Вычисление тройных интегралов: теория и примеры
Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).
Записывается тройной интеграл так:
.
Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.
Вычислить тройной интеграл – значит найти число, равное объёму тела V или, что то же самое – области V.
Практически каждый может понять смысл вычисления тройного интеграла “на своей шкуре”. Точнее – “под шкурой”, а ещё точнее – по своим органам дыхания – лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол – пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое “огромное количество малостей” математически как раз и формулируется понятие тройного интеграла.
Почему именно тройной интеграл служит для нахождения объёма тела V?
Пусть область
.
Если функция f(M) = f(x, y, z)
непрерывна, то будет существовать
В этом случае функция f(M) = f(x, y, z) называется интегрируемой в области V; V – областью интегрирования; x, y, z – переменными интегрирования, dv (или dx dy dz) – элементом объёма.
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.
Рассмотрим трёхмерную область
Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область
V была правильной. Она правильна тогда, когда прямая, параллельная оси
Чтобы наглядно представить отличие правильности от
неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На
рисунке ниже – пример неправильной области V – однополостный гиперболоид,
поверхность которого прямая, параллельная оси
Мы будем рассматривать только правильные области.
Итак, область V – правильная. Тогда для любой функции f(x, y, z), непрерывной в области V, справедлива формула
Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y) и внешнего двойного интеграла по двумерной области D.
Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.
Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три “вложенных” интеграла можно записать так:
.
Из этой записи уже однозначно видно, что:
- сначала нужно интегрировать функцию f(x, y, z)
по переменной z, а в качестве пределов интегрирования взять уравнения
- получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов интегрирования взять уравнения y = y1(x) и y = y2(x) поверхностей, ограничивающих область V с боковых сторон;
- получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов
интегрирования взять уравнения x =
Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу
–
последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.
Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:
.
Вычислим второй интеграл – по переменной y:
.
Теперь вычисляем самый внешний интеграл – по переменной x:
Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.
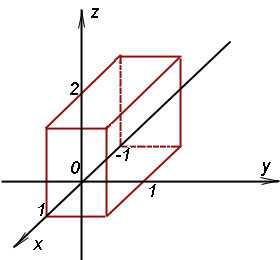
Пример 2. Вычислить тройной интеграл
,
где V – параллелепипед, ограниченный плоскостями x = − 1, x = + 1, y = 0, y = 1, z = 0, z = 2.
Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл – по переменной
.
Вычисляем интеграл “в серединке” – по переменной y. Получаем;
.
Теперь вычисляем самый внешний интеграл – по переменной x:
Ответ: данный тройной интеграл равен -2.
Пример 3. Вычислить тройной интеграл
,
где V – пирамида, ограниченная плоскостью
x + y + z = 1
и координатными плоскостями
x = 0, y = 0,
z = 0. Область
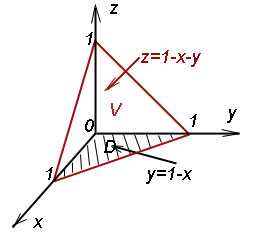
Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0. Чтобы получить верхний предел, выразим z из x + y + z = 1. Получаем 1 − x − y. Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0. Для получения верхнего предела выразим y из x + y
Сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл – по переменной y. Получаем:
Наконец, вычисляем самый внешний интеграл – по переменной x:
Ответ: данный тройной интеграл равен 1/8.
Вычислить тройной интеграл самостоятельно, а затем посмотреть решение
Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность. В первом примере область интегрирования V представляла собой параллелепипед, с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно заданы уравнениями плоскостей. Во втором примере – пирамида: здесь уже требовалось чуть больше подумать и выразить один из пределов из уравнения. А если область V ограничивают не плоские поверхности? Нужно, конечно, определённым образом осмотреть область V.
Начнём с примера “пострашнее”, чтобы почувствовать “обстановку, приближенную к боевой”.
Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V – эллипсоид
.
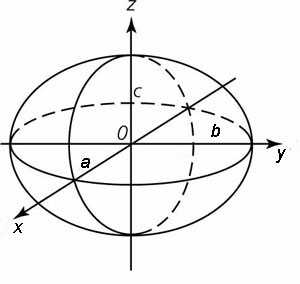
Решение. Пусть центр эллипсоида – начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу. Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена ниже плоскости xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение со знаком минус будет нижним пределом интегрирования по переменной z:
.
Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:
.
Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:
.
Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:
.
Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:
.
Что касается интегрирования по переменной x, то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a: x1 = − a и x2 = a.
Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:
,
где “игрек первое”, “игрек второе”, “зет первое” и “зет второе” – полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc/3.
Следующие примеры – не такие страшные, как только что рассмотренный. При этом они предполагают не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте, чему вы научились, следя за решением “страшного” примера. Думать при расстановке пределов всё равно придётся.
Пример 6. Вычислить тройной интеграл
,
если область интегрирования ограничена плоскостями x + y = 1, x + 2y = 4, y = 0, y = 1, z = 1, z = 5.
Решение. “Курортный” пример по сравнению с примером 5, так как пределы интегрирования по “игрек” и “зет” определены однозначно. Но придётся разобраться с пределами интегрирования по “иксу”. Проекцией области интегрирования на плоскость xOy является трапеция ABCD.
В этом примере выгоднее проецировать трапецию на ось Oy, иначе, чтобы вычислить тройной интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по “иксу” чисто алгебраически. Для этого выразим “икс” из первого и второго уравнений, данных в условии примера. Из первого уравения получаем нижний предел 1 − y, из второго – верхний 4 − 2y. Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Внимание! В этом примере самый внешний интеграл – не по переменной “икс”, а по переменной “игрек”, а “средний” – по переменной “икс”! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox, на на ось Oy.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл – по переменной x. Получаем:
.
Наконец, вычисляем самый внешний интеграл – по переменной y:

Ответ: данный тройной интеграл равен 43.
Пример 7. Вычислить тройной интеграл
,
если область интегрирования ограничена поверхностями x = 0, y = 0, z = 2, x + y + z = 4.
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.

Нижние пределы интегрирования по всем переменным заданы в условии примера. Найдём верхний предел интегирования по “иксу”. Для этого выразим “икс” из четвёртого уравнения, считая “игрек” равным нулю, а “зет” равным двум. Получаем x = 2. Найдём верхний предел интегирования по “игреку”. Для этого выразим “игрек” из того же четвёртого уравнения, считая “зет” равным двум, а “икс” – переменной величиной. Получаем y = 2 − x. И, наконец, найдём верхний предел интегрирования по переменной “зет”. Для этого выразим “зет” из того же четвёртого уравнения, считая “игрек” и “зет” переменными величинами. Получаем z = 4 − x − y.
Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл – по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл – по переменной y. Получаем:
.
Вычисляем самый внешний интеграл – по переменной x и окончательно находим данный тройной интеграл:

Ответ: данный тройной интеграл равен 2.
Если проекцией области интегрирования на какую-либо из координатных плоскостей является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами (r, φ, z), где r – расстояние от начала координат до проекции N точки M на плоскость xOy, φ – угол между вектором ON и положительным направлением оси Ox, z – аппликата точки M (рисунок ниже).
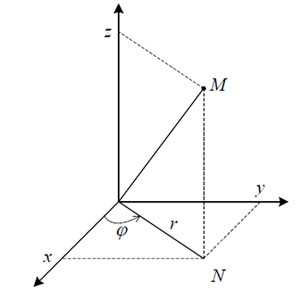
Прямоугольные координаты x, y, z с цилиндрическими координатами r, φ, z связывают формулы
x = rcosφ,
y = rsinφ,
z = z.
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:
.
То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:
.
Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Если область интегрирования в тройном интеграле представляет собой шар или часть шара, то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M характеризуют три величины (ρ, φ, θ), где ρ – расстояние от точки M до начала координат 0, φ – угол между вектором ON и положительным направлением оси Ox (N – проекция точки M на плоскость xOy), θ – угол между вектором OM и положительным направлением оси Oz.
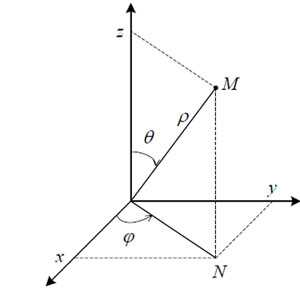
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями
x = ρsinθcosφ,
y = ρsinθsinφ,
z = ρcosθ.
Элемент объёма в сферических координатах выражается следующим образом:
.
Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:
Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же, как при вычислениях в прямоугольных декартовых и цилиндрических координатах – перейти к повторным интегралам (последовательности трёх определённых интегралов):
Пример 9. Вычислить тройной интеграл
переходом к сферическим координатам, где V – область, ограниченная неравенствами и .

Решение. Снизу область интегрирования ограничена конической поверхностью , а сверху – сферой . Так как область интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную функцию:
Учитывая, что , получаем
Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому

Итак, тройной интеграл вычислен. Так как все три интеграла – независисмые друг от друга, мы смогли интегрировать каждый отдельно и результаты перемножить.
Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:
.
Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:
.
Статические моменты материального тела. Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции материального тела. Моменты инерции относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции относительно осей Ox, Oy, Oz определяются по формулам:
Центр тяжести материального тела. Координаты центра массы C(xc, yc, zc) материального тела с плотностью ρ = ρ(x, y, z) определяются по формулам:

Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
∫∫∫ Тройной интеграл – Калькулятор Он-лайн
Введите подинтегральную функцию, для которой необходимо вычислить тройной интеграл
Найдём решение тройного интеграла от функции f(x, y, z)
Введите вверхние и нижние пределы для области интегрирования и
подинтегральную функцию для тройного интеграла.
Если подинтегральной функции нету, то укажите 1
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число – “Пи”, которое примерно равно 3.14
- sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- – умножение
- 3/x
- – деление
- x^3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
www.kontrolnaya-rabota.ru
ТРОЙНЫЕ ИНТЕГРАЛЫ
ρ ≥ 0, ϕ [0,2π] z – любое. Цилиндрические координаты связаны с
декарторыми соотношениями: |
|
x = ρ cosϕ,y = ρ sinϕ,z = z . | (2.7) |
Преобразование тройного интеграла от декартовых | координат |
x , y, z к цилиндрическим координатамϕ, ρ, z осуществляется по
следующей формуле перехода
∫∫∫ f(x, y, z)dxdydz=∫∫∫ f(ρ cosϕ, ρsin ϕ, z)ρdρdϕdz,
V V
где dv = ρdρdϕdz – элемент объема в цилиндрических координатах.
Выразим уравнения нижней и верхней частей поверхности S , ограничивающей данную областьV , в цилиндрических координатах –
z = z1(ρ,ϕ) иz = z2 (ρ,ϕ) соответственно и запишем формулу для вычисления интеграла в цилиндрических координатах, аналогичную (2.3)
∫∫∫ f (ρ cosϕ,ρsinϕ,z)ρdρdϕdz = ∫∫ρdρdϕ | z2 (ρ,ϕ) |
| ||
∫ f (ρ cosϕ,ρsinϕ,z)dz, | ||||
V |
| D | z1 (ρ,ϕ) |
|
где D есть проекция областиV на плоскостьxOy.Воспользовавшись |
| |||
заданием плоской области D в полярных координатах (пункт 1.4) получим | ||||
| z2 | ( ρ,ϕ) |
|
|
∫∫ρdρdϕ | ∫ f (ρ cosϕ,ρsinϕ,z)dz = |
| ||
D | z1 (ρ,ϕ) |
|
| |
β | ρ2 (ϕ) | z2 (ρ,ϕ) |
|
|
= ∫dϕ | ∫ ρdρ | ∫ f (ρ cosϕ,ρsinϕ,z)dz . | (2.8) | |
αρ1 (ϕ)z1 (ρ,ϕ)
Формулу (2.8) удобно использовать, если область V проектируется в круг или часть круга.
Пример 2.3. Вычислить∫∫∫(x2 + y2 )dxdydz по области, ограни-
V
ченной плоскостью z = 2 и параболоидомx2 + y2 = 2z.
Решение. ОбластьV (рис. 2.4) снизу ограничена параболоидомx2 + y2 = 2z , сверху
плоскостью z = 2 . Эта область проектируется на плоскостьxOy в облстьD , ограниченную
| окружностью | x2+ y2= 4, | уравнение которой | ||
| получено | при | исключении | переменной z | из |
| уравнений | параболоида | x2+ y2= 2z | и | |
Рис. 2.4 | плоскости z = 2 . | x2+ y2= ρ2, |
| ||
Введем цилиндрические координаты. Так как | то | ||||
studfiles.net
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному / Тройной интеграл / 3dstroyproekt.ru
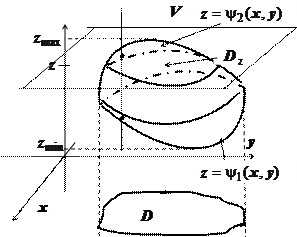
Будем называть ограниченную замкнутую область $\mathbf { \textit { V } } \textbf { простой правильной } $, если выполняются два условия : проекция $\mathbf { \textit { V } } $ на какую-либо координатную плоскость, например, на плоскость $\mathbf { \textit { Оху } } $ – простая область $\mathbf { \textit { D } } $, и любая прямая, перпендикулярная этой плоскости и проходящая через внутреннюю точку $\mathbf { \textit { V } } $, пересекает границу $\mathbf { \textit { V } } $ в двух точках. Такую область можно описать следующим образом: $V=\left( { (x,y,z)\vert (x,y)\in D,\;\psi _1 (x,y)\leqslant z\leqslant \psi _2 (x,y) }\right)$ поверхность $z=\psi _1 (x,y)$ образована множеством нижних точек пересечения прямой, параллельной оси$\mathbf { \textit { Oz } } $, с границей $\mathbf { \textit { V } } $; поверхность $z=\psi _2 (x,y)$ – множеством верхних точек пересечения).
Теорема
Если $\mathbf { \textit { V } } $ – простая область с кусочно-гладкой границей, $\mathbf { \textit { f } } (\mathbf { \textit { P } } )$ – непрерывная функция, то $\iiint\limits_V { f(P)dv } =\iint\limits_D { dxdy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } $.
$\textbf { Доказать } $эту теорему можно так, как мы доказали теорему о переходе от двойного интеграла к повторному: установить, что для повторного интеграла в правой части формулы имеют место все свойства интеграла, разбить область $\mathbf { \textit { V } } $ на подобласти $\mathbf { \textit { V } } _ { i } (\mathbf { \textit { i } } = 1,2, { \ldots } ,\mathbf { \textit { n } } )$, пользуюсь свойствами аддитивности и теоремой о среднем, представить повторный интеграл как интегральную сумму для тройного $\left( { \sum\limits_ { i=1 } ^n { f(P_i )v(V_i ) } }\right)$ и перейти к пределу при $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(V_i )\to 0$.
Если расписать двойной интеграл по простой области $\mathbf { \textit { D } } \quad \left( { D=\left[{ (x,y)\left| { \begin{array} { l } a\leqslant x\leqslant b, \\ \varphi _1 (x)\leqslant y\leqslant \varphi _2 (x) \\ \end{array} }\right. }\right] }\right)$ в виде повторного, получим ещё более детализированную формулу для вычисления тройного интеграла: $\iiint\limits_V { f(P)dv } =\iint\limits_D { dxdy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } =\int\limits_a^b { dx\int\limits_ { \varphi _1 (x) } ^ { \varphi _2 (x) } { dy\int\limits_ { \psi _1 (x,y) } ^ { \psi _2 (x,y) } { f(x,y,z)dz } } } $.
Можно также доказать, что тройной интеграл можно представить в виде повторного с другим порядком интегрирования. Обозначим $z_ { \min } =\mathop { \min z } \limits_ { (x,y,z)\in V } ,\;z_ { \max } =\mathop { \max z } \limits_ { (x,y,z)\in V } $ т.е. минимальное и максимальное значения ординаты для точек области $\mathbf { \textit { V } } )$, $D_z $ – плоскую область, получающуюся при сечении $\mathbf { \textit { V } } $ плоскостью $\mathbf { \textit { z } } $ = const. Тогда $\iiint\limits_V { f(P)dv } =\int\limits_ { z_ { \min } } ^ { z_ { \max } } { dz\iint\limits_ { D_z } { f(x,y,z) } } dxdy$. Естественно, для конкретной задачи может оказаться предпочтительней проектировать $\mathbf { \textit { V } } $ не на плоскость $\mathbf { \textit { Оху } } $, а на другую координатную плоскость.
Примеры решения задач
Пример 1
$I=\iiint\limits_V { \frac { dxdydz } { \left( { 1+x+y+z }\right)^3 } } ,\;V:\left[{ \begin{array} { l } x=0,\;y=0,\;z=0, \\ x+y+z=1. \\ \end{array} }\right.$
Проекция области $\mathbf { \textit { V } } $ на плоскость $\mathbf { \textit { Оху } } $ – треугольник $D:\left[{ x=0,\;y=0,\;x+y=1 }\right]$, поэтому $I=\iiint\limits_V { \frac { dxdydz } { \left( { 1+x+y+z }\right)^3 } } =\iint\limits_D { dxdy\int\limits_0^ { 1-x-y } { \frac { dz } { (1+x+y+z)^3 } } } =\iint\limits_D { \left. { \left[ { -\frac { 1 } { 2 } \cdot \frac { 1 } { (1+x+y+z)^2 } }\right] }\right|_0^ { 1-x-y } dxdy } =$
$=-\frac { 1 } { 2 } \int\limits_0^1 { dx } \int\limits_0^ { 1-x } { \left[ { \frac { 1 } { 4 } -\frac { 1 } { (1+x+y)^2 } }\right]dy } =-\frac { 1 } { 2 } \int\limits_0^1 { \left. { \left[ { \frac { y } { 4 } +\frac { 1 } { 1+x+y } }\right] }\right|_0^ { 1-x } dx } =-\frac { 1 } { 2 } \int\limits_0^1 { \left[ { \frac { 1-x } { 4 } +\frac { 1 } { 2 } -\frac { 1 } { 1+x } }\right]dx } = \\ =-\frac { 1 } { 2 } \int\limits_0^1 { \left[ { \frac { 1-x } { 4 } +\frac { 1 } { 2 } -\frac { 1 } { 1+x } }\right]dx } =-\frac { 1 } { 2 } \left( { \frac { 3x } { 4 } -\frac { x^2 } { 8 } -\ln (1+x) }\right)_0^1 =-\frac { 1 } { 2 } \left( { \frac { 3 } { 4 } -\frac { 1 } { 8 } -\ln 2 }\right)=\frac { 1 } { 2 } \left( { \ln 2-\frac { 5 } { 8 } }\right)$
Пример 2
$I=\iiint\limits_V { z\cdot dxdydz } ,\;V:\left[{ \begin{array} { l } z^2=\frac { h^2 } { R^2 } \left( { x^2+y^2 }\right), \\ z=h. \\ \end{array} }\right.$ Здесь $\mathbf { \textit { V } } $ – внутренность конуса, $\mathbf { \textit { D } } $ – проекция круга, получающегося при сечении этого конуса плоскостью $\mathbf { \textit { z } } =\mathbf { \textit { h } } $ на $\mathbf { \textit { Оху } } $, т.е. круг, ограниченный кривой $h^2=\frac { h^2 } { R^2 } \left( { x^2+y^2 }\right)\Rightarrow x^2+y^2=R^2$, поэтому $I=\iint\limits_D { dxdy\int\limits_ { \frac { h } { R } \sqrt { x^2+y^2 } } ^h { zdz } = } \iint\limits_D { \left. { \frac { z^2 } { 2 } }\right|_ { \frac { h } { R } \sqrt { x^2+y^2 } } ^h dxdy= } \frac { 1 } { 2 } \iint\limits_D { \left[ { h^2-\frac { h^2 } { R^2 } \left( { x^2+y^2 }\right) }\right]dxdy } =$
$=\frac { h^2 } { 2R^2 } \iint\limits_D { \left[ { R^2-\left( { x^2+y^2 }\right) }\right]dxdy } =$ { переходим к полярным координатам } $=\frac { h^2 } { 2R^2 } \int\limits_0^ { 2\pi } { d\varphi } \int\limits_0^R { \left[ { R^2-r^2 }\right]rdr } = \frac { h^2 } { 2R^2 } \int\limits_0^ { 2\pi } { \left[ { R^2\frac { r^2 } { 2 } -\frac { r^4 } { 4 } }\right]_0^R d\varphi } =\frac { h^2 } { 2R^2 } 2\pi \frac { R^4 } { 4 } =\frac { \pi h^2R^2 } { 4 } $.
Вычислим тот же интеграл по другой формуле перехода к повторному интегралу: $I=\int\limits_0^h { dz\iint\limits_ { D_z } { zdxdy } } =\int\limits_0^h { zdz\iint\limits_ { D_z } { zdxdy } } =\int\limits_0^h { zdz\iint\limits_ { D_z } { dxdy } } =\int\limits_0^h { zdz\cdot s(D_z ) } =$ внутренний двойной интеграл – интеграл от функции, равной 1, поэтому он равен площади круга, получающегося при сечении конуса плоскостью $z=const$, уравнение ограничивающей окружности, площадь $s(D_z )=\frac { \pi z^2R^2 } { h^2 } )=\int\limits_0^h { z\frac { \pi z^2R^2 } { h^2 } dz } =\frac { \pi R^2 } { h^2 } \cdot \left. { \frac { z^4 } { 4 } }\right|_0^h =\frac { \pi h^2R^2 } { 4 } $.
Это решение оказалось проще; мы сыграли на том, что подынтегральная функция не зависит от $\mathbf { \textit { х } } $ и $\mathbf { \textit { у } } $.
3dstroyproekt.ru
Тройной интеграл, вычисление тройного интеграла
Объем тела. Представим область $V$ как некоторое тело. Если везде в области $V$ положить $f\left(x,y,z\right)\equiv 1$, то тройной интеграл дает объем тела, а именно: $V=\iiint \limits _{V}dx\cdot dy\cdot dz $. Для цилиндрических и сферических кординат этот объем можно вычислить по формулами $V=\iiint \limits _{V}\rho \cdot d\rho \cdot d\phi \cdot dz $ и $V=\iiint \limits _{V}\rho ^{2} \cdot \sin \theta \cdot d\rho \cdot d\phi \cdot d\theta $ соответственно.
Масса тела. Масса неоднородного тело распределена в замкнутой области $V$ с объемной плотностью $\rho \left(x,y,z\right)\ge 0$. При этом тройной интеграл дает массу $M\; =\; \iiint \limits _{V}\rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz $ этого тела.
Координаты центра массы тела. Масса неоднородного тела распределена в замкнутой области $V$ с объемной плотностью $\rho \left(x,y,z\right)$. Координаты $x_{c} $, $y_{c} $, $z_{c} $ центра массы тела можно вычислить по следующим формулам:
\[x_{c} \; =\; \frac{\iiint \limits _{V}x\cdot \rho \left(x,y,z\right)\cdot \; dx\cdot \; dy\cdot \; dz }{M} ,\] \[y_{c} \; =\; \frac{\iiint \limits _{V}y\cdot \rho \left(x,y,z\right)\cdot \; dx\cdot \; dy\cdot \; dz }{M} ,\] \[z_{c} \; =\; \frac{\iiint \limits _{V}z\cdot \rho \left(x,y,z\right)\cdot \; dx\cdot \; dy\cdot \; dz }{M} .\]Величины в числителях приведенных формул называются статическими моментами относительно плоскостей $yOz$, $xOz$ и $xOy$ соответственно.
В частном случае, когда тело однородное, то есть его плотность постоянна, формулы для координат центра массы упрощаются:
\[x_{c} \; =\; \frac{\iiint \limits _{V}x\cdot dx\cdot dy\cdot dz }{V} , y_{c} \; =\; \frac{\iiint \limits _{V}y\cdot dx\cdot dy\cdot dz }{V} , z_{c} \; =\; \frac{\iiint \limits _{V}z\cdot dx\cdot dy\cdot dz }{V} . \]Моменты инерции тела. Масса неоднородного тело распределена в замкнутой области $V$ с объемной плотностью $\rho \left(x,y,z\right)$. Формулы для моментов инерции тела $I_{x} $, $I_{y} $, $I_{z} $ относительно осей координат и момента инерции $I_{O} $ относительно начала координат имеют вид:
\[I_{x} \; =\; \iiint \limits _{V}\left(y^{2} +z^{2} \right)\; \cdot \rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz ,\] \[I_{y} \; =\; \iiint \limits _{V}\left(x^{2} +z^{2} \right)\; \cdot \rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz ,\] \[I_{z} \; =\; \iiint \limits _{V}\left(x^{2} +y^{2} \right)\; \cdot \rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz ,\] \[I_{O} \; =\; \iiint \limits _{V}\left(x^{2} +y^{2} +z^{2} \right)\; \cdot \rho \left(x,y,z\right)\cdot dx\cdot dy\cdot dz .\]Вычисление тройного интеграла
С целью вычисления тройного интеграла осуществляют его приведение к повторному. Вследствие этого результат удается получить путем последовательного вычисления трех обычных определенных интегралов.
Предположим, что область $V$ является правильной в направлении оси $Oz$. Это значит, что любая прямая, проведенная через внутреннюю точку области параллельно оси $Oz$, пересекает поверхность $S$, ограничивающую область $V$, в двух точках. Кроме того, вся область $V$ должна проецироваться на плоскость $xOy$ в правильную область $D$.
Пусть правильная область $V$ снизу и сверху ограничена поверхностями $z=z_{1} \left(x,y\right)$ и $z=z_{2} \left(x,y\right)$. По бокам область $V$ ограничена цилиндрической поверхностью $P$, образующая которой параллельная оси $Oz$. Область $V$ проецируется на плоскость $xOy$ в область $D$. Граница $L$ области $D$ является направляющой цилиндрической поверхности $P$.
Предположим также, что область $D$ является правильной в направлении оси $Oy$. Пусть она ограничена непрерывными кривыми $y=\vartheta _{1} \left(x\right)$ и $y=\vartheta _{2} \left(x\right)$, а также прямыми линиями $x=a$ и $x=b$, причем $\vartheta _{1} \left(x\right)
Тогда справедливая следующая формула:
Можно построить тройной интеграл и с другим порядком интегрирования, если это позволяют свойства области $V$.
Замена переменных в тройном интеграле осуществляется следующим образом.
Пусть при вычислении тройного интеграла оказалось целесообразным перейти к новым переменным $u$, $v$ и $w$ с помощью формул $x=\vartheta \left(u,v,w\right)$, $y=\psi \left(u,v,w\right)$ и $z=\chi \left(u,v,w\right)$. Пусть этими функциями устанавливается взаимно однозначное соответствие между точками заданной области $V$ в прямоугольных координатах $x$, $y$, $z$ и точками некоторой области $V^{*} $ в криволинейных кооодинатах $u$, $v$, $w$. В этих условиях формула общей замены переменных в тройном интеграле приобретает вид:
\[\iiint \limits _{V}f\left(x,y,z\right)\cdot dx\cdot dy\cdot dz =\] \[=\iiint \limits _{V^{*} }f\left(\vartheta \left(u,v,w\right),\psi \left(u,v,w\right),\chi \left(u,v,w\right)\right)\cdot \left|J\left(u,v,w\right)\right|\cdot du\cdot dv\cdot dw .\]В этой формуле $J\left(u,v,w\right)=\left|\begin{array}{ccc} {{\partial \vartheta \mathord{\left/ {\vphantom {\partial \vartheta \partial u}} \right. } \partial u} } & {{\partial \vartheta \mathord{\left/ {\vphantom {\partial \vartheta \partial v}} \right. } \partial v} } & {{\partial \vartheta \mathord{\left/ {\vphantom {\partial \vartheta \partial w}} \right. } \partial w} } \\ {{\partial \psi \mathord{\left/ {\vphantom {\partial \psi \partial u}} \right. } \partial u} } & {{\partial \psi \mathord{\left/ {\vphantom {\partial \psi \partial v}} \right. } \partial v} } & {{\partial \psi \mathord{\left/ {\vphantom {\partial \psi \partial w}} \right. } \partial w} } \\ {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial u}} \right. } \partial u} } & {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial v}} \right. } \partial v} } & {{\partial \chi \mathord{\left/ {\vphantom {\partial \chi \partial w}} \right.} \partial w} } \end{array}\right|$ — якобиан третьего порядка.
Переходы от прямоугольных координат к цилиндрическим и сферическим в тройном интеграле являются частными случаями общей замены переменных.
В случае цилиндрических координат имеем $x=\rho \cdot \cos \phi $, $y=\rho \cdot \sin \phi $, $z=z$. Согласуем обозначения: $u=\rho $, $v=\phi $ , $w=z$.
Итак, $x=\vartheta \left(\rho ,\phi ,z\right)=\rho \cdot \cos \phi $, $y=\psi \left(\rho ,\phi ,z\right)=\rho \cdot \sin \phi $, $z=\chi \left(\rho ,\phi ,z\right)=z$.
Якобиан преобразования прямоугольных координат $x$, $y$, $z$ в цилиндрические координаты $\rho $, $\phi $, $z$ приобретает следующий вид:
\[J\left(\rho ,\phi ,z\right)=\left|\begin{array}{ccc} {\cos \phi } & {-\rho \cdot \sin \phi } & {0} \\ {\sin \phi } & {\rho \cdot \cos \phi } & {0} \\ {0} & {0} & {1} \end{array}\right|=\] \[=\left|\begin{array}{cc} {\cos \phi } & {-\rho \cdot \sin \phi } \\ {\sin \phi } & {\rho \cdot \cos \phi } \end{array}\right|=\rho \cdot \cos ^{2} \phi +\rho \cdot \sin ^{2} \phi =\rho .\]В случае сферических координат имеем $x=\rho \cdot \sin \theta \cdot \cos \phi $, $y=\rho \cdot \sin \theta \cdot \sin \phi $, $z=\rho \cdot \cos \theta $. Согласуем обозначения: $u=\rho $, $v=\phi $ , $w=\theta $.
Итак, $x=\vartheta \left(\rho ,\phi ,\theta \right)=\rho \cdot \sin \theta \cdot \cos \phi $, $y=\psi \left(\rho ,\phi ,\theta \right)=\rho \cdot \sin \theta \cdot \sin \phi $, $z=\chi \left(\rho ,\phi ,z\right)=\rho \cdot \cos \theta $.
Якобиан преобразования прямоугольных координат $x$, $y$, $z$ в сферические координаты $\rho $, $\phi $, $\theta $ приобретает следующий вид:
\[J\left(\rho ,\phi ,\theta \right)=\left|\begin{array}{ccc} {\sin \theta \cdot \cos \phi } & {-\rho \cdot \sin \theta \cdot \sin \phi } & {\rho \cdot \cos \theta \cdot \cos \phi } \\ {\sin \theta \cdot \sin \phi } & {\rho \cdot \sin \theta \cdot \cos \phi } & {\rho \cdot \cos \theta \cdot \sin \phi } \\ {\cos \theta } & {0} & {-\rho \cdot \sin \theta } \end{array}\right|=\] \[=\cos \theta \cdot \left|\begin{array}{cc} {-\rho \cdot \sin \theta \cdot \sin \phi } & {\rho \cdot \cos \theta \cdot \cos \phi } \\ {\rho \cdot \sin \theta \cdot \cos \phi } & {\rho \cdot \cos \theta \cdot \sin \phi } \end{array}\right|-\] \[-\rho \cdot \sin \theta \cdot \left|\begin{array}{cc} {\sin \theta \cdot \cos \phi } & {-\rho \cdot \sin \theta \cdot \sin \phi } \\ {\sin \theta \cdot \sin \phi } & {\rho \cdot \sin \theta \cdot \cos \phi } \end{array}\right|=-\rho ^{2} \cdot \sin \theta .\]spravochnick.ru
Лекции Тройной интеграл
Скачать с Depositfiles
Тройной интеграл.
Контрольные вопросы.
Тройной интеграл, его свойства.
Вычисление тройного интеграла в декартовых координатах.
Замена переменных в тройном интеграле. Вычисление тройного интеграла в цилиндрических координатах.
Вычисление тройного интеграла в сферических координатах.
Пусть функция u = f(x,y,z) определена в ограниченной замкнутой области V пространства R3. Разобьём область V произвольным образом наn элементарных замкнутых областей V1, … , Vn, имеющих объемы V1, …, Vn соответственно. Обозначим d – наибольший из диаметров областей V1, … , Vn. В каждой области Vk выберем произвольную точку Pk (xk , yk , zk) и составим интегральную сумму функции f(x, y, z)
S = 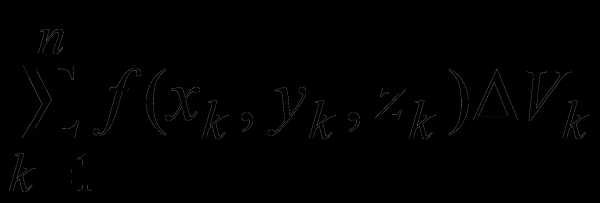
Определение. Тройным интегралом от функции f(x, y, z) по области V называется предел интегральной суммы 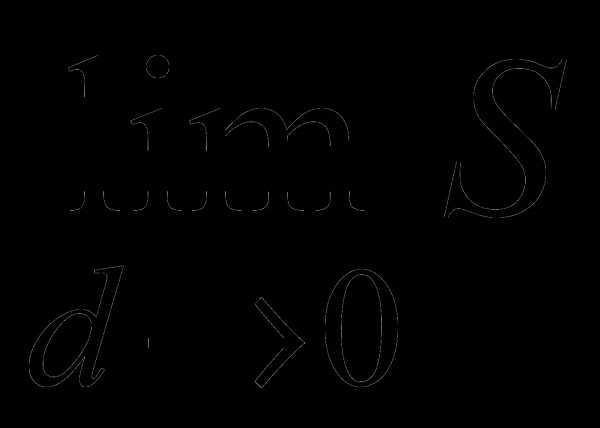 , если он существует.
, если он существует.
Таким образом,
(1)
Замечание. Интегральная сумма S зависит от способа разбиения области V и выбора точек Pk (k=1, …, n). Однако, если существует предел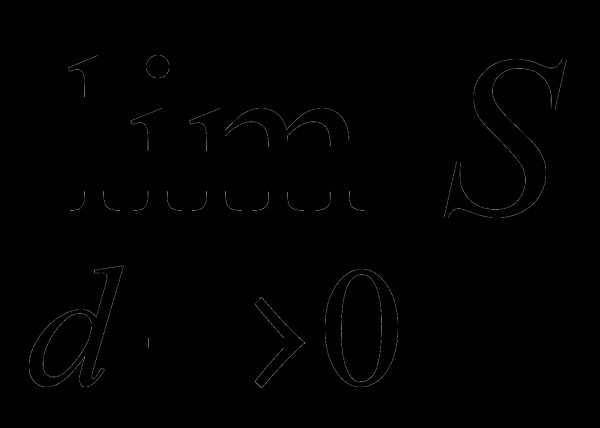 , то он не зависит от способа разбиения области V и выбора точек Pk . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.
, то он не зависит от способа разбиения области V и выбора точек Pk . Если сравнить определения двойного и тройного интегралов, то легко увидеть в них полную аналогию.
Достаточное условие существования тройного интеграла. Тройной интеграл (13) существует, если функция f(x, y, z) ограничена в V и непрерывна в V, за исключением конечного числа кусочно-гладких поверхностей, расположенных в V .
В дальнейшем будем считать, что все рассматриваемые тройные интегралы существуют.
Некоторые свойства тройного интеграла.
1) Если С – числовая константа, то
3) Аддитивность по области. Если область V разбита на области V1 и V2, то
.
4) Объем тела V равен
 (2)
(2)
Вычисление тройного интеграла в декартовых координатах.
Пусть D проекция тела V на плоскость xOy, поверхности z=φ1(x, y), z=φ2(x, y) ограничивают тело V снизу и сверху соответственно. Это значит, что
V = {(x, y, z): (x, y) D, φ1(x, y) ≤ z ≤ φ2(x, y)} .
D, φ1(x, y) ≤ z ≤ φ2(x, y)} .
Такое тело назовем z-цилиндрическим. Тройной интеграл (1) по z-цилиндрическому телу V вычисляется переходом к повторному интегралу, состоящему из двойного и определенного интегралов:

(3)
В этом повторном интеграле сначала вычисляется внутренний определенный интеграл по переменной z, при этом x, y считаются постоянными. Затем вычисляется двойной интеграл от полученной функции по области D.
Если V x-цилиндрическое или y-цилиндрическое тело, то верны соответственно формулы
В первой формуле D проекция тела V на координатную плоскость yOz, а во второй на плоскость xOz
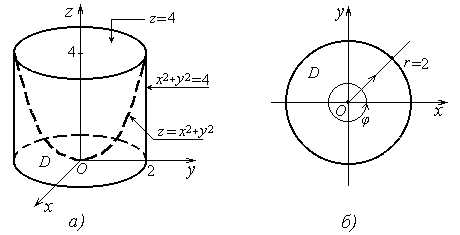
Примеры. 1) Вычислить объем тела V, ограниченного поверхностями z = 0, x2 + y2 = 4, z = x2 + y2 .
Решение. Вычислим объём при помощи тройного интеграла по формуле (2) 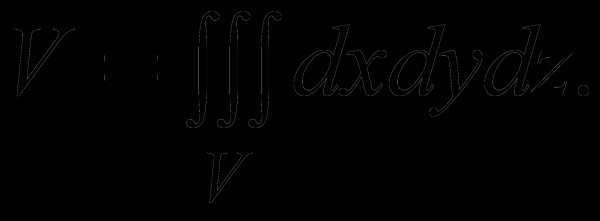
Перейдем к повторному интегралу по формуле (3).
Пусть D круг x2 + y2 ≤ 4, φ1(x, y) = 0, φ2(x, y)= x2 + y2 . Тогда по формуле (3) получим
Для вычисления этого интеграла перейдем к полярным координатам. При этом круг D преобразуется во множество
Dr ={ (r, φ) : 0 ≤ φ < 2π , 0 ≤ r ≤ 2 }.

2) Тело V ограничено поверхностями z=y, z= –y, x=0 , x=2, y=1. Вычислить
Плоскости z = y, z = –y ограничивают тело соответственно снизу и сверху, плоскости x=0 , x=2 ограничивают тело соответственно сзади и спереди, а плоскость y=1 ограничивает справа. V – z-цилиндрическое тело, его проекцией D на плоскость хОу является прямоугольник ОАВС. Положим φ1(x, y) = –y, φ2(x, y)= y и применим формулу (3):

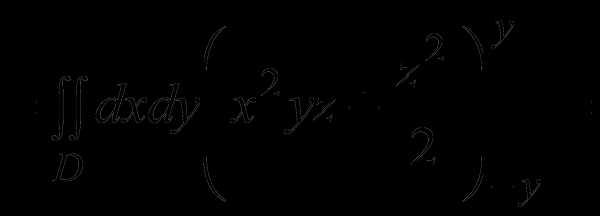
greleon.ru
Тройной интеграл
По аналогии с двойным интегралом вводится
понятие тройного интеграла. Рассмотрим
ограниченную замкнутую пространственную
область  и определенную в ней непрерывную функцию.
Область
и определенную в ней непрерывную функцию.
Область разобьем на
разобьем на элементарных пространственных областей.
Предполагается, что область
элементарных пространственных областей.
Предполагается, что область и элементарные областиимеют объемы, которые будем обозначать
соответственно теми же символами. В
каждой элементарной области
и элементарные областиимеют объемы, которые будем обозначать
соответственно теми же символами. В
каждой элементарной области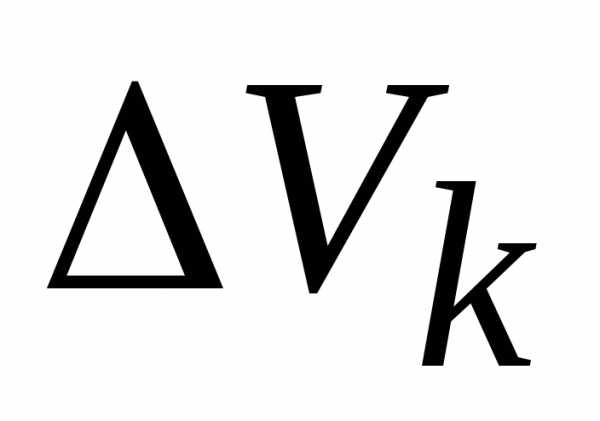 (
(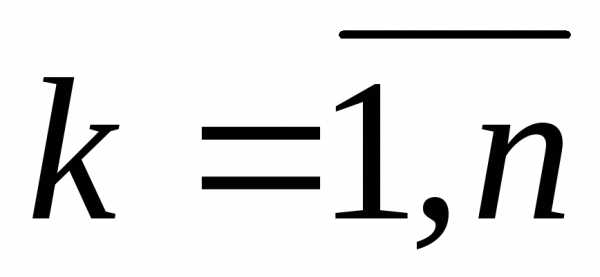 )
выберем произвольную точку,
значение функции в этой точкеумножим на объем элементарной области
)
выберем произвольную точку,
значение функции в этой точкеумножим на объем элементарной области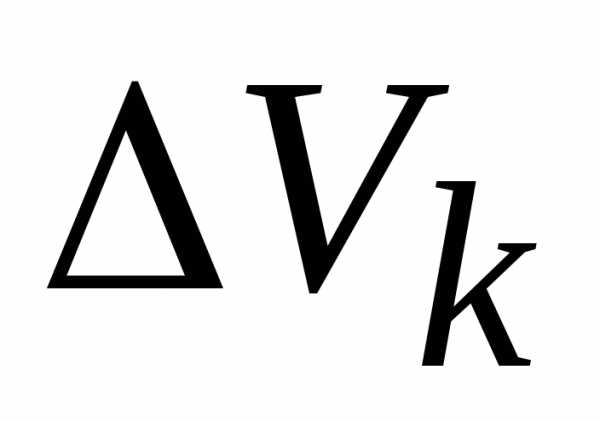 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
,
которая называется интегральной суммой данной функции по данному объему.
Обозначим через 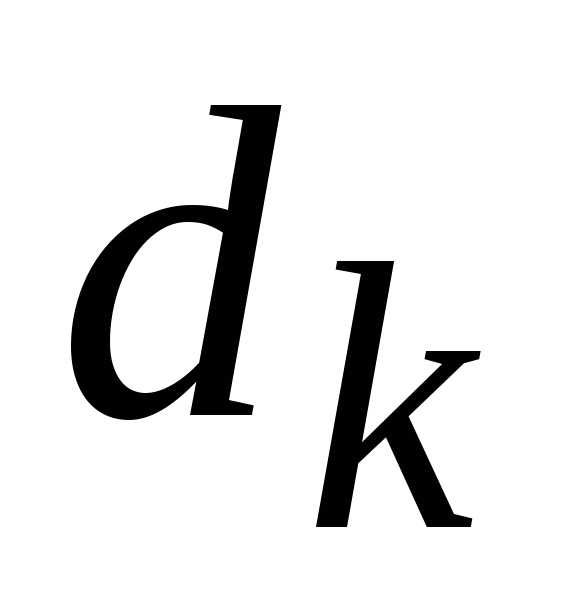 диаметр области
диаметр области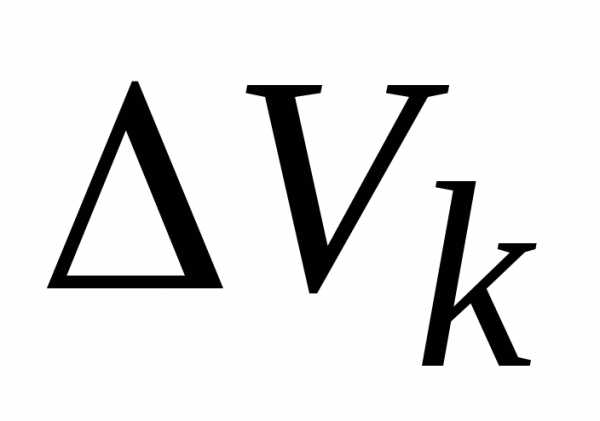 .
Пусть
.
Пусть — наибольший из этих диаметров. И
перейдем в последнем равенстве к пределу
при
— наибольший из этих диаметров. И
перейдем в последнем равенстве к пределу
при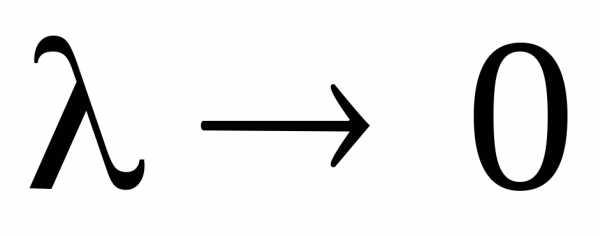 .
.
Если предел интегральной суммы существует,
то он и называется тройным интегралом
от функции
по пространственной области .
.
Итак, по определению
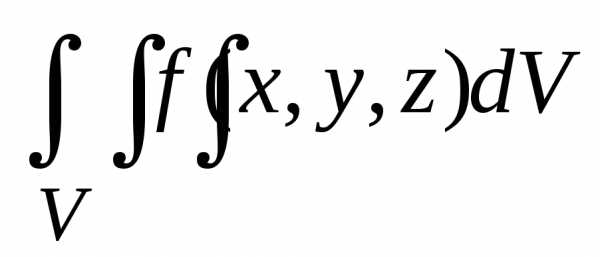 .
(1)
.
(1)
Тройной интеграл от функции
по пространственной области также обозначается следующим образом:
также обозначается следующим образом:
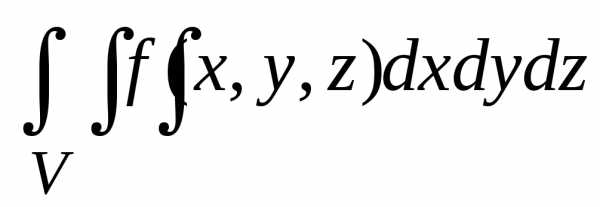 .
.
Отметим без доказательства, что если
функция
непрерывна в рассматриваемой замкнутой
области ,
то предел в правой части формулы (1)
существует и не зависит от способа
разбиения области
,
то предел в правой части формулы (1)
существует и не зависит от способа
разбиения области на элементарные и выбора точкив элементарной области
на элементарные и выбора точкив элементарной области .
.
Предположим, что в области  распределено вещество, объемная плотность
которого задана непрерывной функцией
распределено вещество, объемная плотность
которого задана непрерывной функцией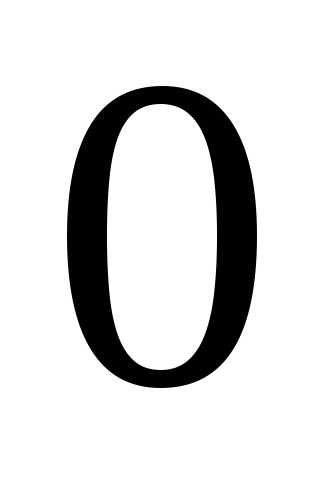 ,
тогда произведение
,
тогда произведение выражает приближенную массу элементарной
области
выражает приближенную массу элементарной
области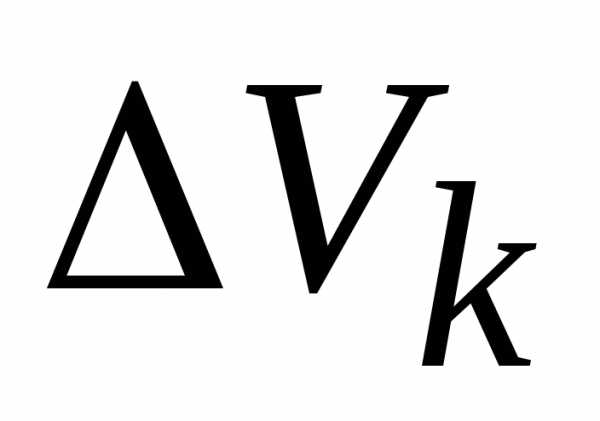 ,
интегральная сумма — приближенную
массу всей области
,
интегральная сумма — приближенную
массу всей области ,
а тройной интеграл — точное значение
этой массы, т. е.
,
а тройной интеграл — точное значение
этой массы, т. е.
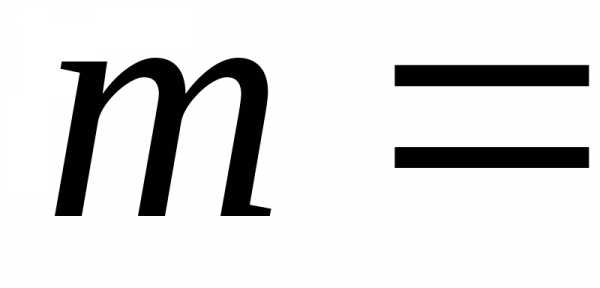
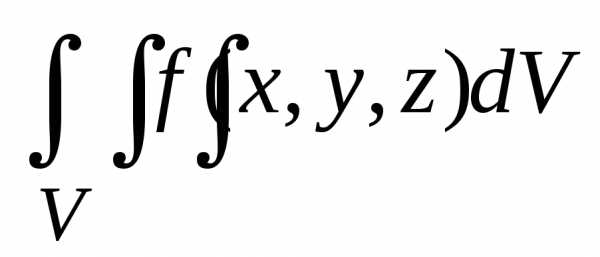 .
.
Данная формула выражает механический
смысл тройного интеграла: тройной
интеграл представляет массу, заполняющую
область интегрирования  .
.
Если в формуле 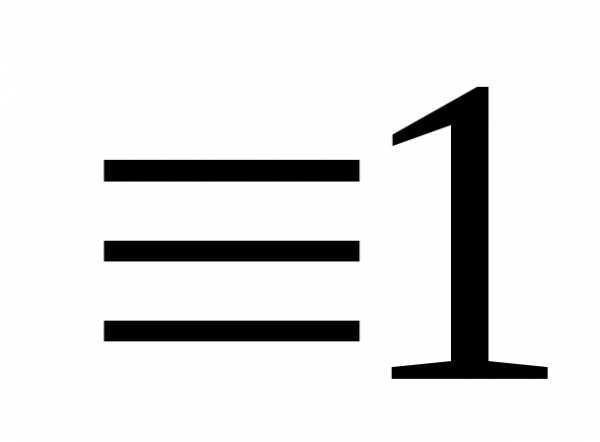 ,
томы получаем формулу для вычисления
объема с помощью тройного интеграла:
,
томы получаем формулу для вычисления
объема с помощью тройного интеграла:
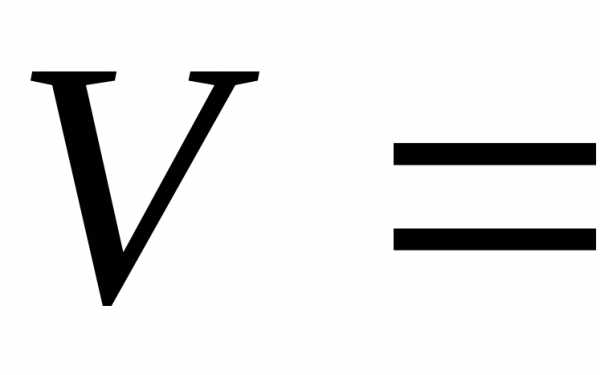
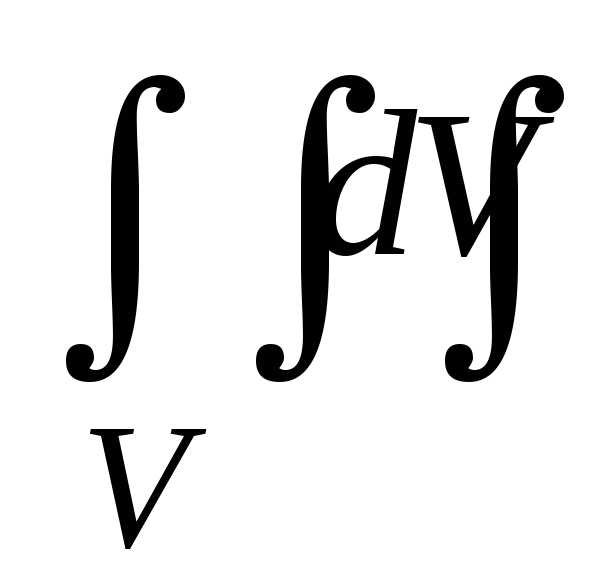 или
или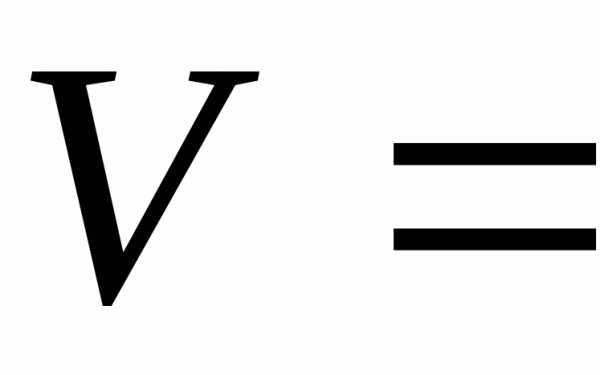
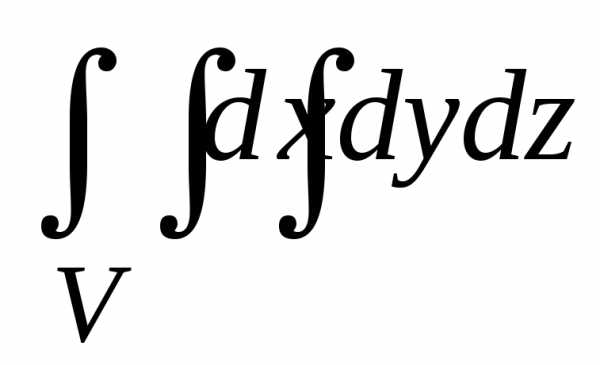
Тройной интеграл обладает свойствами, аналогичными свойствам двойного интеграла.
Перейдем к вопросу о вычислении тройного
интеграла в прямоугольных декартовых
координатах. Предположим, что область  является стандартной в направлении оси
является стандартной в направлении оси ,
т. е. удовлетворяющей следующим условиям:
,
т. е. удовлетворяющей следующим условиям:
1) всякая прямая, параллельная этой оси и имеющая с данной областью общие точки, пересекает границу области только в двух точках;
2) проекция  области
области на плоскость
на плоскость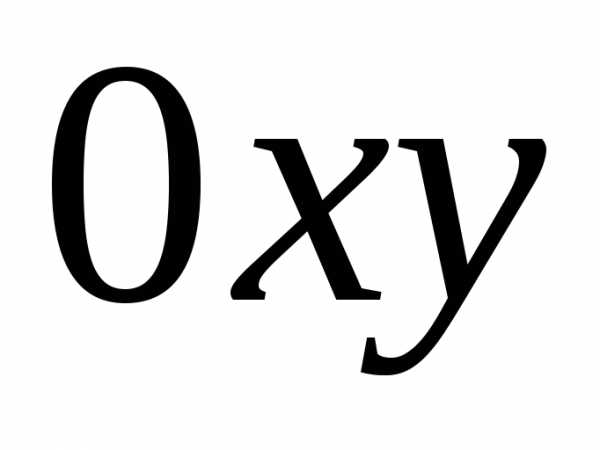 представляет собой стандартную область
в направлении оси
представляет собой стандартную область
в направлении оси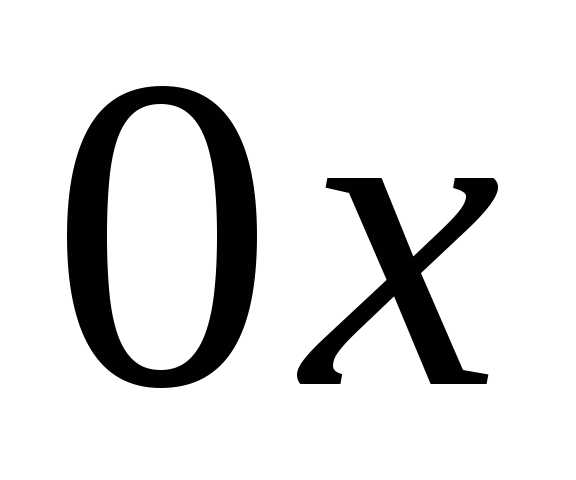 или оси
или оси .
.
Пусть стандартная область  ограничена сверху поверхностью,
снизу — поверхностью,
тогда можно показать, что
ограничена сверху поверхностью,
снизу — поверхностью,
тогда можно показать, что
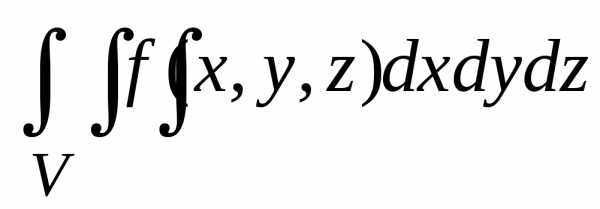
 .
.
Если область 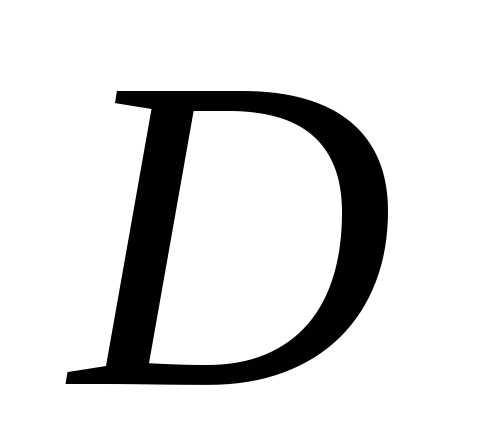 является стандартной в направлении оси
является стандартной в направлении оси и определяется неравенствами
и определяется неравенствами
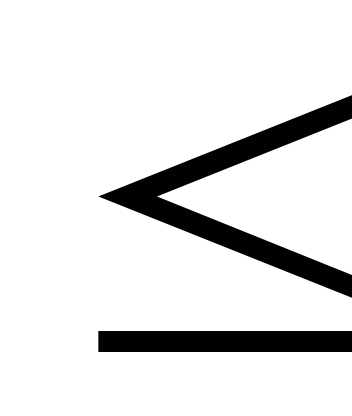
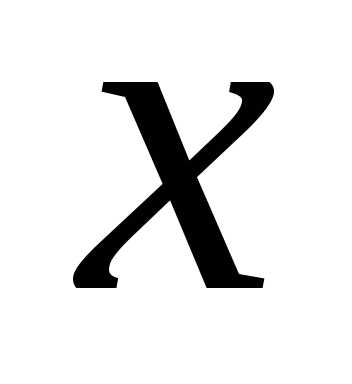
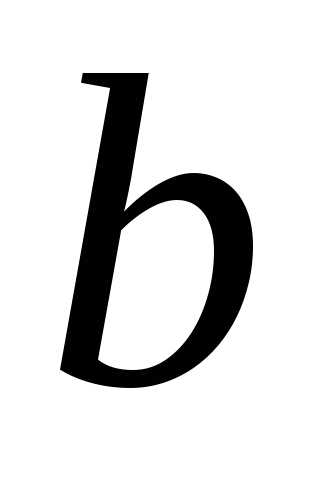 ,
,


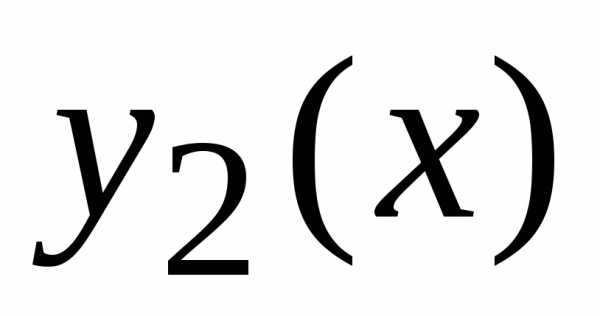 ,
то
,
то
 .
.
Следовательно, в этом случае
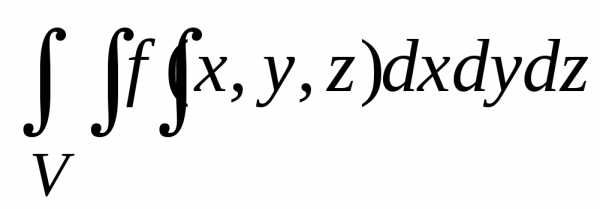 .
.
Замечание.Если область является стандартной в направлении оси
является стандартной в направлении оси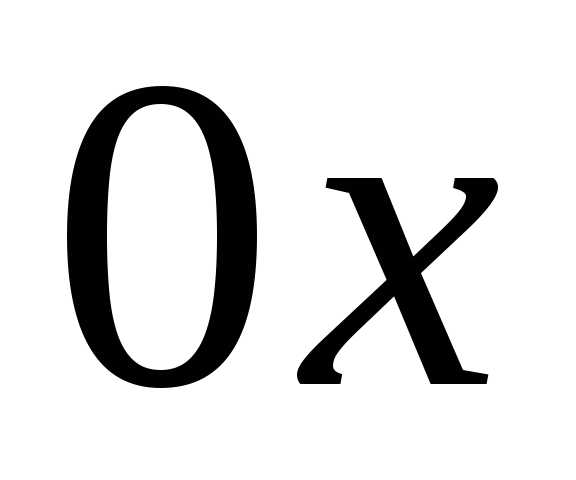 и определяется неравенствами
и определяется неравенствами
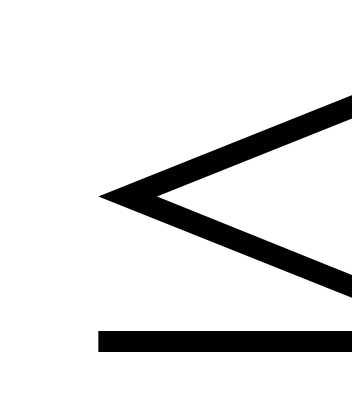

 ,
,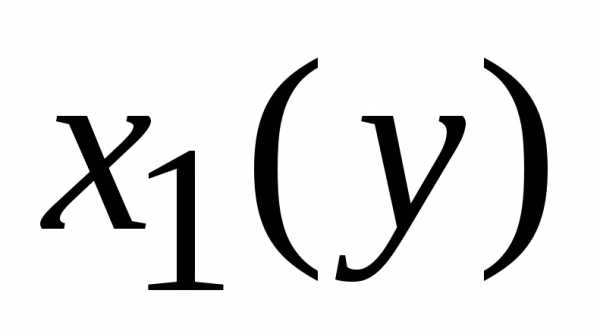
 ,
то
,
то
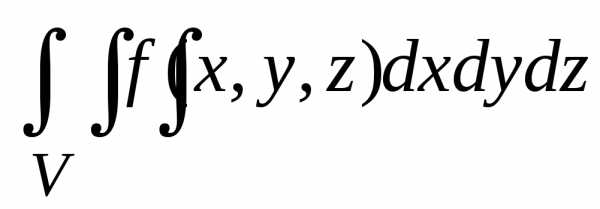 .
.
Замечание.Если область является стандартной в направлении
каждой координатной оси и ее проекции
на координатные плоскости являются
стандартными в направлении каждой
соответствующей оси, то пределы
интегрирования в трехкратном интеграле
можно расставить шестью различными
способами.
является стандартной в направлении
каждой координатной оси и ее проекции
на координатные плоскости являются
стандартными в направлении каждой
соответствующей оси, то пределы
интегрирования в трехкратном интеграле
можно расставить шестью различными
способами.
Пример. Вычислить тройной интеграл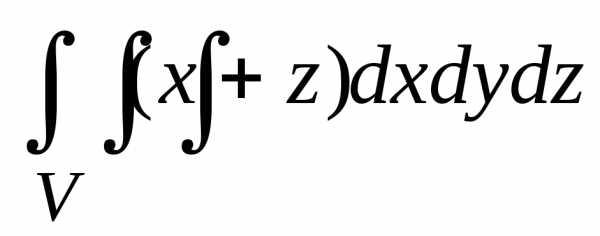 по области
по области ,
ограниченной поверхностями,
,
ограниченной поверхностями, ,
,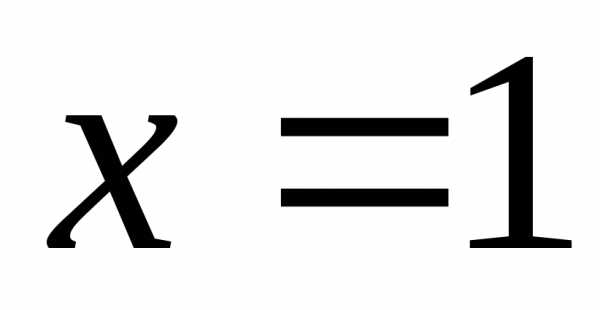 ,
,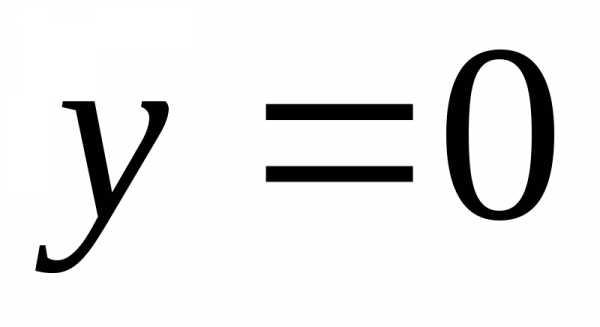 ,
,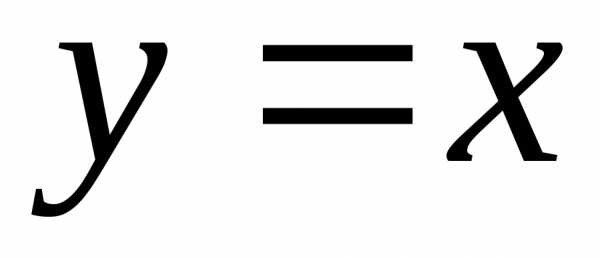 ,.
,.
Решение. Изобразим область .
.

Эта область является стандартной в
направлении оси  ,
а проекция
,
а проекция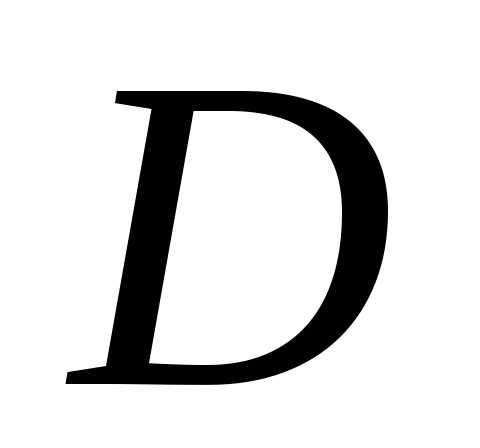 области
области на плоскость
на плоскость представляет собой стандартную область
в направлении оси
представляет собой стандартную область
в направлении оси .
Следовательно,
.
Следовательно,
 .
.
Пример. Найти объем тела, ограниченного
поверхностями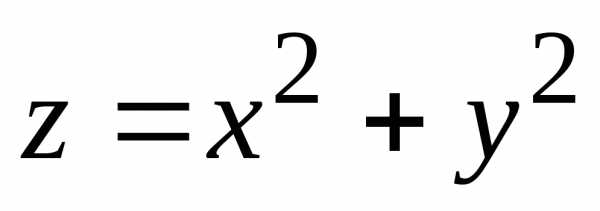 ,
,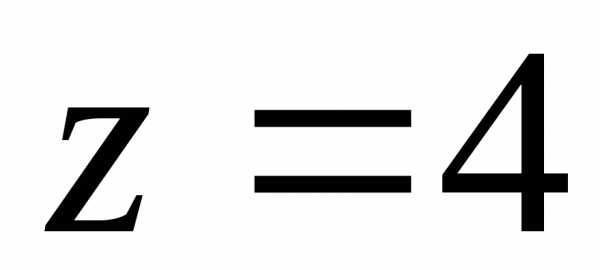 .
.
Решение.Уравнения поверхностей, ограничивающих тело имеют наиболее простой вид в цилиндрических координатах, связь которых с декартовыми осуществляется по формулам:
,,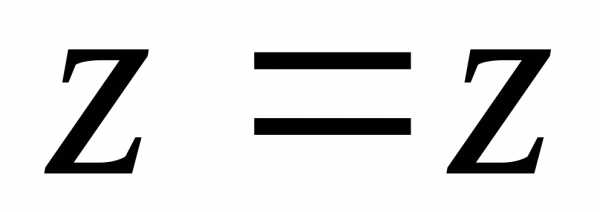 .
.
Первая поверхность являющаяся параболоидом вращения примет вид:
.
Уравнение плоскости 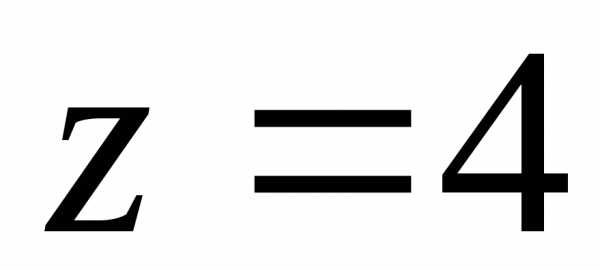 в цилиндрических координатах останется
без изменений.
в цилиндрических координатах останется
без изменений.
Изобразим тело, объем которого необходимо найти, на рисунке.

Решая совместно уравнения  и
и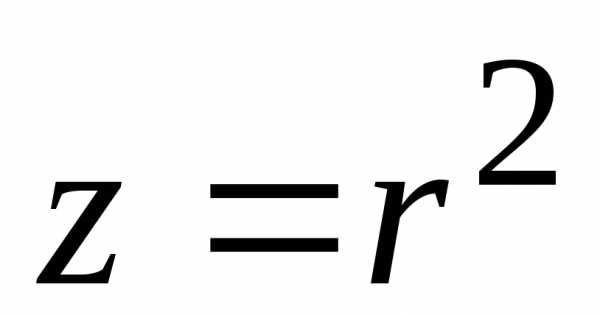 ,
получаем, что область
,
получаем, что область проектируется в плоскость
проектируется в плоскость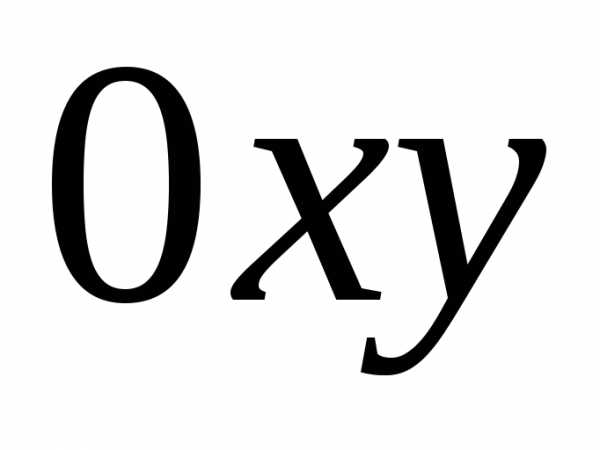 в круг
в круг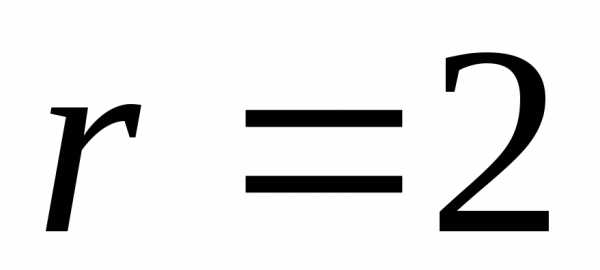 .
.
Следовательно,

.
studfiles.net
