Практическое применение и нахождение обратной матрицы
Матрица – это таблица, которая заполнена определенным набором чисел в определенном порядке. Данный термин был введен в оборот выдающимся английским ученым-теоретиком Джеймсом Сильвестром. Он является одним из основоположников теории применения данных математических элементов.

На сегодняшний день они нашли широкое применение при проведении различных расчетов, которые построены на основе такого способа, как, например, нахождение обратной матрицы в различных отраслях человеческой деятельности. Этот способ базируется на определении неизвестных параметров системы различных уравнений и часто используется при проведении экономических расчетов.
Бывают следующие частные случаи данных математических компонентов: строчная, столбцовая, нулевая, квадратная, диагональная, единичная. Строчная состоит только из одной строки элементов, а столбцовая – из одного столбика чисел. Нулевая – все ее элементы равны 0. У квадратного такого математического элемента количество столбиков равно количеству строк. В свою очередь, в диагональной, расположенные на главной диагонали элементы, отличны от «0», а остальные в ней должны быть равны «0». Единичная – это один из подвидов диагональной матрицы. У нее на главной диагонали расположены только «1».
Примеры матриц:
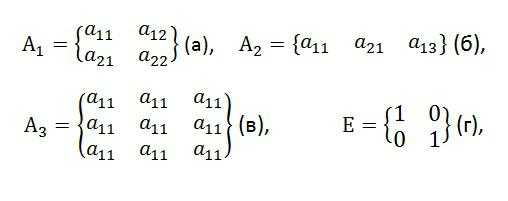
где: Ak – это общее обозначение, aij – элементы ,
(а) –2-го порядка;
(б) – строчная;
(в) –3-го порядка;
(г) – пример единичной таблицы 2-го порядка;
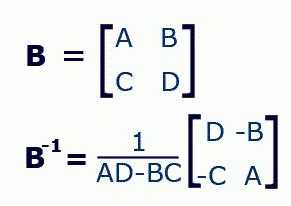 Также существует обратная матрица, определение которой заключается в следующем. При умножении на первоначальную таблицу обратной получается единичная. Разработано множество методов, которые обеспечивают нахождение обратной матрицы. Наиболее простой из них основан на определении алгебраических дополнений и определителя (его также иногда называют детерминантом).
Также существует обратная матрица, определение которой заключается в следующем. При умножении на первоначальную таблицу обратной получается единичная. Разработано множество методов, которые обеспечивают нахождение обратной матрицы. Наиболее простой из них основан на определении алгебраических дополнений и определителя (его также иногда называют детерминантом).
 Определителем матрицы называется выражение a11a22-a12a21, обозначается он следующим образом: ǀАǀ. Приведенная формула справедлива для таблицы соответствующей второму порядку. Есть формулы для определителей матриц более высокого порядка. Обязательное условие существования определителя – таблица должна быть квадратной. На практике этот элемент данной теории чаще всего используется при такой процедуре, как нахождение обратной матрицы.
Определителем матрицы называется выражение a11a22-a12a21, обозначается он следующим образом: ǀАǀ. Приведенная формула справедлива для таблицы соответствующей второму порядку. Есть формулы для определителей матриц более высокого порядка. Обязательное условие существования определителя – таблица должна быть квадратной. На практике этот элемент данной теории чаще всего используется при такой процедуре, как нахождение обратной матрицы.
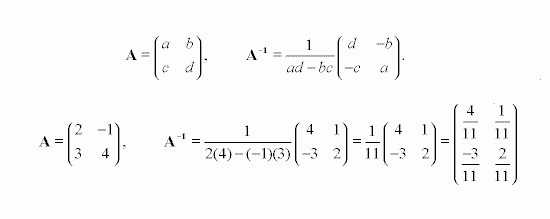
 Второй важный компонент, с помощью которого можно найти значения ее элементов, является алгебраическое дополнение. Вычисляется оно по формуле: Aij=(-1) i+j * Mij, где М – это минор. По существу – это дополнительный определитель, который можно получить путем мысленного удаления строки и столбца, в которых расположен данный элемент. Например, для таблицы, соответствующей второму порядку, которая приведена ранее по тексту, у элемента a11 алгебраическим дополнением будет элемент a22.
Второй важный компонент, с помощью которого можно найти значения ее элементов, является алгебраическое дополнение. Вычисляется оно по формуле: Aij=(-1) i+j * Mij, где М – это минор. По существу – это дополнительный определитель, который можно получить путем мысленного удаления строки и столбца, в которых расположен данный элемент. Например, для таблицы, соответствующей второму порядку, которая приведена ранее по тексту, у элемента a11 алгебраическим дополнением будет элемент a22.
Нахождение обратной матрицы выполняется в 3 этапа. На первом этапе определяется детерминант. На следующем шаге – все алгебраические дополнения, которые потом записываются в соответствии со своими индексами, и получается таблица алгебраических дополнений. На завершающем этапе получается обратная матрица, нахождение которой заканчивается перемножением каждого алгебраического дополнения на детерминант.
Наиболее часто матрицы используются при проведении экономических расчетов. С их помощью можно легко и быстро обработать большой объем информации. При этом конечный результат будет представлен в удобном для восприятия виде.
Еще одной сферой человеческой деятельности, в которой матрицы также нашли большое применение – это моделирование 3D-изображений. Подобные инструменты интегрированы в современные пакеты для реализации 3D-моделей и позволяют конструкторам производить быстро и точно необходимые расчеты. Наиболее ярким представителем таких систем является Компас-3D.
Еще одной программой, в которую интегрированы инструменты для проведения подобных расчетов, является Microsoft Office, а конкретнее – табличный процессор Excel.
fb.ru
От действий над матрицами к пониманию их сути… / Хабр
Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья “Математика на пальцах”, и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше…
Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.
Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что “площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма”. Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.
Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.
Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…
Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.
Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?
Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…
Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.
В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.
habr.com
Матрица, её история и применение
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
Термин «матрица» имеет много значений. Например, в математике матрицей называется система элементов, имеющая вид прямоугольной таблицы, в программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Покерные фишки также имеют непосредственное отношение к матрице. Фишки для покера изготавливаются из высококачественного композиционного материала, зачастую с металлической сердцевиной. В свою очередь композиционный материал или композит имеет матрицу и включенные в нее армирующие элементы (исключение составляют слоистые композиты).
Матрица в фотографии – это интегральная микросхема (аналоговая или цифро-аналоговая), которая состоит из фотодиодов (светочувствительных элементов). Благодаря светочувствительной матрице происходит преобразование спроецированного на нее оптического изображения в электрический сигнал аналогового типа, а при наличии в составе матрицы АЦП, то преобразование происходит в поток цифровых данных.
Матрица – основной элемент цифровых фотоаппаратов, всех современных видео- и телекамер, фотокамер, встроенных в мобильный телефон и системы видеонаблюдения.
Основное значение термин «матрица» имеет в математике.
Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Основные операции над матрицами
Сумма матриц
Суммой двух матриц, например: A и B, имеющих одинаковое количество строк и столбцов, иными словами, одних и тех же порядков m и nназывается матрица С=( С[i, j] ) ( i = 1, 2, …m; j = 1, 2, …n ) тех же порядков m и n, элементы C[i, j] которой равны.
C [i, j] = A [i, j] + B [i, j] (i = 1, 2, …, m; j = 1, 2, …, n)
Для обозначения суммы двух матриц используется запись C = A + B. Операция составления суммы матриц называется их сложением
Итак, по определению имеем:
=
=
Рисунок 1.1 Операция суммы
Пример: + =
Разность матриц
Разностью двух матриц A иB одинаковых порядков естественно называется такая матрица C тех же порядков, которая в сумме с матрицей B дает матрицу A. Для обозначения разности двух матриц используется естественная запись: C = A – B.
Пример: – =
Произведение матриц
Произведением матриц Aи Bбудет матрица Cтакая, что элемент матрицы C, стоящий в i-той строке и j-том столбце (C[i, j]), равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B:
C [i, j] =A [i, 1] * B [1, j] + A [i, 2] * B [2, j] + … + A [i, n] * B [n, j]
Для обозначения произведения матрицы A на матрицу B используют запись C = AB.
Пример: * =
Примечание. Две матрицы можно перемножить между собой тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Деление Матриц
В теории матриц нет понятия «деления матрицы», матрицы можно только умножать. Чтобы «разделить матрицу Aна матрицу B» говорят, что нужно умножить на матрицу A, где B-1 – обратная матрица к матрице B.
Рекомендуемые страницы:
lektsia.com
09. Матрицы и их использование
Статистические, производственные показатели, а также расчеты, производимые на основе полученной информации, часто требуют сохранения результатов для их дальнейшего использовния. В этом случае создаются числовые таблицы, в которых информация в той или иной степени упорядочена. В таблицу могут быть внесены характеристики элементов какого-либо множества, параметры состояния системы и порядок применения операций, так как и операции могут являться элементами определенных множеств (в теории групп симметрии). Экономические и финансовые расчеты, которые являются наиболее широко используемыми во всех сферах деятельности человека (от семейного бюджета до бюджета государства), также должны быть упорядочены. Одной из форм такого упорядоченного состояния любой системы является наличие множества таблиц с определенной информацией. Возникает проблема оптимального использования таблиц, то есть проблема операций (действий) с таблицами данных. Рассмотрим конкретные примеры.
Пусть, в простейшем случае, ежемесячные затраты из семейного бюджета Y складываются из трех основных видов товара (Q1, Q2, Q3), приобретаемых в трех различных магазинах (МJ) по различным ценам (разного сорта). Количество товаров QЯ, купленных в январе и QФ, купленных в феврале, составят таблицы следующего вида:
.
Численное значение в каждой таблице, то есть ее элемент Qij, определяется двумя параметрами – индексами при Qi и Mj. Так, например, из первой таблицы Q12 = 15, а из второй таблицы Q22 = 4. Если количество индексов в строке таблицы или в столбце будет более десяти, то между индексами придется писать запятую. В общем виде каждая из таблиц может быть представлена следующим образом:
. (26)
Таблица элементов Qij, расписанных по M строкам и N столбцам, называется Матрицей. Если число строк и столбцов совпадают (M = N), то матрица называется Квадратной. Наибольшее число строк (или столбцов) в квадратной матрице определяют ее порядок.
Матрица товаров (26) является, таким образом, квадратной матрицей третьего порядка. Рассмотрим действия (операции), которые можно производить с матрицами.
Имея матрицы закупок товаров за каждый месяц, легко подсчитать количество товаров, приобретенных за два месяца. Для этого, действуя по смыслу, необходимо сложить числа в соответствующих местах обеих матриц. В результате получаем общую матрицу товаров.
.
Таким образом, матрицы Можно складывать по правилу: Qij = Qij(Я) +Qij(Ф). Очевидно, что если матрицы закупок за каждый месяц одинаковы, то при поиске общего количества товаров за k месяцев, каждый элемент матрицы необходимо сложить k раз, то есть умножить на k. В общем виде это записывается следующим образом: Q = KQЯ. Поэтому матрицы Можно умножать На одно и то же число.
Пусть теперь нас интересуют ежедневные затраты, производимые за три дня покупок товаров трех сортов в трех различных магазинах, то есть, в общем случае, по разной цене. Теперь мы имеем две матрицы: матрицу закупок товаров Q = {Qij} за три дня и матрицу цен P = {Pij} Товаров различного сорта в трех магазинах. Очевидно, что произведение количества товаров на соответствующие им цены, позволит определить произведенные затраты Y.

В таблицах закупок товара и цен использованы следующие обозначения: Д – дни ; С – сорт товара; М – номер магазина. Теперь опишем матрицу
Y = {Yij}, которая получилась в результате расчетов. Для этого выберем произвольный элемент, например Y23 , и рассмотрим процедуру его вычисления. Индексы при элементе указывают, что речь идет о затратах второго дня при покупке товаров всех сортов в третьем по номеру магазине. Для того, чтобы получить соответствующее число, необходимо выбрать из матрицы товара за второй день товары первого сорта (Q21) и умножить это количество на цену товаров первого сорта по ценам третьего магазина (P13). Затем сюда прибавить затраты на закупку во второй день товаров второго сорта (Q22) по ценам третьего магазина (P23) и, наконец, сложить с затратами за второй день по закупке товаров третьего сорта (Q23) по ценам третьего магазина (P33). В итоге получаем: Y23 = Q21· P13+ Q22· P23+ Q23· P33 . Можно заметить, что при сложении первый и последний индексы не изменяются, а суммирование производится по промежуточному индексу, стоящему между первым и последним. Поэтому для произвольного элемента матрицы затрат следует (по смыслу) составить равенство: , (27)
Где N – порядок матрицы Y. Таким образом, матрицы Можно умножать и правилом умножения является равенство (27).
(?): Как следует интерпретировать следующее равенство (28), в котором появляются матрицы – столбцы {Pij} и {Yij}? Заметим только, что второй индекс у элементов этих матриц можно опустить, так как он везде одинаковый.
(28)
Правило умножения матриц было в неявной форме использовано нами раньше (§2) при решении вопросов, связанных с поиском равновесия на рынке. Еще раз представим систему линейных уравнений (3) из этого параграфа: , которую перепишем следующим образом:
, (29)
где произведена замена: A1 = a11, b1 = a12, A2 = a21, b2 = a22, x = x1, y = x2, c1 = y1, c2 = y2. При этом смысл системы уравнений не изменился, а запись получила новую интерпретацию в матричной форме. Действительно, по правилу умножения матриц, будем иметь:.(30)
Теперь очевидно, что записано равенство типа (28), в котором использованы квадратная матрица второго порядка А = {АIj} и две матрицы – столбцы – для переменных (X1,X2) и (Y1,Y2). Первую из них обозначим Х = {ХI}, а вторую Y = {Yj}. Тогда вместо системы уравнений (29) будем иметь матричное уравнение: AX = Y.
Рассмотрим пример не связанный напрямую с рассмотренными выше экономическими проблемами. Речь пойдет о симметрии и ее описании с помощью преобразований систем координат.
Несмотря на то, что с реальными объектами всегда происходят какие-либо изменения (преобразования), существуют такие характеристики объекта, которые в результате этих преобразований остаются неизменными, т. е. сохраняются. Например, при изменении положения какой-либо фигуры можно заметить, что соответствующие этим изменениям преобразования системы координат (перенос, поворот) оставляют сохраняющимися (инвариантными) такие характеристики геометрической фигуры, как расстояние между его точками, углы между прямыми, площадь поверхности и т. п. (рис. 23).
Рис. 23. Движение фигуры (а) и соответствующее преобразование
системы координат (б)
Направленный отрезок 0А на рис.23а называется Вектором точки А и определяется координатами точки А (x1,x2), а направленный отрезок 0А’ называется Вектором точки А’(x’1,x’2).
Словами «расстояние АВ» или «расстояние АС» характеризуется то, как «относится А к В или А к С», т. е. задается Отношение. Можно представить себе, что точка пространства в заданной системе координат, как-то «относится» ко всем остальным точкам этого пространства. Существуют такие же отношения и для других точек пространства. Если у каждой точки «отношение» к остальным точкам такое же, как и у других точек, то пространство из всех точек «выглядит» одинаково и такое пространство можно охарактеризовать как Однородное.
Можно представить себе другой вариант, когда условие равноправности свойств точек пространства, связанных с сохранением расстояний, углов и т. п. не выполняется, т. е. пространство неодинаково «выглядит» из разных точек, тогда его следует охарактеризовать как Неоднородное.
Проверка пространства на однородность каких-либо характеристик, например, тех же расстояний и углов, осуществляется простым переходом от одной системы координат к другой и расчетом соответствующих характеристик. Параллельный перенос системы координат проверяет однородность по отношению к расстояниям, а поворот проверяет однородность по отношению к углам (последний тип однородности называют Изотропностью).
Будем понимать под Симметрией свойство объектов Сохранять определенные характеристики при преобразованиях. В свою очередь, преобразования, сохраняющие определенные свойства или характеристики пространства, объектов, структур, систем и т. п., будем считать Симметрическими преобразованиями. Так как при некоторых преобразованиях сохраняются расстояния и углы геометрических объектов, можно говорить о том, что Однородность и Изотропность есть Симметрические свойства пространства.
Очевидные соотношения, приведенные во многих справочниках по математике, связывают старую и новую Системы координат: или, в общем виде: . Более коротко обе системы уравнений можно записать следующим образом: , где матрица называется матрицей преобразований вращения.
Под R Можно понимать также определенную симметрическую операцию. Если после перехода из системы координат к системе координат какая-либо величина, зависящая от координат, не меняется, т. е. сохраняется, то можно говорить о «законе сохранения» этой величины.
В рассмотренном примере важно отметить, что преобразования симметрии записываются в матричной форме так же, как и в примерах экономических, связанных с расчетом затрат. Матрицы – столбцы, которые в последнем примере оказались геометрически связаны с определением вектора, получили обобщение при описании любой матрицы.
Всякая строка в произвольной матрице называется Вектор – строка, а всякий столбец называется Вектор – столбец.
Определение симметрии с помощью матричного уравнения, в котором векторы после симметрических преобразований остаются прежними, можно записать следующим образом: АХ = Х. На рис. 24 представлен пример мозаики, которая совмещается сама с собой после операции вращения на угол φ = 360о/5 = 72о. Этот тип симметрии называют симметрией 5 –го порядка.
(?): Каким преобразованием можно продолжить эту мозаику, чтобы в результате она занимала все большую и большую площадь? Мозаика становится фрактальной, так как эту процедуру можно продолжать, переходя как к бесконечно большим, так и бесконечно малым размерам.
 |
Рис. 24. Пример фрактальной мозаики с симметрией 5 – го порядка
Понятие симметрии явно или неявно играет ключевую роль при обсуждении вопросов Устойчивого развития региона или его экономики. Достаточно представить себе процесс развития периодическим (это тип трансляционной симметрии), секториальным с самоподобием (как в приведенной мозаике) или даже нелинейным, Устойчивая Тенденция роста всегда Носит упорядоченный (а следовательно, симметричный) Характер. Именно так решается проблема устойчивого роста в природе. Если Вам удалось понять, каким образом происходит расширение мозаики (рис. 24), то несложно получить формулу увеличения количества элементов мозаики (пятиугольников) после каждого преобразования:
Sn = 5(6N) = 5Qn, а сумма представляет собой геометрическую прогрессию Sn = Aq0 + Aq1 + Aq2 + …. + Aqn , с которой мы уже имели дело в §5 при анализе накоплений в пенсионный фонд. Поэтому можно говорить о том, что приведенная мозаика является геометрической моделью накоплений.
Возвращаясь к системе уравнений (3) в §2, можно заметить, что при поиске координат точки равновесия полученное решение (4) и (5) содержит в знаменателе дробей одну и ту же «конструкцию» (а1B2 – A2B1), составленную из элементов матрицы преобразований. В соответствии с матричным уравнением (30) эту разность представим в виде:
(A11A22 – A12A21). Полученное выражение ставит в соответствие всем элементам матрицы Определенное число, которое называется Определителем матрицы. Определитель (детерминант) матрицы обозначается символом Δ или D = det(A). Если в матрице выбрать элемент Aij и вычеркнуть строку и столбец, которым он принадлежит, то оставшиеся элементы составят новую матрицу с определителем Dij. Этот определитель с соответствующим знаком, зависящим от индекса элемента Ij, определяет число Aij, которое называется Алгебраическим дополнением элемента Aij: Aij = (-1)i+jDij. (31)
Лапласом доказана Теорема о том, что Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. На основе этой теоремы можно, последовательно вычисляя произведения элементов на их дополнения, получить определитель квадратной матрицы любого порядка. Важность операции вычисления определителя связана с упрощением поиска решения системы из большого количества уравнений с соответствующим количеством неизвестных.
Применение теоремы Лапласа рассмотрим на примере поиска определителя матрицы третьего порядка. При поиске определителя матрицу будем записывать, используя вместо скобок вертикальные линии.
.
Конкретные примеры на запись матричного уравнения по заданной системе и вычисление соответствующих определителей матриц приведены в Приложении I.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Математическая матрица. Умножение матриц
Ещё математики древнего Китая использовали в своих вычислениях запись в виде таблиц с определённым количеством строк и столбцов. Тогда подобные математические объекты именовались как «волшебные квадраты». Хотя известны и случаи использования таблиц в виде треугольников, которые так и не получили широкого распространения.
На сегодняшний день под математической матрицей принято понимать объёкт прямоугольной формы с заданным количеством столбцов и символов, которые и определяют размеры матрицы. В математике такая форма записи нашла широкое применение для записи в компактном виде систем дифференциальных, а также линейных алгебраических уравнений. Принято, что количество строк в матрице равно числу присутствующих в системе уравнений, количеству столбцов соответствует, сколько неизвестных необходимо определить в ходе решения системы.
Кроме того, что сама по себе матрица в ходе её решения приводит к нахождению неизвестных, заложенных в условие системы уравнений, существует ряд алгебраических операций, которые допускается осуществлять над данным математическим объектом. Этот перечень включает в себя сложение матриц, имеющих одинаковые размеры. Умножение матриц с подходящими размерами (можно перемножить лишь матрицу, с одной стороны имеющую количество столбцов, равное количеству строк у матрицы с другой стороны). Также допускается умножать матрицу на вектор, или на элемент поля или основного кольца (иначе скаляр).
Рассматривая умножение матриц, следует внимательно следить, чтобы количество столбцов первой строго соответствовало числу строк второй. Иначе данное действе над матрицами будет не определено. Согласно правилу, по которому осуществляется умножение матрицы на матрицу, каждый элемент в новой матрице приравнивается к сумме произведений соответствующих элементов из строк первой матрицы на элементы, взятые из столбцов другой.
Для наглядности рассмотрим пример, как происходит умножение матриц. Берём матрицу A
2 3 -2
3 4 0
-1 2 -2,
умножаем её на матрицу B
3 -2
1 0
4 -3.
Элемент первой строки первого столбца результирующей матрицы равен 2*3+3*1+(-2)*4. Соответственно, в первой строчке во втором столбце будет элемент равный 2*(-2)+3*0+(-2)*(-3), и так далее до заполнения каждого элемента новой матрицы. Правило умножения матриц предполагает, что результатом произведения матрицы с параметрами m x n на матрицу, имеющую соотношение n x k, станет таблица, которая обладает размерами m x k. Следуя этому правилу, можно сделать вывод, что произведение так называемых квадратных матриц соответственно одного порядка всегда определено.
Из свойств, которыми обладает умножение матриц, следует выделить в качестве одного из основных то, что эта операция не является коммутативной. То есть произведение матрицы M на N не равно произведению N на M. Если в квадратных матрицах одного порядка наблюдается, что их прямое и обратное произведения всегда определены, отличаясь лишь результатом, то для прямоугольных матриц подобное условие определенности не всегда выполняется.
У умножения матриц существует ряд свойств, которые имеют чёткие математические доказательства. Ассоциативность умножения подразумевает верность следующего математического выражения: (MN)K=M(NK), где M,N, и K – матрицы, имеющие параметры, при которых умножение определено. Дистрибутивность умножения предполагает, что M(N+K)= MN+MK, (M+N)K= MK+NK, L(MN)= (LM)N+ M(LN), где L – число.
Следствием из свойства умножения матриц, именуемого «ассоциативность», следует, что в произведении, содержащем от трёх и больше сомножителей, допускается запись без использования скобок.
Использование свойства дистрибутивности даёт возможность раскрывать скобки при рассмотрении матричных выражений. Обращаем внимание, если мы раскрываем скобки, то нужно сохранять порядок сомножителей.
Использование матричных выражений позволяет не только компактно производить запись громоздких систем уравнений, но и облегчает процесс их обработки и решения.
fb.ru
Реферат по математике на тему Матрица читать бесплатно
Матрица
Матрицы уже давно стали неотъемлемой частью решения множества математических задач и вопросов. Они представляют собой прямоугольную или квадратную таблицу чисел, в зависимости от количества строк и столбцов в ней. Общепринятое обозначение количества строк в матрице – латинская буква m, и количество столбцов, в свою очередь, обозначается n. Таким образом, если в матрице m=n, значит это квадратная матрица порядка n. С матрицами можно выполнять стандартные алгебраические операции: сложение, вычитание, умножение, деление. Подразумевается как сложение, умножение, вычитание матрицы с одним числом, отличным от нуля и так же все эти операции между двумя матрицами. Однако их можно проделывать не с любыми матрицами, а лишь теми, что соразмерны друг другу. Все эти сведения общеизвестны и широко применяемы. Но существуют так же и другие операции, специфические именно для матриц. Прежде, чем рассказать о них, обратимся к истории и узнаем некоторые факты о возникновении матриц.
История возникновения матриц.
Первые упоминания о матрицах дошли до нас ещё из Древнего Китая, а так же и из работ древних арабских математиков. В те давние времена матрицы называли «волшебными квадратами», и уже тогда стали зарождаться правила сложения двух и более матриц. Уже некоторое время спустя в XXVII в, когда появилась теория определетилей, выдающийся математик Габриэль Крамер опубликовал свое, по сей день известное и используемое «Правило Крамера». Приблизительно в этот же период появился не менее популярный «Метод Гауса». Ну а непосредственно введение самого термина «матрица» – заслуга Джеймса Сильвестра. Термин появился в 1850 году.
Определитель матрицы.
Сущeствует опрeделитель лишь для квадратной матрицы, т е для матрицы, в которой количество строк соответствует количеству столбцов (m=n). Матрицы в математике обозначаются заглавными латинскими буквами (A, B, C), а определители, в свою очередь обозначаются как (det A, det B, det C)
Пример матрицы:
Пример опредeлителя матрицы:
Данное выражение является формулой, по которой вычисляется определитель:
Помимо простых алгебраических операции, над матрицами выполняются и другие специфические действия, для приведения матрицы к наиболее удобному виду для выполнения последующих операций над ней. Рас смотрим некоторые из них.
Транспонирование матриц.
При произведении этой операции матрица меняется таким образом, что первая ее строка заменяется первым столбцом, вторая строка вторым столбцом и так далее. В результате мы получаем, так называемую, транспонированную матрицу, которая обозначается так же, как и обычная матрица, только добавляется индекс T.
Обратная матрица.
Обратная матрица для матрицы А обозначается как А в степени -1. A-1 При умножении матрицы на обратную ей получается единичная матрица (E), то есть матрица, все элементы которой нули, кроме чисел на главной диагонали (от верхнего левого угла до нижнего правого), которые равны 1.
см. также: Все рефераты по математике
www.sdamna5.ru
