Лекция Матрицы. Основные виды матриц. Действия над матрицами.
Скачать с Depositfiles
Лекция № 3. Тема 3 : Матрицы
3.1. Основные виды матриц
Определение 1. Матрицей называется совокупность чисел, располо-женных в т строках и п столбцах и обозначается


Число, стоящее на пересечении 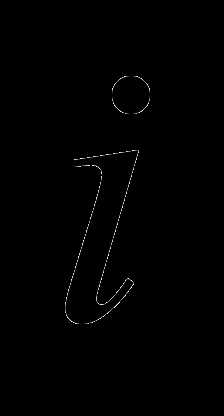 -ой строки и
-ой строки и  -го столбца, обозначается
-го столбца, обозначается 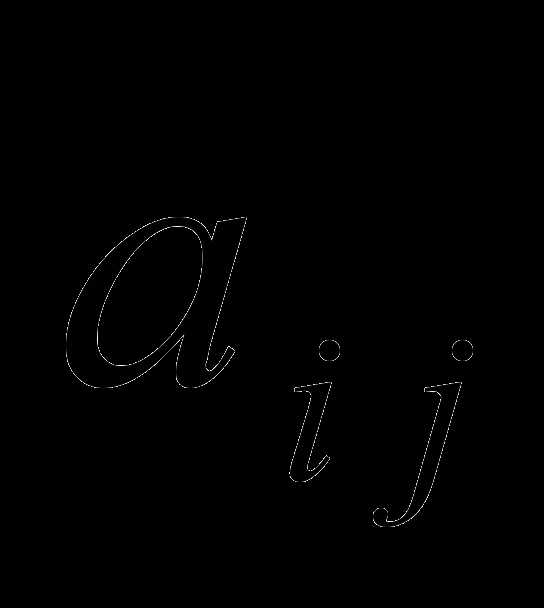 и называется элементом матрицы; размерность матрицы.
и называется элементом матрицы; размерность матрицы.
Существуют следующие виды матриц:
Матрица – строка

Нулевая матрица все ее элементы нули.
Единичная матрица

Диагональная матрица
 .
.Симметрическая матрица – для ее элементов выполняется равенство
 для всех
для всех 
Важной характеристикой квадратной матрицы А
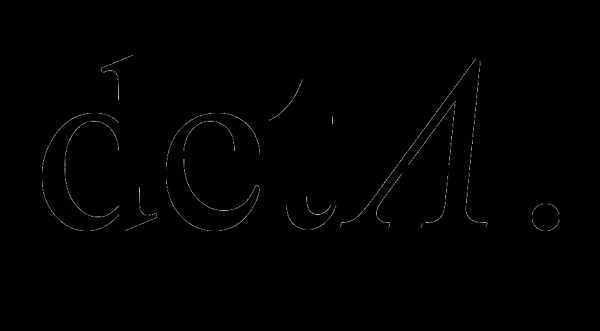 Если
Если  , то матрица А назы-вается невырожденной. В противном случае – вырожденной.
, то матрица А назы-вается невырожденной. В противном случае – вырожденной.Определение 2. Две матрицы 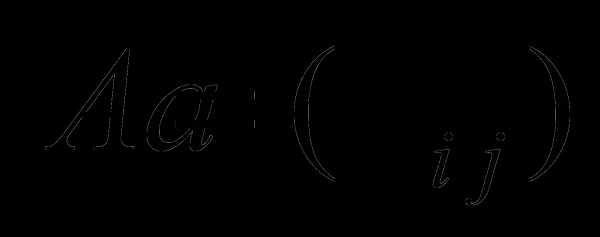 и
и 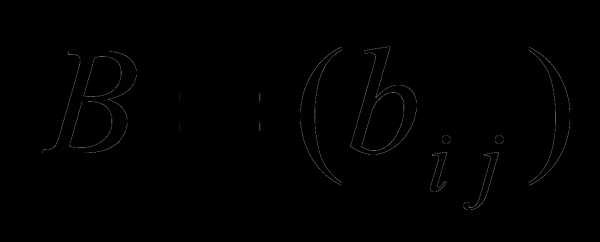 одинаковой размер-ности называются равными, если равны все их соответствующие элементы
одинаковой размер-ности называются равными, если равны все их соответствующие элементы  для всех
для всех
3.2. Действия над матрицами
Определение 3. Транспонированием матрицы называется замена её строк столбцами с сохранением их номеров.
Транспонированная матрица обозначается А Т.
Пример 1. Найти А Т, если матрица 
Тогда 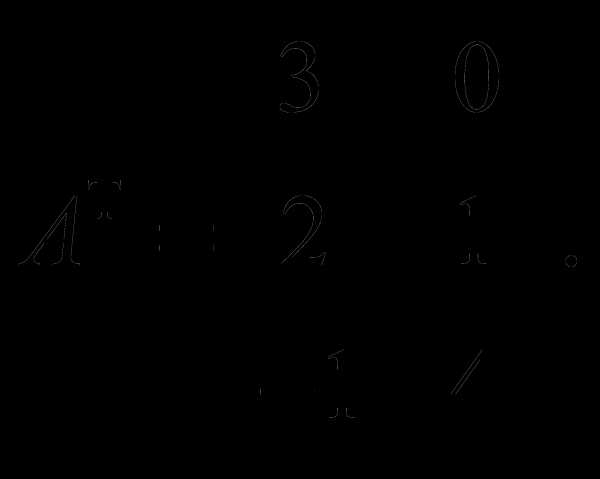
2. Сложение матриц.
Определение 4. Суммой двух матриц 
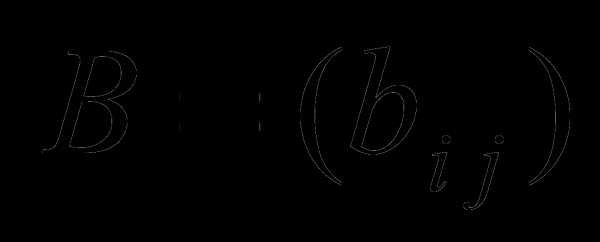 одинаковой размерности называется матрица С той же размерности, элементы которой определяются равенствами и обозначается .
одинаковой размерности называется матрица С той же размерности, элементы которой определяются равенствами и обозначается .3. Умножение матрицы на число.
Определение 5. Произведением матрицы  на некоторое число
на некоторое число  называется матрица
называется матрица 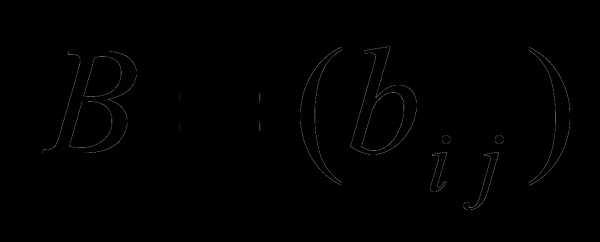 , элементы которой равны элементам матрицы А, умноженным на это число
, элементы которой равны элементам матрицы А, умноженным на это число  , т.е.
, т.е. 
 .
.Пример 2. Найти матрицу , если
4. Умножение матриц.
Определение 6. Произведением матрицы  размерности
размерности  и матрицы
и матрицы 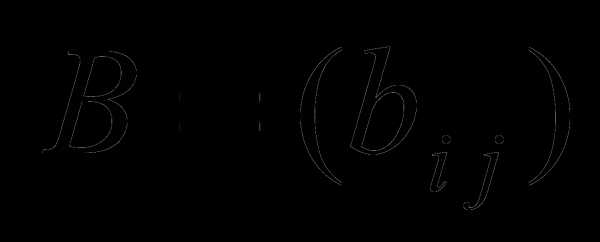 размерности
размерности  , называется матрица
, называется матрица  , размерности
, размерности 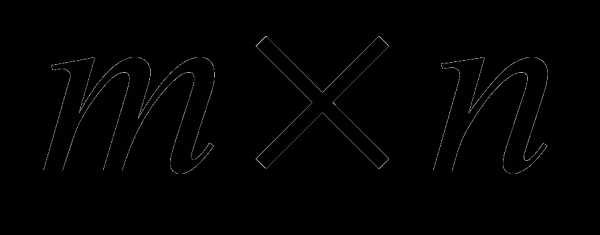
и обозначается  .
.
Замечание 1. Как видно из определения, произведение двух матриц будет определено, если число столбцов первой матрицы равно числу строк второй.
Пример 3. Найти произведение матриц
Тогда
Замечание 2. Легко убедиться в том, что в общем случае произведение матриц не обладает коммутативным свойством, т.е. что видно из следующего примера.
Тогда имеем
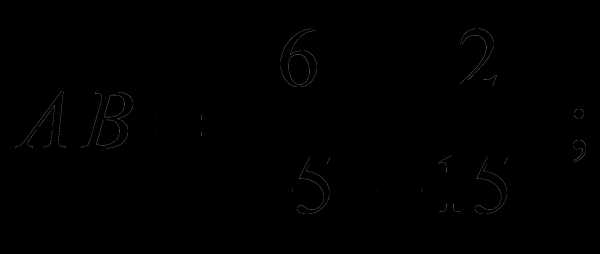
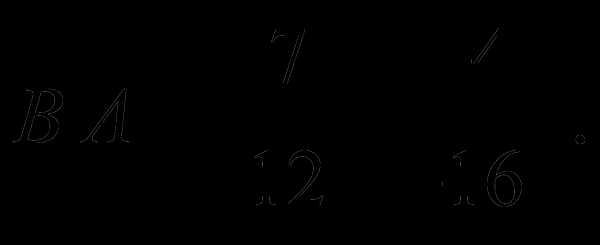
3.3. Обратная матрица
Определение 7. Обратной матрицей матрицы А называется матрица  , для которой выполняется равенство
, для которой выполняется равенство
Из этого определения следует, что понятие обратной матрицы является взаимообратным и определено только для квадратных матриц. При этом для существования обратной матрицы необходимо, чтобы матрица
 .
.Покажем, что обратной матрицей  для случая матрицы А размер-ности
для случая матрицы А размер-ности  будет матрица
будет матрица

где  алгебраические дополнения элемента
алгебраические дополнения элемента 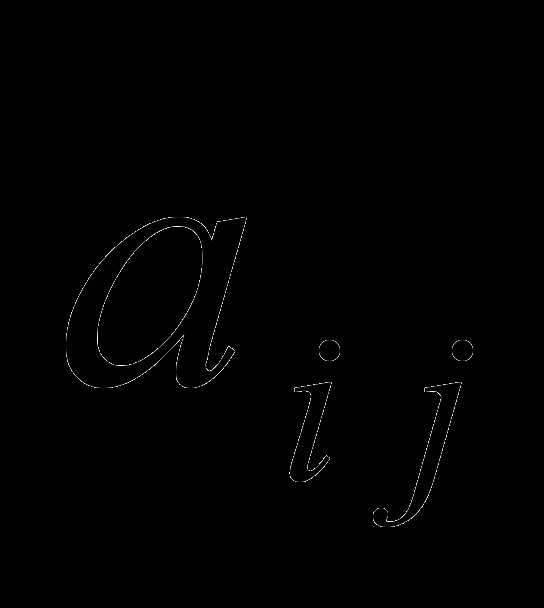 .
.
Например,
и т.д.
Так же можно проверить и равенство 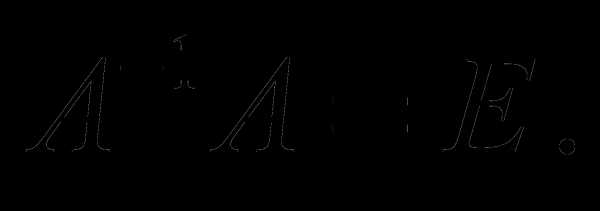
Замечание 4. Аналогично для матрицы А размерности  обратная матрица
обратная матрица 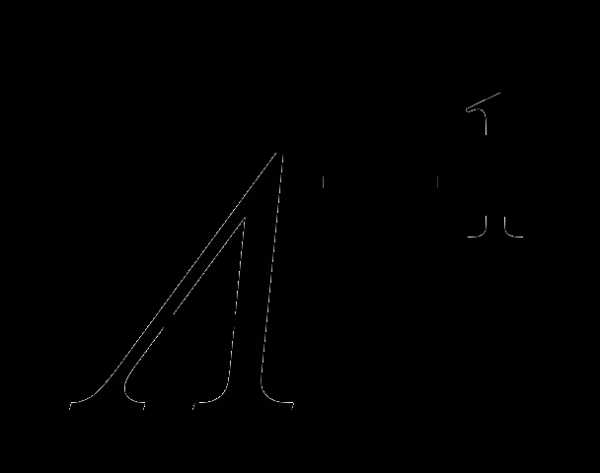 имеет вид
имеет вид

3.4. Решение систем линейных уравнений с помощью обратной матрицы
 (1)
(1)
Введем следующие матрицы
Тогда, используя правило умножения матриц, систему (1) можно пред-ставить в следующем виде (матричная форма системы уравнений (1))
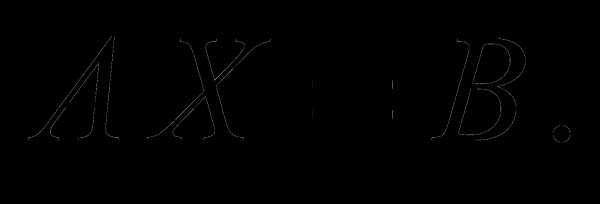 (2)
(2)
Пусть 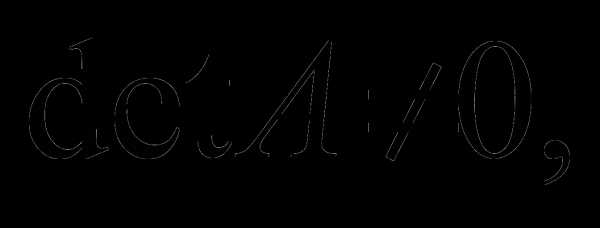 тогда для матрицы А существует обратная
тогда для матрицы А существует обратная 
 , получим
, получим(3)
В силу равенств и 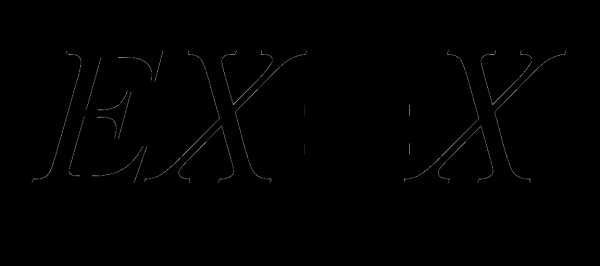 формула (3) принимает вид
формула (3) принимает вид
(4)
Не трудно убедиться в том, что выражение (4), полученное для Х, действительно является решением уравнения (1). Подставляя это выражение в уравнение (2), имеем
Замечание 5. Решение, полученное по формуле (4), то же самое, что было получено по формулам Крамера. Этот факт, вытекающий из единственности решения системы (1), можно непосредственно проверить, если подставить в формулу (4) выражение для обратной матрицы.
Пример 5. Матричным методом решить систему уравнений
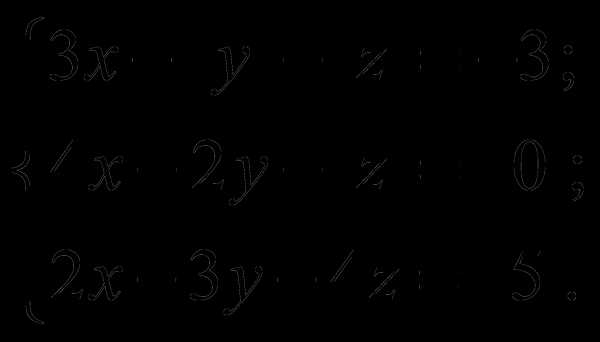
Здесь
Тогда
следовательно, обратная матрица существует.
Вычисляем алгебраические дополнения
аналогично далее
Таким образом, получим окончательное решение
.
Скачать с Depositfiles
greleon.ru
Матрицы – Введение
Каталин Дэвид
Матрица – это прямоугольная таблица, состоящая из строк и столбцов, содержащих числа.
Общий вид матрицы выглядит таким образом:
Элементы матрицы обозначаются $a_{n,m}$, где m – номер строки, а n – номер столбца, на пересечении которых находится данный элемент.
Пример 1
$A= \begin{pmatrix} 1 & 0 & 2\\ 3 & 1 & 4\\ \end{pmatrix} $
A – матрица из 2 строк и 3 столбцов, в которой число 2 стоит в первой строке, третьем столбце.
Пример 2
$A= \begin{pmatrix} 1 & 5 & 2\\ 8 & 7 & 3\\ \end{pmatrix} $
B – матрица из 3 строк и 2 столбцов, в которой число 8 стоит во второй строке, втором столбце.
Матрица с равным числом строк и столбцов называется квадратной матрицей.
Пример 3 $A= \begin{pmatrix} 1 & 2 & 3\\ 2 & 5 & 1\\ \end{pmatrix} $
C – матрица из 3 строк и 3 столбцов
D – общий вид квадратной матрицы.
$D= \begin{pmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3} & . & . & \color{blue}{a_{1,n}}\\ a_{2,1} & \color{red}{a_{2,2}} & a_{2,3} & . & \color{blue}{a_{2,n-1}} & a_{2,n}\\ a_{3,1} & a_{3,2} & \color{red}{a_{3, \color{blue}{3}}} & . & . & a_{3,n}\\ . & \color{blue}{a_{n-1,2}} & . & . & .& .\\ \color{blue}{a_{n,1}} & a_{n,2} & a_{n,3} & . & . & \color{red}{a_{n,n}}\\ \end{pmatrix}$
Элементы главной диагонали выделены красным цветом, а на побочной диагонали – синим.
Квадратная матрица, у которой все элементы главной диагонали равны 1, а все остальные элементы равны 0, называется единичной матрицей.
Пример 4
$A= \begin{pmatrix} 1 & 0 & 2\\ 0 & 1 & 4\\ \end{pmatrix} $
Пример 5
$I_{3}= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix}$
Транспонированная матрица получается, если в исходной матрице заменить строки на столбцы. Если дана матрица A, то транспонированная матрица A обозначается $A^{T}$.
Пример 6
| $A=\begin{pmatrix} 1 & 3\\ 5 & 9 \end{pmatrix}$ | тогда | $A^{T}=\begin{pmatrix} 1 & 5\\ 3 & 9 \end{pmatrix}$ |
www.math10.com
Матрица (математика) | Virtual Laboratory Wiki
У этого термина существуют и другие значения, см. Матрица.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.
Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.
Обычно матрицу обозначают Заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями “||…||”).
Числа, составляющие матрицу (элементы матрицы), обозначают той же буквой, что и саму матрицу, но маленькой.
У каждого элемента матрицы есть 2 нижних индекса ($ a_{ij} $) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят матрица размерности $ n \times m $ подразумевая, что в матрице n строк и m столбцов.
Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.
Матрица как запись коэффициентов системы линейных уравнений Править
Cистему из $ m $ уравнений с $ n $ неизвестными
$ a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n = b_1 $
$ a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n = b_2 $
$ \cdots \cdots \cdots \cdots \cdots $
$ a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n = b_m $
можно представить в матричном виде
- $ A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} ;\quad X = \begin{pmatrix} x_{1} \\ x_{2} \\ \cdots \\ x_{n} \end{pmatrix} ;\quad B = \begin{pmatrix} b_{1} \\ b_{2} \\ \cdots \\ b_{m} \end{pmatrix} $
и тогда всю систему можно записать так:
$ AX = B $, где $ A $ имеет смысл таблицы коэффициентов $ a_{ij} $ cистемы уравнений.
Если $ m = n $ и матрица $ A $ невырожденная, то решение этого уравнение состоит в нахождении обратной матрицы $ A^{-1} $, поскольку умножив обе части уравнения на эту матрицу слева
$ A^{-1}AX = A^{-1}B $
$ A^{-1}A $ — превращается в $ E $ (единичную матрицу). И это даёт возможность получить столбец корней уравнений
$ X = A^{-1}B $.
Все правила, по которым проводятся операции над матрицами выводятся из операций над системами уравнений.
Операции над матрицами Править
Пусть $ a_{ij} $ элементы матрицы $ A $, а $ b_{ij} $ — матрицы $ B $.
Умножение матрицы $ A $ на число $ \lambda $ (обозначение: $ \lambda A $) заключается в построении матрицы $ B $, элементы которой получены путём умножения каждого элемента матрицы $ A $ на это число, то есть каждый элемент матрицы $ B $ равен
- $ b_{ij} = \lambda a_{ij} $
Сложение матриц $ A + B $ есть операция нахождения матрицы $ C $, все элементы которой равны попарной сумме всех соответствующих элементов матриц $ A $ и $ B $, то есть каждый элемент матрицы $ C $ равен
- $ c_{ij} = a_{ij} + b_{ij} $
- $ A+B= \begin{bmatrix} 2 & 0 & -1\\ 1 & 3 & 0 \end{bmatrix} + \begin{bmatrix} 3 & 1 & 0\\ 8 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 2+3 & 0+1 & -1+0\\ 1+8 & 3+2 & 0+3 \end{bmatrix} = \begin{bmatrix} 5 & 1 & -1\\ 9 & 5 & 3 \end{bmatrix} $
Вычитание матриц $ A – B $ определяется аналогично сложению, это операция нахождения матрицы $ C $, элементы которой
- $ c_{ij} = a_{ij} – b_{ij} $
- $ A-B= \begin{bmatrix} 2 & 0 & -1\\ 1 & 3 & 0 \end{bmatrix} – \begin{bmatrix} 3 & 1 & 0\\ 8 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 2-3 & 0-1 & -1-0\\ 1-8 & 3-2 & 0-3 \end{bmatrix} = \begin{bmatrix} -1 & -1 & -1\\ -7 & 1 & -3 \end{bmatrix} $
Сложение и вычитание допускается только для матриц одинакового размера.
Существует нулевая матрица $ \Theta $ такая, что её прибавление к другой матрице A не изменяет A, то есть
- $ A + \Theta = A $
Все элементы нулевой матрицы равны нулю.
Умножение матриц (обозначение: $ A B $, реже со знаком умножения $ A\times B $) — есть операция вычисления матрицы $ C $, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
- $ c_{ij} = \sum_k a_{ik} b_{kj} $
В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица $ A $ имеет размерность $ m \times n $, $ B $ — $ n \times k $, то размерность их произведения $ A B = C $ есть $ m \times k $. Умножение матриц не коммутативно.
- $ F L= \begin{bmatrix} a & d \\ b & e \\ c & f \\ \end{bmatrix} \times \begin{bmatrix} g & i & k \\ h & j & l \\ \end{bmatrix} = \begin{bmatrix} (a \cdot g + d \cdot h) & (a \cdot i + d \cdot j) & (a \cdot k + d \cdot l)\\ (b \cdot g + e \cdot h) & (b \cdot i + e \cdot j) & (b \cdot k + e \cdot l)\\ (c \cdot g + f \cdot h) & (c \cdot i + f \cdot j) & (c \cdot k + f \cdot l)\\ \end{bmatrix} $
- $ A B= \begin{bmatrix} 2 & 3\\ 5 & 7 \end{bmatrix} \times \begin{bmatrix} -1 & 2\\ -2 & 3 \end{bmatrix} = \begin{bmatrix} 2 \cdot -1 + 3 \cdot -2 & 2 \cdot 2 + 3 \cdot 3\\ 5 \cdot -1 + 7 \cdot -2 & 5 \cdot 2 + 7 \cdot 3 \end{bmatrix} = \begin{bmatrix} -8 & 13\\ -19 & 31 \end{bmatrix} $
- $ B A= \begin{bmatrix} -1 & 2\\ -2 & 3 \end{bmatrix} \times \begin{bmatrix} 2 & 3\\ 5 & 7 \end{bmatrix} = \begin{bmatrix} -1 \cdot 2 + 2 \cdot 5 & -1 \cdot 3 + 2 \cdot 7\\ -2 \cdot 2 + 3 \cdot 5 & -2 \cdot 3 + 3 \cdot 7 \end{bmatrix} = \begin{bmatrix} 8 & 11\\ 11 & 15 \end{bmatrix} $
Умножение матриц ассоциативно.
Возводить в степень можно только квадратные матрицы.
Транспонирование матрицы (обозначение: $ A^T $) — операция, при которой матрица отражается относительно главной диагонали, то есть
- $ a^T_{ij} = a_{ji} $
Если $ A $ — матрица размера $ m \times n $, то $ A^T $ — матрица размера $ n \times m $
Свойства матриц Править
- $ A + (B + C) = (A + B) + C $
- $ A + B = B + A $
- $ A(BC) = (AB)C $
- $ A(B + C) = AB + AC $
- $ (B + C)A = BA + CA $
- $ 0 \cdot A = 0 $
- $ 1 \cdot A = A $
- $ A_{k \times l} \cdot B_{l \times n} = C \Rightarrow c_{ij} = \sum_{k = 1}^l a_{ik} b_{kj} $
- $ (A^T)^T=A $
- $ (A*B)^T=B^T*A^T $
Элементарные преобразования матриц Править
Элементарными преобразованиями строк матрицы называются следующие преобразования:
- Умножение строки на число отличное от нуля
- Прибавление одной строки к другой строке
Элеменатрные преобразование столбцов матрицы определяются аналогично.
Матрица линейного оператора Править
Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы.
Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис $ \mathbf{e}_k $. Пусть $ \mathbf{x} $ — произвольный вектор. Тогда его можно разложить по этому базису:
$ \mathbf{x} = x^k\mathbf{e}_k $, где $ x^k $ — координаты вектора $ \mathbf{x} $ в выбранном базисе.
Здесь и далее предполагается суммирование по немым индексам.
Пусть $ \mathbf{A} $ — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим
$ \mathbf{Ax} = x^k\mathbf{Ae}_k $.
Вектора $ \mathbf{Ae}_k $ также разложим в выбранном базисе, получим
$ \mathbf{Ae}_k = a^j_k\mathbf{e}_j $, где $ a^j_k $ — $ j $-я координата $ k $-го вектора из $ \mathbf{Ae}_k $.
Подставим разложение в предыдущую формулу, получим
$ \mathbf{Ax} = x^ka^j_k\mathbf{e}_j = (a^j_kx^k)\mathbf{e}_j $.
Выражение $ a^j_kx^k $, заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица $ a^j_k $ при умножении на столбец $ x^k $ даёт в результате координаты вектора $ \mathbf{Ax} $, возникшего от действия оператора $ \mathbf{A} $ на вектор $ \mathbf{x} $, что и требовалось получить.
- Тензор — многомерный аналог матриц
Ресурсы на сайте Eqworld:
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Матрица (математика). Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .
ru.vlab.wikia.com
Минор и алгебраическое дополнение матрицы.
Определение.
Минором Mij к элементу aij определителя n-го порядка называется определитель (n – 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.Пример 1.
Найти миноры матрицы AA = 571-410203
Решение:
| M11 = | = 1·3 – 0·0 = 3 – 0 = 3 |
| M12 = | = -4·3 – 0·2 = -12 -0 = -12 |
| M13 = | = -4·0 – 1·2 = 0 – 2 = -2 |
| M21 = | = 7·3 – 1·0 = 21 – 0 = 21 |
| M22 = | = 5·3 – 1·2 = 15 – 2 = 13 |
| M23 = | = 5·0 – 7·2 = 0 – 14 = -14 |
| M31 = | = 7·0 – 1·1 = 0 – 1 = -1 |
| M32 = | = 5·0 – 1·(-4) = 0 + 4 = 4 |
| M33 = | = 5·1 – 7·(-4) = 5 + 28 = 33 |
Определение.
Алгебраическим дополнением Aij к элементу aij определителя n-го порядка называется числоAij = (-1)i + j · Mij
Пример 2.
Найти алгебраические дополнения матрицы AA11 = 571-410203
Решение:
A11 = (-1)1 + 1·M11 = (-1)2·1003 = 1·3 – 0·0 = 3 – 0 = 3
A12 = (-1)1 + 2·M12 = (-1)3·-4023 = -(-4·3 – 0·2) = -(-12 -0) = 12
A13 = (-1)1 + 3·M13 = (-1)4·-4120 = -4·0 – 1·2 = 0 – 2 = -2
A21 = (-1)2 + 1·M21 = (-1)3·7103 = -(7·3 – 1·0) = -(21 – 0) = -21
A22 = (-1)2 + 2·M22 = (-1)4·5123 = 5·3 – 1·2 = 15 – 2 = 13
A23 = (-1)2 + 3·M23 = (-1)5·5720 = -(5·0 – 7·2) = -(0 – 14) = 14
A31 = (-1)3 + 1·M31 = (-1)4·7110 = 7·0 – 1·1 = 0 – 1 = -1
A32 = (-1)3 + 2·M32 = (-1)5·51-40 = -(5·0 – 1·(-4)) = -(0 + 4) = -4
A33 = (-1)3 + 3·M33 = (-1)6·57-41 = 5·1 – 7·(-4) = 5 + 28 = 33
ru.onlinemschool.com
Определитель матрицы 2×2, 3×3, 4×4…
Определитель (детерминант) квадратной матрицы A – это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.
Обозначения
Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$
Свойства определителя
- Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$ - Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$ - Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)
или
$\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны) - Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или$ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
- При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 16
В определителе
$\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:
$3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:
$6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$ - При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.
Пример 17
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
Пример 18
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$ - При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.
Пример 19
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$Пример 20
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$ - Определитель матрицы равен определителю транспонированной матрицы.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
Один из миноров матрицы A есть $\begin{vmatrix} 1 & 2\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
Другим минором является $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)
Пример 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $
Один из миноров матрицы B есть $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)
Другим минором является $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Пусть $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n}\\ a_{3,1} & a
www.math10.com
Расчет определителя комплексной матрицы онлайн
| Вы ввели следующие элементы массива |
| Определитель(детерминант) матрицы равен |
Расчет детерминанта комплексной матрицы(DETERMINANT OF THE COMPLEX MATRIX)
Сервис позволяет рассчитывать определитель(детерминант) квадратной матрицы любой размерности с комплексными коэффициентами.
Где же может применяться расчет определителя матрицы( в том числе и с комплексными коэффициентами)?
1. в методе Крамера решения определенных СЛАУ,
2. для вычисления мер в n-мерных пространствах,
3. для определения ранга матрицы через невырожденные миноры,
4. в криптографии для некоторых шифров (например, шифр Хилла, шифрование аффинными блочными шифрами),
5. в нахождении экстремумов функций нескольких переменных,
Многие спрашивают в чем же физический смысл расчета определителя матрицы?
Ответ прост: его нет.
Несмотря на то, что расчет определителя, детерминанта матрицы используется в множесте задач, от экономики до ядерной физики, смысла именно физического у детерминанта нет.
Интересный взгляд на расчет определителя матрицы есть в материале:Определитель матрицы. Альтернативный взгляд.
А кто хочет узнать свойства матриц, то добро пожаловать Свойства определителя матрицы (Property determinant)
Синтаксис
Если используете XMPP клиента: op_i <значения матрицы>
Матрица должна быть квадратной, то есть число столбцов и строк должно быть одинаково.
Как например здесь
Значением матрицы являются как действительные, так и комплексные числа.
Элементы матрицы вводятся по принципу слева направо и сверху вниз, в одну или несколько строк.
Каждый элемент матрицы должен быть разделен пробелами.
Если в строке будет встречен любой символ не являющийся числовым, то он будет автоматически заменен на нуль.
Нет никаких ограничений на количество элементов матрицы. Вернее, не надо вводить больше 300-400 элементов. Устанете.. 🙂
Убедительная просьба: Если уж пишете мнимые единицы то обозначайте их знаком i (ай) а не j(джи). Будьте внимательнее в написании исходных данных!!.
Примеры
Значит в запросе надо писать op2 1 2+2i 3-1.5i 4
Обязательно учтите синтаксис, если вы делаете запрос через сайт, то пишите просто 1 2+2i 3-1.5i 4
и в ответе получим
Матрица квадратная 2х2.
Определитель такой матрицы равен
-5-3i
То есть комплексное число
Записываем элементы
op_i -1 2.2:-2 -7 11 3 4:0.1 1 0:1 7 7 -1.4533 5 0 11 -1:-1 1
Ответ
Матрица квадратная 4х4.
Определитель такой матрицы равен
Где действительная часть -347.94292
Где мнимая часть -644.46077
Посчитаем определитель вот такой “несложной” матрицы.
Пишем cos(2+i) sin(-2+i) tan(i) ln(i^2)
и получаем ответ
Матрица квадратная 2х2.
Определитель такой матрицы равен
2.98466684-0.94876041i
Расчет определителя комплексной матрицы онлайн | 2012-10-22 07:57:36 | Варламов Дмитрий | Алгебра |
5 3 51
Онлайн расчет определителя или детерминанта квадратной матрицы (determinant complex matrix) в поле вещественных и комплексных чисел | определитель, матрица, комплексное, determinant, complex, matrixwww.abakbot.ru



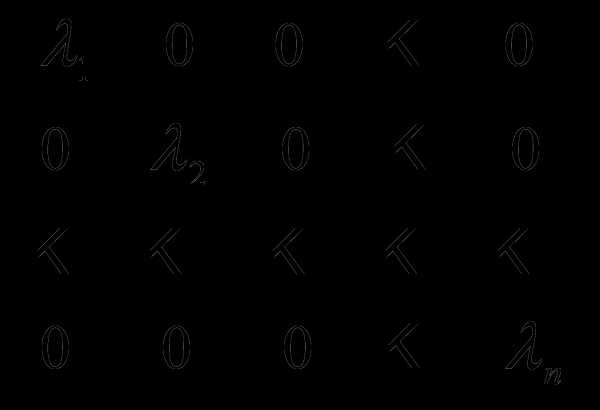 .
.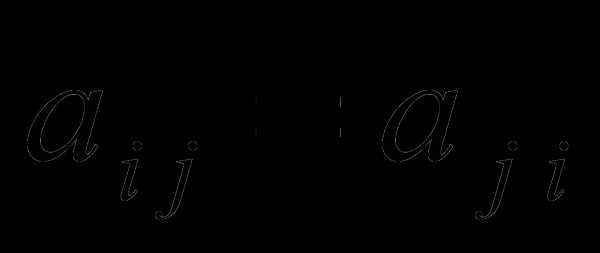 для всех
для всех 