Правило Крамера и метод Гаусса. Лекция
ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство.
Итак, рассмотрим систему 3-х уравнений
с тремя неизвестными. Умножим 1-ое
уравнение системы на алгебраическое
дополнение A11
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
.
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и .
Наконец несложно заметить, что
Таким образом, получаем равенство: .
Следовательно, .
Аналогично выводятся равенства и, откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений
Итак, х=1, у=2, z=3.
Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.
. Поэтому .
При
При p = 30 получаем систему уравнений которая не имеет решений.
При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решенийx=y, yR.
МЕТОД ГАУССА
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на , умножим наи сложим со вторым. Тогда будем иметь систему уравнений:
Отсюда из последнего
уравнения легко найти x
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.
Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
studfiles.net
5 Метод Гаусса и теорема Крамера
Лекция 5
ТЕМА: Построение решений систем линейных уравнений
Пусть задана система линейных уравнений
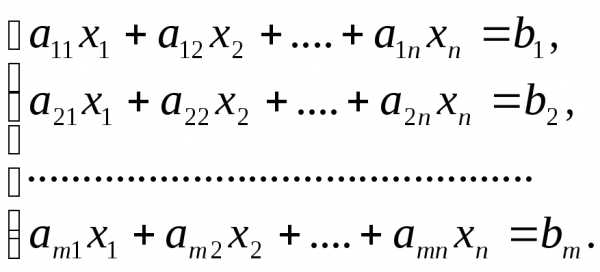 (4.1)
(4.1)
Если в заданной
системе
,
то берут любой отличный от нуля минор
основной матрицы порядка
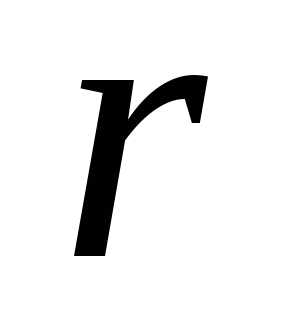 уравнений, коэффициенты которых входят
в этот базисный минор, а остальные
уравнения отбрасывают. Неизвестные,
которые входят в выбранный минор
объявляютглавными, а остальные неизвестные – свободными.
Новую систему переписывают так, что в
левых частях уравнений остаются только
члены, содержащие
уравнений, коэффициенты которых входят
в этот базисный минор, а остальные
уравнения отбрасывают. Неизвестные,
которые входят в выбранный минор
объявляютглавными, а остальные неизвестные – свободными.
Новую систему переписывают так, что в
левых частях уравнений остаются только
члены, содержащие 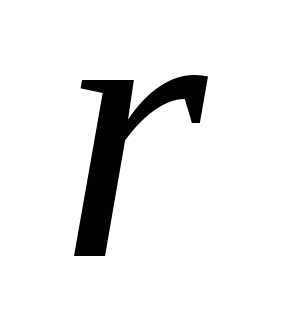 главных неизвестных, а остальные члены
уравнений, содержащие
главных неизвестных, а остальные члены
уравнений, содержащие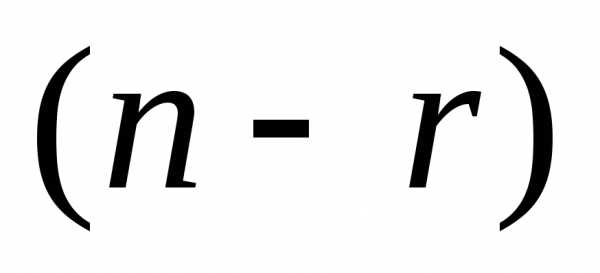
Полученные решения
новой системы с 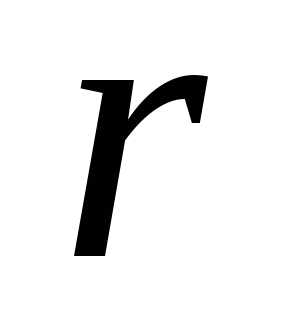 главными неизвестными называетсяобщим
решением системы (4.1).
главными неизвестными называетсяобщим
решением системы (4.1).
Придавая свободным неизвестным некоторые числовые значения, из общего решения находят соответствующие значения главных неизвестных и тем самым находят частное решение исходной системы уравнений (4.1).
Решить систему линейных уравнений:
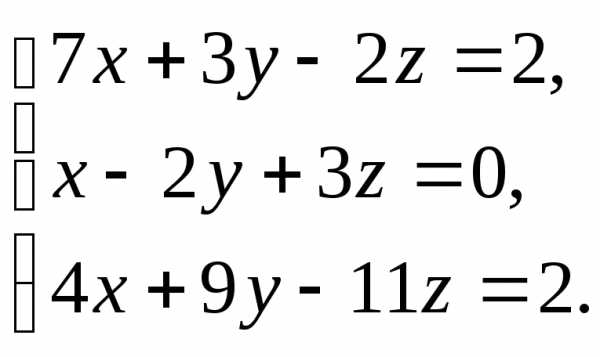 ,
найдем ранг матрицы методом «окаймляющих
миноров»:
,
найдем ранг матрицы методом «окаймляющих
миноров»:
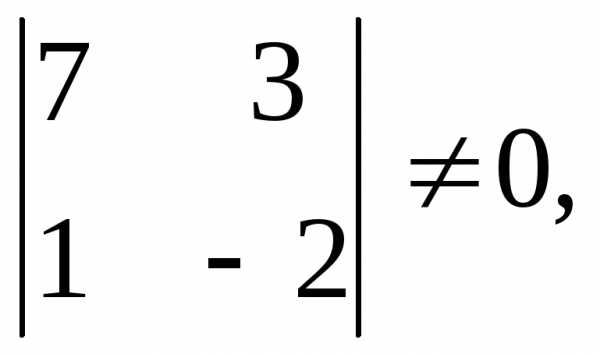
 Рассмотрим
миноры третьего порядка:
;
Рассмотрим
миноры третьего порядка:
;
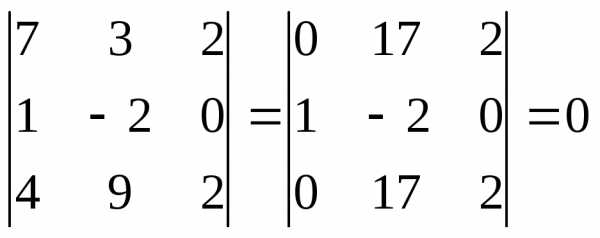
 система
совместна,
система
совместна,
 –
базисный минор;
–
базисный минор;
x, y – главные переменные,
z – свободная переменная.
 решим
систему по правилу Крамера.
решим
систему по правилу Крамера.
,
.
Общим решением
исходной системы является бесконечное
множество наборов 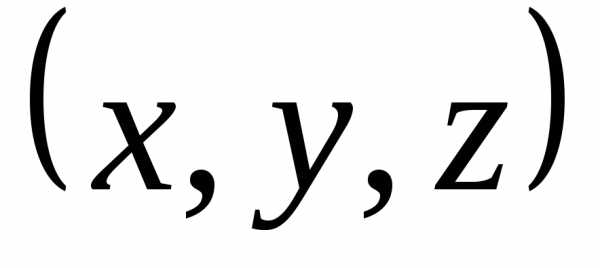 вида
вида
Частным решением
будет, например, числовой набор  ,
получающийся приt=o.
,
получающийся приt=o.
Метод Гаусса
(метод последовательного исключения переменных)
На практике чаще всего применяется метод Гаусса – построения решения систем линейных уравнений.
При исследовании
и решении систем линейных уравнений
производятся элементарные преобразования
строк расширенной матрицы 
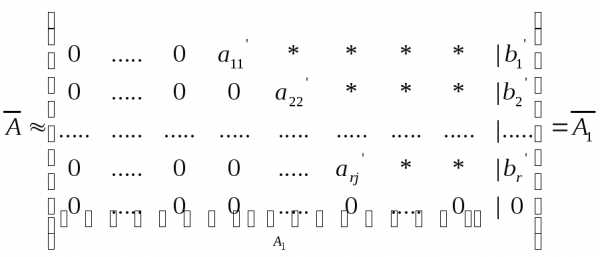 ,
(5.1).
,
(5.1).
Выберем в матрице  ненулевой минор порядка
ненулевой минор порядка ,
т.е. базисный минор (его можно выбрать
на пересечении первых
,
т.е. базисный минор (его можно выбрать
на пересечении первых строк и столбцов, с которых начинаются
ненулевые элементы строк). Будем считать,
что этот минор расположен в левом верхнем
углу матрицы
строк и столбцов, с которых начинаются
ненулевые элементы строк). Будем считать,
что этот минор расположен в левом верхнем
углу матрицы
Этот минор является верхнетреугольным и равен произведению .
Нулевые строки матрицы отбросим
(им соответствуют уравнения ).
(5.2)
(отбросили нулевые столбцы и перенумеровали переменные).
Все элементы базисного минора выше главной диагонали можно сделать равными нулю, а элементы главной диагонали равными единице. Таким образом, исходная система (4.1) приведена к эквивалентной системе:
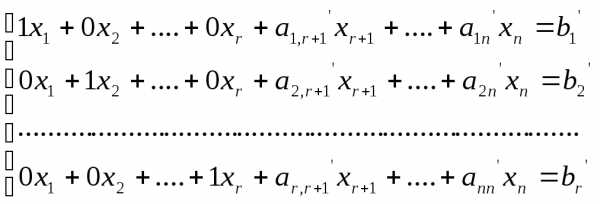 (5.3),
(5.3),
или к системе 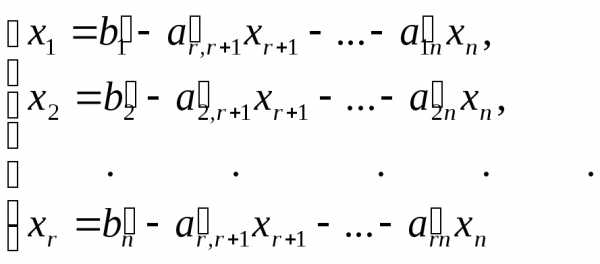 (5.4)
(5.4)
из которой видно,
что если 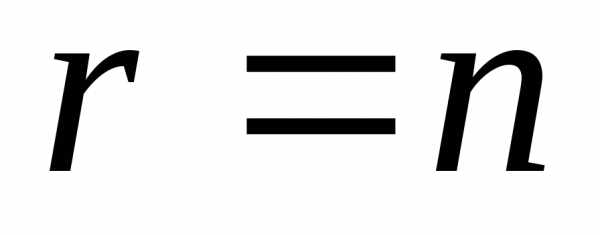 ,
то система (5.4) имеет единственное
решение:
,
то система (5.4) имеет единственное
решение:
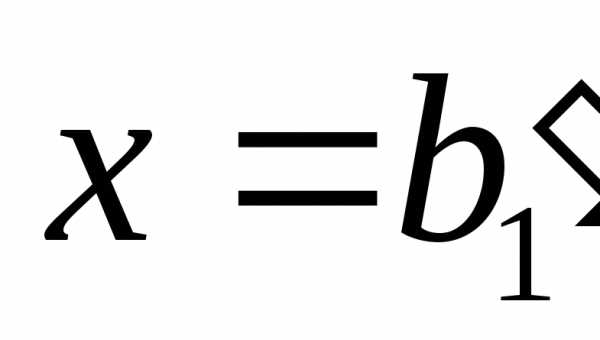 ,
…,
,
…, 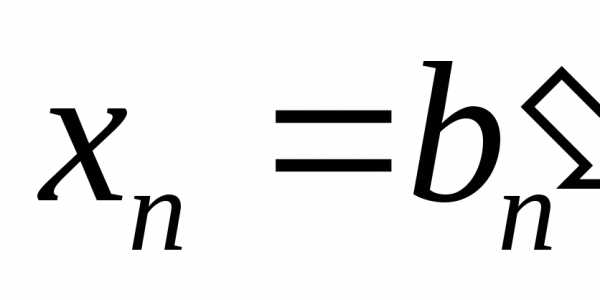 .
.
Если  ,
то переменные
,
то переменные – базисные,
– базисные,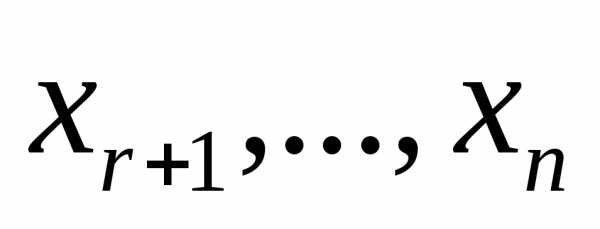 – свободные и придавая им произвольные
значения
– свободные и придавая им произвольные
значения ,
…,,
можно записать общее решение системы
в виде:
,
…,,
можно записать общее решение системы
в виде:
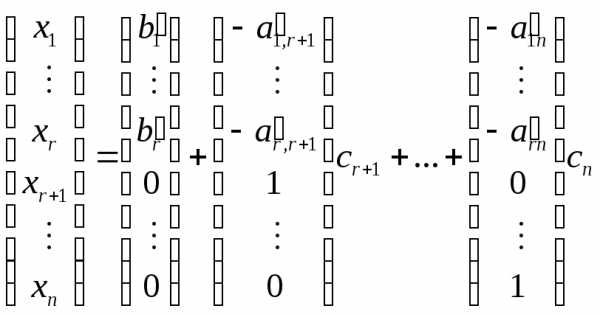 (5.5).
(5.5).
Итак, метод Гаусса состоит в следующем:
расширенную матрицу системы элементарными преобразованиями приводят к ступенчатому виду;
сравнивают ранги основной и расширенной матриц и делают вывод о совместности или несовместности системы;
в случае совместности системы в основной матрице выбирают базисный минор и дальнейшими элементарными преобразованиями строк добиваются того, чтобы в этом миноре все элементы вне главной диагонали стали равными нулю, а элементы главной диагонали стали равными единице;
выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, оставляя базисные неизвестные слева и переведя остальные слагаемые в правую часть;
если
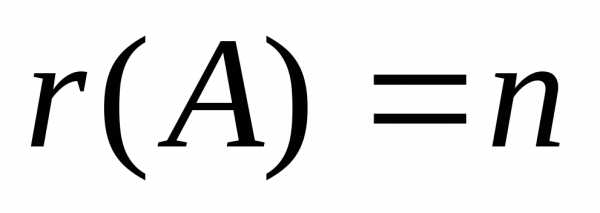 ,то
в правой части стоят только свободные
члены и получено единственное решение;
,то
в правой части стоят только свободные
члены и получено единственное решение;если
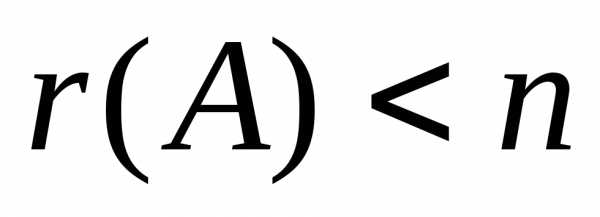 ,
то в правой части есть свободные
неизвестные. Придавая им произвольные
значения, получаем общее решение по
формуле (5.5).
,
то в правой части есть свободные
неизвестные. Придавая им произвольные
значения, получаем общее решение по
формуле (5.5).
Пример 5.2
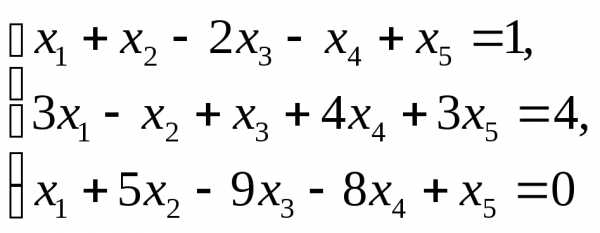
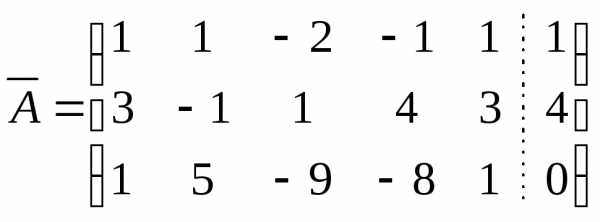

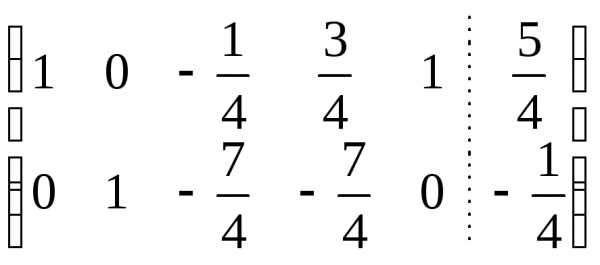

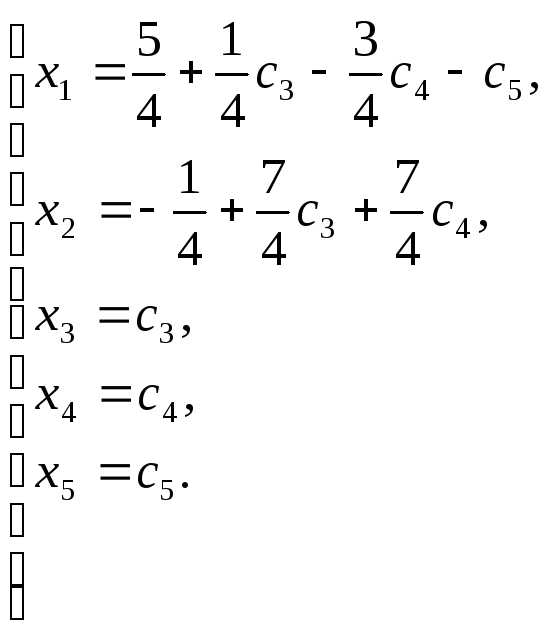 .
.
Теорема Крамера 5.1
Линейная система
(4.2) с квадратной матрицей  имеетрешение,
притом единственное,
тогда и только тогда, когда
.
имеетрешение,
притом единственное,
тогда и только тогда, когда
.
Доказательство

 Пусть система
(4.2) имеет и притом единственное решение.
Допустим, что
.
Это значит, что единственный минор
Пусть система
(4.2) имеет и притом единственное решение.
Допустим, что
.
Это значит, что единственный минор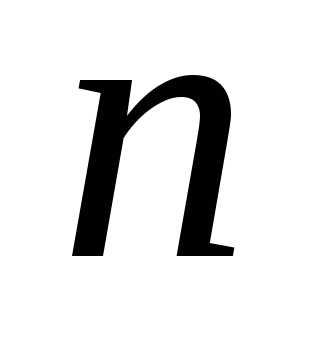 -го
порядка в основной матрице (который
является ее определителем), равен нулю,
и потому
-го
порядка в основной матрице (который
является ее определителем), равен нулю,
и потому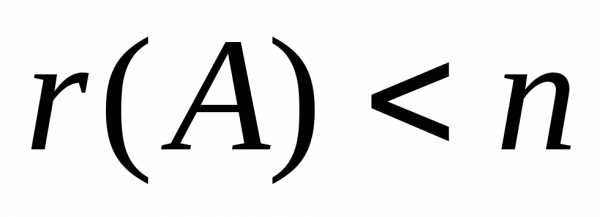 (т.е. ранг матрицы меньше числа неизвестных).
Но согласно следствию (2) теоремы (4.1) в
этом случае система имеет бесконечное
множество решений, что противоречит
условию. Значит допущенноеневерно, и потому.
(т.е. ранг матрицы меньше числа неизвестных).
Но согласно следствию (2) теоремы (4.1) в
этом случае система имеет бесконечное
множество решений, что противоречит
условию. Значит допущенноеневерно, и потому.
 Пусть
.
Тогда
Пусть
.
Тогда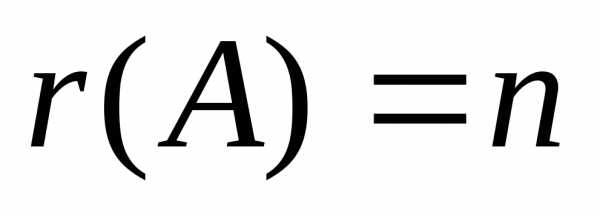 ,
а так как,
то и
,
а так как,
то и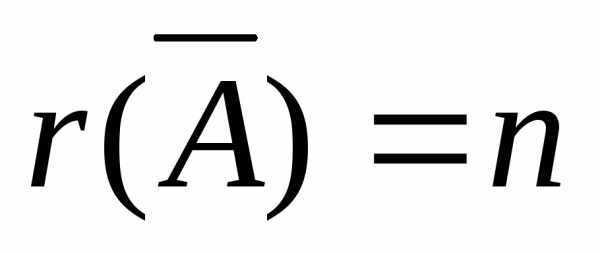 .
Но по теореме (4.1) это означает, что СЛУ
(4.2) имеет решение, а так как ранг основной
матрицы системы равен числу неизвестных,
то в силу следствия (1) теоремы (4.1) это
решение единственное.
.
Но по теореме (4.1) это означает, что СЛУ
(4.2) имеет решение, а так как ранг основной
матрицы системы равен числу неизвестных,
то в силу следствия (1) теоремы (4.1) это
решение единственное.
Нахождение обратной матрицы методом Гаусса
Напомним, что
матрица
называется обратной к ,
если.
Обратные матрицы существуют лишь для
невырожденных матриц, т.е..
Было показано, что,
где
,
если.
Обратные матрицы существуют лишь для
невырожденных матриц, т.е..
Было показано, что,
где – присоединенная матрица, полученная
из алгебраических дополнений, т. е.
вычислением определителей
– присоединенная матрица, полученная
из алгебраических дополнений, т. е.
вычислением определителей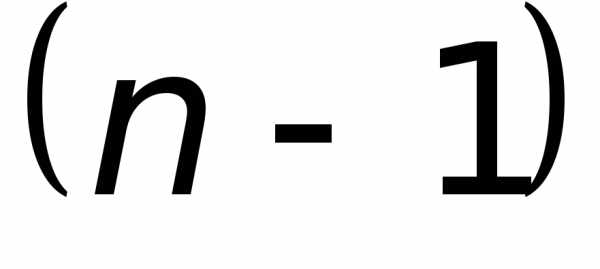 -ого
порядка. Вместе с тем, операция вычисления
определителя, запрограммированная в
ЭВМ, требует больших машинных ресурсов.
Поэтому более предпочтительным выглядит
вычисление обратной матрицы с помощью
метода Гаусса.
-ого
порядка. Вместе с тем, операция вычисления
определителя, запрограммированная в
ЭВМ, требует больших машинных ресурсов.
Поэтому более предпочтительным выглядит
вычисление обратной матрицы с помощью
метода Гаусса.
Для этого
воспользуемся определением обратной
матрицы 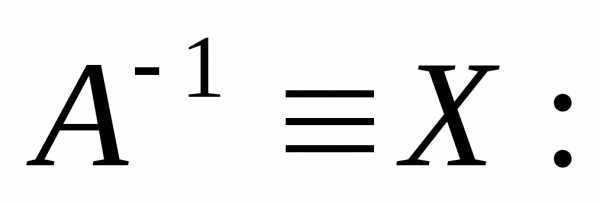



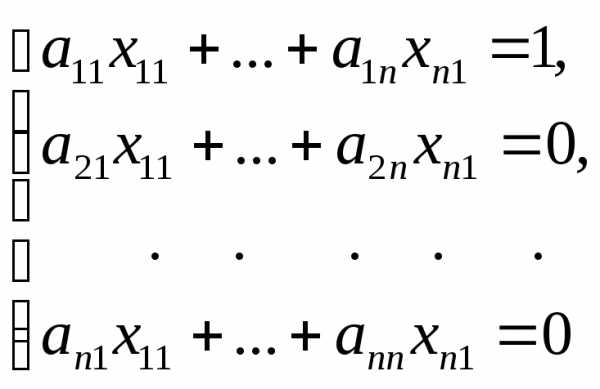
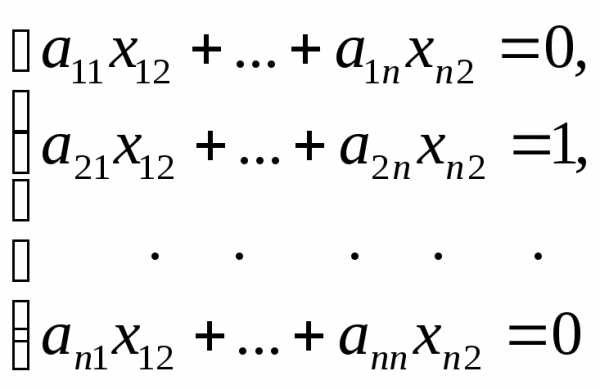
…
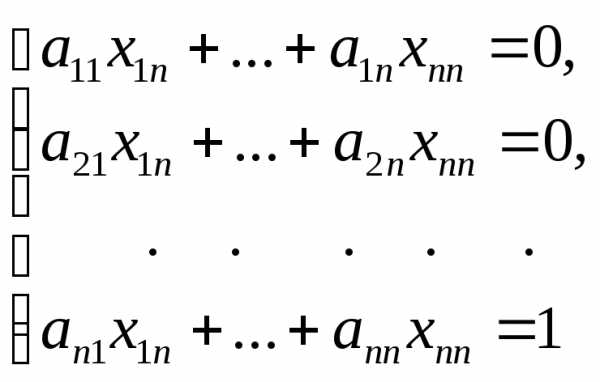 .
.
Таким образом,
матричное уравнение
эквивалентно системе линейных уравнений,
состоящей из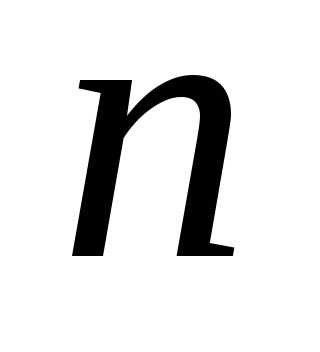 систем, каждая из которых является
системой из
систем, каждая из которых является
системой из  переменных и все они имеют одну и ту же
основную матрицу системы:
переменных и все они имеют одну и ту же
основную матрицу системы:
 ;
;  ;
…;
;
…;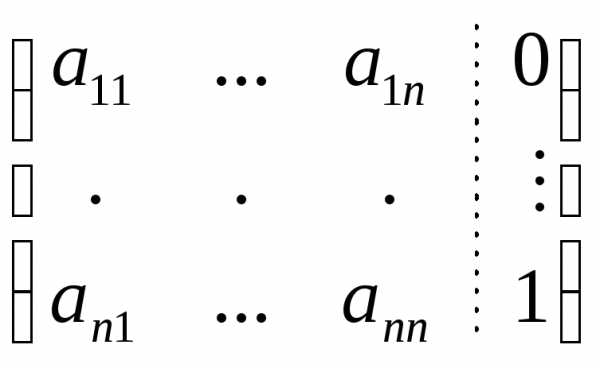
Все эти системы объединим в одной расширенной матрице:
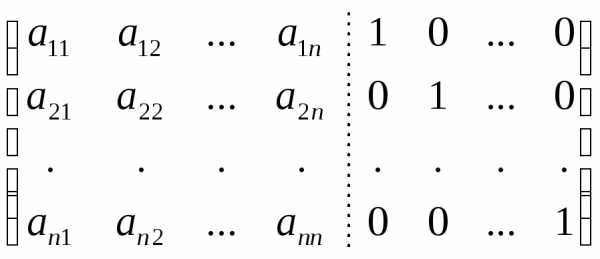 .
.
Приведение этой
матрицы к ступенчатому виду должно
обозначать приведение к ступенчатому
виду всех расширенных матриц подсистем.
Так как 
 она может быть приведена к следующему
виду:
она может быть приведена к следующему
виду:
 .
.
Решение каждой из подсистем имеет вид:
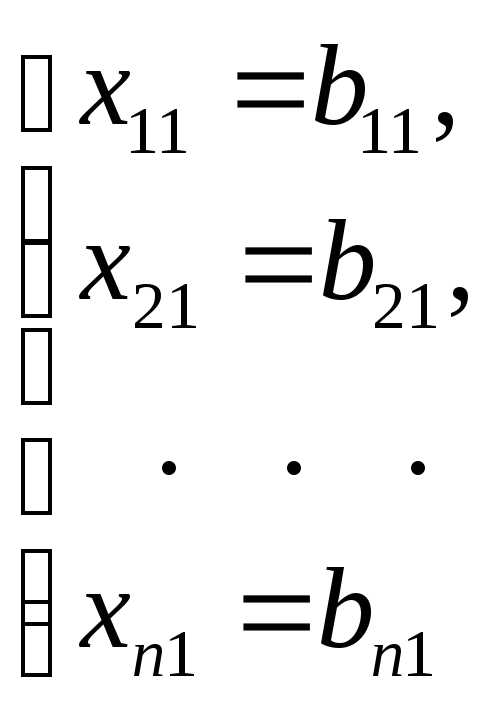 ,
,  ,
…,
,
…, 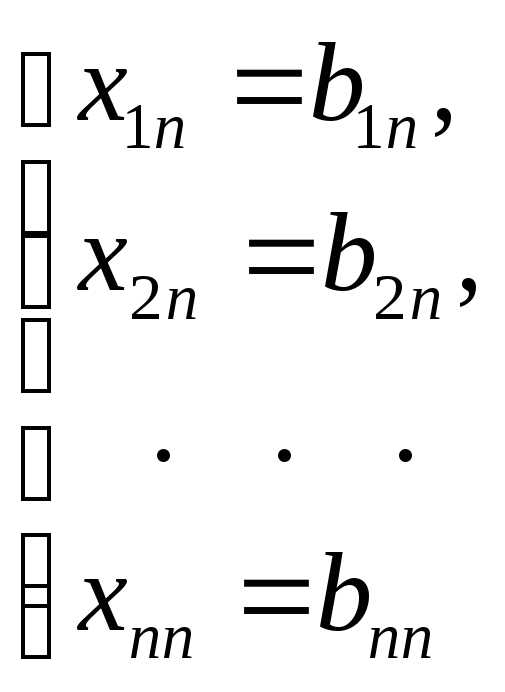

матрица 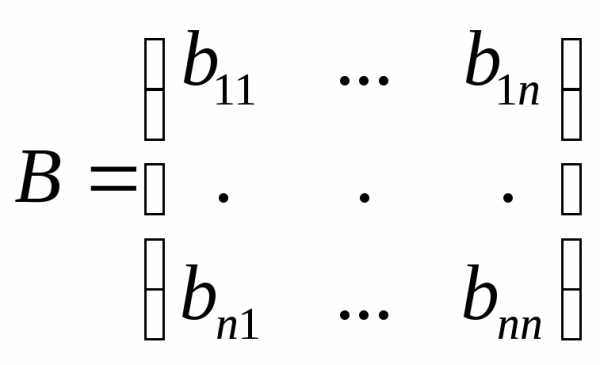 ,
стоящая за вертикальной чертой, является
обратной матрицей
,
стоящая за вертикальной чертой, является
обратной матрицей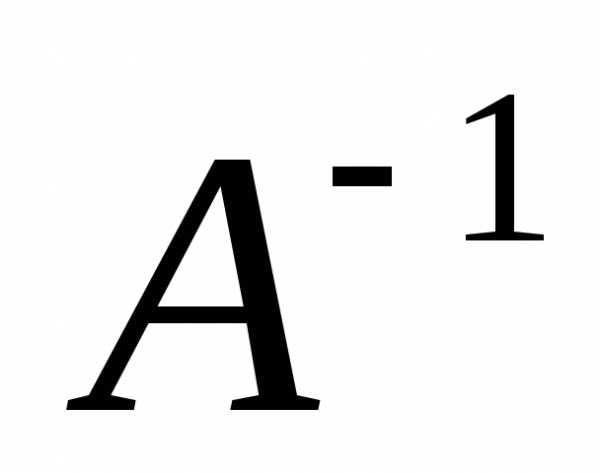 .
.
Пример 5.3
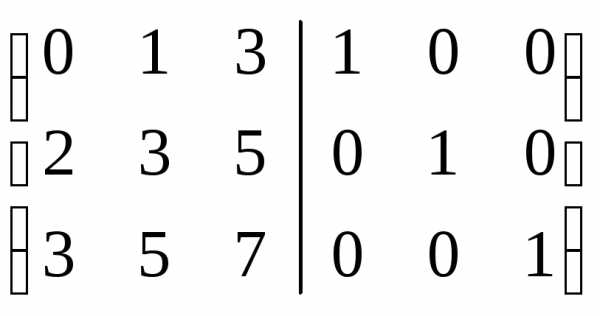
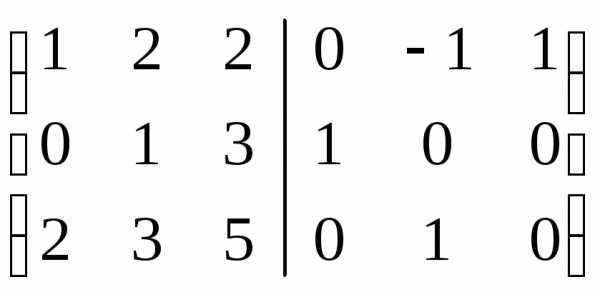

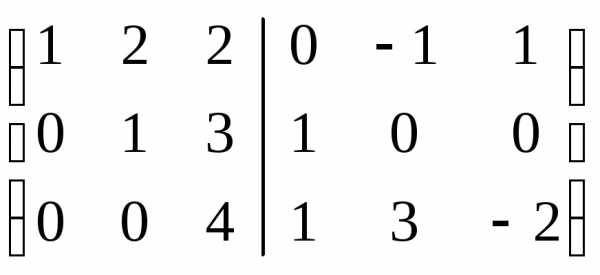
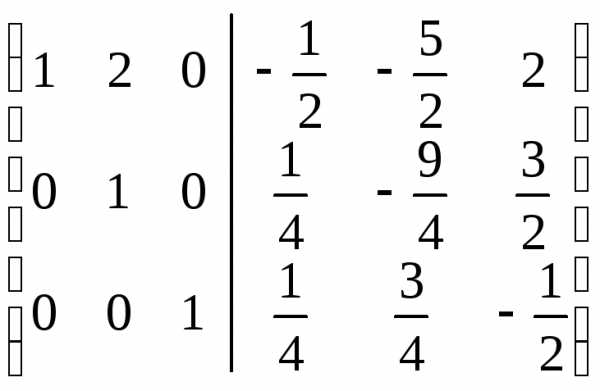
 .
.
7
studfiles.net
Тема 1. Методы решения систем линейных уравнений
нейной илинелинейной в зависимости от математической природы входящих в нее уравнений.
Решение линейного уравнения с одним неизвестным получается достаточно просто и здесь не рассматривается.
Концепция методов
Способы решения систем линейных уравнений делятся на две группы:
•точные (прямые) методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, метод Крамера, метод Гаусса и др.), т.е. при использовании таких методов за конечное число действий получаем точное решение системы. Точное реше-
ние получается в том случае, если вычисления проводить без округлений, т.е. понятие точное относится к алгоритму решения 1.
•итерационные (приближенные) методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов
(метод итерации, метод Зейделя и др.).
Вследствие неизбежных округлений результаты даже точных методов являются приближенными. При использовании итерационных методов, сверх того, добавляется погрешность метода.
Эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.
В общем виде линейная система уравнений записывается следующим образом:
a | 11 | x | 1 | + a | 12 | x | 2 | + a | 13 | x | 3 | + …+a | 1n | x | n | = b |
| |||||||||
|
|
|
|
|
|
|
|
|
| 1 |
| |||||||||||||||
a21x1+ a22x2+ a23x3 | + …+ a2n xn | = b2 | , | |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
………………………………………………………….. |
| |||||||||||||||||||||||||
a | n1 | x | 1 | + a | n2 | x | 2 | + a | n3 | x | 3 | + …+a | nn | x | n | = b |
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n |
| ||||||||||
или чаще в матричном виде: a x = B , гдеа – квадратная матрица размеромn xn,B иx – векторы размеромn (n – размерность системы).
Метод Гаусса
Рассмотрим систему n линейных алгебраических уравнений относительно
n неизвестныхх1,х2,…,хn: |
|
|
|
|
|
|
|
| |||||||||||
a | 11 | x | 1 | + a | 12 | x | 2 | + …+a | 1n | x | n | = b |
| ||||||
|
|
|
|
|
|
| 1 |
| |||||||||||
a21x1+ a22x2+ …+ a2nxn | = b2 | (1.1) | |||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
………………………………………… |
| ||||||||||||||||||
a | n1 | x | 1 | + a | n2 | x | 2 | + …+a | nn | x | n | = b |
| ||||||
|
|
|
|
|
|
|
|
|
|
| n |
| |||||||
Метод Гаусса, его еще называют методом Гауссовых исключений(методом последовательных исключений), состоит в том, что систему (1.1) приво-
1 Метод Крамера для ЭВМ не всегда удобен. Ведь чтобы вычислить определитель nго порядка нужно сделать(n-1)·n!вычислений. Тогда, при n=20 получаем 19·20!=4,5·1019 действий, что для ЭВМ с быстродействием в 1 млн. операций в секунду потребует 1,4·106 лет!
Метод Гаусса дает 2n3/3+0(n2) операций, что гораздо меньше и вполне приемлемо.
studfiles.net
ПРАВИЛО КРАМЕРА – Лекция – Правило Крамера и метод Гаусса
Лекция – Правило Крамера и метод Гаусса
скачать (76.5 kb.)
Доступные файлы (1):
содержание
1.doc
Реклама MarketGid:ПРАВИЛО КРАМЕРА
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
^ Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
.
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и .
Наконец несложно заметить, что
Таким образом, получаем равенство: .
Следовательно, .
Аналогично выводятся равенства и , откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений
Итак, х=1, у=2, z=3.
Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.
. Поэтому .
При
При p = 30 получаем систему уравнений которая не имеет решений.
При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y, yR.
^
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
перестановка строк или столбцов;
умножение строки на число, отличное от нуля;
прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.
Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
Скачать файл (76.5 kb.)
gendocs.ru
Лекция 8. МЕТОД ГАУССА РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Количество просмотров публикации Лекция 8. МЕТОД ГАУССА РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ – 148
- Матричное представление метода Гаусса
- Метод Гаусса с частичным выбором главного элемента
- Метод Гаусса с полным выбором главного элемента
- Матричное представление метода Гаусса
Для получения матричного представления метода Гаусса рассмотрим пример.
Размещено на реф.рф
Пусть крайне важно решить СЛАУ вида :
,
где . На первом шаге метода Гаусса производятся исключения в первом столбце матрицы СЛАУ при помощи первого уравнения, ᴛ.ᴇ. путем элементарных эквивалентных преобразований системы в первом столбце матрицы ниже элемента главной диагонали (ниже 10) делаются нули, а это означает, что переменная исключается из всех уравнений системы, кроме первого. Это достигается следующим образом: для получения 0 на месте (2,1) нужно первое уравнение (первую строку матрицы и элемент ) умножить на 0.3 и сложить со вторым уравнением; для получения 0 на месте (3,1) нужно первое уравнение умножить на -0.5 и сложить с третьим уравнением. В итоге получена эквивалентная СЛАУ . Величины 0.3 и -0.5 называются множителями. Запишем их рядом с уравнениями СЛАУ , для которых они использовались:
,
где . Элемент, стоящий на месте (2,2) в полученной матрице , имеет значение, малое по сравнению с другими элементами второго столбца матрицы . Ниже мы остановимся подробно на отрицательных последствиях такого явления для решения СЛАУ, а сейчас просто поменяем местами второе и третье уравнения последней системы, что выведет на место (2,2) элемент 2.5. Получим СЛАУ :
.
Здесь .
На втором шаге метода Гаусса исключим при помощи второго уравнения из третьего, обнулив элемент (3,2) второго столбца. Это достигается путем умножения второго уравнения на 0.04 и сложения с третьим. В итоге получаем эквивалентную СЛАУ :
,
где . Заметим, что проводить исключение во втором столбце (обнуление элемента (3,2)) при помощи первого уравнения было нецелесообразно, т.к. это могло сделать ненулевым элемент (3,1) и ʼʼиспортитьʼʼ результат, полученный на предыдущем шаге метода Гаусса (обнуление элементов первого столбца матрицы СЛАУ).
Система – это результат прямого хода метода Гаусса, результат проведенных исключений. В итоге прямого хода получается СЛАУ с верхней треугольной матрицей. Теперь решение треугольной системы осуществляется путем обратной подстановки (снизу вверх). Так последнее уравнение СЛАУ имеет вид: , откуда . Это полученное значение должна быть подставлено в предпоследнее уравнение:
.
Подставляя полученные и в первое уравнение , получим .
Решение рассмотренного примера должна быть записано в матричном виде. Обозначим
.
Заметим, что матрица отличается от единичной только первым столбцом, куда записаны множители, использованные при проведении исключений в первом столбце в прямом ходе метода Гаусса.
Непосредственно проверяем, что
.
Обозначим
, тогда .
Матрица отличается от единичной только вторым столбцом, куда записан множитель, использованный при проведении исключения во втором столбце в прямом ходе метода Гаусса. С использованием получаем:
.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, из исходной СЛАУ мы пришли к эквивалентной СЛАУ:
,
матрица которой является верхней треугольной, а вектор правой части .
Аналогичные соотношения справедливы и в общем случае для СЛАУ с матрицей размера . Обозначим , матрицу, полученную из единичной матрицы той же перестановкой строк, какая применялась к строкам матрицы СЛАУ на ом шаге исключения (исключения в ом столбце). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, , – это матрицы перестановок (матрица принято называть матрицей перестановок, в случае если в каждом ее столбце и в каждой ее строке в точности один элемент равен 1, а все остальные равны 0). Умножение произвольной матрицы на матрицу перестановок слева поменяет местами в матрице строки с соответствующими номерами, а умножение на матрицу перестановок справа поменяет в столбцы с теми же номерами.
Пусть , обозначает матрицу, полученную из единичной матрицы записью в поддиагональные позиции го столбца множителей, используемых на ом шаге исключения. Матрицы , называются матрицами исключения, являются нижними треугольными. Элементы го столбца вычисляются в соответствии с формулой
,
где – соответствующие элементы матрицы СЛАУ после 1 шага метода Гаусса (после исключения, проведенного в 1 столбце).
В принятых обозначениях матричный вид прямого хода метода Гаусса следующий:
.
Матрица итоговой СЛАУ – верхняя треугольная. Полученная СЛАУ легко решается путем обратной подстановки. В случае если предположить, что перестановки в ходе исключений не делались, то
.
Матрица как произведение нижних треугольных матриц является нижней треугольной. Исключения, проводимые на каждом шаге метода Гаусса, требуют пересчета элементов матрицы СЛАУ и вектора правой части. Для го шага исключения пересчет происходит в соответствии с формулой:
Здесь – элементы матрицы СЛАУ после 1 го шага исключения, – элементы матрицы СЛАУ после го шага исключения. В матричном виде эти действия просто эквивалентны умножению на матрицу исключения. Поскольку , при этом матрица невырожденная, а значит, обратимая, обратная к ней – нижняя треугольная, то , а это есть ничто иное, как треугольное разложение матрицы .
Диагональные элементы матрицы называются ведущими, или главными; ый ведущий элемент – ϶ᴛᴏ коэффициент при ом неизвестном в ом уравнении на ом шаге исключения Гаусса (исключений в ом столбце матрицы). В предыдущем примере ведущими элементами были 10, 2.5 и 6.2.
При вычислении множителей, а также в ходе обратной подстановки происходит деление на ведущие элементы, в связи с этим ведущие элементы обязательно должны быть отличны от 0. Более того, как показывает следующий пример, ведущие элементы не должны быть малыми по сравнению с другими элементами матрицы.
Пример. Решить СЛАУ :
.
Точное решение этой системы: . Здесь , вектор . Первый шаг метода Гаусса – исключения в первом столбце матрицы СЛАУ за счёт матрицы исключения, имеющей вид: . Тогда исходна система за счёт исключений преобразуется к эквивалентному виду:
. (10)
Для решения полученной СЛАУ с верхней треугольной матрицей применяем обратный ход метода Гаусса. Второе уравнение СЛАУ имеет вид: , откуда . Предположим, что в нашей вычислительной системе количество разрядов в мантиссе равно , тогда . В случае если полученное значение сравнить с точным значением решения данной СЛАУ, то качественно очевидно, что хорошо приближает . Продолжим обратный ход метода Гаусса подставляя в первое уравнение СЛАУ : , откуда , что ʼʼабсольтно не похожеʼʼ на точное значение решения данной СЛАУ.
Что произошло, где была допущена катастрофическая ошибка? Здесь не было накопления ошибок округления, вызываемого выполнением большого количества аоифметических операций. Матрица исходной СЛАУ далека от вырожденной: . Полученный результат имеет только одно объяснение: при проводимом исключение ведущий элемент 0.0001 имел значение, малое по сравнению с другими элементами матрицы, что привело в процессе исключения к колосальному росту коэффициентов второго уравнения: . Эти коэффициенты в 104 раз стали превосходить коэффициенты исходной задачи. Ошибка округления, произошедшая при вычислении и равная , является малой и приемлемой по отношению к большим коэффициентам уравнения , но совершенно неприемлемой с точки зрения уровня элементов исходной матрицы (ведь там есть элемент 0.0001, который меньше, чем абсолютная погрешность ). Таким образом крайне важно при проведении процесса исключения обеспечивать следующее условие: модули значений ведущих элементов не должны быть малыми по сравнению с модулями других элементов матрицы СЛАУ.
- Метод Гаусса с частичным выбором главного элемента
Для обеспечения устойчивости процесса исключения Гаусса крайне важно позаботиться о том, чтобы ведущие элементы имели значения, сравнимые со значениями остальных элементов матрицы СЛАУ. Это можно обеспечить различными способами. Рассмотрим один из них, который принято называть частичным выбором главного элемента.
Частичный выбор главного элемента может осуществляться по столбцу или по строке. Начнем с выбора по столбцу.
Рассматривается СЛАУ :
. (20)
Перед проведением исключений в первом столбце выберем в данном столбце максимальный по модулю элемент. Пусть данный элемент . Выведем данный элемент на место ведущего (на место (1,1)) для первого шага метода Гаусса. Для этого в СЛАУ (20) поменяем местами первое и ое уравнения. Получим СЛАУ:
(30)
Теперь проведем исключение в первом столбце матрицы СЛАУ (30). В результате исключения СЛАУ (30) примет вид:
(40)
В (40) выделены те коэффициенты, которые изменяются (подвергаются пересчету в соответствии с формулой (5)) в процессе исключения. Обозначим полученную систему :
.
Перед проведением исключений второго шага метода Гаусса выберем максимальный по модулю элемент второго столбца матрицы СЛАУ (40), исключая при выборе элемент стоящий в первой строке (область выбора обозначена в предыдущей формуле). Пусть данный элемент . Выводим его на место ведущего элемента для второго шага исключений – на место (2,2) путем перестановки второго и го уравнений (элемент не участвовал при выборе максимального по модулю элемента в силу того, что перестановка первой строки на место второй, в том случае, в случае если бы оказался максимальным по модулю, привела бы к порче структуры матрицы, полученной на первом шаге исключения: нулевой элемент первого столбца, стоящий во второй строке, стал бы ненулевым за счёт того, что на место (2,1) попал бы элемент ). В результате получим СЛАУ:
(50)
Теперь проведем исключение во втором столбце матрицы СЛАУ (50). В результате исключения СЛАУ (50) примет вид:
Перед проведением третьего шага исключения Гаусса (обнуления элементов третьего столбца матрицы СЛАУ ниже главной диагонали) выберем максимальный по модулю элемент третьего столбца среди элементов, исключающих элементы первой и второй строк. Выведем данный элемент на позицию (3,3) – позицию ведущего элемента для третьего шага. И т.д.
Частичный выбор главного элемента можно проводить по строке. В этом случае перед проведением исключений в ом столбце матрицы СЛАУ, которую обозначим , нужно выбрать максимальный по модулю элемент ой строки среди элементов (пусть это элемент ), вывести его на главную диагональ путем перестановки го и го столбцов, и произвести исключение, как описано выше. Необходимо учитывать и помнить, что перестановка столбцов в матрице СЛАУ повлечет за собой соответствующее изменение порядка неизвестных в векторе .
Частичный выбор главного элемента обеспечит сравнимость ведущих элементов на всех шагах исключения Гаусса с остальными элементами соответствующих столбцов (строк) матрицы СЛАУ, ᴛ.ᴇ. обеспечит устойчивость исключений Гаусса.
- Метод Гаусса с полным выбором главного элемента
Выбор главного элемента͵ предваряющий исключение на очередном шаге метода Гаусса, можно проводить, учитывая большее количество элементов матрицы СЛАУ. Так перед исключением в первом столбце выберем максимальный по модулю элемент во всей матрице системы . Пусть данный элемент – . Для того, чтобы вывести данный элемент на место (1,1), переставим в первую и ую строки (соответственно в векторе – первый и ый элементы), первый и ый столбец, после чего проведем исключения в первом столбце.
Перед исключением в ом столбце выберем максимальный по модулю элемент в матрице СЛАУ среди ее элементов , где . И т.д.
Очевидно, что полный выбор главного элемента обеспечит сравнимость ведущих элементов на всех шагах исключения Гаусса с остальными элементами всей матрицы СЛАУ, ᴛ.ᴇ. обеспечит устойчивость исключений Гаусса, причем, как вытекает из стратегии поиска главного элемента͵ погрешность метода Гаусса с полным выбором главного элемента будет меньше, чем при частичном выборе.
referatwork.ru
Лекции – матрицы, метод Гаусса
Лекции – матрицы, метод Гаусса
скачать (34.3 kb.)
Доступные файлы (1):
содержание
Матрицы.rtf
Реклама MarketGid:КОСТРОМСКОЙ ФИЛИАЛ ВОЕННОГО УНИВЕРСИТЕТА РХБ ЗАЩИТЫ
Кафедра «Автоматизации управления войсками»
Только для преподавателей
“Утверждаю”
Начальник кафедры № 9
полковник ЯКОВЛЕВ А.Б.
«____»______________ 2004 г.
доцент СМИРНОВА А.И.
“МАТРИЦЫ. МЕТОД ГАУССА”
ЛЕКЦИЯ № 2 / 3
Обсуждено на заседании кафедры № 9
«____»___________ 2003г.
Протокол № ___________
Кострома, 2003
Cодержание
Введение
Действия над матрицами.
Решение систем линейных уравнений методом Гаусса.
Заключение
Литература
В.Е. Шнейдер и др., Краткий курс высшей математики,том I, гл.2,§6, 7.
В.С. Щипачев, Высшая математика, гл. 10, § 1, 7.
ВВЕДЕНИЕ
На лекции рассматривается понятие матрицы, действия над над матрицами, а также метод Гаусса для решения систем линейных уравнений. Для частного случая, так называемых квадратных матриц, можно вычислять определители, понятие о которых рассмотрено на предыдущей лекции. Метод Гаусса является более общим, чем рассмотренный ранее метод Крамера решения линейных систем. Разбираемые на лекции вопросы используются в различных разделах математики и в прикладных вопросах.
1-ый учебный вопрос ^
ОПРЕДЕЛЕНИЕ 1. Прямоугольная таблица из m, n чисел, содержащая m – строк и n – столбцов, вида:
называется матрицей размера m ´ n
Числа, из которых составлена матрица, называются элементами матрицы.
Положение элемента аi j в матрице характеризуются двойным индексом:
первый i – номер строки;
второй j – номер столбца, на пересечении которых стоит элемент.
Сокращенно матрицы обозначают заглавными буквами: А, В, С…
Коротко можно записывать так:
ОПРЕДЕЛЕНИЕ 2. Матрица, у которой число строк равно числу столбцов, т.е. m = n , называется квадратной.
Число строк (столбцов) квадратной матрицы называется порядком матрицы.
ПРИМЕР.
ЗАМЕЧАНИЕ 1. Мы будем рассматривать матрицы, элементами которых являются числа. В математике и ее приложениях встречаются матрицы, элементами которых являются другие объекты, например, функции, векторы.
ЗАМЕЧАНИЕ 2. Матрица – специальное математическое понятие. С помощью матриц удобно записывать различные преобразования, линейные системы и т.д., поэтому матрицы часто встречаются в математической и технической литературе.
ОПРЕДЕЛЕНИЕ 3. Матрица размера 1 ´ n, состоящая из одной строки, называется матрицей – строкой.
Матрица размера т ´ 1, состоящая из одного столбца, называется матрицей – столбцом.
ОПРЕДЕЛЕНИЕ 4. Нулевой матрицей называют матрицу, все элементы которой равны нулю.
Рассмотрим квадратную матрицу порядка n:
побочная диагональ
главная диагональ
Диагональ квадратной матрицы, идущая от верхнего левого элемента таблицы к правому нижнему, называется главной диагональю матрицы (на главной диагонали стоят элементы вида а i i).
Диагональ, идущая от правого верхнего элемента к левому нижнему, называется побочной диагональю матрицы.
Рассмотрим некоторые частные виды квадратных матриц.
Квадратная матрица называется диагональной, если все элементы, не стоящие на главной диагонали, равны нулю.
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной. Обозначается:
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю:
верхняя нижняя
треугольная матрица треугольная матрица
Для квадратной матрицы вводится понятие: определитель матрицы. Это определитель, составленный из элементов матрицы. Обозначается:
Ясно, что определитель единичной матрицы равен 1: ½Е½ = 1
ЗАМЕЧАНИЕ. Неквадратная матрица определителя не имеет.
Если определитель квадратичной матрицы отличен от нуля, то матрица называется невырожденной, если определитель равен нулю, то матрица называется вырожденной.
ОПРЕДЕЛЕНИЕ 5. Матрица, полученная из данной заменой ее строк столбцами с теми же номерами, называется транспонированной к данной.
Матрицу, транспонированную к А, обозначают АТ.
ПРИМЕР.
2 3 3 2
ОПРЕДЕЛЕНИЕ. Две матрицы одного и того же размера называются равными, если равны все их соответственные элементы.
Рассмотрим действия над матрицами.
СЛОЖЕНИЕ МАТРИЦ.
Операция сложения вводится только для матриц одинакового размера.
^ i j) и В = (bi j) одинакового размера называется матрица С = (сi j) того же размера, элементы которой равны суммам соответствующих элементов слагаемых матриц, т.е. с i j = a i j + b i j
Обозначается сумма матриц А + В.
ПРИМЕР.
УМНОЖЕНИЕ МАТРИЦ НА ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО
ОПРЕДЕЛЕНИЕ 8. Чтобы умножить матрицу на число k, надо умножить на это число каждый элемент матрицы:
если А= (а i j ), то k · A= (k · a i j )
ПРИМЕР.
СВОЙСТВА СЛОЖЕНИЯ МАТРИЦ И УМНОЖЕНИЯ НА ЧИСЛО
1. Переместительное свойство: А + В = В + А
2. Сочетательное свойство: ( А + В ) + С = А + ( В + С )
3. Распределительное свойство: k · ( A + B ) = k A + k B, где k – число
УМНОЖЕНИЕ МАТРИЦ
Матрицу А назовем с о г л а с о в а н н о й с матрицей В , если число столбцов матрицы А равно числу строк матрицы ^ , т.е. для согласованных матриц матрица А имеет размер m ´ n , матрица В имеет размер n ´ k . Квадратные матрицы согласованы, если они одного порядка.
ОПРЕДЕЛЕНИЕ 9. Произведением матрицы А размера m ´ n на матрицу В размера n ´ k называется матрица С размера m ´ k, элемент которой аi j , расположенный в i –ой строке и j – ом столбце, равен сумме произведений элементов i – ой строки матрицы А на соответствующие элементы j – столбца матрицы В, т.е.
cij= a i 1 b 1 j + ai 2 b 2 j +……+ ainbnj
Обозначим: С = А · В.
Если то
Произведение В ´ А не имеет смысла, т.к. матрицы не согласованы.
ЗАМЕЧАНИЕ 1. Если А ´ В имеет смысл, то В ´ А может не иметь смысла.
ЗАМЕЧАНИЕ 2. Если имеет смысл А ´ В и В ´ А, то, вообще говоря
А ´ В ¹ В ´ А, т.е. умножение матриц не обладает переместительным законом.
ЗАМЕЧАНИЕ 3. Если А – квадратная матрица и Е – единичная матрица того же порядка, то А ´ Е = Е ´ А = А.
Отсюда следует, что единичная матрица при умножении играет роль единицы.
ПРИМЕРЫ. Найти , если можно, А ´ В и В ´ А.
Решение: Квадратные матрицы одного и того же второго порядка согласованы в томи другом порядке, поэтому А ´ В и В ´ А существуют.
2.
Решение: Матрицы А и В согласованы
Матрицы В и А не согласованы, поэтому В ´ А не имеет смысла.
Отметим, что в результате перемножения двух матриц получается матрица, содержащая столько строк, сколько их имеет матрица–множимое и столько столбцов, сколько их имеет матрица-множитель.
СВОЙСТВА УМНОЖЕНИЯ МАТРИЦ
Сочетательное свойство: А ´ ( В ´ С ) = (А ´ В ) ´С
Распределительное свойство: (А + В) ´ С = А ´ С + В ´С
Можно показать, что , если А и В – две квадратные матрицы одного порядка с определителями ½ А ½ и ½ В ½, то определитель матрицы С = А ´ В равен произведению определителей перемножаемых матриц, т.е.
½С½ = ½ А ½ ½ В ½
Отметим следующий любопытный факт. Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, т.е. произведение двух ненулевых матриц может оказаться равным нуль – матрице.
Действие “деление” для матриц не вводится. Для квадратных невырожденных матриц вводится обратная матрица. С понятием обратной матрицы можно познакомиться в рекомендуемой литературе.
2 – ой учебный вопрос ^
УРАВНЕНИЙ МЕТОДОМ ГАУССА
Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.
Система т линейных уравнений с п неизвестными имеет вид:
x1 , x2, …, xn – неизвестные.
ai j – коэффициенты при неизвестных.
bi – свободные члены (или правые части)
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.
Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.
Две совместные системы называются равносильными, если они имеют одно и то же множество решений.
К элементарным преобразованиям системы отнесем следующее:
перемена местами двух любых уравнений;
умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;
прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.
Элементарные преобразования переводят систему уравнений в равносильную ей.
Элементарные преобразования системы используются в методе Гаусса.
Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:
Дана система:
( 1 )
^
На первом шаге исключим неизвестное х1 из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а11. Получим уравнение:
( 2 )
где
Исключим х1 из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х1 (соответственно а21 и а31).
Система примет вид:
( 3 )
Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.
^
На втором шаге исключим неизвестное х2 из третьего уравнения системы (3). Пусть коэффициент . Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:
( 4 )
где
Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:
Предполагая, что находим
В результате преобразований система приняла вид:
(5)
Система вида (5) называется треугольной.
Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.
Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.
Для этого найденное значение х3 подставляют во второе уравнение системы (5) и находят х2. Затем х2 и х3 подставляют в первое уравнение и находят х1.
В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.
Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.
Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ¹ 0, то это означает, что система несовместна и решений не имеет.
В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.
Треугольная система имеет вид:
Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.
^ имеет вид:
Такая система имеет бесчисленное множество решений. Чтобы найти эти решения, во всех уравнениях системы члены с неизвестными хk+1, … , xk переносят в правую часть. Эти неизвестные называются свободными и придают им произвольные значения. Из полученной треугольной системы находим х1, … , xk, которые будут выражаться через свободные неизвестные. Подробнее об этом можно узнать в рекомендуемой литературе.
Рассмотренный метод Гаусса легко программируется на ЭВМ и является более экономичным (по числу действий), чем другие методы.
ЗАКЛЮЧЕНИЕ
Рассмотренные на лекции матрицы являются удобным инструментом для записи различных математических преобразований и широко используется в научно-технической литературе. Метод Гаусса позволяет решать любые линейные системы, он находит широкое применение и содержится в пакетах стандартных программ для ЭВМ.
доцент Смирнова А.И.
Скачать файл (34.3 kb.)
gendocs.ru
Лекция 5. Метод исключения Гаусса и Жордана-Гаусса.
Лекция 3. Особые виды матриц
Международный институт экономики и финансов (Государственный университет Высшая школа экономики) Лекции по линейной алгебре Владимир Черняк, 23 Лекция 3 Особые виды матриц Читать под музыку Tnit Ticrm
ПодробнееЛинейная алгебра Вариант 4
Линейная алгебра Вариант Задание. Систему уравнений привести к равносильной разрешенной системе, включив в набор разрешенных неизвестных,,. Записать общее решение, найти соответствующее базисное решение:
Подробнее0.5 setgray0 0.5 setgray1
5 setgray 5 setgray Лекция 3 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Основные определения Рассмотрим следующую систему m уравнений относительно n неизвестных в поле K: a x + a 2 + + a nx n b, a 2 x + a 2 2 + + a2 nx
ПодробнееТеорема Кронекера-Капелли
Установить совместность и решить систему линейных уравнений 5xx x xx 5x 0 x4x x 0 а) по формулам Крамера, б) матричным способом, в) методом Гаусса Совместность Совместность системы можно установить: а)
ПодробнееТема 1: Системы линейных уравнений
Тема 1: Системы линейных уравнений А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров
ПодробнееГлава 1. Начала линейной алгебры
Глава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
ПодробнееТема 1-5: Системы линейных уравнений
Тема 1-5: Системы линейных уравнений А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков
ПодробнееГлава 4. Матрицы. Лекция Основные понятия.
Лекция 0. Глава 4. Матрицы. В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений. 4.. Основные понятия.
ПодробнееПрактикум по линейной алгебре
Министерство образования и науки РФ Нижегородский государственный университет им. Н.И. Лобачевского В.К. Вильданов Практикум по линейной алгебре Учебно-методическое пособие Нижний Новгород Издательство
ПодробнееРАЗДЕЛ 1. Линейная алгебра.
-й семестр. РАЗДЕЛ. Линейная алгебра. Основные определения. Определение. Матрицей размера mn где m- число строк n- число столбцов называется таблица чисел расположенных в определенном порядке. Эти числа
ПодробнееТема 3: Определители
Тема 3: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало
ПодробнееТема 1-7: Определители
Тема 1-7: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр) Перестановки
ПодробнееМатематика (БкПл-100)
Математика (БкПл-100) М.П. Харламов 2011/2012 учебный год, 1-й семестр Лекция 3. Элементы линейной алгебры (матрицы, определители, системы линейных уравнений и формулы Крамера) 1 Тема 1: Матрицы 1.1. Понятие
Подробнее1. Линейные системы и матрицы
1. Линейные системы и матрицы 1. Дать определение умножения матриц. Коммутативна ли эта операция? Ответ пояснить. Произведение C матриц A и B определяется как m p m p A B ij = A ik B kj. Операция не коммутативна.
ПодробнееПримеры решений контрольных работ
Примеры решений контрольных работ Л.И. Терехина, И.И. Фикс 1 Контрольная работа 1 Линейная алгебра Решить матричное уравнение ( ( 3 1 2 1 X + 2 4 2 3 3 ( 1 0 = 3 2 3 Выполним вначале умножение матриц на
ПодробнееСистемы линейных уравнений
Министерство образования и науки РФ Уральский государственный экономический университет Ю. Б. Мельников Системы линейных уравнений Раздел электронного учебника для сопровождения лекции Изд. 4-е, испр.
ПодробнееИтерационные методы решения СЛАУ.
4 Итерационные методы решения СЛАУ Метод простых итераций При большом числе уравнений прямые методы решения СЛАУ (за исключением метода прогонки) становятся труднореализуемыми на ЭВМ прежде всего из-за
ПодробнееЛекция 10: Умножение матриц
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания В данной лекции вводится операция умножения матриц, изучаются
ПодробнееСИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ После изучения данной темы вы сможете: проводить численное решение задач линейной алгебры. К решению систем линейных уравнений сводятся многочисленные практические задачи, решение
ПодробнееЗадача 1 Вычислить определитель матрицы
Задача Вычислить определитель матрицы 4 4 A 4 4 Решение Для вычисления определителя приведем матрицу к треугольному виду. После этого определитель будет равен произведению элементов главной диагонали.
ПодробнееТема: Системы линейных уравнений
Линейная алгебра и аналитическая геометрия Тема: Системы линейных уравнений (Метод Гаусса. Системы линейных однородных уравнений) Лектор Рожкова С.В. 0 г. Метод Гаусса (метод исключения неизвестных) Две
ПодробнееСистемы линейных уравнений
Глава 1 Системы линейных уравнений 1.1 Определители второго и третьего порядка Определителем (детерминантом) 2-го порядка называется a 11 a 12 a 21 a 22 = a 11a 22 a 12 a 21. Определителем (детерминантом)
Подробнеесайты:
Федеральное агентство по образованию Уральский государственный экономический университет Ю. Б. Мельников Системы линейных уравнений Раздел электронного учебника для сопровождения лекции Изд. 3-е, испр.
ПодробнееМАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА
ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу
ПодробнееЛекция 7. . = [A 1,A 2,…,A n ], AX = B,
Лекция 7 СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Рассмотрим систему, состоящую из m линейных уравнений с n неизвестными: a x + a x + + a nx n = b, a x + a x + + a nx n = b, a m x + a m x + + a m n x n = b m Сокращенно
ПодробнееЛекция 5: Определители
Уральский федеральный университет, Институт математики и компьютерных наук, кафедра алгебры и дискретной математики Вступительные замечания В курсе аналитической геометрии уже говорилось об определителях
ПодробнееГлава 2. Системы линейных равнений
Глава истемы линейных равнений Метод Гаусса решения систем линейных алгебраических уравнений истема m линейных алгебраических уравнений (ЛАУ) с неизвестными имеет вид a a a b a a a b () am am am bm Здесь
ПодробнееМАТРИЦЫ И ОТОБРАЖЕНИЯ
ЛЕКЦИЯ 7 РАНГ МАТРИЦЫ КРИТЕРИЙ СОВМЕСТНОСТИ МАТРИЦЫ И ОТОБРАЖЕНИЯ 1 РАНГ МАТРИЦЫ В векторном пространстве R m столбцов высоты m рассмотрим n векторов A (j) = [a 1j, a 2j,…, a mj ], j = 1, 2,…, n, и
ПодробнееПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
ПодробнееТЕКСТЫ ЛЕКЦИЙ по учебной дисциплине
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра высшей математики Допущены к проведению занятий в – учгоду Заведующий кафедрой профессор АП Господариков
Подробнееdocplayer.ru

