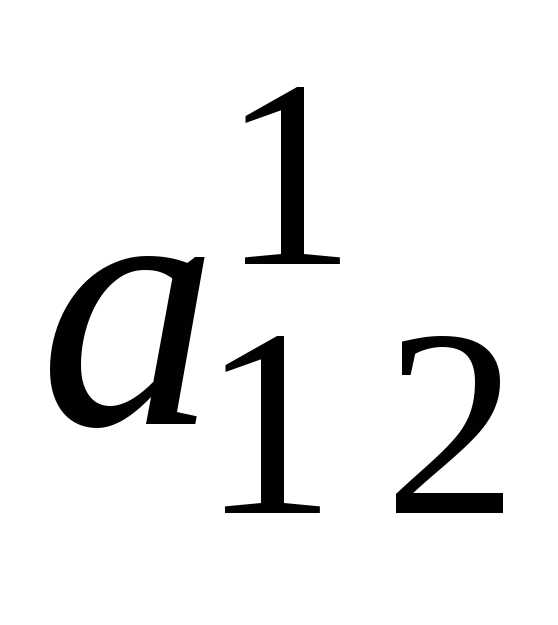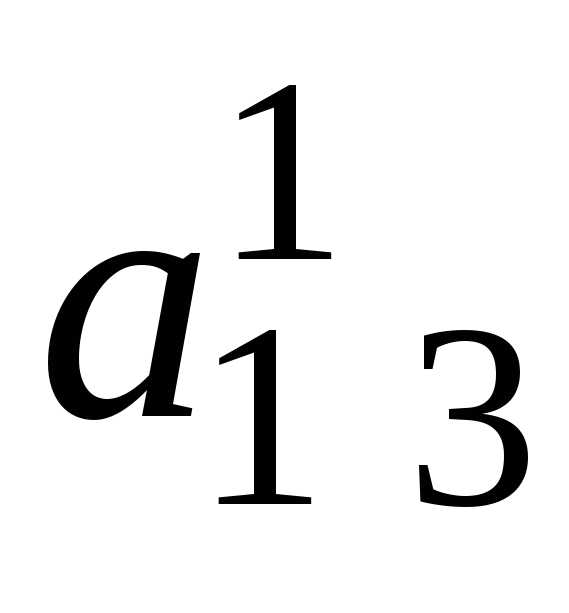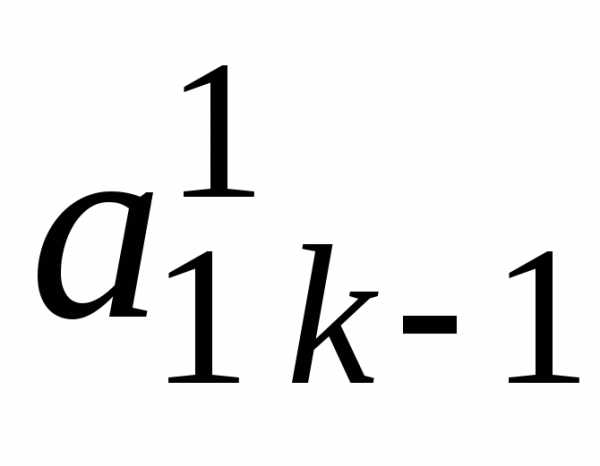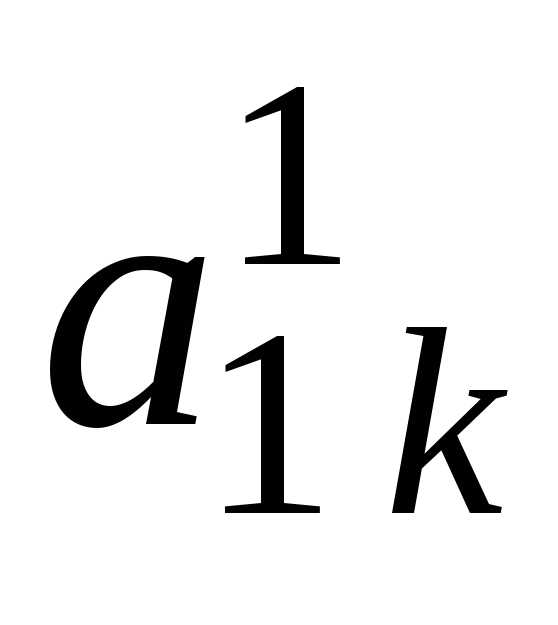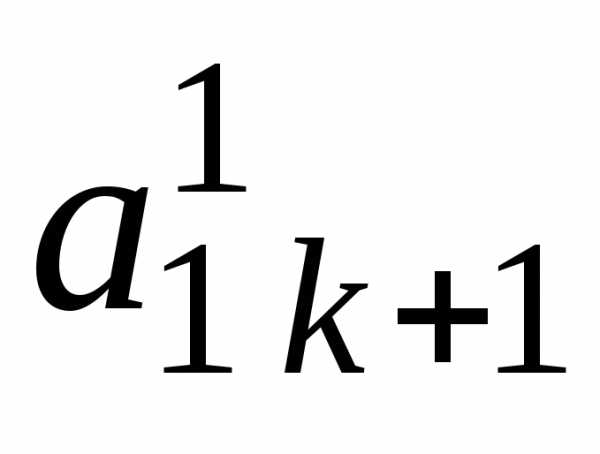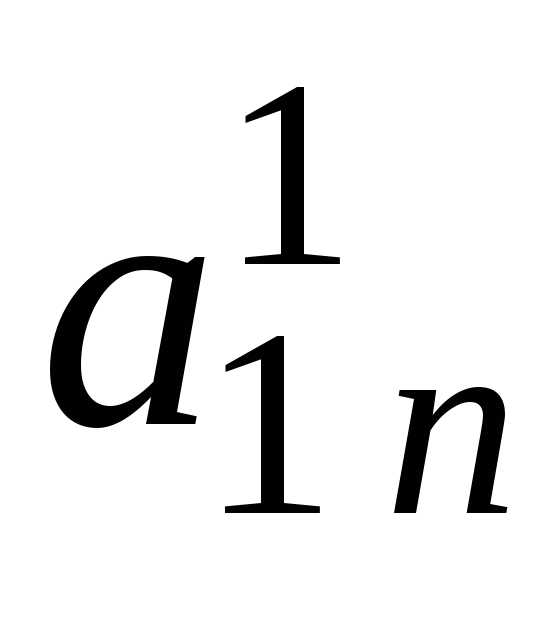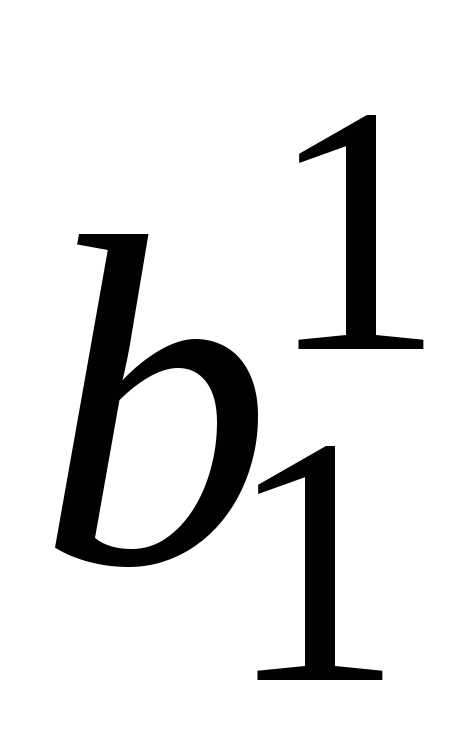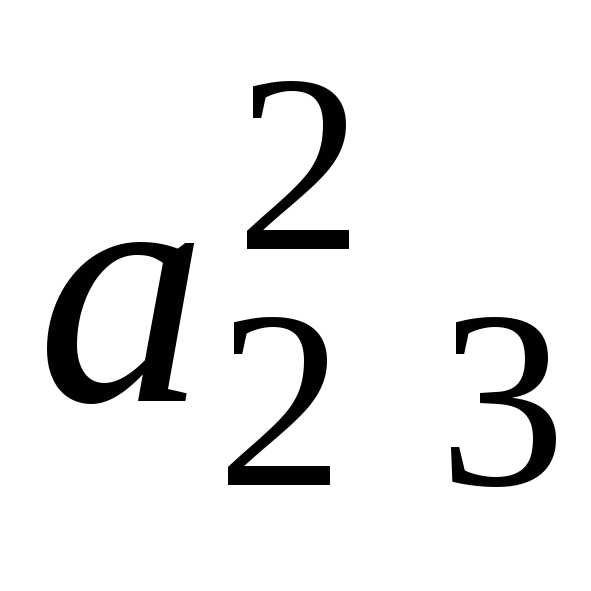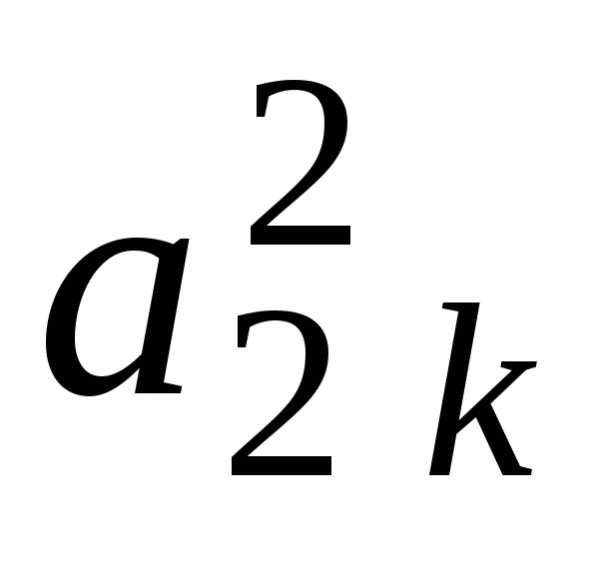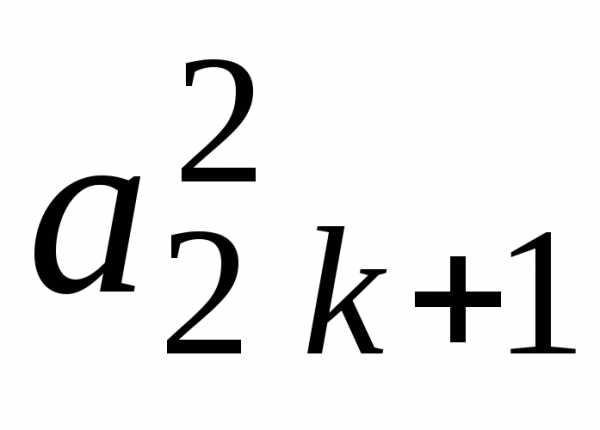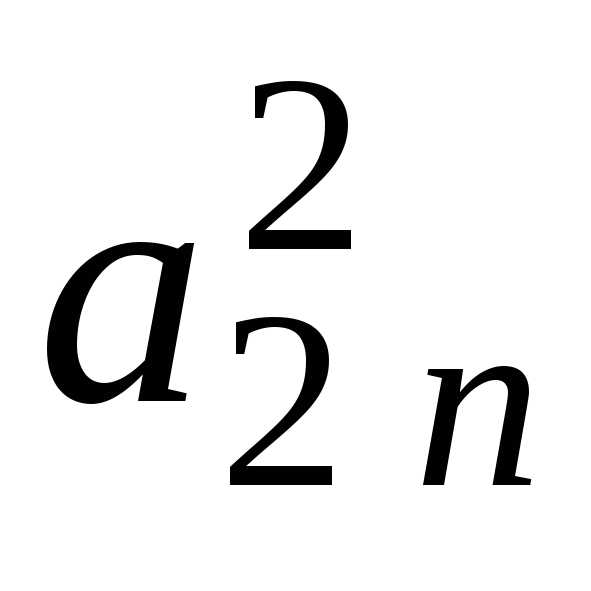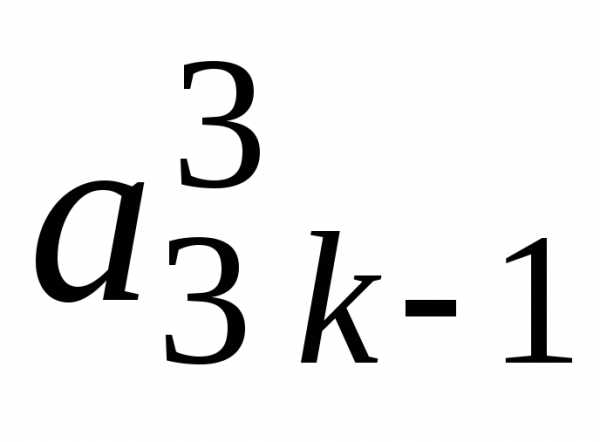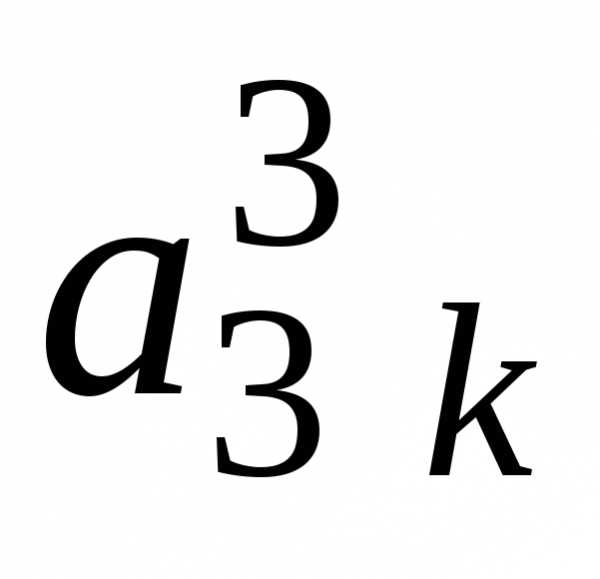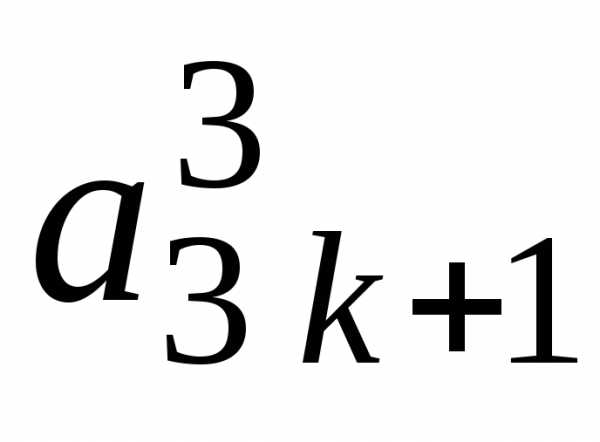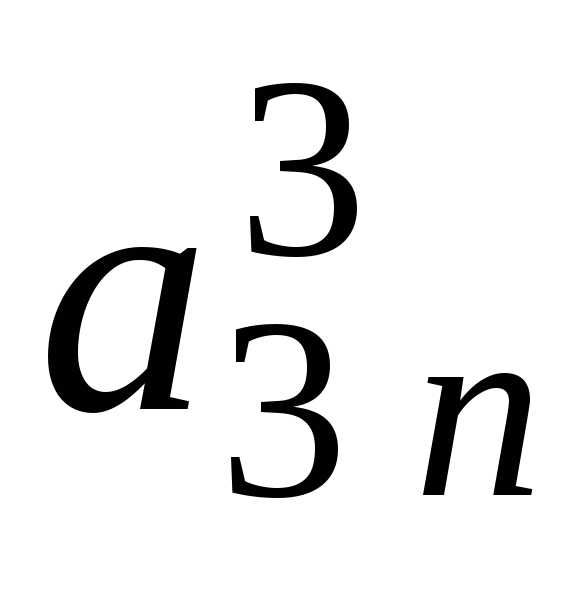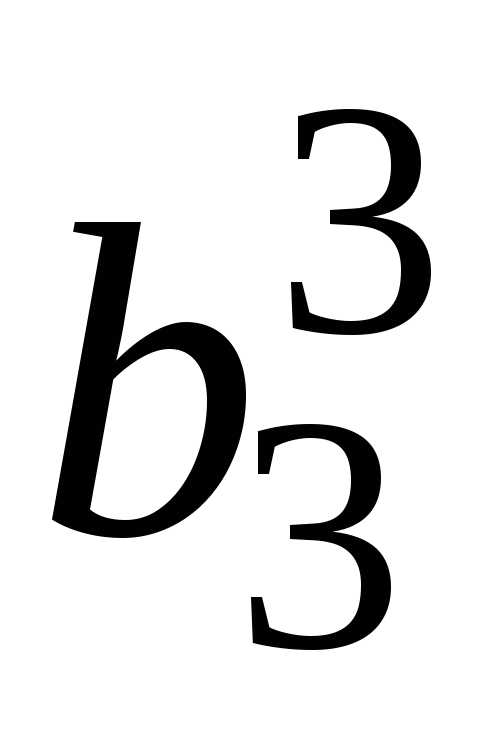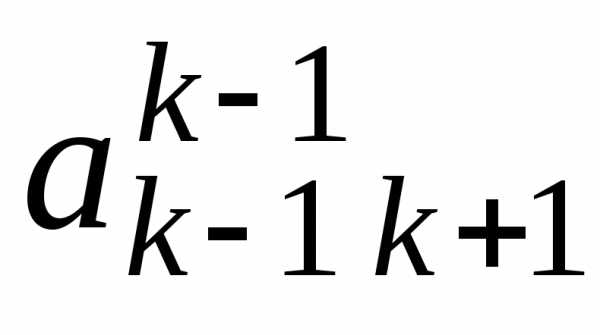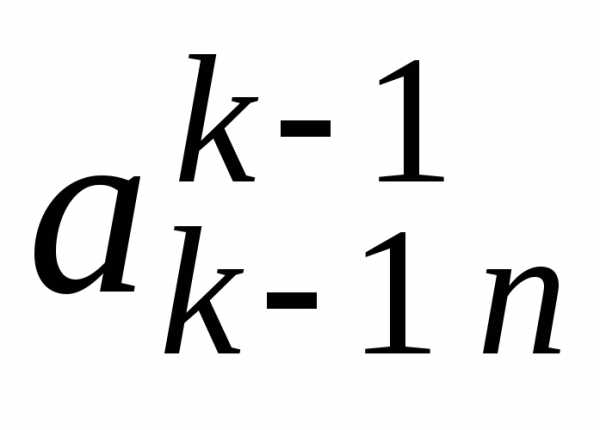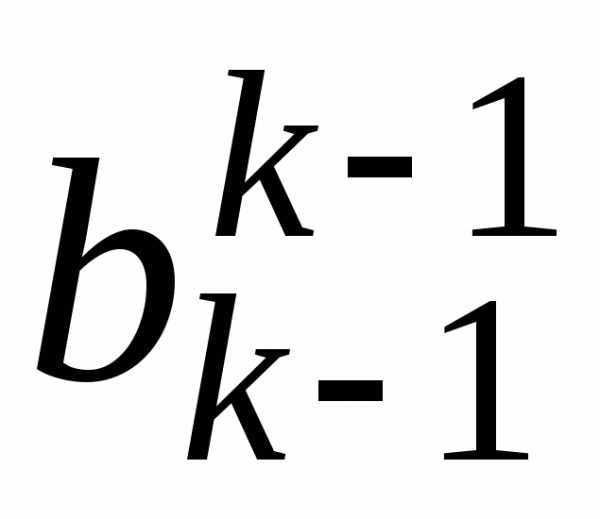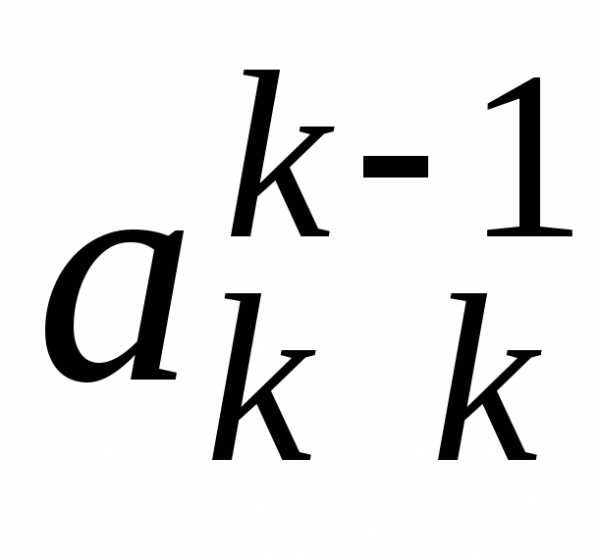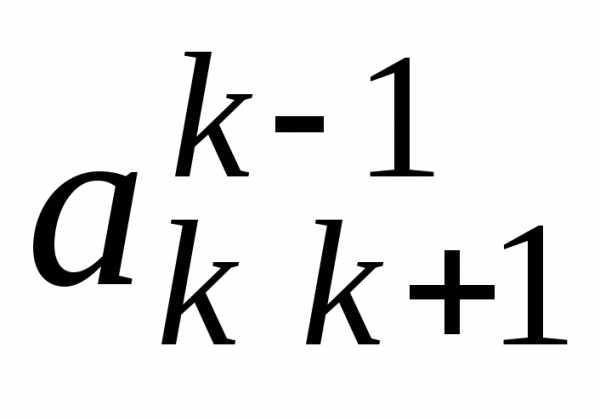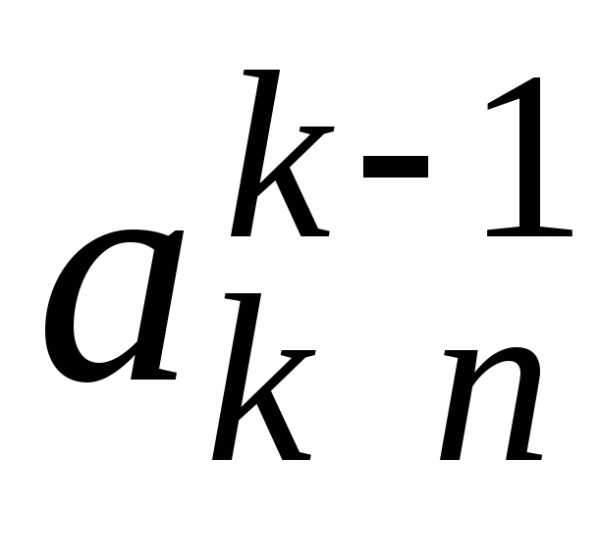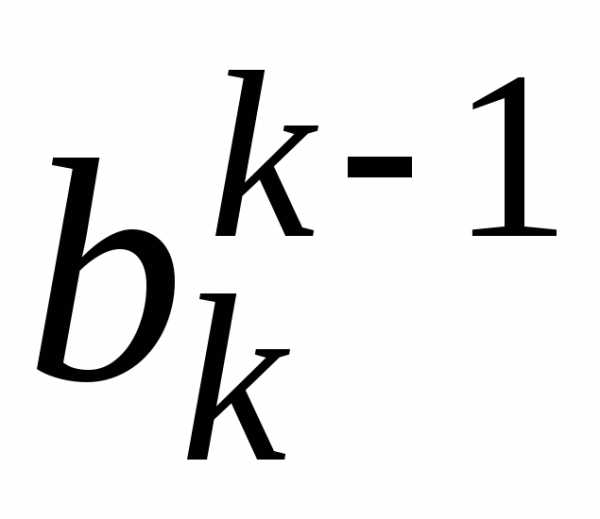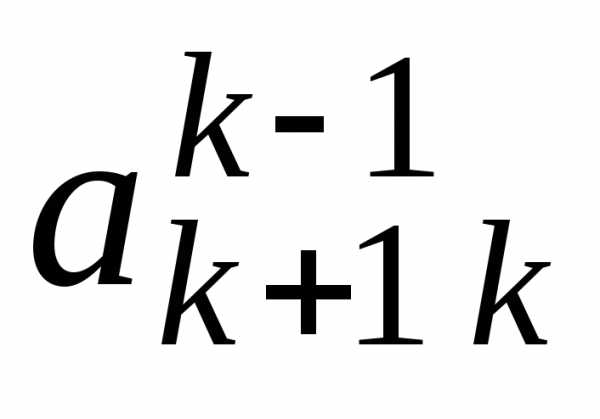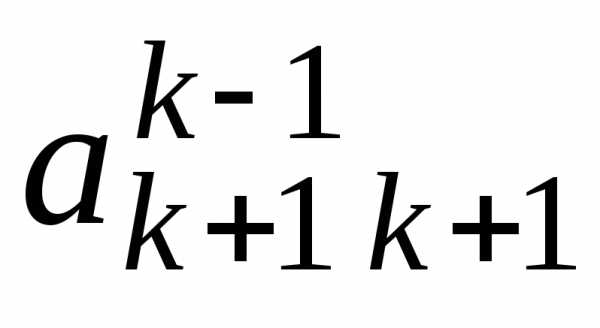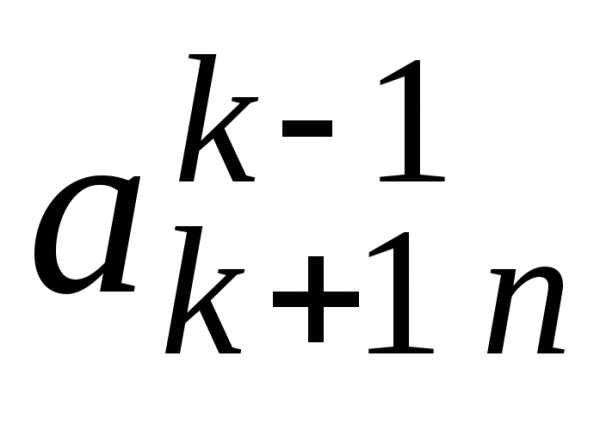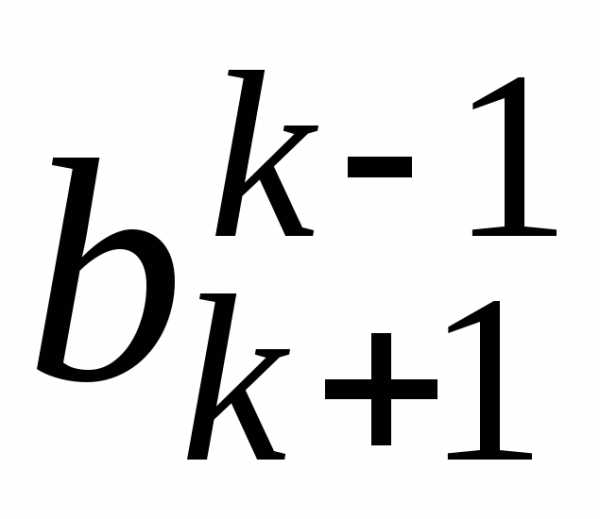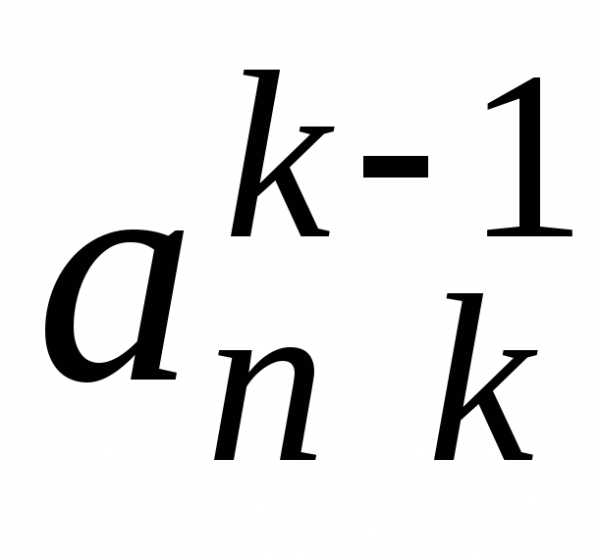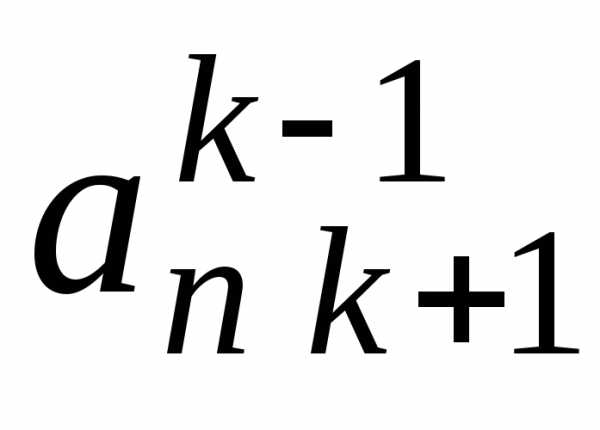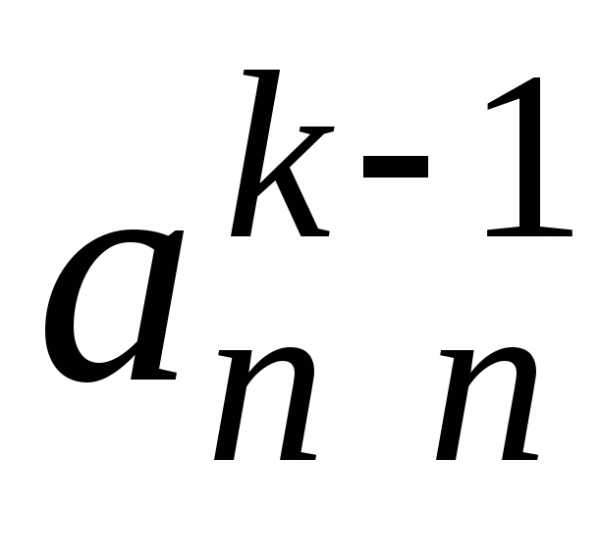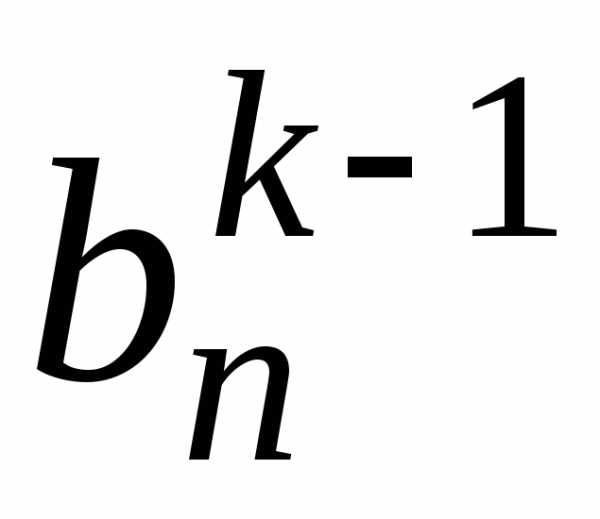Метод Гаусса
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы – матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) строки матрицы можно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует
4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) к строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» – с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х1, стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»).
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по апробированной методике:
2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг. Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x3 = 1
x2 = 3
x1 + x2 – x3 = 1, следовательно x1 + 3 – 1 = 1, x1 = –1
Ответ: x1 = –1, x2 = 3, x3
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х3 = 0,96 или приблизительно 1.
х2 = 3 и х1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
3.2. Метод Гаусса Постановка задачи решения линейной системы
Рассмотрим систему линейных алгебраических уравнений с постоянными коэффициентами (СЛАУ)
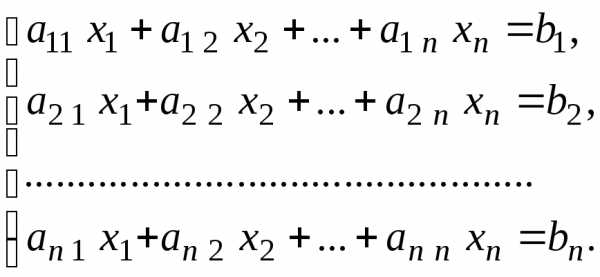(3.2.1)
Введем обозначения для матрицы системы, столбца правых частей и столбца решений
,
,.
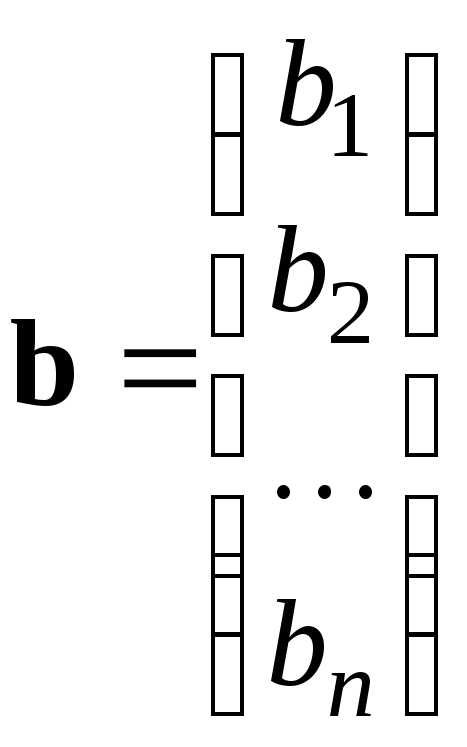Помимо введенной матрицы А, введем расширенную матрицу системы, получающуюся из матрицы А добавлением столбца правых частей
Матрица системы А и столбец правых частей b считаются заданными, а столбец x
.
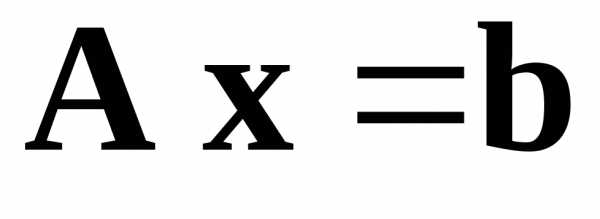(3.2.2)
Из общей теории линейных систем известно, что если
, (3.2.3)
то система (3.1.1) имеет единственное решение. Мы в дальнейшем будем рассматривать только такие линейные системы.
Метод Гаусса с выбором главных элементов в столбцах Прямой ход метода Гаусса с выбором главных элементов в столбцах
Алгоритм решения линейной системы методом Гаусса состоит из прямого и обратного хода. Прямой ход метода Гаусса состоит из однотипных шагов, преобразующих расширенную матрицу системы (3.1.1). На k-м шаге прямого хода с помощью элементарных преобразований в k-м столбце устанавливается единица на главной диагонали матрицы системы и нули под главной диагональю. К элементарным преобразованиям относятся преобразования расширенной матрицы:
1) перестановка строк;
2) деление строки на число, отличное от нуля;
3) вычитание из одной строки расширенной матрицы другой строки, умноженной на некоторое число, отличное от нуля (при этом вторая строка не меняется).
Применение элементарных преобразований к расширенной матрице системы не изменяет решения системы. Поэтому линейная система, получаемая в результате элементарных преобразований над ее расширенной матрицей, должна быть равносильна исходной системе.
Прямой ход метода Гаусса имеет (n-1) шаг. В результате прямого хода метода Гаусса матрица системы становится верхней треугольной матрицей (под главной диагональю стоят нули, а на главной диагонали стоят единицы везде, за исключением последней строки).
Полученная в результате прямого хода система уравнений решается последовательно снизу вверх. В этом и состоит обратный ход метода Гаусса. Рассмотрим описанный в общих чертах алгоритм метода Гаусса подробнее и получим расчетные формулы.
Прямой
ход метода Гаусса с выбором главного
элемента в столбцах представляет собой
цикл, выполняемый последовательно для
.
Для того чтобы установить, что необходимо
делать наk-м
шаге этого цикла, запишем расширенную
матрицу системы, которая получается
после (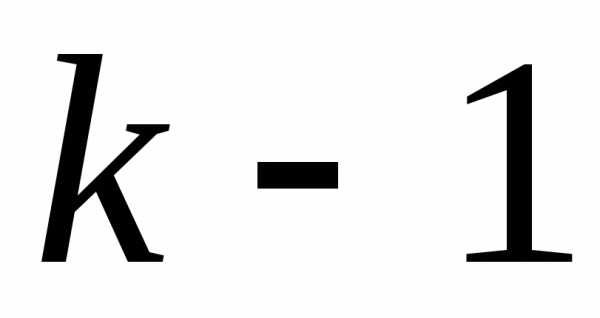
)
шага прямого хода (см. табл. 3.1):
Таблица 3.1
|
i j |
1 |
2 |
3 |
… |
k-1 |
k |
k+1 |
… |
n | |
|
1 |
1 |
|
|
… |
|
|
|
… |
|
|
|
2 |
0 |
1 |
|
… |
|
|
… |
|
| |
|
3 |
0 |
0 |
1 |
… |
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
K-1 |
0 |
0 |
0 |
… |
1 |
|
… |
|
| |
|
k |
0 |
0 |
0 |
… |
0 |
|
|
… |
|
|
|
k+1 |
0 |
0 |
0 |
… |
0 |
|
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
n |
0 |
0 |
0 |
… |
0 |
|
|
… |
|
|
Верхние
индексы элементов расширенной матрицы
указывают на номер шага прямого хода,
в результате которого получено значение
этого элемента. На k-м
шаге преобразуются строки матрицы с
номерами от k
до n.
В результате преобразований на месте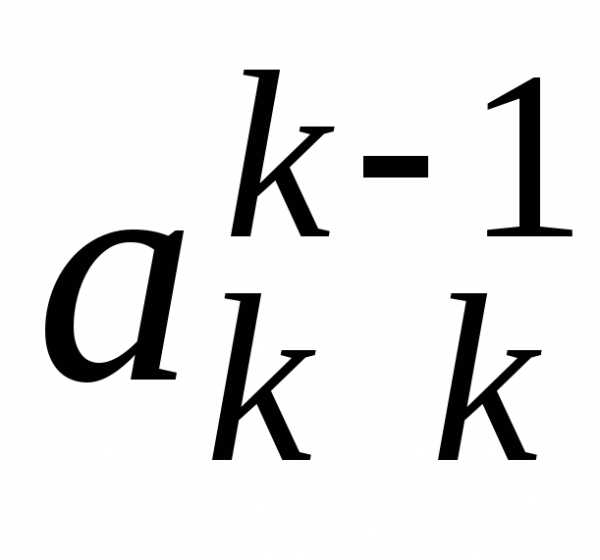
должна быть установлена 1, а на месте
,
…,
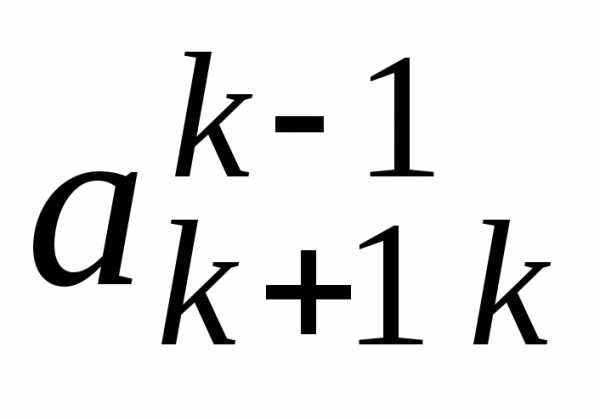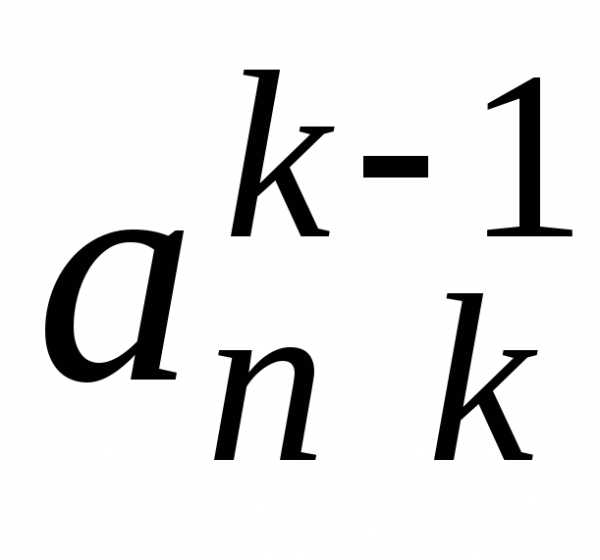должны быть установлены нули. При этом
столбцы с 1-го до (k-1)-й
не должны измениться.
studfiles.net
Прямой ход – метод – гаусс
Прямой ход – метод – гаусс
Cтраница 1
Прямой ход метода Гаусса состоит из L этапов. [1]
На этом заканчивается прямой ход метода Гаусса. [2]
На атом заканчивается прямой ход метода Гаусса. Эту часть процесса вычислений называют обратным ходом метода Гаусса. При этом следует отметить следующее. [3]
Отметим, что прямой ход метода Гаусса требует я3 / 34 – 0 ( / г2) операций сложения, столько же операций умножения и п2 / 2 0 () операций деления, обратный ход требует п2 / 2 0 ( п) операций сложения, столько же операций умножения и п операций деления. [4]
На этом заканчивается прямой ход метода Гаусса. [5]
Операции по выполнению прямого хода метода Гаусса в соответствии с теоремами линейной алгебры не изменяют величины определителя. Очевидно, что определитель треугольной матрицы равен произведению ее диагональных элементов. [6]
Решение (3.5) называется прямым ходом метода Гаусса, решение (3.4) – обратным ходом метода Гаусса. [7]
Нетрудно проверить, что реализация прямого хода метода Гаусса требует N – 2т3 / 3 арифметических операций, а обратного – N – т2 арифметических операций. [8]
Разложение А – ВС соответствует прямому ходу метода Гаусса, а решение системы ( 6) – ( 7) – обратному ходу. Заметим, что в алгоритме, изложенном в § 1, разложение А ВС и решение системы ( 6) проводится одновременно. [9]
Начиная с блока 2, осуществляется прямой ход метода Гаусса, в котором преобразуется п – 1 строка матрицы коэффициентов. Основные преобразования прямого хода выполняются в блоке 4 алгоритма. Блоки 5 и 6 определяют обратный ход метода Гаусса. [10]
Получение системы ( 8) составляет прямой ход метода Гаусса. Поскольку матрица системы имеет треугольный; вид, можно последовательно, начиная с хт, найти все неизвестные. [11]
Перейдем теперь к случаю, когда в прямом ходе метода Гаусса для системы ( 3) возможно т п шагов преобразований. [12]
Преобразованием исходной системы (2.1) к виду (2.5) завершается прямой ход метода Гаусса. [14]
Преобразование системы (2.1) к виду (2.5) в результате прямого хода метода Гаусса связано с преобразованием матрицы А к треугольному виду, что может быть использовано для вычисления ее определителя. Прямой ход метода Гаусса основан на многократно выполняемой операции сложения элементов одной из строк матрицы с элементами другой строки, умноженными на некоторое число. Известно, что в результате такой операции определитель матрицы не изменяется. Однако при этом может возникнуть необходимость перестановки строк матрицы, чтобы перед началом очередного шага ведущий элемент а – – был отличен от нуля. В результате этой операции изменяется знак определителя. [15]
Страницы: 1 2
www.ngpedia.ru