Метод узловых и контурных уравнений
Метод узловых и контурных уравнений используется для расчетов сложных электрических цепей и подразумевает составление системы уравнений по законам Кирхгофа.
Порядок расчета цепи:
Произвольно в ветвях выбираем и показываем на схеме направления токов;
По первому закону Кирхгофа составляем (n-1) уравнение, гдеn– число узлов в схеме;
Остальные уравнения составляются по второму закону Кирхгофа для любых контуров, общее число уравнений должно быть равно числу неизвестных токов в цепи.
Метод контурных токов
Метод контурных токов также предполагает решение системы уравнений, но количество уравнений в ней меньше, чем при решении методом узловых и контурных уравнений. Для решения задачи этим методом составляют систему уравнений по второму закону Кирхгофа для всех независимых контуров, входящих в данную цепь.
Контуры называются независимыми, если отличаются хотя бы одной ветвью.
Порядок расчета:
В каждой ветви выбираем и показываем на чертеже произвольно направление токов;
Выделим все независимые контуры;
В каждом контуре обозначим контурные токи;
Составим для каждого контура уравнение по второму закону Кирхгофа, решить систему уравнений, найти все контурные токи;
Записать связь между контурными токами и токами ветвей, вычислить токи ветвей.
МАГНИТНОЕ ПОЛЕ
Тема 2.1 Магнитное поле и его характеристики
Пространство, в котором обнаруживается действие сил на магнитную стрелку или ток называется магнитным полем.
Магнитное поле создается электрическим током.
Магнитная индукция характеризуется силой, действующей на движущийся в магнитном поле заряд.
Магнитное поле, магнитная индукция в каждой точке которого имеет одинаковое значение и магнитные линии параллельны друг другу, называется однородным.
Абсолютная магнитная проницаемость характеризует способность среды намагничиваться.
Магнитный поток – параметр магнитного поля, определяется соотношением: Ф=Bн*S, гдеBн– нормальная составляющая вектора магнитной индукции.
Напряженность в каждой точке магнитного поля – это расчетная величина, характеризующая интенсивность магнитного поля, в этой точке, созданного током, без учета среды, в которой создается поле.
H=B/μa–напряженность магнитного поля.
Математическое выражение закона полного тока: Hl=∑I;
Магнитное напряжение поля по замкнутому контуру равно полному току, пронизывающему поверхность, ограниченную этим контуром.
Электромагнитная сила определяется соотношением: Fm=I*B*l*sinα;
Тема 2.2 Магнитные цепи
Магнитная цепь представляет собой сочетание тел преимущественно из ферромагнитных материалов, в которых замыкается магнитный поток.
Магнитные цепи бывают разветвленными и неразветвленными. В неразветвленных цепях магнитный поток, созданный токами обмоток для всех участков и сечений, имеет одинаковое значение. Магнитные цепи могут быть однородными и неоднородными. Однородные цепи по всей длине имеют одинаковое сечение и выполнены из одного определенного материала.
studfiles.net
Расчёт электрической цепи постоянного тока методом узловых и контурных уравнений.
Этот принцип основан на первом и втором законе Кирхгофа. Он не требует преобразования схемы.
Порядок расчёта:
- Произвольно задаёмся направлением токов в ветвях. (Токи в ветвях надо направлять так, что бы хотя бы один ток выходил из узла и один входил в узел)
Красным выделены изменения после первого действия
Синим выделены изменения после второго пункта
- Составляем уравнение для узлов по первому закону Кирхгофа. Их должно быть n минус 1 . (n – число узлов)
- Обозначаем узлы буквами.
- Берём один конкретный узел (Например узел А) и смотрим как направлены токи в ветвях образующих узел. Если ток направлен в узел, то записываем его со знаком плюс, если из него то со знаком минус. 0=I1-I4-I6 (Полученное уравнение)
- Повторяем пункт B ещё для двух узлов.0=-I3+I4+I5(Узел В) 0=I3-I1-I2(Узел D)
- Произвольно задаёмся обходом контура (по часовой или против часовой). И составляем уравнения для контуров цепи по второму закону Кирхгофа. В данном примере направление обхода контура выберем по часовой стрелке.
3.1 Смотрим, как направлена ЭДС относительно обхода контура. Если направление обхода контура совпадает, то значение ЭДС записываем со знаком плюс (в левой части уравнения), если не совпадает, то со знаком минус (записываем также в левой части уравнения)
3.2 Смотрим, как направлено падение напряжения на сопротивлении контура.(То есть смотрим как направлены токи, только записываем в уравнение произведение тока на сопротивление через которое ток протекает в данном контуре). Если направление обхода контура совпадает, то падение напряжения записываем со знаком плюс (в правой части уравнения), если не совпадает, то со знаком минус (записываем также в правой части уравнения)
3.3 Произвести действия 3.1 и 3.2 для остальных контуров. У вас должна получится система из n уравнений, где n — количество контуров в цепи.
Контур ABDA E1=I1*(R1+R01)+I4*R4+I3*R3
Контур BCDB E2=I2*(R2+R02)+I3*R3+I5*R5
Контур ABCA 0=I6*R6-I4*R4+I5*R5
- Решаем полученную систему уравнений и находим величины токов во всех ветвях.
Уберём лишние токи из системы используя уравнения полученные во втором пункте поскольку у нас три уравнения поэтому мы оставляем только три любых тока. Для данного примера я рекомендую оставить токи I1 I2 I4.
0=I1-I4-I6 (Узел А)
0=-I3+I4+I5(Узел В)
0=I3-I1-I2(Узел D)
Выражаем из трёх уравнений токи I3 I5 I6 через токи I1 I2 I4.
I6=I1-I4(Узел А)
I3=I1+I2(Узел D)
I5=I3-I4(Узел В)
I5=I3-I4(Узел В) В этом уравнении сразу не получилось выразить I5 через токи I1 I2 I4, поэтому вместо тока I3 подставим уравнение для узла D и получим:
I5=I1+I2-I4
Заменим токи I3 I5 I6 и получим уравнения с тремя токами :
E1=I1*(R1+R01)+I4*R4+(I1+I2)*R3
E2=I2*(R2+R02)+(I1+I2)*R3+(I1+I2-I4)*R5
0=(I1-I4)*R6-I4*R4+(I1+I2-I4)*R5
Раскрываем скобки подставляем значения сопротивлений из условия и получаем например вот такие три уравнения:
40 = 71*I1 + 24*I2 + 14*I4
20 = 55*I1 + 93*I2 — 61*I4
0 = 60*I1 + 16*I2 — 81*I4
Дальше для решения системы можно воспользоваться бесплатной онлайн программой на нашем сайте.
- Если при решении системы ток получается отрицательным (со знаком —), значит его действительное направление противоположно тому направлению которое мы задали в первом действии.
- Правильность решения можно проверить с помощью баланса мощностей.
electrikam.com
Метод узловых и контурных уравнений — Мегаобучалка
1 Выбираем произвольно направления токов в ветвях (рис.1.45)
2Составляем систему уравнений по законам Кирхгофа для определения токов в ветвях. Так как в схеме три ветви, то то необходимо составить три уравнения: по первому закону Кирхгофа – одно уравнение (на единицу меньше числа узлов) и по второму закону Кирхгофа недостающее число уравнений, т.е. два уравнения.
Система уравнений для расчёта токов имеет вид:
{E1+E2 = I1 (R1+r01+R2+R3)+ I2 (R4+r02) (2)
{-E2 = -I2 (R4+r02) + I3 (R5+R6+R7) (3)
В уравнении (1) притекающие к узлу В токи принимают положительными, оттекающие от узла токи – отрицательными. В уравнении (2) и (3) все ЭДС и напряжение, совпадающие с напряжениями обхода по контуру (по часовой стрелке), записывали положительными, не совпадающие – отрицательными.
Решая полученную систему уравнений, найдём токи в ветвях. Подставим значения ЭДС и сопротивлений:
I1 – I2 – I3 = 0
40+20 = I1 (15+1+27+5) +I2 (2+15)
-20 = -I2 (15+2) + I3 (12+10+5)
I1 – I2 – I3 = 0 (4)
60 = I1*48+I2*17 (5)
-20 =-I2*17+I3 =27 (6)
Выразим I1 из (5) -го уравнения, I3 из (6) -го уравнения
I1 – I2 – I3 = 0
48 I1 = 60 – 17 I2
27 I3 = – 20+17 I2
I1 – I2 – I3 = 0
I1 = 60 – 17 I2 / 48 = 60 /48 – 17 / 48 I2 = 1,25 – 0,35 I2 (7)
I3 = -20+17 I2 / 27 = -20 / 27+17 / 27 I2 = -0,74+0,63 I2 (8)
Подставим полученные значения I1 и I3 в (4)-е уравнение:
(1,25 – 0,35 I2) – I2 – (-0,74+0,63 I2) = 0
1,25 – 0,35 I2 – I2+0,74 – 0,63 I2 = 0
-0,35 I2 – I2 – 0,63 I2 = -0,74 – 1,25
-1,98 I2 = -1,99
I2 = -1,99 / -1,99 » 1А
Подставим найденное значение тока I2 в уравнение (7) и (8), и определим токи I1 и I3
I1 = 1,25 – 0,35 I2 = 1,25 – 0,35*1 =0,9 A
I3 = -0,74+0,63 I2 = -0,74+0,63*1 = -0,11
Рассмотренный метод в большинстве случаев является громоздким. Для упрощения расчёта разработаны методы, в основе которых также положены уравнения Кирхгофа, но количество уравнений сокращено.
1.3.2.2 Определим токи в ветвях методом контурных токов. Считаем, что в каждом независимом контуре схемы (рис 1.45) течёт свой контурный ток Iк1, Iк2. Выбираем направления токов в одну сторону, по часовой стрелке.
Составляем уравнения по второму закону Кирхгофа относительно контурных токов. Направление обхода контуров примем совпадающими с направлением контурных токов. Определим контурные ЭДС:
EI = E1+E2 = 40+20 = 60 B
EII = -E2 = -20B
Это алгебраическая сумма ЭДС, входящих в контур.
Определим собственные сопротивления контуров:
RI = R1+R2+R3+R4+r01+r02 = 15+27+5+15+1+2 = 65 Ом
RII = R4+R5+R6+R7+r02 = 15+12+10+5+2 = 44 Ом
Оно определяется как алгебраическая сумма всех сопротивлений , входящих в контур.
Общим для контуров является сопротивление (R4+r02).
Составим систему уравнений :
EI = Iк1*RI – Iк2*(R4+r02) (9)
EII = Iк2*RII – Iк1 *(R4+r02) (10)
В уравнении (9) слагаемое Iк2*(R4+r02) записывается со знаком минус, так как из-за второго контурного тока на общих сопротивлениях (R4+r02) создаётся падение напряжения, причём направление токов Iк2 и Iк1 на этих сопротивления не совпадают.
Аналогично в уравнении (10) из-за тока Iк1 создаётся падение напряжения на общих сопротивлениях (R4+r02).
Подставим известные значения сопротивлений и ЭДС:
60 = Iк1 *65 – Iк2 *(15+2)
-20 = Iк2*44 – Iк1*(15+2)
60 = Iк1 *65 – Iк2 *17 (11)
-20 = Iк2*44 – Iк1*17 (12)
выразим из (11)-го уравнения Iк1 и подставим его значения в (12)-ое уравнение:
65 Iк1 = 60 + 17Iк2
-20 = 44Iк2 – 17 Iк1
Iк1 = 60+17 Iк2 /65 = 60/65+17Iк2 /65 = 0,92+0,26 Iк2
-20 = 44 Iк2 – 17Iк1
-20 = 44 IК2 – 17(0,92+0,26 IK2)
-20 = 44 IK2 – 15,64 – 4,42 I K2
-20+15,64 = 44 IK2 – 4,42 IK2
-4,36 = 39,58 IK2
IK2 = -4,36 / 39,58 = -0,11 A
Из уравнения (13) определим IK1:
IK1 = 0,92+0,26 IK2 = 0,92+0,26 (-0,11) = 0,89 A
Определяем действительные токи в ветвях.
Ток в ветви равен алгебраической сумме контурных токов, протекающих в зтой же ветви.
Рассчитываем значения токов в ветвях схемы (рис. 1.2), сравнивая направления контурных токов в ветвях с направлением действующих токов:
I1 = IK1 = 0,89 A
I2 = IK1 – IK2 =0,95 – (-0,11) = 1,1 A
I3 = IK2 =-0,11 A
1.3.2.3.Определим токи методом наложения токов.
При решении этим методом из схемы поочерёдно исключаем по одному источнику ЭДС. Тогда схема решается как простая схема с одним источником ЭДС и смкшанным соединением сопротивлений. Токи в такой схеме называются частичными. Исключаем из схемы источник Е1:
Рисунок 1.46
Вычислим эквивалентное сопротивление цепи:
R123, r02 = R1+R2+R3+r02 = 15+27+5+2 = 49 Ом
R123567, r02 = R123, r02*R567 / R123, r02+R567 = 49*27 / 49+27 = 1323 / 76 = 17,41 Ом
R = R123567, r02+R4 = 17,41+15 = 32,41 Ом
По закону Ома для полной цепи, общей для данной схемы ток I2’ определяется:
I2’ = E2 / R+r02 = 20 / 32,41+2 = 0,58 A
Для определения токов I1’ и I3’ найдём падение напряжения на участке АВ.
UAB = I2’*R123567, r02 = 0,58*17,41 = 10,1 B
I1’ = UAB / R123, r02 = 10,1 / 49 = 0,21 A
I3’ = UAB / R567 = 10,1 / 27 = 0,37 A
Исключим из схемы источник Е2:
Рисунок 1.47
Вычислим эквивалентное сопротивление цепи:
R567 = R5+R6+R7 = 12+10+5 = 27 Ом
R4,r02 = R4+r02 = 15+2 = 17 Ом
R4567,r02 = R567*R4,r02 / R567+R4,r02 = 27*17 / 27+17 = 459/44 = 10,43 Ом
R = R4567,r02+R1+R2+R3= 10,43+15+27+5 = 57,43 Ом
По закону Ома для полной цепи общий для данной схемы I1’’ определиться:
I1’’ = E1/R+r01 = 40/57,43+1 = 0,68 A
Для определения токов I2’’ и I3’’ найдём падение напряжения на участке СД:
UСД = I1’’ R4567,r02 = 0,6810,43 = 7,09 B
I2’’ = UСД/R4,r02 = 7,09/17 = 0,42 A
I3’’ = UСД/R567 = 7,09/27 = 0,26 A
Вычислим действительные токи в ветвях наложением частичных токов с учётом их направления:
I1 = I1’+I1’’ = 0,21+0,68 = 0,89 A
I2 = I2’+I2’’ = 0,58+0,42 = 1 A
I3 = I3’ – I3’’ = 0,26 – 0,37 = -0,11 A
Действительное направление тока I3 противоположно заданному (об этом свидетельствует знак “минус”)
1.3.2.4 Составим баланс мощностей
на основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источниками питания.
Уравнение баланса мощностей:
Pи = Pп+Pо
где Pи = ЕI – мощность источника энергии;
Pп = I*I*R – мощность потребителя энергии;
Pо = I*I*r – мощность потерь.
В нашем случае:
Pи = E1*I1+E2*I2 = 40*0,89+20*1 = 35,6+20 = 55,6 Вт
Pп = I1*I1(R1+R2+R3) + I2*I2*R4+I3*I3 (R5+R6+R7) = 0,89*0,89 (15+27+5) +
+1*1*15+(-0,11)*(-0,11)*12+10+5) = 0,79*47+15+0,012*27 = 37,13+15+0,324 = 52,45 Вт
Pо = I1*I1*r01+I2*I2*r02 = 0,89*0,89*1+1*1*2 = 0,79+2 = 2,79 Вт
55,6 = 52,45+2,79
55,6 = 55,24
Расхождение в результатах вычислений не превышают 1%, это означает, что токи рассчитаны правильно.
megaobuchalka.ru
Метод узловых и контурных уравнений для расчета сложных электрических цепей
Задача
На рисунке 2 изображена схема сложной электрической цепи. ЭДС источников энергии Е1, Е2, их внутренне сопротивление R01, R02, сопротивление резисторов R1, R2, R3. Чиcловые значения величин приведены в таблице 3. Начертить схему цепи, показав направления токов в ветвях.
Определить токи I1, I2, I3 методом узловых и контурных уравнений (при помощи первого и второго законов Кирхгофа).
Проверить решение методом узлового напряжения. Составить уравнение баланса мощности.
Дано
Е1 =260В
Е2=244В
R01 =0,1Ом
R02 =0,2Ом
R1 =0
R2=0
R3=1Ом
I1-3= ?, Составить баланс мощности.
Схема цепи
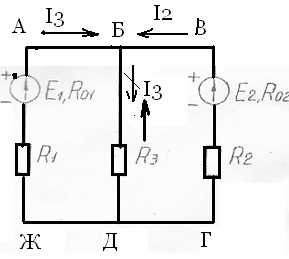
Решение
1.Обозначим контуры электрической цепи:
АБДЖА, БВГДБ, АБВГДЖА..
2. Так как узловых точек две: Б,Д, то число уравнений по первому закону Кирхгофа – одно, а по второму закону Кирхгофа два.
I3 = I1+ I2(1)
E1 =I1(R1+R01) + I3R3(2) контур АБДЖА
-E2 =I2 (R2 + R02) + I3 R3(3) контур БВГДБ
3. Подставляем числовые значения в уравнения, решаем систему из трех уравнений и получаем значения токовI1, I2, I3.
I3 = I1+ I2
250= I1(0+0,1) + I3R3 = 0,1I1+ I3
-244= I2(0+0,2) + I3R3 = 0,2I1+ I3
I1=
I2=
I3 = 175 +57,5 = 232,5А
Проверяем правильность определения токов в сложной цепи при помощи первого и второго законов Кирхгофа методом узлового напряжения
4. Проводимости ветвей:
g1=
g2=
g3=
5.Узловое напряжение (напряжение между узлами Б,Д):
UВД=
6. Токи ветвей:
I1 =(Е1– UВД) g1 =(250-232,5)10=175А
I2 =(Е2– UВД) g2 =(244 -232,5)5=57,5А
I1 = -UВД * g3 =-232,5*1=-232,5А
Значение токов соответствует значениям, полученным при помощи законов Кирхгофа. Так как токи I3 получились отрицательными, его направление, указанное на рисунке, должно быть изменено на противоположное.
Составим баланс мощности
7.Уравнение баланс мощности будет иметь вид:
Рист1+Рист2 =Рист0+Рист0 +Р3
Рист1= Е1*I1=250*175=43750Вт
Рист2= Е2*I2=244*57,5=14030Вт
Рист01= * R01 = =3062,5Вт
Рист02= * R02 = =661,25Вт
Р3= * R3 = =54056,25Вт
Рист =3750Вт +14030Вт=57780Вт
Рист0+Рист0 +Р3 = 3062,5Вт +661,25Вт +54056,25Вт=57780Вт
57780Вт=57780Вт
Баланс выполняется, задача решена, верно.
infourok.ru
Пр. 5. Кирхгоф
ПРАКТИЧЕСКАЯ РАБОТА № 5
«Расчет сложной электрической цепи методом узловых и контурных уравнений, составленных по законам Кирхгофа»
Определить токи во всех ветвях цепи, если даны ЭДС источников Е1 и Е2, внутренние сопротивления R01 и R02, сопротивление резистора R3. Задачу решить методом узловых и контурных уравнений, составленных по законам Кирхгофа. Составить уравнение баланса мощностей. Данные для задачи взять из таблицы.
№ вар. | рис. | Заданные величины | ||||||
Е1, В | Е2, В | R01, Ом | R02, Ом | R1, Ом | R2, Ом | R3, Ом | ||
1 | а | 180 | 220 | 0,1 | 0,1 | 3,9 | 1,9 | 40 |
2 | б | 110 | 84,5 | 0,2 | 0,1 | 7,8 | 9,9 | 12 |
3 | в | 104 | 220 | 0,01 | 0,1 | 1,99 | 3,9 | 36 |
4 | г | 140 | 100 | 0,01 | 0,02 | 1,99 | 7,98 | 16 |
5 | д | 123 | 120 | 0,1 | 1 | 19,9 | 9 | 13,5 |
6 | е | 200 | 160 | 2 | 0,1 | 35,6 | 17,9 | 4,4 |
7 | ж | 75 | 100 | 0,1 | 3 | 4,9 | 3,4 | 4,6 |
8 | з | 200 | 96 | 0,2 | 4 | 9,8 | 19,3 | 10,7 |
9 | и | 110 | 150 | 0,01 | 3 | 14,99 | 5,2 | 4,8 |
10 | к | 110 | 115 | 4 | 0,02 | 10,1 | 23,98 | 3,9 |
11 | а | 110 | 220 | 0,1 | 0,1 | 3,9 | 3,9 | 9 |
12 | б | 227 | 160 | 1 | 1 | 7 | 8 | 35 |
13 | в | 133 | 173 | 2 | 1 | 38 | 9 | 25 |
14 | г | 94 | 224 | 1 | 2 | 7 | 23 | 60 |
15 | д | 171 | 113 | 0,1 | 1 | 9,9 | 24 | 75 |
16 | е | 320 | 400 | 4 | 0,2 | 71,2 | 25,8 | 8,8 |
17 | ж | 200 | 145 | 0,2 | 6 | 18,8 | 7,8 | 13,2 |
18 | з | 186 | 380 | 0,4 | 8 | 19,6 | 41,6 | 21,4 |
19 | и | 300 | 220 | 0,02 | 6 | 29,98 | 11,4 | 13,6 |
20 | к | 330 | 210 | 8 | 0,04 | 21,2 | 47,96 | 7,8 |
21 | а | 360 | 400 | 0,2 | 0,2 | 7,8 | 3,8 | 60 |
22 | б | 220 | 118 | 0,4 | 0,2 | 15,6 | 19,8 | 20 |
23 | в | 205 | 160 | 0,02 | 0,2 | 3,98 | 16,8 | 50 |
24 | г | 280 | 200 | 0,02 | 0,04 | 4,98 | 14,96 | 25 |
25 | д | 150 | 125 | 0,2 | 2 | 39,8 | 18 | 12 |
26 | е | 85 | 100 | 1 | 0,01 | 16,3 | 8,98 | 2,7 |
27 | ж | 175 | 145 | 0,01 | 2 | 7,98 | 5,5 | 8,5 |
28 | з | 65 | 135 | 0,1 | 3 | 13,8 | 14,4 | 9,8 |
29 | и | 450 | 310 | 0,2 | 9 | 44,8 | 24,2 | 16 |
30 | к | 260 | 180 | 2 | 0,06 | 16,4 | 36,96 | 6,7 |
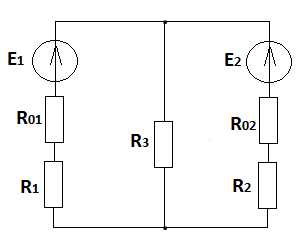
а) б)
в) г)
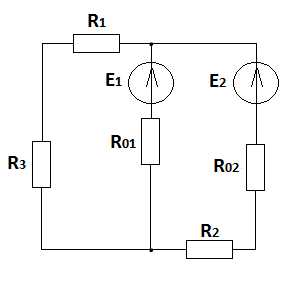
д) е)
ж) з)
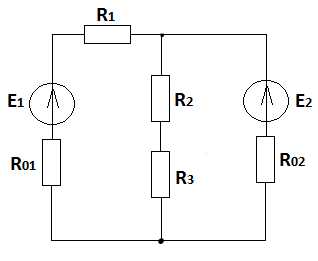
и) к)
ПРИМЕР
Определить токи во всех ветвях цепи, если ЭДС источников энергии Е1=180 В, Е2=96 В, их внутренние сопротивления R01=0,1 Ом, R02=2 Ом; сопротивления резисторов R1=7,9 Ом, R2=20 Ом, R3=32 Ом, R4=10 Ом.
Задачу решить методом узловых и контурных уравнений, составленных по законам Кирхгофа. Составить уравнение баланса мощностей.
Дано: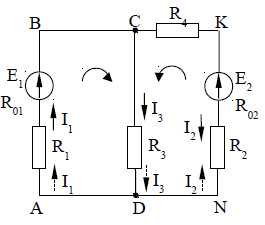
Е1=180 В;
Е2=96 В;
R01=0,1 Ом;
R02=2 Ом;
R1=7,9 Ом;
R2=20 Ом;
R3=32 Ом;
R4=10 Ом.
Определить: I1, I2, I3.
Решение.
Количество неизвестных токов равно количеству ветвей в цепи. На рисунке три ветви, следовательно, неизвестных токов три, для их нахождения необходимо составить систему из трех уравнений.
1 Обозначим контуры буквами.
2 На схеме произвольно показываем предварительное направление токов (пунктир).
3 Сначала составляем уравнение по первому закону Кирхгофа. Количество этих уравнений равно числу узлов в схеме без одного. На схеме два узла – С и D, следовательно, составляем одно уравнение по первому закону Кирхгофа, например, для узловой точки С: I1+I2=I3.
Остальные уравнения (3-1=2) составляются по второму закону Кирхгофа, т. е. два уравнения.
Второе уравнение составим для контура ABCDA, направление обхода контура примем «по часовой стрелке»:
E1=I1(R1+R01)+I3R3.
Третье уравнение составим для контура CKNDC; направление обхода контура примем
«против часовой стрелки»:
E2=I2(R2+R02+R4)+I3R3.
4 Подставляем исходные данные в полученную систему из трех уравнений и решаем эту систему относительно неизвестных токов:
Из второго уравнения получаем:
Из третьего уравнения получаем:
Подставляем выражения (а) и (б) в первое уравнение и находим ток I3.
Значение тока I3 подставляем в выражения (а) и (б) и определяем токи I1 и I2:
Ток I2 получился отрицательным, это значит, что первоначально произвольно принятое
направление тока I2 от точки D к точке С оказалось неверным и должно быть изменено на
противоположное. На схеме показываем действительное направление токов.
5 Составим уравнение баланса мощностей цепи.
В любой электрической цепи алгебраическая сумма мощностей источников энергии равна сумме мощностей, потребляемых сопротивлениями цепи, и мощности потерь внутри источников, т. е.
.
В левой части уравнения мощность источника, работающего в режиме генератора учитывается со знаком «плюс», в режиме потребителя – со знаком «минус».
Режим работы источника определяется по направлению действия ЭДС и положительному направлению тока данной ветви: если эти направления совпадают, то источник работает в режиме генератора; если не совпадают, то источник работает в режиме потребителя.
Для данной цепи:
studfiles.net
Метод узловых и контурных уравнений — Мегаобучалка
Метод контурных токов
Метод узлового напряжения (метод двух узлов)
Метод эквивалентного генератора
Метод наложения.
Порядок расчета:
На исходной схеме произвольно выбирают и указывают положительное направление токов в ветвях.
На основании исходной схемы составляют частные схемы, в каждой из которых действует только одна ЭДС, а остальные источники ЭДС закорачиваются (кроме их внутренних сопротивлений).
Каждая частная схема рассчитывается отдельно методом эквивалентных сопротивлений, и определяются частные токи.
Ток в конкретной ветви исходной схемы определяется как алгебраическая сумма частных токов, протекающих по данной ветви.
Задача:
Дано: Е1 = 120 В, Е2 = 100 В, R1 = 20 Ом, R2 = 10 Ом, R3 = 30 Ом, R4 = 20 Ом.
Определить: I1, I2, I3, I4, I4,1, I3,2.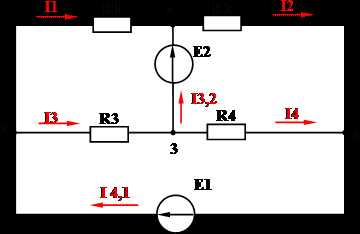 
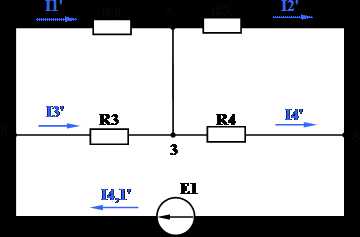
Метод узловых и контурных уравнений.
Порядок расчета:
1. Определить число узлов у и число ветвей b в электрической цепи.
2. Найти количество уравнений, которые необходимо составить по первому закону Кирхгофа (их число равно у – 1) и по второму закону Кирхгофа (их число равно к = b – (y – 1)).
Выбрать произвольно направление токов в ветвях и показать их на схеме.
Составить систему уравнений по первому и второму законам Кирхгофа, и решить её относительно неизвестных токов.
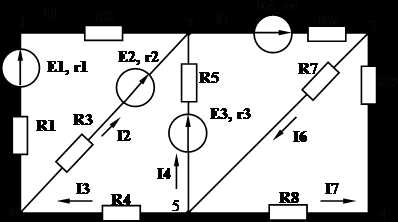
Задача:
Дано: Е1 = 110 В, Е3= 111 В, Е4 = 108 В, r1 = 0,5 Ом, r3 = 1 Ом, r4 = 0,2 Ом, R1 = 4,5 Ом, R2 = 20 Ом, R4 = 25,8 Ом.
Определить: I1, I2, I3, I4.
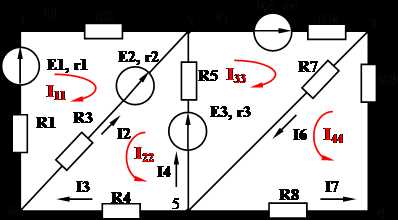
Метод контурных токов.
 | |||
 | |||
Порядок расчета:
1. Определяют количество уравнений, составляемых по второму закону Кирхгофа. Их число равно к = b – (y – 1).
На схеме произвольно указывают направление токов в ветвях.
Произвольно выбирают и указывают направление контурных токов, но желательно, чтобы их направление совпадало с направлением обхода контура.
Составляют систему уравнений и определяют контурные токи.
Рассчитывают искомые токи в ветвях как алгебраическая сумма контурных токов, протекающих через данную ветвь.
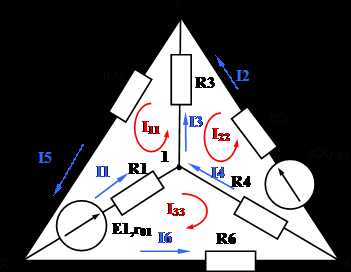
Задача:
Дано: Е1 = 110 В, Е3 = 111 В, Е4 = 108 В, r1 = 0,5 Ом, r3 = 1 Ом, r4 = 0,2 Ом, R1 = 4,5 Ом, R2 = 20 Ом, R4 = 25,8 Ом.
Определить: I1, I2, I3, I4.
 |
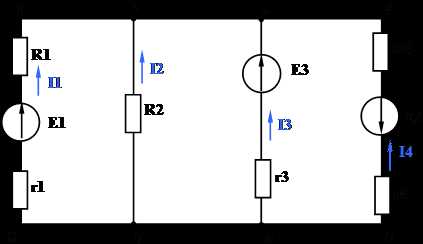
1.4.4. Метод узлового напряжения (метод двух узлов).
Порядок расчета:
Указывают произвольно направление токов в ветвях, но одинаково во всех ветвях.
Рассчитывают проводимости всех ветвей.
3. Определяют межузловое напряжение:
, где
∑(Еn·gn) – алгебраическая сумма произведений ЭДС источника и проводимости соответствующей ветви. ЭДС записывается со знаком «плюс», если направление ЭДС совпадает с направлением тока в ветви, со знаком «минус» – если не совпадает.
∑gn – сумма проводимостей всех ветвей.
4. Рассчитывают токи в ветвях:
Знак ЭДС устанавливается так же, как и в пункте 3.
Задача:
Дано: Е1 = 110 В, Е3 = 111 В, Е4 = 108 В, r1 = 0,5 Ом, r3 = 1 Ом, r4 = 0,2 Ом, R1 = 4,5 Ом, R2 = 20 Ом, R4 = 25,8 Ом.
Определить: I1, I2, I3, I4.
megaobuchalka.ru
1.4.2 Примеры решения задач
Задача №1.6
Определить методом наложения токи (I1 , I2 , I3) в электрической цепи (рисунок 1.7) при следующих исходных данных:Е1=100В,Е2= 40В,R1=20Ом,R2=40Ом, R3=50Ом.
2
Дано: Е1=100В
Е2= 40В
R1=20Ом
R2=40Ом
R3=50Ом
————————-
Определить: I1 , I2 , I3
Решение задачи
Рассматриваем первую расчетную схему. Е2закорачиваем и находим эквивалентное сопротивление полученной схемы (рисунок 1.8):
Rобщ= 20+40*50/(40+50)=42,2 Ом
Находим частичные токи при включенном первом источнике:
I11=E1/Rобщ
I11=2,37 А
U1=I11*R1
U1=20*2,37=47,37В
U12=Е1-U1
U12=100-47,37=52,63В
I12= U12/R2
I12=1,32А
I13= U12/R3
I13=1,05А
Рассматриваем вторую расчетную схему. E1закорачиваем и рассчитываем частичные токи для второй схемы (рисунок1.9):
Rобщ=40+50*20/(50+20)=54,3Ом
I21=E2/Rобщ
I22=0,74 А
U2=I22*R2
U2=40*0,74=29,5В
U22=Е2-U2
U22=40-29,5=10,5В
I21= U22 /R1
I21=0,53А
I23= U22/R3
I23=0,21А
Находим искомые токи
I1 = I11 – I21
I1 = 2,37-0,53=1,84А
I2 = I12– I22
I1 = 1,32-0,74=0,58А
I3 = I13 +I23
I1 =1,05+0,21=1,26А
1.5 Метод узлового напряжения
1.5.1 Рекомендации для студента
Метод узлового напряжения используется для расчета сложных электрических цепей с несколькими источниками и несколькими узлами.
1.Определяем один из узлов базовым и приравниваем его потенциал нулю;
2.Выбираем второй узел, который связан с базовым узлом несколькими ветвями;
3.Опредеяем проводимости ветвей, соединяющих второй узел с базовым;
4.Определяем узловое напряжение относительно базового узла:
,
где
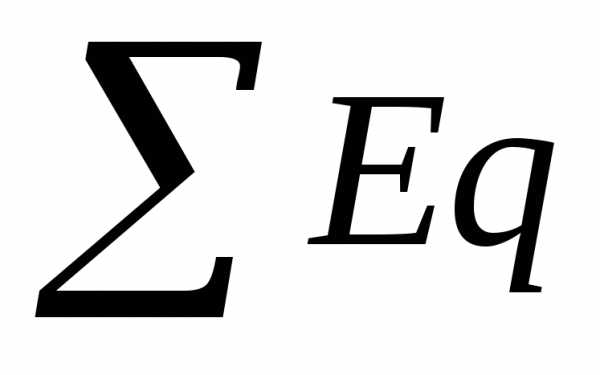– алгебраическая сумма произведений
ЭДС и проводимости ветвей;
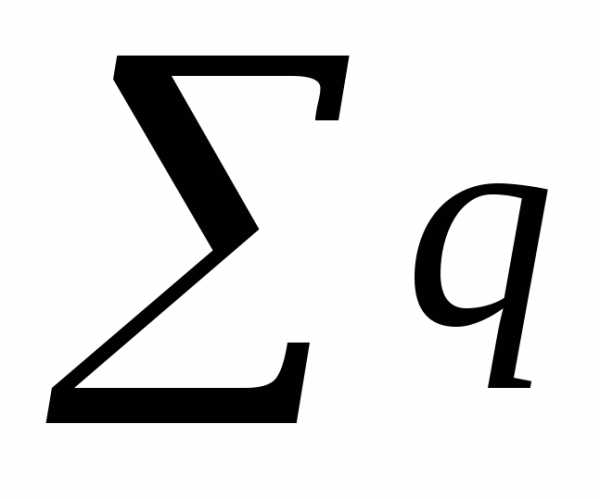– сумма проводимостей ветвей.
5.Токи в ветвях находятся по соотношению:
1.5.2 Примеры решения задач
Задача №1.7
Определить методом узлового напряжения токи ( I1, I2, I3) в электрической цепи (рисунок 1.10) при следующих исходных данных:Е1=100В,Е2= 40В,R1=20Ом,R2=40Ом, R3=50Ом.
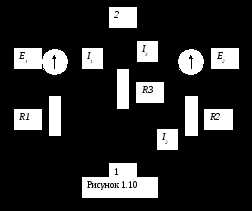
Дано: Е1=100В
Е2= 40В
R1=20Ом
R2=40Ом
R3=50Ом
————————-
Определить: I1, I2, I3
Решение задачи
1.Узел 1 принимаем базовым и считаем его потенциал равным нулю.
2.Определяем проводимости ветвей:
q1=1/R1
q1=0,05См
q2=1/R2
q2=0,025См
q3=1/R3
q3=0,02См
3.Определяем узловое напряжение относительно базового узла:
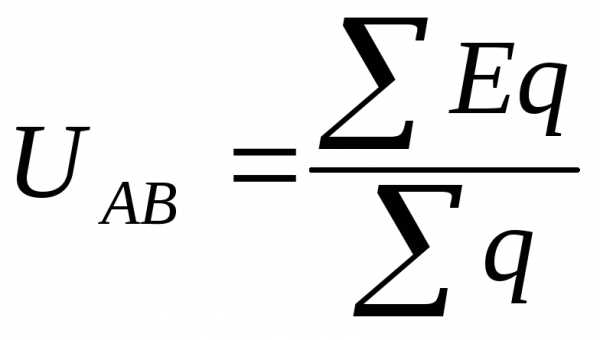
UAB=(100*0,05+40*0,025)/(0,05+0,025+0,02)=63,15В
4.Определяем токи в ветвях:
I1 =(100-63,15)*0,05=1,84А
I2 =(63,15-40)*0,025=0,58А
I3=63,15*0,02=1,26А
1.6 Метод узловых и контурных уравнений
1.6.1 Рекомендации для студента
Расчеты сложных электрических цепей методом узловых и контурных уравнений сводится к составлению уравнений по законам Кирхгофа. Общее число уравнений должно быть равно числу неизвестных токов в ветвях электрической цепи. Порядок расчета:
1.Произвольно задаем направления токов в цепи;
2.Составляем (n-1) уравнение по первому закону Кирхгофа, гдеn– число узловых точек в схеме;
3.Остальные уравнения составляются по второму закону Кирхгофа;
4.Решаем систему уравнений, находим искомые токи. Если значение тока имеет знак «минус», это означает, что на схеме задано его противоположное значение.
studfiles.net