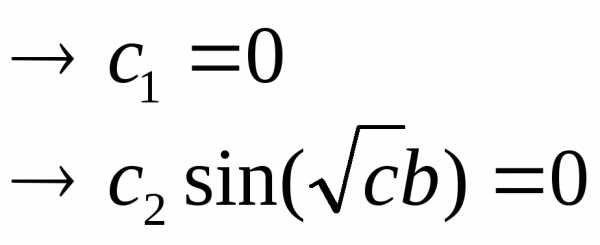4. Метод разделения переменных
Определение. Уравнением с разделенными переменными называется дифференциальное уравнение первого порядка вида
, (4)
с
непрерывными функциями  и
и
Смысл
этого термина заключается в том, что
переменные  и
и разделены по разным частям равенства
(4).
разделены по разным частям равенства
(4).
Напомним,
что, согласно определению, дифференциал
функции 
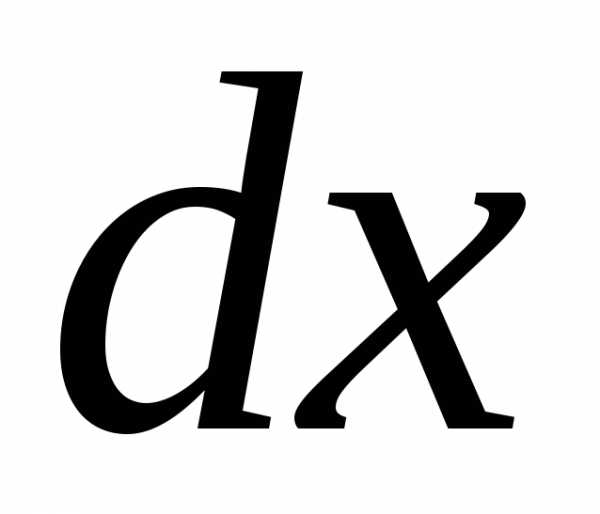 ,
получим:
,
получим:. (5)
Это другой, более традиционный способ записи уравнения с разделенными переменными.
Теорема. Если в уравнении (5) функции  и
и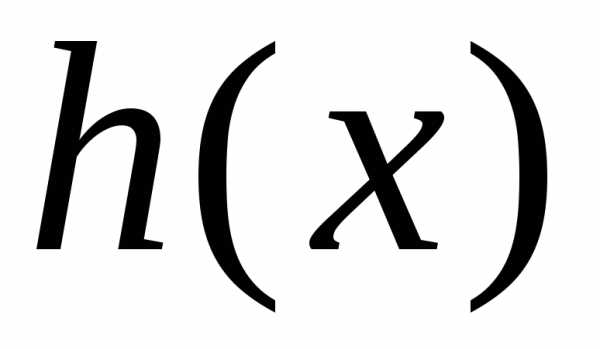 имеют первообразные
имеют первообразные
 ,
то общий интеграл уравнения имеет вид:
,
то общий интеграл уравнения имеет вид:, (6)
где  —
произвольная постоянная.
—
произвольная постоянная.
Замечание. Если для обозначения первообразных использовать символ неопределенного интеграла, то общий интеграл записывается в виде:
. (7)
Доказательство.
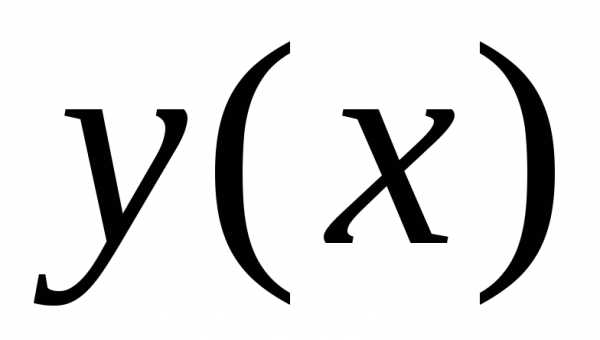 ,
убедимся, что
,
убедимся, что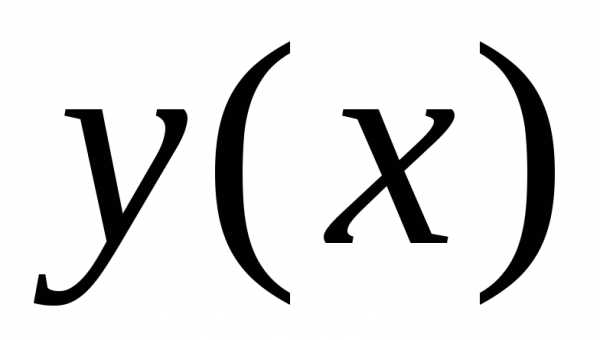 удовлетворяет уравнению (4). Для этого
продифференцируем по
удовлетворяет уравнению (4). Для этого
продифференцируем по равенство (6), применяя для левой части
правило производной сложной функции с
промежуточной переменной
равенство (6), применяя для левой части
правило производной сложной функции с
промежуточной переменной :
:,
 и
и первообразные для
первообразные для и
и :
:.
Остается
убедиться, что за счет выбора значения
произвольной постоянной  можно обеспечить выполнение любых
начальных условий.
Подставляя начальные условия в (6),
получаем:
можно обеспечить выполнение любых
начальных условий.
Подставляя начальные условия в (6),
получаем:
. ▄
Примеры. 1. Для уравнения
найдем общий интеграл и частный интеграл
для начальных условий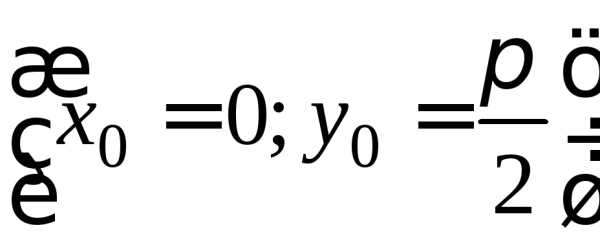 .
Имеем:
.
Имеем:
—
это общий интеграл.
Подставим
теперь в общий интеграл начальные
условия и найдем соответствующее
значение константы  :
:
.
Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:
.
 с начальными условиями.
Умножая обе части уравнения на
с начальными условиями.
Умножая обе части уравнения на и затем интегрируя, получаем:
и затем интегрируя, получаем: –это
общий интеграл. Выражая отсюда явно  через
через и
и ,
получаем общее решение:
,
получаем общее решение:
 ,
так что
,
так что .
Следовательно, функция
.
Следовательно, функция является решением задачи Коши.
является решением задачи Коши.Определение. Уравнением с разделяющимися переменными называется дифференциальное уравнение первого порядка вида
, (8)
с непрерывными функциями .
В
этом уравнении каждая из частей является
произведением двух множителей, один из
которых зависит только от  ,
а другой – только от
,
а другой – только от .
.
От этого уравнения легко перейти к уравнению с разделенными переменными, деля обе части на произведение («разделяя переменные»):
.
Примеры. 1.
.
Обе части разделим на
 :
: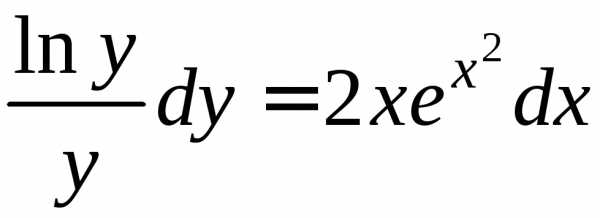 .
Интегрируем:
.
Интегрируем:  —
—
общий интеграл.
2.
;
начальные условия: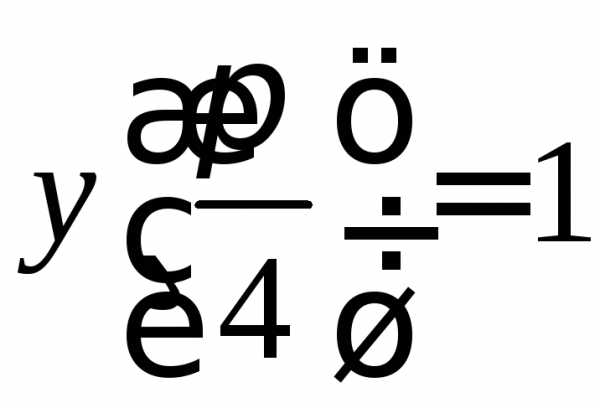 .
Записываем производную
.
Записываем производную как отношение дифференциалов:
как отношение дифференциалов:
Обе
части умножим на  ,
разделим на
,
разделим на и проинтегрируем:
и проинтегрируем:
—
общий интеграл. Найдем теперь частный интеграл, удовлетворяющий начальным условиям. Подставляя начальные условия в полученное уравнение, имеем:
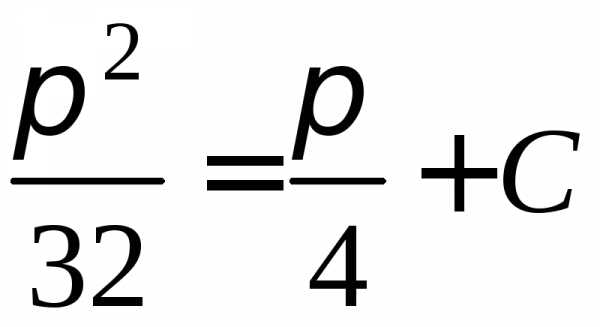 ;
;  .
.
Следовательно, частный интеграл, дающий решение задачи Коши, имеет вид:
.
5. Однородное уравнение первого порядка
Определение. Однородным уравнением первого порядка называется уравнение, разрешенное относительно производной:
, (9)
в
котором функция  при всех вещественных
при всех вещественных удовлетворяет условию:
удовлетворяет условию:
.
Полагая
в этом равенстве 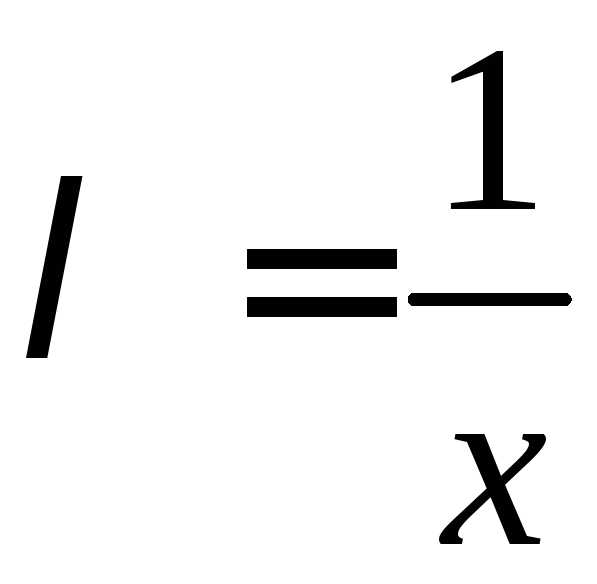
 :
: .
.Приведем примеры таких функций:
1)  ;
2)
;
2) .
Напротив, функция
.
Напротив, функция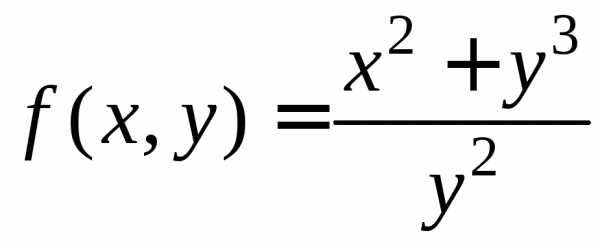 ,
как легко проверить, не удовлетворяет
условию.
,
как легко проверить, не удовлетворяет
условию.
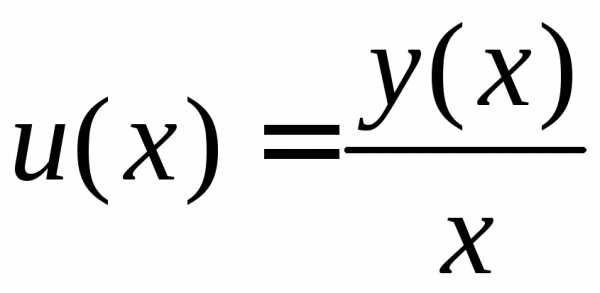 ,
так что.
Тогда формула для производной произведения
дает:,
и уравнение (9) принимает вид:
,
так что.
Тогда формула для производной произведения
дает:,
и уравнение (9) принимает вид:—
уравнение
с разделяющимися переменными относительно
новой искомой функции  .
Если для него найден общий интеграл
(методом, описанным в предыдущем разделе):
.
Если для него найден общий интеграл
(методом, описанным в предыдущем разделе):
,
то,
заменяя в нем  на
на ,
получим общий интеграл для исходной
неизвестной функции
,
получим общий интеграл для исходной
неизвестной функции :
:
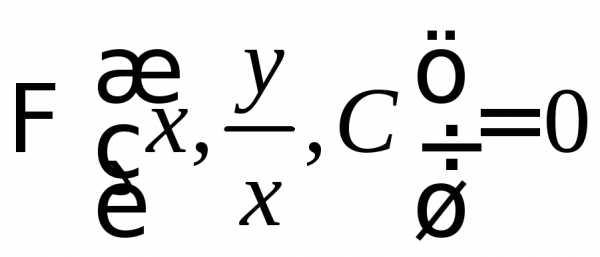 .
.
Алгоритм решения однородного уравнения первого порядка:
1. Проверка однородности: .
2.
Введение новой искомой функции 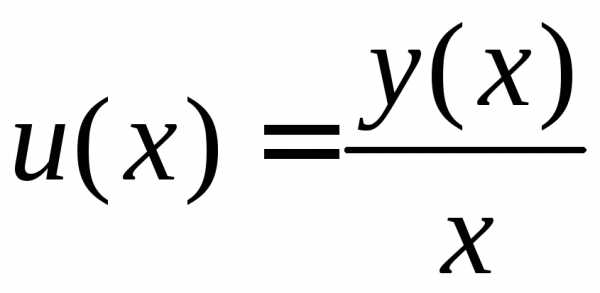 .
.
3.
Замена в уравнении  на
на ,
, на
на .
.
4.
Решение полученного уравнения с
разделяющимися переменными относительно  .
.
5.
Замена в полученном общем интеграле  на
на .
.
Пример. Решим уравнение 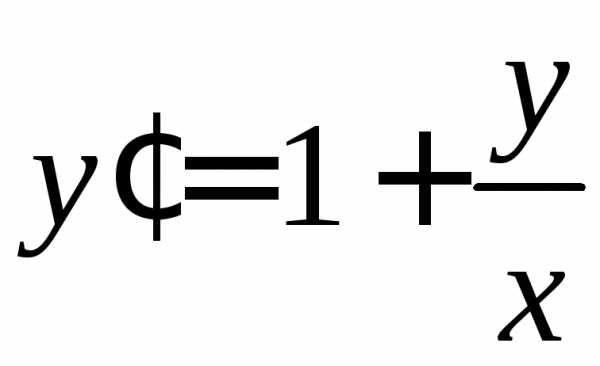 .
Здесь,
так что уравнение, действительно,
является однородным. После введения
новой переменной
.
Здесь,
так что уравнение, действительно,
является однородным. После введения
новой переменной получаем уравнение:
получаем уравнение:
.
Заменяя  на
на ,
получаем общий интеграл для исходной
неизвестной функции
,
получаем общий интеграл для исходной
неизвестной функции :
: .
.
studfiles.net
3.Метод разделения переменных Фурье
Метод разделения переменных Фурье
1. Введение в основные типы уравнений в частных производных II степени.
Многочисленные задачи математической физики, включая задачи механики, теплофизики, электродинамики описываются уравнениями в частных производных II степени. К некоторым, наиболее распространенным основным уравнениями с ч.п. II степени относятся:
а) уравнение Лапласа (в трехмерном случае)  или(здесь- неизвестная функция,
или(здесь- неизвестная функция, и
т.д. – сокращенные обозначения частных
производных) рассматривается в задаче
со стационарным распределением
температуры или электрического потенциала
внутри пространственной области.
и
т.д. – сокращенные обозначения частных
производных) рассматривается в задаче
со стационарным распределением
температуры или электрического потенциала
внутри пространственной области.
б) волновое уравнение 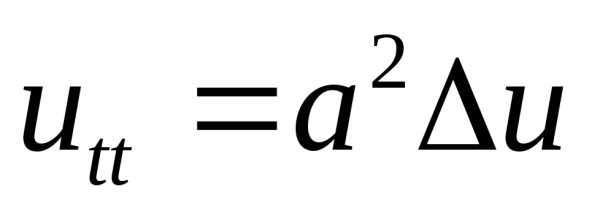 (здесь,
(здесь, – время,
– время, – параметр) рассматривается в задаче
распространения механических или
электромагнитных колебаний в среде.
– параметр) рассматривается в задаче
распространения механических или
электромагнитных колебаний в среде.
в) уравнение теплопроводности 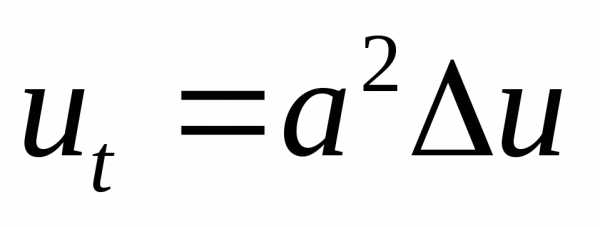 рассматривается в задаче распространения
тепла.
рассматривается в задаче распространения
тепла.
Отметим, что данные уравнения также рассматриваются в задачах для двух- и одномерного пространства. Так отдельно выделяется класс линейных уравнений в частных производных II степени относительно функции двух переменных. Общий вид данных уравнений:
где
– функции независимых переменных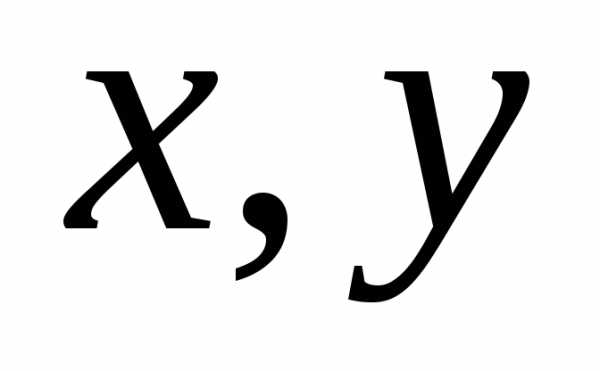 ,- неизвестная функция,
,- неизвестная функция, ,
, и т.д. – сокращенные обозначения частных
производных.
и т.д. – сокращенные обозначения частных
производных.
Все уравнения данного класса, в зависимости от знака дискриминанта можно разделить на три основных типа:
а) уравнения эллиптического типа (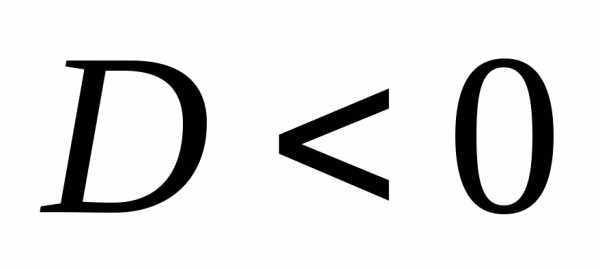 )
– описывают стационарные процессы,
т.е. процессы не изменяющиеся по времени,
пример- уравнение Лапласа для двумерной
поверхности (мембрана, круг и т.д.)
)
– описывают стационарные процессы,
т.е. процессы не изменяющиеся по времени,
пример- уравнение Лапласа для двумерной
поверхности (мембрана, круг и т.д.)
б) уравнения гиперболического типа ( )
– описывают процессы распространения
волн, пример
)
– описывают процессы распространения
волн, пример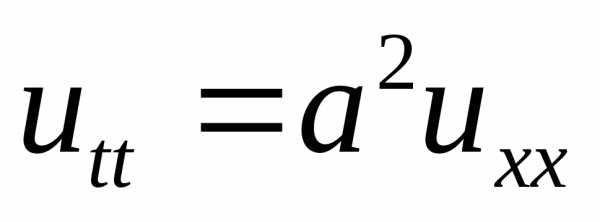 – волновое уравнение в задаче колебания
струны.
– волновое уравнение в задаче колебания
струны.
в)
уравнения параболического типа
( )
– описывают процессы распространения
тепла, пример
)
– описывают процессы распространения
тепла, пример – уравнение теплопроводности в задаче
нагрева/охлаждения стержня.
– уравнение теплопроводности в задаче
нагрева/охлаждения стержня.
Понятие задачи
Общее решение уравнения в частных производных представляет собой бесконечное множество функций от независимых переменных. Для того чтобы выделить единственное решение необходимо задать дополнительные условия – временные и/или краевые. Тем самым вводится понятие задача – это уравнения с дополнительными условиями. Примерами задач являются:
а) задачи распространения волн и тепла в бесконечном стержне:





здесь
указано, что пространственная координата
не имеет ограничений (нет краевых
условий), но вводится начальное условие:
при  функция
функция имеет заданный вид
имеет заданный вид (для гиперболического уравнения –
дополнительное условие на скорость
функции –
(для гиперболического уравнения –
дополнительное условие на скорость
функции – в начальный момент). Данного типа задачи
с начальными условиями именуются
задачамиКоши.
в начальный момент). Данного типа задачи
с начальными условиями именуются
задачамиКоши.
Если вышеуказанные процессы рассматривать в ограниченной области пространства, то начальные условия дополняются граничными, тем самым рассматриваются смешанные задачи:
б) задача колебания закрепленной на концах струны:

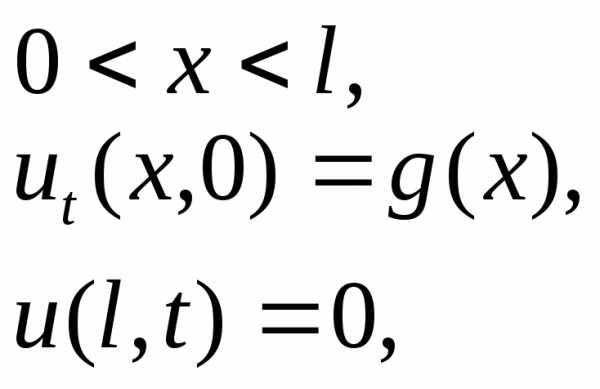

здесь
область пространства ограниченна
,
кроме начального заданы также краевые
условия (т.к. струна закреплена, то ее
колебания в точках
в точках и
и в любой момент времени отсутствуют)
в любой момент времени отсутствуют)
в) задача нагрева/охлаждения стержня:
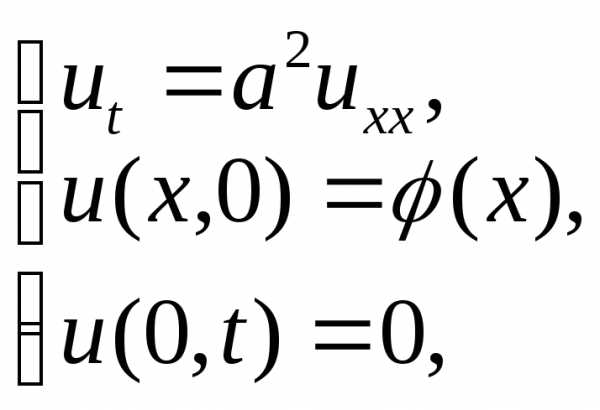


Отметим,
что возможны и другие виды граничных
условий (в частности производные от
функции  на концах стержня и т.д.)
на концах стержня и т.д.)
Для эллиптических задач (при рассмотрении стационарных явлений) вводятся краевые (граничные) условия, среди которых выделяют три основных:
а) граничное
условие I
рода (условие Дирихле) – решение
эллиптического уравнения ищется в
некоторой области пространства  при заданном значении на границе этой
области
при заданном значении на границе этой
области ,
например для уравнения Лапласа:
,
например для уравнения Лапласа:


Пример задачи Дирихле для уравнения Лапласа – распространение температуры/эл. заряда внутри некоторого тела при заданной температуре/потенциале на его поверхности.
б) граничное
условие II
рода (условие Неймана) – решение
эллиптического уравнения ищется в
некоторой области пространства  при заданном значении на границе этой
области
при заданном значении на границе этой
области внешней нормальной производной искомой
функции –
внешней нормальной производной искомой
функции – :
:
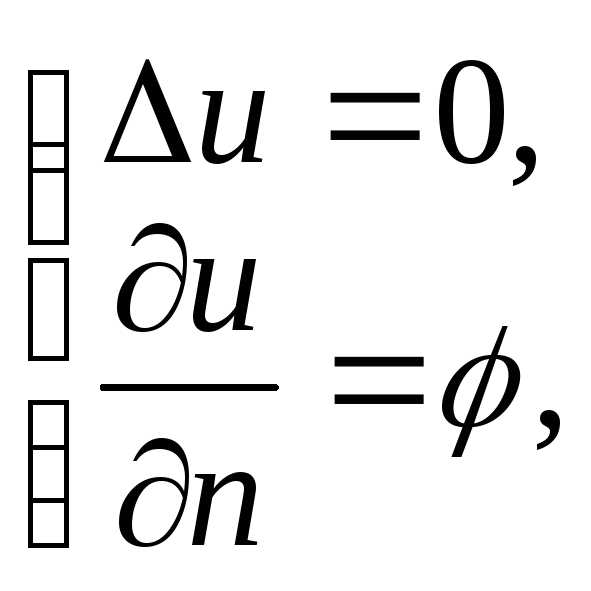

Пример задачи Неймана для уравнения Лапласа – распространение температуры/эл. заряда внутри некоторого тела при заданном потоке температуры/заряде на его поверхности.


в) граничное
условие III
рода (условие Робэна) – решение
эллиптического уравнения ищется в
некоторой области пространства  ,
удовлетворяющее на границе этой области
,
удовлетворяющее на границе этой области условию
условию ,
где
,
где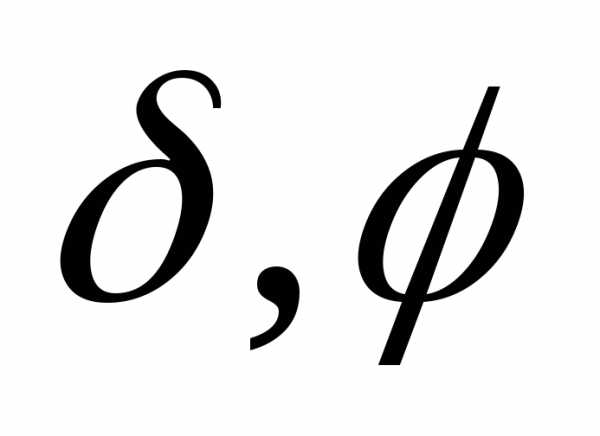 – некоторые функции:
– некоторые функции:
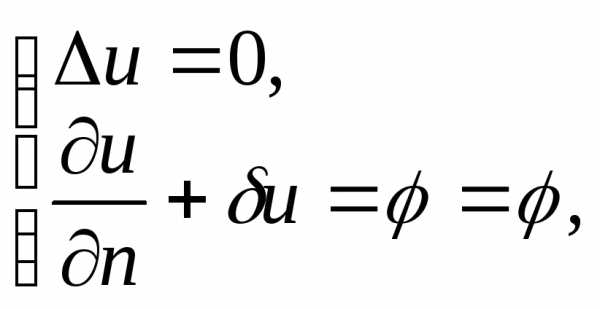

Отметим,
что для различных уравнений, описанных
в эллиптических задачах, необходимо
выполнение дополнительных условий,
связанных с физической сутью задач. Так
для уравнения Лапласа в задаче Неймана
накладывается ограничение: 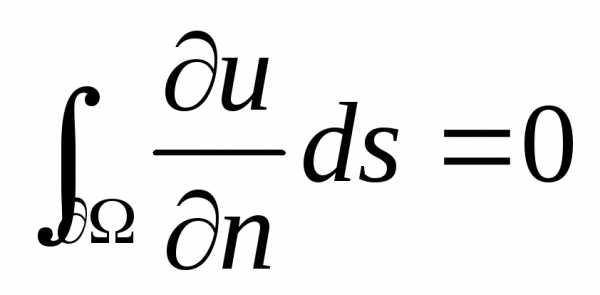 – т.е. полный поток через всю поверхность
тела должен равняться нулю (входящий
поток равен исходящему).
– т.е. полный поток через всю поверхность
тела должен равняться нулю (входящий
поток равен исходящему).
2. Метод Фурье
Одним из наиболее изученных методов решений частных производныхII порядка является метод разделения переменных (метод Фурье). Для рассмотрения данного метода воспользуемся следующим примером: дана задача о распределении заряда на прямоугольной пластине в случае, если на левую сторону нанесен потенциал (переменный вдоль стороны)
Данная задача представляет собой задачу Дирихле для эллиптического уравнения Лапласа на плоскости:


В методе Фурье решение ищется в виде функции с разделенными переменными, в данном случае . При подстановке данной функции в исходное уравнение все частные производные обратятся в обыкновенные:
При этом само уравнение обратится в уравнение с разделенными переменными (в дальнейшем будем опускать обозначения переменных функций):
Непосредственно разделяя переменные, получим:
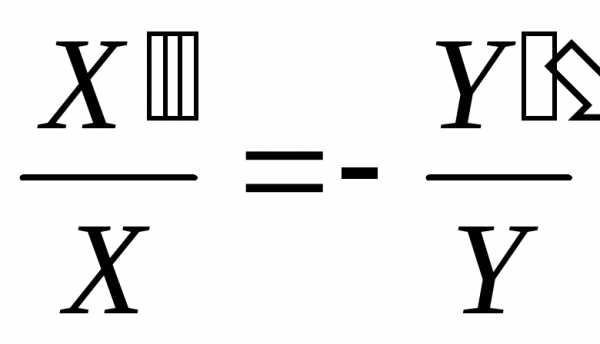
Так как правая и левая части уравнений зависят от разных переменных, то они равны только в том случае, если являются константой, т.е.
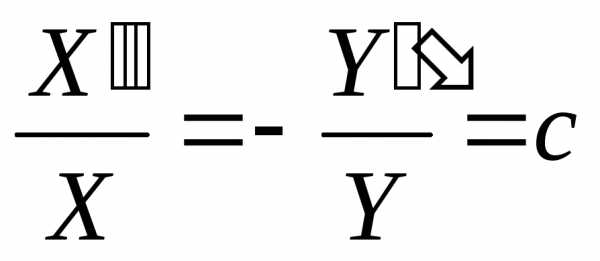
Отсюда можно записать систему из двух обыкновенных дифференциальных уравнений:
(1) 
Далее рассматривают решение одного из этих уравнений, учитывая заданные граничные условия. В данном случае возьмем второе уравнение, для которого граничные условия выводятся следующим образом:
для
нетривиальных значений 
Аналогично:
– т.е. оба граничных условия для данного уравнения однородны.
В итоге получаем обыкновенное однородное дифференциальное уравнение с однородными граничными условиями:

Решение
данной системы представляет собой задачу
Штурма-Лиувилля.
Эта задача связанна с поиском собственных
значений (чисел) константы  и связанных с ними собственными функциями
и связанных с ними собственными функциями ,
при этом доказано, что существует счетное
(дискретное) множество этих функций
(чисел).
,
при этом доказано, что существует счетное
(дискретное) множество этих функций
(чисел).
Задача Штурма-Лиувилля
Рассмотрим однородное дифференциальное уравнение системы. Для нахождения его общего решения необходимо составить характеристическое уравнение и найти его корни:
В зависимости от знака константы, структура общего решения будет различаться. При этом для нахождения частных решений необходимо использовать краевые условий . Возможны три ситуации:
а)
общее решение:
частное решение: , можно показать, что данная система имеет нетривиальное решение только в случае, если
 ,
что противоречит условию данной
структуры общего решения.
,
что противоречит условию данной
структуры общего решения.
б) 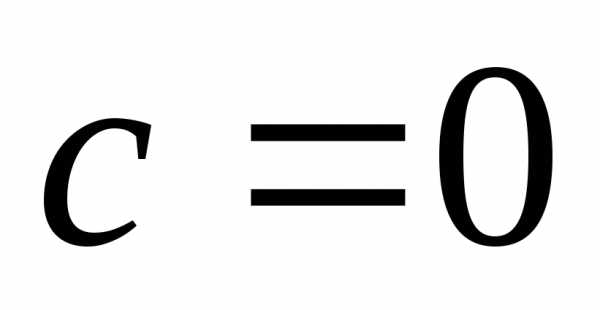
общее решение:
частное решение:
 и данная система не имеет нетривиальных
решений.
и данная система не имеет нетривиальных
решений.
в) 
общее решение: т.к. , то
частное решение:

Последнее уравнение обладает бесконечным множеством нетривиальных решений:
где
Отсюда
искомая функция 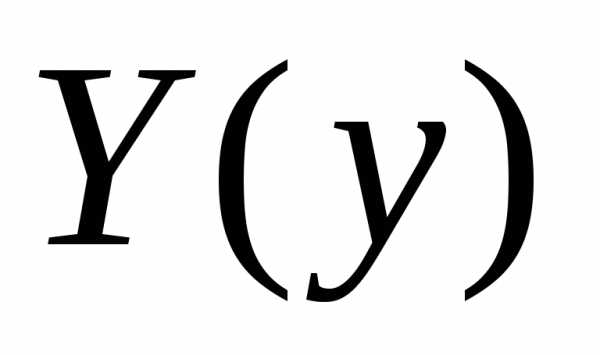 запишется в виде:
запишется в виде:
Непосредственной
подстановкой в исходное уравнение можно
доказать что данная функция является
частным решением для любых значений 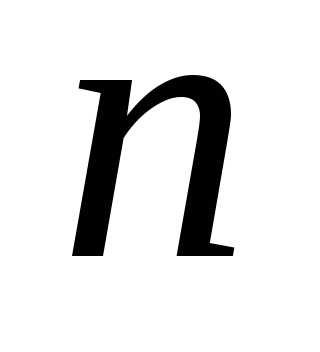 .
Для счетного множества значений
.
Для счетного множества значений ,
множества собственных чисел и функций
запишутся в виде:
,
множества собственных чисел и функций
запишутся в виде:
(2)  ,
,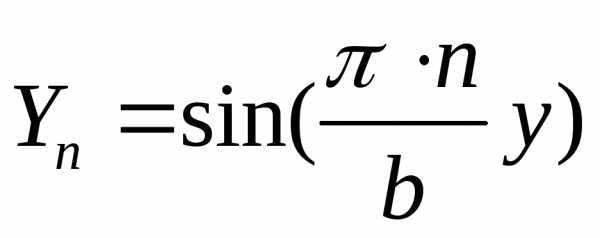
Метод Фурье (продолжение)
Рассмотрим первое уравнение системы (1):
Его
общее решение с учетом корней
характеристического уравнения ( )
и положительности значений константы
(
)
и положительности значений константы
(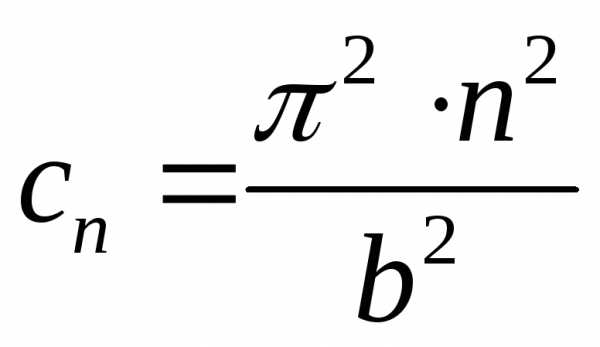 )
запишется в виде:
)
запишется в виде:
(здесь 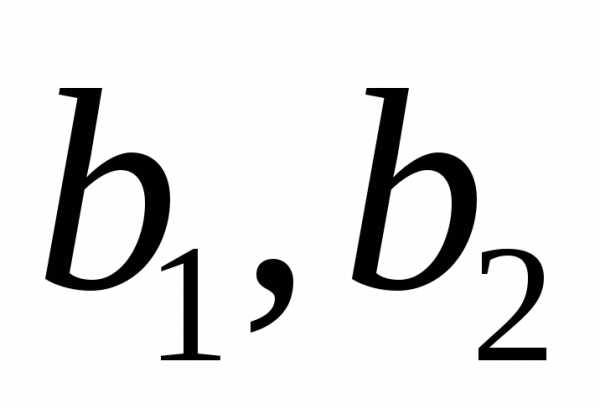 –
константы интегрирования)
–
константы интегрирования)
Для дальнейших построений, воспользуемся одним из граничных условий уравнения (1), а именно однородным условием: . Подставляя в него полученное выше решение, получим:
Т.е.
формула для  запишется следующим образом:.
Данное выражение обычно записывают в
более удобном виде, приводя к формуле
для гиперболического синуса:
запишется следующим образом:.
Данное выражение обычно записывают в
более удобном виде, приводя к формуле
для гиперболического синуса:
Множество собственных функций в данном случае:
Теперь можно обратиться к общей идеи метода Фурье – к поиску всего многообразия частных решений в виде . Доказано, что линейная комбинация частных решений также является частным решением, поэтому наиболее «полное» решение исходной задачи представляется следующей зависимостью:
где  – константы, значение которых необходимо
определить, используя условия задачи.
– константы, значение которых необходимо
определить, используя условия задачи.
В
нашем случае однородные граничные
условия для 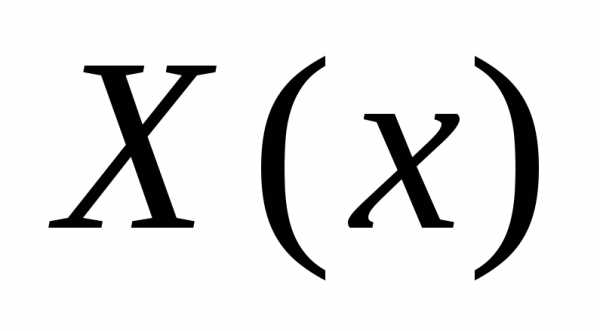 и
и использовались для решения задачи
Штурма – Лиувилля, поэтому для определения
использовались для решения задачи
Штурма – Лиувилля, поэтому для определения используем неоднородное граничное
условие:.
Имеем:
используем неоднородное граничное
условие:.
Имеем:
(при
этом можно показать, что  ).
Подставляя данное выражение в граничное
условие,
получим:
).
Подставляя данное выражение в граничное
условие,
получим:
Учитывая выражения для коэффициентов Фурье для тригонометрического ряда (для нечетных функций: ), запишем:
Тем самым мы получили искомый ответ исходной задачи:
,
где
Для
проверки этого решения его необходимо
подставить в исходное уравнение, что с
учетом наличия рядов является трудоемкой
задачей. Для упрощения процедуры,
преобразуем исходную задачу, а именно
выберем конкретный вид функции  :.
:.
Находя
коэффициенты  ,
получим:
,
получим:
для 
для 
Окончательный
результат: 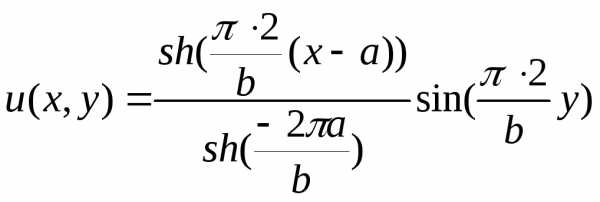 можно проверить непосредственно
подстановкой в исходное уравнение.
можно проверить непосредственно
подстановкой в исходное уравнение.
Представленный вывод может быть получен более простым способом – непосредственной анализом «общей» линейной последовательности по известному (конкретному) граничному условию.
Имеем:
.
Для любых нет значений
нет значений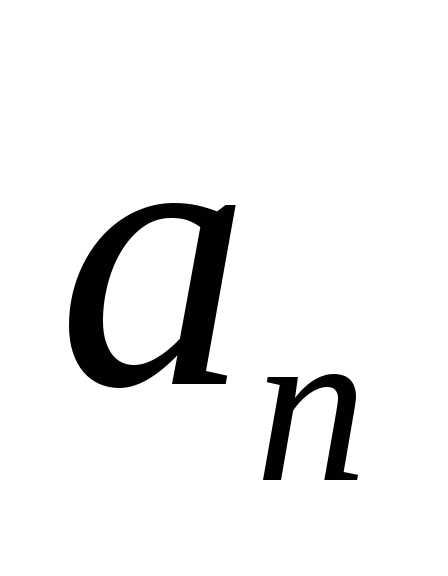 приводящих данное выражение в верное
тождество. Соответственно для
приводящих данное выражение в верное
тождество. Соответственно для получаем:
получаем:
Задания
Для рассмотренного в методичке примера решить следующие задачи






Проверить решения на примерах с заданными функциями неоднородных граничных условий (как в приведенном ранее примере, где ).
studfiles.net
Метод разделения переменных — WiKi
Рассмотрим обыкновенное дифференциальное уравнение, правая часть которого есть произведение функции только от x{\displaystyle x} на функцию только от y{\displaystyle y} [4]:
dydx=g(x)h(y).(1){\displaystyle {\frac {dy}{dx}}=g(x)h(y).\qquad (1)}
При h(y)≠0{\displaystyle h(y)\neq 0} это уравнение можно переписать в виде
dyh(y)=g(x)dx{\displaystyle {\frac {dy}{h(y)}}=g(x)dx} .
Пусть y(x){\displaystyle y(x)} — некоторое решение уравнения (1). Из равенства дифференциалов следует, что их неопределённые интегралы отличаются лишь произвольным постоянным слагаемым:
∫dyh(y)=∫g(x)dx+C{\displaystyle \int {\frac {dy}{h(y)}}=\int g(x)dx+C} .
Вычисляя интегралы, получим общий интеграл уравнения (1).
Если уравнение задано в виде[5]:
M(x)N(y)dx+P(x)Q(y)dy=0,{\displaystyle M(x)N(y)dx+P(x)Q(y)dy=0,}
то для разделения переменных не нужно приводить его к виду (1). Достаточно разделить обе части на N(y)P(x){\displaystyle N(y)P(x)} :
M(x)dxP(x)+Q(y)dyN(y)=0,{\displaystyle {\frac {M(x)dx}{P(x)}}+{\frac {Q(y)dy}{N(y)}}=0,}
откуда получится общий интеграл
∫M(x)dxP(x)+∫Q(y)dyN(y)=C.{\displaystyle \int {\frac {M(x)dx}{P(x)}}+\int {\frac {Q(y)dy}{N(y)}}=C.}
Пример
Пусть
xdy−ydx=0{\displaystyle xdy-ydx=0} [6].
Разделяя переменные, получим
dyy=dxx.{\displaystyle {\frac {dy}{y}}={\frac {dx}{x}}.}
Интегрируя обе части последнего равенства, будем иметь
ln|y|=ln|x|+lnC1,{\displaystyle \ln |y|=\ln |x|+\ln C_{1},}
где C1{\displaystyle C_{1}} — положительная постоянная. Отсюда
|y|=C1|x|{\displaystyle |y|=C_{1}|x|}
или
y=Cx,{\displaystyle y=Cx,}
где C=±C1{\displaystyle C=\pm C_{1}} — произвольная постоянная, которая может принимать как положительные, так и отрицательные значения.
Решениями данного дифференциального уравнения являются также функции x=0{\displaystyle x=0} и y=0{\displaystyle y=0} . Последнее решение получается из общего решения y=Cx{\displaystyle y=Cx} при C=0{\displaystyle C=0} .
Метод разделения переменных применяется для решения краевых задач для линейных уравнений второго порядка гиперболического, параболического и эллиптического типов, а также для некоторых классов нелинейных уравнений и уравнений высших порядков [7].
Однородное уравнение
Приведем схему метода для задачи о колебаниях струны, закрепленной на концах[8]:
utt=a2uxx,(2){\displaystyle u_{tt}=a^{2}u_{xx},\qquad (2)}
u(0,t)=0,u(l,t)=0,(3){\displaystyle u(0,t)=0,\quad u(l,t)=0,\qquad (3)}
u(x,0)=φ(x),ut(x,0)=ψ(x).(4){\displaystyle u(x,0)=\varphi (x),\quad u_{t}(x,0)=\psi (x).\qquad (4)}
Будем искать тождественно не равные нулю решения уравнения (2), удовлетворяющие краевым условиям (3) в виде произведения
u(x,t)=X(x)T(t).(5){\displaystyle u(x,t)=X(x)T(t).\quad (5)}
Подставим предполагаемый вид решения в уравнение (2) и поделим на a2X(x)T(t){\displaystyle a^{2}X(x)T(t)} :
X″(x)X(x)=T″(t)a2T(t).(6){\displaystyle {\frac {X”(x)}{X(x)}}={\frac {T”(t)}{a^{2}T(t)}}.\qquad (6)}
Левая часть равенства (6) является функцией только переменного x{\displaystyle x} , правая — только t{\displaystyle t} . Следовательно, обе части не зависят ни от x{\displaystyle x} , ни от t{\displaystyle t} и равны некоторой константе −λ{\displaystyle -\lambda } . Получаем обыкновенные дифференциальные уравнения для определения функций X(x){\displaystyle X(x)} и T(t){\displaystyle T(t)} :
X″(x)+λX(x)=0,X(x)≢0,(7){\displaystyle X”(x)+\lambda X(x)=0,\quad X(x)\not \equiv 0,\qquad (7)}
T″(t)+a2λT(t)=0,T(t)≢0,(8){\displaystyle T”(t)+a^{2}\lambda T(t)=0,\quad T(t)\not \equiv 0,\qquad (8)}
Подставляя (5) в краевые условия (3), получаем
X(0)=X(l)=0.(9){\displaystyle X(0)=X(l)=0.\qquad (9)}
Приходим к задаче задаче Штурма-Лиувилля (7),(9). Эта задача только при значениях λ{\displaystyle \lambda } , равных собственным значениям
λn=(πnl)2,n=1,2,3,…{\displaystyle \lambda _{n}=\left({\frac {\pi n}{l}}\right)^{2},\quad n=1,2,3,\dots }
имеет нетривиальные решения (собственные функции)
Xn(x)=sinπnlx,{\displaystyle X_{n}(x)=\sin {\frac {\pi n}{l}}x,}
определяемые с точностью до произвольного множителя. Этим же значениям λn{\displaystyle \lambda _{n}} соответствуют решения уравнения (8)
Tn(t)=Ancosπnlat+Bnsinπnlat,{\displaystyle T_{n}(t)=A_{n}\cos {\frac {\pi n}{l}}at+B_{n}\sin {\frac {\pi n}{l}}at,}
где An{\displaystyle A_{n}} и Bn{\displaystyle B_{n}} — произвольные постоянные.
Таким образом, функции
un(x,t)=Xn(x)Tn(t){\displaystyle u_{n}(x,t)=X_{n}(x)T_{n}(t)}
являются частными решениями уравнения (2), удовлетворяющими условиям (3). Решение задачи (2)-(4) получается в виде бесконечной суммы частных решений
u(x,t)=∑n=1∞un(x,t)=∑n=1∞(Ancosπnlat+Bnsinπnlat)sinπnlx,{\displaystyle u(x,t)=\sum _{n=1}^{\infty }u_{n}(x,t)=\sum _{n=1}^{\infty }\left(A_{n}\cos {\frac {\pi n}{l}}at+B_{n}\sin {\frac {\pi n}{l}}at\right)\sin {\frac {\pi n}{l}}x,}
где константы An{\displaystyle A_{n}} и Bn{\displaystyle B_{n}} могут быть найдены из начальных условий (4) как коэффициенты Фурье функций φ(x){\displaystyle \varphi (x)} и ψ(x){\displaystyle \psi (x)} :
An=2l∫0lφ(x)sinπnlxdx,Bn=2πna∫0lψ(x)sinπnlxdx.{\displaystyle A_{n}={\frac {2}{l}}\int _{0}^{l}\varphi (x)\sin {\frac {\pi n}{l}}xdx,\quad B_{n}={\frac {2}{\pi na}}\int _{0}^{l}\psi (x)\sin {\frac {\pi n}{l}}xdx.}
Метод разделения переменных также применим к уравнению колебаний струны общего вида
∂∂x[k(x)∂u∂x]−q(x)u=ρ(x)∂2u∂t2,{\displaystyle {\frac {\partial }{\partial x}}\left[k(x){\frac {\partial u}{\partial x}}\right]-q(x)u=\rho (x){\frac {\partial ^{2}u}{\partial t^{2}}},}
где k{\displaystyle k} , q{\displaystyle q} и ρ{\displaystyle \rho } — непрерывные положительные на отрезке 0<x<l{\displaystyle 0<x<l} функции[9]. В этом случае решение строится в виде ряда по собственным функциям задачи Штурма-Лиувилля
ddx[k(x)dXdx]−q(x)X+λρ(x)X=0,X(0)=X(l)=0.(10){\displaystyle {\frac {d}{dx}}\left[k(x){\frac {dX}{dx}}\right]-q(x)X+\lambda \rho (x)X=0,\quad X(0)=X(l)=0.\qquad (10)}
Основополагающие работы по обоснованию метода Фурье принадлежат В. А. Стеклову[10]. Теорема Стеклова утверждает, что при определенных условиях любая функция единственным образом разлагается в ряд Фурье по собственным функциями краевой задачи (10).
Неоднородное уравнение
Метод разделения переменных для неоднородных уравнений иногда называют методом Крылова в честь А. Н. Крылова[2]. При решении краевой задачи для уравнения неоднородного уравнения колебаний струны
utt=a2uxx+f(x,t)(11){\displaystyle u_{tt}=a^{2}u_{xx}+f(x,t)\quad (11)}
функции u{\displaystyle u} и f{\displaystyle f} разлагаются в ряды Фурье по системе собственных функций задачи Штурма-Лиувилля для соответствующего однородного уравнения (2):
u(x,t)=∑n=1∞Tn(t)sinπnlx,{\displaystyle u(x,t)=\sum _{n=1}^{\infty }T_{n}(t)\sin {\frac {\pi n}{l}}x,}
f(x,t)=∑n=1∞fn(t)sinπnlx.{\displaystyle f(x,t)=\sum _{n=1}^{\infty }f_{n}(t)\sin {\frac {\pi n}{l}}x.}
Подстановка полученных рядов в уравнение (11) с учетом ортогональности системы {sinπnlx}{\displaystyle \left\{\sin {\frac {\pi n}{l}}x\right\}} даёт уравнение относительно Tn(t){\displaystyle T_{n}(t)} :
Tn″(t)+a2λnTn(t)=fn(t).(12){\displaystyle T”_{n}(t)+a^{2}\lambda _{n}T_{n}(t)=f_{n}(t).\qquad (12)}
Функции Tn(t){\displaystyle T_{n}(t)} могут быть найдены как решения задач Коши для уравнений (12) с начальными условиями, полученными из начальных условий исходной краевой задачи.
ru-wiki.org
3.. Решение однородной краевой задачи теплопроводности методом разделения переменных
Вернемся к задаче охлаждения стержня ограниченных размеров (3.5).
Оба края стержня находятся при фиксированной нулевой температуре.
Представим искомую функцию, в виде
и подставим в дифференциальное уравнение.
,
Разделим переменные:
.
Левая часть зависит только от , а правая только от . Такое возможно, только если обе части одна и та же константа. Если эта константа отрицательна, то решение для есть, если константа положительная или равна нулю, то решения нет. Это было доказано в теме 2.
Обозначим
.
Для функций и получаем уравнения
,
.
Построим краевые задачи для этих функций.
Для функции :
Найдем решение этой задачи:
,
,
.
Если , то решение будет нулевое, оно нас не интересует, значит,
→ .
Получаем дискретный набор (собственных значений):
, ему соответствует дискретный набор собственных функций:
, где произвольная константа.
Пользуясь произвольностью выбора , положим что , в таком случае получаем
.
Для функции T: .
Решение дифференциального уравнения имеет вид
.
Найдем из начальных условий:
Пусть , где .
Тогда
,
.
.
Нашли частное решение в виде
.
Чтобы найти общее решение, построим бесконечный ряд
, где (3.8)
Чтобы ряд (3.8) был общим решением задачи (3.5),надо чтобы ряды для , , равномерно сходились.
,
.
Чтобы ряды равномерно сходились, надо чтобы сходились мажорантные ряды:
,
,
Будем считать, что , то есть начальная температура ограничена сверху:
.
Нас интересуют ряды: и
Проверим их сходимость.
Условие сходимости ряда .
Применим его для наших рядов:
, возьмем и рассмотрим отношение:
.
Мы доказали сходимость мажорантных рядов, значит,равномерно сходятся ряды для , , , а значит (3.8) является общим решением задачи (3.5).
, где . (3.8)
3.. Решение неоднородной краевой задачи теплопроводности методом разделения переменных
Задача на подогрев стержня ограниченных размеров имеет вид
(3.9)
Представим её решение в виде суммы решений (метод редукции):
, и для каждого решения составим свои задачи.
(3.9a)
(3.9б)
Задача (3.9a) ранее уже решена. Её решением является:
.
Будем искать решение задачи (3.9б). Представим функцию в виде ряда
, чтобы сразу удовлетворить краевым условиям.
, где
. После подстановки получим:
.
Приравниваем коэффициенты при одинаковых гармониках и получаем дифференциальное уравнение:
(3.9в)
Решение будем искать в виде
.
Покажем, что
– удовлетворяет (3.9в),если – удовлетворяет (3.9г).
(3.9г)
Доказательство:
Складывая оба уравнения системы получим
.Лемма доказана.
Осталось найти решение (3.9г).
Введем переменную . . Получаем измененное условие задачи (3.9г):
, .
Подставим в , получим:
,
,
. (3.10)
При (3.10) сводится к (3.8).
studfiles.net
Дифференциальные уравнения.
Основные понятия о дифференциальных уравнениях.
Дифференциальным уравнением называется алгебраическое равенство, связывающее независимую переменную х, искомую функцию y = (x) и её производные. Если искомая функция является функцией одной переменной х, то дифференциальное уравнение называется обыкновенным дифференциальным уравнением. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком данного дифференциального уравнения.
Общий вид дифференциального уравнения n-порядка следующий:
F(х, у, у…. у(n)) = 0 (1)
Всякая функция у =(x), подставленная в уравнение (1), и обращающая его в верное равенство, называется решением данного дифференциального уравнения.
Дифференциальное уравнение первого порядка имеет следующий общий вид:
F(x, y, y) = 0 (2)
Если его можно разрешить относительно у, то
у = (x, y) (3)
Решение уравнения (3), которое содержит произвольную постоянную С, то есть имеющее вид:
y = (х, С) (4)
называется общим решением данного дифференциального уравнения. Если это решение имеет вид:
(х, у, С) = 0 или (х, у) = С (5),
то в этом случае выражение (5) называется общим интегралом уравнения (3). Решить или проинтегрировать дифференциальное уравнение (3) – значит найти его общее решение в виде (4) или общий интеграл в виде (5).
5.2. Уравнения с разделяющимися переменными.
Запишем уравнение у = (x, y) в виде:
dydx = (x, y),
dy = (x, y)dx
Данному уравнению можно придать следующую форму:
M(x, y)dx + N(x, y)dy = 0 (6)
Предположим, что функции M(x, y) и N(x, y) можно представить следующим образом:
M(x, y) = M1(x) M2(y)
N(x, y) = N1(x) N2(y)
Тогда уравнение (6) можно переписать в виде:
M1(x) M2(y)dx + N1(x) N2(y)dy = 0 (7)
Разделим данное уравнение на M2(y) N1(x), получим
M1(x)N1(x)dx + M2(y)N2(y)dy = 0 (8)
Уравнение (7) называется уравнением с разделяющимися переменными, а уравнение (8) – уравнением с разделенными переменными. Чтобы окончательно решить уравнение (8) перепишем его в следующем виде:
M2(y)N2(y)dy = M1(x)N1(x)dx (9)
Переменные разделились относительно знака равенства: слева от знака равенства алгебраическое выражение зависящее только от у, справа от знака равенства алгебраическое выражение зависящее только от х. Проинтегрируем обе части уравнения (9):
M2(y)N2(y)dy = M1(x)N1(x)dx +C (10)
Данное решение (10) есть общее решение уравнения (7)
Частным решением уравнения(3) называется функция (х,С0), которая получается из общего решения у = (х,С) при определенном значении константы С = С0, которое определяется из начальных условий у0 = (х0,С). Геометрически общее решение у = (х,С) представляет собой семейство интегральных кривых на плоскости Оху, а частное решение у = (х,С0) – одну интегральную кривую, проходящую через заданную точку (х0, у0).
studfiles.net
Метод разделения переменных — Википедия (с комментариями)
Ты – не раб!
Закрытый образовательный курс для детей элиты: “Истинное обустройство мира”.
http://noslave.org
Материал из Википедии — свободной энциклопедии
Метод разделения переменных — метод решения дифференциальных уравнений, основанный на алгебраическом преобразовании исходного уравнения к равенству двух выражений, зависящих от разных независимых переменных.
В применении к уравнениям в частных производных схема разделения переменных приводит к нахождению решения в виде ряда или интеграла Фурье. В этом случае метод также называют методом Фурье (в честь Жана Батиста Фурье, построившего решения уравнения теплопроводности в виде тригонометрических рядов[1]) и методом стоячих волн[2][3].
Обыкновенные дифференциальные уравнения
Рассмотрим обыкновенное дифференциальное уравнение, правая часть которого есть произведение функции только от <math>x</math> на функцию только от <math>y</math> [4]:
<math>\frac{dy}{dx} = g(x) h(y). \qquad (1)</math>
При <math>h(y) \ne 0</math> это уравнение можно переписать в виде
<math>\frac{dy}{h(y)} = g(x) dx</math>.
Пусть <math>y(x)</math> — некоторое решение уравнения (1). Из равенства дифференциалов следует, что их неопределённые интегралы отличаются лишь произвольным постоянным слагаемым:
<math> \int \frac{dy}{h(y)} = \int g(x) dx + C </math>.
Вычисляя интегралы, получим общий интеграл уравнения (1).
Если уравнение задано в виде[5]:
<math> M(x)N(y)dx + P(x)Q(y)dy = 0, </math>
то для разделения переменных не нужно приводить его к виду (1). Достаточно разделить обе части на <math> N(y) P(x)</math>:
<math> \frac{M(x) dx}{P(x)} + \frac{ Q(y)dy}{N(y)} = 0, </math>
откуда получится общий интеграл
<math> \int \frac{M(x) dx}{P(x)} + \int \frac{ Q(y)dy}{N(y)} = C. </math>
Пример
Пусть
<math>x dy – y dx = 0</math>[6].
Разделяя переменные, получим
<math> \frac{dy}{y} = \frac{dx}{x}. </math>
Интегрируя обе части последнего равенства, будем иметь
<math> \ln|y| = \ln|x| + \ln C_1, </math>
где <math>C_1</math> — положительная постоянная. Отсюда
<math> |y| = C_1 |x| </math>
или
<math> y = Cx, </math>
где <math>C = \pm C_1</math> — произвольная постоянная, которая может принимать как положительные, так и отрицательные значения.
Решениями данного дифференциального уравнения являются также функции <math> x = 0 </math> и <math> y = 0 </math>. Последнее решение получается из общего решения <math> y = C x </math> при <math> C = 0 </math>.
Уравнения в частных производных
Метод разделения переменных применяется для решения краевых задач для линейных уравнений второго порядка гиперболического, параболического и эллиптического типов, а также для некоторых классов нелинейных уравнений и уравнений высших порядков [7].
Однородное уравнение
Приведем схему метода для задачи о колебаниях струны, закрепленной на концах[8]:
<math> u_{tt} = a^2 u_{xx}, \qquad (2) </math>
<math> u(0,t) = 0, \quad u(l, t) = 0, \qquad (3) </math>
<math> u(x, 0) = \varphi(x), \quad u_t(x, 0) = \psi(x). \qquad (4) </math>
Будем искать тождественно не равные нулю решения уравнения (2), удовлетворяющие краевым условиям (3) в виде произведения
<math> u(x, t) = X(x) T(t). \quad (5) </math>
Подставим предполагаемый вид решения в уравнение (2) и поделим на <math> a^2 X(x) T(t) </math>:
<math> \frac{X(x)}{X(x)} = \frac{T(t)}{a^2 T(t)}. \qquad (6) </math>
Левая часть равенства (6) является функцией только переменного <math>x</math>, правая — только <math>t</math>. Следовательно, обе части не зависят ни от <math>x</math>, ни от <math>t</math> и равны некоторой константе <math>-\lambda</math>. Получаем обыкновенные дифференциальные уравнения для определения функций <math>X(x)</math> и <math>T(t)</math>:
<math> X(x) + \lambda X(x) = 0, \quad X(x) \not \equiv 0, \qquad (7) </math>
<math> T(t) + a^2 \lambda T(t) = 0, \quad T(t) \not \equiv 0, \qquad (8) </math>
Подставляя (5) в краевые условия (3), получаем
<math> X(0) = X(l) = 0. \qquad (9) </math>
Приходим к задаче задаче Штурма-Лиувилля (7),(9). Эта задача только при значениях <math>\lambda</math>, равных собственным значениям
<math> \lambda_n = \left(\frac{\pi n}{l}\right)^2, \quad n = 1, 2, 3, \dots </math>
имеет нетривиальные решения (собственные функции)
<math> X_n(x) = \sin \frac{\pi n }{l} x, </math>
определяемые с точностью до произвольного множителя. Этим же значениям <math>\lambda_n</math> соответствуют решения уравнения (8)
<math> T_n(t) = A_n \cos \frac{\pi n}{l} at + B_n \sin \frac{\pi n}{l} at, </math>
где <math> A_n </math> и <math> B_n </math> — произвольные постоянные.
Таким образом, функции
<math> u_n(x, t) = X_n(x) T_n(t) </math>
являются частными решениями уравнения (2), удовлетворяющими условиям (3). Решение задачи (2)-(4) получается в виде бесконечной суммы частных решений
<math> u(x, t) = \sum_{n = 1}^{\infty} u_n(x, t) = \sum_{n = 1}^{\infty} \left(A_n \cos \frac{\pi n}{l} at + B_n \sin \frac{\pi n}{l} at \right) \sin \frac{\pi n }{l} x, </math>
где константы <math>A_n</math> и <math>B_n</math> могут быть найдены из начальных условий (4) как коэффициенты Фурье функций <math> \varphi(x)</math> и <math> \psi(x) </math>:
<math> A_n = \frac{2}{l} \int_0^l \varphi(x) \sin \frac{\pi n}{l} x dx, \quad B_n = \frac{2}{\pi n a} \int_0^l \psi(x) \sin \frac{\pi n}{l} x dx. </math>
Метод разделения переменных также применим к уравнению колебаний струны общего вида
<math> \frac{\partial}{\partial x} \left[ k(x) \frac{\partial u}{\partial x} \right] – q(x) u = \rho(x) \frac{\partial^2 u}{\partial t^2}, </math>
где <math>k</math>, <math>q</math> и <math>\rho</math> — непрерывные положительные на отрезке <math> 0 < x < l </math> функции[9]. В этом случае решение строится в виде ряда по собственным функциям задачи Штурма-Лиувилля
<math> \frac{d}{d x} \left[ k(x) \frac{d X}{d x} \right] – q(x) X + \lambda \rho(x) X = 0, \quad X(0) = X(l) = 0. \qquad (10) </math>
Основополагающие работы по обоснованию метода Фурье принадлежат В. А. Стеклову[10]. Теорема Стеклова утверждает, что при определенных условиях любая функция единственным образом разлагается в ряд Фурье по собственным функциями краевой задачи (10).
Неоднородное уравнение
Метод разделения переменных для неоднородных уравнений иногда называют методом Крылова в честь А. Н. Крылова[2]. При решении краевой задачи для уравнения неоднородного уравнения колебаний струны
<math> u_{tt} = a^2 u_{xx} + f(x, t) \quad (11) </math>
функции <math>u</math> и <math>f</math> разлагаются в ряды Фурье по системе собственных функций задачи Штурма-Лиувилля для соответствующего однородного уравнения (2):
<math> u(x, t) = \sum_{n = 1}^{\infty} T_n(t) \sin \frac{\pi n}{l}x, </math>
<math> f(x, t) = \sum_{n = 1}^{\infty} f_n(t) \sin \frac{\pi n}{l} x. </math>
Подстановка полученных рядов в уравнение (11) с учетом ортогональности системы <math> \left \{ \sin \frac{\pi n}{l} x \right \} </math> даёт уравнение относительно <math>T_n(t)</math>:
<math> T_n(t) + a^2 \lambda_n T_n(t) = f_n(t). \qquad (12) </math>
Функции <math>T_n(t)</math> могут быть найдены как решения задач Коши для уравнений (12) с начальными условиями, полученными из начальных условий исходной краевой задачи.
См. также
Напишите отзыв о статье “Метод разделения переменных”
Примечания
- ↑ Клейн Ф. Лекции о развитии математики в XIX столетии. — М.-Л.: ГОНТИ, 1937. — Т. I. — С. 103.
- ↑ 1 2 Юрко В. А. Уравнения математической физики, 2004.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 88.
- ↑ Смирнов В. И. Курс высшей математики, 1974, Т. 2, с. 14.
- ↑ Степанов В. В. Курс дифференциальных уравнений, 1950, с. 24.
- ↑ Демидович Б. П., Моденов В. П. Дифференциальные уравнения, 2008, с. 19.
- ↑ Зайцев В. Ф., Полянин А. Д. Метод разделения переменных в математической физике, 2009.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 82.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 113.
- ↑ Тихонов А. Н., Самарский А. А. Уравнения математической физики, 1999, с. 119.
Литература
- Смирнов В. И. Курс высшей математики. — 21-е издание. — Наука, 1974. — Т. 2.
- Степанов В. В. Курс дифференциальных уравнений. — Изд. 6-е. — 1950.
- Демидович Б. П., Моденов В. П. Дифференциальные уравнения: учебное пособие. — 3-е изд.. стер.. — СПб.: Лань, 2008. — 288 с.
- Зайцев В. Ф., Полянин А. Д. Метод разделения переменных в математической физике. — СПб., 2009. — 92 с. — ISBN 978–5–94777–211–1.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики: Учебное пособие.. — 6-е изд., испр. и доп.. — М.: Изд-во МГУ, 1999. — 798 с. — ISBN 5-211-04138-0.
- Юрко В. А. Уравнения математической физики: учеб. пособие для студентов механико-математического и физического факультетов. — Саратов: Изд-во Сарат. ун-та, 2004. — 118 с. — ISBN 5-292-03022-8.
Отрывок, характеризующий Метод разделения переменных
Через два часа после этого князь Андрей тихими шагами вошел в кабинет к отцу. Старик всё уже знал. Он стоял у самой двери, и, как только она отворилась, старик молча старческими, жесткими руками, как тисками, обхватил шею сына и зарыдал как ребенок.Через три дня отпевали маленькую княгиню, и, прощаясь с нею, князь Андрей взошел на ступени гроба. И в гробу было то же лицо, хотя и с закрытыми глазами. «Ах, что вы со мной сделали?» всё говорило оно, и князь Андрей почувствовал, что в душе его оторвалось что то, что он виноват в вине, которую ему не поправить и не забыть. Он не мог плакать. Старик тоже вошел и поцеловал ее восковую ручку, спокойно и высоко лежащую на другой, и ему ее лицо сказало: «Ах, что и за что вы это со мной сделали?» И старик сердито отвернулся, увидав это лицо.
Еще через пять дней крестили молодого князя Николая Андреича. Мамушка подбородком придерживала пеленки, в то время, как гусиным перышком священник мазал сморщенные красные ладонки и ступеньки мальчика.
Крестный отец дед, боясь уронить, вздрагивая, носил младенца вокруг жестяной помятой купели и передавал его крестной матери, княжне Марье. Князь Андрей, замирая от страха, чтоб не утопили ребенка, сидел в другой комнате, ожидая окончания таинства. Он радостно взглянул на ребенка, когда ему вынесла его нянюшка, и одобрительно кивнул головой, когда нянюшка сообщила ему, что брошенный в купель вощечок с волосками не потонул, а поплыл по купели.
Участие Ростова в дуэли Долохова с Безуховым было замято стараниями старого графа, и Ростов вместо того, чтобы быть разжалованным, как он ожидал, был определен адъютантом к московскому генерал губернатору. Вследствие этого он не мог ехать в деревню со всем семейством, а оставался при своей новой должности всё лето в Москве. Долохов выздоровел, и Ростов особенно сдружился с ним в это время его выздоровления. Долохов больной лежал у матери, страстно и нежно любившей его. Старушка Марья Ивановна, полюбившая Ростова за его дружбу к Феде, часто говорила ему про своего сына.
– Да, граф, он слишком благороден и чист душою, – говаривала она, – для нашего нынешнего, развращенного света. Добродетели никто не любит, она всем глаза колет. Ну скажите, граф, справедливо это, честно это со стороны Безухова? А Федя по своему благородству любил его, и теперь никогда ничего дурного про него не говорит. В Петербурге эти шалости с квартальным там что то шутили, ведь они вместе делали? Что ж, Безухову ничего, а Федя все на своих плечах перенес! Ведь что он перенес! Положим, возвратили, да ведь как же и не возвратить? Я думаю таких, как он, храбрецов и сынов отечества не много там было. Что ж теперь – эта дуэль! Есть ли чувство, честь у этих людей! Зная, что он единственный сын, вызвать на дуэль и стрелять так прямо! Хорошо, что Бог помиловал нас. И за что же? Ну кто же в наше время не имеет интриги? Что ж, коли он так ревнив? Я понимаю, ведь он прежде мог дать почувствовать, а то год ведь продолжалось. И что же, вызвал на дуэль, полагая, что Федя не будет драться, потому что он ему должен. Какая низость! Какая гадость! Я знаю, вы Федю поняли, мой милый граф, оттого то я вас душой люблю, верьте мне. Его редкие понимают. Это такая высокая, небесная душа!
Сам Долохов часто во время своего выздоровления говорил Ростову такие слова, которых никак нельзя было ожидать от него. – Меня считают злым человеком, я знаю, – говаривал он, – и пускай. Я никого знать не хочу кроме тех, кого люблю; но кого я люблю, того люблю так, что жизнь отдам, а остальных передавлю всех, коли станут на дороге. У меня есть обожаемая, неоцененная мать, два три друга, ты в том числе, а на остальных я обращаю внимание только на столько, на сколько они полезны или вредны. И все почти вредны, в особенности женщины. Да, душа моя, – продолжал он, – мужчин я встречал любящих, благородных, возвышенных; но женщин, кроме продажных тварей – графинь или кухарок, всё равно – я не встречал еще. Я не встречал еще той небесной чистоты, преданности, которых я ищу в женщине. Ежели бы я нашел такую женщину, я бы жизнь отдал за нее. А эти!… – Он сделал презрительный жест. – И веришь ли мне, ежели я еще дорожу жизнью, то дорожу только потому, что надеюсь еще встретить такое небесное существо, которое бы возродило, очистило и возвысило меня. Но ты не понимаешь этого.
– Нет, я очень понимаю, – отвечал Ростов, находившийся под влиянием своего нового друга.
Осенью семейство Ростовых вернулось в Москву. В начале зимы вернулся и Денисов и остановился у Ростовых. Это первое время зимы 1806 года, проведенное Николаем Ростовым в Москве, было одно из самых счастливых и веселых для него и для всего его семейства. Николай привлек с собой в дом родителей много молодых людей. Вера была двадцати летняя, красивая девица; Соня шестнадцати летняя девушка во всей прелести только что распустившегося цветка; Наташа полу барышня, полу девочка, то детски смешная, то девически обворожительная.
В доме Ростовых завелась в это время какая то особенная атмосфера любовности, как это бывает в доме, где очень милые и очень молодые девушки. Всякий молодой человек, приезжавший в дом Ростовых, глядя на эти молодые, восприимчивые, чему то (вероятно своему счастию) улыбающиеся, девические лица, на эту оживленную беготню, слушая этот непоследовательный, но ласковый ко всем, на всё готовый, исполненный надежды лепет женской молодежи, слушая эти непоследовательные звуки, то пенья, то музыки, испытывал одно и то же чувство готовности к любви и ожидания счастья, которое испытывала и сама молодежь дома Ростовых.
В числе молодых людей, введенных Ростовым, был одним из первых – Долохов, который понравился всем в доме, исключая Наташи. За Долохова она чуть не поссорилась с братом. Она настаивала на том, что он злой человек, что в дуэли с Безуховым Пьер был прав, а Долохов виноват, что он неприятен и неестествен.
– Нечего мне понимать, – с упорным своевольством кричала Наташа, – он злой и без чувств. Вот ведь я же люблю твоего Денисова, он и кутила, и всё, а я всё таки его люблю, стало быть я понимаю. Не умею, как тебе сказать; у него всё назначено, а я этого не люблю. Денисова…
– Ну Денисов другое дело, – отвечал Николай, давая чувствовать, что в сравнении с Долоховым даже и Денисов был ничто, – надо понимать, какая душа у этого Долохова, надо видеть его с матерью, это такое сердце!
– Уж этого я не знаю, но с ним мне неловко. И ты знаешь ли, что он влюбился в Соню?
– Какие глупости…
– Я уверена, вот увидишь. – Предсказание Наташи сбывалось. Долохов, не любивший дамского общества, стал часто бывать в доме, и вопрос о том, для кого он ездит, скоро (хотя и никто не говорил про это) был решен так, что он ездит для Сони. И Соня, хотя никогда не посмела бы сказать этого, знала это и всякий раз, как кумач, краснела при появлении Долохова.
Долохов часто обедал у Ростовых, никогда не пропускал спектакля, где они были, и бывал на балах adolescentes [подростков] у Иогеля, где всегда бывали Ростовы. Он оказывал преимущественное внимание Соне и смотрел на нее такими глазами, что не только она без краски не могла выдержать этого взгляда, но и старая графиня и Наташа краснели, заметив этот взгляд.
Видно было, что этот сильный, странный мужчина находился под неотразимым влиянием, производимым на него этой черненькой, грациозной, любящей другого девочкой.
Ростов замечал что то новое между Долоховым и Соней; но он не определял себе, какие это были новые отношения. «Они там все влюблены в кого то», думал он про Соню и Наташу. Но ему было не так, как прежде, ловко с Соней и Долоховым, и он реже стал бывать дома.
С осени 1806 года опять всё заговорило о войне с Наполеоном еще с большим жаром, чем в прошлом году. Назначен был не только набор рекрут, но и еще 9 ти ратников с тысячи. Повсюду проклинали анафемой Бонапартия, и в Москве только и толков было, что о предстоящей войне. Для семейства Ростовых весь интерес этих приготовлений к войне заключался только в том, что Николушка ни за что не соглашался оставаться в Москве и выжидал только конца отпуска Денисова с тем, чтобы с ним вместе ехать в полк после праздников. Предстоящий отъезд не только не мешал ему веселиться, но еще поощрял его к этому. Большую часть времени он проводил вне дома, на обедах, вечерах и балах.
wiki-org.ru
Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
Начальная задача (задача Коши) и теорема существования и единственности решения задачи Коши. Общее и частное решения (интегралы) дифференциального уравнения. Уравнения с разделяющимися переменными
В элементарной математике в основном рассматриваются алгебраические уравнения. Корнями (или решениями) таких уравнений являются, как правило, числа. В линейной алгебре мы имели дело с системами уравнений, решениями которых совокупности чисел (векторы). После изучения дифференциального и интегрального исчисления резонно рассмотреть уравнения, содержащих в качестве неизвестных не числа, а функции. Простейшим примером такого уравнения является следующее: Здесь решением является такая функция производная которой совпадает с известной функцией Эту функцию, как известно называется первообразной для Она имеет вид Это и есть решение уравнения которое называется дифференциальным уравнением. Перейдём к рассмотрению таких уравнений.
1. Общие понятия
Уравнения, в которых неизвестная функция входит под знак производной или диффе-ренциала, называется дифференциальным уравнением. Например,
Если неизвестная функция зависит только от одной переменной, то соответствующее уравнение называется обыкновенным уравнением (таковыми являются уравнения 1-3). Если же она зависит от двух и более переменных, то соответствующее уравнение называется уравнением в частных производных (таковым является уравнение 4).
Здесь рассматриваются только обыкновенные уравнения. Они часто встречаются на практике. Например, уравнение выражает собой второй закон Ньютона, а уравнение описывает вынужденные колебания линейного осциллятора (точкой обозначено дифференцирование по ).
Порядком дифференциального уравнения называется максимальный порядок входящей в него производной неизвестной функции или её дифференциала. Например, уравнения 1 и 3 – дифференциальные уравнения первого порядка, а уравнение 2 – уравнение го порядка.
2. Дифференциальные уравнения первого порядка, его частное и общее решения (интегралы). Теорема Коши существования и единственности решения начальной задачи. Геометрическийсмысл дифференциального уравнения. Метод изоклин
Рассмотрим дифференциальное уравнение первого порядка:
где неизвестная функция. Областью определения уравнения (1) называется множество
Определение 1.Функция называется решением уравнения (1) на отрезке[1] если выполнены следующие условия:
1) точка
2) функция дифференцируема на отрезке и имеет место тождество
График решения называется интегральной кривой уравнения (1). Например, функция является решением уравнения на всей числовой оси (проверьте это!). Часто вместо слов “ решить уравнение” говорят “проинтег-
рировать уравнение”.
 Пусть – область определения уравнения (1). Тогда в каждой точке мы можем построить вектор Поскольку угловой коэффициент интегральной кривой в фиксированной точке равен то вектор касается в точке интегральной кривой. Важно заметить, что саму интегральную кривую можно и не знать, а вектор всегда известен. Таким образом, уравнение задаёт в своей области определения множество векторов которое называют векторным полем (или просто полем) дифференциального уравнения (1). В этом и состоит геометрический смысл уравнения (1).
Пусть – область определения уравнения (1). Тогда в каждой точке мы можем построить вектор Поскольку угловой коэффициент интегральной кривой в фиксированной точке равен то вектор касается в точке интегральной кривой. Важно заметить, что саму интегральную кривую можно и не знать, а вектор всегда известен. Таким образом, уравнение задаёт в своей области определения множество векторов которое называют векторным полем (или просто полем) дифференциального уравнения (1). В этом и состоит геометрический смысл уравнения (1).
В связи с этим задачу интегрирования дифференциального уравнения (1) можно свести к построению кривых, касающихся в каждой своей точке векторного поля На такой интерпретации уравнения (1) основан геометрический метод решения, называемый методом изоклин. Поясним его смысл.
Определение 2.Кривая задаваемая уравнением называется изоклиной уравнения (1).
Из геометрического смысла уравнения (1) вытекает, что все его интегральные кривые в произвольной точке изоклины имеют касательные векторы одного и того же наклона (см. рис.1). Построив довольно густую сетку изоклин (с различными постоянными ) и изобразив на них векторы мы, двигаясь от фиксированной точки с изображённым на ней вектором проводим эскиз кривой, которая коснётся вектора на следующей ближайшей изоклине, и т.д. В результате будет нарисована приближенная интегральная кривая уравнения (1) (на рис. 1 изображены не сами векторы , а их небольшие отрезки).
Рассматривая уравнение видим, что оно имеет бесконечное множество реше-
 ний где произвольная постоянная. Такая ситуация имеет место для любого дифференциального уравнения. Для выделения конкретного решения надо задать вместе с равнением (1) ещё так называемое начальное условие означающее, что при решение должно иметь значение Полученная задача называется начальной задачей или задачей Коши и её кратко записывают так:
ний где произвольная постоянная. Такая ситуация имеет место для любого дифференциального уравнения. Для выделения конкретного решения надо задать вместе с равнением (1) ещё так называемое начальное условие означающее, что при решение должно иметь значение Полученная задача называется начальной задачей или задачей Коши и её кратко записывают так:
Геометрически задача Коши означает, что среди всех интегральных кривых уравнения (1) надо найти ту, которая проходит через заданную начальную точку (см. рис. 2). В каком случае задача Коши (2) имеет решение и будет ли оно единственным? Ответ на этот вопрос содержится в следующем утверждении, которое мы даём без доказательства.
Теорема Коши(существования и единственности решения начальной задачи). Пусть в уравнении (1) правая часть и её частная производная непрерывны в области определения уравнения (1). Тогда какова бы ни была начальная точка
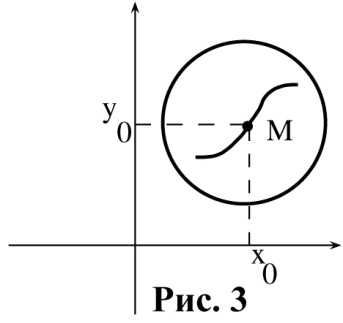 лежащая внутри области существует число такое, что начальная задача (2) с указанной начальной точкой имеет на отрезке решение и это решение единственно на этом отрезке.
лежащая внутри области существует число такое, что начальная задача (2) с указанной начальной точкой имеет на отрезке решение и это решение единственно на этом отрезке.
Геометрически это означает, что при выполнении условий теоремы Коши существует окрестность начальной точки в которой содержится лишь одна интегральная кривая уравнения (1), проходящая через точку (см. рис. 3) . Сделаем два замечания.
Замечание 1.Теорема Коши носит достаточный характер. Это означает, что при выполнении её условий решение задачи (2) обязательно существует и единственно. Однако решение может существовать и тогда, когда не выполняются условия этой теоремы. Правда, в этом случае не гарантируется единственность решения. Например, задача Коши имеет два решения: и
В этой задаче правая часть не удовлетворяет условиям теоремы Коши: в окрестности начальной точки частная производная не существует.
Замечание 2. Теорема Коши носит локальный характер. Это означает, что при выполнении её условий существование решения гарантируется лишь в достаточно малой окрестности точки (число вообще говоря, достаточно мало̀).
Перейдём теперь к описанию частного и общего решений и интегралов.
Определение 3.Частным решением уравнения (1) называется решениекакой-нибудь его фиксированной задачи Коши (2), а частным интегралом этого уравнения называется
частное решение записанное в неявной форме
Например, функция является частным решением уравнения а соотношение – частным интегралом того же уравнения.
Определение 4.Общим решением уравнения (1) в области ( область определения уравнения (1))называется функция удовлетворяющая следующим требованиям:
1) какова бы ни была допустимая постоянная функция является решением уравнения (1) на некотором отрезке
2) какова бы ни была начальная точка существует значение постоянной такое, что функция является решением задачи Коши (2) с этой начальной точкой.
Общим интегралом уравнения (1) называется общее решение, записанное в неявной форме
Чтобы проверить, будет ли соотношение общим интегралом уравнения (1), надо из системы уравнений
исключить постоянную Если при этом будет получено дифференциальное уравнение (1) (или эквивалентное ему уравнение), то – общий интеграл уравнения (1).
Пример 1.Проверить, что соотношение является общим интегралом уравнения
Решение. Составляем систему (3) и исключаем постоянную
Получено данное дифференциальное уравнение, значит, – его общий интеграл.
Дифференциальные уравнения с разделяющимися переменными. Однородные уравнения
Опишем теперь аналитические методы решения некоторых дифференциальных уравнений.
1. Уравнения с разделенными переменными:
Ясно, что общий интеграл этого уравнения может быть получен интегрированием обеих частей (функции и непрерывны в своих областях определения):
Отметим, что здесь часто вместо определённых интегралов пишут неопределённые.
2. Уравнения с разделяющимися переменными:
(здесь перед дифференциалами стоят произведения функций с разделёнными переменными).
Предполагая, что функции непрерывны в своих областях определения, разделим обе части уравнения (4) на произведение будем иметь
Получено уравнение с разделёнными переменными. Интегрируя его, получим общий интеграл
Однако это верно в случае, когда Случаи или надо рассматривать отдельно. Если при этом будут получены решения уравнения (4), то их надо присовокупить к уже полченным.
Пример 2.Решить уравнение
Решение. Разделяем переменные, поделив обе части уравнения на произведение
и интегрируем полученное уравнение:
Рассматриваем отдельно случай При исходное уравнение обращается в тождество, значит, – решение. Оно может быть получено из при Функция также удовлетворяет данному уравнение. Однако она не может быть получена из . Следовательно, решениями исходного уравнения является совокупность функций
3. Однородные уравнения:
Такие уравнения приводятся к уравнению с разделяющимися переменной заменой где новая неизвестная функция. Действительно, дифференцируя замену и подставляя её в исходное уравнение, будем иметь
Заметим, что к однородным приводятся уравнения вида
В первом случае надо разделить числитель и знаменатель входящей под знак функции дроби на во втором случае сделать замену переменных где решение системы уравнений
Пример 3.Решить уравнение
Решение.Найдем решение системы Делаем замену переменных Вместо исходного получим следующее уравнение:
 jj
jj
Это уравнение однородно, поэтому делаем замену В итоге получим уравнение решая которое методом разделения переменных, будем иметь
Получен общий интеграл данного уравнения.
Лекция 2. Линейные уравнения первого порядка. Дифференциальные уравнения высшего порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Общее решение и общий интеграл. Методы понижения порядка дифференциального уравнения
Наиболее часто встречаются линейные дифференциальные уравнения. Так называются уравнения, у которых правая часть линейна относительно неизвестной функции. Перейдём к их рассмотрению.
Похожие статьи:
poznayka.org

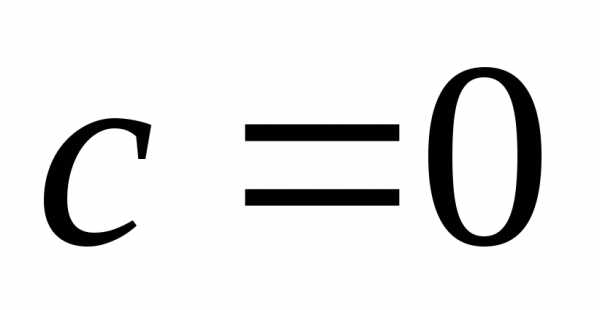 ,
что противоречит условию данной
структуры общего решения.
,
что противоречит условию данной
структуры общего решения. и данная система не имеет нетривиальных
решений.
и данная система не имеет нетривиальных
решений.