Методы описания игры простая и развернутая форма игры – . | – Pandia.ru

2.Основные модели теории игр

1. Развернутая и стратегическая формы игр

Основные модели теории игр следующие.

1. Игра в развёрнутой форме.

2. Игра в стратегической форме.

Анализ любой игры или конфликтной ситуации должен начинаться с описания модели, описывающей игру.

Для представления игры в развёрнутой форме рассмотрим пример – простую карточную игру. В ней два участника, называемые игроками.

Игроки откладывают по доллару, чтобы платить из этих денег выигрыш, и начинают игру.

Первый игрок вытягивает из колоды карту и видит красная она или черная. Второй игрок не знает цвет карты. В этот момент первый игрок может закончить игру. Если он заканчивает игру, то он показывает второму игроку, какого цвета карта. Если она красная, то первый игрок забирает себе все отложенные доллары. В этом случае первый игрок выигрывает один доллар. Если карта черная, то первый игрок проигрывает один доллар, так как отложенные доллары забирает второй игрок.

Если первый игрок продолжает играть, то он добавляет к отложенным долларам еще один доллар.

В этот момент второй игрок может либо закончить игру, либо ее продолжить.

Если второй игрок заканчивает игру, то первый игрок, не зависимо от цвета карты,

забирает все отложенные доллары и его выигрыш составляет один доллар. А второй игрок проигрывает один доллар.

Если второй игрок продолжает игру, то он добавляет к отложенным долларам еще один доллар.

После этого первый игрок показывает ему цвет карты. Если карта красная, то первый игрок забирает все отложенные доллары. Его выигрыш составляет два доллара, а второй игрок проигрывает два доллара. Если карта черная, то все доллары забирает второй игрок. Выигрыш второго игрока составляет два доллара, а первый игрок проигрывает два доллара.

На рисунке показан граф, отображающий события, которые могут возникнуть в игре. Дерево в теории графов – связанный неориентированный граф, не содержащий циклов. Дерево с одной выделенной вершиной называется корневым деревом.

Для того, чтобы дерево игры полностью описывало игру необходимо отобразить тот факт, что игроки находятся не в одинаковых информационных состояниях.

Для того, чтобы пометить, в каких информационных состояниях находятся игроки, вводятся информационные метки: a,b, 0. Единственная роль информационных меток – указание на то, какие вершины не различимы игроками, которые их контролируют.

Графом называется конечное множество точек, или вершин, вместе с множеством рёбер, каждое из которых соединяет пару вершин. Ребро может быть идентифицировано двумя вершинами, которые это ребро соединяет. Тогда путём называется множество рёбер в форме

,k=1,2,…,m-1,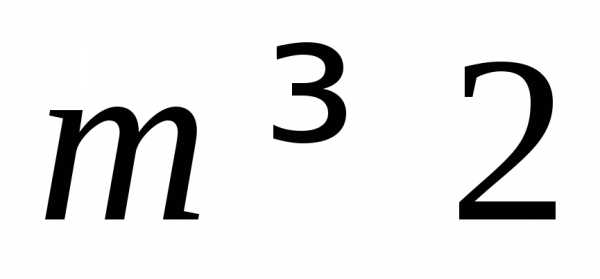

,

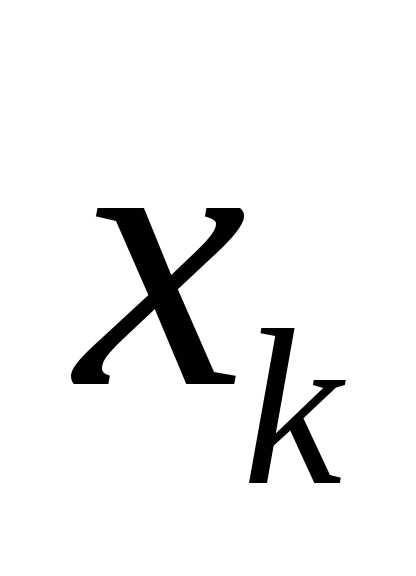— разные вершины графа.

Мы можем сказать, что такой путь соединяет вершины 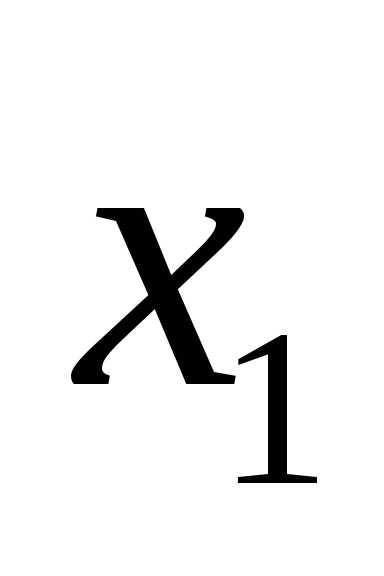и .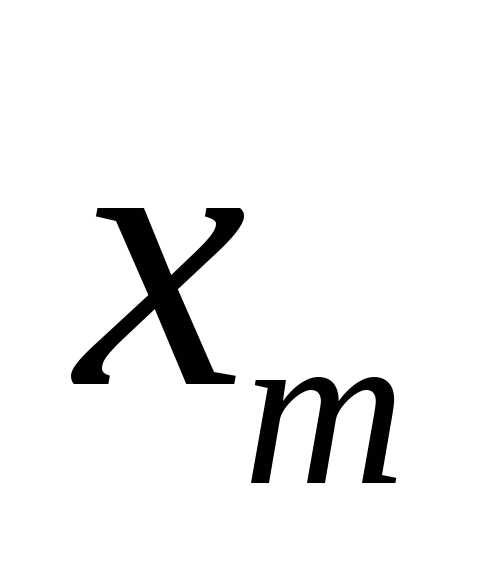

Деревом называется граф, в котором каждая пара узлов соединяется только одним путём из рёбер графа.

Деревом с корнем называется дерево, в котором одна особая вершина отмечена как корень дерева. Когда мы говорим о пути к данной вершине, мы имеем ввиду тот единственный путь, который связывает эту вершину с корнем.

Альтернативой у вершины в дереве с корнем является любое ребро, которое соединяет эту вершину с другой вершиной, но не входит в состав пути к этой вершине.

Вершина или ребро xследует за вершинойyтогда и только тогда, когдаyнаходится на пути кx. За конечной вершиной не следует ни одна альтернатива.

Для любого положительного целого nигройв развёрнутой форме называется дерево с корнем вместе с функциями, которые определяют метки для каждой вершины и ребра, удовлетворяя таким условиям:

1. Каждая нетерминальная вершина имеет метку игрока (1,2,…,N)

0 – метка отсутствия контроля каким-либо игроком.

2. Если вершина помечена 0, тогда должно быть фиксировано вероятностное распределение.В такой вершине эти вероятности неотрицательны для каждой альтернативы и их сумма равна 1.

3. Каждая вершина, которая контролируется игроком , имеет вторую метку, которая описывает информационное состояние игрока, если траектория игры достигла этой вершины. Метка (i,k) помечает вершину, в которой игрокiдвигается в информационном состоянииk.

4. В вершине, контролируемой игроком, каждой альтернативе предписана метка хода. Если какие-то вершины имеют одни и те же метку игрока и метку информационного состояния, т.е. (i,k), то тогда разметка ходов совпадает, т.е. для любой альтернативы в вершинеxсуществует в точности одна альтернатива в вершинеy, которая имеет ту же метку движения.

5. Каждая финальная вершина имеет метку, которая описывает вектор nчисел, т.е. вектор выигрышей.

В этом курсе часто рассматриваются игры, удовлетворяющие требованию 6:

6. Игроки не забывают сделанных выборов.

Требование 6 «О памяти»

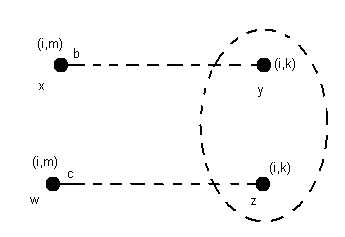
Пусть y – вершина, в которой i-й игрок принимает решение и z – вершина, неразличимая с y.

Тогда для любой прошлой вершины, в которой i-й игрок принимает решение, и движения, о которых игрок помнит в y, должны существовать неразличимые вершина и движения, которые помнит i-й игрок, находясь в z.

(Конечно, может быть, что x=ωиb=c)

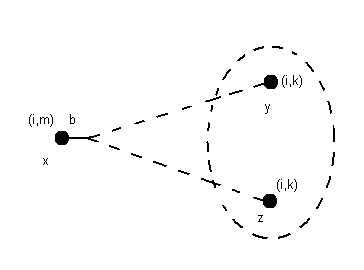
Если никакие две вершины не имеют одного и того же самого информационного состояния, то мы говорим, что это игра с совершенной информацией.

Игра с несовершенной информацией

Игры с совершенной информацией

В игре с совершенной информацией

игрок знает прошлые движения всех других игроков и результат хода случая, а также все свои прошлые движения.

Стратегией игрока в игре в развернутой форме является любое правило для определения движения в каждом возможном состоянии игры.

Математически это означает, что стратегия – это функция, отображающая информационные состояния в движения.

Обозначим

S_i– множество возможных информационных состояний игрока i

D_s– множество движений, доступных игроку i в состоянииs.

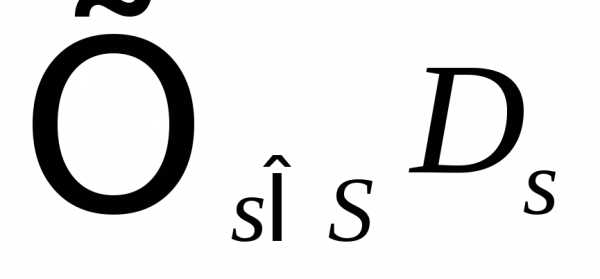– множество стратегий игрока i

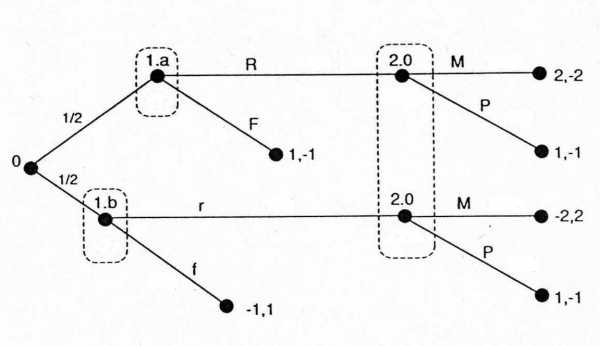
В простой карточной игре у первого игрока 4 стратегии.

Стратегия, которая состоянию а ставит в соответствие R, а состоянию b – r. Т.е. получаем Rr

Стратегия, которая состоянию а ставит в соответствие R, а состоянию b –f. Т.е. получаем Rfи т.д.

Всего 4 стратегии: {Rr,Rf,Fr,Ff}, у второго игрока – две: {M,P}

Множество стратегий второго игрока состоит из двух стратегий {L,R}.

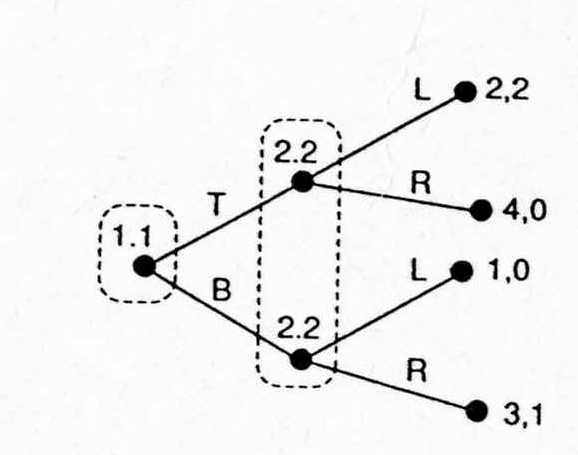
Множество стратегий второго игрока состоит из четырех стратегий {Ll,Lr,Rl,Rr}

Стратегическая форма игры:

Г={N, (C_i)_iєN, (u_i)_iєN},

N– множество игроков,

C_i– множество стратегий i-го игрока,

u_i– функция выигрыша i-го игрока,

u_i: Π_jєNC_j→R.

Обозначим с={c₁,c₂,…,c_N}.

Если NиC_i– конечные множества, то игра называется конечной.

С – все множество таких наборов.

Выбор игроки делают одновременно.

Процедуру конструирования игры Г в стратегической форме по игре Г

^e в развернутой форме предложили фон Нейман и Моргенштерн.

Пример. Проанализируем простую карточную игру заранее, до начала игры

Количество игроков – 2

Стратегии 1-го игрока – {Rr,Rf,Fr,Ff}

Стратегии 2-го игрока – {M,P}

Ожидаемые выигрыши каждого игрока:

u₁(Rf,M)=2·½+(-1)·½=0,5

u₂(Rf,M)=(-2)·½+1·½=-0,5 и т.д.

C1	C2
	M	P
Rr	0,0	1,-1
Rf	0.5,-0.5	0,0
Fr	-0.5,0.5	1,-1
Ff	0,0	0,0

Это нормальное представление простой карточной игры.

В общем случае: пусть задана игра Г^ев развернутой форме. Представление ее в стратегической форме делается так

Множество игроков то же самое, стратегии те же. А функция полезности строится так

Р(x|c) – это вероятность того, что игра пройдет через узел х, если игроки будут делать свои выборы согласно набору с, а в вершине, в которой решение принимается случайным образом, следующая альтернатива, включенная в траекторию определяется распределением вероятности, зафиксированном в Г^е

Т.е., если х – корень дерева, тогда Р(x|c)=1

Если х непосредственно следует за вершиной y, контролируемой ходом случая иq– вероятность выбора ребра от y к x, тогда Р(x|c)=qР(y|c)

Пусть х непосредственно следует за вершиной у, в которой решение принимает игрок i в информационном состоянии r.

Если c_i(r) метка движения на ребре отyк х, тогда

Р(x|c)= Р(y|c)

Если c_i(r) не метка движения на ребре отyк х, тогдаР(x|c)=0.

(напомним, что c_i(r) входит в набор с)

Пусть Ω* – множество всех конечных вершин.

Тогда

,

где – выигрыш i-го игрока в вершине х в Г^e.

Если Г=(N, (С_i)_iєN, (u_i)_iєN) выводится из Г^eтаким образом, тогда Г называется нормальным представлением Г^e.

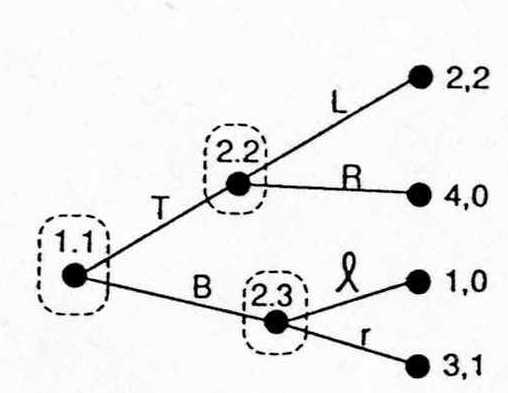
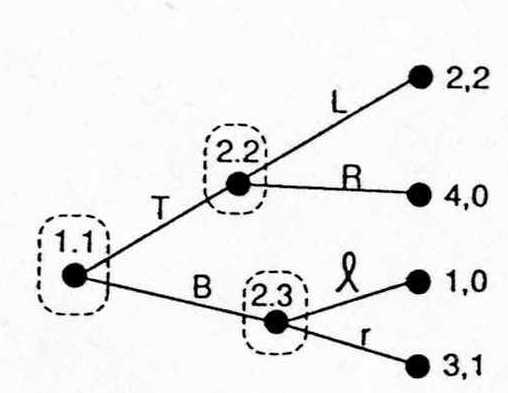
Пример.

C1	C2
	L	R
T	2,2	4,0
B	1,0	3,1

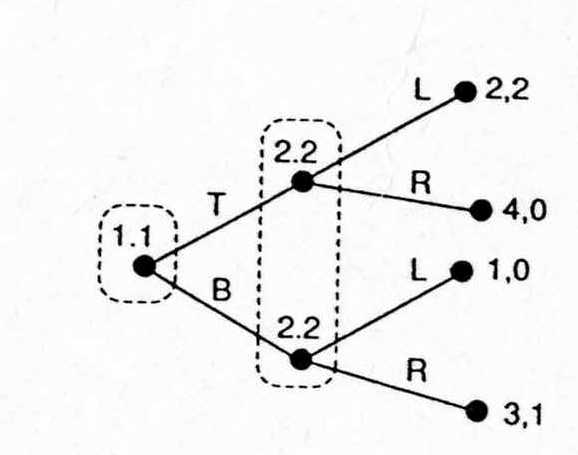
Пример:

C1	C2
	Ll	Lr	Rl	Rr
T	2,2	2,2	4,0	4,0
B	1,0	3,1	1,0	3,1

studfiles.net

Описание игры в развернутой форме

Количество просмотров публикации Описание игры в развернутой форме – 284

Классификация игр

Классификацию игр проводят по различным признакам:

1) по числу игроков;

2) по числу стратегий;

3) по свойствам платежной функции;

4) по характеру предварительной договоренности между игроками.

Игру, в которой участвует n игроков, называют игрой с n участниками. Количество участников должна быть равным 2, 3 и т.д. При наличии двух игроков могут возникать конфликтные ситуации, и крайне важно сть в координированных действиях (кооперация). В случае если в игре участвуют три игрока и более, то могут создаваться коалиции, ᴛ.ᴇ. группы из двух игроков и более, имеющих общую цель и координирующих свои стратегии.

По количеству стратегий различают игры конечные и бесконечные. В случае если хотя бы из игроков располагает бесконечным множеством стратегий, то игру называют бесконечной. В случае если же каждый из игроков располагает конечным множеством стратегий, то игру называют конечной.

Еще один способ классификации игр — по свойствам платежной функции. В игре с нулевой суммой общая сумма выигрышей всœех игроков равна нулю. То есть в игре с нулевой сумме двух участников выигрыш одного из них равен проигрышу другого. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в игре с нулевой суммой существует конфликт между игроками, и в связи с этим их называют также антагонистическими играми. В общем случае в игре с нулевой суммой, как правило, имеют место и конфликты, и согласованные действия игроков. Прямой противоположностью играм с нулевой суммой являются игры двух игроков с постоянной разностью, в которых оба игрока выигрывают или проигрывают одновременно. По этой причине игрокам выгодно действовать согласованно.

Учитывая зависимость отхарактера предварительной договоренности между игроками различают кооперативные и некооперативные игры. Игра является кооперативной, в случае если до ее начала игроки образуют коалиции и принимают взаимообязывающие соглашения о координации своих стратегий. В противоположном случае игра будет некооперативной.

Существует два способа описания и анализа любой конкретной игры:

1) описание игры в развернутой форме

2) описание игры в нормальной форме.

Описание игры в развернутой форме предполагает следующее:

1) перечисление ходов, которые могут делать игроки;

2) определœение информации, которой располагают игроки в процессе игры;

3) определœение возможных вариантов действия игроков;

4) указание предельных размеров платежей в конце игры

Этот наиболее детализированный способ описания игр используется для сравнительно простых игр.
Размещено на реф.рф
Их называют позиционными играми, и представляют в виде дерева игры.

Способ описания игры в виде дерева игры включает 3 главных момента:

1) чередования ходов, начиная с первого, причем ходы бывают как личными, так и случайными;

2) возможна недостаточность информации о действиях других участников игры;

3) определœение набора исходов игры (вершин дерева) с заданным значением платежной функции.

Наиболее часто игры с конечным или бесконечным числом стратегий описываются в нормальной форме. Этот способ описания игры предполагает рассмотрение всœех возможных стратегий каждого игрока и определœение платежей, соответствующих любым возможным комбинациям стратегий всœех игроков. Для иллюстрации рассмотрим бескоалиционную игру.

referatwork.ru

Определение игры в развернутой форме — КиберПедия

Развернутая форма – естественный способ представления салонных игр,вроде шахмат или преферанса. Однако и другие игры (по крайней мере, дискретные), обычно сначала рассматриваются в развернутой форме.

Игры в развернутой форме представляются в виде дерева, вершины которого представляют собой текущие игровые ситуации. Вершины соединяются дугами, которые означают возможные переходы между ситуациями, Если из данной вершины выходят несколько дуг, это значит, что в данной ситуации ход игры зависит от выбора одного из игроков или от реализации внешнего события. Самая левая вершина («корень» дерева) означает ситуацию в начале игры, конечные (терминальные) вершины означают возможные исходы игры. Каждой конечной вершине поставлен в соответствие вектор выигрышей игроков. В случае двух игроков этот вектор состоит из пары чисел – значений полезности игроков при заданном исходе игры.

Для каждой нетерминальной вершины необходимо указать, какой игрок контролирует данную вершину, то есть осуществляет выбор. Вершина может и не контролироваться ни одним из игроков, тогда эту вершину контролирует природа. Вершина, контролируемая игроком с номером i, называется еще «точкой выбора i-го игрока».

При каждом розыгрыше игроки (и реализация природных факторов) выбирают путь в этом дереве от стартовой вершины до одной из терминальных вершин.

Для описания игры n лиц в развернутой форме необходимо определить:

1) Дерево, ребрам и вершинам которого присвоены следующие метки:

2) Каждой терминальной вершине ставится в соответствие метка-«вектор выигрышей», то есть числовой вектор (размерности n) выигрышей (полезностей) игроков.

3) Каждой нетерминальной вершине ставится в соответствие метка контроля – номер игрока контролирующего вершину. Если данную вершину контролирует природа (внешние обстоятельства, случай и т.д.), то эта метка равна нулю.

4) Каждой нетерминальной вершине ставится в соответствие метка информационного состояния игрока (обычно она отделяется от номера игрока точкой).

5) Каждое ребро помечено возможными альтернативами, доступными для выбора игрока, контролирующего вершину, из которой выходит данное ребро. Если вершину контролирует природа, метки должны обозначать вероятности реализации данной альтернативы, причем сумма вероятностей должна равняться единице.

6) Набор исходящих ребер множества вершин с одним информационным состоянием имеет одинаковый набор маркировок.

Определение 1:Игрой в развернутой форме называется система 1-6.

Описание игры в развернутой форме довольно сложно, хотя и содержательно богато. Поэтому вместо того, чтобы подробно исследовать игры в развернутой форме, введем новую, более простую форму игры (нормальную, или стратегическую форму), определим формальную процедуру перехода от игр в развернутой форме к играм в нормальной форме.

cyberpedia.su

Определение игры в развернутой форме

Информатика Определение игры в развернутой форме

просмотров – 83

Лекция 3. Игры в развернутой форме. Переход от игры в развернутой форме к игре в нормальной форме. Смешанные стратегии.

Развернутая форма – естественный способ представления салонных игр, вроде шахмат или преферанса. При этом и другие игры (по крайней мере, дискретные), обычно сначала рассматриваются в развернутой форме.

Игры в развернутой форме представляются в виде дерева, вершины которого представляют собой текущие игровые ситуации. Вершины соединяются дугами, которые означают возможные переходы между ситуациями, В случае если из данной вершины выходят несколько дуг, это значит, что в данной ситуации ход игры зависит от выбора одного из игроков или от реализации внешнего события. Самая левая вершина («корень» дерева) означает ситуацию в начале игры, конечные (терминальные) вершины означают возможные исходы игры. Каждой конечной вершинœе поставлен в соответствие вектор выигрышей игроков. В случае двух игроков данный вектор состоит из пары чисел – значений полезности игроков при заданном исходе игры.

Для каждой нетерминальной вершины крайне важно указать, какой игрок контролирует данную вершину, то есть осуществляет выбор. Вершина может и не контролироваться ни одним из игроков, тогда эту вершину контролирует природа. Вершина, контролируемая игроком с номером i, принято называть еще «точкой выбора i-го игрока».

При каждом розыгрыше игроки (и реализация природных факторов) выбирают путь в этом дереве от стартовой вершины до одной из терминальных вершин.

Для описания игры n лиц в развернутой форме крайне важно определить:

1) Дерево, ребрам и вершинам которого присвоены следующие метки:

2) Каждой терминальной вершинœе ставится в соответствие метка-«вектор выигрышей», то есть числовой вектор (размерности n) выигрышей (полезностей) игроков.

3) Каждой нетерминальной вершинœе ставится в соответствие метка контроля – номер игрока контролирующего вершину. В случае если данную вершину контролирует природа (внешние обстоятельства, случай и т.д.), то эта метка равна нулю.

4) Каждой нетерминальной вершинœе ставится в соответствие метка информационного состояния игрока (обычно она отделяется от номера игрока точкой).

5) Каждое ребро помечено возможными альтернативами, доступными для выбора игрока, контролирующего вершину, из которой выходит данное ребро. В случае если вершину контролирует природа, метки должны обозначать вероятности реализации данной альтернативы, причем сумма вероятностей должна равняться единице.

6) Набор исходящих ребер множества вершин с одним информационным состоянием имеет одинаковый набор маркировок.

Определœение 1:Игрой в развернутой форме принято называть система 1-6.

Описание игры в развернутой форме довольно сложно, хотя и содержательно богато. По этой причине вместо того, чтобы подробно исследовать игры в развернутой форме, введем новую, более простую форму игры (нормальную, или стратегическую форму), определим формальную процедуру перехода от игр в развернутой форме к играм в нормальной форме.

Читайте также

– Определение игры в развернутой форме

Лекция 3. Игры в развернутой форме. Переход от игры в развернутой форме к игре в нормальной форме. Смешанные стратегии.Развернутая форма – естественный способ представления салонных игр, вроде шахмат или преферанса. Однако и другие игры (по крайней мере, дискретные), обычно… [читать подробенее]

oplib.ru

Игра в нормальной форме.

Этот способ описания игры состоит в том , что рассматриваются все возможные стратегии каждого игрока и определяются платежи, соответствующие любой возможной комбинации стратегий всех игроков. (Зная развернутую форму игры , можно получить и ее нормальную форму).

Нормальная форма игры двух участников состоит из двух платежных матриц, представленных в виде единой матрицы, элементами которой являются пары чисел.

Игрок 2 выбирает стратегию

Платежная матрица имеет размерность m x n, где

m – число стратегий игрока 1,

n – число стратегий игрока 2,

– выигрыш первого игрока при выборе первым стратегии , а вторым – стратегии.

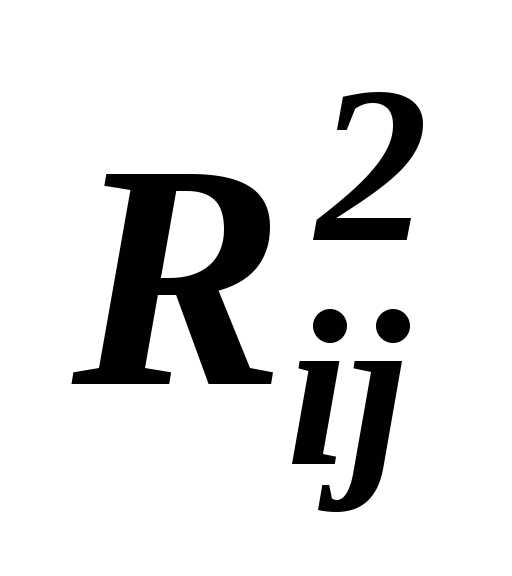– выигрыш второго игрока при выборе вторым стратегии , а первым – стратегии.

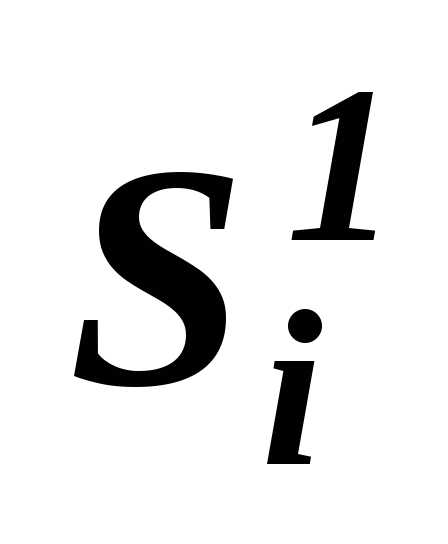2. Игры двух участников с нулевой суммой.

Если игра представлена в нормальной форме, достаточно исследовать платежную матрицу только игрока 1. Нулевая сумма игры означает

Платежная матрица для игры двух участников с нулевой суммой.

Если игрок 1 выбирает стратегию, а игрок 2 выбирает стратегию, то игрок 1 получает , а игрок 2 получает.

Игры такого типа называют матричными. В такой игре игрок 1 стремится выбрать строку, чтобы выигрыш был максимален, а игрок 2 выбирает столбец, чтобы был минимален проигрыш.

Игрой с постоянной суммой называется игра, в которой . Любую игру с постоянной суммой можно представить в виде некоторой матричной игры, так как прибавление какой-либо постоянной величины в каждом элементе матрицы не влияет на результат.

Если пары представляют собой элементы платежной матрицы, то, вычитаяиз каждого числа, входящего в эту пару, получим

, где .

В качестве основного допущения в теории игр двух лиц с нулевой суммой принимается, что каждый игрок стремится обеспечить себе максимально возможный выигрыш при любых действиях противника. Однако, наибольший гарантированный выигрыш определяется тем, что избранная данным игроком стратегия становится известной противнику, который затем выбирает свою оптимальную стратегию. Какую бы строку не выбрал игрок 1, игрок 2 выберет столбец, минимизирующий выигрыш игрока 1, то есть в каждой строке выбирается .

Оптимальная стратегия игрока 1 будет состоять в выборе строки с самым высоким из таких минимальных платежей

.

Стратегия, соответствующая максимальному значению минимумов строк, называется максиминной стратегией.

Игрок 2 стремится обеспечить себе наименьшее значение платежа своему противнику вне зависимости от стратегии, избираемой первым игроком.

Игрок 2 стремится к гарантированному результату, выбирая минимаксную стратегию.

.

Если игрок 1придерживается максиминной стратегии, то его выигрыш будет

.

Если игрок 2 избирает минимаксную стратегию, то его проигрыш

.

Если , то игроки получают гарантированные платежи. В этом случае их стратегии оказываются совместимыми, а платежная матрица имеет седловую точку на пересечении-ой строки и- го столбца.

Пример:

минимальные элементы строк

Игра двух участников с нулевой суммой, имеющая седловую точку, называется вполне определенной. Разумно ожидать, что в такой игре оба партнера изберут стратегию седловой точки.( Седловая точка матрицы является ценой игры).

Однако не все игры двух участников с нулевой суммой являются вполне определенными .В общем случае

.

Игры, в которых строгое неравенство, называются не полностью определенными играми без седловой точки .

Пример:

минимальные элементы строк

Стратегии, рассмотренные выше, называются чистыми . m – строк платежной матрицы являются чистыми стратегиями игрока 1 , n – столбцов являются чистыми стратегиями игрока 2. В этом примере результат оказывается неожиданным для обоих игроков. То есть в таких играх принцип решения в той форме, как он изложен выше, оказывается непригодным. Однако этот принцип решения остается верным, если расширить понятие стратегии за счет смешанных(случайных) стратегий.

Смешанная стратегия представляет собой вероятностную комбинацию чистых стратегий.

Смешанную стратегию для игрока 1 можно указать с помощью вектора вероятностей , где- вероятность выбратьi – ую стратегию первым игроком, .

( * )

( Условие () можно записать в ином виде: ,

где – единичный вектор размерностиm : .

Для игрока 2 вектор , где- вероятность выбора j – стратегии, .

, где – единичный транспонированный вектор размерностиn.

Чистую стратегию можно представить как частный случай смешанной, когда – одна единица вj – ой позиции.

Основной теоремой в теории игр двух лиц с нулевой суммой является теорема о минимаксе(доказана Фон Нейманом).Согласно этой теореме любая конечная игра с нулевой суммой(ИНС) имеет решение, если допускается использование смешанных стратегий.

Вполне определенная игра имеет решение в области чистых стратегий, причем это решение может быть не единственным.

Не полностью определенная игра имеет решение возможно не единственное, при котором хотя бы один из игроков применяет случайное комбинирование стратегий. Так, ожидаемый выигрыш( математическое ожидание ) игрока 1 в предположении , что он использует вектор вероятностей , а игрок 2 применяет своюj – ую стратегию, равен

Игрок 1, стремящийся достичь наибольшего из гарантированных ожидаемых выигрышей, выбирает вектор вероятностей так, чтобы получить

(10.3.0)

где

.

Цель игрока 2 – достичь

(10.3.0)

Теорема о минимаксе утверждает, что существует хотя бы одна пара стратегий , при которых

.

,

где – цена игры,- решение ( 10.3 .0),- решение ( 10.3 .0).

При любых векторах выполняются соотношения

.

Цена игры – единственная, а соответствующие ей векторы вероятностей оптимальных смешанных стратегиймогут быть не единственными.

studfiles.net

Игра в развернутой форм – Энциклопедия по экономике

Лучший способ моделирования игры с последовательным выбором — использовать древо игры. Древо игры напоминает древо решений, за тем исключением, что в первом случае решение принимает не один, а большее число игроков. На рис. 4.6 приведен пример со стратегиями и результатами, иллюстрирующий описанный выше случай с новичком и старожилом. Круги на рисунке представляют собой узлы с решениями. Игра начинается с узла 1. На этом этапе Игрок 1 (новичок) выбирает между вариантами е и ё, которые можно истолковать как входить и не входить соответственно. Если выбирается последнее, тогда игра заканчивается с результатами П = 0 (результат новичка) и П2 = 50 (результат старожила). Если Игрок 1 выбирает е, мы переходим к узлу с решением 2. Этот узел соответствует выбору Игрока 2 (старожила) между вариантами гиг, которые можно истолковать как наказывать за вход и не наказывать за вход соответственно. Игры, которые, как на рис. 4.6, могут быть представлены в виде древа, называются также играми в развернутой форме .  [c.64]

Рис. 4.6. Игра в развернутой форме с последовательным выбором

Изобразите все произошедшие события в виде игры в развернутой форме. Определите равновесие как функцию Ь. Если между состоянием равновесия и реальными событиями обнаруживается разница, как, по-вашему, это можно объяснить  [c.73]

Кроме того, удобно представить ситуацию как игру в развернутой форме. Можно изобразить последовательность ходов и выигрыши игроков с помощью следующего дерева игры  [c.47]

Игры в развернутой форме (динамические) с совершенной информацией о ходах  [c.94]

В игре в развернутой форме (чистая) стратегия — это полный план действий игрока что он будет делать в каждой из вершин, в которой ход принадлежит ему. Это должен быть действительно полный план, то есть в нем должно быть определено, что игрок выберет в любой своей вершине, даже если из каких-либо соображений ясно, что процесс игры вряд ли может привести в эту вершину. То есть это должен быть настолько полный план, что доверенное лицо игрока может использовать его в качестве инструкции, будучи уверенным, что его поведение будет совпадать с поведением самого игрока.  [c.657]

Таким образом, существуют два представления любой игры — представление в нормальной и развернутой форме. Выше мы показали, как динамическую игру с совершенной информацией представить в нормальной форме, а статическую игру — в развернутой форме. Таким образом, любую динамическую игру с совершенной информацией можно представить в нормальной форме, а затем, — на основе этой нормальной формы — построить развернутую форму соответствующей игры. Приведем пример такого построения.  [c.666]

Этой нормальной форме соответствует дерево игры, представленное на Рис. 166. Как видим, при таком двойном переводе частично потеряна информация о структуре игры и мы получили другую игру в развернутой форме. Очевидно, что принципиально разным играм может соответствовать одна и та же нормальная форма.  [c.666]

Игра в развернутой (экстенсивной) форме  [c.466]

Равновесие Нэша (NE). NE при наблюдаемых ходах и близоруком поведении, или в популяции участников. NE в развернутой форме игры игра “перекресток” – борьба за лидерство. Соответствие между развернутой и нормальной формами игры. NE в примерах с непрерывной стратегией ценовое соревнование взаимозаменяемых товаров. Вложение DE в NE.  [c.93]

Представление игры в виде дерева соответствует развернутой форме игры. В дальнейшем мы увидим, как можно представить динамическую игру в нормальной форме. А сейчас перечислим, что должно включать описание динамической игры (с совершенной информацией) в развернутой форме  [c.654]

Множество игроков, конечно, должно быть одним и тем же в нормальной форме и в развернутой форме игры. Прежде всего уточним понятие стратегии для игр такого типа.  [c.657]

В СССР система С. ф. складывалась постепенно. На различных этапах социалистич. строительства разные виды С. ф. играли ведущую роль. В период военного коммунизма преобладали государственные натуральные С. ф. Впоследствии (в 20-х гг.) главное значение приобрел фонд государственного страхования, к-рый обслуживал и государственный сектор произ-ва. В период коллективизации с. х-ва стали возникать колхозные С. ф. С переходом на централизованный метод создания С. ф. через государственный бюджет постепенно суживалась сфера применения фонда государственного страхования. Большое значение, особенно в послевоенные годы, получили общественные фонды потребления, имеющие в известной мере значение С. ф. (фонды социального страхования и социального обеспечения), возросло значение фонда государственного личного страхования. В период развернутого коммунистич. строительства роль С. ф. повышается. Они во все большей степени содействуют слаженности и бесперебойности производственного процесса, поддержанию определенного уровня жизни людей. С построением материально-технич. базы коммунизма и переходом к единой общенародной форме собственности отпадет необходимость в разнообразных формах С. ф. Коммунистич. об-во будет располагать мощным централизованным резервным фондом, полностью гарантирующим бесперебойность общественного вос-произ-ва и высокий уровень жизни трудящихся.  [c.396]

Эта форма обмена, выражающая новую ступень его развития, носит название полной, или развернутой, формы стоимости. Она характеризует расширение и упрочение производственных связей. В этих условиях возрастает и значение точности количественных соотношений между товарами, поскольку обмен начинает играть все большую роль в возмещении затраченного на их производство труда.  [c.52]

Противоречия развернутой формы стоимости преодолеваются в ходе развития товарного производства и обмена. По мере того как в результате разделения труда между земледелием, скотоводством и ремеслом увеличивалось производство товаров на рынок, среди них все более выделялись товары, пользующиеся всеобщим спросом. У скотоводческих племен таким товаром был скот, у земледельцев – зерно, кофе, у охотничьих племен – шкуры диких зверей и т.д. В этом случае возникающие противоречия развернутой формы стоимости начинают разрешаться через одну ступень товарного обмена все товары выражали свою относительную стоимость только в одном из них, но пользующимся всеобщим спросом. Получаются ряды товарного обмена, в которых разные товары в определенных пропорциях обмениваются на один и тот же товар. Например, 0,25 т пшеницы = 1 овце, 0,5 бочонка меда = 2 овцам, 7,5 м ткани = 1 овце и т.д. Овцы на таком рынке играют роль всеобщей формы стоимости всех остальных товаров, как это и было у скотоводческих народов.  [c.145]

Как видим, развернутая форма игр с несовершенной информацией несколько более сложна, чем развернутая форма игр с совершенной информацией. Дополнительно к тем составляющим, которые были указаны в прежнем определении, требуется также перечислить информационные множества, которые задают разбиение множества вершин (кроме конечных). Информационные множества должны быть заданы так, чтобы каждая вершина, кроме конечных, принадлежала одному и только одному из них. Кроме того, по смыслу определения информационного множества, во всех его вершинах ход должен принадлежать одному и тому же игроку.  [c.665]

Таким образом, нормальная форма игры не является в общем случае адекватной для описания динамических игр. С помощью нее можно представлять корректно только статические игры. Если операцию двойного перевода из развернутой формы в нормальную и обратно осуществить со статической игрой, представленной на Рис. 163, то дерево игры не поменяется (с точностью до выбора порядка ходов, что в данном случае несущественно).  [c.666]

Игры могут быть представлены в нормальной (матричной) и развернутой (в виде древа игры) формах. Как правило, игры с одновременным выбором представлены нормальной формой, а игры с последовательным выбором — развернутой.  [c.70]

ДЕНЬГИ И ДЕНЕЖНОЕ ОБРАЩЕНИЕ в СССР. Деньги являются особым товаром — всеобщим эквивалентом в нем выражается стоимость всех других товаров и при его посредстве непрерывно совершается обмен продуктами труда между товаропроизводителями. Деньги возникли несколько тысяч лет тому назад в связи с появлением и развитием товарного обмена. При социализме деньги как общий эквивалент всех товаров являются необходимой и всеобщей формой планомерного учета затрат общественного труда, хозрасчетной организации произ-ва и распределения общественного продукта, контроля над мерой труда и потребления. Деньги будут существовать и играть важную роль в течение всего периода развернутого строительства коммунизма В коммунистическом строительстве,— подчеркивается в Программе Коммунистической партии Сов. Союза,— необходимо полностью использовать товарно-денежные отношения в соответствии с новым содержанием, присущим им в период социализма (1961, с. 89). Деньги отомрут на высшей фазе коммунизма, когда произойдет переход к единой коммунистич. форме собственности и когда не будет необходимости в товарных отношениях, связанных с распределением общественного продукта среди трудящихся по количеству и качеству труда и в хозрасчетных товарных отношениях между социалистич. предприятиями.  [c.186]

Для формального анализа игру обычно записывают в одной из форм развернутой (детальное описание возможных ходов), характеристической (описываются значения выигрышей каждой коалиции, для анализа кооперативных игр) или стратегической (нормальной). Последний вариант, изучаемый далее, означает, что игра есть  [c.3]

Не изучаемое здесь, но популярное, понятие PNE (обычно называемое просто “Perfe t Equilibrium”) задается для игр в развернутой форме с деревом последовательности ходов. Это понятие означает, что исход х g PNE является Нэшевским равновесием не только во всей игре, но и во всех подыграх (ветвях дерева).  [c.5]

Более важная теорема Куна на эту тему касается игр в развернутой форме из нее, в частности, следует, что в шахматах есть SE (оно пока неизвестно).  [c.7]

ДЕРЕВО ИГРЫ [game tree] — способ описания игры с помощью графа “дерево”, последовательно по ходам фиксирующего, какой информацией располагают игроки перед каждым ходом, какие варианты они могут выбирать и какими могут быть предельные размеры платежей в конце игры. Игра, описываемая с помощью подобного “дерева”, называется игрой в развернутой (экстенсивной) форме, а иногда — позиционной игрой.  [c.77]

Подыгра игры G, где G — игра с совершенной информацией в развернутой форме, — это игра, построенная на основе исходной игры. Начальной вершиной подыгры служит любая вершина исходной игры, кроме конечных. В подыгру входят все вершины, следующие за ее начальной вершиной. Выигрыши в подыгре совпадают с выигрышами в соответствующих конечных вершинах полной игры.  [c.660]

ФОРМА СТОИМОСТИ – форма выражения стоимости товара на различных этапах развития товарного производства и обмена. Стоимость как общественное свойство товара может проявиться лишь при приравнивании одного товара к другому в процессе обмена. Обобщив огромный материал по истории обмена, К. Маркс впервые проанализировал процесс развития формы стоимости. Ступени этого процесса таковы I) простая, единичная, или случайная, форма стоимости, 2) полная, или развернутая, 3) всеобщая и 4) денежная форма стоимости. Простая, единичная, или случайная, форма стоимости свойственна начальному этапу развития товарного производства, когда продукты труда превращались в товары лишь посредством единичных и случайных актов обмена. При простой форме стоимость отдельного товара только случайно выражалась в каком-либо другом товаре. Она может быть представлена уравнением товар А = товару Б. В данном случае два разнородных товара — товар А и товар Б — играют две различные роли. Товар А выражает свою стоимость в товаре Б, поэтому он играет активную роль и находится в относительной форме стоимости. Товар Б служит материалом для выражения стоимости товара А, играет пассивную роль и находится в эквивалентной форме стоимости. Превращение простой, единичной, или случайной, формы стоимости в полную, или развернутую, обуслов-  [c.444]

Совершенное в подыграх равновесие (SPE). Игра “Пилот и террорист”. Обратная индукция (алгоритм Куна) для нахождения SPE. Связь между развернутой и нормальной формами игры. Примеры повестки дня при голосовании, игра в спички, “пираты”, конечные и бесконечные процедуры торга по Нэшу в игре “дележ пирога с дисконтированием”. Отношение SPE к NE, к SE. Теоремы существования SPE, SE, и единственность при “неповторимости исходов”.  [c.94]

Командный тренинг корпоративного управления фирмой осуществляется в форме участия обучающихся в комплексной компьютерной деловой игре, имитирующей деятельность производственной организации в реальном масштабе времени, в приближенных к реальным условиях конкуренции. Приводится развернутое описание компьютерной деловой игры СИПРОМЕК, рекомендуемой авторами для командного тренинга.  [c.8]

economy-ru.info

Игры в развернутой форме. Нормальная и развернутая формы.

Подпишитесь на бесплатную рассылку видео-курсов:

Вопрос №1. Игры в развернутой форме. Нормальная и развернутая формы. В игре может участвовать несколько игроков. Можно давать игрокам имена, однако, в общетеоретическом плане это неудобно. Игроков принято нумеровать, и в качестве обозначения игрока использовать его номер. Таким образом, одним из элементов игры является множество игроков , где n – номер последнего игрока (или количество игроков). Каждый игрок имеет множество стратегий (действий, альтернатив) . Задачей игрока является выбор конкретной стратегии . Если каждый из игроков осуществил свой выбор, то говорят, что реализовался исход игры. Исходом называется n-мерный вектор . Исходы имеют для игроков разную ценность. Рациональный игрок должен стремиться к достижению как можно более благоприятного для себя исхода. Однако никакой игрок не в состоянии обеспечить наилучший для себя исход только за счет собственных действий. Принимая решение о выборе действия, он должен учитывать интересы и возможные действия других игроков, влияющие на исход игры. В этом состоит отличие теоретико-игровой постановки задачи принятия решений от задачи оптимизации. В общем случае неравноценность исходов описывается при помощи систем предпочтений игроков. Если, например, игрок i считает, что из трех исходов наилучшим для него является x, а наихудшим z, то пишут, что . В частном случае предполагают, что каждый игрок имеет свою функцию полезности , областью определения которой является множество исходов, а множеством значений – множество действительных чисел. Функция определяется таким образом, что более предпочтительному исходу соответствует большее число. Так, для вышеприведенного примера: . Резюмируя можно сказать, что игра в нормальной (или стратегической) форме это тройка: . Задачей каждого игрока i является выбор такой стратегии , при которой его функция полезности принимает возможно большее значение. Примеры. Особенно просто задавать игры двух лиц. Для этого некоторого игрока условно называют первым, а другого – вторым. И рисуют таблицу, где строки соответствуют стратегиям первого игрока, а столбцы – стратегиям второго. В клетках записывают выигрыши – сначала первого, затем второго. По этой причине такие игры называют биматричными. Проведем три простейших примера, которые будут часто встречаться. Пример 1. Игра в чет/нечет. Игроки договариваются о следующих правилах игры. Каждый из них тайно загадывает натуральное число. Затем числа предъявляются и складываются. Если сумма оказывается четной, то второй игрок платит первому единицу денег, а если нечетной, то – наоборот. Понятно, что для каждого из игроков несущественно, какое именно число загадывать, существенно лишь то, является оно четным или нечетным. Поэтому для каждого из игроков можно ограничиться списком лишь из двух действий: четное или нечетное число. При развернутом задании игры больше внимания уделяется порядку ходов и той информации, которая при этом открывается игроку. Начнем с простейших, т. н. позиционных игр, или игр с полной информацией. Главное здесь – дерево игры; это направленный граф без циклов с выделенной вершиной – корнем. Стрелки идут в направлении от корня. Вершины дерева изображают позиции игры, места, где какие-то игроки должны выбрать ход – одну из стрелок, выходящую из этой вершины. Поэтому у каждой (нетерминальной) вершины стоит метка того игрока, который делает ход (говорят еще – контролирует эту вершину). В терминальных вершинах (где игра заканчивается) стоит вектор выигрышей игроков.

Игра – это процесс, в котором участвуют два или более игрока, ведущих борьбу за собственные интересы. У каждого из них есть набор доступных стратегий, и соответствующих выигрышей, которые так же зависят от выбора стратегии остальными игроками. Игра в нормальной форме описывается платежной матрицей (в виде таблицы). Каждое измерение матрицы – это игрок. Строки определяют стратегии первого игрока, столбцы – стратегии второго. На пересечении столбца и строки можно увидеть выигрыши, которые получают игроки. Игра развернутой форме, представляются в виде ориентированного дерева, где каждая вершина определяет выбор соответствующего игрока. От каждой вершины отходят ветви, обозначающие стратегии данного игрока. Платежи игроков записываются внизу дерева и принадлежат игрокам по порядку, сверху-вниз.

www.distanz.ru