Методы первого порядка решения дифференциальных уравнений – 3. Основные типы дифференциальных уравнений первого порядка и способы их решения Уравнения с разделенными и разделяющимися переменными

3. Основные типы дифференциальных уравнений первого порядка и способы их решения Уравнения с разделенными и разделяющимися переменными

Простейшим д .у.1 является уравнение вида 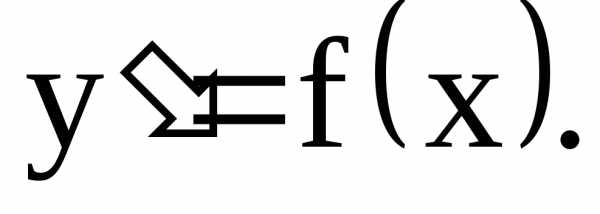Как известно из курса интегрального исчисления, функцияy находится интегрированием

Определение. Уравнение вида называется дифференциальным уравнением сразделенными переменными. Его можно записать в виде

Проинтегрируем обе части уравнения, получим так называемый общий интеграл (или общее решение).

Пример.

Решение. Запишем уравнение в виде Проинтегрируем обе части уравнения:

(общий интеграл дифференциального уравнения).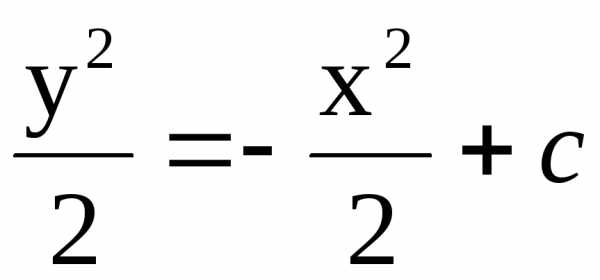

Определение. Уравнение вида называется уравнениемс разделяющимися переменными, если функции можно представить в виде произведения функций

,

,

т. е. есть уравнение имеет вид

Чтобы решить такое дифференциальное уравнение, нужно привести его к виду дифференциального уравнения с разделенными переменными, для чего разделим уравнение на произведение Действительно, разделив все члены уравненияна произведение,

получим

–дифференциальное уравнение с разделенными переменными.

Для решения его достаточно почленно проинтегрировать

При решении дифференциального уравнения с разделяющимися переменными можно руководствоваться следующим алгоритмом (правилом) разделения переменных.

Первый шаг. Если дифференциальное уравнение содержит производную , ее следует записать в виде отношения дифференциалов: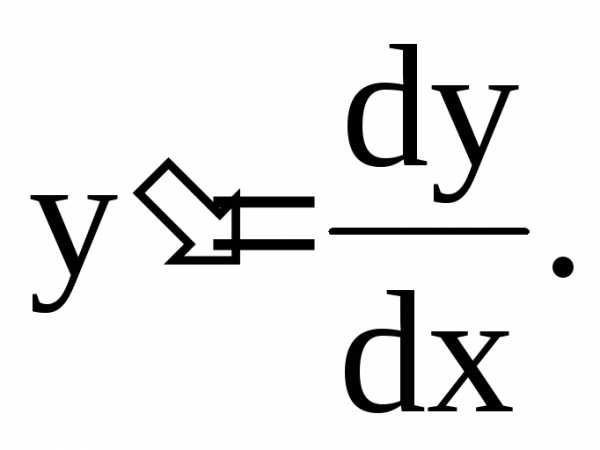

Второй шаг. Умножим уравнение на 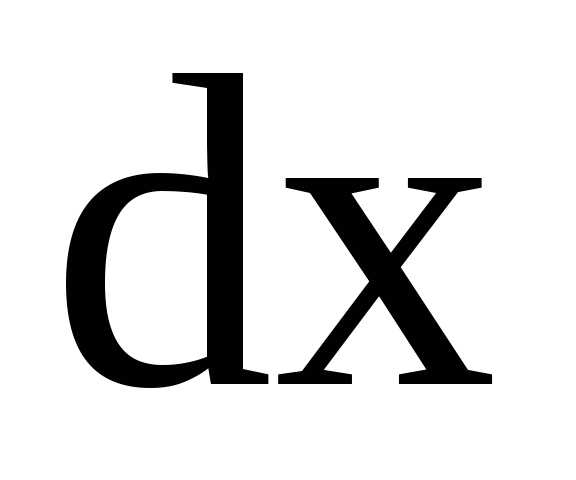, затем сгруппируем слагаемые, содержащие дифференциал функции и дифференциал независимой переменной.

Третий шаг. Выражения, полученные при , представить в виде произведения двух множителей, каждый из которых содержит только одну переменную (). Если после этого уравнение примет видто, разделив его на произведение , получим дифференциальное уравнение с разделенными переменными.

Четвертый шаг. Интегрируя почленно уравнение, получим общее решение исходного уравнения (или его общий интеграл).

Рассмотрим уравнения

№ 1.

№ 2.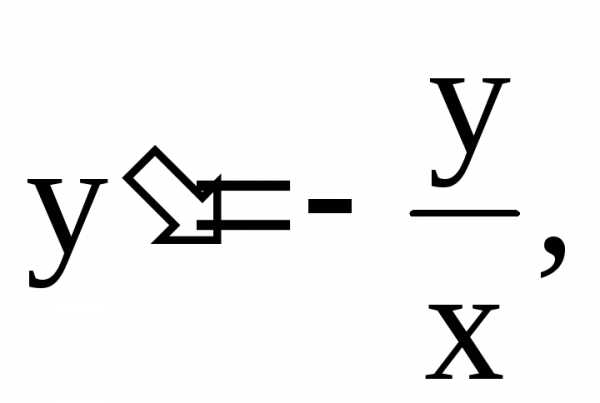

№ 3.

Дифференциальное уравнение № 1 является дифференциальным уравнением с разделяющимися переменными, по определению. Разделим уравнение на произведение 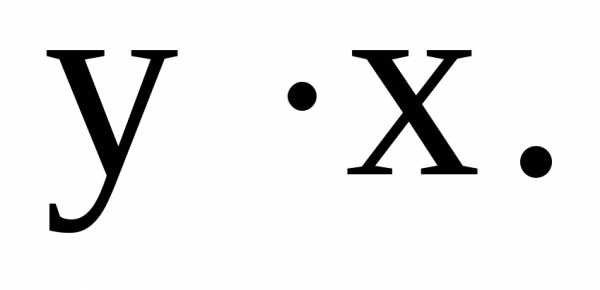Получим уравнение

Интегрируя, получим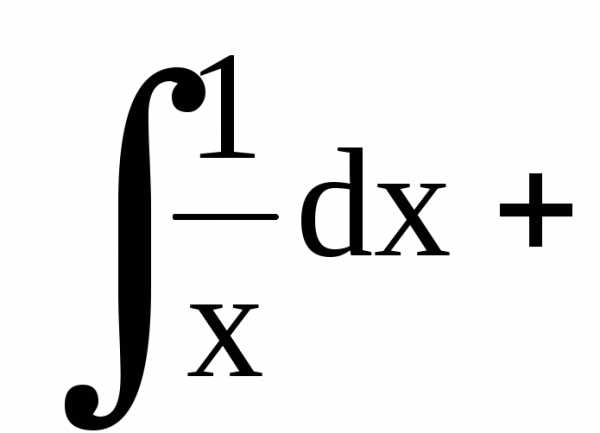

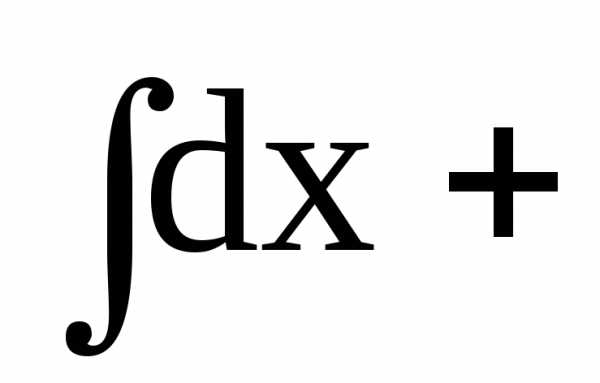
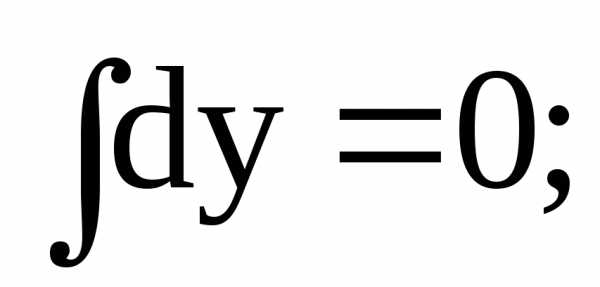
или

Последнее соотношение есть общий интеграл данного дифференциального уравнения.

В дифференциальном уравнении № 2 заменим умножим на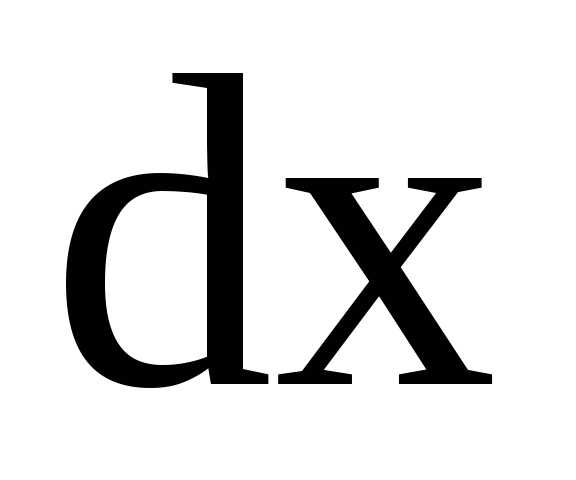, получим

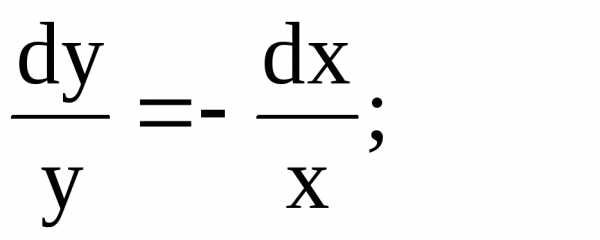
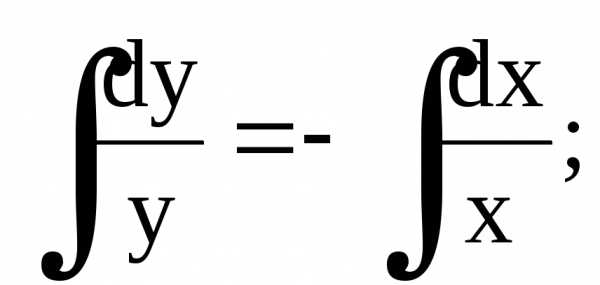
общее решение дифференциального уравнения.

Дифференциальное уравнение № 3 не является уравнением с разделяющимися переменными, т. к., записав его в виде

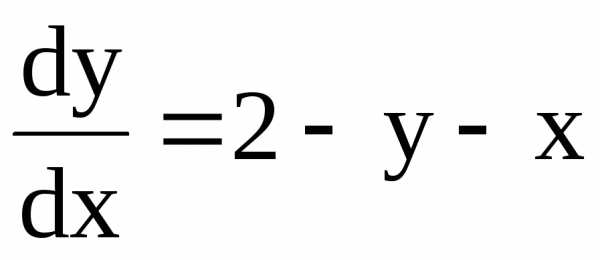или ,

видим, что выражение в виде произведения двух множителей (один –

только с y, другой – только с х) представить невозможно. Заметим, что иногда нужно выполнить алгебраические преобразования, чтобы видеть, что данное дифференциальное уравнение – с разделяющимися переменными.

Пример № 4. Дано уравнение Преобразуем уравнение, вынося общий множитель слева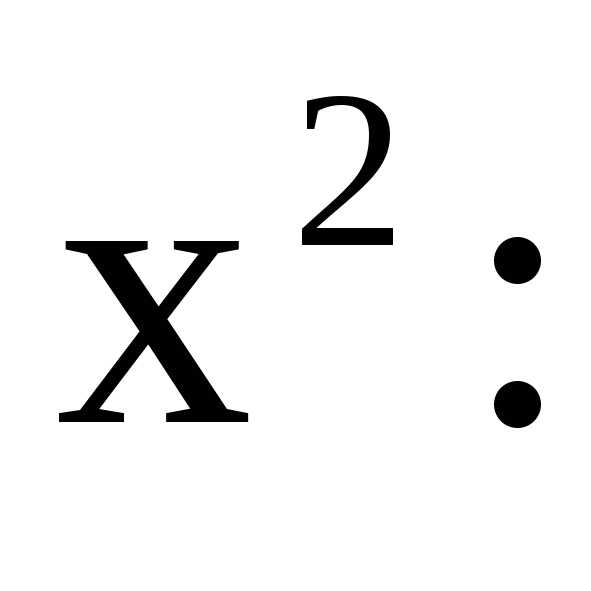Разделим левую и правую части уравнения на произведение

получим

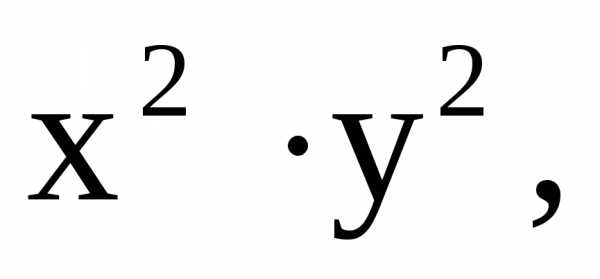
Проинтегрируем обе части уравнения:

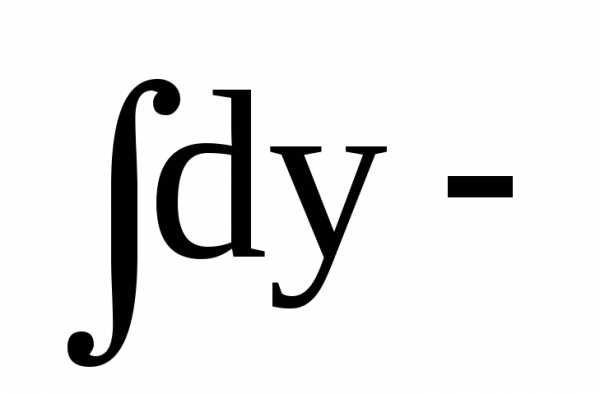
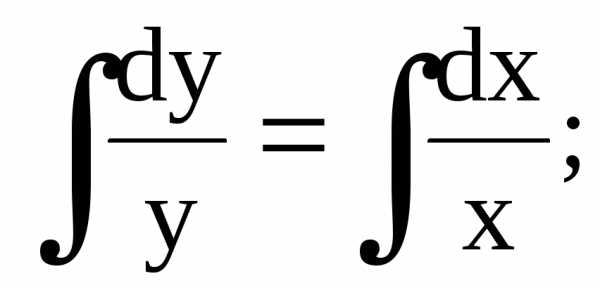
откуда – общий интеграл данного уравнения. (а)

Заметим, что если постоянную интегрирования записать в виде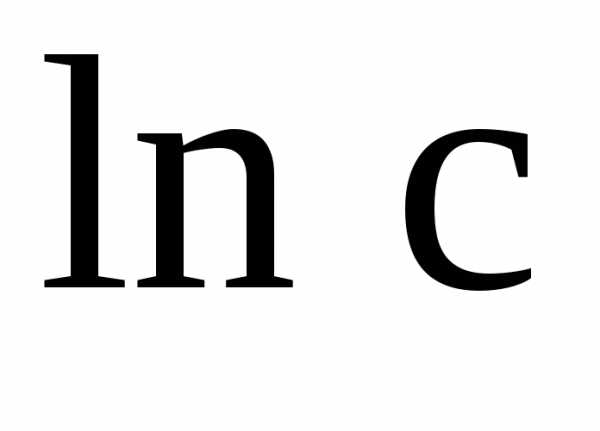

, то общий интеграл данного уравнения может иметь другую форму:

или – общий интеграл. (б)

Таким образом, общий интеграл одного и того же дифференциального уравнения может иметь различную форму. Важно в любом случае доказать, что полученный общий интеграл удовлетворяет данному дифференциальному уравнению. Для этого нужно продифференцировать по

х обе части равенства, задающего общий интеграл, учитывая, что y есть функция от х. После исключения с получим одинаковые дифференциальные уравнения (исходное). Если общий интеграл , (вид (а)), то

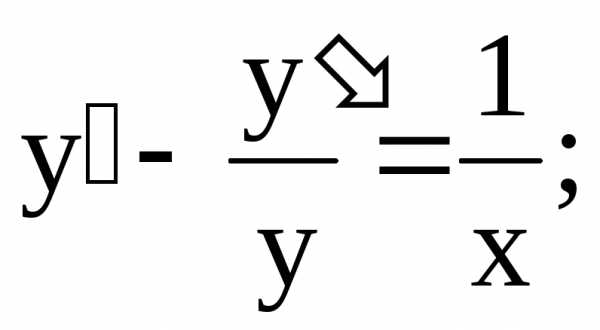
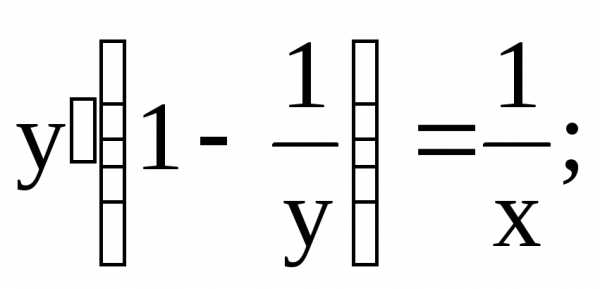
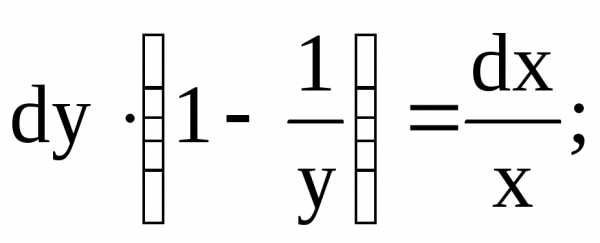
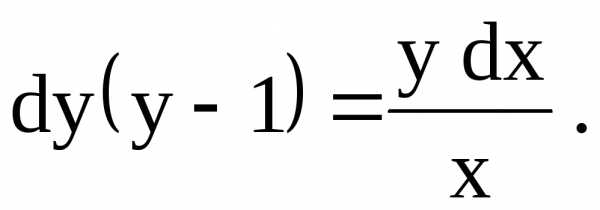
Если общий интеграл (вид (б)), то

Получим то же уравнение, что и в предыдущем случае (а).

Рассмотрим теперь простые и важные классы уравнений первого порядка, приводящиеся к уравнениям с разделяющимися переменными.

studfiles.net

Численное решение дифференциальных уравнений (1)

Численное решение дифференциальных уравнений

Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:

, где x – независимая переменная, – i-ая производная от искомой функции. n – порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных, т.е. общее решение имеет вид.

Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.

Ясно, что при n=1 можно говорить только о задачи Коши.

Примеры постановки задачи Коши:

Примеры краевых задач:

Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.

Численные методы решения задачи Коши для ОДУ первого порядка

Постановка задачи. Найти решение ОДУ первого порядка

 на отрезке при условии

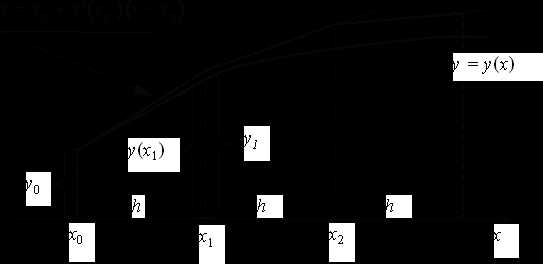
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом , расчетными узлами служат точкипромежутка [x₀, x_n].

Целью является построение таблицы

xi	x0	x1	…	xn
yi	y0	y1	…	yn

т.е. ищутся приближенные значения y в узлах сетки.

Интегрируя уравнение на отрезке , получим

Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка

,

то получим явную формулу Эйлера:

, .

Порядок расчетов:

Зная , находим, затемт.д.

Геометрическая интерпретация метода Эйлера:

Пользуясь тем, что в точке x₀ известно решение y(x₀) = y₀ и значение его производной , можно записать уравнение касательной к графику искомой функциив точке:. При достаточно малом шагеh ордината этой касательной, полученная подстановкой в правую часть значения, должна мало отличаться от ординатыy(x₁) решенияy(x) задачи Коши. Следовательно, точка пересечения касательной с прямойx = x₁ может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую , которая приближенно отражает поведение касательной кв точке. Подставляя сюда(т.е. пересечение с прямойx = x₂), получим приближенное значение y(x) в точке x₂: и т.д. В итоге дляi–й точки получим формулу Эйлера.

Явный метод Эйлера имеет первый порядок точности или аппроксимации.

Если использовать формулу правых прямоугольников: , то придем к методу

, .

Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения по известному значениютребуется решать уравнение, в общем случае нелинейное.

Неявный метод Эйлера имеет первый порядок точности или аппроксимации.

Модифицированный метод Эйлера: в данном методе вычисление состоит из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.

Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(x_i+1) по формуле вида

,

где

…………………………………………….

.

Здесь a_n, b_nj, p_n, – некоторые фиксированные числа (параметры).

При построения методов Рунге–Кутты параметры функции (a_n, b_nj, p_n) подбирают таким образом, чтобы получить нужный порядок аппроксимации.

Схема Рунге – Кутта четвертого порядка точности:

Пример. Решить задачу Коши:

.

Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.

Точное решение: 

Расчетные формулы по явному методу Эйлера для данного примера:

Расчетные формулы модифицированного метода Эйлера:

Расчетные формулы метода Рунге – Кутта:

x	y1	y2	y3	точное
0	1.0000	1.0000	1.0000	1.0000
0.1	1.2000	1.2210	1.2221	1.2221
0.2	1.4420	1.4923	1.4977	1.4977
0.3	1.7384	1.8284	1.8432	1.8432
0.4	2.1041	2.2466	2.2783	2.2783
0.5	2.5569	2.7680	2.8274	2.8274
0.6	3.1183	3.4176	3.5201	3.5202
0.7	3.8139	4.2257	4.3927	4.3928
0.8	4.6747	5.2288	5.4894	5.4895
0.9	5.7377	6.4704	6.8643	6.8645
1	7.0472	8.0032	8.5834	8.5836

y1 – метод Эйлера, y2 – модифицированный метод Эйлера, y3 – метод Рунге Кутта.

Видно, что самым точным является метод Рунге – Кутта.

Численные методы решения систем ОДУ первого порядка

Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений первого порядка.

Покажем это для случая системы двух уравнений первого порядка:

Явный метод Эйлера:

Модифицированный метод Эйлера:

Схема Рунге – Кутта четвертого порядка точности:

К решению систем уравнений ОДУ сводятся также задачи Коши для уравнений высших порядков. Например, рассмотрим задачу Коши для уравнения второго порядка

Введем вторую неизвестную функцию . Тогда задача Коши заменяется следующей:

Т.е. в терминах предыдущей задачи: .

Пример. Найти решение задачи Коши:

 на отрезке [0,1].

Точное решение: 

Действительно:

Решим задачу явным методом Эйлера, модифицированным методом Эйлера и Рунге – Кутта с шагом h=0.2.

Введем функцию .

Тогда получим следующую задачу Коши для системы двух ОДУ первого порядка:

Явный метод Эйлера:

Модифицированный метод Эйлера:

Метод Рунге – Кутта:

Схема Эйлера:

X	y	z	y теор	z теор	y-y теор
0	1	0	1	0	0
0.2	1	-0.2	0.983685	-0.14622	0.016315
0.4	0.96	-0.28	0.947216	-0.20658	0.012784
0.6	0.904	-0.28	0.905009	-0.20739	0.001009
0.8	0.848	-0.2288	0.866913	-0.16826	0.018913
1	0.80224	-0.14688	0.839397	-0.10364	0.037157

Модифицированный метод Эйлера:

X	ycv	zcv	y	z	y теор	z теор	y-y теор
0	1	0	1	0	1	0	0
0.2	1	-0.2	1	-0.18	0.983685	-0.14622	0.016315
0.4	0.96	-0.28	0.962	-0.244	0.947216	-0.20658	0.014784
0.6	0.904	-0.28	0.9096	-0.2314	0.905009	-0.20739	0.004591
0.8	0.848	-0.2288	0.85846	-0.17048	0.866913	-0.16826	0.008453
1	0.80224	-0.14688	0.818532	-0.08127	0.839397	-0.10364	0.020865

Схема Рунге – Кутта:

x	Y	z	k1	l1	k2	l2	k3	l3	k4	l4
0	1	0	0	-1	-0.1	-0.7	-0.07	-0.75	-0.15	-0.486
0.2	0.983667	-0.1462	-0.1462	-0.49127	-0.19533	-0.27839	-0.17404	-0.31606	-0.20941	-0.13004
0.4	0.947189	-0.20654	-0.20654	-0.13411	-0.21995	0.013367	-0.2052	-0.01479	-0.2095	0.112847
0.6	0.904977	-0.20734	-0.20734	0.10971	-0.19637	0.208502	-0.18649	0.187647	-0.16981	0.27195
0.8	0.866881	-0.16821	-0.16821	0.269542	-0.14126	0.332455	-0.13497	0.317177	-0.10478	0.369665
1	0.839366	-0.1036	-0.1036	0.367825	-0.06681	0.40462	-0.06313	0.393583	-0.02488	0.423019

Max(y-y теор)=4*10^-5

Метод конечных разностей решения краевых задач для ОДУ

Постановка задачи: найти решение линейного дифференциального уравнения

, (1)

удовлетворяющего краевым условиям:. (2)

Теорема. Пусть . Тогда существует единственное решение поставленной задачи.

К данной задаче сводится, например, задача об определении прогибов балки, которая на концах опирается шарнирно.

Основные этапы метода конечных разностей:

1) область непрерывного изменения аргумента ([a,b]) заменяется дискретным множеством точек, называемых узлами: .

2) Искомая функция непрерывного аргумента x, приближенно заменяется функцией дискретного аргумента на заданной сетке, т.е. . Функцияназывается сеточной.

3) Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена называется разностной аппроксимацией.

Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки, которые находятся из решения алгебраических уравнений.

Аппроксимация производных.

Для аппроксимации (замены) первой производной можно воспользоваться формулами:

 – правая разностная производная,

 – левая разностная производная,

 – центральная разностная производная.

т.е., возможно множество способов аппроксимации производной.

Все эти определения следуют из понятия производной как предела: .

Опираясь на разностную аппроксимацию первой производной можно построить разностную аппроксимацию второй производной:

(3)

Аналогично можно получить аппроксимации производных более высокого порядка.

Определение. Погрешностью аппроксимации n- ой производной называется разность: .

Для определения порядка аппроксимации используется разложение в ряд Тейлора.

Рассмотрим правую разностную аппроксимацию первой производной:

Т.е. правая разностная производная имеет первый по h порядок аппроксимации.

Аналогично и для левой разностной производной.

Центральная разностная производная имеет второй порядок аппроксимации.

Аппроксимация второй производной по формуле (3) также имеет второй порядок аппроксимации.

Для того чтобы аппроксимировать дифференциальное уравнение необходимо в нем заменить все производные их аппроксимациями. Рассмотрим задачу (1), (2) и заменим в(1) производные:

.

В результате получим:

 (4)

Порядок аппроксимации исходной задачи равен 2, т.к. вторая и первая производные заменены с порядком 2, а остальные – точно.

Итак, вместо дифференциальных уравнений (1), (2) получена система линейных уравнений для определения в узлах сетки.

Схему можно представить в виде:

т.е., получили систему линейных уравнений с матрицей:

Данная матрица является трехдиагональной, т.е. все элементы, которые расположены не на главной диагонали и двух прилегающих к ней диагоналях равны нулю.

Решая полученную систему уравнений, мы получим решение исходной задачи.

studfiles.net

Геометрическая интерпретация решений дифференциальных уравнений первого порядка.

у a

b

A S

x

Как уже говорилось выше (см. Интегральные кривые. ), линия S, которая задается функцией, являющейся каким- либо решением дифференциального уравнения, называется интегральной кривой уравнения

Производная y’ является угловым коэффициентом касательной к интегральной кривой.

В любой точке А(х, у) интегральной кривой этот угловой коэффициент касательной может быть найден еще до решения дифференциального уравнения.

Т.к. касательная указывает направление интегральной кривой еще до ее непосредственного построения, то при условии непрерывности функции f(x, y) и непрерывного перемещения точки А можно наглядно изобразить поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.

Определение. Множество касательных в каждой точке рассматриваемой области называется полем направлений.

С учетом сказанного выше можно привести следующее геометрическое истолкование дифференциального уравнения:

1) Задать дифференциальное уравнение первого порядка – это значит задать поле направлений.

2) Решить или проинтегрировать дифференциальное уравнение – это значит найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.

Определение. Линии равного наклона в поле направлений называются изоклинами.

Численные методы решения дифференциальных уравнений.

Известные методы точного интегрирования дифференциальных уравнений позволяют найти решение в виде аналитической функции, однако эти методы применимы для очень ограниченного класса уравнений. Большинство уравнений, встречающихся при решении практических задач нельзя проинтегрировать с помощью этих методов.

В таких случаях используются численные методы решения, которые представляют решение дифференциального уравнения не в виде аналитической функции, а в виде таблиц значений искомой функции в зависимости от значения переменной.

Существует несколько методов численного интегрирования дифференциальных уравнений, которые отличаются друг от друга по сложности вычислений и точности результата.

Рассмотрим некоторые из них.

Метод Эйлера.

(Леонард Эйлер (1707 – 1783) швейцарский математик )

Известно, что уравнение задает в некоторой области поле направлений. Решение этого уравнения с некоторыми начальными условиями дает кривую, которая касается поля направлений в любой точке.

Если взять последовательность точек х₀, х₁, х₂, …. и заменить на получившихся отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную линию.

y

M₂

M₁ M₃

M₀

y₀ M₄

0 x₀ x₁ x₂ x₃ x₄ x

При подстановке заданных начальных условий (х₀, у₀) в дифференциальное уравнение получаем угловой коэффициент касательной к интегральной кривой в начальной точке

Заменив на отрезке [x₀, x₁] интегральную кривую на касательную к ней, получаем значение

Производя аналогичную операцию для отрезка [x₁, x₂], получаем:

Продолжая подобные действия далее, получаем ломаную кривую, которая называется ломаной Эйлера.

Можно записать общую формулу вычислений:

Если последовательность точек х_i выбрать так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое шагом вычисления, то получаем формулу:

Следует отметить, что точность метода Эйлера относительно невысока. Увеличить точность можно, конечно, уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на практике применяется так называемый уточненный метод Эйлера или формула пересчета.

Суть метода состоит в том, что в формуле вместо значения

берется среднее арифметическое значений f(x₀, y₀) и f(x₁, y₁). Тогда уточненное значение:

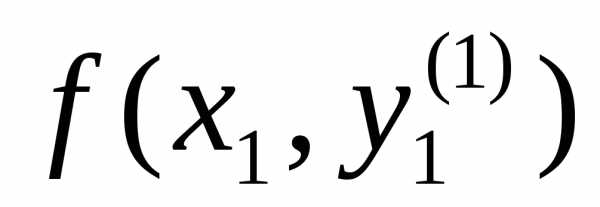Затем находится значение производной в точке . Заменяяf(x₀, y₀) средним арифметическим значений f(x₀, y₀) и , находят второе уточненное значениеу₁.

Затем третье:

и т.д. пока два последовательных уточненных значения не совпадут в пределах заданной степени точности. Тогда это значение принимается за ординату точки М₁ ломаной Эйлера.

Аналогичная операция производится для остальных значений у.

Подобное уточнение позволяет существенно повысить точность результата.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая решает любое дифференциальное уравнение первого порядка методом Эйлера и уточненным методом Эйлера. На каждом шаге вычислений подробно выводятся все указанные выше значения.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple ( Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Метод Рунге – Кутта.

Метод Рунге – Кутта является более точным по сравнению с методом Эйлера.

Суть уточнения состоит в том, что искомое решение представляется в виде разложения в ряд Тейлора. (См. Формула Тейлора. )

Если в этой формуле ограничиться двумя первыми слагаемыми, то получим формулу метода Эйлера. Метод Рунге – Кутта учитывает четыре первых члена разложения.

.

В методе Рунге – Кутта приращения y_i предлагается вычислять по формуле:

где коэффициенты k_i вычисляются по формулам:

Пример. Решить методом Рунге – Кутта дифференциальное уравнение при начальном условии у(0) = 1 на отрезке [0; 0,5] с шагом 0,1.

Для i = 0 вычислим коэффициенты k_i.

Последующие вычисления приводить не будем, а результаты представим в виде таблицы.

i	xi	k		yi	yi
0	0	1	0,1000	0,1104	1
		2	0,1100
		3	0,1105
		4	0,1155
1	0,1	1	0,1210	0,1325	1,1104
		2	0,1321
		3	0,1326
		4	0,1443
2	0,2	1	0,1443	0,1569	1,2429
		2	0,1565
		3	0,1571
		4	0,1700
3	0.3	1	0,1700	0,1840	1,3998
		2	0,1835
		3	0,1842
		4	0,1984
4	0,4	1	0,1984	0,2138	1,5838
		2	0,2133
		3	0,2140
		4	0,2298
5	0,5				1,7976

Решим этот же пример методом Эйлера.

Применяем формулу

Производя аналогичные вычисления далее, получаем таблицу значений:

i	0	1	2	3	4	5
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi	1	1,1	1,22	1,362	1,528	1,721

Применим теперь уточненный метод Эйлера.

i	0	1	2	3	4	5
xi	0,0	0,1	0,2	0,3	0,4	0,5
yi	1	1,1	1,243	1,400	1,585	1,799

Для сравнения точности приведенных методов численного решение данного уравнения решим его аналитически и найдем точные значения функции у на заданном отрезке.

Уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Решим соответствующее ему однородное уравнение.

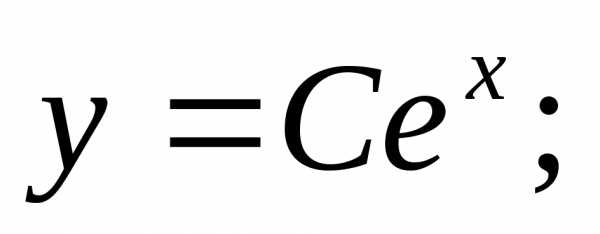
Решение неоднородного уравнения имеет вид

Общее решение:

C учетом начального условия:

Частное решение:

Для сравнения полученных результатов составим таблицу.

i	xi	yi
		Метод Эйлера	Уточненный метод Эйлера	Метод Рунге – Кутта	Точное значение
0	0	1	1	1	1
1	0,1	1,1	1,1	1,1104	1,1103
2	0,2	1,22	1,243	1,2429	1,2428
3	0,3	1,362	1,4	1,3998	1,3997
4	0,4	1,528	1,585	1,5838	1,5837
5	0,5	1,721	1,799	1,7976	1,7975

Как видно из полученных результатов метод Рунге – Кутта дает наиболее точный ответ. Точность достигает 0,0001. Кроме того, следует обратить внимание на то, ошибка (расхождение между точным и приближенным значениями) увеличивается с каждым шагом вычислений. Это обусловлено тем, что во – первых полученное приближенное значение округляется на каждом шаге, а во – вторых – тем, что в качестве основы вычисления принимается значение, полученное на предыдущем шаге, т.е. приближенное значение. Таким образом происходит накопление ошибки.

Это хорошо видно из таблицы. С каждым новым шагом приближенное значение все более отличается от точного.

При использовании кмпьютерной версии “Курса высшей математики” возможно запустить программу, которая решает любое дифференциальное уравнение первого порядка рассмотренным выше методом Рунге- Кутта. Программа подробно выводит результаты вычислений на каждом шаге.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple ( Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

studfiles.net