Механика в физике определение – Определения по Механике | Объединение учителей Санкт-Петербурга

Термины и определения по физике

Механика

Механика – часть физики, в которой изучаются закономерности механического движения и причины, вызывающие или изменяющие это движение.

Кинематика

  Кинематика- раздел физики, описывающий движение тел, не рассматривающий причин, вызвавших это движение. Система отсчета-тело отсчета, система координат, прибор для измерения времени. Тело отсчета- тело, по отношению к которому рассматривается данное механическое движение. Материальная точка- тело, размерами которого в данных условиях можно пренебречь. Механическое движение- изменение взаимного положения тел или их частей в пространстве с течением времени. Твердое тело- система материальных точек, расстояние между которыми не изменяется при движении. Траектория- линия, описываемая в пространстве движущейся материальной точкой. Длинна пути S- сумма длины всех участков траекторий, пройденных материальной точкой за рассматриваемый промежуток времени. Характеристики механического движения: перемещение, скорость, ускорение. Перемещение- направленный отрезок прямой, соединяющий начальное положение тела с ее последующим положением. Ускорение- величина, характеризующая быстроту изменения скорости. Равномерное движение- движение, при котором тело за любые промежутки времени совершает одинаковые перемещения. Равноускоренное движение-движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково. Вращательное движение Угловое перемещение- угол поворота радиуса-вектора за время dt Угловая скорость- векторная величина, модуль которой равен первой производной по времени от угла поворота радиуса вектора. Период обращения Т- время одного полного поворота тела вокруг оси вращения. Угловое ускорение- векторная величина, модуль которой равен первой производной по времени от угловой скорости.

---

Динамика

  Динамика- раздел механики, изучающий законы движения тел Первый закон Ньютона: Всякое тело сохраняет состояние относительного покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не изменит это состояние. Инерциальные системы отсчета- системы отсчета, в которых выполняется первый закон Ньютона. Инертность- свойство тела сохранять состояние покоя или равномерного прямолинейного движения. Масса- физическая величина, являющаяся мерой инертности тела при поступательном движении. Скалярная величина. Сила F- векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел. Принцип независимости действия сил: если на тело одновременно действуют несколько сил, то каждая из сил действует независимо от других. Второй закон Ньютона: ускорение, приобретаемое телом в инерциальной системе отсчета, пропорционально действующее на тело силе и обратно пропорционально массе это тело. Третий закон Ньютона: Силы, с которыми две материальные точки действуют друг на друга равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки. Закон всемирного тяготения: две любые материальные точки притягиваются друг к другу с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Сила тяжести — сила, с которой тело притягивается Землей. Сила тяжести равна произведению массы тела т на ускорение свободного падения g Вес тела — сила, с которой тело вследствие притяжения к вращающейся Земле действует на опору или подвес, удерживающие его от свободного падения. Импульс тела р — векторная величина, равная произведению массы тела на скорость его движения Замкнутая система тел — система тел, на которую не действуют внешние тела (внешние силы), т. е. тела, не входящие в эту систему.

 

---

Законы сохранения

  Закон сохранения импульса справедлив и для незамкнутой системы, если: 1. результирующая всех внешних сил, действующих на систему, равна нулю: 2. проекция суммы всех внешних сил на какую-либо координатную ось равна нулю, тогда сохраняется проекция импульса незамкнутой системы на эту координатную ось. Потенциальная энергия Е- энергия, которая определяется взаимным расположением тел или частей одного и того же тела. Кинетическая энергия Ек — энергия, которой обладает тело вследствие своего движения. Мощность N – скалярная физическая величина, характеризующая скорость выполнения работы. Закон сохранения энергии в механических процессах. Любое тело или система тел может одновременно обладать как потенциальной Е, так и кинетической Ек энергией. В механических явлениях возможен переход кинетической энергии системы тел в потенциальную и наоборот, но полная энергия замкнутой системы тел сохраняет неизменное значение с течением времени

 

Механические колебания и волны

  Колебательные движения- движения или процессы, точно или приблизительно повторяющиеся через одинаковые промежутки времени. Осциллятор- колебательная система вне зависимости от ее физической природы Полное колебание- один законченный цикл колебательного движения, после которого оно повторяется в том же порядке. Период колебаний Т — время, в течение которого совершается полное колебание. Частота периодических колебаний v — число полных колебаний, совершаемых за еди¬ницу времени Амплитуда А — значение максимального отклонения колеблющейся материальной точки от положения равновесия. Гармонические колебания — колебания, при которых колеблющаяся величина со временем изменяется по закону синуса (или косинуса). Фаза колебаний — угловая мера времени, прошедшего от начата колебаний. Свободные колебания – колебания, совершаемые в колебательной системе без внешнего воздействия за счет первоначально сообщенной энергии. Математический маятник – идеализированная система, представляющая собой материальную точку массой т, подвешенную на тонкой, невесомой и нерастяжимой нити длиной /. Период колебаний математического маятника не зависит от его массы и амплитуды колебаний, а зависит от длины маятника I и ускорения свободного падения Пружинный маятник — груз массой т, подвешенный на абсолютно упругой пружине. Период колебаний пружинного маятника зависит от массы колеблющегося тела m и жесткости пружины к Незатухающие колебания — колебания материальной точки (тела), происходящие с постоянной амплитудой. Затухающие колебания — колебания материальной точки (тела), происходящие с постепенно уменьшающейся амплитудой. Вынужденные механические колебания — незатухающие колебания, совершаемые под действием внешней периодически изменяющейся силы Волновой процесс — процесс распространения колебаний в упругой среде. Луч – линия, вдоль которой распространяется волна. Волновая поверхность – множество точек, колеблющихся в одинаковой фазе. Фронт волны — множество точек, до которых дошло колебание к данному моменту времени. Длина волны — кратчайшее расстояние между двумя соседними частицами среды, колеблющимися в одинаковой фазе. Звуковые волны — механические колебания, распространяющиеся в твердой, жидкой или газообразной упругой среде и воспринимаемые органами слуха. Сила звука (или интенсивность) зависит от энергии, ежесекундно переносимой через единичную площадку, расположенную перпендикулярно направлению распространения звуковой волны. Громкость звука зависит от его интенсивности. Звук большой интенсивности вызывает болевые ощущения. Простои, или чистый, тон — звук, источник которого совершает гармонические колебания. Тембр звука определяется его спектром и зависит от громкости отдельных обертонов.

---

Молекулярная физика и термодинамика.

Молекулярная физика

  Первое положение молекулярно-кинетической теории: термодинамическая температура пропорциональна средней кинетической энергии хаотичного движения молекул газа. Второе положение молекулярно-кинетической теории: средние кинетические энергии молекул разных газов, находящихся при одинаковой температура, равны между собой. Третье положение молекулярно-кинетической теории: средняя квадратическая скорость молекул пропорциональна корню квадратному из термодинамической температуры. Атом – наименьшая частица данного химическою элемента. Молекула – наименьшая устойчивая частица данного вещества, обладающая его основными химическими свойствами. Количество вещества — это отношение числа N молекул (атомов) в данном макроскопическом теле к числу NA атомов в 0,012 кг углерода Моль — количество вещества, содержащего столько же молекул (атомов), сколько содержится атомов в 0,012 кг углерода. Броуновское движение- тепловое движение взвешенных в жидкости (или газе) частичек. Межмолекулярное взаимодействие- взаимодействие электрически нейтральных молекул или атомов.

 

---

Агрегатные состояния вещества

  Термодинамический процесс- всякое изменение состояния газа. Изохорный процесс – процесс, протекающий в газе, при котором объем остается постоянным. Идеальный газ – газ, для которого можно пренебречь размерами молекул, силами молекулярного взаимодействия; соударения молекул в таком газе происходят по закону соударения упругих шаров. Плазма — газ, в котором имеется большое количество положительно и отрицательно заряженных ионов, а также свободных электронов Закон Бойля – Мариотта. Всякое изменение состояния газа называется термодинамическим процессом. Парообразование – явление перехода вещества в пар. Испарение- парообразование с открытой поверхности жидкости. Сублимация или возгонка- испарение твердых тел. Удельная теплота парообразования -количество теплоты Q, необходимое для превращения в пар 1 кг жидкости при постоянной температуре. Критическая температура — это наивысшая температура, при которой газ может быть превращен в жидкость. Относительная влажность — отношение парциального давления водяного пара к давлению насыщенного пара при данной температуре. Абсолютная влажность — количество воды, содержащейся в одном кубическом метре воздуха. Жидкость — это агрегатное состояние вещества, промежуточное между газообразным и твердым. Теплоемкость тела- отношение количества теплоты Q, необходимого для повышения его температуры от значения Т1 до значения Т-2, к разности этих температур Поверхностное натяжение различно для разных жидкостей и зависит от температуры. Поверхностное натяжение равно отношению работы, которую нужно затратить при постоянной температуре, чтобы создать поверхность жидкости площадью дельтаS, к площади этой поверхности. Если силы взаимодействия молекул твердого тела и молекул жидкости больше сил взаимодействия между молекулами жидкости, то жидкость смачивает твердое тело (ртуть — железо). В другом случае жидкость не смачивает твердого тела (ртуть — стекло). Анизотропия – зависимость ряда физических свойств, таких, как скорость распространения света, теплопроводность, модуль упругости и др., от направления Изотропные тела- тела, свойства которых одинаковы по всем направлениям. Монокристаллы- крупные одиночные кристаллы. Полиморфизм -Свойство вещества одного состава образовывать различные кристаллические структуры, обладающие разными физическими свойствами. Упругие деформации- деформации, которые полностью исчезают при снятии деформирующих факторов. Пластические деформации -деформации, которые не исчезают при снятии деформирующих- факторов. Прочность материала- это его способность выдерживать нагрузки без разрушения. Предел прочности- это значение нормального механического напряжения, которому соответствует наибольшая выдерживаемая телом нагрузка Предел упругости (пропорциональности)— значение, до которого сохраняется пропорциональность между деформацией и приложенной силой, т.е. выполняется закон Гука. Удельная теплота плавления – это отношение количества теплоты Q, необходимого для того, чтобы перевести твердое тело в жидкость при температуре плавления, к массе этого тела. Кристаллизация— переход вещества из жидкого состояния в твердое кристаллическое. Фазовый переход – переход вещества из одного состояния (фазы) в другое. Если система разделяется на граничащие друг с другом однородные части, находящиеся в физически различных состояниях, то эти части называются фазами системы. Температура, при которой происходит фазовый переход второго рода, называется точкой Кюри Сублимация – переход твердого состояния в газообразное минуя жидкое. Любой процесс, сопровождаемый трением или теплопередачей от нагретого тела к холодному, является необратимым.

 

---

Основы термодинамики

  Внутренняя энергия — это сумма энергий молекулярных взаимодействий и энергии теплового движения молекул. Одноатомный газ – это газ, состоящий из отдельных атомов, а не молекул. Теплообмен- это процесс передачи внутренней энергии без совершения механической работы. Количество теплоты- мера энергии, получаемая или отдаваемая телом в процессе теплообмена. Теплоемкость тела- это отношение количества теплоты Q, необходимого для повышения его температуры от значения T1 до значения Т2, к разности этих температур Первое начало термодинамики — это закон сохранения и превращения энергии Изменение внутренней энергии тела равно разности сообщенного телу количества теплоты и произведенной над ним механической работы. Количество теплоты, сообщенное телу, идет на увеличение его внутренней энергии и на совершение телом работы над внешними телами. Если в замкнутой системе, состоящей из нескольких тел, имеющих первоначально различные температуры, происходит теплообмен, то никакой работы внутри системы не совершается. Изменение внутренней энергии идеального газа при изохорном процессе пропорционально изменению его температуры. При изотермическом нагревании вся теплота, сообщенная газу, расходуется на работу газа против внешних сил. Адиабатным называется процесс, происходящий без теплообмена с окружающими телами. При адиабатном процессе работа совершается только за счет изменения внутренней энергии газа. Равновесным называют процесс, в котором газ проходит ряд следующих друг за другом равновесных состояний.

 

---

Электрическое поле

Закон сохранения заряда: Суммарный заряд электрически изолированной системы не изменяется. Электрические заряды не создаются и не исчезают, а только передаются от одного тела к другому или перераспределяются внутри данного тела   Электростатика- Раздел электродинамики, в котором изучается взаимодействие неподвижных электрических зарядов. Сила электрического взаимодействия между двумя неподвижными точечными электрически заряженными телами в вакууме пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстоя¬ния между ними. Если заряд неподвижен, электрическое поле называется электростатическим. Электростатическое иоле не меняется во времени и создается только электрическими зарядами. Напряженность – силовая характеристика поля, она численно равна силе, действующей на единичный положительный заряд Силовыми линиями, или линиями напряженности поля, называют линии, касательные к которым в каждой точке совпадают с вектором напряженности в данной точке поля. Линии напряженности электростатического поля никогда не могут быть замкнуты сами на себя. Они имеют обязательно начало и конец либо уходят в бесконечность. линии напряженности электрического поля направлены от положительного заряда к отрицательному, т. е. выходят из положительного, а входят в отрицательный заряд. Линии напряженности никогда не пересекаются. Система, состоящая из двух одинаковых по значению, но разноименных точечных зарядов, расположенных на некотором расстоянии I друг от друга, называется электрическим диполем Вектор напряженности электрического поля Е всегда перпендикулярен поверхности равного потенциала. Два важных свойства эквипотенциальных поверхностей: 1) В каждой точке эквипотенциальной поверхности вектор напряженности поля перпендикулярен ей и направлен в сторону убывания потенциала: 2) Работа по перемещению заряда по эквипотенциальной поверхности равна нулю. Диэлектриками называют вещества, не проводящие электрического тока. Электрической поляризацией называют особое состояние вещества, при котором электрический момент некоторого объема этого вещества не равен пулю. Явление перераспределения зарядов внутри проводника под действием внешнего электрического поля называется электростатической индукцией. Заряды, появляющиеся на поверхности проводника, называются наведенными или индуцированными Электрическая емкость (емкость) проводника или системы проводников есть физическая величина, характеризующая способность проводника или системы проводников накапливать электрические заряды. Фарад — емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл Система проводников, емкость которой не зависит от расположения окружающих тел, получила название конденсатора. Конденсаторы — это обычно система из двух проводников, называемых обкладками и разделенных диэлектриком, толщина которого мала по сравнению с размерами обкладок.

 

---

Законы постоянного тока

  Под электрическим током понимают упорядоченный перенос или направленное движение электрически заряженных частиц. Постоянным называется электрический ток, сила и направление которого с течением времени не изменяются. Сила тока — скалярная величина, равная отношению количества электричества ∆Q, которое за время ∆T переносится через данное сечение проводника, ко времени ∆T Кулон — это количество электричества, проходящее через поперечное сечение проводника при силе тока 1 А за время 1 с. Закон Ома для участка цепи без ЭДС: сила тока в проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника Работа, которую совершают сторонние силы при перемещении единичного положительного электрического заряда вдоль всей цени, равна электродвижущей силе (ЭДС) источника тока. Физическая величина, численно равная полной работе, которая совершается кулоновскими и сторонними силами при перемещении единичного положительного заряда вдоль участка цепи (например, А В) из точки А в точку В, называется напряжением (падением напряжения) UBA на этом участке. Закон Ома для полной цепи: сила тока цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника. Узлом А в разветвленной цепи называют точку, в которой сходится не меньше трех проводников Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю Второе правило Кирхгофа: в любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура Закон Джоуля-Ленца: количество теплоты, которое выделяется в проводнике с током, пропорционально квадрату силы тока, времени его прохождения и сопротивлению проводника. Мощность — это отношение роботы электрического тока ко времени T, за которое совершается работа Прибор, служащий для измерения энергии электрического тока, называется электрическим счетчиком.

 

Электрический ток в различных средах

  Удельная проводимость полупроводника складывается из электронной и дырочной проводимости. Движение дырок эквивалентно движению положительно заряженных частиц с зарядом, равным заряду электронов. Число дырок в кристалле равно числу атомов примеси.

 

---

Магнитное поле

  Взаимодействие между проводчиками с током, т. е. взаимодействие между дви¬жущимися электрическими зарядами, называют магнитным. Силы, с которыми проводники с током действуют друг на друга, называют магнитными силами. Магнитное поле представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом. Правило левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением тока в проводнике, то отогнутый большой палец укажет направление силы, действующей на проводник с током, помещенный в магнитное поле Тепловое движение атомов и молекул разрушает взаимную ориентацию магнитных моментов молекул, поэтому намагниченность парамагнетика зависит от температуры, и относительная магнитная проницаемость парамагнетиков убывает с увеличением температуры. Магнитная проницаемость парамагнетиков, как и диамагнетиков, не зависит от индукции внешнего магнитного поля. Магнитная индукция является силовой характеристикой магнитного поля в данной точке пространства. Линии магнитной индукции — это линии, касательные к которым в данной точке совпадают по направлению с вектором В в этой точке. Линии магнитной индукции всегда замкнуты и охватывают проводники с токами. Работа, совершаемая сипами Ампера при перемещении проводника с током в магнитном поле, равна произведению силы тока на магнитный поток через поверхность, охватываемую проводником при его движении. Закон электромагнитной индукции Фарадея: В отличие от электростатического ноля индуцированное электрическое ноле является не потенциальным, так как работа, совершаемая в индуцированном электрическом поле, при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции, а не нулю. Явление возникновения индуцированною тока в цепи в результате изменения тока в этой цепи называют самоиндукцией.

---

Электромагнитные колебания

  Переменный ток- электрический ток, изменяющийся со временем Время, в течение которого переменный периодический ток совершает полный цикл своих изменений, возвращаясь к своей исходной величине, называется периодом переменного тока. Автоколебания- незатухающие колебания. Поддерживаемые в колебательной системе за счет постоянного внешнего источника энергии. Генераторы электрического тока — это устройства для преобразования различных видов энергии — механической, химической, тепловой, световой и др. — в электрическую. Трансформатор представляет собой выполненный из мягкого ферромагнетика сердечник замкнутой формы, на котором находятся две обмотки

 

---

Электромагнитные волны

  электромагнитные волны — это распространяющееся в пространстве переменное электромагнитное поле. Расстояние, на которое перемещается электромагнитная волна за время, равное одному периоду колебания, называется длиной волны. Диполь — это система двух разноименных точечных зарядов + Q и -Q, расположенных на расстоянии I друг от друга. Под светом в настоящее время понимают электромагнитное излучение, воспринимаемое человеческим глазом. Длина волн воспринимаемого электромагнитного излучения лежит в интервале от 0,38 до 0,76 мкм. В физике часто называют светом и невидимые электромагнитные волны, лежащие за пределами этого интервала: от 0,01 до 340 мкм. Свет — это электромагнитные волны, которые могут распространяться как в среде, так и в вакууме. Принцип Гюйгенса: каждая точка среды, до которой доходит световое возбуждение, является, в свою очередь, центром вторичных волн. Непрерывное геометрическое место точек среды, колеблющихся в одинаковой фазе, называют волновой поверхностью, а множество точек, до которых дошло колебание к данному моменту времени. – фронтом волны. Дисперсией называют зависимость от длины волны скорости света в веществе, т. е. показателя преломления вещества. Дисперсию называют нормальной, если показатель преломления возрастает с уменьшением длины волны. Цвет непрозрачного тела определяется смесью цветов, которые оно отражает. Способность тел поглощать определенные цветные лучи называют избирательным поглощением. Интерференцией называют явление, возникающее при наложении двух (или нескольких) световых волн одинаковою периода в однородной изотропной среде, в результате чего происходит перераспределение энергии волн в пространстве. Люминесценцией называют излучение, представляющее собой избыток над тепловым излучением тела при данной температуре, длительность которого значительно превышает период световых волн .

Строение атома и квантовая физика

Квантовая физика

  Гипотеза планка: энергия испускается телом не непрерывно, как это предполагалось в классической физике, а отдельными дискретными порциями — квантами, энергия Е которых пропорциональна частоте v колебаний Фотоэлектрический эффект — вырывание электронов из атомов или молекул вещества под действием света (излучения) Если электроны, выбитые светом, вылетают за пределы вещества, фотоэффект называют внешним. Если же оторванные от своих атомов или молекул электроны остаются внутри освещаемого вещества в качестве свободных, то фотоэффект называют внутренним. Законы фотоэффекта: 1. Сила фототока насыщения, возникающего при освещении монохроматическим светом, пропорциональна световому потоку, падающему на катод 2. Скорость фотоэлектронов увеличивается с ростом частоты (с уменьшением длины волны) падающего света и не зависит от интенсивности светового потока. 3. Независимо от интенсивности светового потока фотоэффект начинается только при определенной для данного металла минимальной частоте (максимальной длине волны) света, называемой красной границей фотоэффекта.

Строение атома

  Основные положения боровской теории атома: 1. Электроны могут двигаться в атоме только по определенным орбитам, находясь на которых они, несмотря на наличие у них ускорения, не излучают. 2. Атом излучает или поглощает квант электромагнитной энергии при переходе электрона из одного стационарного состояния в другое. Под индуцированным понимают излучение возбужденных атомов, вызванное действием падающего на них света. Радиус атомных ядер- линейные размеры области, в которой проявляется действие ядерных сил.

 

---

Физика атомного ядра

  Удельной энергии связи- это физическая величина, равная работе, которую нужно совершить для удаления нуклона из ядра. Стабильными являются ядра элементов, у которых число протонов равно числу нейтронов. Экспозиционной дозой излучения называют меру ионизации воздуха, происходящей под действием данного излучен

 

---

 

fizikakkep.ru

Механика.

§1. Механическое движение.

Простейший вид движения, встречающиеся в природе – это механическое движение.

Определение: Механическим движением называется движение, состоящие в изменении взаимного расположения тел или их частей в пространстве с течением времени.

Определение: Механикой называется раздел физики, занимающийся изучением законов механического движения.

В более узком смысле под механикой понимают ньютоновскую или классическую механику, то есть механику, в основе которой лежат законы Ньютона. Классическая механика состоит из трех разделов – статики, кинематики и механики.

Определение: Статикой называется раздел механики рассматривающий законы сложения сил и условия равновесия тел.

Определение: Кинематикой называется раздел механики, дающий математическое описание всевозможных видов механического движения, безотносительных к тем причинам, которые обеспечивают осуществление каждого конкретного вида движения.

Определение: Динамика называется раздел механики, исследующий влияние взаимодействия между телами на их механическое движение.

Для описания реально движущегося тела в механике используются, в зависимости от условий каждой конкретной задачи, различными упрощенными моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело и т.д.

Определение: Материальной точкой называют тело, форма и размеры которого не существенны в условиях данной задачи.

Определение: Механической системой называют совокупность тел, выделенных из окружающего мира для последующего механического исследования.

При определенных условиях систему тел можно рассматривать как систему материальных точек. Любое про? материальное тело рассматривают как систему материальных точек. Для этого данное тело необходимо разбить на такое количество частей, что размеры каждой части будут много меньше размера самого тела. Каждую такую часть рассматривают материальную точку.

Определение: Абсолютно твердое тело – тело, деформациями которого в условиях данной задачи можно пренебречь.

Расстояние между двумя точками всегда неизменны. Под твердым телом понимают реальное тело, деформации которого не сказываются на его движении.

Определение: Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука

После снятия внешних воздействий такое тело полностью восстанавливает свою форму и размеры.

Определение: Абсолютно неупругое тело – тело, которое после снятия внешних воздействий полностью сохраняет деформированное состояние, вызванное этим воздействием.

§2. Вектор перемещения точки.

Положение тела в пространстве можно определить только по отношению к другим телам.

Определение: Система отсчета – система координат, жестко связанная с абсолютно твердым телом, снабженная часами и используемая для определения положения в пространстве тел или их частей в любые моменты времени. Иногда система отсчета называют хронометрированной системой координат.

Тело отсчета – абсолютно твердое тело, с которым жестко связана система координат. Обычно это инерциальная система отсчета. Наиболее часто используется прямоугольная декартова система координат, в основе которой лежит базис .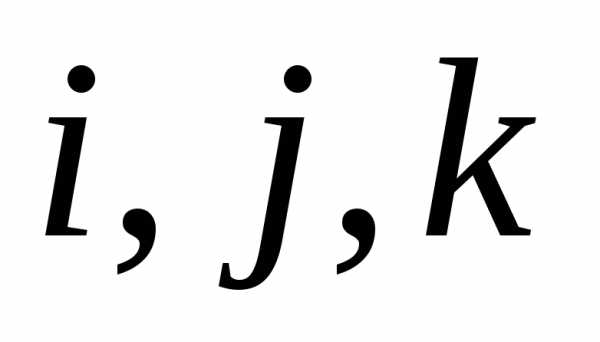

Определение: Радиус-вектор – вектор, направленный из начала координат в текущее положение материальной точки.

В координатном представлении, гдеx, y, я – координаты точки. В общем случае , x, y,z являются функциями времени.

x, y, z – проекции радиус-векторов на оси: OX, OY, OZ.

M – текущее положение точки.

M₁ – проекция точки на плоскость XOY

Движение материальной точки полностью определено, если заданны три непрерывные функции:

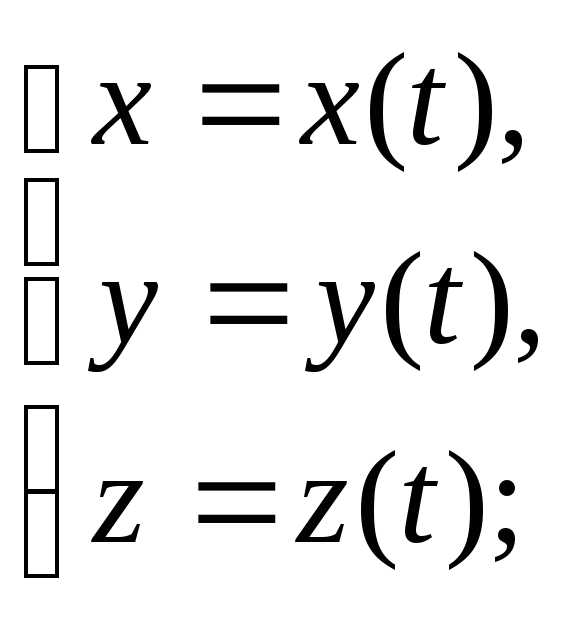
Данная система уравнений является системой кинематических уравнений движения материальной точки. Кинетические уравнения движения точки задают уравнение её траектории в параметрической форме, где параметр время.

Определение: Траекторией называется линия, описываемая в пространстве движущейся точки.

Пример:

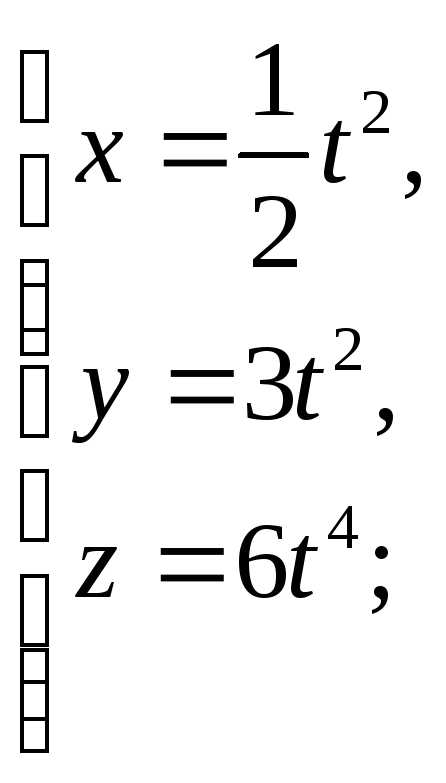Определяем уравнение траектории 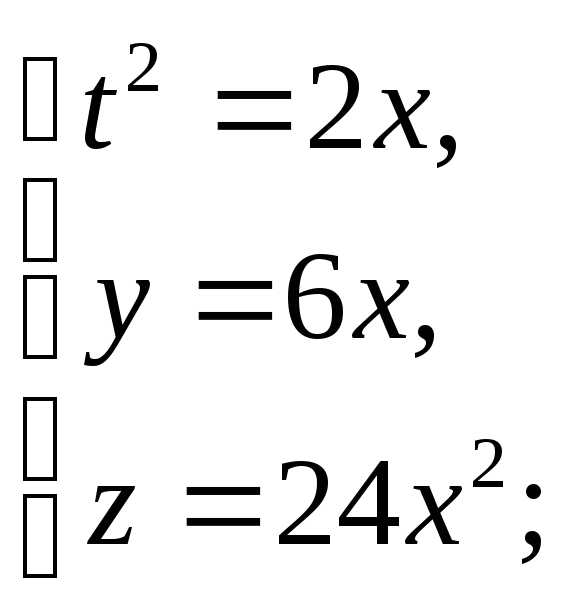;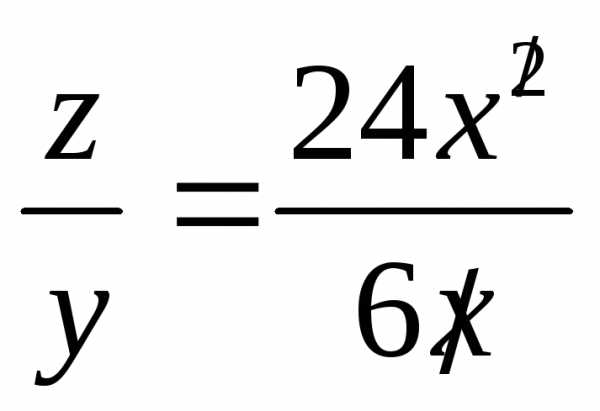Итого:

В зависимости от формы траектории различают прямолинейное, вращательное, криволинейное движение точки.

Определение: Плоским называют такое движение точки, если её траектория целиком лежит в одной плоскости.

Механическое движение тела относительно, то есть характер и, в частности, вид траекторий точки тела зависят от выбора системы отсчёта.

В общем случае траектория материальной точки представляет пространственную кривую.

Определение: Длинной пути называется расстояние пройденного материальной точкой за рассматриваемый промежуток времени, измеряемое вдоль траектории.

Длина пути 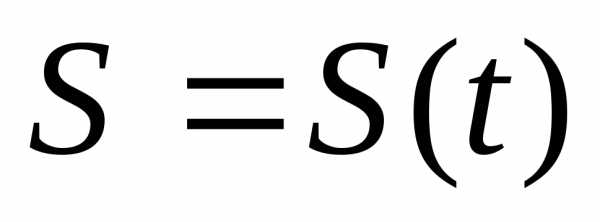– скалярная функция,.

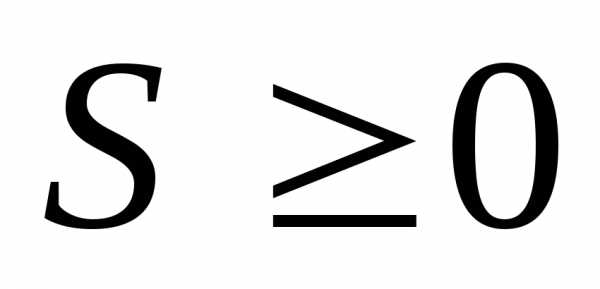Определение: Вектор перемещения материальной точки – это вектор, соединяющий начальное и конечное её положение в рассматриваемые моменты времени. Он равен приращению радиус-вектора за заданный промежуток времени.

– перемещение или приращение радиус-вектора

где – изменение координатыx материальной точки

где – изменение координатыy материальной точки

где – изменение координатыz материальной точки

x₀, x – «иксовые» координаты начального и конечного положения точки, аналогично y₀, y и z₀, z.

Определение: Числом степеней свободы механической системы называется число независимых движений, которые она может совершать.

Пример:

Материальная точка имеет три степени свободы; две материальные точки, соединенные невесомым стержнем – пять степеней свободы; три материальные точки, соединенные невесомым стержнем – шесть степеней свободы.

studfiles.net

МЕХАНИКА | Энциклопедия Кругосвет

Содержание статьи

МЕХАНИКА, раздел физики, в котором изучается движение тел под действием сил. Механика охватывает очень широкий круг вопросов – в ней рассматриваются объекты от галактик и систем галактик до мельчайших, элементарных частиц вещества. В этих предельных случаях выводы механики представляют, конечно, чисто научный интерес. Но предметом механики является также проектирование строений, мостов и механизмов; этот раздел, обычно называемый прикладной механикой, сам по себе достаточно обширен.

Фундаментальное значение для всей этой тематики имеет механика материальной точки, разделяющаяся на кинематику, предметом которой является математическое описание возможных движений материальной точки, и динамику, которая рассматривает движение материальных точек под действием заданных сил. Основные принципы динамики сведены в законы движения, которые в случае материальных точек имеют самый простой вид. Эти законы были впервые сформулированы в 1687 И.Ньютоном. Если материальные точки движутся с очень большими скоростями, то ньютоновские законы движения следует модифицировать в соответствии с теорией относительности; если же это частицы атомных масштабов, то необходима иная формулировка законов движения – так называемая квантовая механика. Ниже будет изложена ньютоновская механика; ее модификациям посвящены статьи ОТНОСИТЕЛЬНОСТЬ; КВАНТОВАЯ МЕХАНИКА.

Протяженное тело можно формально рассматривать как совокупность идеализированных материальных точек, совершенно не имея в виду атомное строение вещества. Выводы о движении таких тел можно делать, исходя из совокупности движений материальных точек. Здесь тоже проводится различие между кинематикой и динамикой и, кроме того, существует статика, изучающая условия равновесия твердых тел, на которые действуют внешние силы. Эти вопросы обсуждаются ниже.

Механические свойства газов и жидкостей в какой-то мере сходны, и законы, которым подчиняется их движение, тоже можно вывести, рассматривая их как системы материальных точек. Этот раздел, обычно называемый «механикой жидкостей и газов», подразделяется на гидростатику и гидродинамику. Им посвящена статья ГИДРОАЭРОМЕХАНИКА. Специальные вопросы течения газов рассматриваются в статье АЭРОДИНАМИКА, а вопросы движения электропроводящих жидкостей и газов – в статье МАГНИТНАЯ ГИДРОДИНАМИКА. Остаются еще три специальных раздела – аналитическая динамика, небесная механика и статистическая механика. Аналитическая динамика – это математическая дисциплина, в центре внимания которой находятся общие методы составления уравнений движения и их решения, а не анализ конкретных механических систем. В небесной механике методы аналитической динамики применяются при изучении чрезвычайно сложного движения планетных систем. Статистическая механика опирается на теорию газов и рассматривает в общем виде поведение системы, содержащей огромное число молекул или атомов, исходя из свойств таких отдельных частиц и законов, управляющих их поведением. По этим вопросам имеются отдельные статьи НЕБЕСНАЯ МЕХАНИКА; СТАТИСТИЧЕСКАЯ МЕХАНИКА.

Подобное деление механики отражает историческое развитие физики и, кроме того, соответствует использованию различных математических методов. В конечном итоге механика и физика как наука составляют единое целое, ибо чем больше мы узнаем, например, о таких явлениях, как свет и электричество, которые обычно не рассматриваются в механике, тем яснее становится их фундаментальная связь с атомными явлениями, тесно связанными с механикой.

Исторически развитие статики началось с Архимеда в 3 в. до н.э. До этого периода и много столетий спустя проблемы динамики обсуждались лишь с качественной стороны и соотносились с принципами, которые мы полагаем сегодня ошибочными либо не имеющими отношения к делу. Начало динамике было положено Ньютоном, который сформулировал законы движения и закон всемирного тяготения, опубликованные в первом издании Математических начал натуральной философии (Philosophiae naturalis principia mathematica, 1687). Ньютону удалось в своей книге заложить основы, а в ряде случаев и далеко продвинуться в изучении динамики, небесной механики, механики твердого тела, гидродинамики и баллистики. Хотя принципы статики к тому времени были хорошо известны, Ньютон впервые рационально обосновал их, показав, как их можно вывести из законов динамики. На протяжении примерно двух столетий после этого механика развивалась путем построения более совершенных математических методов без необходимости внесения каких-либо изменений в основные принципы, и лишь после 1900 развитие теории электромагнетизма и атомной физики потребовало модификации механики для распространения ее принципов на явления, которые она не могла удовлетворительно описывать. Но теория относительности и квантовая механика не отменили ньютоновской теории – она по-прежнему точна, как и раньше, и можно показать, что она строго вытекает из обеих новых теорий в том случае, когда рассматриваемые тела имеют макроскопические размеры и движутся с умеренными скоростями. В остальной части этой статьи мы будем иметь дело только с такими ситуациями.

Механика материальной точки.

Чтобы можно было описывать движение материальной точки, нужно определить ее положение в данный момент. На рис. 1 показана прямоугольная система координат, которая позволяет характеризовать положение материальной точки, находящейся в точке Р, координатами (x, y, z). Поскольку материальная точка не имеет размеров и, следовательно, не может быть ориентирована в том или ином направлении, эти три числа полностью характеризуют ее положение в любой момент. Если раcсматривать их как функции времени t, то функция [x (t), y(t), z (t)] прочерчивает в пространстве траекторию, полностью определяющую движение материальной точки. Основная задача динамики материальной точки – найти зависимость x, y и z от t, если заданы силы, действующие на материальную точку. (Возможна, конечно, задача о нескольких материальных точках, оказывающих силовое воздействие друг на друга; подобные задачи решаются труднее.)

Рассмотрим сначала материальную точку, движущуюся прямолинейно, скажем, вдоль оси x, в отсутствие каких-либо сил. В средневековой механике вслед за Аристотелем утверждалось, что тело движется, пока на него действует сила. Однако Галилей, а за ним и Ньютон установили, что единственное действие силы состоит в изменении движения тела и что в отсутствие силы тело либо остается в покое, либо продолжает двигаться равномерно и прямолинейно. В этом заключается первый закон механики Ньютона. Под равномерным движением подразумевается движение с постоянной скоростью v, при котором путь x, проходимый за время t, равен:

x = vt.

Точнее было бы формулировать это определение, рассматривая короткие интервалы пути и времени: если частица начинает двигаться из точки x₀ в момент времени t₀ и достигает точки х в момент t, то средняя скорость за это время определяется как

Конечно, если материальная точка движется с постоянной скоростью, то нет необходимости говорить о среднем значении. Но если на материальную точку действует сила, то ее движение не является равномерным. В этом случае скорость меняется во времени, и можно говорить о мгновенной скорости v (t) в момент времени t как пределе представленного выше выражения при очень малых интервалах времени и пути. Это записывается следующим образом:

Точно так же можно говорить об изменении скорости во времени, т.е. об ускорении. Если мгновенная скорость изменяется от v₀ в момент t₀ до vв момент t, то среднее ускорение за этот промежуток определяется как

а мгновенное ускорение в момент времени t –

Таким образом, скорость характеризует быстроту изменения положения, а ускорение – быстроту изменения скорости. Рассматривать скорость изменения ускорения и т.д. не имеет особого смысла, поскольку, как это первым понял Ньютон, сила создает лишь ускорение. Действительно, если к небольшому телу приложена сила F, то, как показывает опыт, его ускорение остается постоянным, если сила постоянна, и в любой момент времени ускорение пропорционально этой силе. Данное положение можно записать в виде a ~ F или F ~ a. В этом соотношении коэффициент пропорциональности m есть величина, постоянная для рассматриваемой частицы независимо от того, где и как она движется. Эта величина m называется массой (инертной массой) частицы, и, следовательно, равенство

F = ma

есть установленное опытным путем соотношение между мгновенными значениями величин F и a. В этом суть второго закона Ньютона. Третий закон, который мы приведем в дальнейшем, относится к случаю, когда имеется более одного тела.

Единицы измерения механических величин вводятся следующим образом. На основе эталонов единиц длины и времени – метра и секунды – определяются единицы скорости – метр в секунду (м/с) и ускорения – метр в секунду в квадрате (м/с²). Единица массы килограмм (кг) определяется как масса международного прототипа килограмма, изготовленного из сплава иридия с платиной и хранящегося в Международном бюро мер и весов в Севре под Парижем. Единица силы в системе СИ называется ньютоном (Н) и определяется как сила, сообщающая телу массой 1 кг ускорение 1 м/с². Таким образом, согласно второму закону Ньютона,

1 H = 1 кгЧм/с².

Направление вектора ускорения совпадает с направлением вектора силы.

Тяготение.

Представленное выше определение единицы силы, основанное на незыблемых физических принципах, тем не менее, не удобно для практических измерений. Удобнее исходить из понятия веса, т.е. силы притяжения Земли. Согласно закону всемирного тяготения, сформулированному тоже Ньютоном, между любыми двумя телами во Вселенной действует сила притяжения, пропорциональная произведению масс этих тел и обратно пропорциональная квадрату расстояния между ними. Это положение математически выражается соотношением

где G – универсальная гравитационная постоянная, а m_G и M_G – гравитационные массы тел. Если тела протяженные, то все материальные точки этих тел попарно взаимодействуют друг с другом в соответствии с этой формулой и, чтобы найти полную силу, нужно суммировать все отдельные взаимодействия. В чрезвычайно важном случае тел сферической формы оказывается, что притяжение будет в точности таким, как если бы масса каждого из них находилась в центре сферы.

Предположим теперь, что телу с гравитационной массой m_G и инертной массой m, удерживаемому не очень высоко над поверхностью Земли, предоставляется возможность свободно падать. Сила тяжести ускоряет тело вниз, и мы имеем

где M_G – гравитационная масса Земли, а R – ее радиус. Ускорение падающего тела можно записать в виде

где первый множитель не зависит от свойств тела. Экспериментально установлено, что ускорение несколько изменяется в разных точках на поверхности Земли, поскольку Земля не является идеальной сферой и к тому же вращается. Однако в данном месте оно в точности одно и то же для всех тел. Это означает, что величины m и m_G всегда и всюду пропорциональны, а при надлежащем выборе единиц измерения одинаковы. В таком случае нет необходимости различать гравитационную и инертную массы, и выражение для F_G приобретает вид

где

Аналогично выражению для ускорения a, ускорение силы тяжести g в любой точке дается формулой

Величина g составляет примерно 9,81 м/с² и позволяет определить массу Земли (5,97Ч10²⁴ кг) и ее среднюю плотность, в 5,5 раз превышающую плотность воды. Предположим, теперь, что вес тела равен W. Так как сила веса создает ускорение g, соотношение между массой, весом и ускорением приобретает вид

W = mg.

Между экватором и полюсами на поверхности земли величина g изменяется от 9,78 до 9,83 м/с². Соответственно этому изменяется и вес, но в одной точке вес двух тел с одинаковой массой всегда одинаков, и на этом опытном факте основан гораздо более удобный способ измерения массы и силы, нежели основанный на втором законе Ньютона. Массы двух тел равны, если в одном и том же месте равны их веса.

Импульс и энергия.

Импульс тела р определяется как произведение его массы на скорость:

p = mv.

Эта величина имеет важное значение. В самом деле, предположим, что два тела с массами m и M действуют друг на друга с силой, стремящейся ускорить оба тела. На рис. 2 такую силу создает пружина (происхождение силы может быть любым). Согласно третьему закону Ньютона, в любой момент времени сила, с которой масса m действует на массу M, равна по величине и противоположна по направлению силе, с которой масса M действует на m (действие равно противодействию). Предположим, что в момент времени t₀ скорости масс равны v₀ и V₀. Комбинируя выражение для ускорений со вторым законом Ньютона, мы найдем, что скорости изменяются в соответствии с выражениями

где F_m и F_M – силы, действующие на m и M. Поскольку эти силы равны и противоположно направлены, имеем

откуда, умножая на (t – t₀) получаем

Из этого равенства следует, что хотя отдельные импульсы изменяются, их сумма в момент времени t₀ равна их же сумме в момент t, т.е. в процессе всего движения остается постоянной. Это – так называемый закон сохранения импульса. Он универсален в том смысле, что справедлив независимо от природы сил и длительности их действия между телами.

Работа U, совершаемая силой, приложенной к движущемуся телу, определяется как произведение силы на расстояние:

U = F(x – x₀),

где (как и далее) точки x и x₀ должны выбираться достаточно близко друг к другу, чтобы силу F можно было считать постоянной. Воспользуемся тем, что, как легко доказать, точка, движущаяся с постоянным ускорением, проходит за время (t – t₀) такое же расстояние, как если бы все это время она двигалась со средней скоростью ¹/₂(v + v₀). Таким образом, из выражения для второго закона Ньютона вытекает:

или

Величина ¹/₂mv² называется кинетической энергией. Если обозначить ее через Т, то выражение

U = T – T₀

означает, что работа, совершаемая за любой малый промежуток времени, а следовательно (если просуммировать), и за любой произвольный промежуток времени, равна разности конечной и начальной кинетических энергий. Это положение справедливо независимо от того, какова сила и как она изменяется со временем, а также от того, каково расстояние, на котором она действует.

Путем точно таких же рассуждений можно показать, что тело, обладающее кинетической энергией Т, может совершить работу, равную T – T₀, если его Т уменьшится до величины T₀, или равную Т, если тело в конце останавливается. Таким образом, всю работу, совершенную над телом при его ускорении, можно снова получить, остановив тело. Поэтому движущееся тело можно рассматривать как «носителя» работы. Под энергией понимается способность совершать работу, а запасенная телом кинетическая энергия зависит только от его скорости (и массы) и не зависит от того, как эта скорость была приобретена.

Предположим, что тело массой m поднято на высоту h над поверхностью земли, а затем свободно падает. Если оно падает в течение времени t с постоянным ускорением g, то соотношение между g, h и t можно получить из правила для средних скоростей

где v – скорость, с которой тело ударяется о землю, причем мы положили v₀ = 0, поскольку до начала падения тело покоится. Вновь, поскольку v = gt, можно написать h = v²/2g, а умножив обе части равенства на mg, получим

mgh = ¹/₂mv².

Поскольку mg – вес тела, величина mgh есть работа по подъему тела на высоту h, а ¹/₂mv² – кинетическая энергия тела в момент достижения им земли, равная работе, которую тело может совершить при ударе. Анализируя весь процесс, мы видим, что работа по подъему тела, равная mgh, запасается телом в виде его потенциальной энергии перед тем, как оно начинает падать. По мере падения потенциальная энергия переходит в кинетическую, которая может снова перейти в работу, равную mgh, при ударе тела о землю. Когда тело окончательно приходит в состояние покоя, то на первый взгляд энергия исчезает. Но более тщательный анализ показывает, что она сохранилась в форме усилившегося молекулярного движения в месте падения, т.е. в форме звука и теплоты. В отличие от импульса, энергия принимает разные формы, но при переходе из одной формы в другую полное количество энергии не меняется. Это – так называемый закон сохранения энергии.

В качестве примера применения двух законов сохранения рассмотрим соударение двух шаровых маятников (рис. 3,а). Предположим, что шары маятников имеют одинаковую массу и изготовлены из абсолютно упругого материала. Это означает, что кинетическая энергия при ударе не рассеивается. Пусть V₁ – скорость первого маятника в момент, предшествующий соударению, и нам надо найти v₁ и v₂ – скорости сразу после удара.

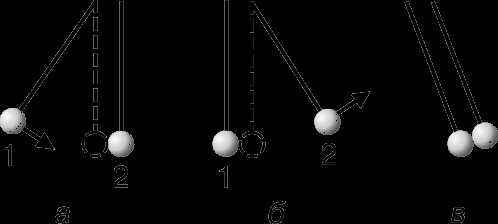
При соударении энергия и импульс сохраняются, и мы имеем

Производя сокращения и возводя обе части второго равенства в квадрат, получаем

Эти соотношения могут выполняться одновременно только при v₁v₂ = 0. Таким образом, либо v₁ = 0, либо v₂ = 0, но не то и другое. Поскольку второй шар служит препятствием для первого, в нуль обратится v₁, и в силу закона сохранения импульса системы имеем v₂ = V₁. Первый шар останавливается, а второй движется со скоростью V₁, как показано на рис. 3,б.

Предположим теперь, что на второй шар нанесена мастика, так что при соударении шары прилипают друг к другу и дальше движутся вместе (рис. 3,в). В этом случае v₂ = v₁ и импульс по-прежнему сохраняется, так что

mV₁ = 2mv₁,

откуда v₁ = ¹/₂V₁, т.е. шары будут двигаться со скоростью, которая в два раза меньше начальной скорости первого шара. Начальное значение кинетической энергии равнялось T₁ = ¹/₂mV₁², а конечное значение 2 ґ¹/₂m(¹/₂V₁)² = ¹/₂T₁. Таким образом, кинетическая энергия, равная ¹/₂T₁, рассеивается, причем основная часть этой потери идет на деформацию и нагрев мастики и шаров.

Динамика и статика в трех измерениях.

Чтобы обобщить предыдущие результаты на случай трех измерений, потребуется ввести лишь еще один принцип, который заключается в том, что законы Ньютона справедливы для движения вдоль каждой оси координат независимо от движения по другим осям. Так, если пренебречь сопротивлением воздуха, снаряд вдоль оси z движется с замедлением (рис. 4), а вдоль горизонтальной оси – без внешних сил и без ускорения. Обозначим через t время полета. Половину этого времени снаряд поднимается, а остальное время опускается. Таким образом, его скорость по вертикали изменяется на v_0z за время ¹/₂t, так что

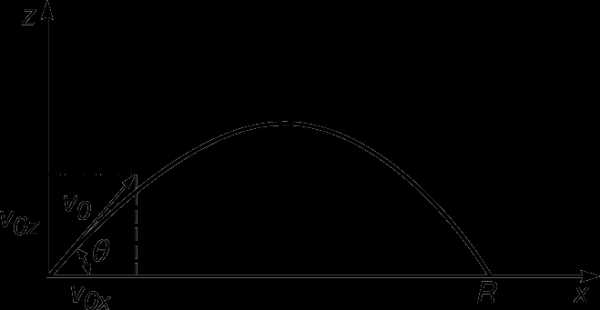
v_0z = ¹/₂gt, t = 2v_0z/g,

и все это время горизонтальное движение происходит со скоростью v_0x и без ускорения. Таким образом, дальность полета равна:

R = v_0xt = 2v_0xv_0z/g.

Если v₀ – начальная скорость, а q – угол возвышения, то легко понять, что v_0x = v₀cosq и v_0x = v₀sinq, так что

и максимальное значение этой величины, равное v₀²/g, достигается при q = 45°.

В приведенном примере начальная скорость v₀ характеризовалась и величиной, и направлением. Такие величины называются векторами, а величины v_0x и v_0z – соcтавляющими или компонентами вектора. (Обычно векторы обозначают полужирными буквами.) Предположим теперь, что в трехмерном пространстве к покоящейся материальной точке приложено несколько сил, под действием которых она остается в покое. О подобной системе сил говорят, что они уравновешены, и законы динамики позволяют определить, каким должно быть соотношение между ними. Если материальная точка покоится и сохраняет это состояние, ее ускорения вдоль осей x, y или z равны нулю, а поскольку ускорения вдоль этих осей не зависят друг от друга, полные силы в каждом из этих трех направлений тоже должны быть равны нулю. (Полная сила, действующая на материальную точку вдоль оси х и стремящаяся привести ее в движение вдоль этой оси, равна сумме x-компонент всех действующих сил; то же самое справедливо и для двух других осей.)

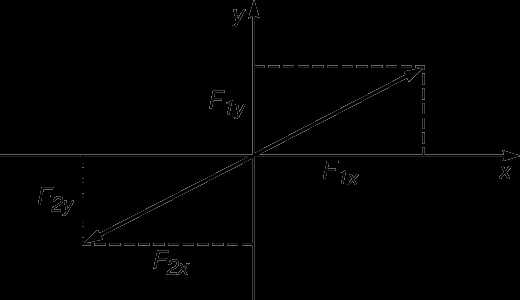
Предположим, что имеются только две силы с компонентами F_1x, F_1y, F_2x и F_2y (для упрощения рисунка ограничимся двумя измерениями). В случае равновесия имеем

F_1x + F_2x = 0 и F_1y + F_2y = 0,

или

F_1x = –F_2x и F_1y = –F_2y.

Так как F_1x и F_1y – компоненты вектора силы F₁, и аналогично F_2x и F_2y – компоненты вектора F₂, то возникает ситуация, показанная на рис. 5, где векторы двух уравновешивающих друг друга сил изображены равными по величине и направленными в противоположные стороны.

Предположим, теперь, что имеются три вектора, причем F₃ уравновешивает F₁ и F₂. В этом случае F_1x + F_2x + F_3x = 0, F_1y + F_2y + F_3y = 0.

Эти соотношения можно переписать в виде

F_1x + F_2x = –F_3x, F_1y + F_2y = –F_3y.

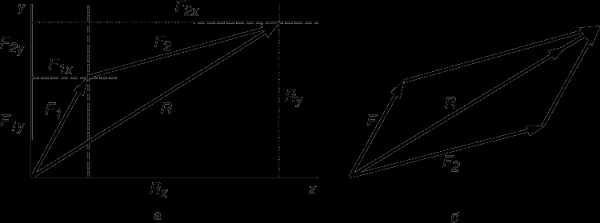
Сравнение с аналогичными соотношениями в случае двух сил показывает, что если мы введем новый вектор R с компонентами

R_x = F_1x + F_2x, R_y = F_1y + F_2y,

который называется равнодействующей сил F₁ и F₂, то R будет в точности уравновешивать F₃. Таким образом, сила R воспроизводит суммарное действие сил F₁ и F₂ в том смысле, что если удалить силы F₁ и F₂, заменив их силой R, то материальная точка по-прежнему останется бы в равновесии. Все сказанное представлено графически на рис. 6,а, где показано сложение компонент. На рис. 6,б вспомогательные линии убраны и оставлены только векторы. Последний рисунок называется параллелограммом сил. Он иллюстрирует один из фундаментальных принципов статики, который, как мы видели, является следствием динамической теории. Этот принцип был установлен С.Стевином (1548–1620), который показал, что если бы это было не так, то имелась бы возможность создать машину, которая производила бы работу, даже если бы к ней не подводилась энергия. Сегодня мы рассматривали бы такую машину как пример нарушения закона сохранения энергии; для Стевина это просто противоречило здравому смыслу, но при этом положения статики тоже обосновывались динамическими соображениями.

Механика твердого тела.

Твердое тело, которое может принимать различные ориентации в пространстве, можно считать состоящим из материальных точек. (Это просто математический прием, позволяющий расширить применимость законов движения материальных точек, но не имеющий ничего общего с гипотезой атомного строения вещества.) Поскольку материальные точки такого тела будут двигаться в разных направлениях с разными скоростями, приходится прибегать к процедуре суммирования.

Рассмотрим систему, изображенную на рис. 7. Сила F, приложенная к тросу, заставляет массу, имеющую форму цилиндра, изменять свою скорость вращения. Будем характеризовать ориентацию цилиндра углом q между радиусом, проведенным из центра цилиндра в некоторую точку на нем, и произвольно выбранным направлением отсчета. Угол q измеряется в радианах; один радиан (примерно 57°) есть центральный угол, стягивающий дугу длиной r на окружности радиуса r. Таким образом, произвольный угол q стягивает дугу s, равную rq, а вся окружность сoответствует углу 2p радиан. Скорость любой точки на окружности равна

где под q /t понимается скорость, с которой изменяется угол q при вращении. Обозначив эту угловую скорость через w, мы наряду с равенством

s = rq

получим

v = rw.

Нетрудно вычислить кинетическую энергию цилиндра, вращающегося вокруг неподвижной оси с угловой скоростью w. Обозначим через m одну из материальных точек цилиндра, расположенную на расстоянии r_m от оси. Ее кинетическая энергия равна ¹/₂m(r_mw)², а полная кинетическая энергия всех материальных точек может быть представлена в виде суммы

или

T = ¹/₂Iw²,

где . Величина I, называемая моментом инерции, зависит от распределения массы в цилиндре и является его характеристикой. Момент инерции можно вычислить путем интегрирования, и для однородного цилиндра он равен ¹/₂Ma², где M – масса цилиндра, а a – его радиус. Если цилиндр вращается свободно и нет сил, которые совершали бы над ним работу, то из закона сохранения энергии следует, что его кинетическая энергия остается постоянной. В таком случае постоянна и величина w, и мы имеем вращательный аналог первого закона Ньютона.

Предположим теперь, что к тросу, намотанному на цилиндр, на короткое время от t₀ до t прилагается сила F и за это время точка, отмеченная на тросе, проходит расстояние от x₀ до х, а цилиндр поворачивается на угол от q₀ до q, причем

x – x₀ = a(q –q₀).

Работа, совершенная при этом силой, равна:

U = F(x – x₀) = Fa(q – q₀),

и точно так же, как при выводе выражения U = ¹/₂mv² – ¹/₂mv₀², мы можем выразить угловое перемещение через среднюю угловую скорость на этом интервале:

q – q₀ = ¹/₂(w +w₀)(t – t₀),

так что

U = ¹/₂Fa(w +w₀)(t – t₀).

За счет этой работы кинетическая энергия цилиндра изменяется от T₀ до T , так что

U = ¹/₂ I(w²– w₀²).

Приравнивая два последних выражения и производя упрощения, получаем выражение

напоминающее формулу для ускорения частицы. Поэтому мы можем ввести угловое ускорение

и тогда для малого интервала от t₀ до t получим L = Ia, т.е. вращательный аналог второго закона Ньютона, в котором величина Fa, вызывающая вращение, обозначена через L. Она называется вращающим моментом.

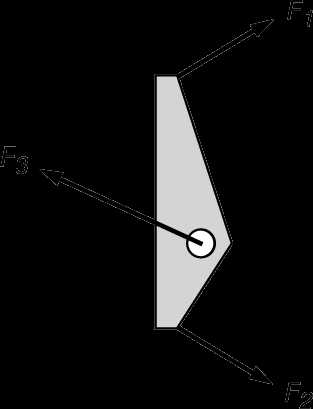
Изложенное можно обобщить на случай, когда отсутствуют неподвижные оси и тело свободно вращается в пространстве. В этом случае имеются три момента инерции, относящиеся к «главным осям». Мы не будем углубляться в рассмотрение этих вопросов. Однако можно вывести второй основной принцип статики для случая твердых тел. Пусть силы F₁ и F_2, приложенные к пластине, которая может вращаться, таковы, что вращения нет (рис. 8). Равновесие означает отсутствие углового ускорения, и поэтому полный вращающий момент равен нулю. Моменты сил F₁ и F₂ компенсируют друг друга при условии:

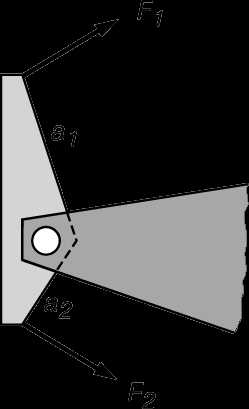
F₁a₁ = F₂a₂,

т.е. получается закон рычага, известный со времен Архимеда. Удалим ось и заменим ее действие третьей силой, как показано на рис. 9, предполагая, что весом пластины можно пренебречь. Для равновесия всех этих сил нужно, во-первых, чтобы пластина не перемещалась и, следовательно, компоненты сил удовлетворяли условию векторного равновесия и, во-вторых, чтобы не было вращения, т.е. выполнялось выведенное только что соотношение. Оба эти принципа составляют основу теории строительной механики и важны при проектировании мостов и зданий.

Проводившиеся выше рассуждения упрощаются, если пользоваться обозначениями математического анализа, в которых подразумевается предельный переход (t → t₀), так что нет необходимости все время говорить о нем. Ньютон первым применил методы дифференциального и интегрального исчисления при решении физических задач, а последующее развитие механики как науки было делом таких математиков, как Л.Эйлер, Ж.Лагранж, П.Лаплас и К.Якоби, каждый из которых находил в ньютоновской механике источник вдохновения для своих математических изысканий.

www.krugosvet.ru

Классическая механика

Классическая механика – это раздел классической физики, изучающий механическое движение макроскопических объектов, которые движутся со скоростями много меньше скорости света ( =3 108 м/с). Под макроскопическими объектами понимаются объекты, размеры которых м. (размер типичной молекулы).

Таким образом, предмет изучения классической механики – законы и причины механического движения, понимаемого как взаимодействие макроскопических (состоящих из огромного числа частиц) физических тел и составляющих их частей, и порождаемое этим взаимодействием изменение их положения в пространстве, происходящее с досветовыми (нерелятивистскими) скоростями.

Место классической механики в системе физических наук и границы её применимости показаны на рисунке 1.

Рисунок 1. Область применимости классической механики

Классическая механика подразделяется на статику (которая рассматривает равновесие тел), кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин) и динамику (которая рассматривает движение тел с учётом вызывающих его причин).

Существует несколько эквивалентных способов формального математического описания классической механики: законы Ньютона, Лагранжев формализм, Гамильтонов формализм, формализм Гамильтона — Якоби.

Когда классическая механика применяется к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул, и при расстояниях или условиях, когда скорость распространения гравитации можно считать бесконечной, она даёт исключительно точные результаты. Потому и сегодня классическая механика сохраняет своё значение, поскольку она намного проще в понимании и использовании, чем остальные теории, и достаточно хорошо описывает повседневную реальность. Классическую механику можно использовать для описания движения очень широкого класса физических объектов: и обыденных объектов макромира (таких, как волчок и бейсбольный мяч), и объектов астрономических размеров (таких, как планеты и звёзды), и многих микроскопических объектов.

Классическая механика – древнейшая из физических наук. Ещё в доантичные времена люди не только опытным путём осознавали законы механики, но и применяли их на практике, конструируя простейшие механизмы. Уже в эпоху неолита и бронзового века появилось колесо, несколько позже применяются рычаг и наклонная плоскость. В античный период накопленные практические знания начали обобщаться, были сделаны первые попытки определить основные понятия механики, такие как сила, сопротивление, перемещение, скорость, и сформулировать некоторые её законы. Именно в ходе развития классической механики закладывались основы научного метода познания, предполагающего некие общие правила научных рассуждений об эмпирически наблюдаемых явлениях, выдвижения предположений (гипотез), эти явления объясняющих, построения моделей, упрощающих изучаемые явления при сохранении существенных их свойств, формирования систем идей ли принципов (теорий) и их математической интерпретации.

Однако качественная формулировка законов механики началась только в XVII веке н. э., когда Галилео Галилей открыл кинематический закон сложения скоростей и установил законы свободного падения тел. Через несколько десятилетий после Галилея Исаак Ньютон сформулировал основные законы динамики. В механике Ньютона движение тел рассматривается при скоростях, много меньше скорости света в пустоте. Ее называют классической или ньютоновской механикой в отличие от релятивистской механики, созданной в начале XX века, главным образом благодаря работам Альберта Эйнштейна.

Современная классическая механика в качестве метода исследования природных явлений использует их описание с помощью системы основных понятий и построения на их основе идеальных моделей реальных явлений и процессов.

Основные понятия классической механики

Пространство. Считается, что движение тел происходит в пространстве, являющимся евклидовым, абсолютным (не зависит от наблюдателя), однородным (две любые точки пространства неотличимы) и изотропным (два любых направления в пространстве неотличимы).

Время — фундаментальное понятие, постулируемое в классической механике. Оно считается является абсолютным, однородным и изотропным (уравнения классической механики не зависят от направления течения времени).

Система отсчёта состоит из тела отсчёта (некоего тела, реального или воображаемого, относительно которого рассматривается движение механической системы), прибора для измерения времени и системы координат. Те системы отсчета по отношению, к которым пространство однородно, изотропно и зеркально – симметрично и время однородно называются инерциальными системами отсчета (ИСО).

Масса — мера инертности тел.

Материальная точка — модель объекта, имеющего массу, размерами которого в решаемой задаче пренебрегают.

Абсолютно твердое тело – система материальных точек, расстояния между которыми не меняются в процессе их движения, т.е. тело, деформациями которого можно пренебречь.

Элементарное событие – явление с нулевой пространственной протяженностью и нулевой длительностью (например, попадание пули в мишень).

Замкнутая физическая система – система материальных объектов, в которой все объекты системы взаимодействуют между собой, но не взаимодействуют с объектами, которые не входят в систему.

Основные принципы классической механики

Принцип инвариантности относительно пространственных перемещений: сдвигов, поворотов, симметрий: пространство однородно, и на протекании процессов внутри замкнутой физической системы не сказывается ее место положения и ориентация относительно тела отсчета.

Принцип относительности: на протекании процессов в замкнутой физической системе не сказывается ее прямолинейное равномерное движение относительно системы отсчета; законы, описывающие процессы, одинаковы в разных ИСО; сами процессы будут одинаковы, если одинаковы начальные условия.

spravochnick.ru

Что такое механическое движение в физике определение

Механическое движение это:

Механическое движение

Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.

Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой.

В более общем значении движением называется изменение состояния физической системы с течением времени. Например, можно говорить о движении волны в среде.

Содержание 1 Виды механического движения 2 Геометрия движения 3 Относительность движения 4 См. также 5 Ссылки

Виды механического движения

Механическое движение можно рассматривать для разных механических объектов:

• Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
  • Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
  • Криволинейное движение�— движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
• Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
  • Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Движение при этом не обязательно является прямолинейным.
  • Для описания вращательного движения�— движения тела относительно выбранной точки, например закреплённого в точке,�— используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
  • Также для твёрдого тела выделяют плоское движение�— движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела�— положением любых двух точек.
• Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).

Геометрия движения

• По окружности (см. Первая космическая (круговая) скорость)
• По эллипсу
• По параболе (см. Вторая космическая (параболическая) скорость), под действием однородного гравитационного поля
• По гиперболе
• Равномерное движение
  • Квадратриса
  • Кривая погони. Эволюта (огибающая нормалей) трактрисы: (цепная линия, поверхность которой — катеноид)
• Под действием однородного гравитационного поля
  • Кривая скорейшего спуска Время спуска под действием только силы тяжести не зависит от расположения начальной точки на дуге циклоиды
  • Лемниската Бернулли: материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки. Движение под действием однородного гравитационного поля

Относительность движения

Относительность�— зависимость механического движения тела от системы отсчёта. Не указав систему отсчёта, не имеет смысла говорить о движении.

Два стрелка неподвижны относительно друг друга, но движутся, если рассматривать другие системы отсчёта.

См. также

• Теория относительности

Ссылки

• Механическое движение (видеурок, программа 10 класса)

Категория:

• Механическое движение

Wikimedia Foundation. 2010.

dic.academic.ru>

2. Механика. Механическое движение.

Понятие механики. Механика – это часть физики, в которой изучают движение тел, взаимодействие тел или, движение тел под каким-либо взаимодействием.

Главная задача механики – это определение местоположения тела в любой момент времени.

Разделы механики: кинематика и динамика. Кинематика – это раздел механики, изучающий геометрические свойства движений без учета их масс и действующих на них сил. Динамика – это раздел механики, изучающий движение тел под действием приложенных к ним сил.

Движение. Характеристики движения. Движение – это изменение положения тела в пространстве с течением времени относительно других тел. Характеристики движения: пройденный путь, перемещение, скорость, ускорение.

Механическое движение – это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Поступательное движение. Демонстрируется видеопоказом с объяснениями.

Равномерное движение тела. Демонстрируется видеопоказом с объяснениями.

Неравномерное механическое движение – это движение, при котором за равные промежутки времени тело совершает неравные перемещения.

Относительность механического движения. Демонстрируется видеопоказом с объяснениями.

Точка отсчёта и система отсчёта в механическом движении. Тело, относительно которого рассматривается движение, называется точкой отсчёта. Система отсчёта в механическом движении – это точка отсчёта и система координат и часами.

Система отсчета. Характеристики механического движения. Система отсчета демонстрируется видеопоказом с объяснениями. Механическое движение имеет характеристики: Траектория; Путь; Скорость; Время.

Траектория прямолинейного движения – это линия, вдоль которой движется тело.

Криволинейное движение. Демонстрируется видеопоказом с объяснениями.

Путь и понятие скалярной величины. Демонстрируется видеопоказом с объяснениями.

Физические формулы и единицы измерения характеристик механического движения:

Обозначение величины	Единицы измерения величины	Формула для определения величины
Путь-s	м, км	S=vt
Время- t	с, час	T = s/v
Скорость –v	м/с, км/ч	V = s/t

Понятие ускорения. Раскрывается демонстрацией видеопоказа, с объяснениями.

Формула для определения величины ускорения:

3. Законы динамики Ньютона.

Великий физик И. Ньютон. И. Ньютон развенчал античные представления, что законы движения земных и небесных тел совершенно различны. Вся Вселенная подчинена единым законам, допускающим математическую формулировку.

Две фундаментальные задачи, решенные физикой И. Ньютона:

1. Создание для механики аксиоматической основы, которая перевела эту науку в разряд строгих математических теорий.

2. Создание динамики, связывающей поведение тела с характеристиками внешних воздействий на него (сил).

Законы динамики И. Ньютона в его авторской редакции:

1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.

3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Первый закон динамики И. Ньютона. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Понятия инерции и инертности тела. Инерция – это явление, при котором тело стремится сохранить свое первоначальное состояние. Инертность – это свойство тела сохранять состояние движения. Свойство инертности характеризуется массой тела.

Развитие Ньютоном теории механики Галилея. Долгое время считалось, что для поддержания любого движения необходимо осуществлять нескоменсированное внешнее воздействие со стороны других тел. Ньютон разбил эти убеждения, выведенные Галилеем.

Инерциальная система отсчета. Системы отсчёта, относительно которых свободное тело движется равномерно и прямолинейно, называются инерциальными.

Первый закон Ньютона – закон инерциальных систем. Первый закон Ньютона – это постулат о существовании инерциальных систем отсчёта. В инерциальных системах отсчёта механические явления описываются наиболее просто.

Второй закон динамики И. Ньютона. В инерциальной системе отсчёта прямолинейное и равномерное движение может происходить только в том случае, если на тело не действуют другие силы или действие их скомпенсировано, т.е. уравновешено. Демонстрируется видеопоказом с объяснениями.

Принцип суперпозиции сил. Демонстрируется видеопоказом с объяснениями.

Понятие массы тела. Масса – одна из самых фундаментальных физических величин. Масса характеризует сразу несколько свойств тела и обладает рядом важных свойств.

Сила – центральное понятие второго закона Ньютона. Второй закон Ньютона определяет, что тело тогда будет двигаться с ускорением, когда на него действует сила. Сила – мера взаимодействия двух (или больше) тел.

Два вывода классической механики из второго закона И. Ньютона:

1. Ускорение тела напрямую связано с приложенной к телу силой.

2. Ускорение тела напрямую связано с его массой.

Демонстрация прямой зависимости ускорения тела от его массы

Третий закон динамики И. Ньютона. Демонстрируется видеопоказом с объяснениями.

Значение законов классической механики для современной физики. Механика, основанная на законах Ньютона, называется классической механикой. В рамках классической механики хорошо описывается движение не очень маленьких тел с не очень большими скоростями.

Демонстрации:

Физические поля вокруг элементарных частиц.

Планетарная модель атома Резерфорда и Бора.

Движение, как физическое явление.

Поступательное движение.

Равномерное прямолинейное движение

Неравномерное относительное механическое движение.

Видеоанимация системы отсчета.

Криволинейное движение.

Путь и траектория.

Ускорение.

Инерция покоя.

Принцип суперпозиции.

2-й закон Ньютона.

Динамометр.

Прямая зависимость ускорения тела от его массы.

3-й закон Ньютона.

Контрольные вопросы:.

1. Сформулируйте определение и научный предмет физики.

2. Сформулируйте физические свойства, общие для всех явлений природы.

3. Сформулируйте основные этапы эволюции физической картины мира.

4. Назовите 2 основных принципа современной науки.

5. Назовите особенности механистической модели мира.

6. В чем суть молекулярно-кинетической теории.

7. Сформулируйте основные признаки электромагнитной картины мира.

8. Объясните понятие физического поля.

9. Определите признаки и различия электрического и магнитного полей.

10. Объясните понятия электромагнитного и гравитационного полей.

11. Объясните понятие «Планетарная модель атома»

12. Сформулируйте признаки современной физической картины мира.

13. Сформулируйте основные положения современной физической картины мира.

14. Объясните значение теории относительности А. Эйнштейна.

15. Объясните понятие: «Механика».

16. Назовите основные разделы механики и дайте им определения.

17. Назовите основные физические характеристики движения.

18. Сформулируйте признаки поступательного механического движения.

19. Сформулируйте признаки равномерного и неравномерного механического движения.

20. Сформулируйте признаки относительности механического движения.

21. Объясните смысл физических понятий: «Точка отсчёта и система отсчёта в механическом движении».

22. Назовите основные характеристики механического движения в системе отсчета.

23. Назовите основные характеристики траектории прямолинейного движения.

24. Назовите основные характеристики криволинейного движения.

25. Дайте определение физическому понятию: «Путь».

26. Дайте определение физическому понятию: «Скалярная величина».

27. Воспроизведите физические формулы и единицы измерения характеристик механического движения.

28. Сформулируйте физический смысл понятия: «Ускорение».

29. Воспроизведите физическую формулу для определения величины ускорения.

30. Назовите две фундаментальные задачи, решенные физикой И. Ньютона.

31. Воспроизведите основные смыслы и содержание первого закона динамики И. Ньютона.

32. Сформулируйте физический смысл понятия инерции и инертности тела.

33. В чем проявилось развитие Ньютоном теории механики Галилея.

34. Сформулируйте физический смысл понятия: «Инерциальная система отсчета».

35. Почему первый закон Ньютона это закон инерциальных систем.

36. Воспроизведите основные смыслы и содержание второго закона динамики И. Ньютона.

37. Сформулируйте физические смыслы принципа суперпозиции сил, выведенного И. Ньютоном.

38. Сформулируйте физический смысл понятия массы тела.

39. Обоснуйте, что сила является центральным понятием второго закона Ньютона.

40. Сформулируйте два вывода классической механики на основании второго закона И. Ньютона.

41. Воспроизведите основные смыслы и содержание третьего закона динамики И. Ньютона.

42. Объясните значение законов классической механики для современной физики.

Литература:

1. Ахмедова Т.И., Мосягина О.В. Естествознание: Учебное пособие / Т.И. Ахмедова, О.В. Мосягина. – М.: РАП, 2012. – С. 34-37.

StudFiles.ru>

Что такое точка отсчета? Что такое механическое движение?

Andreus-папа-ndrey

Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики. Раздел механики, описывающий геометрические свойства движения без учёта причин, его вызывающих, называется кинематикой

В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.
Механическое движение можно рассматривать для разных механических объектов:

* Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости) . Изучением этого занимается кинематика точки.
o Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна эта прямой)
o Криволинейное движение это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности) .
* Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
o Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Заметим, что при этом оно не обязательно является прямолинейным.
o Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
o Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела положением любых двух точек.
* Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости) , поэтому число определяющих координат бесконечно (неизестными становятся функции) .
Относительность — зависимость механического движения тела от системы отсчёта, не указав систему отсчёта — не имеет смысла говорить о движении.

Даниил юрьев

Виды механического движения [править | править вики-текст]
Механическое движение можно рассматривать для разных механических объектов:
Движение материальной точки полностью определяется изменением её координат во времени (например, для плоскости — изменением абсциссы и ординаты). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
Криволинейное движение — движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки. Движение при этом не обязательно является прямолинейным.
Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, — используют Углы Эйлера. Их количество в случае трёхмерного пространства равно трём.
Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела — положением любых двух точек.
Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).

Механическое движение. Путь. Скорость. Ускорение

Лара

Механическим движением называют изменение положения тела (или его частей) относительно других тел.
Положение тела задается координатой.
Линию, вдоль которой движется материальная точка, называют траекторией. Длину траектории называют путем. Единица пути — метр.
Путь = скорость* время. S=v*t.

Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением.

Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением (s). Перемещение — величина векторная. Единица перемещения — метр.

Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка времени.
Формула скорости имеет вид v = s/t. Единица скорости — м/с. На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с) .

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Формула для вычисления ускорения: a=(v-v0)/t; Единица ускорения – метр/(секунда в квадрате) .

Читайте также

zna4enie.ru

краткое определение относительности и поступательности, что такое система отсчета

В физике существует такое понятие, как механическое движение, определение которого трактуется как изменение координат тела в трехмерном пространстве относительно иных тел с затратой времени. Как ни странно, но можно никуда не двигаясь превысить, к примеру, скорость автобуса. Эта величина относительна и зависима от заданной точки. Главное, зафиксировать систему отсчета, чтобы наблюдать за точкой по отношению к предмету.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Описание

Понятия из физики:

1. Материальная точка — часть тела или предмет с небольшими параметрами и массой, которые не принимаются в учет при изучении процесса. Это величина, которой в физике пренебрегают.
2. Перемещение — это расстояние, пройденное материальной точкой из одной координаты в другую. Понятие не следует путать с движением, так как в физике это определение пути.
3. Пройденный путь — это участок, который прошел предмет. Что такое пройденный путь рассматривает раздел физики под названием «Кинематика».
4. Траектория в пространстве — это прямая или ломаная линия, по которой объект проходит путь. Представить, что такое траектория, согласно определению из области физики, можно мысленно начертив линию.
5. Механическим называют перемещение по заданной траектории.

Внимание! Взаимодействие тел осуществляется по законам механики, и этот раздел называется кинематикой.

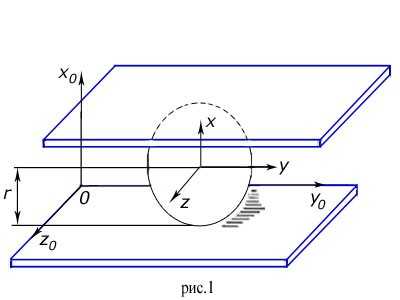Понять, что такое система координат, и что такое траектория на практике?

Достаточно мысленно найти точку в пространстве и от нее провести координатные оси, относительно ее будет двигаться предмет по ломаной или прямой линии, причем виды движения тоже будут разные, в их числе поступательное, осуществляемое при колебании и вращении.

Например, кот находится в комнате, перемещается к любому объекту или изменяет свое нахождение в пространстве, двигаясь по разным траекториям.

Расстояние между объектами может отличаться, так как выбранные траектории неодинаковые.

Типы

Известные виды движения:

1. Поступательное. Характеризуется параллельностью двух соединенных между собой точек, одинаково движущихся в пространстве. Предмет движется поступательно, когда проходит по одной линии. Достаточно представить замену стержня в шариковой ручке, то есть стержень двигается поступательно по заданному пути, при этом каждая его часть движется параллельно и одинаково. Довольно часто такое встречается в механизмах.
2. Вращательное. Предмет описывает окружность во всех плоскостях, которые расположены параллельно друг другу. Оси вращения — центры описываемых окружностей, а точки, расположенные на оси неподвижны. Сама вращающая ось может быть расположена внутри тела (ротационное), а также соединятся с внешними его точками (орбитальное). Чтобы уяснить, что это такое, можно взять обычную иглу с ниткой. Последнюю зажать между пальцами и постепенно раскручивать иглу. Игла будет описывать окружность, и подобные виды движения следует относить к орбитальным. Пример ротационного вида: раскручивание предмета на твердой поверхности.
3. Колебательное. Все точки тела, перемещающегося по заданной траектории, с точностью или приближено повторяются через одинаковое время. Наглядный пример — шайба, подвешенная на шнуре, колеблющаяся вправо и влево.

Внимание! Особенность поступательного движения. Предмет двигается по прямой линии, и в любой временной промежуток все его точки перемещаются в одном направлении — это поступательное движение. Если едет велосипед, то в любое время можно отдельно рассмотреть траекторию его любой точки, она будет одинаковой. При этом не важно, ровная поверхность или нет.

Данные виды движения встречаются ежедневно на практике, поэтому проиграть их мысленно не составит труда.

Что такое относительность

Согласно законам механики, двигается предмет относительно какой-либо точки.

К, примеру, если человек стоит на месте, а автобус движется, это и называется относительность движения рассматриваемого транспортного средства к объекту.

С какой скоростью перемещается объект по отношению к определенному телу в пространстве тоже учитывается относительно этого тела и, соответственно, ускорение также имеет относительную характеристику.

Относительность — прямая зависимость заданной при движении тела траектории, проходимого пути, скоростной характеристики, а также перемещения по отношению к системам отсчета.

Как проводится отсчет

Что представляет собой система отсчета и как она характеризуется? Отсчет во взаимосвязи с пространственной системой координат, первичным отсчетом времени передвижения — это и есть система отсчета. В разных системах у одного тела может быть разное местонахождение.

Точка находится в системе координат, когда она начинает двигаться, учитывается ее время перемещения.

Тело отсчета — это абстрактный предмет, находящийся в заданной точке пространства. При ориентации на его положение рассматриваются координаты иных тел. К примеру, машина стоит на месте, а человек движется, в данном случае тело отсчета — это машина.

Равномерное перемещение

Понятие равномерное движение — это определение в физике трактуется следующим образом:

» Предмет проходит одно расстояние за одинаковое время» Равномерно предмет двигается при постоянной скорости.

Пример: Каждую минуту машина проезжает по 100 метров.

Равномерное движение можно отнести к части неравномерного.

Всем известно, что любое техническое средство, в основном двигаются с ускорением и торможением.

Механическое движение — изучаем физику

Механика — что такое траектория, перемещение и прочее

Вывод

В нашей жизни примеры данного физического явления можно встретить повсюду. Так, автомобили едут на прямой магистрали поступательно, а их колеса совершают вращательные ротационные движения. Земля вращается вокруг Солнца на орбите и одновременно вокруг своей оси. Природные комбинации могут быть и более сложными. К примеру, футбольный мяч, во время матча отправленный нападающим в ворота, одновременно будет передвигаться поступательно и вращательно. Тоже самое можно наблюдать при работе отдельных частей различных механизмов.

Это интересно! Что такое закон всемирного тяготения: формула великого открытия

uchim.guru

Теория классической механики

Определение 1

Классическая механика — особый вид механики, изучающий законы изменения положений физических тел в пространстве, принципы которого основаны на законах Ньютона и гипотезе относительности Галилея.

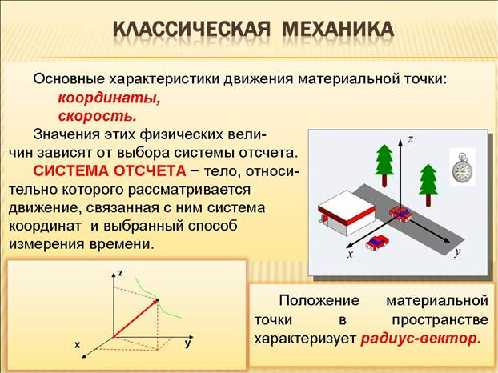
Рисунок 1. Классическая механика. Автор24 — интернет-биржа студенческих работ

Классическую механику или «ньютоновскую философию» ученые подразделяется на:

• кинематику – исследующую геометрическое свойство стабильного движения тел без рассмотрения его причин;
• статику – рассматривающую равновесие материальных веществ;
• динамику – изучающую движение тел с учётом всех вызывающих его причин.

На сегодняшний день центральным предметом изучения классической механики считается движения любых физических тел, совершаемые с определенными скоростями, значительно меньшими скорости света. При исследовании этого процесса в ньютоновской теории вводят ряд абстрактных определений, которые комплексно отражают конкретные свойства реальных материальных тел.

Существует несколько эквивалентных методов формального и детального математического описания классической механики:

• Лагранжев формализм;
• Законы Ньютона;
• Гамильтонова абстракция;
• Гипотеза Гамильтона — Якоби.

На границе XIX—XX столетия были установлены принципы применимости классической механики. Оказалось, что данное направление в науке дает только точные результаты, но только в тех случаях, когда она применяется к физическим телам, размеры которых существенно превышают величину атомов и молекул и при расстояниях, когда скорость распространения гравитации считается бесконечной.

Инерциальная система отсчета как основная теория в классической механике

Рисунок 2. Системы отсчета. Автор24 — интернет-биржа студенческих работ

Определение 2

Система отсчёта — это совокупность и общность тела отсчета, который связан с ним посредством координат, рассматриваемых движение каких-либо материальных точек или веществ.

Как известно, Первый закон Ньютона предполагает, что все свободные элементы, к которым не приложено никаких усилий, двигаются прямолинейно или е находятся в спокойном состоянии в инерциальной системе отсчета.

Для полноты данного понятия необходимо определить суть инерциальной системы отсчета. В течение многих столетий механики физики пытались описать это явление так как в классической механике часто применяются системы отсчета, базирующиеся на образе твердого тела, в роли которого могут выступать металлы и алмазы. Постулируется, что между любыми веществами расстояния являются неизменными.

Для полного описания системы отсчета необходимо еще изучить понятие прямой.

В современной практике используется две трактовки прямой:

• в качестве образа натянутой нити;
• прямая как образ линии движения света.

В первом приближении эти два определения прямой полностью совпадают, а линия движения света кривой уже устанавливается в конкретных условиях.

Для определения пространственного масштаба изначально требуется указать отрезок прямой между двумя выбранными физическими телами как основной эталон длины.

Это позволяет сформировать и внедрить в науку метрику пространства и трехмерную систему координат. Для измерения временных параметров ученые применяют разные периодические процессы.

Элементы системы отсчета на базе твердого тела для сохранения своей неподвижности напрямую связаны друг с другом силовыми показателями, следовательно, находятся в невесомом состоянии.

Пример 1

Например, во вращающейся отчетной системе весомость тел записывается так: $W = ρ$, где $ρ$ ─ расстояние до центральной оси вращения.

Элементы жестких концепций отсчета в гравитационной среде также являются весомыми, однако могут существовать и теории с невесомыми телами отсчета. Такие системы физики называют «мягкими». И наконец, возможны системы отсчета, которые могут иметь разные формы одновременно, где все неподвижные относительно друг друга материальные элементы отсчета не имеют общей силовой связи. Такие концепции и являются инерциальными системами отсчета.

История становления классической механики

Основы м методы классической механики были впервые заложены великим мыслителем Галилеем, а затем Кеплером и Коперником при исследовании закономерностей движения существующих на планете небесных тел, поэтому, в течение длительного периода времени физика и механика рассматривались исключительно в контексте толкования астрономических событий.

В своих научных работах Коперник указывал, что определение принципов движения материальных элементов возможно значительно упростить, если отойти от закономерностей, заложенных ранее Аристотелем, и считать именно Солнце отправной точкой для таких научных вычислений. Это помогло ученым осуществить переход от геоцентрической к гелиоцентрической концепции.

Далее методы и идеи классической механики были формализованы трех законах Кеплера движения небесных тел, согласно которым, все планеты нашей солнечной системы движутся только эллиптическими орбитами. Следующий весомый вклад в становлении классической механики был осуществлен Галилеем, который смог сформулировать и описать пять уникальных законов движения, изучая главные закономерности механического движения материальных веществ.

Но все же лавры самого известного основателя изучаемого научного течения относятся Исааку Ньютону, который в своей работе “Математические истоки натуральной философии” представил синтез тех определений по физике механического стабильного движения, которые были созданы его предшественниками. Ньютон смог описать три основных законы движения тел, которые впоследствии были названы его именем, а также теорию всемирного тяготения, подводящую черту под экспериментами Галилеем в качестве процесса свободного падения веществ.

Ограничения классической механики

Рисунок 3. Ограничения классической механики. Автор24 — интернет-биржа студенческих работ

Классическая механика дает исследователям точные результаты для концепций, которые часто встречаются в повседневной жизни. Но они считаются некорректными для систем, скорость которых практически одинакова со скоростью света. В таких ситуациях это направление в физике заменяется релятивистской механикой, где действуют другие законы светового излучения и поглощения. Для учений, объединяющих оба эти свойства, используется квантовая гипотеза поля вместо классической механики. Для систем с огромным количеством составляющих, или уровней свободы, классическая механика не может быть адекватной, зато применяет способы статистической физики.

Классическая механика достаточно широко применяется в современном мире так как она гораздо проще в использовании, чем перечисленные выше гипотезы, следовательно, имеет большие возможности для аппроксимации физических объектов, начиная с обычных и заканчивая совсем микроскопическими в виде органических молекул.

Хотя классическая механика является в целом совместимой с другими классическими идеями, в ней возможно определить некоторые несоответствия, которые были обнаружены только в конце 19 столетия. Все ограничения в этом разделе физики могут быть решены с помощью методов современной науки. В частности, уравнения и формулы электродинамики не действуют относительно химических преобразований Галилея.

Скорость света входит в них как основная константа, поэтому классическая электродинамика и механика могли бы быть абсолютно совместимы только в одной выбранной концепции отсчета.

Однако теоретическая проверка и практика не определила наличие различий, что привело к возникновению универсальной теории относительности, в пределах которой уравнения механики были полностью модифицированы.

Принципы классической механики также невозможно совместить с некоторыми идеями классической термодинамики, что приводит к парадоксу Гиббса, согласно которому точно установить энтропию, в которой абсолютно черное вещество излучает бесконечное количество энергии, – нереально. Для преодоления указанной несовместимости была в результате разработана квантовая механика.

spravochnick.ru