Мгновенная скорость равноускоренного движения – Прямолинейное равноускоренное движение. Ускорение — урок. Физика, 9 класс. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Ускорение. Равноускоренное движение. Зависимость скорости от времени при равноускоренном движении

На данном уроке мы с вами рассмотрим важную характеристику неравномерного движения – ускорение. Кроме того, мы рассмотрим неравномерное движение с постоянным ускорением. Такое движение еще называется равноускоренным или равнозамедленным. Наконец, мы поговорим о том, как графически изображать зависимости скорости тела от времени при равноускоренном движении.

Для того чтобы ответить на вопрос, что же такое равноускоренное движение, обратимся к следующему эксперименту. Возьмем движение автомобиля по наклонной плоскости. Автомобиль начинает движение из состояния покоя. Рассмотрим положение автомобиля через одинаковые промежутки времени (рис. 1). За равные промежутки времени автомобиль проезжал все большие расстояния , совершал все большие и большие перемещения.

Рис. 1. Положение автомобиля через равные промежутки времени

Повторим этот эксперимент, увеличив угол наклона плоскости к поверхности стола (рис. 2). Опять-таки, рассмотрим положение автомобиля через равные промежутки времени.

Рис. 2. Эксперимент с увеличенным углом наклона плоскости к поверхности стола

Обратите внимание, что расстояние, которое проходит автомобиль за равные промежутки времени увеличивается быстрее, чем в предыдущий раз. Таким образом, и скорость автомобиля растет быстрее . В физике говорят, что во втором случае было большее ускорение.

Ускорение – это физическая величина, равная отношению изменения скорости тела ко времени, за которое это изменение произошло (рис. 3).

Рис. 3. Иллюстрация определения ускорения

где – текущая или конечная скорость; – начальная скорость; – промежуток времени, за который произошло изменение скорости.

Ускорение обозначается буквой , так как этот термин произошел от латинского слова acceleration – «ускоряться, увеличивать скорость». В физике очень много величин обозначаются от первой буквы их латинского наименования или английского аналога (рис. 4).

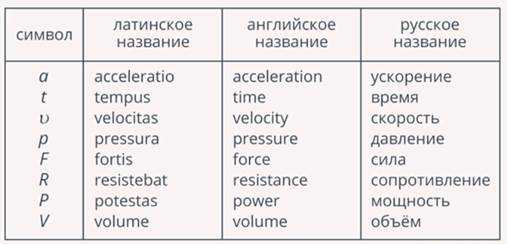
Рис. 4. Некоторые физические величины

Записав векторное определение ускорения, перейдем к его скалярному определению – проекции ускорения, ведь чаще всего в курсе 10 класса мы будем работать с прямолинейным движением, где нам достаточно одной

interneturok.ru

Равномерное и равноускоренное движение

Определение 1

Движение, при котором за одинаковые интервалы времени тело проходит неравное расстояние, называют неравномерным (или переменным).

При переменном движении скорость тела с течением времени меняется, по этой причине для характеристики подобного перемещения применяются определения средней и моментальной скоростей.

Средней скоростью переменного движения $v_{cp}$ называют векторную величину, равную отношению перемещения тела $s$ к промежутку времени $t$ , в течении которого оно совершило перемещение:

$v_{cp} = lim\left(\frac{Ds}{Dt}\right)$.

Переменное перемещение внедряет в процесс только лишь тот интервал времени, для которого эта скорость установлена. Мгновенной скоростью является скорость, какой тело обладает в определенный период времени (и значит, в конкретной точке траектории). Мгновенная скорость $v$ является пределом, к которому устремляется средняя скорость точки $v_{cp}$ , в то время как промежуток времени движения точки стремится к 0:

$v = lim\left(\frac{Ds}{Dt}\right)$.

Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к 0 (если этот порог существует), выступает главной производной этой функции по данному аргументу.

Изучим, как скатывается шарик с наклонной плоскости. Шар перемещается неровно: пути, проходимые им за последовательные одинаковые интервалы периода, увеличиваются. Таким образом, темп передвижения шарика возрастает. Перемещение объекта, скатывающегося с косой плоскости, считается классическим примером прямолинейного равноускоренного перемещения.

Определение 2

Прямолинейным равноускоренным движением именуют прямолинейное перемещение, при котором скорость тела за любые одинаковые интервалы времени меняется на одну и ту же величину.

Прямо равноускорено способен передвигаться, к примеру, транспорт в период разгона. Но необычным может представиться в таком случае, то что во время торможения машина также способна передвигаться прямолинейно равноускорено! Так как в определении равноускоренного перемещения речь никак не идет не о росте стремительности, а только лишь об изменении скорости.

Суть в том, что представление ускорения в физике обширнее, нежели в обыденном понимании. В повседневной речи под ускорением подразумевают как правило только лишь повышение быстроты. Мы в физике станем говорить, то что тело перемещается с ускорением постоянно, если быстрота тела меняется любым способом (возрастает либо снижается согласно модулю, меняется согласно направленности и т. п.).

Может возникнуть вопрос: по какой причине мы уделяем внимание непосредственно прямолинейному равноускоренному перемещению? Забегая немножко вперед, скажем, что с этим перемещением мы будем часто иметь дело при рассмотрении законов механики.

Напомним, что под воздействием стабильной силы тело перемещается прямо равноускорено. (В случае если первоначальная скорость тела равна нулю либо ориентирована по линии воздействия силы.) А в многочисленных задачах из сферы механики рассматривается непосредственно такая ситуация.

Равноускоренное движение тела

Определение 3

Равноускоренное движение – это перемещение тела, при каком его скорость за всевозможные одинаковые интервалы времени меняется (способна расти либо снижаться) одинаково.

Равноускоренное перемещение никак не обладает равной скоростью в течении всего пути прохождения. в этом случае имеется убыстрение, что отвечает за непрерывное повышение скорости. Ускорение перемещения остается постоянным, а темп регулярно и одинаково увеличивается. Кроме равноускоренного имеется также равнозамедленное перемещение, где модуль темп одинаково уменьшается. Таким образом равноускоренное перемещение способно проходить в некоторых измерениях, оно бывает:

одномерным;
многомерным.

В случае первого — перемещение осуществляется по одной оси местоположение. В случае второго могут добавляться и прочие замеры.

Ускорение тела

Применять формулы подобных перемещений возможно в абсолютно различных плоскостях. К примеру, с целью расчета падения жестких тел в свободном падении, места падения. В частности, для различных точных и геометрических расчетов.

Исходя из противопоставления равномерному перемещению, неравномерное – это движение с разной скоростью согласно каждой траектории. В чем его особенность? Это неравномерное передвижение, но оно “равно ускоряется”.

Ускорение мы ассоциируем с увеличением скорости. Так как она ускоряется одинаково, получается равное увеличение скорости. Как понять скорость равно увеличивается или нет? Нам нужно засечь время, оценить скорость через одинаковый промежуток времени.

Пример 1

Например, автомобиль начал движение, за первые 2 сек он развил скорость до 10 м/с, за последующие 2 сек 20 м/с. Еще через 2 сек он уже едет со скоростью 30 м/с. Каждые 2 секунды темп возрастает и каждый раз на 10 м/с.

Такое передвижение и является равноускоренным. Ускорением называется величина, определяющая, насколько каждый раз увеличивается скорость.

Перемещение с убывающей скоростью – замедленное передвижение. Однако физики каждое перемещение с изменяющейся быстротой называют ускоренным перемещением. Трогается ли автомобиль с участка (темп увеличивается), либо притормаживает – скорость снижается), в каждом случае он перемещается с ускорением.

Быстроту изменения скорости характеризует ускорение. Это число, на которое меняется скорость за каждую секунду. Если ускорение точки по модулю большое, значит точка стремительно набирает скорость (при разгоне) или быстро сбрасывает ее (при торможении). Ускорение $a$ – это физическая векторная величина, которая равна отношению перемены скорости $\delta V$ к промежутку времени $\delta t$, за которое оно произошло

$\ vec{a} = \frac{\delta V}{\delta t}$

Равномерное движение

Механическое передвижение, при котором тело за всевозможные одинаковые интервалы времени проходит одну и ту же дистанцию является равномерным. При равномерном перемещении значение скорости точки остаётся стабильной.

$υ = \frac{l}{\delta t}$, где:

$υ$– скорость равномерного движения (м/с)
$l$– пройденный телом путь (м)
$ \delta t$– интервал времени движения (с)

Равномерное перемещение присутствует, если скорость предмета остается равной в каждом интервале пройденного пути, к этом случае период прохождения различных двух одинаковых участков будет одинаково.

В случае если перемещение является не только лишь равномерным, а и прямолинейным, в таком случае путь тела одинаковый с модулем передвижения. По этой причине, воспользовавшись аналогией с предшествующей формулой, в физике определяют скорость равномерного прямолинейного перемещения:

$ \vec{v} = \frac{\vec s}{\vec\delta t}$, где:

$ \vec{v}$ – скорость равно прямолинейного движения, м/с
$ \vec{s}$ – перемещение тела, м
${\vec\delta t}$ – интервал времени движения, с

Скорость равномерного прямолинейного движения является вектором, так как перемещение – величина векторная. А значит, имеет не только числовое значение, но и пространственное направление.

Замечание 1

Равноускоренное перемещение отлично от равномерного тем, что быстрота в этом перемещении регулярно и одинаково увеличивается, вплоть до конкретного предела. В равномерном же перемещении скорость не изменяется ни в коем случае, другим образом подобное перемещение никак не станет называться равномерным.

spravochnick.ru

Отсчёта. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость. Ускорение. Равномерное и равноускоренное движение – Документ

Билет 1.

Вопрос 1. Механическое движение. Относительность движения. Система отсчёта. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость. Ускорение. Равномерное и равноускоренное движение.

Механическим движением называют изменение положения тела (или его частей) относительно других тел. Например, человек едущий на эскалаторе в метро, находится в покое относительно самого эскалатора и перемещается относительно стен туннеля; Гора Эльбрус находится в покое относительно Земли и движется вместе с Землёй относительно Солнца. Из этих примеров видно, что всегда надо указать тело, относительно которого рассматривается движение, его называют телом отсчёта. Система координат, тело отсчёта с которым она связана, и выбранный способ измерения времени образуют систему отсчёта. Рассмотрим два примера. Размеры орбитальной станции, находящейся на орбите около Земли, можно не учитывать, а рассчитывая траекторию движения космического корабля на стыковке со станцией, без учёта её размеров не обойтись. Таким образом, иногда размерами тела по сравнению с расстоянием до него можно пренебречь, в этих случаях тело считают материальной точкой. Линию, вдоль которой движется материальная точка, называют траекторией. Длину части траектории между начальным и конечным положением точки называют путем (l). Единица пути – метр.

Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением. Направленный отрезок прямой, проведённый из начального положения движущейся точки в её конечное положение, называется перемещением (S). Это величина векторная. Единица перемещения – метр.

Скорость – векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка. Промежуток времени считается достаточно малым если скорость в течение этого промежутка не менялась. Определяющая формула скорости имеет вид 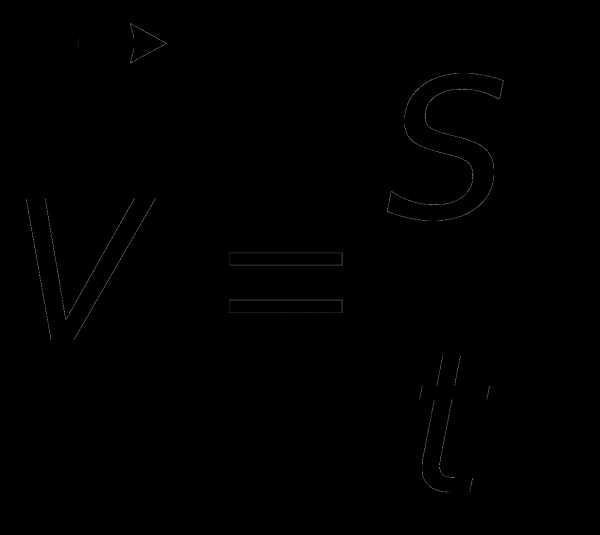Единица измерения скорости – м/с. На практике – км/ч. Измеряют скорость спидометром.

Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле Единица измерения ускорения м/с².

Характеристики механического движения связаны между собой основными кинематическими уравнениями:

Предположим, что тело движется без ускорения (самолёт на маршруте), его скорость в течение продолжительного времени не меняется, а=0. Тогда кинематические уравнения будут иметь вид: V=const, S=Vt.

Движение, при котором скорость тела не меняется, т.е. тело за любые равные промежутки времени перемещается на одну и ту же величину, называют равномерным прямолинейным движением.

Во время старта скорость ракеты быстро возрастает, т.е. ускорение а>0, а=const.

В этом случае кинематические уравнения выглядят так:

При таком движении скорость и ускорение имеют одинаковые направления, причём скорость изменяется одинаково за любые равные промежутки времени. Этот вид движения называют равноускоренным.

При торможении автомобиля скорость уменьшается одинаково за любые равные промежутки времени, ускорение меньше нуля; т.к. скорость уменьшается, то уравнение принимает вид:

Такое движение называется равнозамедленным.

Все физические величины, характеризующие движение тела (скорость, ускорение, перемещение), а также вид траектории, могут изменяться при переходе из одной системы к другой, т.е. характер движения зависит от выбора системы отсчёта, в этом и проявляется относительность движения. Например, в воздухе происходит дозаправка самолёта топливом. В системе отсчёта, связанной с самолётом, другой самолёт находится в покое, а в системе отсчёта, связанной с Землёй, оба самолёта находятся в движении. При движении велосипедиста точка колеса в системе отсчёта, связанной с осью, имеет траекторию:

В системе отсчёта, связанной с Землёй вид траектории будет таким:

Билет 2.

Взаимодействие тел. Сила. Второй закон Ньютона.

Простые наблюдения и опыты, например с тележками, приводят к следующим качественным заключениям: а) тело, на которое другие тела не действуют сохраняет свою скорость неизменной, б) Ускорение тела возникает под действием других тел, но зависит и от самого тела; в) действие других тел друг на друга всегда носят характер взаимодействия. Эти выводы подтверждаются при наблюдении явлений в природе, технике, космическом пространстве только в инерциальных системах отсчёта.

Взаимодействия отличаются друг от друга и количественно, и качественно. Например, ясно, что чем больше деформируется пружина, тем больше взаимодействие её витков. Или чем ближе два одноимённых заряда, тем сильнее они будут притягиваться. В простейших случаях взаимодействия количественной характеристикой является сила. Сила – причина ускорения тел по отношению к инерциальной системе отсчёта или их деформации. Сила – это векторная физическая величина, являющаяся мерой ускорения, приобретаемого телами при взаимодействии. Сила характеризуется: а) модулем; б) точкой приложения; в) направлением.

Единица силы – ньютон. Один ньютон – это сила, которая телу массой 1 кг сообщает ускорение 1 м/с² в направлении действия этой силы, если другие тела на него не действуют. Равнодействующей нескольких сил называют силу, действие которой эквивалентно действию тех сил, которые она заменяет. Равнодействующая является векторной суммой всех сил, приложенных к телу

R=F₁+F₂+…+F_n.

Качественно по своим свойствам взаимодействия также различны. Например, электрическое и магнитное взаимодействия связаны с наличием зарядов у частиц либо с движением заряжённых частиц. Наиболее просто рассчитать силы в электродинамике: сила Ампера – F=IlBsin, Сила Лоренца – F=qvBsin, Кулоновская сила – 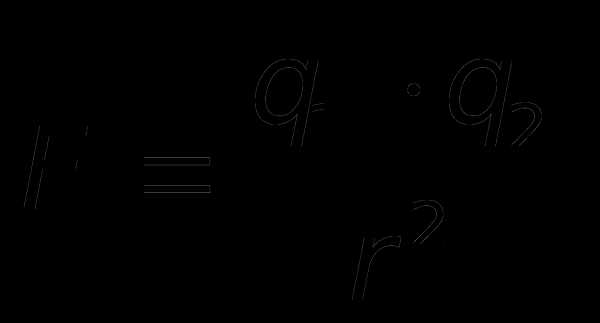и гравитационные силы: закон всемирного тяготения – 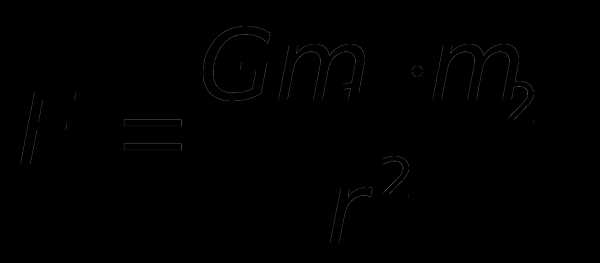Такие механические силы, как сила упругости и сила трения, возникают в результате электромагнитного взаимодействия. Для их расчёта необходимо использовать формулы: закон Гука – F_упр=-kx, сила трения – F_тр=-N.

На основании опытных данных были сформулированы законы Ньютона. Второй закон Ньютона. Ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил, действующих на тело, обратно пропорционально его массе и направлено также, как и равнодействующая сила: 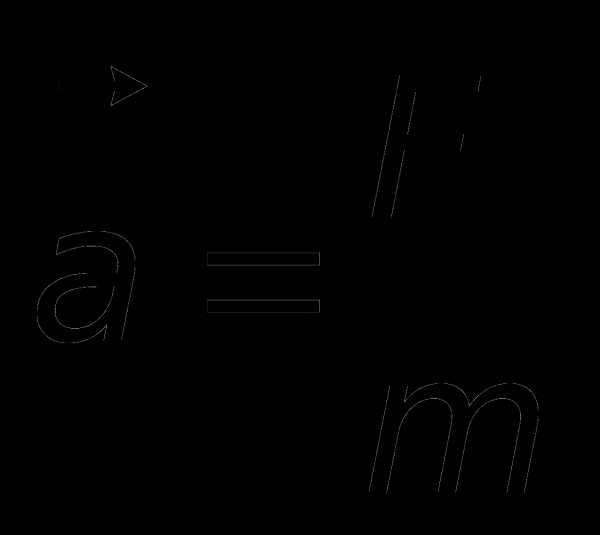Для решения задач закон часто записывают в виде F=ma.

Билет 3.

Импульс тела. Закон сохранения импульса. Закон сохранения энергии.

Простые наблюдения и опыты доказывают, что покой и движение относительны, скорость тела зависит от выбора системы отсчёта; по второму закону Ньютона независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движения может происходить только при действии силы, т.е. в результате взаимодействия с другими телами. Однако существуют величины, которые могут сохраняться при взаимодействии тел. Это энергия и импульс. Импульсом тела называют векторную физическую величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается p. Единица измерения импульса – кг м/с. Импульс тела равен произведению массы тела на его скорость: p=mv. Направление вектора импульса p совпадает с направлением вектора скорости тела v. Рис.

Для импульса тел выполняется закон сохранения, который справедлив только для замкнутых физических систем. В общем случае замкнутой называют систему, которая не обменивается энергией и массой с телами и полями, не входящими в неё. В механике замкнутой называют систему, на которую не действуют внешние силы или действие этих сил скомпенсировано. В этом случае p₁=p₂, где p₁ – начальный импульс системы, а p₂ – конечный. В случае двух тел, входящих в систему, это выражение имеет вид m₁v₁+m₂v₂=m₁v₁’+m₂v₂’, где m₁ и m₂ – массы тел, v₁ и v₂ – скорости до взаимодействия, v₁’ и v₂’ – скорости после взаимодействия. Эта формула и является математическим выражением закона сохранения импульса: импульс замкнутой физической системы сохраняется при любых взаимодействиях, происходящих внутри этой системы; т.е. в замкнутой физической системе геометрическая сумма импульсов тел до взаимодействия равна геометрической сумме импульсов этих тел после взаимодействия. В случае не замкнутой системы импульс тел системы не сохраняется. Однако если в системе существует направление, по которому внешние силы не взаимодействуют или их действия скомпенсировано, то сохраняется проекция импульса на это направление. Кроме того, если время взаимодействия мало (выстрел, взрыв, удар), то за это время даже в случае не замкнутой системы внешние силы не значительно изменяют импульсы взаимодействующих тел. Поэтому для практических расчётов в этом случае тоже можно применять закон сохранения импульса.

Экспериментальные исследования взаимодействий различных тел – от планет и звёзд до атомов и элементарных частиц – показали, что в любой системе взаимодействующих тел при отсутствии действия со стороны других тел, не входящих в систему, или равенстве нулю суммы действующих сил геометрическая сумма импульсов тел действительно остаётся неизменной.

В механике закон сохранения импульса и законы Ньютона связаны между собой. Если на тело массой m в течение времени t действует сила и скорость его движения изменяется от v₀ до v, то ускорение движения a тела равно На основании второго закона Ньютона для силы F можно записать F=ma=m, отсюда следует Ft=mv-mv₀.

Ft – векторная физическая величина, характеризующая действие на тело силы за некоторый промежуток времени и равная произведению силы на время t её действия, называют импульсом силы. Единица импульса в СИ – 1 Н с.

Билет 4.

Основные положения молекулярно-кинетической теории (МКТ) и их опытное обоснование. Масса и размеры молекул. Постоянная Авогадро.

МКТ – это раздел физики, изучающий свойства различных состояний вещества, основывающийся на представлениях о существовании молекул и атомов как мельчайших частиц вещества. В основе МКТ лежат три основных положения:

Все вещества состоят из мельчайших частиц: молекул, атомов или ионов.
Эти частицы находятся в непрерывном хаотическом состоянии, скорость которого определяет температуру вещества.
Между частицами существуют силы притяжения и отталкивания, характер которых зависит от расстояния между ними.

Основные положения МКТ подтверждаются многими опытными фактами. Существование молекул, атомов ионов доказано экспериментально, молекулы достаточно изучены и даже сфотографированы с помощью электронных микроскопов. Способность газов неограниченно расширяться и занимать весь предоставленный им объём объясняется непрерывным хаотическим движением молекул. Упругость газов, твёрдых и жидких тел, способность жидкостей смачивать некоторые твёрдые тела, процессы окрашивания, склеивания, сохранения формы твёрдыми телами и многое другое говорят о существовании сил притяжения и отталкивания между молекулами. Явление диффузии – способность молекул одного вещества проникать в промежутки между молекулами другого – тоже подтверждает основные положения МКТ. Явлением диффузии объясняется, например, распространение запахов, смешивание разнородных жидкостей, процесс растворения твёрдых тел в жидкостях, сварка металлов путём их расплавления или путём давления. Подтверждением непрерывного хаотического движения молекул является также и броуновское движение – непрерывное хаотическое движение микроскопических частиц, не растворимых в жидкости.

Движение броуновских частиц объясняется хаотическим движением частиц жидкости, которые сталкиваются с микроскопическими частицами и приводят их в движение. Опытным путём было доказано, что скорость броуновских частиц зависит от температуры жидкости. Теорию броуновского движения разработал А. Эйнштейн. Законы движения частиц носят статистический, вероятностный характер. Известен только один способ уменьшения интенсивности броуновского движения – уменьшение температуры. Существование броуновского движения убедительно подтверждает движение молекул.

Любое вещество состоит из частиц, поэтому количество вещества v принято считать пропорциональным числу частиц, т.е. структурных элементов, содержащихся в теле.

Единицей количества вещества является моль. Моль – это количество вещества, содержащее столько же структурных элементов любого вещества, сколько содержится атомов в 12 г углерода С¹². Отношение числа молекул вещества к количеству вещества называют постоянной Авогадро:

N_A=N/v. N_A=6,02  10²³ моль^-1.

Постоянная Авогадро показывает, сколько атомов и молекул содержится в одном моле вещества. Молярной массой называют величину, равную отношению массы вещества к количеству вещества: М=M/v.

Молярная масса выражается в кг/моль. Зная молярную массу, можно вычислить массу одной молекулы:

m₀=m/N=m/vN_A=M/N_A.

Средняя масса молекул обычно определяется химическими методами, постоянная Авогадро с высокой точностью определена несколькими физическими методами. Массы молекул и атомов со значительной степенью точности определяются с помощью масс-спектрографа.

Массы молекул очень малы. Например, масса молекулы воды: m=29,910²⁷кг.

Молярная масса связана с относительной молекулярной массой M_r. Относительная молярная масса – это величина, равная отношению массы молекулы данного вещества к 1/12 массы атома углерода С¹². Если известна химическая формула вещества, то с помощью таблицы Менделеева может быть определена его относительная масса, которая, будучи выражена в килограммах, показывает величину молярной массы этого вещества.

Диаметром молекулы принято считать минимальное расстояние, на котором им позволяют сблизиться силы отталкивания. Однако понятие размера молекулы является условным. Средний размер молекулы порядка 10^-10м.

Билет 5.

Идеальный газ. Основное уравнение МКТ идеального газа (без вывода). Температура и её измерение. Температурные шкалы Цельсия и Кельвина.

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если: а) между молекулами отсутствуют силы притяжения, т.е. молекулы ведут себя как абсолютно упругие тела; б) газ очень разряжен, т.е. расстояние между молекулами намного больше размеров самих молекул; в) тепловое равновесие по всему объёму достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрёл свойства идеального, осуществляются при соответствующем разряжении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных. Основными параметрами идеального газа являются давление, объём и температура.

Одним из первых и важных успехов МКТ было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение заключается в том, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.

На основании использования основных положений МКТ было получено основное уравнение МКТ идеального газа, которое выглядит так: p=1/3m₀nv², где p – давление идеального газа, m₀ – масса молекулы, n – концентрация молекул, v² – средний квадрат скорости молекул.

Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа E_k, получим основное уравнение МКТ идеального газа в виде: p=2/3nE_k.

Однако, измерив только давление газа, невозможно узнать ни среднее значение кинетической энергии молекул отдельности, ни их концентрацию. Следовательно, для нахождения микроскопических параметров газа нужно измерение ещё какой-то физической величины, связанной со средней кинетической энергией молекул. Такой величиной в физике является температура. Температура – скалярная физическая величина, описывающая состояние термодинамического равновесия (состояния, при котором не происходит изменения микроскопических параметров). Как термодинамическая величина температура характеризует тепловое состояние системы и измеряется степенью его отклонения от принятого на нулевое, как молекулярно-кинетическая величина – характеризует интенсивность хаотического движения молекул и измеряется их средней кинетической энергией: E_k=3/2kT, где k=1,3810^-23 Дж/К и называется постоянной Больцмана.

Температура всех частей изолированной системы, находящейся в равновесии, одинакова. Измеряется температура термометрами в градусах различных температурных шкал. Существует абсолютная термодинамическая шкала (шкала Кельвина) и различные эмпирические шкалы, которые отличаются начальными точками. До введения абсолютной шкалы температур в практике широкое распространение получила шкала Цельсия (за 0⁰С принята точка замерзания воды, за 100⁰С принята точка кипения воды при нормальном атмосферном давлении).

Единица температуры по абсолютной шкале называется кельвином и выбрана равной одному градусу по шкале Цельсия 1 К=1⁰С. В шкале Кельвина за нуль принят абсолютный нуль температур, т.е. температура, при которой давление идеального газа при постоянном объёме равно –нулю. Вычисления дают результат, что абсолютный нуль температуры равен -273⁰С. Таким образом, между абсолютной шкалой температур и шкалой Цельсия существует связь T=t⁰C+273. Абсолютный нуль температур недостижим, так как любое охлаждение основано на испарении молекул с поверхности, а при приближении к абсолютному нулю скорость поступательного движения молекул настолько замедляется, что испарение практически прекращается. Теоретически при абсолютном нуле скорость поступательного движения молекул равна нулю, т.е. прекращается тепловое движение молекул.

Билет 6.

Вопрос 1. Уравнение состояния идеального газа (уравнение Менделеева-Клайперона). Изотермический, изобарный и изохорный процессы, их графики.

Состояние данной массы полностью определено, если известны давление, температура и объём газа. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.

Для произвольной массы газа единичное состояние газа описывается уравнением Менделеева-Клайперона: pV=mRt/M, где p – давление, V – объём, R – универсальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R=8,31 Дж/мольК).

Уравнение Менделеева-Клайперона показывает, что возможно одновременное изменение пяти параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближённо как процессы, в которых изменяются лишь два параметра из пяти. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.

Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре – температуре, давлении или объёме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.

Изотермическим называют процесс, протекающий при постоянной температуре T=const. Он описывается закон Бойля-Мариотта. pV=const.

Изохорным называют процесс, протекающий пи постоянном объёме. Для него справедлив закон Шарля. V=const, p/T=const.

Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T=const при p=const и называется законом Гей-Люссака. Все процессы можно изобразить графически (рис.).

Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объём молекул пренебрежительно мал по сравнению с объёмом сосуда, в котором находится газ) и при не слишком низких температурах (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т.е. для реального газа это уравнение и его следствия являются хорошим приближением.

Билет 7.

Вопрос 1. Испарение и конденсация. Насыщенный и ненасыщенный пары. Парциональное давление водяного пара. Влажность воздуха. Измерение влажности воздуха (психрометр).

Испарение – парообразование, происходящее при любой температуре со свободной поверхности жидкости. Неравномерное распределение кинетической энергии теплового движения молекул приводит к тому, что при любой температуре кинетическая энергия некоторых молекул жидкости или твёрдого тела может превышать потенциальную энергию их связи с другими молекулами. Большей кинетической энергией обладают молекулы, имеющие большую скорость, а температура тела зависит от скорости движения его молекул, следовательно, испарение сопровождается охлаждением жидкости. Скорость испарения зависит: от площади открытой поверхности, температуры, концентрации молекул вблизи жидкости. Конденсация – процесс перехода вещества из газообразного состояния в жидкое.

Испарение жидкости в закрытом сосуде при неизменной температуре приводит к постепенному увеличению концентрации молекул испаряющегося вещества в газообразном состоянии. Через некоторое время после начала испарения концентрация вещества в газообразном состоянии достигнет такого значения, при котором число молекул возвращающихся в жидкость, становится равным числу молекул, покидающих жидкость за то же время. Устанавливается динамическое равновесие между процессами испарения и конденсации вещества. Вещество в газообразном состоянии, находящееся в динамическом равновесии с жидкостью, называют насыщенным паром. (Паром называют совокупность молекул, покинувших жидкость в процессе испарения.) Пар, находящийся при давлении ниже насыщенного, называют ненасыщенным.

Вследствие постоянного испарения воды с поверхностей водоёмов, почвы и растительного покрова, а также дыхания человека и животных в атмосфере всегда содержится водяной пар. Поэтому атмосферное давление представляет собой сумму давления сухого воздуха и находящегося в нем водяного пара. Давление водяного пара будет максимальным при насыщении воздуха паром. Насыщенный пар в отличие от ненасыщенного не подчиняется законам идеального газа. Так, давление насыщенного пара не зависит от объёма, но зависит от температуры. Эта зависимость не может быть выражена простой формулой, поэтому на основе экспериментального изучения зависимости давления насыщенного пара от температуры составлены таблицы, по которым можно определить его давление при различных температурах.

Давление водяного пара, находящегося в воздухе при данной температуре, называют абсолютной влажностью, или упругостью водяного пара. Поскольку давление пара пропорционально концентрации молекул, можно определить абсолютную влажность как плотность водяного пара, находящегося в воздухе при данной температуре, выраженную в килограммах на метр кубический ().

Большинство явлений, наблюдаемых в природе, например быстрота испарения, высыхание различных веществ, увядание растений, зависит не от количества водяного пара в воздухе, а от –того, насколько это количество близко к насыщению, т.е. от относительной влажности, которая характеризует степень насыщения воздуха водяным паром.

При низкой температуре и высокой влажности повышается теплопередача и человек подвергается переохлаждению. При высоких температурах и влажности теплопередача, наоборот, резко сокращается, что ведёт к перегреванию организма. Наиболее благоприятной для человека в средних климатических широтах является относительная влажность 40-60%. Относительной влажностью называют отношение плотности водяного пара (или давления), находящегося в воздухе при данной температуре, к плотности (или давлению) водяного пара при той же температуре, выраженное в процентах, т.е. =/₀100%.

Относительная влажность колеблется в широких пределах. Причём суточный ход относительной влажности обратен суточному ходу температуры. Днём, с возрастанием температуры и, следовательно, с ростом давления насыщения, относительная влажность убывает, а ночью возрастает. Одно и то же количество водяного пара может либо насыщать, либо не насыщать воздух. Понижая температуру воздуха, можно довести находящийся в нём пар до насыщения. Точкой росы называют температуру, при которой пар, находящийся в воздухе, становится насыщенным. При достижении точки росы в воздухе или на предметах, с которыми он соприкасается, начинается конденсация водяного пара. Для определения влажности воздуха используются приборы, которые называются гигрометрами и психрометрами.

Билет 8.

Вопрос 1. Кристаллические и аморфные тела. Упругие и пластические деформации твёрдых тел.

Каждый может разделить тела на твёрдые и жидкие. Однако это деление будет только по внешним признакам. Для того чтобы выяснить, какими же свойствами обладают твёрдые тела, будем их нагревать. Одни тела начнут гореть (дерево, уголь) – это органические вещества. Другие будут размягчаться (смола) даже при невысоких температурах – это аморфные. Третьи будут изменять своё состояние при нагревании так, как показано на графике (рис.). Это и есть кристаллические тела. Такое поведение кристаллических тел при нагревании объясняется их внутренним строением. Кристаллические тела – это такие тела, атомы и молекулы которых расположены в определённом порядке, и этот порядок сохраняется на достаточно большом расстоянии. Пространственное периодическое расположение атомов или ионов в кристалле называют кристаллической решёткой. Точки кристаллической решётки, в которых расположены атомы или ионы, называют узлами кристаллической решётки.

Кристаллические тела бывают монокристаллами и поликристаллами. Монокристалл обладает единой кристаллической решёткой во всём объёме.

Анизотропия монокристаллов заключается в зависимости их физических свойств он направления. Поликристалл представляет собой соединение мелких, различным образом ориентированных монокристаллов (зерен) и не обладает анизотропией свойств. Большинство твёрдых тел имеют поликристаллическое строение (минералы, сплавы, керамика).

refdb.ru

Скорость прямолинейного равноускоренного движения. График скорости

Вспомним, что такое ускорение.

Определение

Ускорение – это физическая величина, которая характеризует изменение скорости за определенный промежуток времени:

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.

Еще раз о том, что такое равноускоренное движение

Рассмотрим задачу.

Автомобиль за каждую секунду увеличивает свою скорость на . Движется ли автомобиль равноускоренно?

На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на за вторые 0,5 с. Могла быть и другая ситуация: автомобиль разгонялся на да первые , а оставщиеся двигался равномерно. Такое движение не будет равноускоренным.

По аналогии с равномерным движение введем корректную формулировку равноускоренного движения.

Равноускоренным называется такое движение, при котором тело за ЛЮБЫЕ равные промежутки времени меняет свою скорость на одинаковую величину.

Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).

Воспользовавшись уравнением, определяющим ускорение , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:

Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.

К вопросу о направлении скорости и ускорения

В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.

Рассмотрим наиболее типичные примеры направления скорости и ускорения.

1. Скорость и ускорение направлены в одну сторону вдоль одно

interneturok.ru

§ 6. Скорость прямолинейного равноускоренного движения. График скорости. –

Вопросы.
1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.

2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?

3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?

В обоих случаях движение происходит с ускорением, однако в первом случае ускорение положительно, а во-втором отрицательно.

Упражнения.
1. Хоккеист слегка ударил клюшкой по шайбе, придав ей скорость 2 м/с. Чему будет равна скорость шайбы через 4 с после удара, если в результате трения о лёд она движется с ускорением 0,25 м/с²?

2. Лыжник съезжает с горы из состояния покоя с ускорением, равным 0,2 м/с². Через какой промежуток времени его скорость возрастёт до 2 м/с?

3. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v_ox= 1м/с, a_x= 0,5 м/с²; б) v_ox= 1м/с, a_x= 1 м/с²; в) v_ox= 2 м/с, a_x= 1 м/с².
Масштаб во всех случаях одинаков: 1см- 1м/с; 1см – 1с.

4. В одних и тех же координатных осях постройте графики проекции вектора скорости (на ось Х, сонаправленную с вектором начальной скорости) при прямолинейном равноускоренном движении для случаев: а) v_ox= 4,5 м/с, a_x= -1,5 м/с²; б) v_ox= 3 м/с, a_x= -1 м/с²
Масштаб выберите сами.

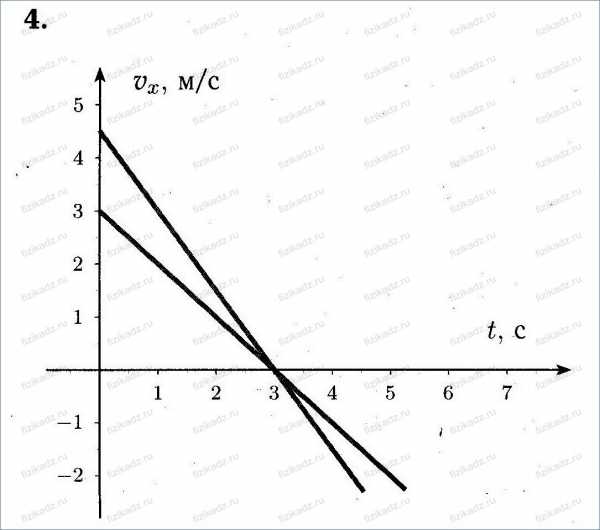
5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I? тело II?

fizikadz.ru

Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение. Физика, 9 класс: уроки, тесты, задания.

1.	Терминология Сложность: лёгкое	2
2.	Единица ускорения в СИ Сложность: среднее	2
3.	Вычисление ускорения лифта Сложность: среднее	2
4.	Равномерное торможение мотоцикла Сложность: среднее	2
5.	Графики равноускоренного движения Сложность: среднее	2
6.	Ускорение Сложность: среднее	2
7.	Средняя скорость Сложность: сложное	3
8.	Равноускоренное движение грузовика Сложность: сложное	3
9.	Характер движения автомобиля Сложность: сложное	3
10.	Длина взлётной полосы Сложность: сложное	3
11.	Полный пройденный путь Сложность: сложное	3

www.yaklass.ru

мгновенная скорость, ускорение, перемещение — методическая рекомендация. Физика, 9 класс.

1.	Терминология	1 вид – рецептивный	лёгкое	2 Б.	Определение понятий.
2.	Единица ускорения в СИ	2 вид – интерпретация	среднее	2 Б.	Перевод единиц ускорения в СИ.
3.	Вычисление ускорения лифта	2 вид – интерпретация	среднее	2 Б.	Требуется найти ускорение лифта.
4.	Равномерное торможение мотоцикла	2 вид – интерпретация	среднее	2 Б.	Требуется определить модуль ускорения мотоцикла.
5.	Графики равноускоренного движения	2 вид – интерпретация	среднее	2 Б.	Требуется выбрать график, на котором представлена зависимость модуля ускорения от времени движения шарика.
6.	Ускорение	2 вид – интерпретация	среднее	2 Б.	Вычисление ускорения вездехода.
7.	Средняя скорость	3 вид – анализ	сложное	3 Б.	Требуется найти среднюю скорость велосипедиста .
8.	Равноускоренное движение грузовика	3 вид – анализ	сложное	3 Б.	Вычисление начальной скорости и ускорения.
9.	Характер движения автомобиля	3 вид – анализ	сложное	3 Б.	Дана ситуации, требуется определить характер движения автомобиля.
10.	Длина взлётной полосы	3 вид – анализ	сложное	3 Б.	Неравномерное движение самолёта при посадке.
11.	Полный пройденный путь	3 вид – анализ	сложное	3 Б.	Равномерное и неравномерное движение автобуса.