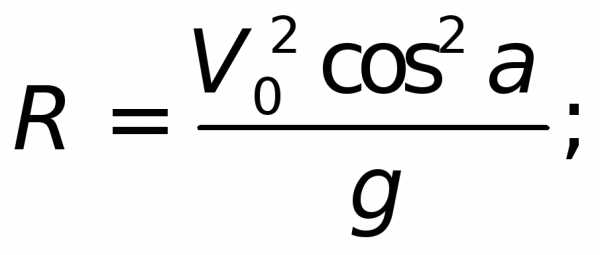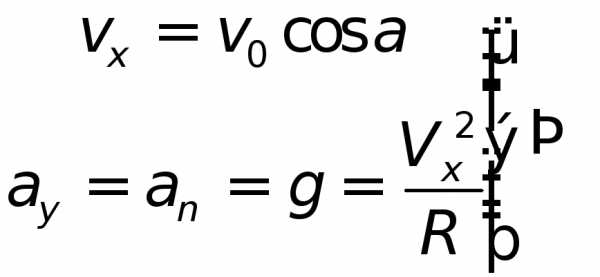1. 1. 4. Ускорение. Мгновенное и среднее ускорение. Нормальное и тангенциальное ускорения.
Скорость
частицы ( )
может изменяться со временем как по
величине, так и по направлению.Быстрота
изменения вектора
)
может изменяться со временем как по
величине, так и по направлению.Быстрота
изменения вектора  называется ускорением
называется ускорением  .
Как и быстрота изменения любой функции
по времени, ускорение
.
Как и быстрота изменения любой функции
по времени, ускорение  определяется производной вектора
определяется производной вектора поt.
Таким образом, по определению ускорения
получаем:
поt.
Таким образом, по определению ускорения
получаем:
| (1.9) |
Разложение
вектора 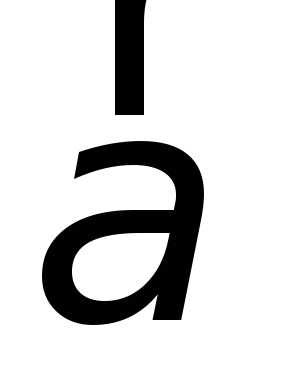 по
базису прямоугольной декартовой системы
координат:
.
по
базису прямоугольной декартовой системы
координат:
.
Проекции
вектора ускорения 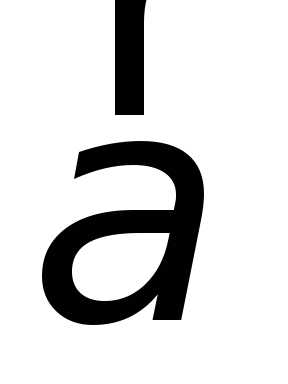 на
оси координат определяются выражениями:
на
оси координат определяются выражениями:
(1.10) |
Модуль вектора ускорения:
(1.11) |
Единица измерения ускорения – 1 м/с2.
Средним
ускорением точки
в интервале времени от t до t + ∆t называется
вектор  , равный
отношению изменения
, равный
отношению изменения 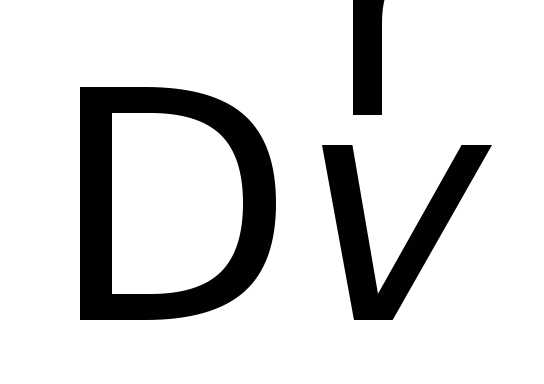 вектора
скорости точки за этот промежуток
времени к его продолжительности
вектора
скорости точки за этот промежуток
времени к его продолжительности :
:
| (1.12) |
Определим ускорение произвольно движущейся точки.
В общем случае траектория точки представляет из себя пространственную кривую. Введем следующие понятия:
Соприкасающейся плоскостью в точке М траектории называется предельное положение плоскости, проходящей через любые три точки траектории, когда эти точки неограниченно приближаются к точке М.
Соприкасающейся окружностью в точке M траектории называется предельная окружность, полученная из произвольной окружности проходящей через три точки траектории при их неограниченном приближении к точке М.
Соприкасающаяся окружность лежит в соприкасающейся плоскости.
Центр соприкасающейся окружность и ее радиус называются соответственно центром кривизны и радиусом кривизны рассматриваемой кривой в точке М.
Прямая, соединяющая точку М с центром кривизны называется главной нормалью к кривой в точке М.
окружности и перемещение точки подобны. Следовательно,
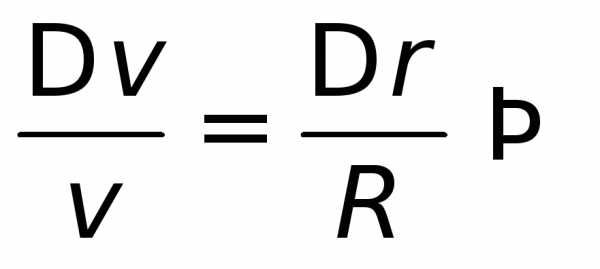
Ускорение 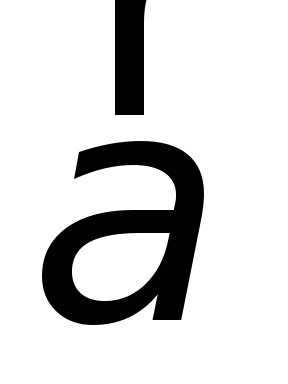 может быть представлено в виде:
может быть представлено в виде:
| (1.13) |
где 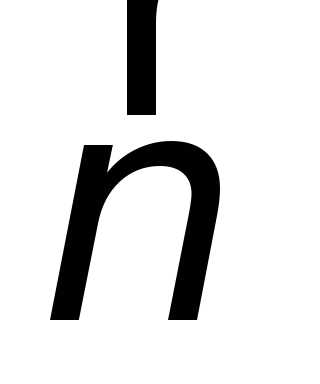 – единичный вектор
нормали к круговой траектории движения
точки (направлен к центру кривизны
траектории).
– единичный вектор
нормали к круговой траектории движения
точки (направлен к центру кривизны
траектории).
Представим вектор скорости в виде:
| (1.14) |
где 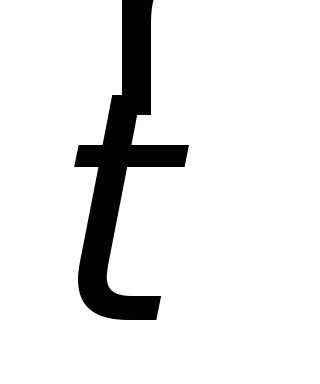 – единичный вектор,
направленный по касательной к окружности
и указывающий направление скорости,
– единичный вектор,
направленный по касательной к окружности
и указывающий направление скорости,  – величина скорости, т.е. ее численное
значение.
– величина скорости, т.е. ее численное
значение.
При
равномерном движении модуль скорости
равен константе ( = const),
меняется только направление вектора
касательной. Тогда для такого случая:
= const),
меняется только направление вектора
касательной. Тогда для такого случая:
| (1.15) |
Сравниваем
с формулой ускорения через 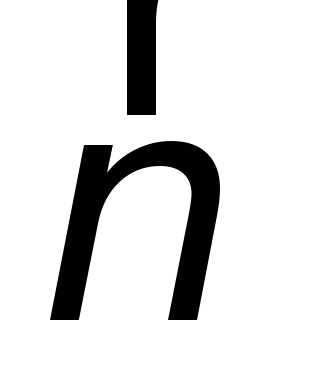 (1), получим:
(1), получим:
| (1.16) | |
При
равномерном движении ускорение Рассмотрим этот случай. тогда | ||
Рисунок 1.4. | ||
Применяем подстановку, исходя из формул (1.13) и (1.15) получаем:
| (1.17) |
Заменим 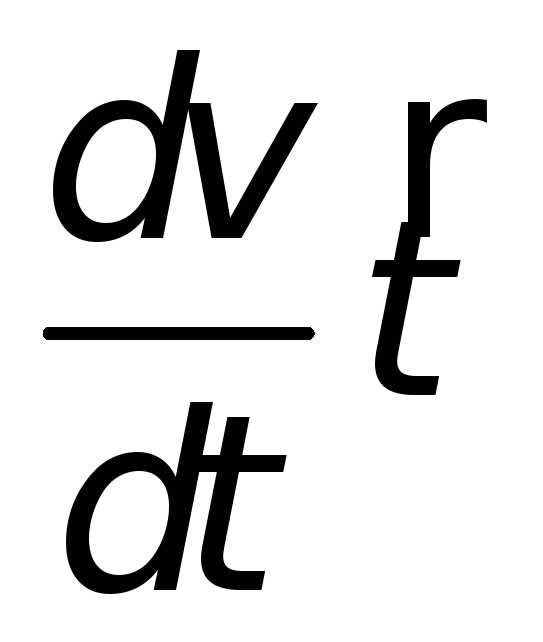
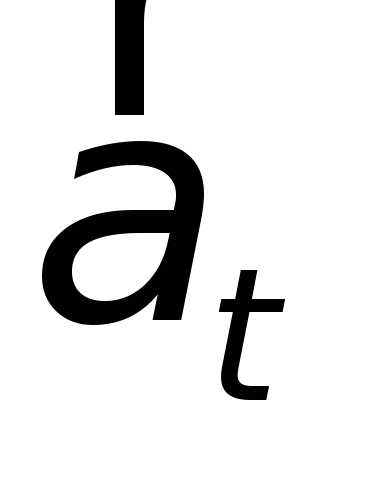 (тангенциальное
ускорение), а
(тангенциальное
ускорение), а 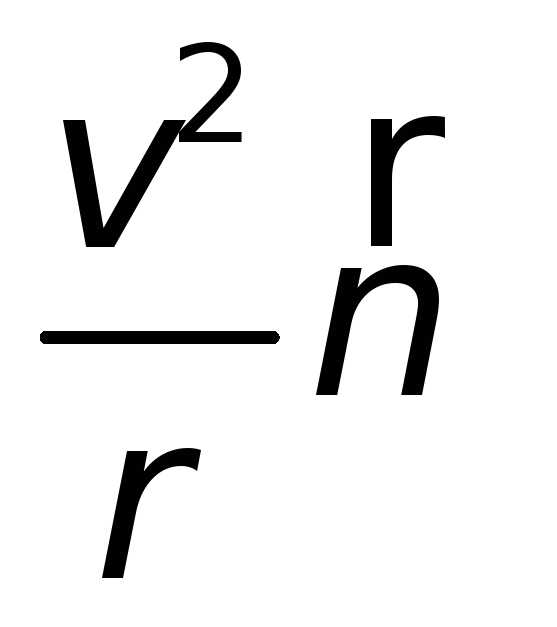 на
на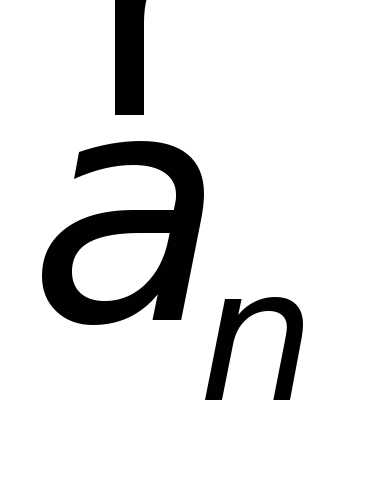 (нормальное ускорение),
получим
(нормальное ускорение),
получим | (1.18) |
Тангенциальное
ускорение 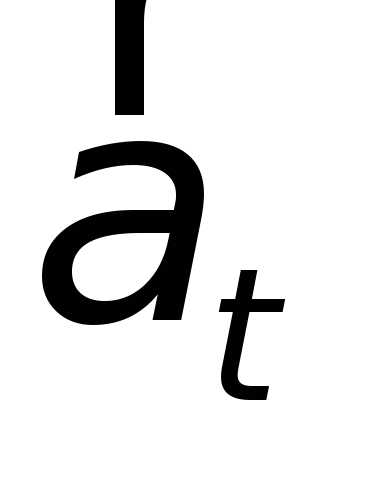 меняет скорость по величине, нормальное
ускорение
меняет скорость по величине, нормальное
ускорение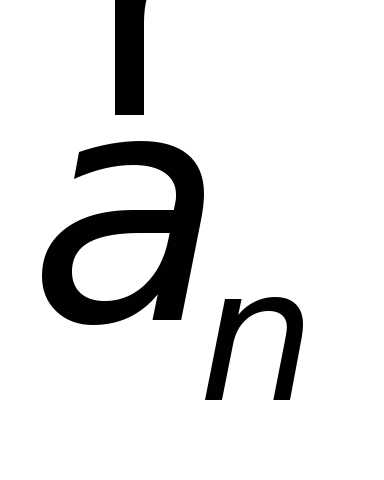
Действительно,
если дана некая траектория (см. рис. 1.5)
есть скорость  в начале и скорость
в начале и скорость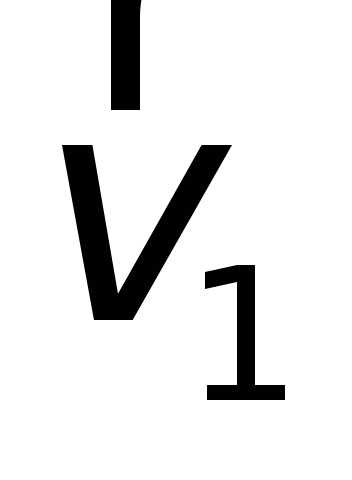 во втором положении,
перенесем параллельным переносом вектор
во втором положении,
перенесем параллельным переносом вектор 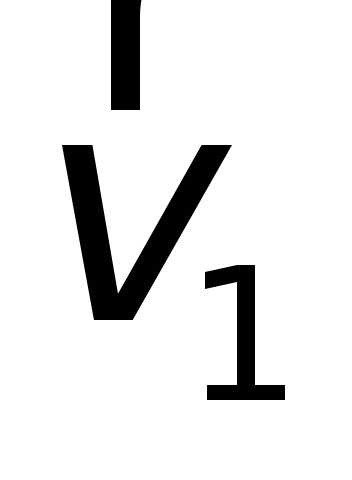 в точку M1,
тогда мы видим, что вектор скорости
получает приращение
в точку M1,
тогда мы видим, что вектор скорости
получает приращение  .
.
В результате, если уменьшать промежутки времени
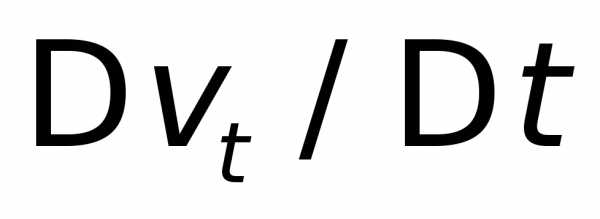 и
и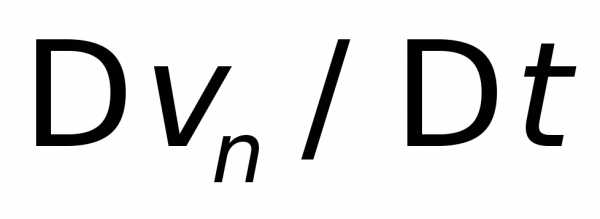 будут стремиться к пределам
будут стремиться к пределамРисунок 1.5. | Рисунок 1.6. |
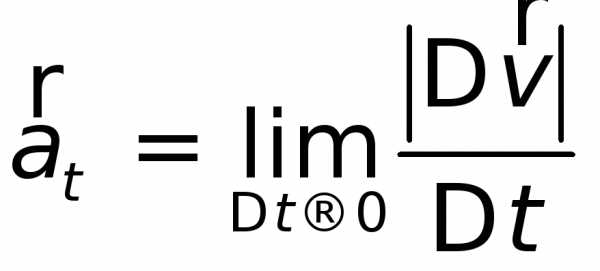 и
и 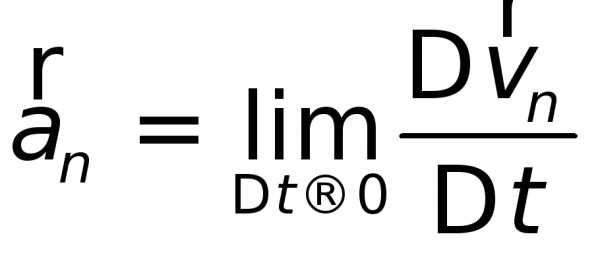
Пример . | Пример: Снаряд выпущен с начальной скоростью V = 200 м/с под углом = 60 к горизонту. Определить кривизну траектории в точке наивысшего подъема снаряда (Рис.1.7). Силами аэродинамического сопротивления пренебречь. | |
Рисунок 1.7. | Решение:
| |
В верхней точке |
studfiles.net
12-и. Мгновенное ускорение и его постоянство
§ 12-и. Мгновенное ускорение и его постоянство
Стробоскопическая фотография в предыдущем параграфе показывает, что свободно падающий шарик движется с ускорением. Различных тел, движущихся с ускорением, вокруг нас множество. Это, например, нога футболиста перед ударом по мячу, взлетающая с космодрома ракета, отъезжающий от станции поезд и так далее.
По аналогии с формулой мгновенной скорости в физике вводят формулу, выражающую определение мгновенного ускорения:
В школьной физике изучают только такие движения, для которых модуль мгновенного ускорения не меняется с течением времени. Поэтому вместо «мгновенное ускорение» часто говорят короче: «ускорение». Например, ускорение поезда, ускорение ракеты, летящего мяча и так далее.
Вспомним, что при равноускоренном движении мгновенная скорость за любые равные интервалы времени изменяется одинаково (см. § 12-з). Поэтому, если равные изменения мгновенной скорости поделить на равные интервалы времени, мы получим равные ускорения. Другими словами, при равноускоренном движении ускорение постоянно (как по числовому значению, так и пространственному направлению), значит, интервал времени наблюдения может быть любым. И тогда из формулы мгновенного ускорения мы получим определение ускорения:
, принимая момент времени to = 0 .
Выпишем начало и конец получившегося равенства и выразим скорость:
, если ускорение постоянно.
Для движения вдоль осей X и Y эта формула может быть записана с использованием проекций векторов на координатные оси:
υx = υox + ax t и υy = υoy + ay t
Как видно из этих равенств, при равноускоренном движении проекции мгновенной скорости зависят от времени по линейному закону, то есть описываются линейными функциями вида y = kx + b.
Ускорение свободного падения. Взглянем ещё раз на чертёж с «векторным треугольником» и последний абзац § 12-з. Обратим внимание: вектор изменения скорости свободно падающего шарика, а значит, и вектор ускорения свободного падения направлен вниз и не зависит от скорости тела. Подтвердим это вторым способом.
Проделаем опыт. В стеклянную трубку с краном помещены скомканный лист бумаги и камешек. Сначала кран трубки открыт, и внутри неё находится атмосферный воздух. Поэтому при переворачивании трубки бумага падает с меньшим по модулю ускорением. Затем воздух откачивают, создавая в трубке вакуум, а кран закрывают. Теперь бумага падает с тем же ускорением, что и камень. Опыт нам продемонстрировал, что ускорение свободного падения одинаково для всех тел. В физике свободным падением называют движение тела при действии только силы тяжести.
Если на тело действуют сравнительно малые силы, препятствующие свободному падению, то их действием можно пренебречь. Тогда измерения показывают: модуль ускорения свободного падения всех тел вблизи поверхности Земли равен 9,8 м/с². Это значение вам уже знакомо из 7 класса как «коэффициент силы тяжести» (см. § 3-г). Вспомнив определение 1 ньютона (см. § 3-а), вы поймёте, что уже известное вам значение 9,8 Н/кг – это именно 9,8 м/с².
Для вычисления (измерения) любых ускорений тел, и ускорения свободного падения в частности, вполне можно использовать метод стробоскопического фотографирования.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
Мгновенное ускорение и его постоянство
Стробоскопическая фотография в предыдущем параграфе показывает, что свободно падающий шарик движется с ускорением. Различных тел, движущихся с ускорением, вокруг нас множество. Это, например, нога футболиста перед ударом по мячу, взлетающая с космодрома ракета, отъезжающий от станции поезд и так далее.
По аналогии с формулой мгновенной скорости в физике вводят формулу, выражающую определение мгновенного ускорения:
| = | . Δ. | – мгновенное ускорение, м/с² Δ – изменение скорости, м/с ( если Δt→0 ) Δt – стремящийся к нулю интервал времени, с | |||
| Δt |
В школьной физике изучают только такие движения, для которых модуль мгновенного ускорения не меняется с течением времени. Поэтому вместо «мгновенное ускорение» часто говорят короче: «ускорение». Например, ускорение поезда, ускорение ракеты, летящего мяча и так далее.
Вспомним, что при равноускоренном движении мгновенная скорость за любые равные интервалы времени изменяется одинаково (см. § 12-з). Поэтому, если равные изменения мгновенной скорости поделить на равные интервалы времени, мы получим равные ускорения. Другими словами, при равноускоренном движении ускорение постоянно (как по числовому значению, так и пространственному направлению), значит, интервал времени наблюдения может быть любым. И тогда из формулы мгновенного ускорения мы получим определение ускорения:
, принимая момент времени to = 0 .
Выпишем начало и конец получившегося равенства и выразим скорость:
, если ускорение постоянно.
Для движения вдоль осей X и Y эта формула может быть записана с использованием проекций векторов на координатные оси:
υx = υox + ax t и υy = υoy + ay t
Как видно из этих равенств, при равноускоренном движении проекции мгновенной скорости зависят от времени по линейному закону, то есть описываются линейными функциями вида y = kx + b.
Ускорение свободного падения. Взглянем ещё раз на чертёж с «векторным треугольником» и последний абзац § 12-з. Обратим внимание: вектор изменения скорости свободно падающего шарика, а значит, и вектор ускорения свободного падения направлен вниз и не зависит от скорости тела. Подтвердим это вторым способом.
Проделаем опыт. В стеклянную трубку с краном помещены скомканный лист бумаги и камешек. Сначала кран трубки открыт, и внутри неё находится атмосферный воздух. Поэтому при переворачивании трубки бумага падает с меньшим по модулю ускорением. Затем воздух откачивают, создавая в трубке вакуум, а кран закрывают. Теперь бумага падает с тем же ускорением, что и камень. Опыт нам продемонстрировал, что ускорение свободного падения одинаково для всех тел. В физике свободным падением называют движение тела при действии только силы тяжести.
Если на тело действуют сравнительно малые силы, препятствующие свободному падению, то их действием можно пренебречь. Тогда измерения показывают: модуль ускорения свободного падения всех тел вблизи поверхности Земли равен 9,8 м/с². Это значение вам уже знакомо из 7 класса как «коэффициент силы тяжести» (см. § 3-г). Вспомнив определение 1 ньютона (см. § 3-а), вы поймёте, что уже известное вам значение 9,8 Н/кг – это именно 9,8 м/с².
Для вычисления (измерения) любых ускорений тел, и ускорения свободного падения в частности, вполне можно использовать метод стробоскопического фотографирования.
questions-physics.ru
6.1. Среднее ускорение и мгновенное ускорение
6.1. Среднее ускорение и мгновенное ускорение
Ускорением называют физическую величину, характеризующую быстроту изменения мгновенной скорости тела. Как и скорость, ускорение − одна из наиболее важных физических величин.
Природа такова, что силовое воздействие на тело порождает именно ускорение тела (не саму скорость, а быстроту ее изменения).
Подробнее об этом будем говорить в главе, посвященной динамике.
Различают среднее ускорение материальной точки за данный промежуток времени и мгновенное ускорение точки в данный момент времени. Среднее ускорение aср за время от t до t + Δt определяют соотношением
Мгновенное ускорение a(t) определяют как предел последовательности средних ускорений при Δt → 0:
Именно мгновенное ускорение является основным понятием, так как именно оно определяется силовым воздействием на тело. В различных задачах важно уметь находить ускорение в каждой точке траектории. Используя в дальнейшем термин «ускорение», будем иметь в виду именно мгновенное ускорение. Среднее же ускорение, как и средняя скорость по перемещению, играет, как правило, вспомогательную роль.
В случае прямолинейного движения векторное соотношение (1) можно заменить на соответствующее скалярное соотношение:
Если скорость v(t) со временем возрастает (если v(t + Δt) > v(t)), то ускорение положительно: a(t) > 0 (тело ускоряется). Если же скорость v(t) со временем уменьшается (если v(t + Δt) < v(t)), то ускорение отрицательно: a(t) < 0 (тело замедляется). При равномерном прямолинейном движении выполняется равенство v(t + Δt) = v(t), ускорение равно нулю, т. е. отсутствует.
Подчеркнем, что ускорение равно нулю только в случае равномерного прямолинейного движения. Если точка движется по какой-либо криволинейной траектории, она будет иметь ускорение даже при равномерном движении. При равномерном движении по криволинейной траектории модуль мгновенной скорости остается неизменным, однако изменяется направление скорости. Поэтому и появляется ускорение.
Применение среднего ускорения при решении задачи на механическое колебание.
fizportal.ru
Мгновенное ускорение – это… Что такое Мгновенное ускорение?
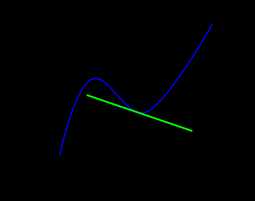
Если движение точки прямолинейно, можно построить график зависимости скорости от времени. При этом величина ускорения будет равна тангенсу угла наклона касательной к графику в указанной точке.
Ускоре́ние (обычно обозначается , в теоретической механике ), производная скорости по времени — векторная величина, показывающая, насколько изменяется вектор скорости точки (тела) при её движении за единицу времени (т.е. ускорение учитывает не только изменение величины скорости, но и её направления).
Например, вблизи Земли падающее на Землю тело, в случае, когда можно пренебречь сопротивлением воздуха, увеличивает свою скорость примерно на 9,8 м/с каждую секунду, то есть, его ускорение равно 9,8 м/с².
Раздел механики, изучающий движение в трёхмерном евклидовом пространстве, его запись, а также запись скоростей и ускорений в различных системах отсчёта, называется кинематикой.
Единицей ускорения служит метр в секунду за секунду (m/s2, м/с2), существует также внесистемная единица Гал (Gal), применяемая в гравиметрии и равная 1 см/с2.
Производная ускорения по времени т.е. величина, характеризующая быстроту изменения ускорения по времени называется рывок.
Вектор ускорения материальной точки в любой момент времени находится путём дифференцирования вектора скорости частицы по времени:
- .
Ускорение точки при прямолинейном движении
Если вектор не меняется со временем, движение называют равноускоренным. При равноускоренном движении справедливы формулы:
- .
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю во всё время движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), так что говорят, что движение прямолинейно и равномерно.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). (Обратное не верно.)
Ускорение точки при движении по окружности
Если точка движется по окружности с постоянной по модулю скоростью, ее ускорение все равно не равно 0, поскольку направление вектора скорости постоянно изменяется. Ускорение в этом случае называется центростремительным, посколку его вектор всегда направлен к центру окружности, а его модуль равен:
Если при движении по окружности модуль скорости изменяется, удобно ввести такое понятие, как угловое ускорение, аналогичное угловой скорости. Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растет, и наоборот.
Ускорение точки при движении по кривой
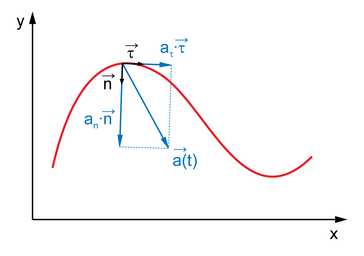
Вектор ускорения можно разложить по сопутствующему базису :
- ,
где
Известно, что всегда равно нулю.
Векторы и называются касательным (тангенциальным), нормальным и бинормальным ускорениями соответственно.
Ускорения в твёрдом теле
Связь ускорений двух точек можно получить, продифференцировав формулу Эйлера для скоростей по времени:
- ,
где — вектор угловой скорости тела, а — вектор углового ускорения тела.
Второе слагаемое называется центростремительным ускорением.
Ускорение при сложном движении
Абсолютное ускорение равно сумме относительно, переносного и кориолисова:
- .
Первый закон Ньютона постулирует существование инерциальных систем отсчета. В этих системах отсчета равномерное прямолинейное движение имеет место всякий раз, когда материальная точка (но не тело!) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчета всегда является некоторое внешнее силовое воздействие.
Второй закон Ньютона утверждает, что приложенная (к точке) сила и порождаемое ей ускорение точки всегда пропорциональны, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется массой материальной точки):
- .
Единицы измерения ускорения
См. также
Ссылки
Wikimedia Foundation. 2010.
xzsad.academic.ru


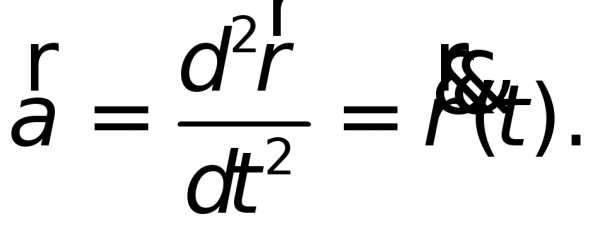
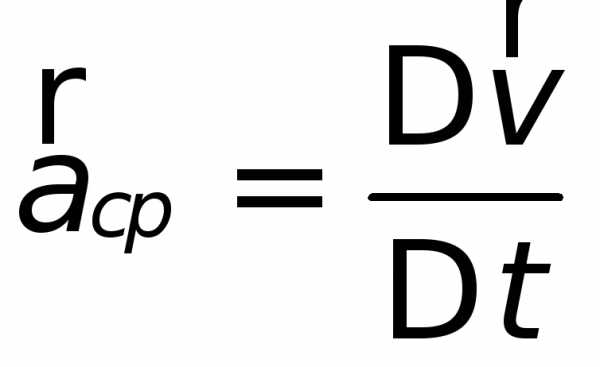 .
.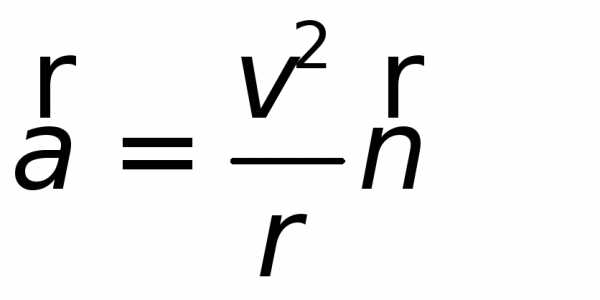 ,
,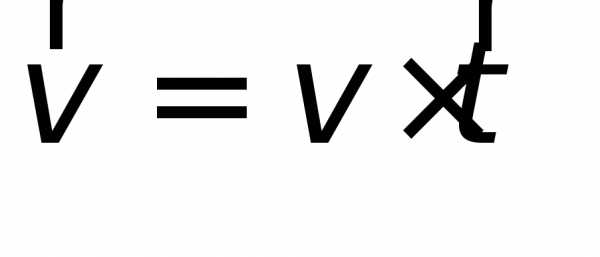
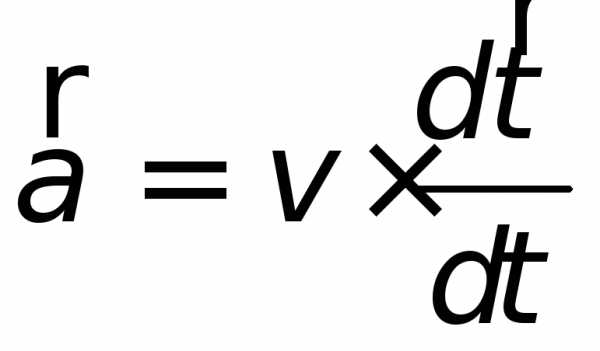 .
.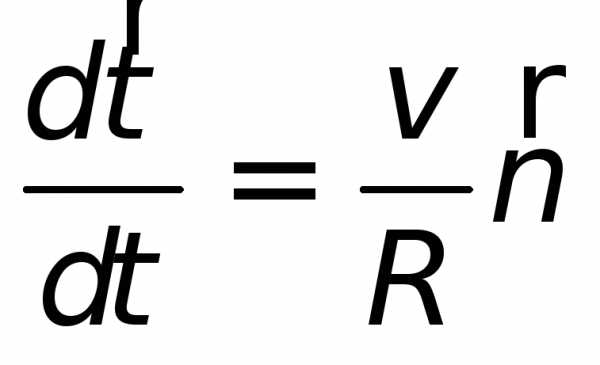 .
. направлено к центру, т.е. перпендикуляр
траектории, но не
так будет обстоять дело, когда скорость
направлено к центру, т.е. перпендикуляр
траектории, но не
так будет обстоять дело, когда скорость  const.
В общем случае произвольной гладкой
кривой радиус кривизны меняется от
точки к точке (см., например, рис. 1.4).
Непрерывно меняется и направление
единичного вектора главной нормали
const.
В общем случае произвольной гладкой
кривой радиус кривизны меняется от
точки к точке (см., например, рис. 1.4).
Непрерывно меняется и направление
единичного вектора главной нормали 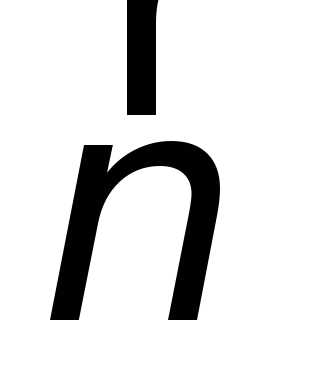 .
.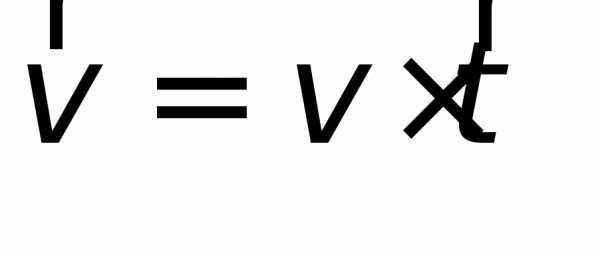
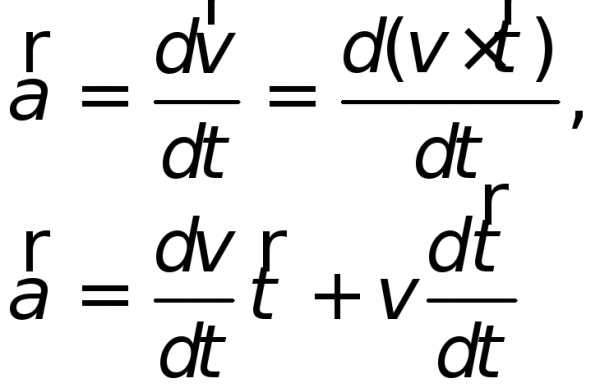
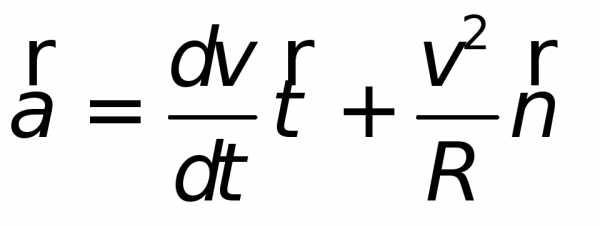
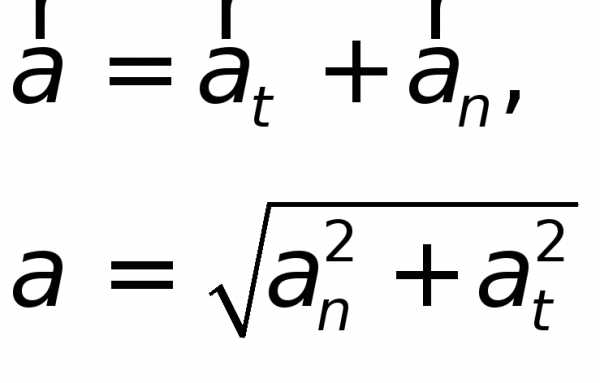 .
.