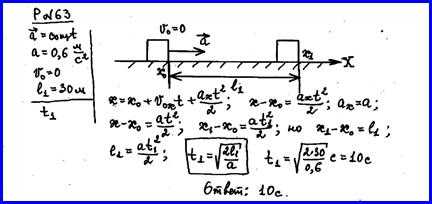
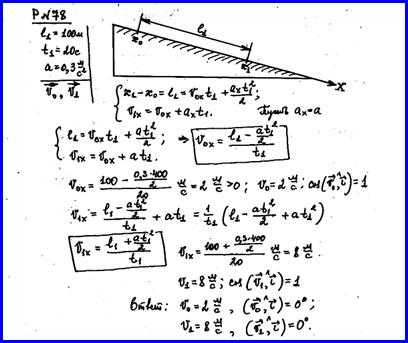
Физические основы механики
Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.
Средняя скорость за время от t1 до t2 равна отношению перемещения за это время к промежутку времени , за которое это перемещение имело место:
Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <…> , как это сделано выше.
Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:
Действительно
Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени
Скорость в момент времени t равна пределу отношения перемещения за время к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
Рис. 2.5. К определению мгновенной скорости.
В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если и есть конечное перемещение и конечный промежуток времени, то и — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
есть ничто иное как дробь — частное от деления на , поэтому последнее соотношение может быть переписано и весьма часто используется в виде
Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:
По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.
Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.
Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей
Учитывая постоянство декартовых единичных векторов , , , продифференцируем это выражение по времени
С другой стороны, разложение по базису вектора скорости имеет вид
опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть
Модуль вектора скорости равен
Получим ещё одно, важное, выражение для модуля вектора скорости.
Уже отмечалось, что при величина || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому
и в пределе (>0)
Иными словами, модуль скорости — это производная пройденного пути по времени.
Окончательно имеем:
Средний модуль вектора скорости, определяется следующим образом:
Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:
Здесь s(t1, t2) — путь за время от t1 до t2 и, соответственно, s(t0, t2) — путь за время от t0 до t2 и s(t0, t2) — путь за время от t0 до t1.
Средний вектор скорости или просто средняя скорость, как указано выше, равен
Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени , в который мгновенная скорость равна средней путевой скорости за первые секунд движения точки.
Рис. 2.6. Определение мгновенной и средней скорости тела
Модуль скорости в данный момент времени
будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости точке соответствующей моменту времени t*. Средний модуль скорости за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
online.mephi.ru
| Археология Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика | КИНЕМАТИКА Движение с постоянным ускорением
Свободное падение тел
Средний модуль скорости
|
studopedya.ru
|
Средний вектор скорости определяется как отношение вектора перемещения Δr
ко времени Δt, за которое это перемещение произошло: .
Вектор совпадает с направлением вектора Δr (рис. 2.4). Мгновенная скорость в точке 1:
Мгновенная скорость υ – вектор скорости в данный момент времени, равный первой производной от r по времени и направлен по касательной к траектории в данной точке в сторону движения точки А. Модуль вектора скорости: . При Δt → 0, т.е. на бесконечно малом участке траектории, ΔS = Δr (перемещение совпадает с траекторией).В этом случае мгновенную скорость можно выразить через скалярную величину – путь: Так вычислять скорость проще, т.к. s – скаляр. Обратное действие – интегрирование (рис. 2.5).
Геометрический смысл этого интеграла в том, что площадь под кривой есть путь тела за время t. Путь, перемещение Принцип суперпозиции |
ens.tpu.ru
Типы движений | Учеба-Легко.РФ – крупнейший портал по учебе
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).
Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.
Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:
vcp = v
Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:
= / t
Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.
Перемещение при равномерном прямолинейном движении определяется формулой:
= • t
Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:
vx = v, то есть v > 0
Проекция перемещения на ось ОХ равна:
s = vt = x – x0
где x0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)
Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:
х = x0 + vt
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
х = x0 - vt
Равномерное прямолинейное движение – это частный случай неравномерного движения.
Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.
vcp = s / t
Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:
Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:
= ‘
Проекция вектора скорости на ось ОХ:
vx = x’
это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).
Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:
Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:
= ‘ = ” Учитывая, что 0 – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:
Отсюда формула скорости равнопеременного движения в любой момент времени:
= 0 + t Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:
vx = v0x ± axt
Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.
Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).
Рис. 1.15. Зависимость ускорения тела от времени.
Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).
Рис. 1.16. Зависимость скорости тела от времени.
График зависимости скорости от времени (рис. 1.16) показывает, что
При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).
Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:
0a = v0 bc = v
Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).
Общая формула для определения проекции перемещения:
График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.
Рис. 1.18. Зависимость перемещения тела от времени.
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
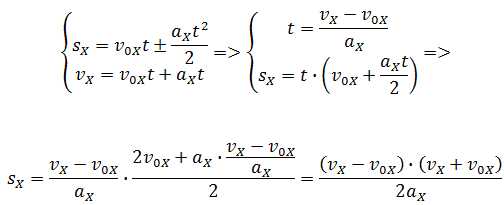
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз (рис. 1.18).
uclg.ru
05.Механические явления – Сайт Александра Таранова
назад к оглавлению
Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
Раздел механики, описывающий геометрические свойства движения без учета причин, его вызывающих, называется кинематикой.
В более общем значении движением называется любое пространственное или временное изменение состояния физической системы. Например, можно говорить о движении волны в среде.
Относительность движения
Относительность — зависимость механического движения тела от системы отсчёта. Не указав систему отсчёта, не имеет смысла говорить о движении.
Траектория материальной точки — линия в трёхмерном пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве. Существенно, что понятие о траектории имеет физический смысл даже при отсутствии какого-либо по ней движения. Кроме того, и при наличии движущегося по ней объекта, траектория сама по себе не может ничего дать в отношении причин движения, то есть о действующих силах.
Путь — длина участка траектории материальной точки, пройденного ею за определённое время.
Скорость (часто обозначается , от англ. velocity или фр. vitesse) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.
В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.
Единицы измерения скорости
Метр в секунду, (м/с), производная единица системы СИ
Километр в час, (км/ч)
узел (морская миля в час)
Число Маха, 1 Мах равен скорости звука в данной среде; Max n в n раз быстрее.
Как единица, зависящая от конкретных условий среды, должна дополнительно определяться.
Скорость света в вакууме (обозначается c)
В современной механике движение тела подразделяется на виды, и существует следующая классификация видов движения тела:
- Поступательное движение, при котором любая прямая линия, связанная с телом, остаётся при движении параллельной самой себе.
-
Вращательное движение или вращение тела вокруг своей оси, считающейся неподвижной.
-
Сложное движение тела, состоящее из поступательного и вращательного движений.
Каждое из этих видов может быть неравномерным и равномерным (с не постоянной и постоянной скоростью соответственно).
Средняя скорость неравномерного движения
Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:
Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.
Средняя скорость по перемещению
Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:
Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).
Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.
Прямолинейное равномерное движение – это движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения. Вектор скорости точки остаётся неизменным, а её перемещение есть произведение вектора скорости на время:
Если направить координатную ось вдоль прямой, по которой движется точка, то зависимость координаты точки от времени является линейной: , где — начальная координата точки, — проекция вектора скорости на координатную ось x.
Точка, рассматриваемая в инерциальной системе отсчёта, находится в состоянии равномерного прямолинейного движения, если равнодействующая всех сил, приложенных к точке, равна нулю.
Вращательное движение — вид механического движения. При вращательном движении абсолютно твердого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землей, ось вращения ротора генератора на электростанции неподвижна.
Характеристики вращения тела
При равномерном вращении (N оборотов в секунду),
Частота вращения — число оборотов тела в единицу времени,
Период вращения — время одного полного оборота. Период вращения T и его частота v связаны соотношением T = 1 / v.
Линейная скорость точки, находящейся на
расстоянии R от оси вращения
,
Угловая скорость вращения тела.
Кинетическая энергия вращательного движения
,
где Iz — момент инерции тела относительно оси вращения. w — угловая скорость.
Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы, пропорциональной смещению.
Если возвращающая сила — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор (см. LC-цепь).
Звук, в широком смысле — упругие волны, продольно распространяющиеся в среде и создающие в ней механические колебания; в узком смысле — субъективное восприятие этих колебаний специальными органами чувств животных или человека.
Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16 Гц до 20 кГц. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, — ультразвуком, более 1 ГГц — гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).
Физические параметры звука
Колебательная скорость — величина, равная произведению амплитуды колебаний А частиц среды, через которую проходит периодическая звуковая волна, на угловую частоту w:
v=Aw, измеряется в м/с или см/с.
В энергетическом отношении реальные колебательные системы характеризуются изменением энергии вследствие частичной её затраты на работу против сил трения и излучение в окружающее пространство. В упругой среде колебания постепенно затухают. Для характеристики затухающих колебаний используются коэффициент затухания (S), логарифмический декремент (D) и добротность (Q).
Коэффициент затухания отражает быстроту убывания амплитуды с течением времени. Если обозначить время, в течение которого амплитуда уменьшается в е = 2,718 раза, через t, то:
.
Скорость звука — скорость распространения звуковых волн в среде.
Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, что связано в основном с убыванием сжимаемости веществ в этих фазовых состояниях соответственно.
В среднем, в идеальных условиях, в воздухе скорость звука составляет 340—344 м/с.
Скорость звука в любой среде вычисляется по формуле:
где В — адиабатическая сжимаемость среды; р — плотность.
Как и световые
волны, звуковые тоже могут отражаться, преломляться и т.д.
Далее – 06.Взаимодействие тел
Если Вам понравилась эта страница, и Вам захотелось, чтобы Ваши друзья тоже её увидели, то выберите внизу значок социальной сети, где вы имеете свою страницу, и выразите своё мнение о содержании.
Ваши друзья и случайные посетители благодаря этому добавят Вам и моему сайту рейтинг
aetaranow.narod.ru
Средняя и мгновенная скорость движения материальной точки. — КиберПедия
Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени.
Физическая величина, равная отношению вектора перемещения к промежутку времени, за который это перемещение произошло называется средней скоростью материальной точки за промежуток времени
Вектор направлен так же, как , т е направлен вдоль хорды, стягивающей участок траектории . В случае прямолинейного движения в одном направлении =
Модуль средней скорости определяется как отношение пути ∆S, пройденного телом за некоторый промежуток времени, к этому промежутку:
Мгновенная скорость есть предел, к которому стремится средняя скорость , когда промежуток времени движения стремится к нулю:
Мгновенная скорость есть векторная величина, равная первой производной радиуса – вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости направлен по касательной к траектории в сторону движения.
По мере уменьшение ∆t путь ∆S все больше будет приближаться к , поэтому модуль мгновенной скорости:
Таким образом, модуль мгновенной скорости равен первой производной пути по времени :
Путь, пройденный материальной точкой при равномерном и равнопеременном движении.
Если выражение ds = vdt проинтегрировать по времени в пределах от t до t+Δt, то найдем длину пути, пройденного точкой за время Δt:
В случае равномерного прямолинейного движения числовое значение мгновенной скорости
постоянно; тогда выражение примет вид
Длина пути, пройденного точкой за промежуток времени от t1 до t2, дается интегралом
Равнопеременным движением (равноускоренным или равнозамедленным) называется такое движение, при котором модуль скорости за любые равные интервалы времени изменяется (увеличивается или уменьшается) на равную величину. При равнопеременном прямолинейном движении вектор ускорения – величина постоянная.
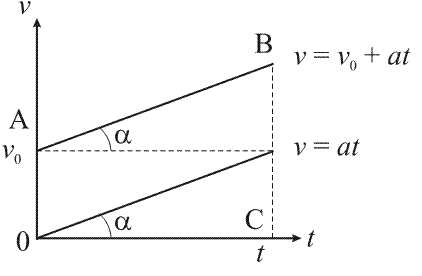
График зависимости модуля скорости равнопеременного движения от времени движения Средняя скорость равна:
 .
.
По графику скорости можно найти путь за интервал времени t. Он численно равен площади трапеции ОАВС:
, где
|OA| = v0, |BC| = v, OC = t.
Подставим эти значения и получим:
Подставим формулу модуля скорости
v = v0 ± a t. И получается:
Формула пути равнопеременного движения
Среднее и мгновенное ускорение материальной точки.
Средним ускорением неравномерного движения в интервале от t до t + ∆t называется векторная величина, равная отношению изменения скорости ∆v к интервалу времени ∆t:
Мгновенным ускорением ав момент времени t будет предел среднего ускорения:
Ускорение ∆а есть векторная величина, равная первой производной скорости по времени.
cyberpedia.su
5.2. Средняя путевая скорость и средняя скорость по перемещению.
5.2. Средняя путевая скорость и средняя скорость по перемещению.
Понятие скорости − одно из главных понятий в кинематике.
Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
Будем рассматривать материальную точку в системе координат x, y, z (рис. а).
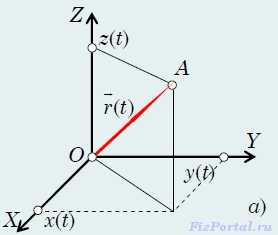
Положение A точки в момент времени t характеризуем координатами x(t), y(t), z(t), представляющими три составляющих радиуса-вектора (t). Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t) описывает кривую, называемую траекторией движущейся точки.
Траектория, описанная за промежуток времени от t до t + Δt, показана на рисунке б.
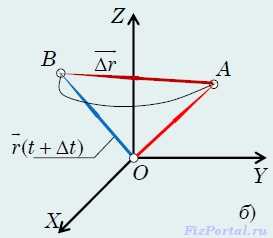
Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt)). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt.
Среднюю путевую скорость точки за данный промежуток времени определяют соотношением
Очевидно, что vп − скалярная величина; она характеризуется только числовым значением.
Показанный на рисунке б вектор
называют перемещением материальной точки за время от t до t + Δt.
Среднюю скорость по перемещению за данный промежуток времени определяют соотношением
Очевидно, что vср − векторная величина. Направление вектора vср совпадает с направлением перемещения Δr.
Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от Δt. Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
Вопрос:
Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?
Ответ:
Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы vср).
Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |vср|). Но направления перемещений (а значит, и векторов vср) и в данном случае будут различными для одинаковых Δt. Это видно на рисунке,
Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB, BC, CD. Хотя векторы перемещений 1, 2, 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.
Примечание
Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.
fizportal.ru