Модуль вектора ускорения
(1.12)
Вектор ускорения можно разложить на два вектора (рис. 1.5) .
Составляющая ускорения, характеризующая изменение мгновенной скорости по величине, называетсякасательным (тангенциальным) ускорением , совпадающимс касательной в точке траектории,а
Составляющая ускорения, направленная к центру кривизны траектории перпендикулярно и характеризующая изменение вектора скорости по направлению, называетсянормальным ускорением ,
где R-радиус кривизны траектории,
Вектор полного ускорения
, (1.12)
а его модуль (1.13)
1.2. Уравнения движения
1.2.1 Равномерно, прямолинейно движение.
В зависимости от векторов скорости
 и ускоренияразличают равномерное и ускоренное
движения.
и ускоренияразличают равномерное и ускоренное
движения. Движение называется равномерным и
прямолинейным, если точка движется по
прямой линии с постоянной скоростью  .
.
Пусть в начальный момент времени t=0координата точких
= х0,
а скорость постоянно и совпадает с направлением
движения (рис. 1.7).
постоянно и совпадает с направлением
движения (рис. 1.7).
За малый интервалdtперемещение точки
,
где – проекция
вектора скорости
Проинтегрируем левую и правую часть последнего равенства в пределах изменения переменных x и t
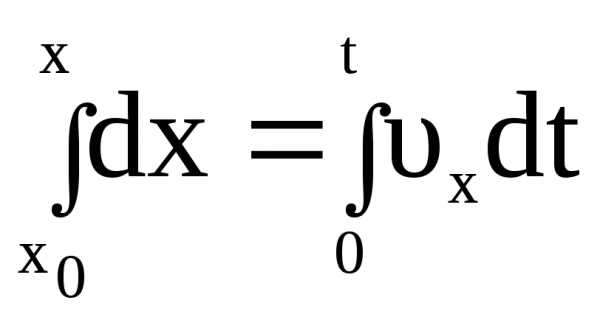 ,
,
, (1.14)
.
В случае когда вектор скорости  не
совпадает с направлением движения
не
совпадает с направлением движения
.
При прямолинейном равномерном движении пройденный точкой
.
1.2.2 Ускоренное, прямолинейное движение
Движение
по прямолинейной траектории с постоянным
ускорением  называется
равноускоренны.
называется
равноускоренны.
Пусть
в начальный момент времени координата
точкиx=х0, скорость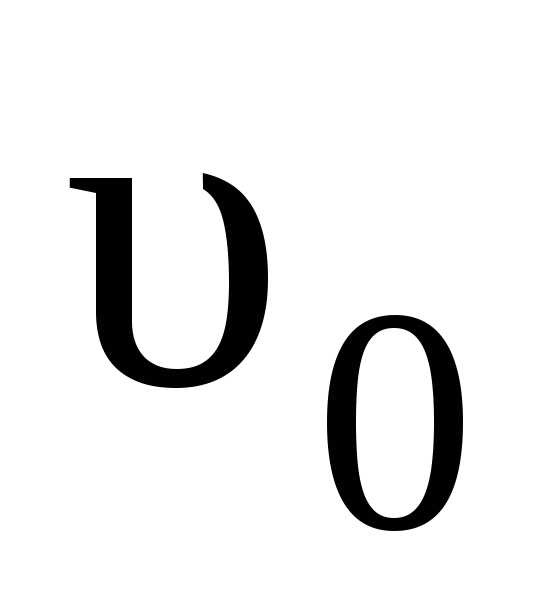 совпадает с направлением оси ОХ. За
время t пройденный точкой путь.
совпадает с направлением оси ОХ. За
время t пройденный точкой путь.
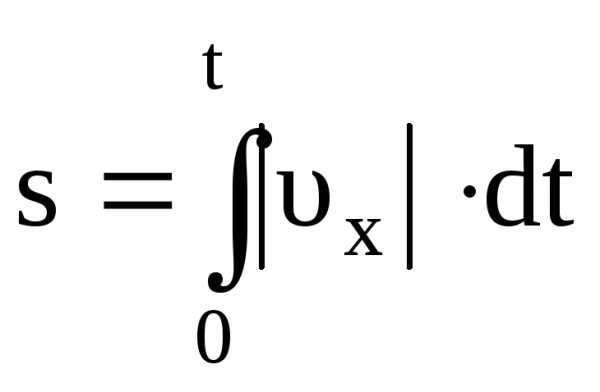 (1.15)
(1.15)
где 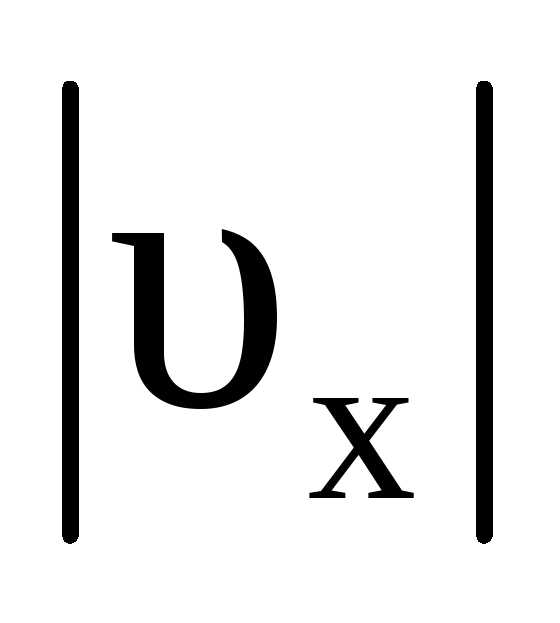 – модуль проекции вектора скорости на
ось OX находится из соотношения
– модуль проекции вектора скорости на
ось OX находится из соотношения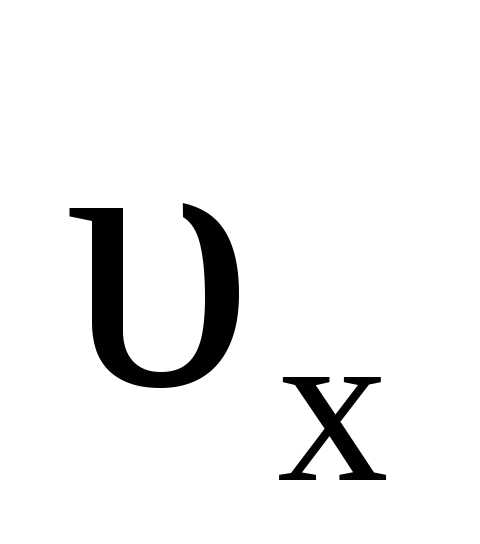 иt
иt
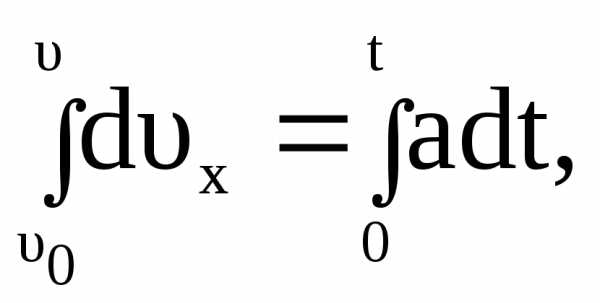

Подставим в соотношение (1.19) скорости и определи пройденный путь и координату точки
,
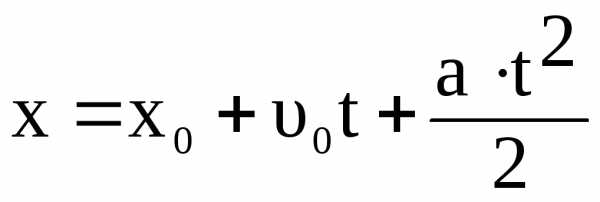 (1.16)
(1.16)
Если вектор
.
. (1.17)
где.
Лекция 2
1.2.3 Кинематика вращательного и колебательного движения Вращательное движение
Рассмотрим
движение м.т. по окружности радиусомRс постоянной линейной скоростью вокруг неподвижной осиZ(рис. 1.8).
вокруг неподвижной осиZ(рис. 1.8).
 Положение
точки определяется радиус-вектором
Положение
точки определяется радиус-вектором ,
проведенным из начала координат. За
малый интервал времени
,
проведенным из начала координат. За
малый интервал времени
 повернется на угол
повернется на угол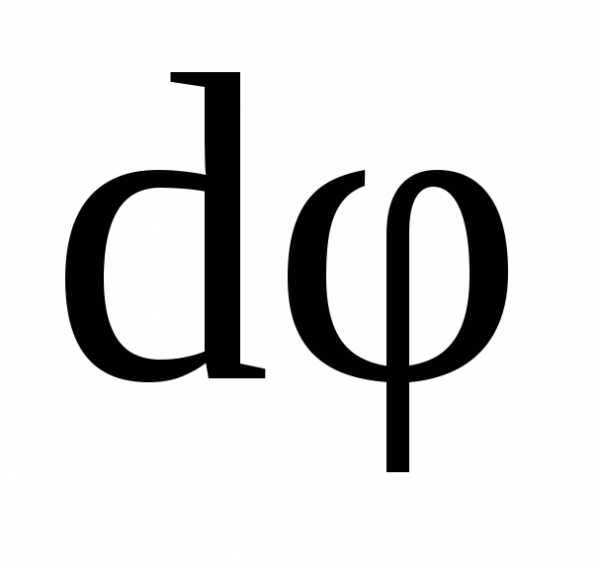 .
Направление поворота м.т. вокруг осиZзадается вектором
.
Направление поворота м.т. вокруг осиZзадается вектором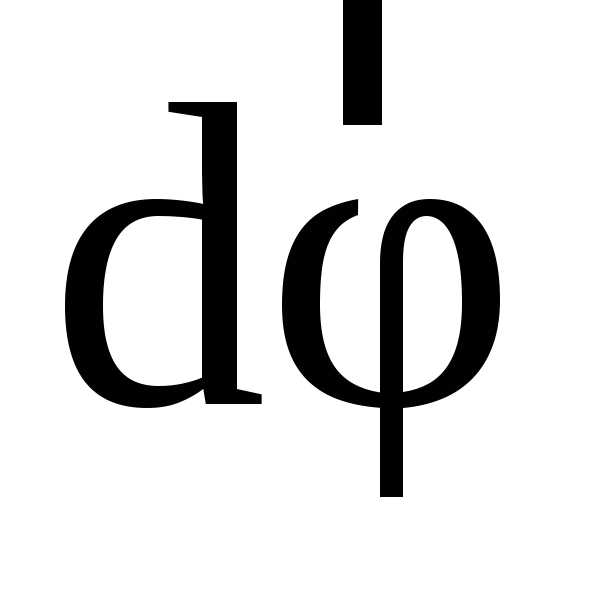 ,
который определяется правиломправого
винта: поступательное движение правого
винта и вектора
,
который определяется правиломправого
винта: поступательное движение правого
винта и вектора  совпадают, если вращение точки и винта
совершается в одинаковом направлении. Модуль вектора
совпадают, если вращение точки и винта
совершается в одинаковом направлении. Модуль вектора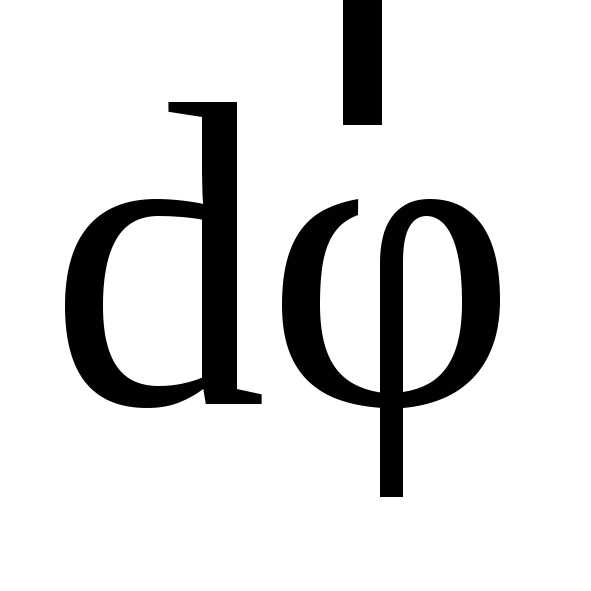
 .
Линейное перемещение вектора
.
Линейное перемещение вектора за времяdt
за времяdt(1.18)

Вектор линейной скорости
, (1.19)
где 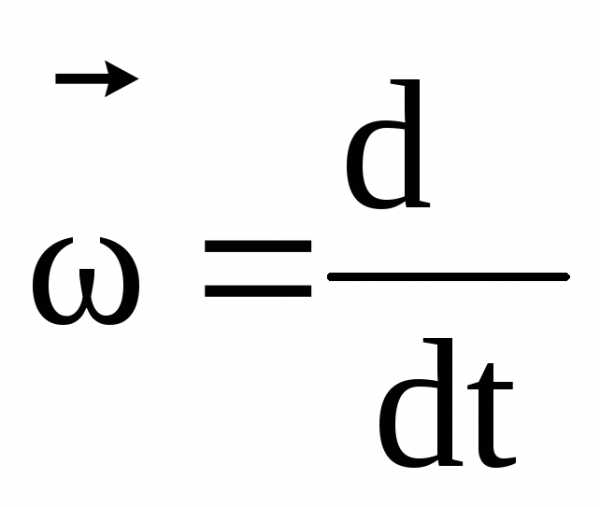 – вектор угловой скорости.
– вектор угловой скорости.
Вектор угловой скорости 
Модуль вектора линейной скорости
(1.20)
Где –
угол между векторами и
и
Вектор линейного ускорения
, (1.21)
где  – вектор углового ускорения, – вектор
касательного ускорения,
–
вектор нормального ускорения.
– вектор углового ускорения, – вектор
касательного ускорения,
–
вектор нормального ускорения.
Направление вектора углового ускорения 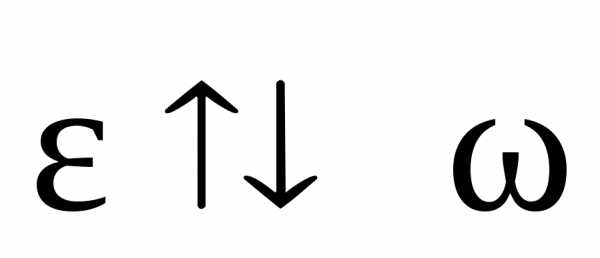 ), если она уменьшается.
), если она уменьшается.
Модули векторов ,
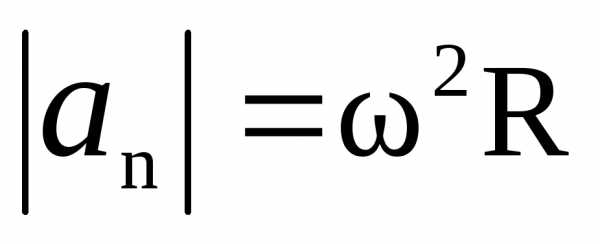 .
.
. (1.22)
Угловой путь м.т., движущейся по окружности за время dt
.
Угловой путь 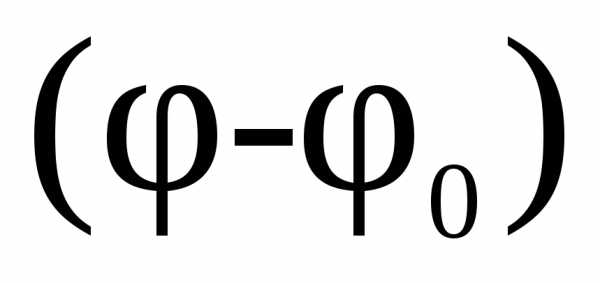 точки
за интервал времениtпри начальном угле
точки
за интервал времениtпри начальном угле
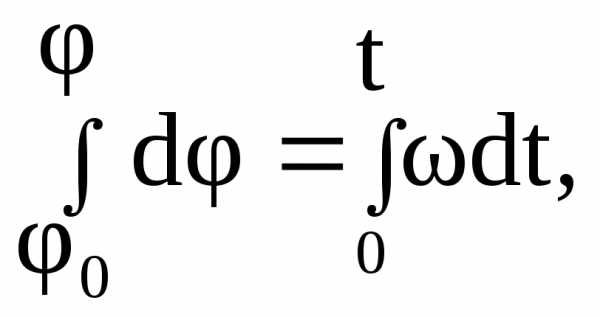
 .
.
studfiles.net
Модуль вектора ускорения
(1.12)
Вектор ускорения можно разложить на два вектора (рис. 1.5) .
Составляющая ускорения, характеризующая изменение мгновенной скорости по величине, называется
Составляющая ускорения, направленная к центру кривизны траектории перпендикулярно и характеризующая изменение вектора скорости по направлению, называетсянормальным ускорением ,
где R-радиус кривизны траектории,
Вектор полного ускорения
,(1.12)
а его модуль (1.13)
1.2. Уравнения движения
1.2.1 Равномерно, прямолинейно движение.
В зависимости от векторов скорости  и ускоренияразличают равномерное и ускоренное
движения.
и ускоренияразличают равномерное и ускоренное
движения.
Движение называется равномерным и
прямолинейным, если точка движется по
прямой линии с постоянной скоростью  .
.
Пусть в начальный момент времени t=0координата точких
= х0,
а скорость постоянно и совпадает с направлением
движения (рис. 1.7).
постоянно и совпадает с направлением
движения (рис. 1.7).
За малый интервалdtперемещение точки
,
где – проекция
вектора скорости на ось ОХ,
на ось ОХ,
Проинтегрируем левую и правую часть последнего равенства в пределах изменения переменных x и t
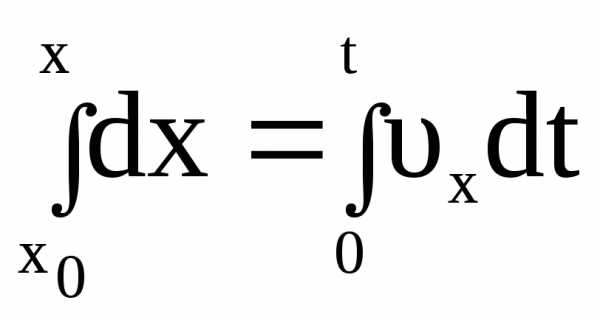 ,
,
, (1.14)
.
В случае когда вектор скорости  не
совпадает с направлением движения
не
совпадает с направлением движения
.
При прямолинейном равномерном движении пройденный точкой
.
1.2.2 Ускоренное, прямолинейное движение
Движение
по прямолинейной траектории с постоянным
ускорением ,
совпадающим со скоростью  называется
равноускоренны.
называется
равноускоренны.
Пусть
в начальный момент времени координата
точкиx=х0, скорость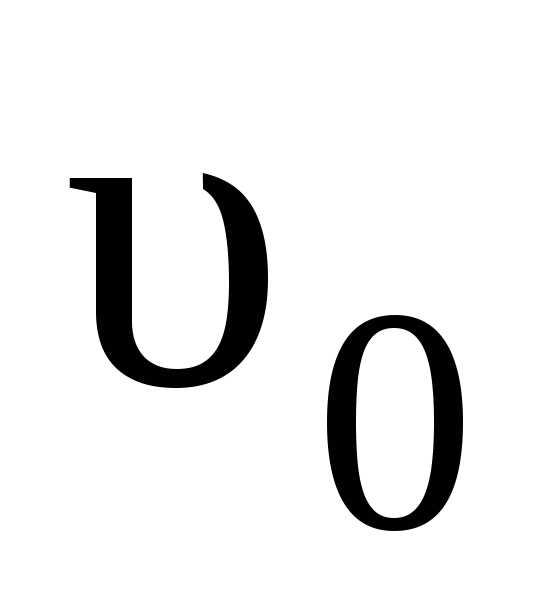 совпадает с направлением оси ОХ. За
время t пройденный точкой путь.
совпадает с направлением оси ОХ. За
время t пройденный точкой путь.
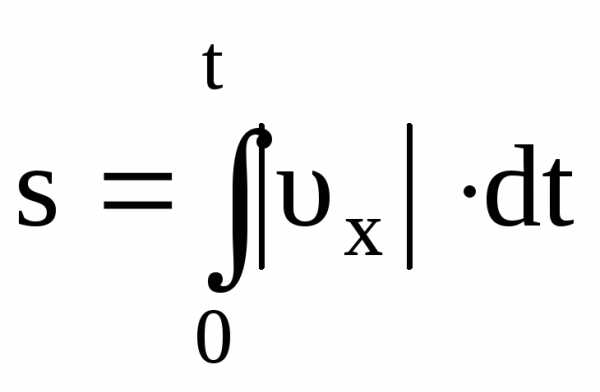 (1.15)
(1.15)
где 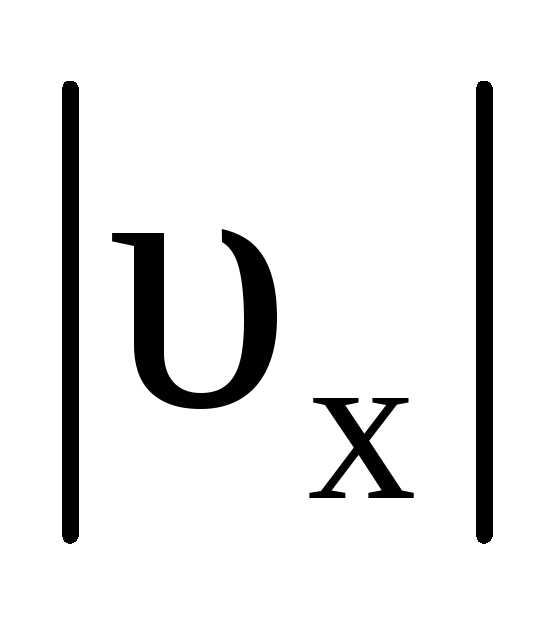 – модуль проекции вектора скорости на
ось OX находится из соотношенияинтегрированием его левой и правой
части в пределах изменения переменных
– модуль проекции вектора скорости на
ось OX находится из соотношенияинтегрированием его левой и правой
части в пределах изменения переменных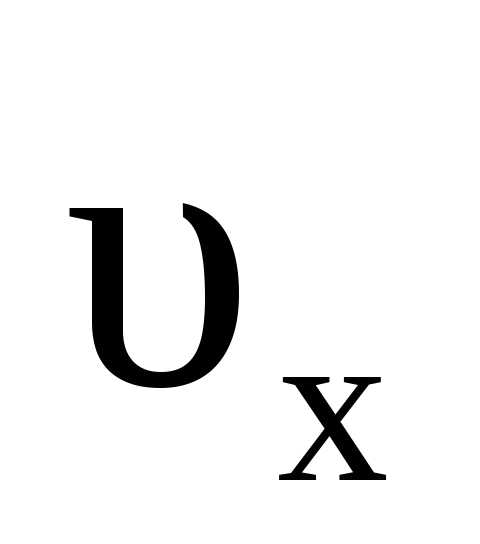 иt
иt


Подставим в соотношение (1.19) скорости и определи пройденный путь и координату точки
,
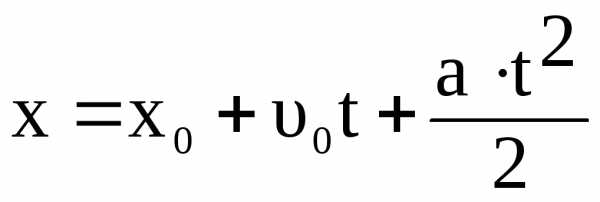 (1.16)
(1.16)
Если вектор противоположен скорости, то движение будетbи путь равнозамедленный то проекция скорости,координата точки пройденной точкой определяются из соотношений:
.
. (1.17)
где.
Лекция 2
1.2.3 Кинематика вращательного и колебательного движения Вращательное движение
Рассмотрим
движение м.т. по окружности радиусомRс постоянной линейной скоростью вокруг неподвижной осиZ(рис. 1.8).
вокруг неподвижной осиZ(рис. 1.8).
 Положение
точки определяется радиус-вектором
Положение
точки определяется радиус-вектором ,
проведенным из начала координат. За
малый интервал времени
,
проведенным из начала координат. За
малый интервал времени радиус-вектор
радиус-вектор повернется на угол
повернется на угол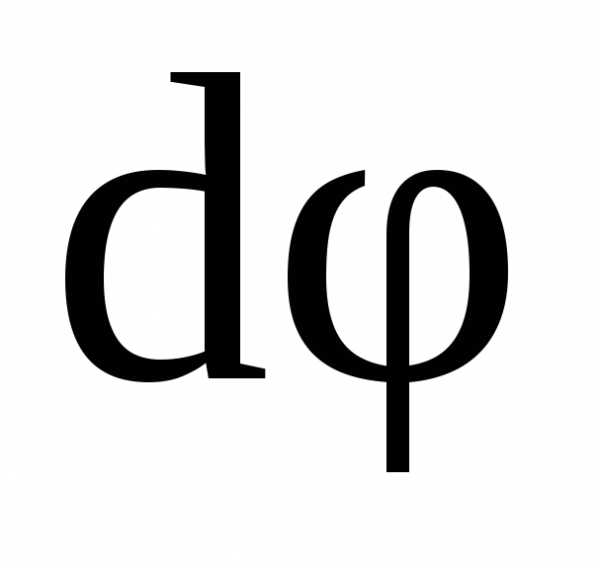 .
Направление поворота м.т. вокруг осиZзадается вектором
.
Направление поворота м.т. вокруг осиZзадается вектором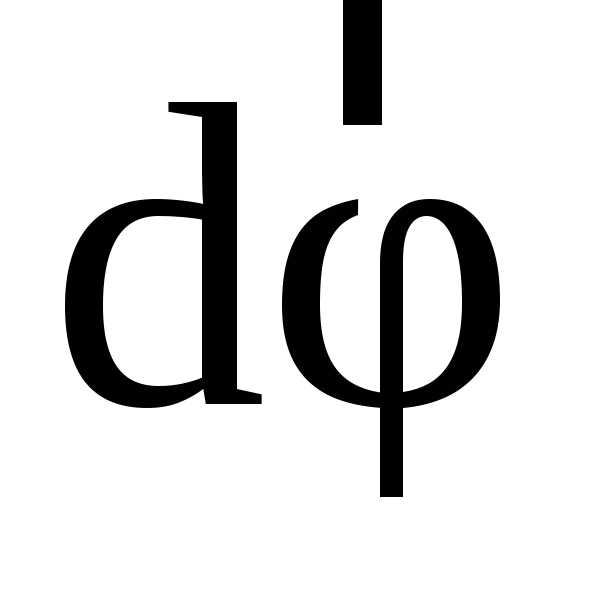 ,
который определяется правиломправого
винта: поступательное движение правого
винта и вектора
,
который определяется правиломправого
винта: поступательное движение правого
винта и вектора 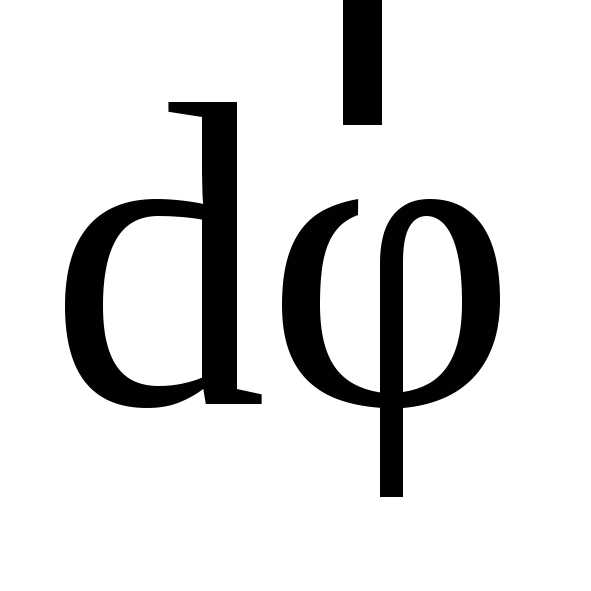 совпадают, если вращение точки и винта
совершается в одинаковом направлении. Модуль вектора
совпадают, если вращение точки и винта
совершается в одинаковом направлении. Модуль вектора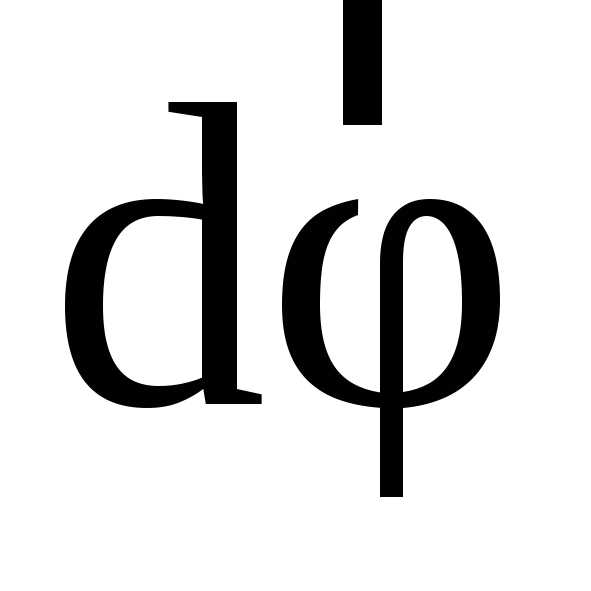 равен углу поворота за интервал времени
равен углу поворота за интервал времени .
Линейное перемещение вектора
.
Линейное перемещение вектора за времяdt
за времяdt
(1.18)
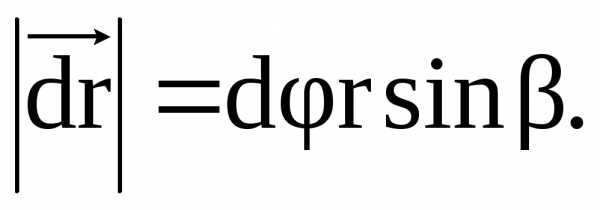
Вектор линейной скорости
, (1.19)
где 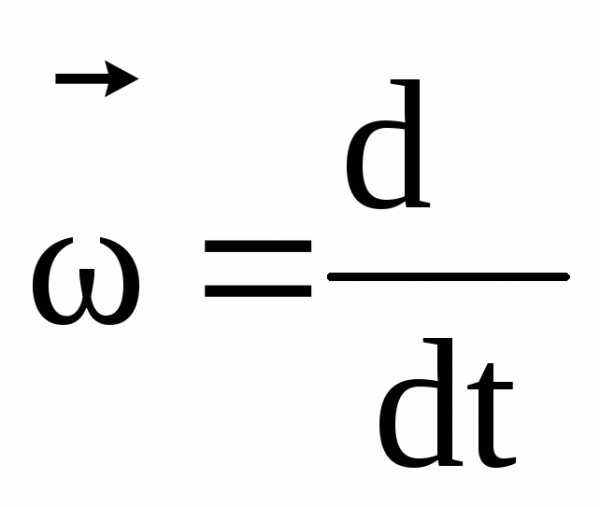 – вектор угловой скорости.
– вектор угловой скорости.
Вектор угловой скорости  совпадает с направлением вектора.
совпадает с направлением вектора.
Модуль вектора линейной скорости
(1.20)
Где –
угол между векторами и
и
Вектор линейного ускорения
, (1.21)
где  – вектор углового ускорения, – вектор
касательного ускорения,
–
вектор нормального ускорения.
– вектор углового ускорения, – вектор
касательного ускорения,
–
вектор нормального ускорения.
Направление вектора углового ускорения совпадает с направлением вектора
, если угловая скорость возрастает,
и противоположно(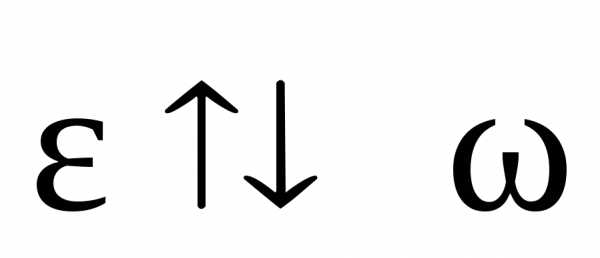 ), если она уменьшается.
), если она уменьшается.
Модули векторов ,
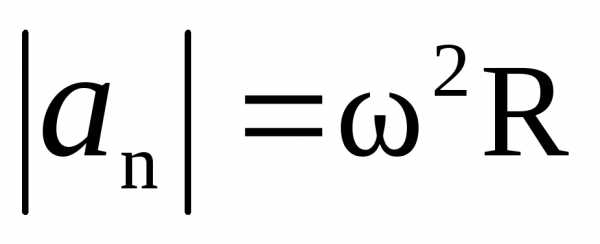 .
.
. (1.22)
Угловой путь м.т., движущейся по окружности за время dt
.
Угловой путь 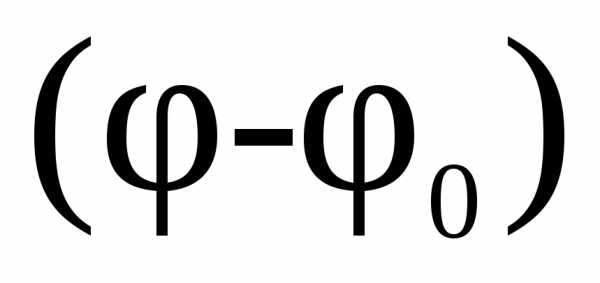 точки
за интервал времениtпри начальном угле
точки
за интервал времениtпри начальном угле
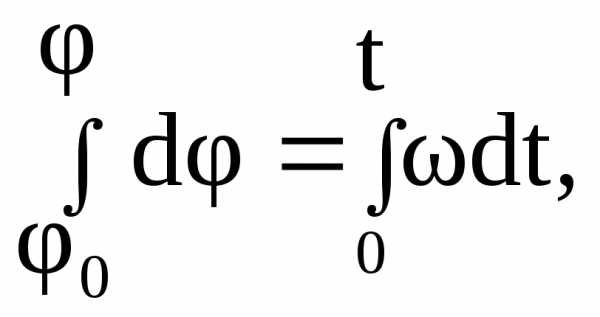
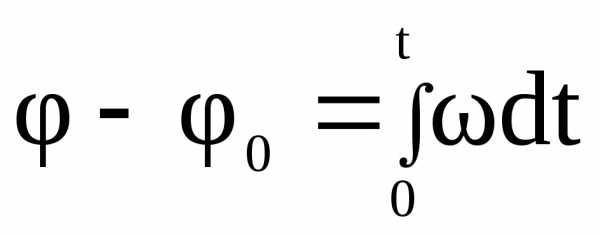 .
.
studfiles.net
Вектор скорости, модуль вектора скорости, вектор ускорения, модуль вектора ускорения.
Вектор скорости, модуль вектора скорости, вектор ускорения, модуль вектора ускорения.Кинематика точки
Вектор скорости, модуль вектора скорости, вектор ускорения, модуль вектора ускорения.
– проекция вектора скорости на координатную ось X может быть найдена как производная координаты x по времени t;
– выражение модуля скорости через проекции вектора скорости на координатные оси;
– вектор скорости по определению – это производная радиус-вектора по времени;
– выражение модуля радиус-вектора материальной точки через ее координаты;
– выражение модуля ускорения через проекции вектора ускорения на координатные оси;
– проекция вектора ускорения на координатную ось X может быть найдена как производная проекции скорости на эту ось по времени t.
1.1. Материальная точка движется вдоль координатной оси X по закону . Вычислите проекцию скорости материальной точки на ось X для момента t = 1 с.
1.2. Материальная точка движется со скоростью . Вычислите модуль скорости материальной точки для момента времени t = 2,67 с.
1.3. Радиус-вектор материальной точки зависит от времени по закону . Найдите зависимости вектора и модуля вектора скорости от времени.
1.5. Закон движения материальной точки дан уравнениями
Вычислите величину скорости материальной точки в позиции x = y = 0.
1.6. Закон движения материальной точки дан уравнениями
Здесь b, c и k положительные постоянные. Найдите величину скорости материальной точки как функцию времени.
1.8. Координаты x и y материальной точки зависят от времени по законам
x = A×cos wt
y = B×sin wt,
где A, B, w – постоянные величины. Найдите величину скорости материальной точки в момент wt = p/4.
1.11. Материальная точка движется вдоль координатной оси X по закону . Через сколько t времени после момента t = 0 с вектор ускорения материальной точки изменит направление на противоположное?
1.12. Координаты x и y материальной точки зависят от времени по законам
где R, w – положительные постоянные величины. Найдите величину ускорения материальной точки.
1.13. Материальная точка движется со скоростью . Вычислите модуль ускорения материальной точки.
Тангенциальное ускорение.
– тангенциальное (касательное) ускорение – это производная от модуля скорости по времени. Оно показывает, как быстро изменяется величина (модуль) скорости со временем. Для нахождения тангенциального ускорения сначала находим модуль скорости как функцию времени и затем дифференцируем эту функцию по времени.
1.36. Для экономии места, въезд на один из высочайших в Японии мостов устроен в виде винтовой линии, обвивающей цилиндр радиуса R. Полотно дороги составляет угол α с горизонтальной плоскостью. Найдите тангенциальное ускорение автомобиля, движущегося с постоянной по модулю скоростью.
1.37. Точка движется в плоскости так, что проекции ее скорости на оси прямоугольной системы координат равны . Вычислите величину тангенциального ускорения точки, соответствующую моменту времени t = 1/p с после старта.
1.39. Небольшое тело бросили горизонтально со скоростью = 3 м/с в поле сил тяжести (g = 10 м/с2). Вычислите величину тангенциального ускорения тела, соответствующую моменту времени t = 0,4 с после старта.
1.40. Закон движения материальной точки дан уравнениями
Здесь b, c и k положительные постоянные. Найдите зависимость величины тангенциального ускорения от времени.
Нормальное ускорение.
Вектору скорости (как и другим векторам) присущи два атрибута (неотъемлемых свойства): модуль (длина) и направление в пространстве. Производная вектора скорости по времени показывающая, как быстро изменяется вектор скорости со временем, может быть представлена в виде суммы двух слагаемых. Одно из этих слагаемых показывает, как быстро изменяется величина скорости – это тангенциальное (касательное) ускорение. Другое слагаемое характеризует быстроту изменения направления скорости – это нормальное (перпендикулярное к касательной, проходящей через точку касания к траектории) ускорение. В средней школе это ускорение называют центростремительным. Таким образом, имеем . Учитывая взаимную перпендикулярность векторов тангенциального и нормального ускорений, в соответствии с теоремой Пифагора, получаем полезную формулу .
1.46. Точка движется в плоскости так, что проекции ее скорости на оси прямоугольной системы координат равны , . Вычислите величину нормального ускорения, соответствующего времени t = 0,5 с.
1.47. Закон движения материальной точки задан уравнениями , , . Вычислите величину нормального ускорения, соответствующего времени t = 1 с.
1.48. Небольшое тело бросили горизонтально со скоростью = 3 м/с в поле сил тяжести (g = 10 м/с2). Вычислите величину нормального ускорения тела, соответствующего времени t = 0,4 с после старта.
Радиус кривизны траектории.
Можно показать, что нормальное ускорение, характеризующее быстроту изменения направления скорости, связано с величиной скорости формулой . Здесь ρ – радиус кривизны траектории. Отсюда получаем . Именно такой формулой будем пользоваться для нахождения радиуса кривизны траектории в этом разделе.
1.54. Небольшое тело бросили горизонтально со скоростью = 5 м/с в однородном поле сил тяжести (g = 10 м/с2). Вычислите радиус кривизны траектории в непосредственной близости от старта.
1.56. Точка движется в плоскости так, что проекции ее скорости на оси прямоугольной системы координат равны , . Вычислите радиус кривизны траектории.
1.57. Закон движения материальной точки задан уравнениями , , . Вычислите радиус кривизны траектории.
Задачи для семинара. В скобках домашнее задание 1.3 (1.1, 1.2), 1.8 (1.5, 1.6), 1.12 (1.11, 1.13), 1.40 (1.36, 1.37, 1.39), 1.47 (1.46, 1.48), 1.57 (1.54, 1.56)
Дата добавления: 2015-11-05; просмотров: 112 | Нарушение авторских прав
mybiblioteka.su – 2015-2018 год. (0.008 сек.)
mybiblioteka.su
