Расчёт моментов инерции некоторых тел
Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массыdm = dV. Тогда момент инерции тела относительно оси равен интегралу по объёму тела:
(1)
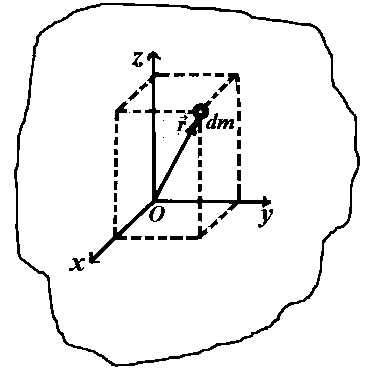
Рис. 1
где r– расстояние элементаdmдо оси.Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его
(2)
где r– расстояние элементаdmдо выбранной точки (относительно которой
вычисляется).
Пусть эта точка является началом системы
координатX, Y, Z(рис. 1). Квадраты
расстояний элементаdmдо координатных осейX, Y, Z и до начала координат равны
соответственноy2+z2, z2+x2, x
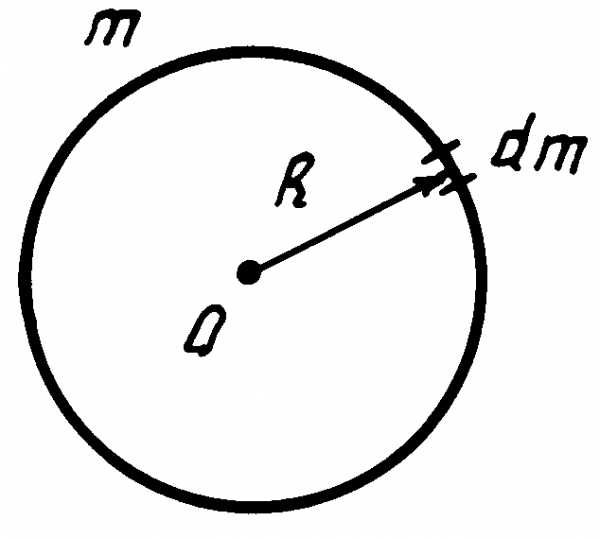
Рис. 2
Из этих соотношений следует, что
(3)
Таким образом, сумма моментов инерции тела относительно трёх любых взаимно перпендикулярных осей , проходящих через одну точку, равна удвоенному моменту инерции тела относительно этой точки.
Момент инерции тонкого кольца.Все элементы кольцаdm(рис. 2) находятся на одинаковом расстоянии, равном радиусу кольцаR,от его оси симметрии (осьY) и от его центра. Момент инерции кольца относительно осиY
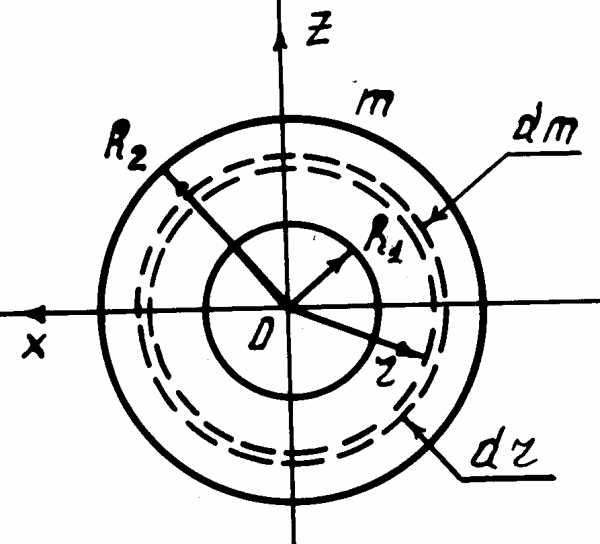
Рис. 3
(4) Момент инерции
тонкого диска.Пусть тонкий
однородный диск массыmс концентрическим отверстием (рис. 3)
имеет внутренний и внешний радиусыR1иR
(5)
Момент инерции диска:
(6)
В частности, полагая в (6) R1 = 0, R2 = R,получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси:
(7)
Момент инерции диска относительно его оси симметрии не зависит от толщины диска
Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = Jy,а моменты инерции относительно осейXиZравны между собой,Jx = Jz. Поэтому, в соответствии с (3): 2Jx +Jy = 2Jy, Jx = Jy/2,или
(8)
Рис. 4
Момент инерции цилиндра.Пусть имеется полый симметричный цилиндр массыm, длины h, внутренний и внешний радиусы которого равныR1 и R2. Найдём его момент инерции относительно осиZ, проведенной через центр масс перпендикулярно оси цилиндра (рис. 4). Для этого мысленно разобьём его на диски бесконечно малой толщиныdy. Один из таких дисков, массойdm = mdy/h, расположенный на расстоянииyот начала координат, показан на рис. 4. Его момент инерции относительно осиZ, в соответствии с (8) и теоремой Гюйгенса – Штейнера(9)
Момент инерции всего цилиндра
(10)
Момент инерции цилиндра относительно оси Z(оси вращения маятника) найдём по теореме Гюйгенса – Штейнера
где d– расстояние от центра масс цилиндра до осиZ. В работе 16 этот момент инерции обозначен какJц
(11)
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Нанесение экспериментальных точек и проведение по ним графика «на глаз», а также определение по графику абсцисс и ординат точек, не отличаются высокой точностью. Её можно повысить, если использовать аналитический метод. Математическое правило построения графика заключается в подборе таких значений параметров «а» и «в» в линейной зависимости вида

Рис. 5
(1)
имела минимум. Здесь x
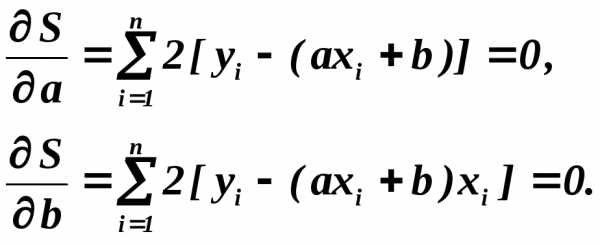
 (2)
(2)
Отсюда наилучшие значения параметров «а» и «b» равны:
(3)
где средние
значения
,
Введем обозначения
и (4)
Абсолютные случайные погрешности асл и bсл определяются по формулам:
и (5)
где tp,n-2 коэффициент Стьюдента для доверительной вероятности P и (n-2) измерений. При P = 0,95 и n 12-15 коэффициент tp,n-2 = 2,25, а при
16
studfiles.net
Моменти инерции некоторых простых сечений
Момент инерции прямоугольного пересечения
Розмеры прямоугольного сечения – b*h
Осевые моменты инерции
$$J_x = {b*h^3\over 12} $$
$$J_y = {h*b^3\over 12} $$
Полярный момент инерции прямоугольного сечения
$$J_p = {b*h\over 12}*(h^2-b^2) $$
Квадратное сечение

a – сторона квадрата.
Осевые моменты инерции
$$J_x = J_y = {a^4\over 12}$$
Полярный момент инерции квадрата
$$J_p = 2J_x = {a^4\over 6}$$
Момент инерции круга
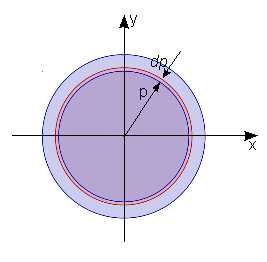
Запишем
$$J_{p}= 2\,\pi \,\int_{0}^{p}{p}^{3}dp$$
Интегрируем выражение и получаем
$$J_p= \frac{\pi \,{p}^{4}}{2}$$
Полярный момент инерции круга
$$J_p=J_x+J_y=2I_x$$
Осевые моменты инерции круга
Момент инерции кругового кольца.

Круговое кольцо с внутренним диаметром d и внешним D
Момент инерции полукруга
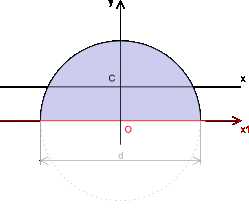
Диаметр полукруга d .
Моменты инерции полукруга относительно осей y и x1 будут равными между собою и в два раза меньшими, нежели осевой центральный момент инерции круга.
$$J_y = J_{x_1} = {\pi d^4\over 128}$$
Площадь полукруга
$$A={\pi*d^2\over 8}$$
Статический момент полукруга относительно оси x1:
$$S_{x_1} = {d^3\over 12}$$
Находим момент инерции полукруга относительно оси x:
$$J_x = \frac{\left( 9\,{\pi }^{2}-64\right) \,{d}^{4}}{1152\,\pi } \approx 0.00686d^4$$
Момент инерции треугольника
вычислим моменты инерции для треугольника относительно центральной оси.
Центр тяжести треугольника: [math]y_o=\frac{1}{3}h[/math].
С выражения dA=b(y)*dy, а также с подобия
треугольников (2/3*h-y)/h=b(y)/b
можем получить
$$dA=\left( \frac{2\,b}{3}-\frac{b\,y}{h}\right)*dy $$
тогда
$$J_x= \int_{\frac{h}{3}}^{\frac{2\,h}{3}}{y}^{2}\,\left( \frac{2\,b}{3}-\frac{b\,y}{h}\right) dy$$
Интегрируем выражение и получаем: $$J_x=\frac{b\,{h}^{3}}{36}$$
Для равнобедренного треугольника [math]J_y=\frac{hb^3}{48}[/math]
Момент инерции двутавра и профилей
Дополнительная информация
В приложенном файле – геометрические характеристики других сечений (из справочника по сопротивлению материалов /Фесик С.П. – 1982)
Связанные статьи
sopromat.in.ua
4.3. Моменты инерции простых фигур
Как уже отмечалось выше, к числу простых плоских фигур относятся три фигуры: прямоугольник, треугольник и круг. Простыми эти фигуры считаются потому, что положение центра тяжести этих фигур заранее известно. Все остальные фигуры могут быть составлены из этих простых фигур и считаются сложными. Вычислим осевые моменты инерции простых фигур относительно их центральных осей.
1. Прямоугольник.Рассмотрим сечение
прямоугольного профиля размерами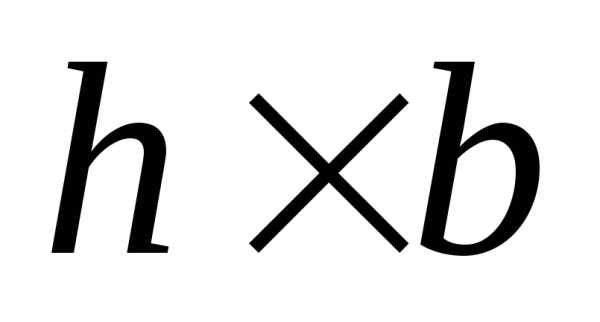 (Рис.4.6). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии
(Рис.4.6). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии от
центральной оси
от
центральной оси .
.
Рис.4.6
Вычислим момент инерции прямоугольного сечения относительно оси :
. (4.10)
Момент
инерции прямоугольного сечения
относительно оси 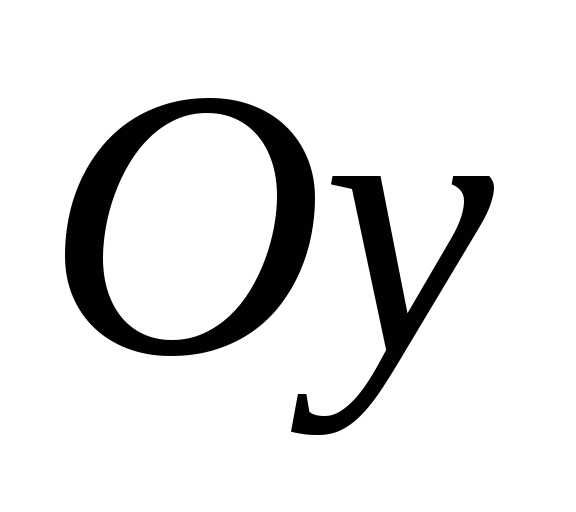 найдем аналогично. Здесь вывод не
приводится.
найдем аналогично. Здесь вывод не
приводится.
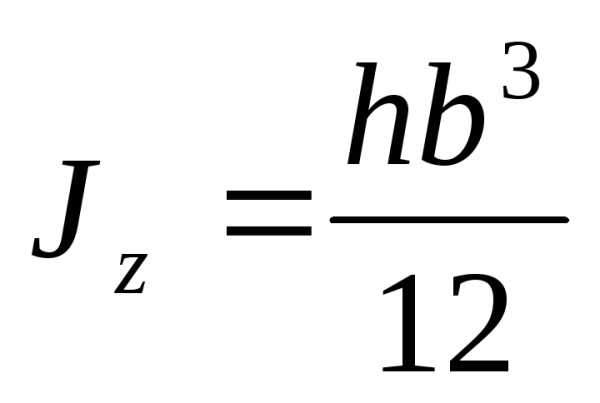 .
(4.11)
.
(4.11)
Центробежный
момент инерции относительно осей  и
и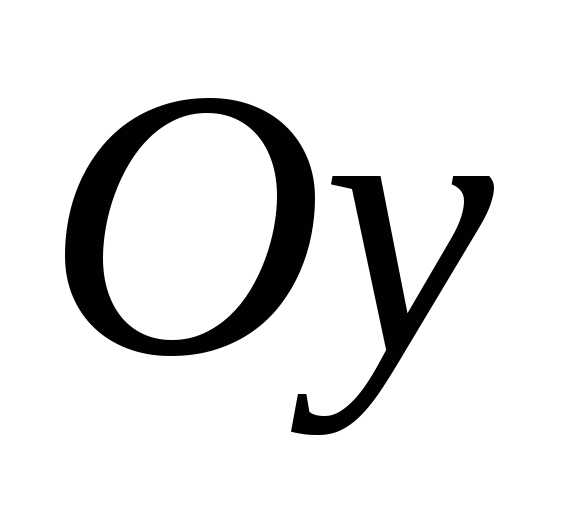 равен нулю, так как оси
равен нулю, так как оси и
и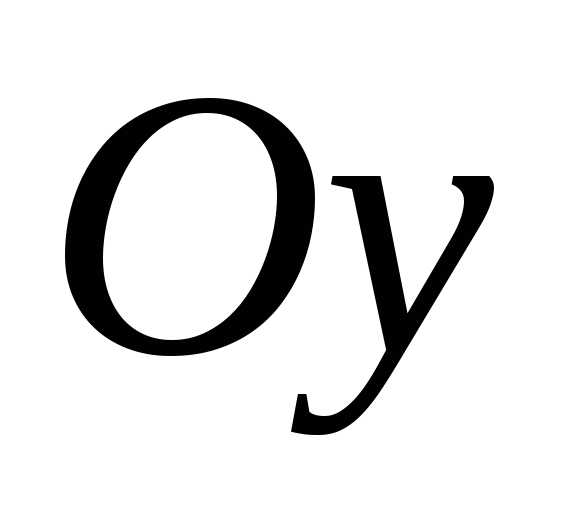 являются осями симметрии, а, следовательно,
главными осями.
являются осями симметрии, а, следовательно,
главными осями.
2. Равнобедренный треугольник.Рассмотрим сечение треугольного профиля
размерами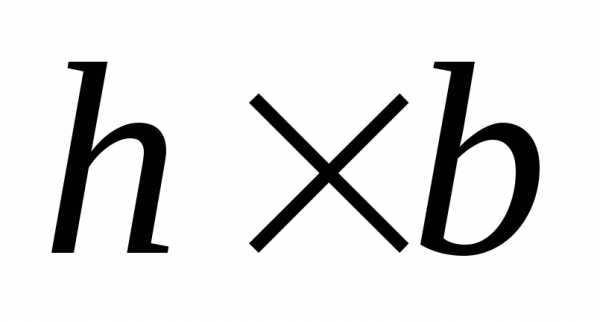 (Рис.4.7). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии
(Рис.4.7). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянии от центральной оси
от центральной оси .
Центр тяжести треугольника находится
на расстояни
.
Центр тяжести треугольника находится
на расстояни от основания. Треугольник принимается
равнобедренным, так что ось
от основания. Треугольник принимается
равнобедренным, так что ось сечения является осью симметрии.
сечения является осью симметрии.
Рис.4.7
Вычислим
момент инерции сечения относительно
оси  :
:
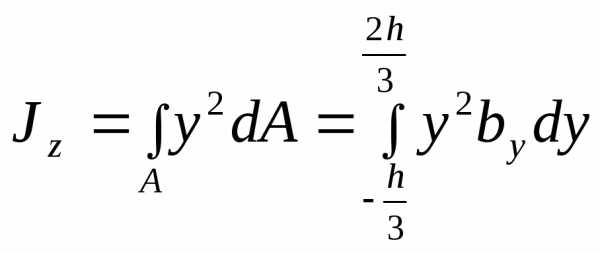 .
(4.12)
.
(4.12)
Величину 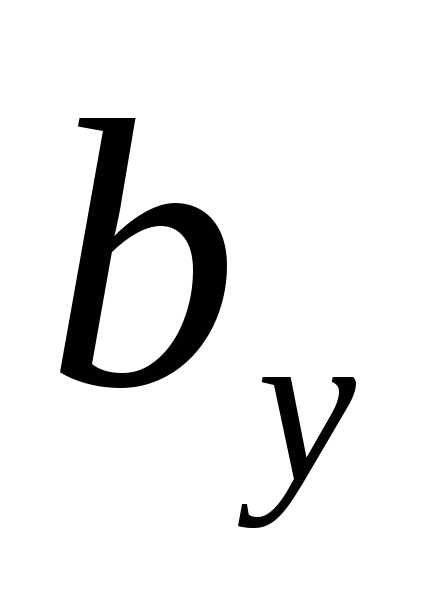 определим из подобия треугольников:
определим из подобия треугольников:
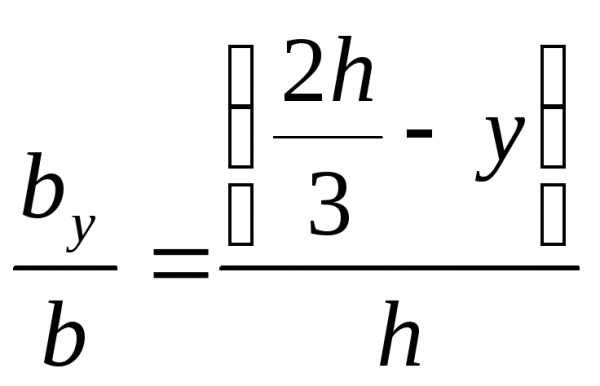 ;
откуда
;
откуда 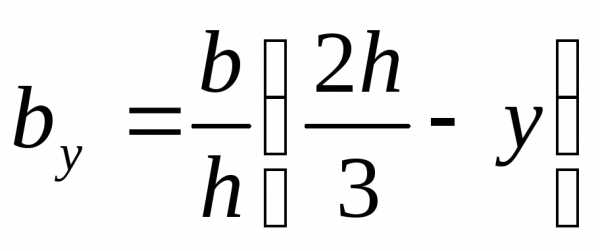 .
.
Подставляя
выражения для 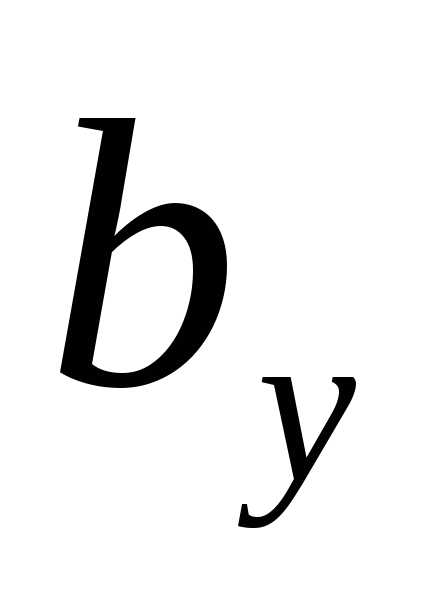 в (4.12) и интегрируя, получим:
в (4.12) и интегрируя, получим:
. (4.13)
Момент
инерции для равнобедренного треугольника
относительно оси  находится аналогичным образом и равен:
находится аналогичным образом и равен:
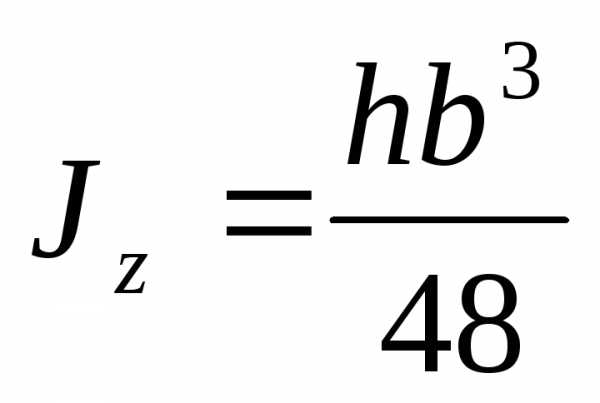 (4.14)
(4.14)
Центробежный
момент инерции относительно осей  и
и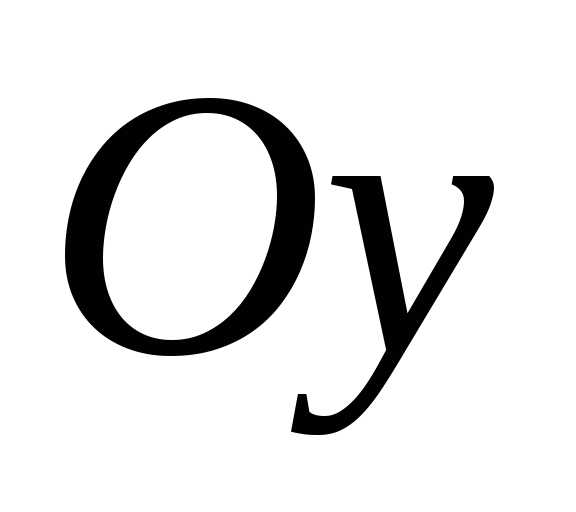 равен нулю, так как ось
равен нулю, так как ось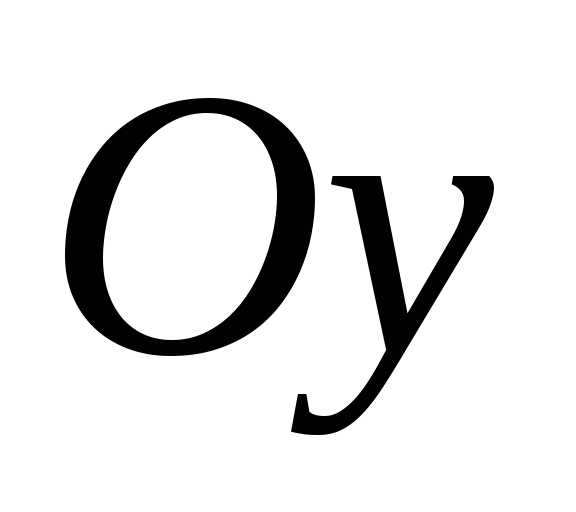 является осью симметрии сечения.
является осью симметрии сечения.
3. Круг. Рассмотрим сечение круглого
профиля диаметром (Рис.4.8).
Выделим элемент сечения двумя бесконечно
близко расположенными концентрическими
окружностями, расположенными на
расстоянии
(Рис.4.8).
Выделим элемент сечения двумя бесконечно
близко расположенными концентрическими
окружностями, расположенными на
расстоянии от центра тяжести круга
от центра тяжести круга .
.
Рис.4.8
Вычислим полярный момент инерции круга, воспользовавшись выражением (4.5):
. (4.15)
Используя условие инвариантности для
суммы осевых моментов инерции относительно
двух взаимно перпендикулярных осей
(4.6) и учитывая, что для круга в силу
симметрии  ,
определяем величину осевых моментов
инерции:
,
определяем величину осевых моментов
инерции:
. (4.16)
Откуда:
. (4.17)
Центробежный
момент инерции относительно осей  иравен нулю, так как оси
иравен нулю, так как оси и
и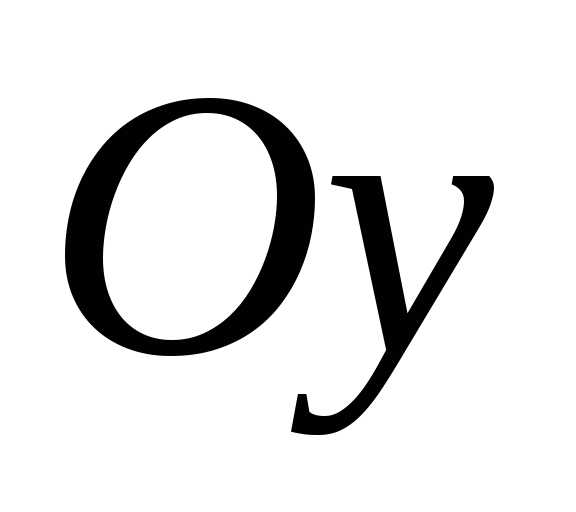 являются осями симметрии сечения.
являются осями симметрии сечения.
4.4. Зависимости между моментами инерции относительно параллельных осей
При вычислении моментов инерции для сложных фигур следует запомнить одно правило: значения для моментов инерции можно складывать, если они вычислены относительно одной и той же оси. Для сложных фигур чаще всего центры тяжести отдельных простых фигур и всей фигуры не совпадают. Не совпадают, соответственно, и центральные оси для отдельных простых фигур и всей фигуры. В связи с этим существуют приемы приведения моментов инерции к одной оси, например, центральной оси всей фигуры. Это может быть связано с параллельным переносом осей инерции и дополнительными вычислениями.
Рассмотрим определение моментов инерции относительно параллельных осей инерции, изображенных на рис.4.9.
Рис.4.9
Пусть
осевые и центробежный моменты инерции
изображенной на рис.4.9. фигуры относительно
произвольно выбранных осей  ис началом координат в точке
ис началом координат в точке известны. Требуется вычислить осевые
и центробежный моменты инерции фигуры
относительно произвольных параллельных
осей
известны. Требуется вычислить осевые
и центробежный моменты инерции фигуры
относительно произвольных параллельных
осей и
и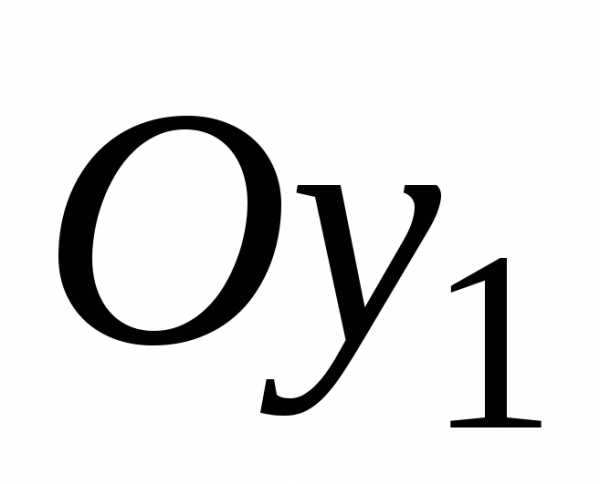 с началом координат в точке
с началом координат в точке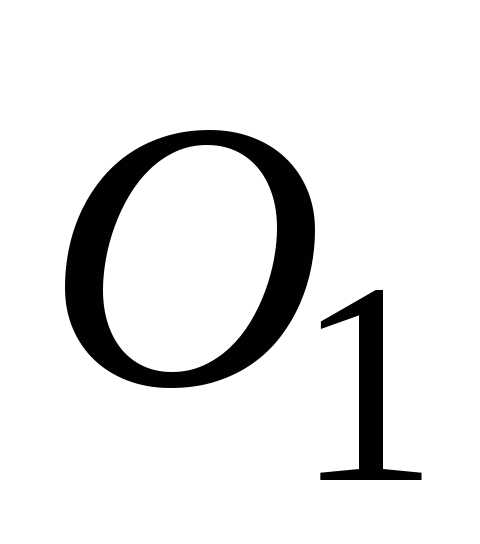 .
Оси
.
Оси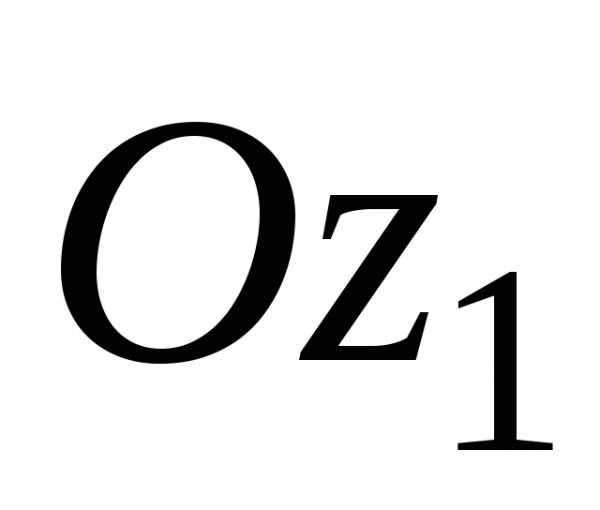 и
и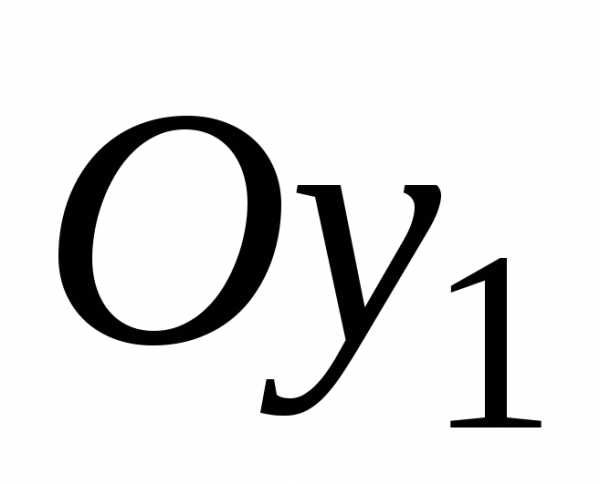 проведены на расстояниях
проведены на расстояниях и
и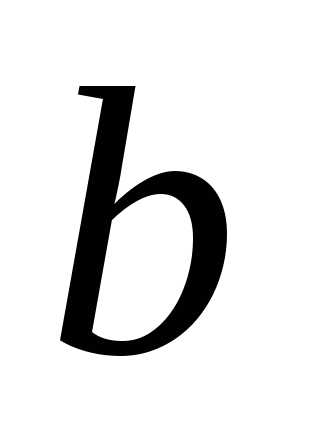 соответственно от осей
соответственно от осей и
и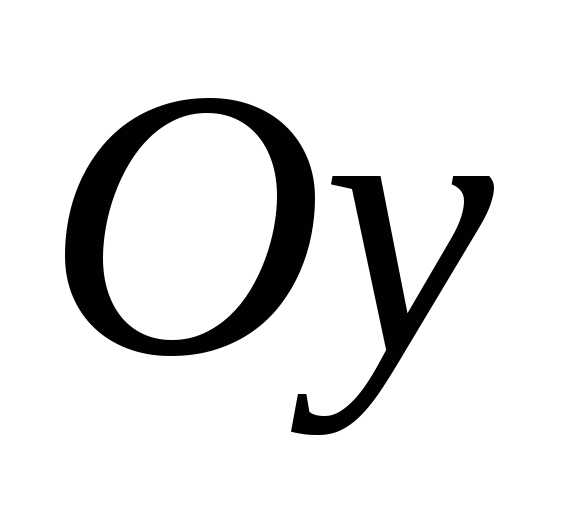 .
.
Воспользуемся
выражениями для осевых моментов инерции
(4.4) и для центробежного момента инерции
(4.7). Подставим в эти выражения вместо
текущих координат  и
и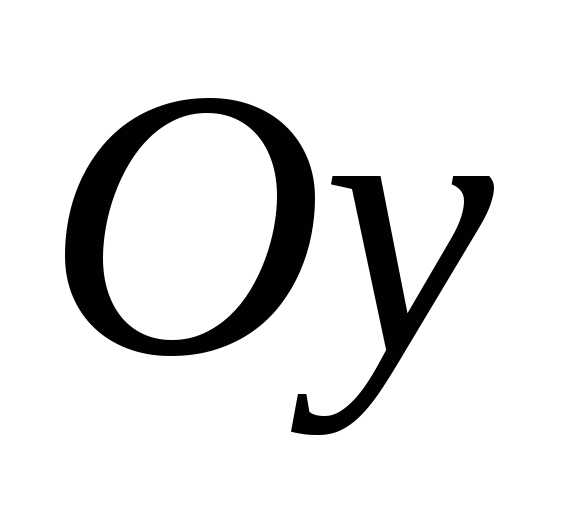 элемента с бесконечно малой площадью
координаты
элемента с бесконечно малой площадью
координаты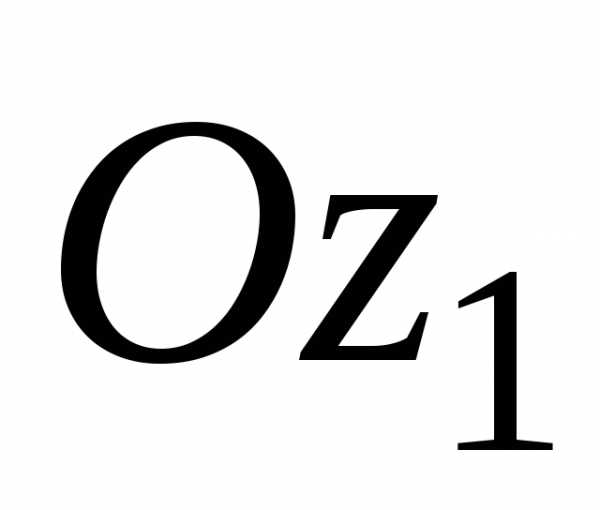 и
и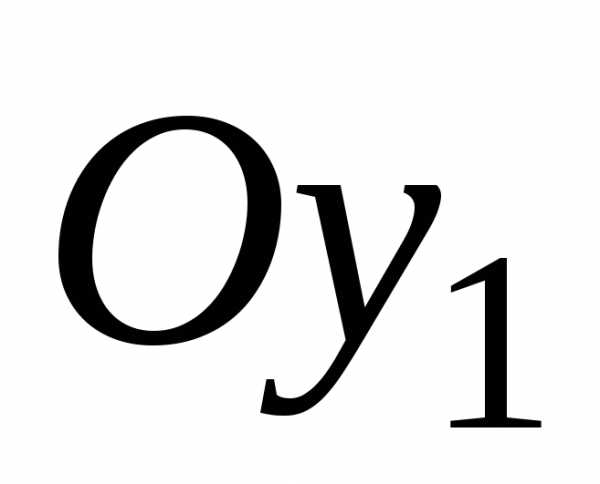 в новой системе координат. Получим:
в новой системе координат. Получим:
. (4.18)
. (4.19)
.
(4.20)
Анализируя полученные выражения, приходим к выводу, что при вычислении моментов инерции относительно параллельных осей к моментам инерции, вычисленных относительно исходных осей инерции, следует призводить добавки в виде дополнительных членов, которые могут оказаться намного больше значений для моментов инерции относительно исходных осей. Поэтому пренебрегать этими дополнительными членами ни в коем случае нельзя.
Рассмотренный случай представляет собой самый общий случай параллельного переноса осей, когда в качестве исходных были взяты произвольные оси инерции. В большинстве расчетов встречаются частные случаи определения моментов инерции.
Первый частный случай. Исходные оси являются центральными осями инерции фигуры. Тогда, используя основное свойство для статического момента площади, можно исключить из уравнений (4.18)(4.20) члены уравнений, в которые входит статический момент площади фигуры. В результате получим:
. (4.21)
. (4.22)
. (4.23)
Здесь оси 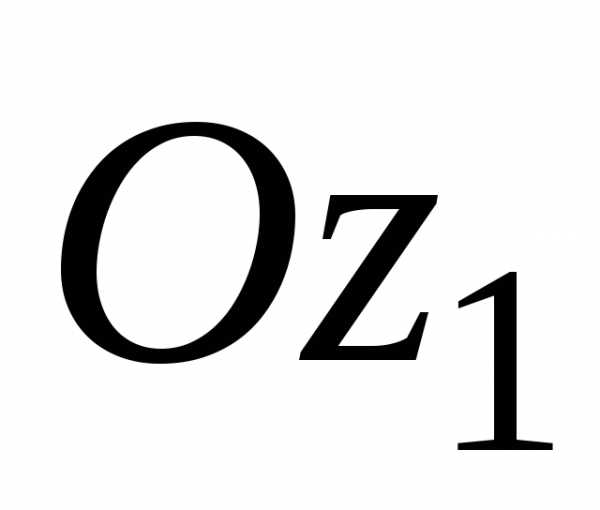 и
и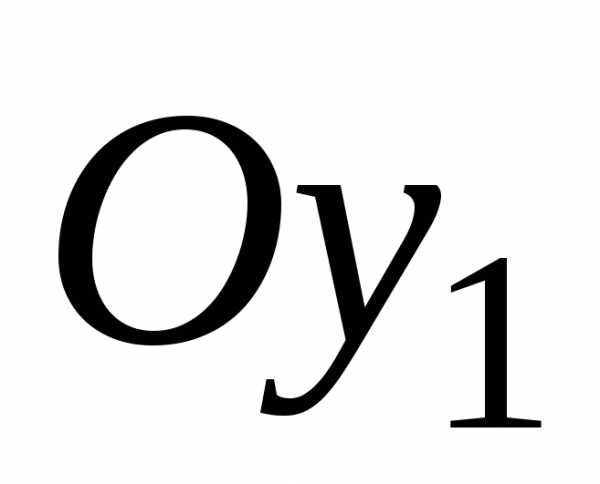 центральные оси
инерции.
центральные оси
инерции.
Второй частный случай. Исходные оси являются главными осями инерции. Тогда, учитывая, что относительно главных осей инерции центробежный момент инерции равен нулю, получим:
. (4.24)
. (4.25)
. (4.26)
Здесь оси 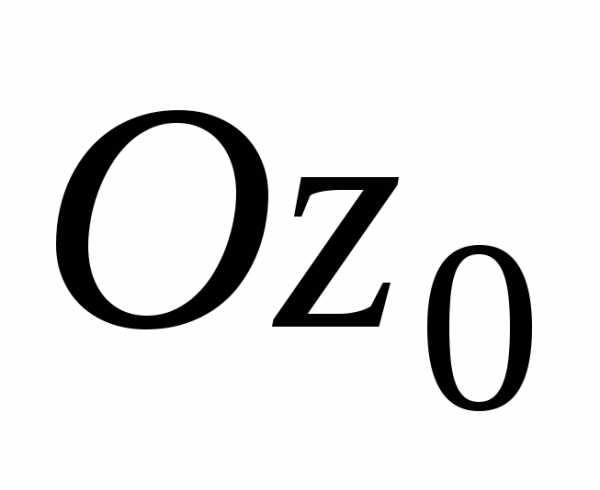 и
и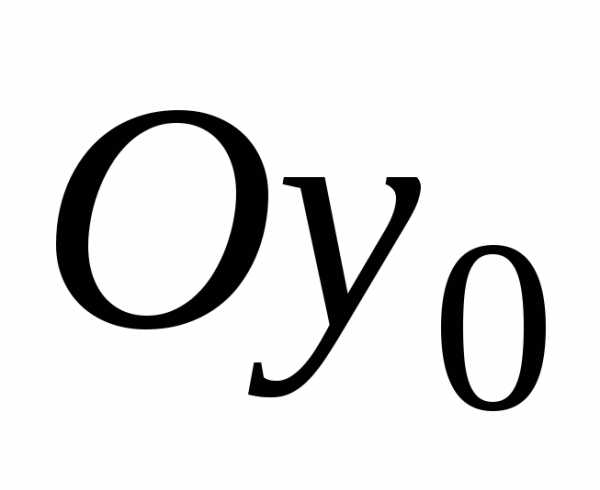 главные оси инерции.
главные оси инерции.
Воспользуемся полученными выражениями и рассмотрим несколько примеров вычисления моментов инерции для плоских фигур.
Пример 4.2.Определить осевые моменты
инерции фигуры, приведенной на рис.
4.10, относительно центральных осей и
и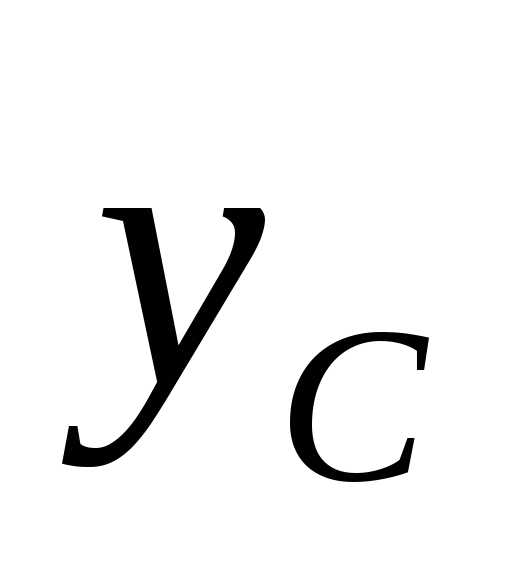 .
.
Рис.4.10
Решение:
В предыдущем примере 4.1 для изображенной
на рис.4.10 фигуры было определено положение
центра тяжести С. Координата центра
тяжести откладывалась от оси  и составила.
Вычислим расстояния
и составила.
Вычислим расстояния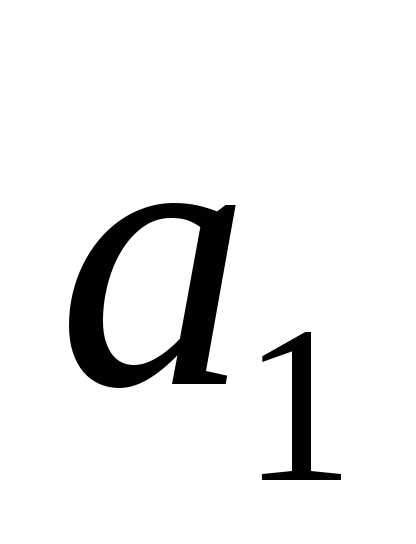 и
и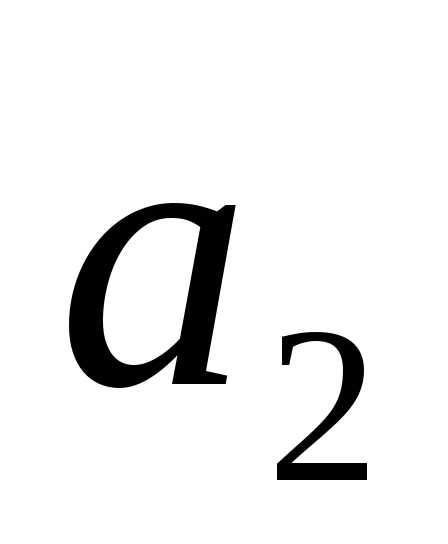 между осями
между осями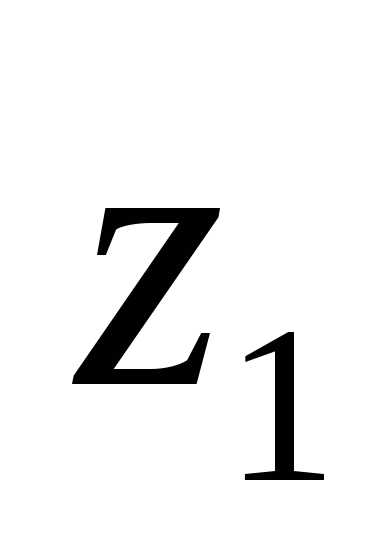 и
и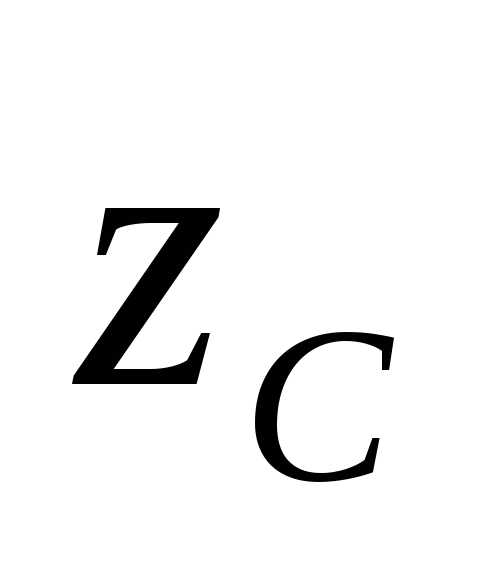 и осями
и осями и
и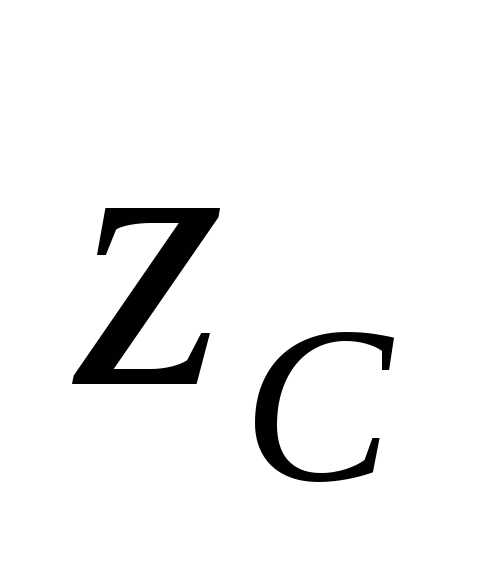 .
Эти расстояния составили соответственнои.
Так как исходные оси
.
Эти расстояния составили соответственнои.
Так как исходные оси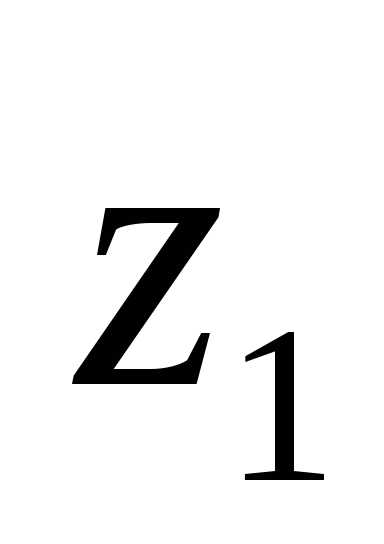 и
и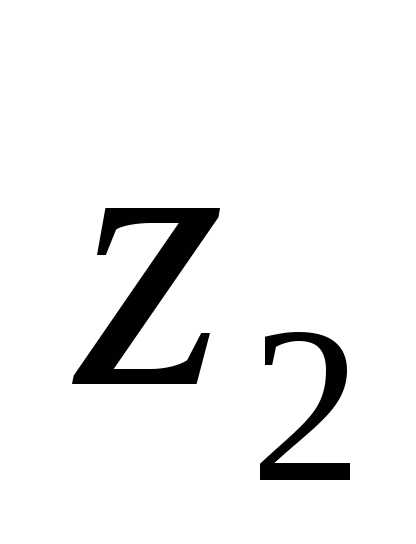
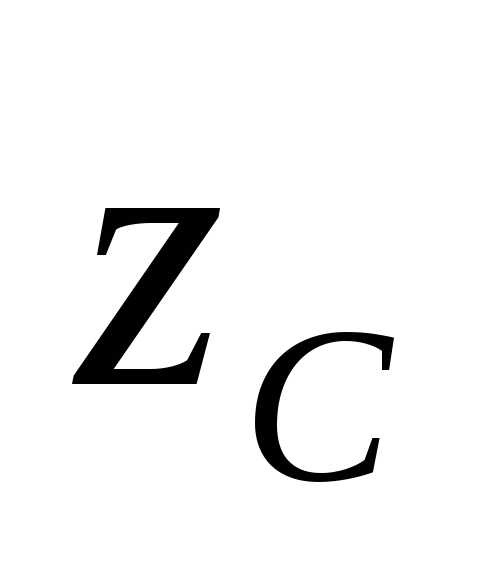 воспользуемся выводами для первого
частного случая, в частности, формулой
(4.21).
воспользуемся выводами для первого
частного случая, в частности, формулой
(4.21).см4.
Момент инерции относительно оси 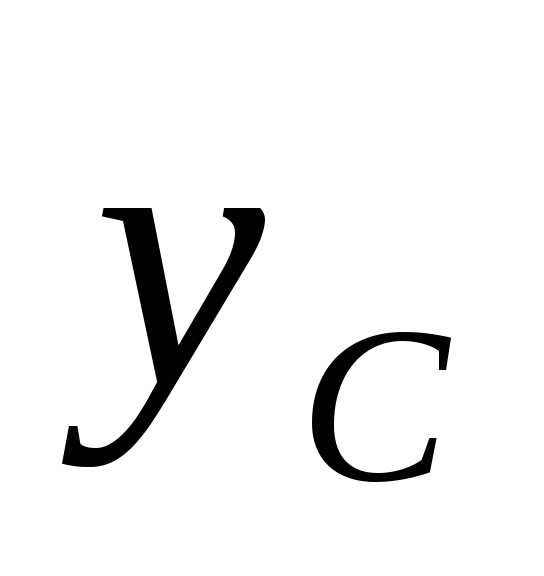 получим путем сложения моментов инерции
простых фигур относительно этой же оси,
так как ось
получим путем сложения моментов инерции
простых фигур относительно этой же оси,
так как ось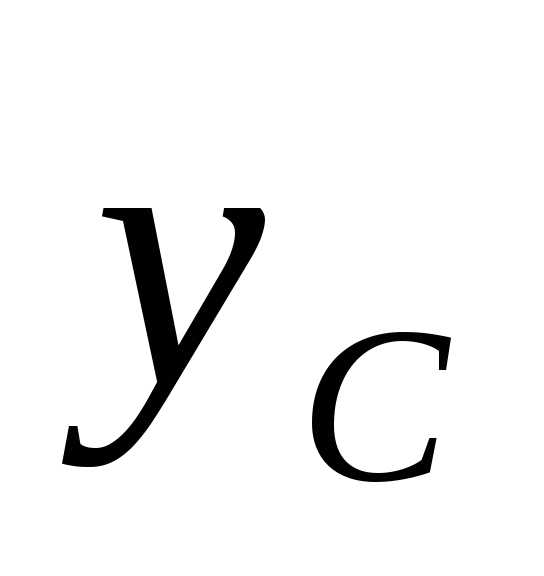 является общей центральной осью для
простых фигур и для всей фигуры.
является общей центральной осью для
простых фигур и для всей фигуры.
см4.
Центробежный момент инерции относительно
осей 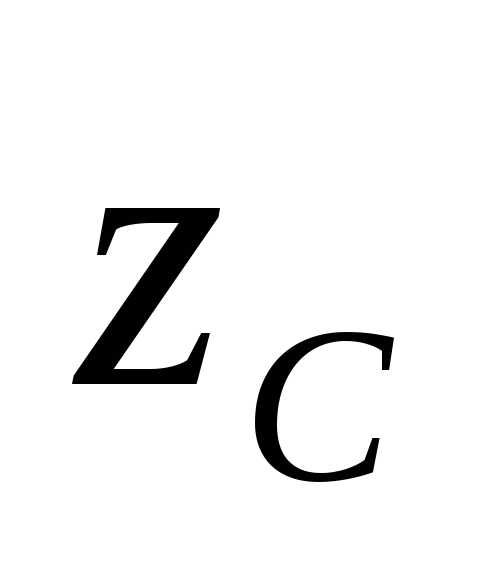 и
и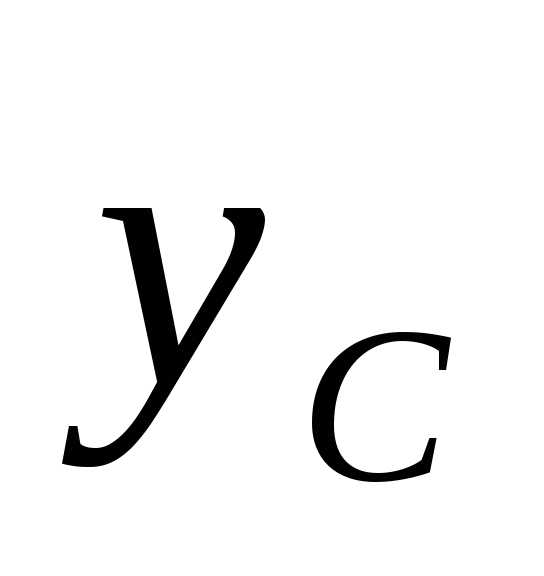 равен нулю, так как ось инерции
равен нулю, так как ось инерции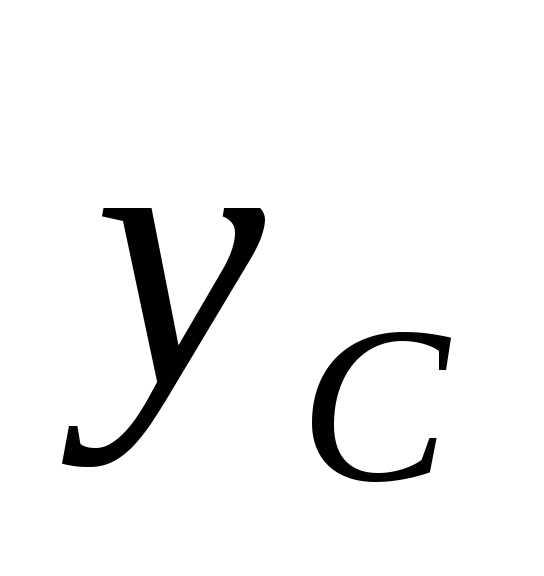 является главной осью (осью симметрии
фигуры).
является главной осью (осью симметрии
фигуры).
Пример
4.3. Чему равен
размер b (в см) фигуры,
изображенной на рис. 4.11, если момент
инерции фигуры относительно оси 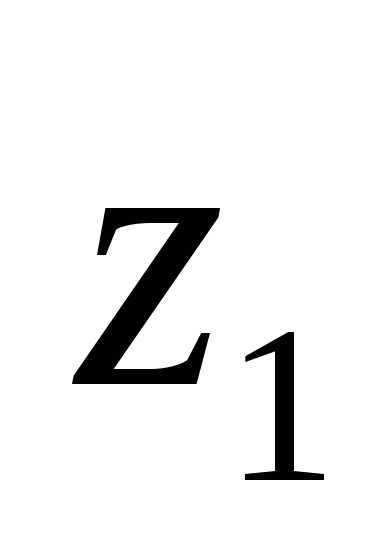 равен 1000 см4?
равен 1000 см4?
Рис.4.11
Решение:
Выразим момент инерции относительно
оси  через неизвестный размер сечения
через неизвестный размер сечения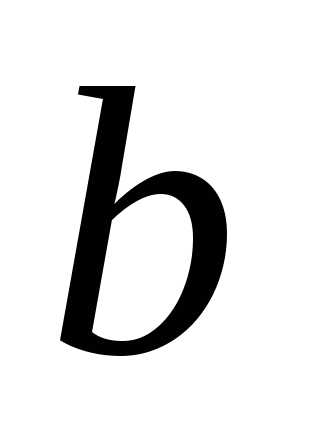 ,
воспользовавшись формулой (4.21), учитывая,
что расстояние между осями
,
воспользовавшись формулой (4.21), учитывая,
что расстояние между осями и
и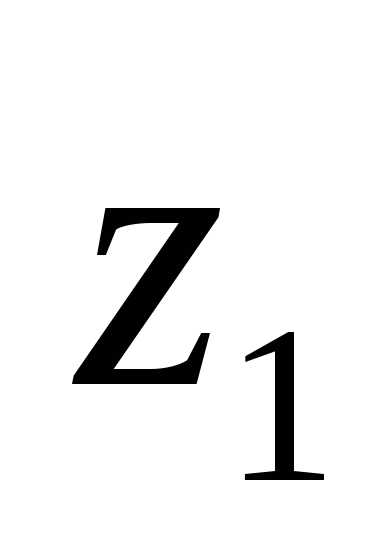 равно 7см:
равно 7см:
см4. (а)
Решая выражение (а) относительно размера
сечения  ,
получим:
,
получим:
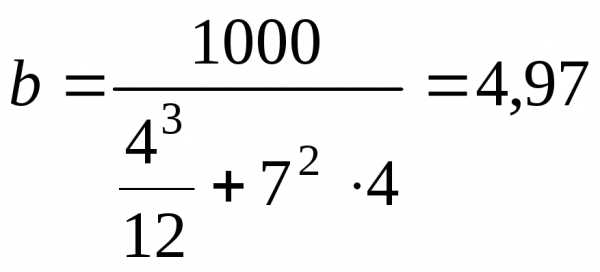 см.
см.
Пример.4.4. Какая из фигур, изображенных на рис.4.12
, имеет больший момент инерции относительно
оси  ,
если обе фигуры имеют одинаковую площадьсм2?
,
если обе фигуры имеют одинаковую площадьсм2?
Рис.4.12
Решение:
1. Выразим площади фигур через их размеры и определим:
а) диаметр сечения для круглого сечения:
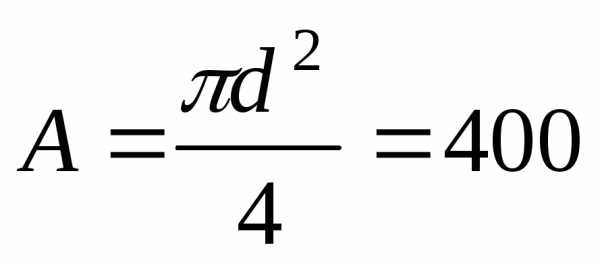 см2; Откудасм.
см2; Откудасм.
б) размер стороны квадрата:
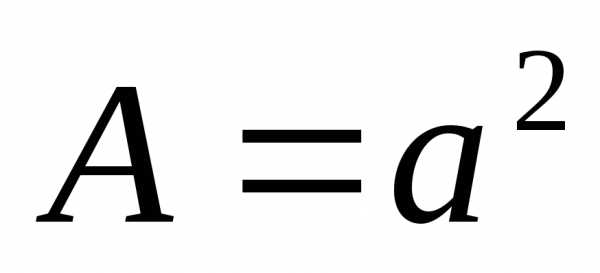 ;
Откудасм.
;
Откудасм.
2. Вычисляем момент инерции для круглого сечения:
см4.
3. Вычисляем момент инерции для сечения квадратной формы:
см4.
Сравнивая полученные результаты, приходим к выводу, что наибольшим моментом инерции будет обладать сечение квадратной формы по сравнению с сечение круглой формы при одинаковой у них площади.
Пример 4.5.Определить полярный момент
инерции (в см4) сечения прямоугольной
формы относительно его центра тяжести,
если ширина сечения 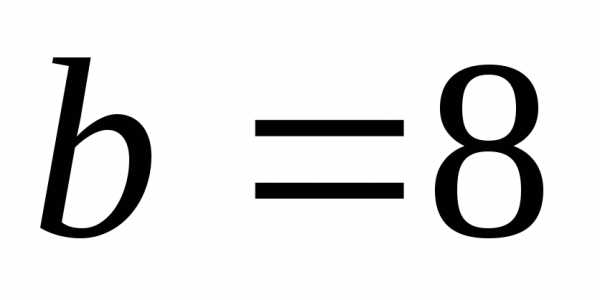 см,
высота сечениясм.
см,
высота сечениясм.
Решение:
1. Найдем моменты инерции сечения
относительно горизонтальной  и вертикальной
и вертикальной центральных осей инерции:
центральных осей инерции:
см4;см4.
2. Определяем полярный момент инерции сечения как сумму осевых моментов инерции:
см4.
Пример
4.6. Определить
момент инерции фигуры треугольной формы
изображенной на рис.4.13, относительно
центральной оси  ,
если момент инерции фигуры относительно
оси
,
если момент инерции фигуры относительно
оси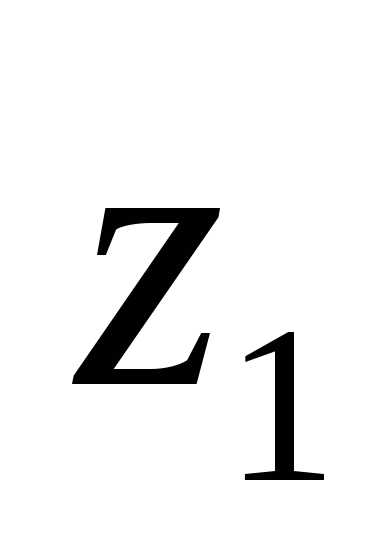 равен 2400 см4.
равен 2400 см4.
Рис.4.13
Решение:
Момент инерции сечения треугольной
формы относительно главной оси инерции  будет меньше по сравнению с моментом
инерции относительно оси
будет меньше по сравнению с моментом
инерции относительно оси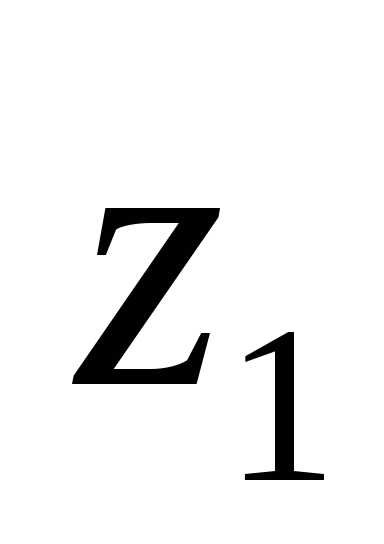 на величину
на величину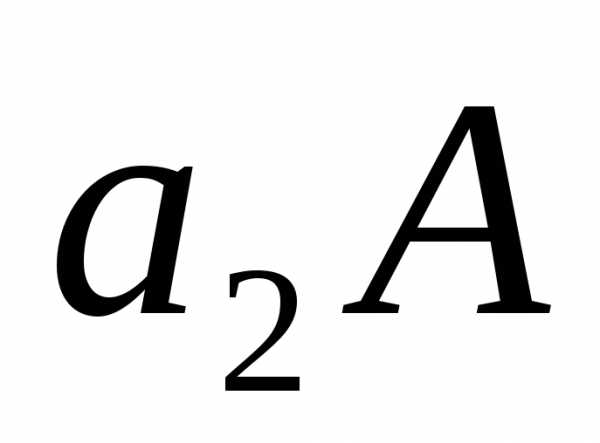 .
Поэтому присм
момент инерции сечения относительно
оси
.
Поэтому присм
момент инерции сечения относительно
оси найдем следующим образом:
найдем следующим образом:
см4.
studfiles.net
Легенда:
|
Легенда:
|
||
|
Форма поперечного сечения |
Осевой момент инерции, J, см4 |
Момент сопротивления W, см3 |
Радиус инерции i, см |
| Круг |
|||
Кольцо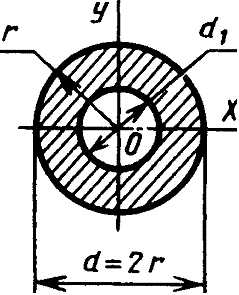 c=d1/d |
|||
Тонкостенное кольцо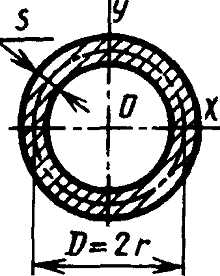 s≤(D/10) |
|||
| Полукруг Vo=2d/3π=0,2122d=0,4244r |
|||
| Круговой сегмент |
|||
| Круговой сектор |
— | 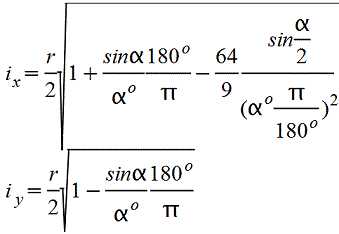 |
|
Круговое полукольцо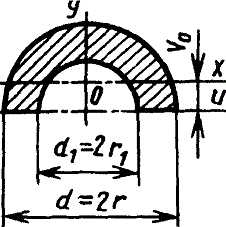 |
|||
| Сектор кругового кольца |
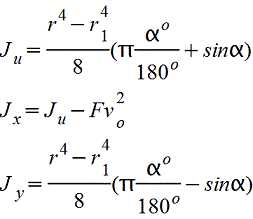 |
— | |
| Профиль с симметричными закруглениями |
— | ||
|
Эллипс |
|||
|
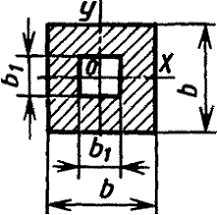
Квадрат |
|||
|
Полый квадрат |
|||
|
Полый тонкостенный квадрат 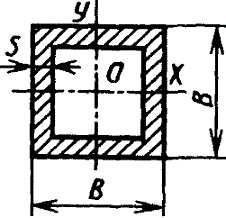 s<(B/15) s<(B/15) |
|||
Квадрат, поставленный на ребро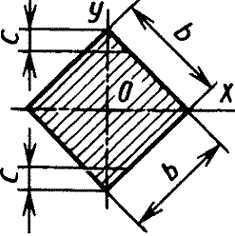 |
Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С=1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx=0,124b3 |
||
Полый квадрат, поставленный на ребро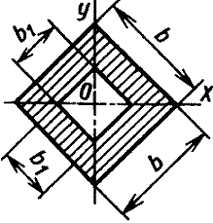 |
|||
|
Прямоугольник |
|||
| Прямоугольник повернутый |
|||
|
Полый прямоугольник |
|||
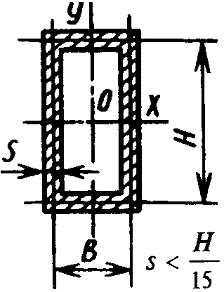
|
Полый тонкостенный прямоугольник
|
|||
|
Сечение из двух равных прямоугольников
|
|||
|
Треугольник
|
При вычислении напряжения в вершине треугольника |
||
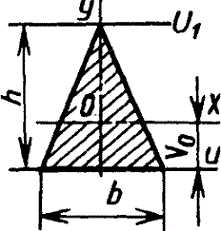
|
Поставленный на ребро треугольник
|
|||
|
Трапеция
|
При вычислении напряжений в точках верхнего основания |
||
|
Трапеция |
|||
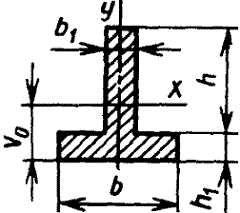
|
Тавр
|
Для нижних волокон Для верхних волокон |
||
|
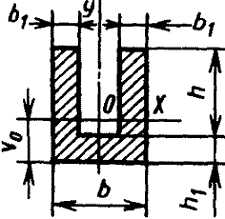
Корытное сечение
|
|||
|
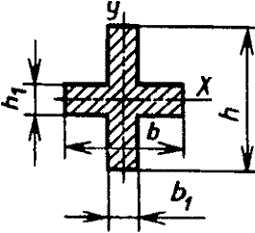
Крестообразное сечение
|
|||
|
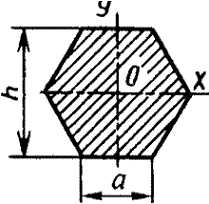
Правильный шестиугольник
|
|||
|
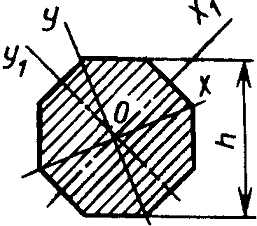
Правильный восьмиугольник
|
|||
www.dpva.ru
Сортамент фасонных профилей: Геометрические характеристики фигур
Геометрические характеристики фигур / Геометрические характеристики простых фигур: прямоугольника, квадрата, треугольника, круга, полукруга
Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур: статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга. Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.
Геометрические характеристики прямоугольника и квадрата
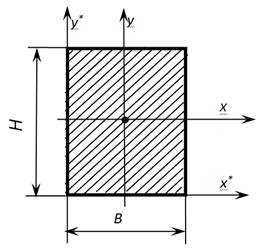
Осевые моменты инерции прямоугольника (квадрата)
Геометрические характеристики прямоугольного треугольника
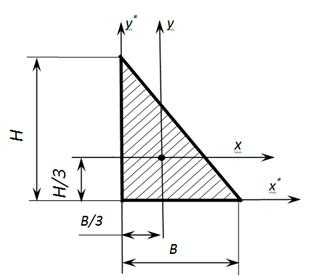
Осевые моменты инерции прямоугольного треугольника
Геометрические характеристики равнобедренного треугольника
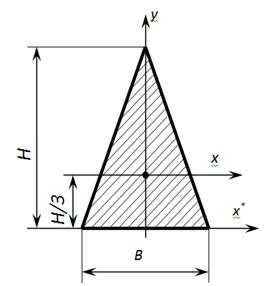
Осевые моменты инерции равнобедренного треугольника
Геометрические характеристики круга
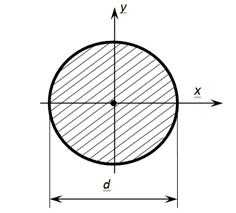
Осевые моменты инерции круга
Геометрические характеристики полукруга
Осевые моменты инерции полукруга
sopromato.ru
Список моментов инерции — Википедия
Материал из Википедии — свободной энциклопедии
Приведены формулы моме́нтов ине́рции для ряда массивных твёрдых тел различной формы. Момент инерции массы имеет размерность масса × длину2. Он является аналогом массы при описании вращательного движения. Не следует путать его с моментом инерции плоских сечений[уточнить], который используется при расчетах изгибов.
Моменты инерции в таблице рассчитаны для постоянной плотности по всему объекту. Также предполагается, что ось вращения проходит через центр масс, если не указано иное.
| Описание | Изображение | Моменты инерции | Комментарии |
|---|---|---|---|
| Тонкая цилиндрическая оболочка с открытыми концами радиуса r и массы m | I=mr2{\displaystyle I=mr^{2}} [1] | Предполагается, что толщина корпуса пренебрежимо мала. Этот объект является частным случаем нижеследующего при r1=r2. Кроме того, точка массы m на конце стержня длиной r имеет тот же момент инерции, а r называется радиусом инерции. | |
| Толстостенная цилиндрическая труба с открытыми концами, внутреннего радиуса r1, внешнего радиуса r2, длиной h и массой m | Iz=12m(r12+r22){\displaystyle I_{z}={\frac {1}{2}}m\left({r_{1}}^{2}+{r_{2}}^{2}\right)} [1][2] Ix=Iy=112m[3(r22+ |
ru.wikipedia.org
Момент инерции прямоугольного сечения
Определение и общие понятия о моменте инерции
Осевым (экваториальным) моментом инерции сечения по отношению к некоторой оси называют взятую по всей его площади S сумму произведений элементарных площадок на квадраты их расстояний от этой оси:
Полярным моментом инерции сечения относительно точки (полюса) называют сумму произведений элементарных площадок на квадраты расстоянии от них до полюса, при этом сумма берется по всей площади S:
где (рис.1)
Если оси, по отношению к которым известны моменты инерции взаимно перпендикулярны, то легко найти полярный момент инерции относительно точки пересечения этих осей, как сумму осевых моментов инерции.
Центробежным моментом инерции сечения по отношению к некоторым взаимно перпендикулярным осям называют сумму произведений элементарных площадок на их расстояния от этих осей, взятых по всей площади сечения S:
Осевой момент инерции прямоугольного сечения
Найдем осевой момент инерции прямоугольника, который имеет высоту h и ширину относительно оси X, которая проходит через основание прямоугольника (рис.2).
Выделим из нашего прямоугольника элементарную площадку dS (рис.2). Основания этой площадки параллельны осям X и Y. Высота полоски составляет dy, ширина b. Площадь данной полоски равна:
Расстояние от полоски до оси X равно y. Используя второе выражение из (1), для момента инерции сечения относительно оси X имеем:
Для получения момента инерции прямоугольного сечения относительно оси Y элементарную полоску выделяют параллельно оси Y. Проводят аналогичную последовательность действий, при этом получают:
Центробежный момент инерции прямоугольного сечения
Центробежный момент инерции прямоугольного сечения относительно осей XY(рис. 2) () равен:
Если оси X и Y провести через центр тяжести прямоугольного сечения, то центробежный момент инерции равен нулю, так ка эти оси совпадают с осями симметрии.
Примеры решения задач
ru.solverbook.com