Момент инерции простых фигур – Определение моментов инерции сложных сечений относительно главных центральных осей (задачи № 29, 30, 31)

1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг)

Прямоугольное сечение.

Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.

Главный центральный момент инерции относительно оси x

Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим

Окончательно

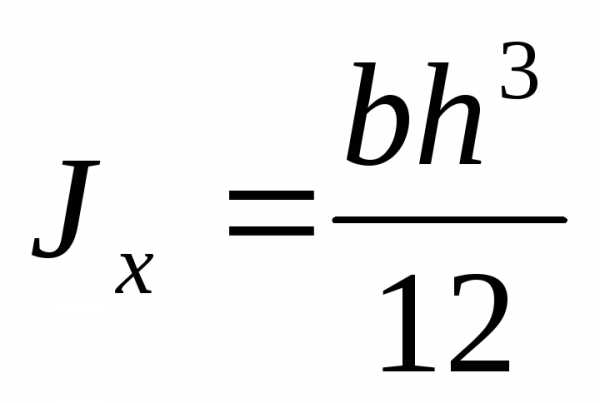
Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:

Круглое сечение

Для круга главные центральные моменты инерции относительно осей x и y равны между собой.

Поэтому из равенства

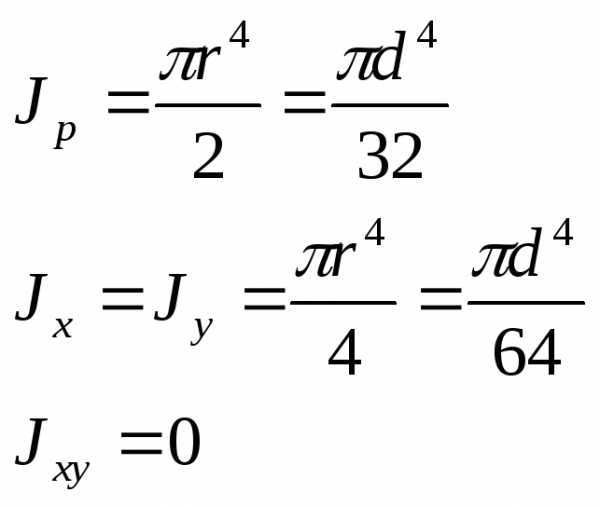
Треугольник

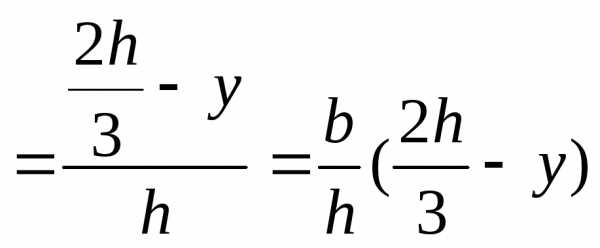
2.Изменение моментов инерции при переходе от центральных осей к параллельным:

J_x1=J_x + a²А;

J_y1=J_y + b²А;

момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. J_y1x1=J_yx + abF; (“a” и “b” подставляют в формулу с учетом их знака).

3.Изменение моментов инерции при повороте осей

J_x1=J_xcos² + J_ysin² — J_xysin2; J_y1=J_ycos² + J_xsin² + J_xysin2;

J_x1y1=(J_x — J_y)sin2 + J

xycos2 ;

Угол >0, если переход от старой системы координат к новой происходит против час.стр. J_y1 + J_x1= J_y + J_x

Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей:

, если

₀>0  оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:

J_max + J_min= J_x + J_y. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:

J_x1=J_maxcos² + J_minsin²; J_y1=J_maxcos² + J_minsin²; J_x1y1=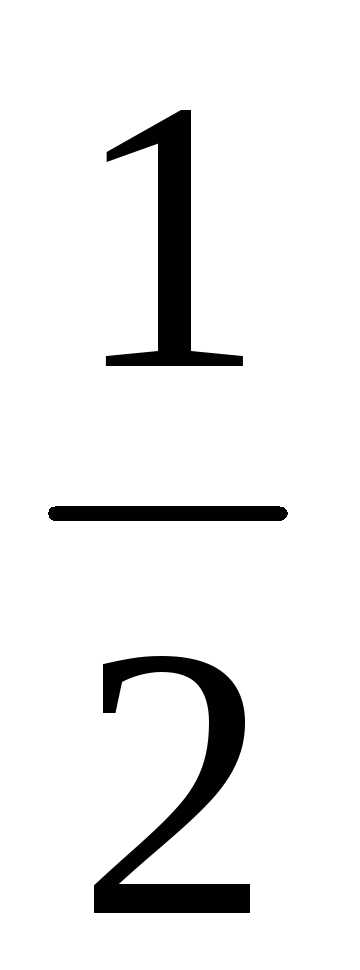(J_max — J_min)sin2;

4.Классификация элементов конструкций

Стержнем наз. Геом тела у которых один из размеров много больше других.

Пластины или оболочки – это геом тела у которых один из размеров << других

Массивные тела– все размеры одного порядка

5.Основные допущения о свойствах материала

Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;

Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;

Изотропны – механич. св-ва не зависят от направления нагружения;

Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.

6.Типы опор

а) Шарнирно – неподвижная (двухсвязная) опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).

б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки. Реакция опоры всегда направлена вдоль опорного стержня, перпендикулярно опорной поверхности

в) Жесткая заделка (трехсвязная)

Реакции в опорах определяют из условия равновесия (уравнение статики).

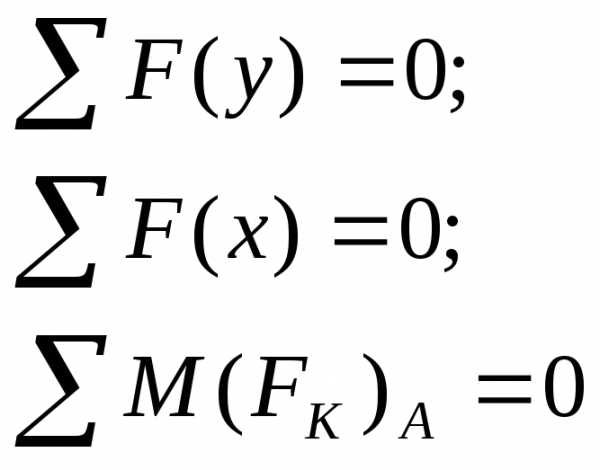
7.Классификация нагрузок

1. По месту действия

Поверхностные и объемные

а) сосредоточенная сила

б) распределенная сила

прямоугольная Rq= qa

треугольная Rq= ½ qa

в) сосредоточенный момент

изгибающий

скручивающий

г) распределенный момент

Rmz= mz a –равнодейств распр мом

2. По времени действия

Постоянные и временные

3. По характеру действия

Статические и динамические

4. По характеру возникновения

Активная(известны) и реактивная (неизвестны)

8.Основные принципы изучаемого курса

При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.

принцип Сен-Венана

на достаточном удалении от места приложения нагрузки характер её воздействия не зависит от способа её приложения, а зависит от величины равнодействующей.

9.Внутренние усилия. Метод сечений (Метод РОЗУ)

Nz=∑z (pi) нормальная с

Qx=∑x (pi) поперечная с

Qy=∑y (pi)

Mz=∑mz (pi) крутящий момент

Mx=∑mx (pi) изгибающий

My=∑my (pi)

Разрезаем мысл тело плоск

Отбрасываем одну из г внутр усил

Заменяем внутр усилиями

Уравновешив внутр ус внеш нагр

10.Правило знаков внутренних усилий

Правило знаков поперечных сил при изгибе:

Крутящий момент

Против ЧС при взгляде со стороны сеч то +

Правило знаков изгибающих моментов:

Правило проверки правильности построения эпюр нагружения:

В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.

11.Эпюры внутренних усилий

ПРИ РАСТЯЖЕНИИ-СЖАТИИ

ПРИ КРУЧЕНИИ

при прямом изгибе

12.Дифференциальные зависимости при изгибе

; ;

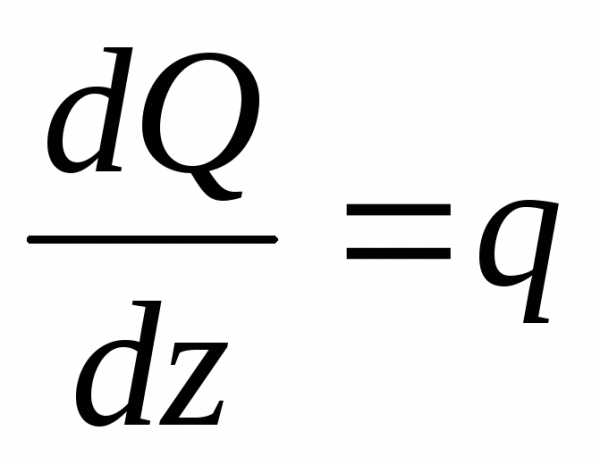13.Следствия из дифференциальных зависимостей

1. Если на участке нет распр нагр (q=0) то поперечная сила на этом участке имеет пост вел., а эпюры изгиб мом меняются по лин закону

2. На уч на котором присутст распр нагр пост интенсивн. Поперечная сила меняется по лин зак , а эпюры по закону квадр параболы. Причем эпюра мх всегда напр навстречу распр нагрузке. Где Qy равно 0 эпюра мх имеет экстремум. Если Qy равно 0 на всем участке, то мх постоян величину

4. На участке где Qy>0 эпюра мх возрастает слева направо

5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента

studfiles.net

5.2. Моменты инерции плоских сечений

Полярным моментом инерции сечения

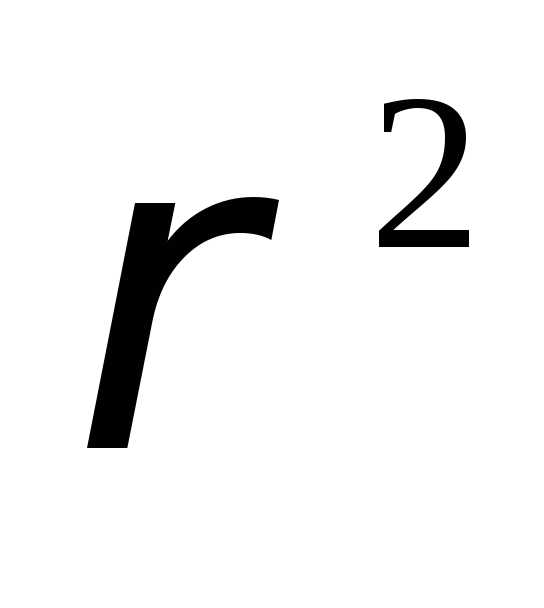называется сумма произведений элементарных площадок(dA) на квадраты их расстояний () до какого-либо полюса, лежащего в плоскости сечения, распространённая на всю площадь сечения (рис. 5.2):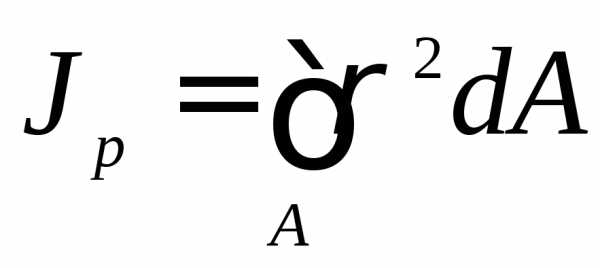

. (5.7)

Рис. 5.2

Осевым моментом инерции площади сечения относительно какой-либо оси, лежащей в её плоскости, называется сумма произведений элементарных площадок на квадраты расстояний их до этой оси:

(5.8)

Из рис. 5.2 видно, что Подставим это выражение в (5.7) и получим

(5.9)

Следовательно, сумма осевых моментов инерции плоского сечения относительно двух перпендикулярных осей равна полярному моменту инерции относительно полюса, представляющего точку пересечения этих осей.

Осевые и полярные моменты инерции измеряются в метрах в четвертой степени (м⁴). Они всегда положительны и не могут быть равны нулю.

5.3. Моменты инерции простых плоских сечений

Определим моменты инерции наиболее распространенных плоских сечений.

1. Прямоугольник (рис. 5.3). Вычислим момент инерции сечения относительно оси х, проходящей через центр тяжести параллельно основанию. Выделим на расстоянии у от оси х бесконечно узкую площадку высотой dy, тогда dA=b dy. В соответствии с (5.8):

. (5.10)

Рис. 5.3

Аналогично находим осевой момент инерции относительно оси у:

(5.11)

Для квадратного сечения со стороной а:

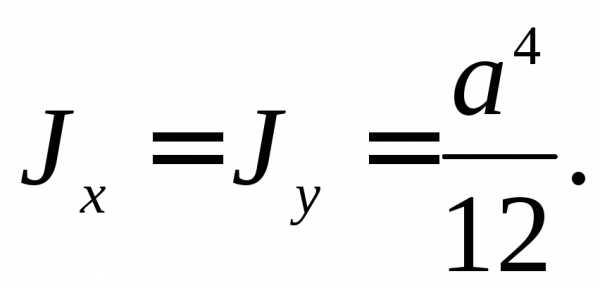(5.12)

2. Круг радиуса r (рис. 5.4). Определим вначале полярный момент инерции относительно центра круга. За dA примем площадь бесконечно тонкого кольца толщиной и радиусом, тогдаПодставим это значение в (5.7):

(5.13)

Определим теперь осевые моменты инерции. Согласно формуле (5.9) для круглого сечения

Следовательно,

(5.14)

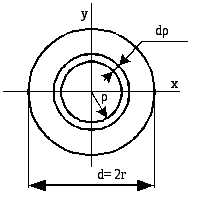
Рис. 5.4

3. Кольцо (рис. 5.5). Воспользуемся формулой (5.13), приняв пределы интегрирования от R до r.

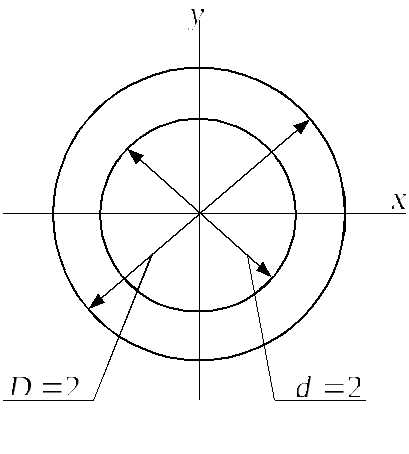
Рис. 5.5

Обозначим отношение . Тогда

(5.15)

Аналогично сплошному сечению (5.14) определим осевой момент инерции кольца:

(5.16)

5.4. Центробежный момент инерции

Центробежным моментом инерции называется сумма произведений элементарных площадок на их координаты, распространённая на всю площадь сечения (рис. 5.6)

. (5.17)

Рис. 5.6

Центробежный момент инерции имеет размерность – метр в четвертой степени (м⁴) и может быть величиной положительной, отрицательной и равной нулю.

Если взаимно перпендикулярные оси х и у или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю.

5.5. Изменение моментов инерции при повороте осей

Найдём зависимость между моментами инерции относительно осей х и у и моментами инерции относительно осей ,,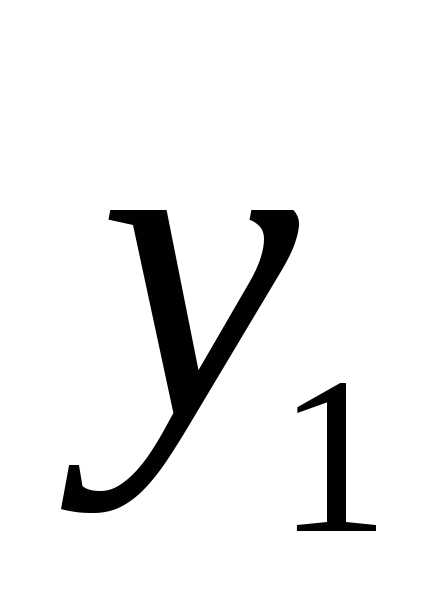 повёрнутых на угол

(рис. 5.7). Пусть J_x > J_y и положительный угол отсчитывается от осих против хода часовой стрелки.

Найдём зависимость между координатами площадки в исходных и повёрнутых осях.

,

.

Теперь определим моменты инерции относительно осей и:

Или

. (5.18)

.

После преобразований

. (5.19)

Рис. 5.7

Центробежный момент инерции

. (5.20)

Сложим (5.18) и (5.19):

(5.21)

Вычтем (5.19) из (5.18):

Анализ формулы (5.21): сумма моментов инерции относительно любых взаимно-перпендикулярных осей не меняется при их повороте.

Формула (5.22) может быть использована для определения центробежного момента инерции по известным осевым моментам инерции относительно осейх, у и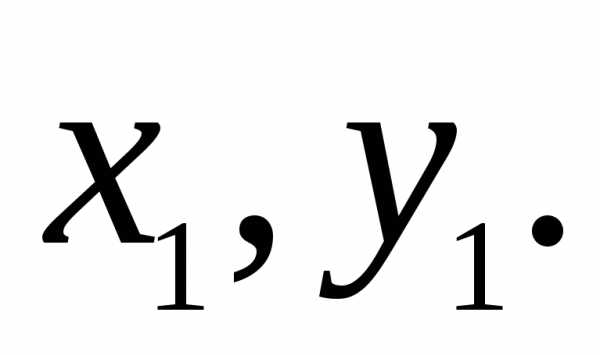

studfiles.net

MYsopromat.ru: Моменты инерции простейших фигур

В расчетной практике часто встречаются сечения в виде простейших фигур (прямоугольников, кругов, треугольников и т. п.) или их комбинаций. При вычислении моментов инерции таких фигур обычно пользуются заранее выведенными расчетными формулами. Рассмотрим некоторые из фигур.

Прямоугольник и параллелограмм (рис. 6.4). Выделим элементарную полоску площадью dF=bdy и подставим это значение dF под знак интеграла (6.5):

Рис. 6.4	Рис. 6.5

.

Следовательно, момент инерции прямоугольника и параллелограмма с основанием b и высотой h относительно центральной оси, параллельной основанию,

.

(6.16)

Моменты инерции этих фигур относительно осей, проходящих через основание, находим по формуле (6.13):

.

(6.17)

Моменты инерции прямоугольника относительно осей y_c и y вычисляются по формулам (6.16) и (6.17), где b заменяется на h, а h на b:

.	(6.18)
.	(6.19)

Треугольник с основанием b и высотой h (рис. 6.5).

Разобьем треугольник на элементарные полоски, параллельные его основанию. Площадь такой полоски

.

Тогда момент инерции треугольника относительно оси, проходящей через основание,

.

(6.20)

Подсчитывая по формулам переноса момент инерции треугольника относительно центральной оси, параллельной основанию, получаем

.

(6.21)

Круг и полукруг диаметра d (рис. 6.6). Подсчитываем сначала полярный момент инерции круга. Для этого выделим в сечении окружностями радиуса ρ и ρ+dρ элементарное кольцо площадью dF=2πρdρ и вычислим I_y по формуле (6.7):

.

(6.22)

Рис. 6.6.

Обычно размеры круглого сечения выражают через диаметр d и подсчитывают I_p по формуле

.

(6.23)

Осевые моменты инерции круга найдем с помощью соотношения (6.8). Замечая, что в силу симметрии круга I_z=I_y, получаем для осевых моментов инерции круга выражение

.

(6.24)

Центральные оси y и z делят круг на четыре совершенно одинаковые части с равными моментами инерции относительно этих осей. Следовательно, моменты инерции круга и полукруга относительно осей y и z должны быть равны соответственно учетверенным и удвоенным моментам инерции относительно тех же осей одной четверти круга. Из сказанного следует, что моменты инерции полукруга относительно оси симметрии y и оси z, проходящей через его основание (рис. 6.2), будут одинаковы и равны половине момента инерции круга,

,

(6.25)

а моменты инерции четверти круга

.

(6.26)

    

mysopromat.ru

4.2. Основные теоремы о моментах инерции

Осевыми моментами инерции сечения называются интегралы

Jx = ∫ y2dA Jy = ∫ x2dA			(4.1)
A	,	A
Центробежным моментом инерции называется интеграл
Jxy	= ∫ xydA		(4.2)
	A
Полярным моментом инерции называется интеграл
Jρ	= ∫ ρ 2dA		(4.3)
	A
Так как ρ 2 = x2 + y2 , то
Jρ	= Jx	+ J y ,

т.е. полярный момент инерции сечения относительно заданной точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку.

4.1.4. Радиусы инерции

Величины, определяемые по формулам:

ix=	J	x	; iy =	J y	, – называются радиусами инерции относительно осей x и y
				A
	A

соответственно

4.2.1. Теорема о моментах инерции относительно осей, параллельных центральным

Осевой момент инерции сечения относительно произвольной оси равен моменту инерции относительно центральной оси параллельной данной плюс произведение квадрата расстояния между осями на площадь сечения.

Центробежный момент инерции сечения относительно произвольных осей координат равен центробежному моменту инерции относительно центральных осей параллельных данным плюс произведение площади сечения на расстояния между осями.

Рассмотрим сечение произвольной формы площадью A. Пусть оси x и y являются центральными (т.е. проходящими через центр тяжести сечения), и известны моменты инерции

Jx, Jy, Jxy. Требуется определить моменты инерцииJx1 ,J y1 ,Jx1y1 относительно осей x1 и y1, смещенных параллельно центральным осям на расстояния a и b соответственно.

44

Координаты элементарной площадки dA в системе координат (x1, y1): x1=x+b; y1=y+a.

По определению осевого момента инерции (4.1)

Jx1 = ∫( y+ a)2 dA= Jx + 2a∫ ydA+ a2 A,

A A

где ∫ ydA =Sx = 0.

A

Таким образом,

J	x1	= J	x	+ a2 A	(4.4)

Рассуждая аналогичным образом, можно получить

J	y1	= J	y	+ b2 A	(4.5)

По определению центробежного момента инерции (4.2):

Jx y		= ∫ x1 y1dA= ∫( y+ a)(x+ b)dA= Jxy + abA.
1	1		A
		A

4.2.2. Вычисление моментов инерций простейших фигур

Прямоугольник.

Сначала определим моменты инерции прямоугольника относительно осей x1 и y1.

Выделим на расстоянии y1 от оси x1 элементарную площадку dA высотой dy1 и шириной, равной ширине прямоугольника:

По определению осевого момента инерции (4.1)

Jx1 = ∫ y12dA.

A

Заменим интеграл по площади интегралом по высоте

h		3			h		3
Jx1 = ∫ y12bdy1	= b	y1				= bh	.
0	3				0	3

Аналогично

45

Jy1 = hb33 .

Моменты инерции относительно центральных осей x и y определим, пользуясь теоремой о моментах инерции относительно осей, параллельных центральным (4.4):

Jx= Jx1 −	h 2		bh =			bh4		bh4	bh4
		2				3	−	4 =	12 .
Аналогично
		J		=	hb3		.
			y		12

Круг.

Определим полярный момент инерции круга. Выделим на расстоянии ρ от центра круга элементарный слой dA толщинойdρ .

По определению полярного момента инерции (4.3)

Jρ	= ∫ ρ 2dA.
	A
Заменим интеграл по площади интегралом по радиусу
Jρ = d∫/ 2 ρ2 2πρdρ= 2πd∫/ 2 ρ3dρ= 2π		ρ 4			d / 2	=	πd 4 .
		4
0	0				0		32

Так как Jp=Jx+Jy и для круга Jx=Jy, то осевой момент инерции

	J		=	J	ρ	=	πd4	.
		x		2			64

Прямоугольный треугольник.

Определим момент инерции треугольника относительно оси x1, совпадающей с его нижней стороной.

Выделим на расстоянии y1 от оси x1 элементарную площадку dA высотой dy1. Ширина площадки из подобия треугольников:

by

= b

h − y1

.

1

h

Момент инерции

h

b(h− y

)

y3

h

b y4

h

bh4

bh4

bh4

J x1 = ∫ y12dA= ∫ y12

1

dy1 = b

1

−

1

=

−

=

.

h

3

h 4

3

4

12

A

0

0

0

Относительно центральной оси

Jx

= Jx

h 2

bh

=

bh4

−

bh4

=

bh4

−

2

12

18

36

.

1

3

Аналогично для второй оси

J y

=

hb3

; J y =

hb3

.

12

36

1

4.2.3. Теорема о моментах инерции при повороте осей координат

Рассмотрим сечение произвольной формы площадью A. Пусть известны моменты инерции относительно осей x и y: Jx, Jy, Jxy. Требуется определить моменты инерцииJx1 ,J y1 ,Jx1y1

относительно осей x1 и y1, повернутых по отношению к осям x и y на угол α. Выделим в окрестности точки K с координатами x и y элементарную площадку dA.

Координаты площадки dA в повернутой системе координат:

x1 = OC+ BD= xcosα + ysinα , y1 = KD− CB= ycosα − xsinα .

Осевые моменты инерции:

J x1 = ∫ y12dA = ∫(y cosα − x sinα )2 dA = Jx cos2 α + J y sin2 α − Jxy sin 2α ,

	A	A
J y1	= ∫ x12dA = ∫(x cosα + y sinα )2 dA = J ycos2 α + Jx sin2 α + Jxy sin 2α .
	A	A

Сложив попарно левые и правые части полученных уравнений, найдем:

J x1 + Jy1 = Jx + Jy .

Таким образом, сумма моментов инерции относительно осей прямоугольной системы координат не изменяется при их повороте. Как было показано выше, эта сумма равна полярному моменту инерции относительно начала координат.

studfiles.net

Какие моменты инерции называются собственными?

Осевые и центробежный моменты инерции относительно осей, проходящих через центр тяжести поперечного сечения стержня, иногда называются собственными моментами инерции.

6. По какой формуле вычисляются моменты инерции фигуры относительно оси, параллельной центральной? Какие моменты инерции называются переносными?

Пусть две взаимно перпендикулярные оси x и y проходят через центр тяжести C поперечного сечения стержня. Проведем другие оси координат и, параллельные осямx и y. Обозначим a и b координаты центра тяжести С в новых осях 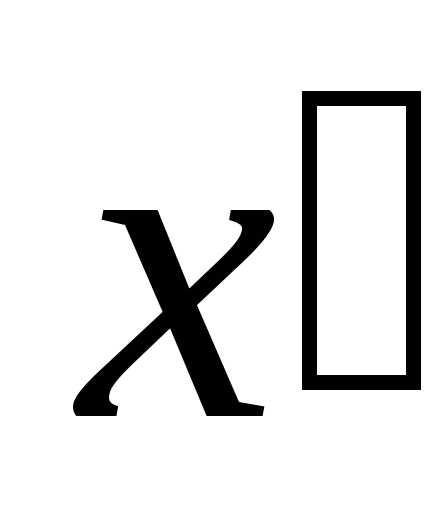и(рис. 4.3,а).

Тогда осевые и центробежный моменты инерции фигуры относительно новых осейибудут определяться по следующим формулам:

. (4.6)

Первые слагаемые в этих формулах ранее нами были названы собственными моментами инерции. Вторые (подчеркнутые) слагаемые в формуле (4.6) называются переносными моментами инерции.

Отметим, что координаты a и b необходимо подставлять в формулы (4.6) с учетом их знаков, что является крайне важным для третьей из этих формул.

7. Как изменяются собственные моменты инерции при повороте координатных осей?

Пусть нам известны собственные моменты инерции ,иотносительно двух взаимно перпендикулярных осейx и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие ос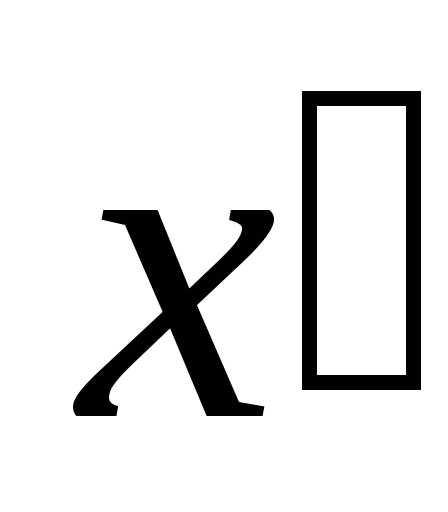и и, повернутые относительно осейx и y на угол (рис. 4.3,б). Будем считать этот угол положительным, если поворот осей происходит против хода часовой стрелки.

Тогда моменты инерции поперечного сечения относительно новых осей определяются по формулам:

;

; (4.7)

.

Из формул (4.7) видно, что

,

то есть сумма собственных осевых моментов инерции является величиной постоянной (она не изменяется при повороте координатных осей).

Как уже отмечалось выше, две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции. Тогда при из третьей формулы (4.7) после несложных преобразований можно определить направления этих осей:

. (4.8)

Из полученного выражения (4.8) мы найдем два значения угла , которые отличаются друг от друга на угол. Они и определяют положение двух главных центральных осей.

8. Какие собственные осевые моменты инерции называются главными моментами инерции?

При повороте центральных осей и приближении их к главным центральным осям, больший из собственных осевых моментов инерции становится еще больше, стремясь к своему максимальному значению ,а меньший – еще меньше, приближаясь к минимальному значению .

Моменты инерции фигуры относительно главных центральных осей и называютсяглавными центральными моментами инерции. Они могут быть вычислены по следующим формулам:

(4.9)

Отметим важное свойство, вытекающее из этих формул. Если в частном случае , то осевые моменты инерцииитоже равны между собой и при повороте осей вообще не изменяются. Тогда любые две взаимно перпендикулярные оси, проходящие через центр тяжести поперечного сечения, являются главными центральными осями.

9. Как для сложной фигуры определить, какая из главных центральных осей является осью max, то есть той осью, относительно которой момент инерции принимает наибольшее значение ?

По определению осевой момент инерции равен интегралу произведений элементарных площадок на квадрат их расстояний до соответствующей оси. Поэтому, чем больше площадки удалены от оси и чем больше таких площадок, тем больше и осевой момент инерции.

studfiles.net

5.2. Моменты инерции простых сечений

Нижеприведенные формулы для определения моментов инерции простых сечений относительно их центральных осей получены из интегральных выражений для моментов инерции (5.4), (5.5), (5.6):

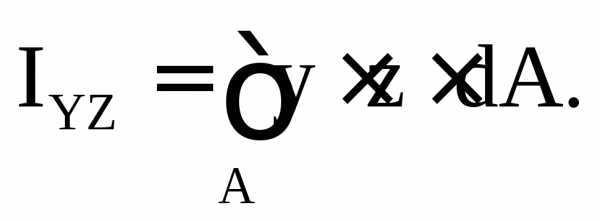
1. Прямоугольник

(5.10)

(5.11)

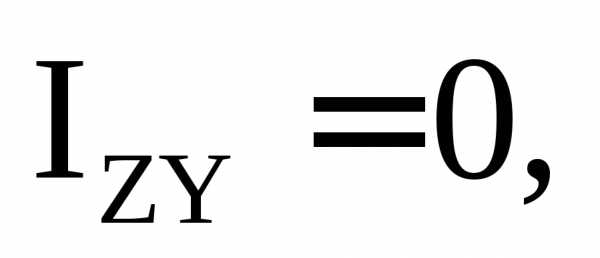так как оси Z иY– оси симметрии.

2. Круг

(5.12)

(5.13)

Здесь – полярный момент инерции сечения.

3. Полукруг

(5.14)

(5.15)

Рис. 5.5

4. Равнобедренный треугольник

(5.16)

(5.17)

5. Прямоугольный треугольник

(5.18)

(5.19)

(5.20)

Полезно запомнить, что в формулах (5.10), (5.11) и (5.16)–(5.19) возводится в куб размер стороны фигуры, перпендикулярной рассматриваемой оси.

В формуле (5.20) при определении центробежного момента инерции знак “минус” ставится тогда, когда острые углы треугольника находятся в отрицательных четвертях (т.е. 2-й и 4-й). В тех случаях, когда эти углы находятся в положительных четвертях (т.е. 1-й и 3-й), в формуле (5.20) ставится знак “плюс”.

5.3. Главные центральные моменты инерции сложных симметричных сечений

Положение главных центральных осей и величины главных центральных моментов инерции для симметричных сечений определяются в следующем порядке:

1. Сложное сечение разбивается на простые фигуры (круг, прямоугольник, двутавр, уголок и т.п.) и проводятся их центральные оси Z_i и Y_i (как правило – горизонтально и вертикально).

2. Определяется по формулам (5.3) положение центра тяжести всего сечения и через эту точку проводятся его центральные оси Z и Y. При наличии двух осей симметрии центр тяжести всего сечения находится в точке их пересечения.

Если сечение обладает только одной осью симметрии, то по формулам (5.3) определяется только одна координата центра тяжести. Поясним это для фигуры, показанной на рис. 5.8:

а) оси Z’ и Y’ выбираем так, чтобы ось Y’ совпала с осью симметрии фигуры, а ось Z’ – чтобы было удобно определить расстояние до этой оси от центральных осей простых фигур;

б) определяем статический момент площади сечения относительно произвольной оси Z’ по формуле:

= А₁у₁+ А₂у₂,

где А_i– площади сечений простых фигур; у_i– расстояния от произвольной осиZ’ до центральных осей простых фигурZ_i. Расстояния у_iнеобходимо брать с учетом знаков;

в) определяем координату у_Cцентра тяжести по формуле (5.3):

=

г) на расстоянии у_Cот осиZпроводим вторую центральную осьZ. Первой центральной осью является ось симметрии Y.

3. Моменты инерции относительно главных центральных осейZиY(рис. 5.8) определяем по формулам (5.9), которые в развернутом виде запишутся так:

так как одна из рассматриваемых осей

(ось Y) является осью симметрии.

В этих формулах:

– осевые моменты инерции простых фигур относительно своих центральных осей (собственные моменты инерции), которые определяются по формулам (5.10)–(5.19) или по таблицам сортаментов для прокатных элементов;

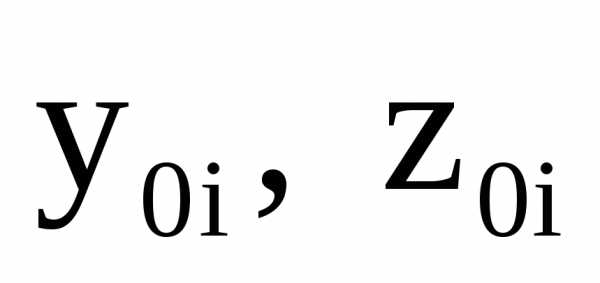– расстояния от общих центральных осей сеченияZиYдо центральных осей простых фигур. В рассматриваемом примереипоказаны на рис. 5.8;

A_i– площади простых фигур. Если простой фигурой является фигура, вырезанная от общей, т.е. “пустая” фигура, то в соответствующие формулы площади таких фигурAи их собственные моменты инерцииподставляются со знаком “минус”.

ПРИМЕР 5.1

Требуется определить главные центральные моменты инерции сечения, изображенного на рис. 5.9.

РЕШЕНИЕ:

1. Разбиваем сечение на простые фигуры и проводим их горизонтальные и вертикальные центральные оси Z_iиY_i

2. Проводим центральные оси для всей фигуры, т.е. оси симметрии ZиY.

3. Определяем расстояния от общих центральных осей ZиYдо центральных осей простых фигур и площади этих фигур:

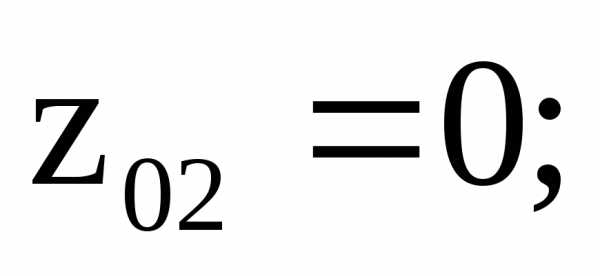
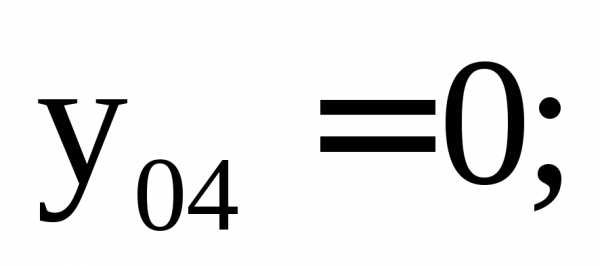
4. Вычисляем собственные центральные моменты фигур по формулам (5.10)–(5.17):

5. Определяем осевые моменты инерции всего сечения относительно центральных осей ZиY:

Центробежный момент инерции так какZиY– оси симметрии. Поэтому вычисленные намиI_ZиI_Yпоэтому являются главными центральными осями:

ПРИМЕР 5.2

Требуетсяопределить главные центральные моменты инерции сечения показанного на (рис. 5.10).

РЕШЕНИЕ

1. Разбиваем сечение на простые фигуры и проводим их центральные оси иY_i.

2. Проводим ось симметрии Y. Она является главной центральной осью заданного сечения.

3. Для определения положения 2-й главной центральной оси выбираем произвольную ось Z, перпендикулярную оси симметрии. Пусть эта ось совпадает с осьюZ₃.

4. По формуле (5.3) определяем ординату у_сцентра тяжести поперечного сечения по оси Y:

Откладываем размер у_Cвверх от осиZ’ и проводим 2-ю главную центральную осьZ.

5. Определяем осевые моменты инерции простых фигур относи­тельно собственных центральных осей (см. формулы (5.10)–(5.17)):

6. Вычисляем расстояния от центральных осей всего сечения ZиYдо центральных осей отдельных фигур (рис. 5.10):

так как оси Y₁,Y₂,Y₃совпадают с осью симметрииY.

7. Вычисляем осевые моменты инерции всего сечения относи­тельно центральных осей ZиYпо формулам (5.9):

Центробежный момент инерции I_ZYвсего сечения равен нулю, так как ось Y является осью симметрии, т.е. осиZиYявляются главными центральными осями инерции сечения, а вычисленные осевые моменты инерции являются главными центральными моментами инерции:

ПРИМЕР 5.3

Требуетсяопределить главные центральные моменты инерции составного сечения, показанного на (рис. 5.11).

РЕШЕНИЕ

Порядок решения подробно рассмотрен в примере 5.2.

1. Разбиваем сечение на отдельные фигуры, геометрические характеристики которых приводятся в таблице сортаментов (двутавр и швеллер) или легко вычисляются по формулам (5.10)–(5.20) (в данном примере прямоугольник) и проводим их центральные оси.

2. Проводим ось симметрии Y. Центр тяжести всего сечения лежит на этой оси.

3. Выбираем произвольную ось Z. Пусть в данном примере эта ось совпадает с осьюZ₃.

4. Расстояние у_Cопределяем от произвольной осиZдо центра тяжести всего сечения:

Расстояния от произвольно выбранной оси Z’ до центральных осей каждой фигуры (у₁, у₂, у₃) показаны на рис. 5.11.

Площади сечений швеллера А₁и двутавра А₂выписываем из соответствующих таблиц сортамента, а площадь прямоугольника А₃вычисляем:

А₁= 23,4 см², А₂= 46,5 см², А₃= 242 = 48 см².

Отложим величину у_Cвверх от осиZ’ (так как у_C > 0) и на этом расстоянии проведем главную центральную осьZ.

5. Геометрические характеристики прокатных профилей выписываем из таблицы сортаментов, учитывая различие в ориентации осей в таблице сортаментов и на рис. 5.12а, в.

1. Швеллер № 20

ГОСТ 8240-89

(рис. 5.12а) ;

Двутавр № 30

ГОСТ 8239-89

(рис. 5.12б) h= 30 см.

Буква “с” в индексе осевых моментов инерции I означает ссылку на обозначение осей в сортаменте.

Моменты инерции прямоугольника (рис. 5.12в) вычисляем отдельно по формулам (5.10) и (5.11):

6. Определяем расстояния от общих центральных осей Y и Z до центральных осей отдельных фигур (они показаны на рис. 5.11):

так как оси Y₁,Y₂,Y₃ совпадают с осью симметрии всего сеченияY.

7. Определяем осевые моменты инерции сложной фигуры относительно центральных осей ZиYпо формулам (5.9):

Центробежный момент инерции так как ось Y является осью симметрии. Поэтому оси Z и Y являются главными центральными осями.

studfiles.net

2. Моменты инерции плоских фигур.

Осевыми моментами инерции площади фигуры называют выражения

; .

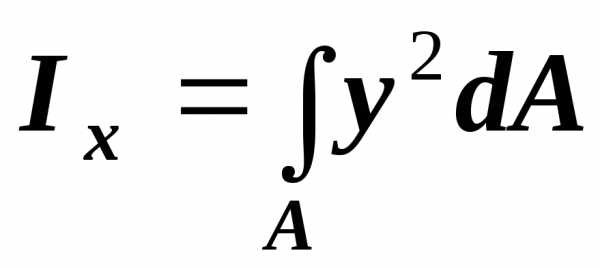Полярным моментом инерции площади фигуры относительно полюса называют

.

Если через полюс проведена система взаимно перпендикулярных осейи(рис. 10), то(как гипотенуза).

Тогда

,

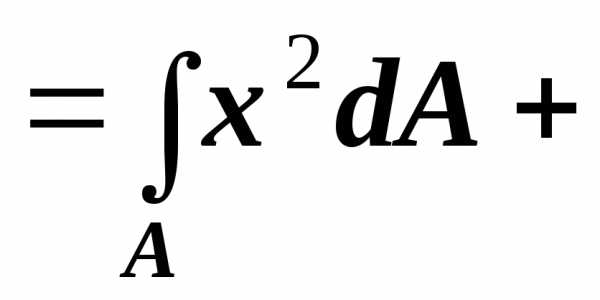то есть полярный момент инерции относительно полюса равен сумме осевых моментов инерции относительно осей, проходящих через полюс.

Отметим, что величины осевых и полярных моментов инерции положительны.

Центробежным моментом инерции называют . Единицы измерения осевых, полярных и центробежных моментов инерции –.

Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называют главными осями. Две взаимно перпендикулярные оси, одна из которых является осью симметрии фигуры, называются главными осями. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.

Вычислим моменты инерции прямоугольника относительно центральных осей, параллельных его сторонам (рис. 11).

Выделим элементарную площадку в виде узкого прямоугольника, параллельного оси. Площадь элемента.

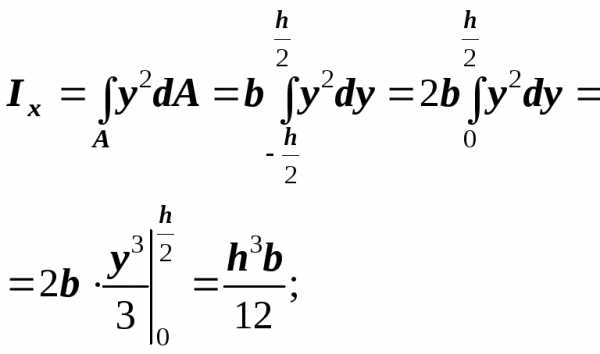
Аналогично, если выделить элементарную вертикальную полоску шириной , получим:и

.

Вычислим полярный момент инерции круга относительно его центра, а также момент инерции относительно центральной оси.

При вычислении полярного момента инерции выделим элементарную полоску в виде тонкого кольца толщиной 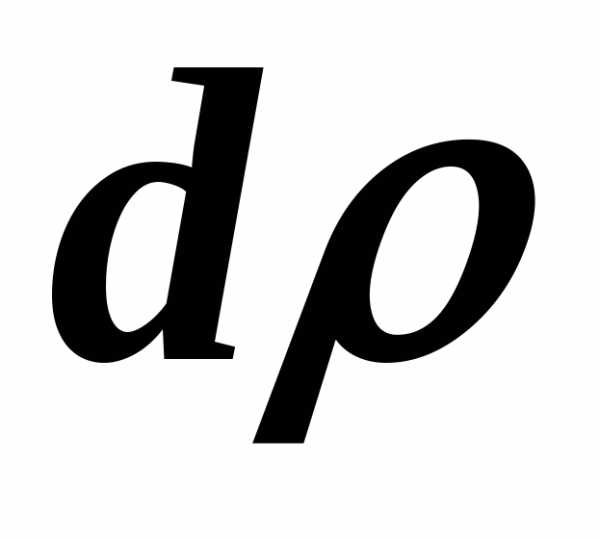(рис. 12). Площадь такого элемента равна

Ввиду малости слагаемым пренебрегаем.

Полярный момент инерции

.

В силу симметрии фигуры 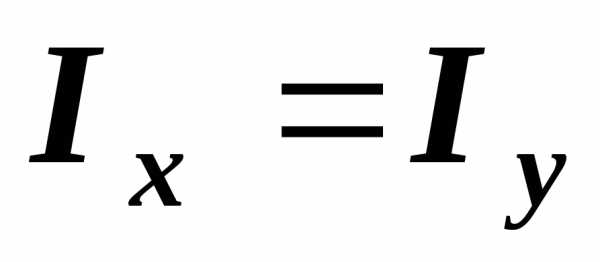. Используя свойство осевых и полярных моментов инерции, получим: . Отсюда

.

3. Моменты инерции сложных сечений.

В расчетной практике часто приходится вычислять моменты инерции сложных сечений. Для прокатных профилей (рис. 13) геометрические характеристики сведены в таблицы, которые называются сортаментом прокатной стали.

Рис. 13.

двутавр

швеллер

Равнобокий уголок

неравнобокий уголок

Пусть требуется определить моменты инерции сложной фигуры относительно осей ,(рис. 14). При вычислении моментов инерции сложных сечений их нужно разбить на простые части, моменты инерции которых известны.

Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей.

;

.

Если в сечении имеется отверстие (рис. 15), то его удобно считать фигурой с отрицательной площадью.

;

.

studfiles.net