5. Выводы
В результате проделанной работы были определены средние значения <t> прохождения грузом пути h с занесением в таблицу измерений времени прохождения груза (таблица 4.1).
Определены случайная, приборная и общая погрешности измерений t и рассчитаны погрешности величин t2.
Был построен линеаризованный график зависимости и рассчитан коэффициент t2, все точки укладываются в пределах погрешностей.
Определены момент инерции блока экспериментально и момент инерции блока аналитический. При сравнивании результатов получена разница в 1,358 %
6. Ответы на контрольные вопросы
1.Что такое момент сил и момент инерции?
Момент силы – это векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы. Характеризует вращательное действие силы на твердое тело.
2.Моменты каких сил действуют на блок?
На блок действуют: момент инерции тела, момент сил натяжения нитей, момент инерции оси вращения.
3.Как рассчитать момент инерции блока? Сформулировать теорему Штейнера.
Рассчитать момент инерции блока можно по формуле:
I=mбR2
Где mб – масса блока;
R – радиус блока.
Теорема Штейнера:
Момент инерции тела I0 относительно произвольной оси равен сумме момента инерции этого тела Ic относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния a между осями:
I0=Ic+ma2
где
Ic – известный момент инерции относительно оси, проходящей через центр масс тела,
I0 – искомый момент инерции относительно параллельной оси,
m – масса тела,
a – расстояние между осями.
4.Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Неточность вычислений; физические допущения при анализе движения грузов; погрешности измерения величин, колебания параметров среды, параметров измерительной установки.
7. ПРИЛОЖЕНИЕ
К работе прилагается регистрационный файл (phyLab2), файл
журнала измерений (Lab2.txt), рецензия:
studfiles.net
Физика 2 (Определение момента инерции твердых тел. Преподаватель Крафт. Год 2011. Зачет.) / Физика Лабораторная 2 ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ Преподователь Крафт
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная работа по курсу “Общая физика”
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
Студент группы: з-161-а, поток 8
Козлов Андрей Владимирович
29 марта 2012г.
2012
1. ЦЕЛЬ РАБОТЫ
Целью настоящей работы является изучение основных законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока и сравнение его с расчетным значением.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Схема экспериментальной установки на основе машины Атвуда приведена на рис. 3.1.
На вертикальной стойке 1 крепится массивный блок 2, через который перекинута нить 3 с грузами 4 одинаковой массы, равной 80 г. В верхней части стойки расположен электромагнит, который может удерживать блок, не давая ему вращаться. На среднем кронштейне 5 закреплен фотодатчик 6. Риска на корпусе среднего кронштейна совпадает с оптической осью фотодатчика. Средний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На стойке укреплена миллиметровая линейка 7, по которой определяют начальное и конечное положение грузов. За начальное, принимают положение нижнего среза груза, за конечное – риску на корпусе среднего кронштейна.
Миллисекундомер 8 представляет собой прибор с цифровой индикацией времени. Опоры 9 используют для регулировки положения установки на лабораторном столе.
Принцип работы машины Атвуда заключается в следующем. Когда на концах нити висят грузы одинаковой массы, система находится в положении безразличного равновесия. Если же на один из грузов (обычно на правый) положить перегрузок, то система выйдет из равновесия, и грузы начнут двигаться с ускорением.
Машина Атвуда
1 – стойка; 2 – блок; 3 – нить; 4 – грузы; 5 – средний кронштейн; 6 – фотодатчик; 7 – линейка; 8 – миллисекундомер; 9 – регулировочная опора.
Рис. 3.1
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Нахождение среднего времени прохождения и его квадрата:
где: td– среднее время прохождения, с
n – количество измерений
ti – время каждого измерения, c
Нахождение общей погрешности:

где: 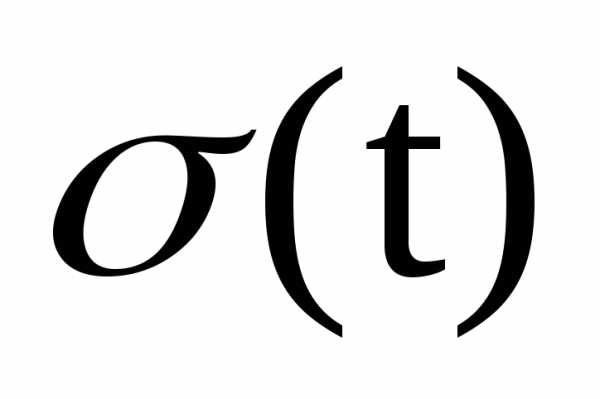 –
общая
погрешность, с
–
общая
погрешность, с
где: 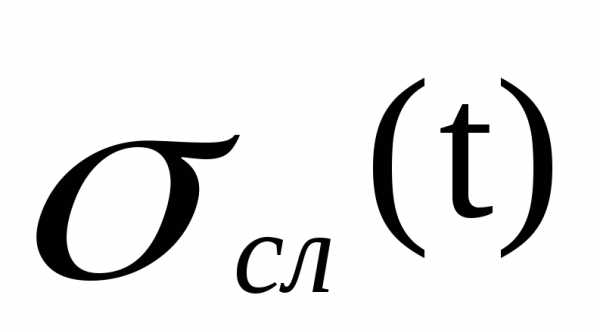 –
случайная погрешность, с
–
случайная погрешность, с
τ – коэффициент Стьюдента
Нахождение абсолютной погрешности и ее квадрата:
где σабс(t)- абсолютная погрешность, с
σсис(t) – системная погрешность, с
Нахождение углового коэффициента прямой и отрезка, отсекаемого прямой от оси OY:
K=k(n,h,t2 )
B=b(n,h,t2)
где К – угловой коэффициент прямой,
h – расстояние от груза до фотодатчика, м
В – отрезок, отсекаемый прямой, с2
Нахождение абсолютных погрешностей вычисления параметров прямой линии:
где σK – погрешность углового коэффициента,
σB – погрешность отрезка, отсекаемой от прямой,
Нахождение момента инерции блока экспериментально и аналитически:
где Iex – экспериментальный момент инерции,
Ian – аналитический момент инерции,
Ic – момент инерции блока относительно оси
вращения,
m – масса перегруза, г
М- масса груза, г
R – радиус блока, м
g – ускорение свободного падения,
Теорема Штейнера:
где Ian – аналитический момент инерции,
Ic – момент инерции блока относительно оси
вращения,
m — масса тела,, г
d — расстояние между указанными осями.
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Измеренные значения и результаты их обработки приведены в таблице 1
Таблица 1.Результаты измерений времени прохождения груза
Номер измерений | h1 =0,070 | h2 =0,079 | h3 =0,090 | h4 =0,099 | h5 =0,110 |
1 | 2,090 | 2,136 | 2,322 | 2,494 | 2,507 |
2 | 2,075 | 2,150 | 2,343 | 2,481 | 2,520 |
3 | 2,070 | 2,183 | 2,324 | 2,417 | |
4 | 2,044 | 2,198 | 2,350 | 2,455 | 2,553 |
5 | 2,093 | 2,163 | 2,372 | 2,361 | 2,622 |
2,074 | 2,166 | 2,342 | 2,442 | 2,553 | |
4,301 | 4,692 | 5,485 | 5,963 | 6,518 |
4.1. Определить средние значения времени прохождения грузом пути:
; сек. среднее значение времени
4.2. Определить случайную, приборную и общую погрешности измерений t и рассчитать погрешности величин t2
; с2 квадрат среднего значения времени
Так как класс точности электронных часов, используемых в работе не указан, то за приборную погрешность принимается единица в младшем разряде часов, то есть:
σсис(t)=0,001c
Чтобы вычислить случайную погрешность измерения времени, необходимо определить коэффициент Стьюдента и среднеквадратичное отклонение. Для серии из 5 измерений и доверительной вероятности 0,95 определяемый коэффициент Стьюдента равен 2,8
Таблица 2. Результаты вычислений средних значении времени и квадрата времени.
Номер измерений | ||
1 | 0,009 | 0,025 |
2 | 0,011 | 0,031 |
3 | 0,009 | 0,026 |
4 | 0,024 | 0,067 |
5 | 0,02 | 0,056 |
Таблица 3. Абсолютные суммарные погрешности измерения времени t и квадратов времени
Номер измерений | ||
1 | 0,026 | 0,108 |
2 | 0,032 | 0,140 |
3 | 0,027 | 0,125 |
4 | 0,068 | 0,334 |
5 | 0,057 | 0,290 |
4.3 Нанести экспериментальные точки на график в координатах
Здесь же указать погрешности в виде доверительных интервалов.
=
Угловой коэффициент
прямой равен K=
49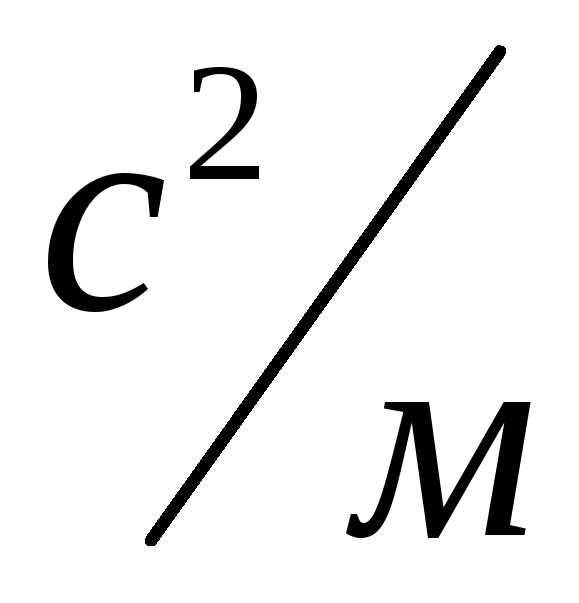
Отрезок отсекаемый прямой от ос OY B= -0,0001
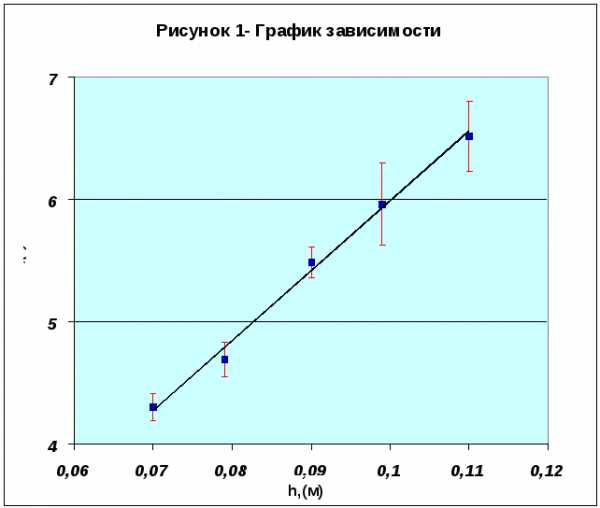
4.4 Провести интерполирующую прямую и вычислить величину k
Абсолютные погрешности вычисления параметров прямой линии:
4.5 Используя
выражение (3.7) для k
и учитывая, что M=100г.
M=2г.
R=75 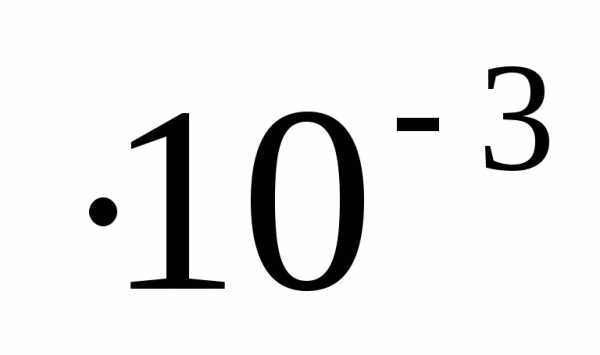 и g=9,807
и g=9,807 вычислить момент инерции I
блока
вычислить момент инерции I
блока
Iex= 1,567
4.6 Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок (латунь ) рассчитаем его момент инерции.
м – радиус блока,
м – радиус выреза,
м – расстояние от оси выреза до оси вращения самого блока,
м – высота блока.
Отсюда находим:
Объем сплошного блока:
Масса сплошного блока: кг
Объем цилиндрического выреза: м2
Масса цилиндрического выреза: кг
Момент инерции блока относительно оси вращения в предположении, что блок является сплошным:
Момент инерции цилиндрического выреза (считая его сплошным цилиндром) относительно центра симметрии выреза:
По теореме Штейнера вычисляем момент инерции цилиндрического выреза относительно (параллельной) оси вращения блока:
Аналитическое значение момента инерции:
4.7 Сравнить расчетное значение момента инерции блока с полученным экспериментально.
Полученные экспериментальным и аналитическим способами моменты инерции можно сравнить, получив отличие между ними в процентах:
5. ВЫВОДЫ
В ходе работы нами изучены основные законов динамики поступательного и вращательного движений твердых тел, экспериментальное определение момента инерции блока и сравнение его с расчетными значениями.
.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Что такое момент сил и момент инерции?
Момент инерции I материальной точки относительно неподвижной оси вращения – физическая величина, равная произведению массы m материальной точки на квадрат расстояния r между точкой и осью вращения: I = m∙r2.
Скалярная величина I = ΣIi = Σ(mi∙ri2) равная сумме моментов инерции всех материальных точек твердого тела и характеризующая инерционность тела по отношению к вращению – есть момент инерции твердого тела относительно выбранной оси вращения.
6.2. Моменты каких сил действуют на блок?
Вращательное движение блока описывается уравнением
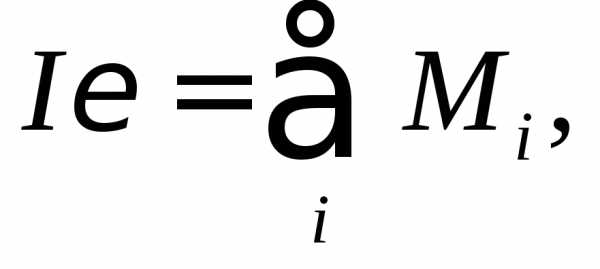
где ε – угловое ускорение блока,
I – его момент инерции,
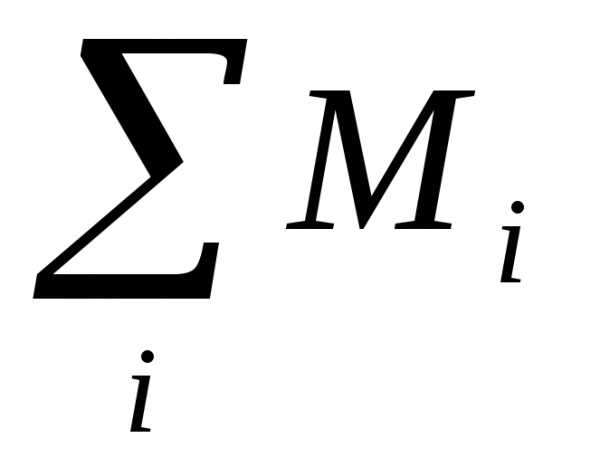 –сумма моментов
сил, приложенных к блоку.
–сумма моментов
сил, приложенных к блоку.
Сумма моментов сил равна T1R – T2R. При движении нерастяжимой нити без скольжения по блоку имеет место равенство
ε = a/R
где а – линейное ускорение точек на поверхности блока, а, следовательно, и самой нити,
R – радиус блока.
6.3. Как рассчитать момент инерции блока? Сформулировать теорему Штейнера.
Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
I = I0 + ml².
6.4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Физические допущения, принятые при теоретическом анализе движения грузов в эксперименте;
Погрешности измерения величин;
Точность вычислений.
7. ПРИЛОЖЕНИЕ
К работе прилагается регистрационный файл (*.REG).
studfiles.net
Определение момента инерции твердых тел
= 2911 г∙см2Момент инерции блока с тремя вырезами в виде малых дисков
I_an= I_CD-3∙ I_can I_an = 16298 г∙см2
Полученные экспериментальным и аналитическим способами моменты инерции можно сравнить, получив отличие между ними в процентах, при помощи нижеследующего соотношения:
5. ВЫВОДЫ
Используя экспериментальные данные, был построен график линеаризованной зависимости и рассчитаны коэффициенты соответствующего уравнения t 2 = f ( h ) = 0,49∙ h с2 . Все точкив этой зависимостиукладываются на прямую в пределах их погрешностей.Это свидетельствует, что экспериментальная зависимость t 2 = f ( h ) соответствует теоретической, т.е. экспериментально доказана справедливость основного уравнения динамики вращательного движения:Значение собственного момента инерции,полученное в ходе эксперимента равно:
I_ex = 1,7 кг∙м2
Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок, рассчитан его момент инерции:
I_an = 1,6кг∙м2
Значение собственного момента инерции,полученное в ходе эксперимента, больше расчетного
Несовпадение экспериментального результата с расчетным можно объяснить тем, что не учитывался момент сил трения. Это и привело к завышенному значению собственного момента инерции блока в эксперименте.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое момент сил и момент инерции?
Моментом силы относительно оси называется физическая величина, численно равная произведению величины составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на плечо этой составляющей, т.е. на кратчайшее расстояниеr от оси вращения до линии действия
Момент силы относительно оси есть вектор, направленный вдоль этой оси и связан с направлением вращения правилом правого винта.
Момент инерции характеризует инерционные свойства вращающихся тел. Чем больше момент инерции тела, тем труднее изменить его угловую скорость. Момент инерции во вращательном движении аналогичен массе тела в поступательном движении. Момент инерции тела относительно некоторой оси зависит от распределения его массы относительно оси вращения.
Для элемента тела массой dm момент инерции dI выражается соотношением: dI = r 2 dm ,
где r – расстояние от элемента dm до оси вращения.
Момент инерции всего тела запишется в виде интегралагде интегрирование осуществляется по всему телу.
2. Моменты каких сил действуют на блок?
Т1 и Т2 – силы натяжения нитей.На блок действуют моменты сил натяжения нитей:
M 1 = T 1 R , M 2 = T 2 R .
Вращательное движение блока описывается уравнением:
Рис. 6.1 где ε – угловое ускорение блока, I – его момент инерции,– сумма моментов сил, приложенных к блоку.
Согласно рис.6.1 вращательное движение блока описывается уравнением
3. Как рассчитать момент инерции блока?
Сформулировать теорему Штейнера.
Момент инерции блока рассчитывается как:
I = I диск – 3× I отв
где I диск – момент инерции сплошного диска;
I отв – момент инерции цилиндрического отверстия (“дырки”).
Момент инерции цилиндрического отверстияI отв относительно оси, проходящей через центр масс блока, определяем согласно теоремы Штейнера.
Теорема Штейнера :
Момент инерции I относительно произвольной оси, равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
I = I 0 + ml 2
4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин; точность вычислений.
7. ПРИЛОЖЕНИЕ
К работе прилагается:
· регистрационный файл – phyLab2.reg
· файл журнала измерений – Ж.лаб2.txt
mirznanii.com
Изучение вращательного и поступательного движения тел на машине Атвуда
Значение
собственного момента инерции, полученное в ходе эксперимента, больше
расчетного на 1,798%. Несовпадение экспериментального
результата с расчетным можно объяснить тем,
что не учитывался момент сил трения. Это и привело
к завышенному значению собственного
момента инерции блока в эксперименте.
.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое момент сил и момент инерции?
Моментом силы относительно оси называется физическая величина, численно равная произведению величины составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на плечо этой составляющей, т.е. на кратчайшее расстояние r от оси вращения до линии действия. Момент силы относительно оси есть вектор, направленный вдоль этой оси и связан с направлением вращения правилом правого винта.
Момент инерции – это скалярная величина, служащая мерой инертности тел при вращательном движении. Обладает свойством аддитивности: момент инерции тела, может быть найден как сумма моментов инерции всех частей тела. Величина момента инерции зависит не только от массы и формы тела, но и от взаимного расположения тела и оси вращения. Аддитивность момента инерции позволяет легко вычислять его значение для тел, обладающих симметрией.
Для элемента тела
массой dm момент инерции dI выражается соотношением:
где r – расстояние от элемента dm до оси вращения.
Момент инерции всего тела запишется в виде интеграла:
где интегрирование осуществляется по всему телу.
2. Моменты каких сил действуют на блок?
На
блок действуют моменты сил
M1= T1R,
M2= T2R,
где Т1 и Т2 – силы натяжения нитей.
Вращательное движение блока относительно неподвижной оси описывается основным законом динамики вращательного движения:
где ε – угловое ускорение блока, I– его момент инерции,
М – сумма моментов сил, приложенных к блоку.
Рис. 6.1
Согласно рис.6.1 вращательное движение блока описывается уравнением:
dI = r2dm,
где r – расстояние от элемента dm до оси вращения.
3. Как рассчитать момент инерции блока?
Сформулировать теорему Штейнера.
Момент инерции блока рассчитывается как:
I = * mб*R2
где mб – масса
блока;
R – радиус блока.
Теорема Штейнера :
Момент инерции I относительно произвольной оси, равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
I = I0 + ml2
4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Физические допущения,
принятые при теоретическом анализе движения
грузов в эксперименте; погрешности измерения
величин; неточность вычислений.
7.
ПРИЛОЖЕНИЕ
К
работе прилагается регистрационный файл
(phyLab2.reg) и файл журнала измерений (лаб.2.txt).
turboreferat.ru
Момент – инерция – блок
Момент – инерция – блок
Cтраница 1
Моменты инерции блока В в барабана Б относительно их осей вращения соответственно равны / 2 и / t; радиус блока равен, г, радиус барабана R. [1]
Момент инерции блока относительно геометрической оси равен /, радиус блока г. Массу нити считать пренебрежимо малой. [2]
Массы и моменты инерции блоков 2 п 5 одинаковы. [3]
Массы и моменты инерции блоков 2 я 5 одинаковы. [4]
Массы и моменты инерции блоков 2 и 5 одинаковы. [5]
Рассмотрим движение ( рузов в машине Атвуда, не пренебрегая моментом инерции блока. [6]
Рассмотрим движение грузов в машине Атвуда до снятия добавочного груза Дт, не пренебрегая моментом инерции блока. [7]
При расчете оптимальных передаточных отношений пар зубчатой передачи, исходя из ее минимальной инерционности, момент инерции блока г-го ведомого колеса и f 1-го ведущего колеса принимается равным моменту инерции цилиндра с диаметром, равным диаметру начальной окружности ведомого колеса, и высотой, равной ширине зуба колеса. Такое допущение приводит к ошибке в оценке инерционности всей передачи, не превышающей 2 – 3 % от оптимального значения. Методика же расчета значительно упрощается. [8]
Определить ускорение, с которым будет опускаться грузик, и силу натяжения веревки, если известен момент инерции блока J. Считать веревку практически нерастяжимой и массой веревки и трением пренебречь. [9]
Это уравнение связывает моменты сил ТУ и ТУ с угловым ускорением блока а / г. i – момент инерции блока, г – его радиус. [11]
Кинетическая энергия системы равна Т – – – тхг – п – / со2, где 3 М № – момент инерции блока относительно оси О, а со ж / Л – угловая скорость вращения блока. Силовая функция равна V – – с ( К – f – х) г т х, где Kmg / c – статическое удлинение пружины. [12]
Масса одного груза на машине Атвуда 500 г, а масса другого 460 г. Радиус блока, смонтированного на подшипниках без трения, равен 5 0 см. Будучи освобожден для движения, более тяжелый груз за 5 сек переместился на 75 см. Как определить из этих данных момент инерции блока. [13]
Момент инерции блока /, радиус соответствующих участков блока. О 2.7.18. На валик радиуса г плотно насажен сплошной диск. [14]
При конструировании шпиндельных блоков большое внимание обращается на уменьшение их габаритов. Увеличение габаритов блока, особенно его наружного диаметра, увеличивает момент инерции блока и уменьшает допустимую скорость его поворота. [15]
Страницы: 1 2
www.ngpedia.ru
Определение момента инерции в машине атвуда — Учись Как На Парах!
Вводная часть
Цель работы
Целью данной работы является изучение вращательного и поступательного движений на машине Атвуда, определение момента инерции блока и момента сил трения в оси блока.
Приборы и принадлежности
Машина Атвуда, набор грузов, секундомер, масштабная линейка.
Исследуемые закономерности
Машина Атвуда является настольным прибором и предназначена для изучения законов поступательного и вращательного движений. На вертикальной стойке основания расположены три кронштейна: нижний, средний и верхний. На верхнем кронштейне крепится блок с узлом подшипников качения, через который переброшена нить с грузом. На верхнем кронштейне находится электромагнит, который при подаче на него напряжения с помощью фрикциона удерживает систему с грузами в неподвижном состоянии.
На среднем кронштейне крепится фотодатчик, выдающий электрический сигнал по окончании счета времени равноускоренного движения грузов. На среднем кронштейне есть риска, совпадающая с оптической осью фотодатчика. Нижний кронштейн представляет собой площадку с резиновым амортизатором, о который ударяется груз при остановке. На вертикальной стойке укреплена миллиметровая линейка, по которой определяют начальное и конечное положения грузов, т. е. пройденный путь.
Начальное положение определяют визуально по нижнему краю груза, конечное положение — по риске среднего кронштейна. времени.
Машина Атвуда предназначена для изучения законов поступательного и вращательного движений. Принцип работы установки основан на том, что, когда на концах нити подвешены грузы различной массы, система начинает двигаться равноускоренно. На каждый груз действуют две силы — сила тяжести и сила натяжения нити, под действием которых грузы движутся. Полагая, что нить невесома и нерастяжима, получим, что ускорения обоих грузов будут постоянны, одинаковы по значению и противоположны по направлению.
На основании второго закона Ньютона для первого груза с перегрузом и второго груза можно записать
Где m1 и m2 — массы 1-го и 2-го грузов; Δm, — масса перегруза, находящегося на 1-м грузе; Т1 и T2 — силы натяжения нити, действующие на 1-й и 2-й грузы; а — ускорение грузов. Вращение блока описывается уравнением
Где r — радиус блока; MTP — момент сил трения в оси блока; I — момент инерции блока; ε — угловое ускорение блока. Из предыдущих уравнений можно получить:
Где S — пройденный грузом за время t путь.
Расчетная часть
В результате проведенных экспериментов были получены следующие эксперименты
№ опыта | № изм-я | Δmi, г | T, с | Mк | ε | |||
1 | 1 | 1,3 | 2,981 | 3,0063 | 0,498 | 0,498 | 5,627 | 5,53 |
2 | 3,038 | 0,498 | 5,417 | |||||
3 | 3,00 | 0,498 | 5,556 | |||||
2 | 1 | 2,2 | 2,433 | 2,429 | 0,832 | 0,832 | 8,447 | 8,479 |
2 | 2,467 | 0,833 | 8,215 | |||||
3 | 2,387 | 0,831 | 8,775 | |||||
3 | 1 | 2,6 | 2,097 | 2,101 | 0,971 | 0,971 | 11,37 | 11,363 |
2 | 2,1 | 0,971 | 11,338 | |||||
3 | 2,096 | 0,971 | 11,381 | |||||
4 | 1 | 4,8 | 1,559 | 1,536 | 1,722 | 1,716 | 20,572 | 21,282 |
2 | 1,458 | 1,698 | 23,521 | |||||
3 | 1,591 | 1,728 | 19,753 | |||||
5 | 1 | 5,8 | 1,391 | 1,401 | 2,031 | 2,034 | 25,841 | 25,476 |
2 | 1,412 | 2,038 | 25,078 | |||||
3 | 1,400 | 2,034 | 25,510 |
Величина | Значение | Приборная погрешность |
S, м | 0,49 | 0,0005 |
R, м | 0,04 | 0,0005 |
M1, кг | 0,07765 | 0,000005 |
M2, кг | 0,07657 | 0,000005 |
Δm, кг | – | 0,00005 |
T, с | – | 0,001 |
1. Проверим значения t на наличие грубых промахов.
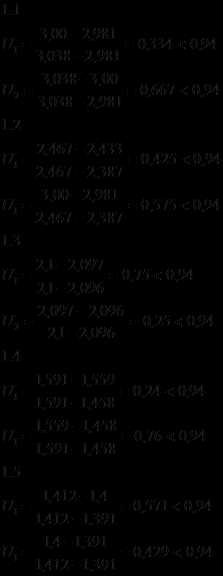
2. Рассчитаем значение погрешности для t.
Коэффициент Стьюдента для N = 3 и Р = 95% tp, n = 4,3
Коэффициент βN, P для N = 3 и Р = 95% tp, n = 4,3 βN, P = 1,3

2. Определим момент инерции блока (I) и момент сил трения в блоке (Мтр) методом наименьших квадратов. Для этого по формулам (3.5) и (3.6) вычислим значения Мк и ε. Из уравнения движения получаем, с учетом :
По этим формулам вычисляем значения Мк и ε.
3. Рассчитаем погрешность для величин Мк и ε
Вычислим средние значения Мк и ε и занесем их в таблицу
Выведем формулы для расчета погрешности для Мк и ε:

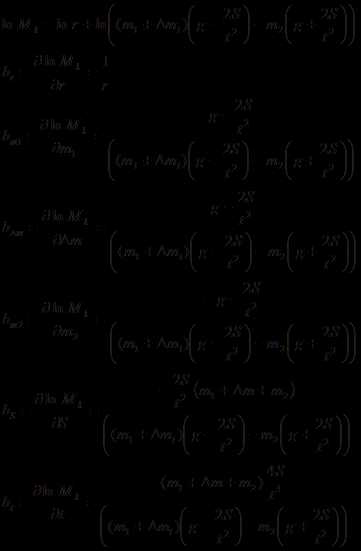
Вычислим значения полной погрешности для εi :
№ опыта | ε, x | Θε | Δε | |
1 | 5,53 | 0,078 | 0,368 | 0,446 |
2 | 8,479 | 0,122 | 0,698 | 0,82 |
3 | 11,363 | 0,164 | 0,162 | 0,326 |
4 | 21,282 | 0,315 | 5,542 | 5,857 |
5 | 25,476 | 0,381 | 1,455 | 1,839 |
Вычислим значения погрешности для Мк
№ опыта | МК, y | ΘМК | ΔМК | |
1 | 0,498 | 0,0063 | 0,0013 | 0,0076 |
2 | 0,832 | 0,01 | 0,0024 | 0,0124 |
3 | 0,971 | 0,012 | 0,0006 | 0,0126 |
4 | 1,716 | 0,022 | 0,027 | 0,049 |
5 | 2,034 | 0,026 | 0,0081 | 0,0341 |
Сопоставив линейную зависимость Y = aX + B и уравнение M = Iε + Mтр получаем, что X = ε; Y = M; a = I; b = Mтр.
Воспользуемся методом наименьших квадратов.
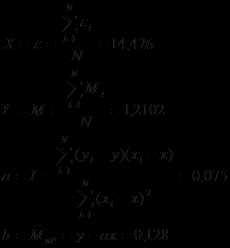
0,004
Mтр = 0,13 ± 0,02
I = 0,075 ± 0,01
Записи по теме
naparah.com
Момент инерции стержня, теория и примеры
Определение и общие понятия момента инерции стержня
Это скалярная (в общем случае тензорная) физическая величина, которую определяют как сумму произведений масс материальных точек () на которые разбивают тело на квадраты расстояний () от них до оси вращения:
Если тело рассматривают как непрерывное, то суммирование в формуле (1) заменяют на интегрирование, массы элементов тела обозначают как , тогда J тела, вращающегося около оси:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела. Для однородного тела выражение (2) представим как:
Формула для вычисления момента инерции однородного стержня
Определим формулу для вычисления момента инерции однородного стержня, вращающегося относительно оси (), которая проходит перпендикулярно стержню и идет через его один конец. Масса стержня равна m, длина l (рис.1).

Выделим в объеме стержня материальную точку (), которая находится от оси вращения на расстоянии r. Ее момент инерции равен:
Будем считать, что толщина стержня много меньше, чем его длина, тогда массу можно считать распределенной по длине стержня
Обозначим линейную плотность стержня как , тогда:
где – объем, стержня, который занимает наша материальная точка. Для нахождения момента инерции всего стержня проинтегрируем выражение (4), учитывая (6) и то, что :
Зная из (5), что:
формулу (7) перепишем в виде:
Мы получили, что момент инерции стержня вращающегося относительно оси, перпендикулярной ему и проходящей через один их его концов равен:
Для того чтобы получить момент инерции относительно оси, перпендикулярной стержню и проходящей через центр масс стержня (), следует рассмотреть интеграл:
в котором расстояние изменяется в пределах: :
Формула (11) дает момент инерции относительно оси, перпендикулярной стержню и проходящей через его центр масс.
Примеры решения задач
ru.solverbook.com
