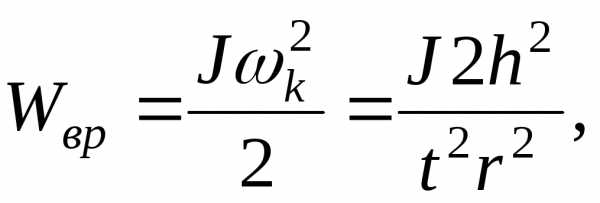Момент инерции сплошного цилиндра формула – Момент инерции цилиндра, теория и примеры

Момент инерции цилиндра, теория и примеры

Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:

   

где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.

Для получения формулы расчета момента инерции однородного цилиндра, мы его представим как совокупность бесконечно тонких дисков, а диск, в свою очередь – совокупность бесконечно тонких колец. Поэтому мы сначала получим выражение для момента инерции кольца, затем диска и только в самом окончании цилиндра.

Момент инерции тонкого кольца

Пусть кольцо имеем радиус R. Его называют бесконечно тонким, если его ширина и толщина много меньше радиуса. Пусть кольцо вращается относительно оси Z, перпендикулярной плоскости кольца и проходит через центр кольца (рис.1).

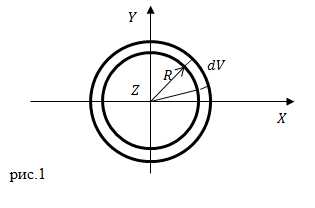
Выделим на кольце элементарную массу (), – плотность кольца; – элементарный объем кольца. Для нахождения момента инерции кольца нам следует найти интеграл (1). Все элементарные массы находятся на одном расстоянии от оси, то есть распределение массы кольца имеет цилиндрическую (осевую) симметрию.

   

Момент инерции бесконечно тонкого однородного диска

Пусть диск имеет радиус R. Он вращается относительно оси, которая проходит через его центр инерции, перпендикулярно его плоскости. Диск представим как систему бесконечно тонких колец, радиусы которых изменяются от нуля до R. Одно из таких колец изображено на рис.2.

Так как момент инерции тонкого кольца мы уже нашли, то его возьмем за элементарный:

   

где – масса выделенного кольца, равная:

   

Найдем момент инерции бесконечно тонкого диска, учитывая: :

   

массу бесконечно тонкого диска можно считать равной:

   

тогда момент инерции диска равен:

   

Момент инерции цилиндра

Для того, чтобы найти момент инерции однородного цилиндра, вращающегося относительно своей оси, представим его как совокупность дисков, толщиной . Формула (7) справедлива для диска имеющего толщину, поэтому в качестве элементарной массы мы возьмем диск. Тогда имеем:

   

где – высота цилиндра. Тогда момент инерции цилиндра относительно его собственной оси равен:

   

где масса цилиндра равна:

   

Примеры решения задач

ru.solverbook.com

Момент инерции цилиндра сплошного и полого: разное положение осей вращения

Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением. В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.

Момент инерции: математическое определение

Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:

I = m*r²

В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:

I = ∫r²dm

По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.

Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько “сильно” система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.

Момент инерции цилиндра относительно оси, его основаниям перпендикулярной

Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.

В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.

Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h – высота фигуры. Учитывая, что dm = ρ*dV, где ρ – плотность цилиндра, получаем:

I = ∫r²dm = ρ*∫r²dV = 2*pi*ρ*h*∫r³dr

Этот интеграл необходимо вычислить для пределов от 0 до R, где R – радиус фигуры. Тогда получим:

I = 2*pi*ρ*h*∫^R₀r³dr = 2*pi*ρ*h/4*(r⁴)∣^R₀ = pi*ρ*h*R⁴/2

Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:

I = m*R²/2, где m = pi*ρ*h*R²

Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.

Момент инерции полого цилиндра

Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R₁ и внутренним R₂. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R₂ до R₁. Имеем:

I = 2*pi*ρ*h/4*(r4)∣R1R2 = pi*ρ*h*R4/2∣R1R2 = pi*ρ*h/2*(R14-R24)

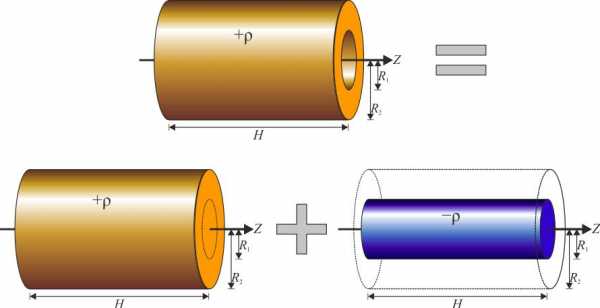
Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:

I = pi*ρ*h*(R₁²-R₂²)*(R₁²+R₂²)/2

Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:

I = m*(R₁²+R₂²)/2

Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R₂²/2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания

В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).

Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.

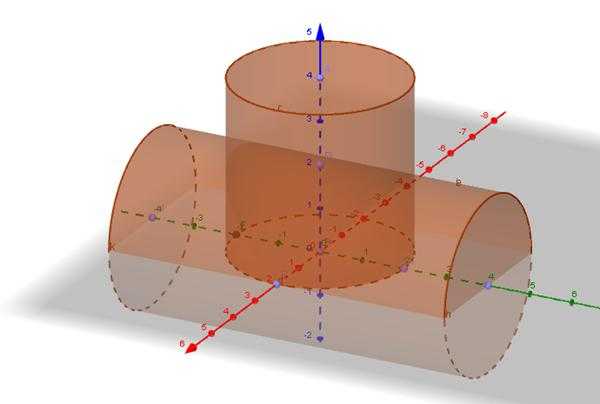
Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:

I_i = R²*dm/4

Чтобы найти, величину I_i для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:

I_i = R²*dm/4 + L²*dm, здесь L – расстояние от оси до тонкого диска.

Зная, что dm = pi*R²*dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L₀/2; +L₀/2), имеем:

I = ∫_mI_i = ∫_m(R²*dm/4 + L²*dm) = pi*R²*ρ*∫^L0/2_-L0/2(R²*dL/4 + L²*dL)

Решение этого интеграла приводит к конечной формуле:

I = m*(R²/4 + L₀²/12)

Пример решения задачи

Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.

Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:

I = m*R²/4 + m*L₀²/12 + m*(L₀/2)² = m*R²/4 + m*L₀²/3

Заметим, что если R<<L₀, тогда первым слагаемым можно пренебречь, и формула сводится к равенству:

I = m*L₀²/3

Этот момент инерции соответствует стержню с осью вращения на его конце.

fb.ru

Момент инерции полого цилиндра (кольца).

Определим момент инерции полого цилиндра, вращающегося вокруг оси симметрии, используя общую формулу (13) для определения момента инерции

(13)

Через R₁ обозначим внутренний радиус кольца высотой h, а через R

2 – внешний (рис.2).Объём кольца определится через разность площадей оснований S₁ и S₂

а масса кольца

(14)

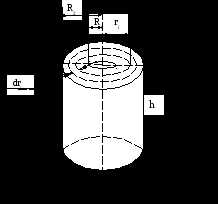
Разобьём кольцо на кольца бесконечно малой толщины dr_i.

Выделим колечко, отстоящее от оси вращения на расстоянии r_i. Объём этого колечка равен:

(15)

Подставим dV_i в формулу (13)

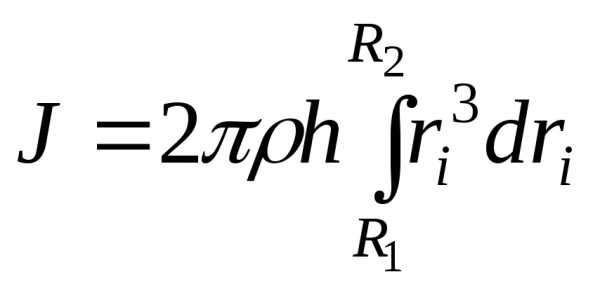и проинтегрируем.

Момент инерции кольца

(16)

Перепишем формулу (16) в виде и, учитывая выражение (14) получим момент инерции кольца

(17)

рис.2

3. Описание установки.

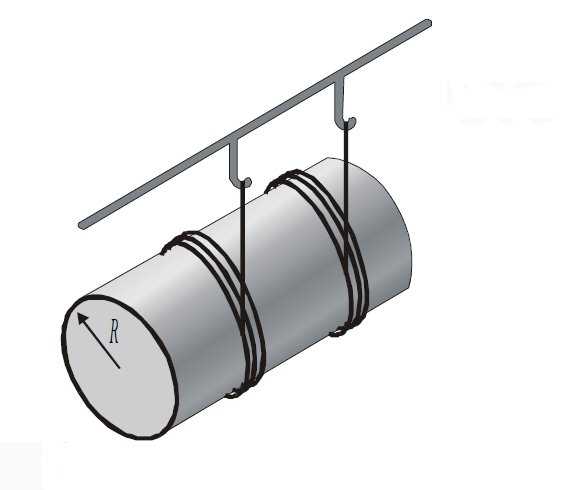
Маятник Максвелла FPM–03 предназначен для исследования закона сохранения энергии и определения на этом основании момента инерции колец.

Общий вид маятника Максвелла FPM–03 показан на рис.3. Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижный нижний кронштейн 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик №1–7 и вороток 8 для закрепления и регулирования длины бифилярной подвески маятника.

Нижний кронштейн вместе с прикрепленным к нему фтоэлектрическим датчиком №2 – 9 можно перемещать вдоль колонки и фиксировать в произвольно избранном положении.

Маятник 10 прибора FPM–03 – это ролик, закрепленный на оси и завешенный по бифилярному способу, на который накладываются заменные кольца 11, изменяющие таким образом момент инерции системы.

Рис.3. Общий вид маятника МаксвеллаFPM– 03.

Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале на колонке прибора.

Время движения маятника фиксируется миллисекундомером. На лицевой панели миллисекундомера находятся следующие манипуляционные элементы:

/сеть/ – выключатель сети. Нажатие этой клавиши включает напряжение питания. Визуально объявляется это свечением цифровых индикаторов (высвечивающих цифру ноль) и свечением лампочек фотоэлектрических датчиков.

/сброс/ – установка ноля измерителя. Нажатие клавиши вызывает сброс схем миллисекундомера FPM– 15.

/пуск/ – управление электромагнитом. Нажатие этой клавиши обозначает освобождение электромагнита и генерирование в схеме миллисекундомера импульса разрешения на измерение.

На задней стенке миллисекундомера находятся зажим заземления.

4. Теория метода.

Метод основан на выполнении фундаментального закона сохранения энергии–механическая энергия замкнутой консервативной системы при движении системы не меняется. Когда маятник Максвелла (основные элементы: ось, ролик и кольца) находятся на высоте hс нитью, намотанной на ось, вся система обладает потенциальной энергией

(18)

Затем маятник, вращаясь, опускается и потенциальная энергия уменьшаясь переходит в кинетическую. Кинетическая энергия системы будет состоять из кинетической энергии поступательного и вращательного движения.

Кинетическая энергия поступательного движения

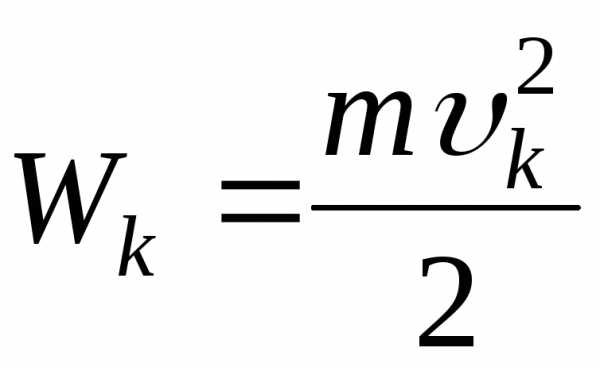, где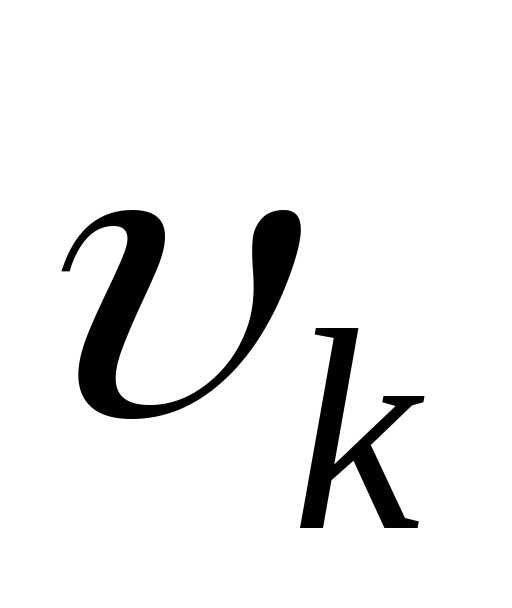– конечная скорость системы.

При равноускоренном движении с нулевой начальной скоростью конечная скорость определится по формуле:

,

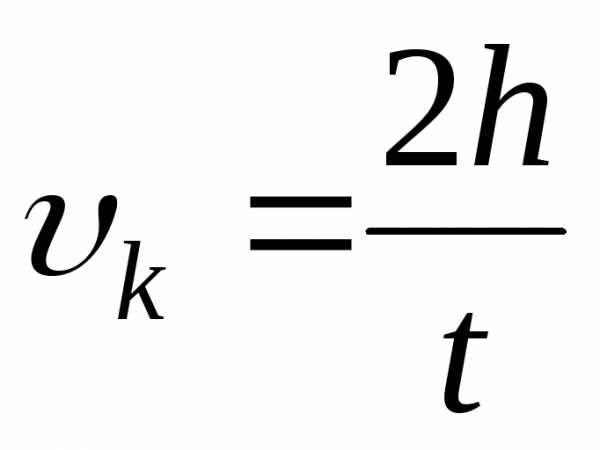т.к. ,,.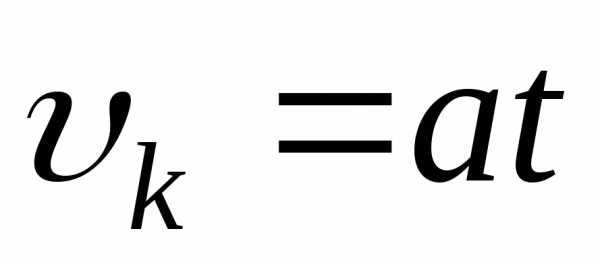

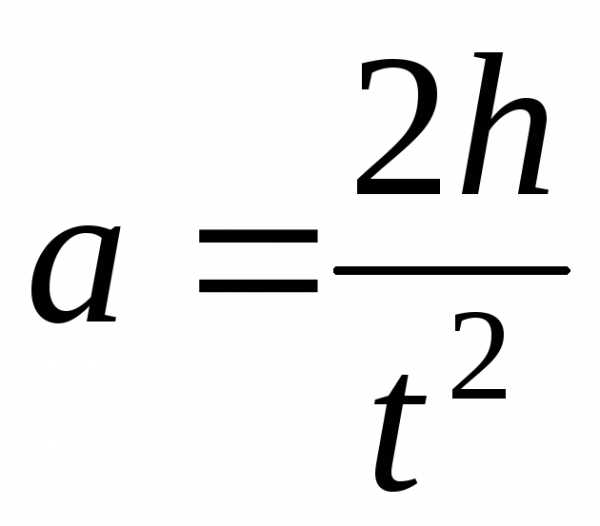Тогда кинетическая энергия поступательного движения будет равна:

(19)

Кинетическая энергия вращательного движения равна:

(20)

т.к.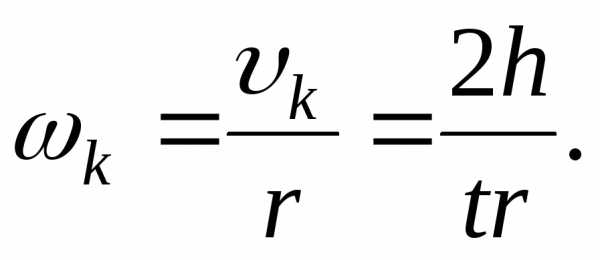

Подставляя формулы (19) и (20) в формулу, выражающую закон сохранения энергии всей системы

.

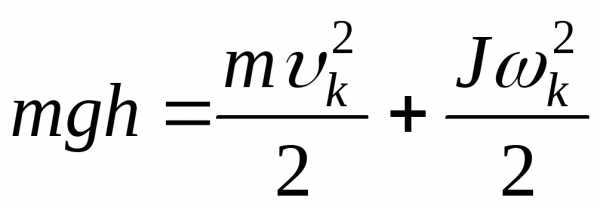
После преобразования получим рабочую формулу для определения момента инерции

(21)

studfiles.net

Момент инерции цилиндра

Момент инерции однородного цилиндра, диска, полого цилиндра и т. п. вычислим относительно его геометрической оси. Любое из этих тел мы можем мысленно разбить на тонкие цилиндрические слои, частицы которых находятся на одинаковом расстоянии от оси. Разобьем цилиндр радиуса R_o на концентрические слои толщиной dR (рис.1.21). Пусть радиус какого-то слоя R; тогда масса частиц, заключенных в этом слое, равна

 

dm = 2pRhr×dR,

 

где h – высота цилиндра;

r – плотность вещества цилиндра.

Все частицы слоя будут находиться на расстоянии R от оси, следовательно, момент инерции этого слоя (рис.1.21):

 

 

 

 

Рисунок 1.21

 

dI = dm×R² = 2prhR³×dR

 

Представим, что весь цилиндр разбит на такие слои; тогда момент инерции всего цилиндра будет равен сумме бесконечно малых моментов или момент инерции всего цилиндра

 

(1.19)

 

Вспоминая, что масса цилиндра m = pR_o²hr, можно записать так:

 

(1.20)

Формула (1.20) выражает момент инерции сплошного однородного цилиндра .

Момент инерции полого цилиндра, имеющего внутренний радиус R₁, а внешний R₀ просто вычислить по формуле (1.19), нужно только в интеграле поставить другие пределы, а именно:

 

 

Замечая, что масса полого цилиндра равна , запишем момент инерции полого толстостенного цилиндра так:

 

(1.21)

 

Таким же простым путем можно вычислить момент инерции любого тела, которое можно разбить на совокупность полых цилиндров, колец, дисков.

 

Похожие статьи:

poznayka.org

Цилиндры — Момент инерции – Энциклопедия по машиностроению XXL

Решение. Рассматривая обод маховика как полый цилиндр, найдем момент инерции его по формуле  [c.181]

Считая барабан однородным круглым сплошным цилиндром, определим момент инерции барабана по формуле  [c.652]

Цилиндры полые — Моменты инерции  [c.795]

Круглый цилиндр. Вычислим момент инерции круглого однородного цилиндра относительно его оси вращения z. Пусть радиус основания цилиндра равен К, а его масса равна М. Разобьем весь цилиндр плоскостями, параллельными его основанию, на бесконечно тонкие круглые пластинки. Момент инерции каждой такой пластинки относительно оси вращения цилиндра на основании формулы (142) будет равен 0,5 где (г — масса пластинки.  [c.506]

Пример 99. Тяжелый цилиндр радиуса г и массы т может скользить по плоскости, наклоненной к горизонту под углом а. Вокруг цилиндра обмотана нить, конец которой тянут вдоль наклонной плоскости с постоянным ускорением а (рис. 203). Определить ускорение центра масс цилиндра, если момент инерции цилиндра относительно оси симметрии равен Мк .  [c.347]

Вычислить момент инерции стального вала радиуса б см и массы 100 кг относительно его образующей. Вал считать однородным сплошным цилиндром.  [c.263]

На шероховатый круглый полуцилиндр радиуса В положен призматический брусок массы М с прямоугольным поперечным сечением. Продольная ось бруска перпендикулярна оси цилиндра. Длина бруска 21, высота 2а. Концы бруска соединены с полом пружинами одинаковой жесткости с. Предполагая, что брусок не скользит по цилиндру, найти период его малых колебаний. Момент инерции бруска относительно поперечной горизонтальной оси, проходящей через центр масс, равен /о.  [c.411]

Произведение модуля упругости второго рода на полярный момент инерции GJp называют жесткостью при кручении. Эта величина, характеризует способность тела из данного материала с поперечным сечением данных размеров и формы сопротивляться деформации кручения. Таким образом, полный угол закручивания цилиндра прямо пропорционален крутящему моменту и длине цилиндра и обратно пропорционален жесткости при кручении.  [c.192]

О — моменты инерции дисков, кг-м , для кругового цилиндра постоянной толщины диаметром D и массой т  [c.335]

Такая же формула получится, очевидно, и для момента инерции Уг однородного круглого цилиндра массой М и радиусом R относительно его оси (рис. 277, б).  [c.268]

Задана 120. Определить момент инерции цилиндра относительно оси Аг , проходящей через его образующую (см. рис. 277,6).  [c.269]

Момент инерции цилиндра относительно оси z определим как сумму моментов инерции А/сг элементарных пластинок относительно этой же оси, пользуясь формулой (36.2)  [c.97]

Для вычисления момента инерции цилиндра относительно оси Сх воспользуемся теоремой о моментах инерции тела относительно параллельных осей ( 35).  [c.97]

Подставив в (а) значение т,- и просуммировав моменты инерции пластинок, получим момент инерции цилиндра  [c.97]

Момент инерции полого цилиндра. Момент инерции полого цилиндра с внешним радиусом R и внутренним радиусом (рис. 82) относительно его центральной продольной оси z можно определить как разность моментов инерции сплошных цилиндров радиусами R и R .  [c.97]

Момент инерции полого цилиндра  [c.98]

Из формул (36.7), (36.8) и (36.4) следует, что моменты инерции конуса, шара и цилиндра, имеющих равные массы и радиусы, относятся как 3 4 5.  [c.99]

Вычислим моменты инерции вала (сплошного цилиндра) и махового колеса fio соответствующим формулам  [c.185]

Момент инерции цилиндра относительно его продольной оси, согласно формуле (36.4), равен J = mR /2. Угловая скорость катка равна отношению линейной скорости его центра масс С к расстоянию от точки С до мгновенного  [c.185]

Момент инерции цилиндра относительно оси g  [c.238]

Считать, что за время подъема цилиндра на наклонную плоскость скорость тележки 2, полученная ею в конце удара, остается постоянной, а вертикальные плоскости соударения тележек — гладкие. Поверхность рельсов абсолютно шероховата, т. е. препятствует проскальзыванию колес при соударении тележек. Моменты инерции колес относительно их осей пренебрежимо малы.  [c.229]

Определим моменты инерции и как разности моментов инерции тела I (сплошного цилиндра) и тела II (конуса) (рис. 205)  [c.263]

Момент инерции сплошного однородного цилиндра 01-носительно его геометрической оси (рис. 215, а)  [c.327]

Сопоставляя между собой при помощи рисунков формулы (1) и (2), а также (3) и (4), необходимо учитывать го, что при о,дной и той же массе стержней и одинаковой длине второй стержень обладает в четыре раза большим моменгом инерции (см. рис. 274, б), а также при одинаковых внешних размерах цилиндров и одинаковой массе (если цилиндры изготовлены из различных материалов, например из алюминия и стали) полый цилиндр обладает большим моментом инерции.  [c.327]

Если определять числовые значения моментов инерции обоих цилиндров, то  [c.328]

Момент инерции сплошного однородного цилиндра массой т относительно его геометрической оси г (рис, 1.176) выражается  [c.147]

Момент инерции полого цилиндра массой т относительно геометрической оси 2 выражается формулой (приводим ее без вывода).  [c.148]

Задача 288. Вычислить момент инерции относительно оси вращения г вала веса 100 мг и радиуса Ю см с насаженным на него маховиком веса 1 т и радиуса 1 м. Вал считать однородным сплошным цилиндром, маховик — однородным кольцом.  [c.198]

Момент инерции выделенного элементарного объема относительно оси 2 вычисляем по формуле момента инерции цилиндра  [c.200]

Задача 1221 (рис. 640). К вороту А, предстапляюгдему собой цилиндр с моментом инерции J и радиусом R, приложен вращающий момент М. Определить угловое ускорение s ворота, если массы грузов и М2 соответственно равны и т.,. Массами блоков, тросов и трением пренебречь.  [c.429]

Если КА имеет систему стабилизации угловой скорости собственного вращения и выполнен в виде цилиндра с моментами инерции — — а стабиплата также имеет форму  [c.48]

Формулы (29) и (30) дают нам хорошо сходящиеся строки, с помощью которых можем вычислять моменты инерции эквивалентных тел для различных углов р. Таким образом, получаем следующий результат если полость тела имеет форму круглого цилиндра, то момент инерции эквивалентного тела около оси цилиндра по формуле (14) равен нулю если же разделим эту полость диаметральными перегородками на двое, четверо или восемь равных частей, то момент инерции эквивалентного т ела составит 0,6211, 0,7904 или 0,9077 от момента инерции всей окидкой массы.  [c.210]

Момент инерции однороокого круглого цилиндра. Определим моменты инерции однородного круглого цилиндра относительно продольной оси цилиндра Сг и осей Сх и Су, проведенных по диаметрам среднего поперечного сечения цилиндра (рис. 81).  [c.347]

Дано = 0,05 м, = 0,25 м, координата центра масс S шатуна = = 0,10 м, диаметр цилиндра Dj = 0,13 м, диаметр штока Dj = 0,11 м, масса шатуна = 1,8 кг. масса поршня = 2,2 кг, момент инерции шатуна относительно оси, проходящей через его центр масс S, равен = 0,025 кгм , момент инерции кривошипа вместе с приведенными к нему массами звеньев редуктора и ротора электромотора / == 0,07 кгм . Давление газа на поршень задано индикаторной диаграммой (рис. 92, б) максимальное давление на поршень в первой ступени = 22,5 hI m , максимальное давление на поршень во второй сту-  [c.166]

Для вычисления центробежного момента инерции в качестве всномо-1 ительных осей координат возьмем главные центральные оси инерции цилиндра Сх у (оси его симметрии). Систему осей координат x y z можно получить  [c.380]

Момент инерции полого однородного цилиндра относи1е-льно его геометрической оси (рис. 275, 5)  [c.327]

---

mash-xxl.info

I = m(R2/4 + h3/12)

“Ось перпендикулярна к цилиндру и проходит через его центр масс” – это мы догадываться должны? Вот вопрос, для каких тел уже известен момент инерции. Я бы в стал так делать: 1. Нашел момент инерции диска для оси, перпендикулярной диску, проходящей через его центр масс. Задачка очень популярная и, возможно, Вами уже решенная. 2. Нашел момент инерции диска для оси, лежащей в плоскости диска, проходящей через его центр масс. Будет половина от предыдущего из соображения симметрии координат в интеграле 3. Проинтегрировал бы цилиндр по дисковым сечением. Теорема Гюйгенса-Штейнера в помощь, да и ответ намекает, что такой подход должен красиво сработать.

По определению момента, как интеграл массы-радиуса по объему цилиндра.

найдем момент инерции относительно оси проходящей через центр масс цилиндра перпендикулярно оси цилиндра. проведем ось ОХ вдоль оси цилиндра, разобьем цилиндр на малые цилиндры. пусть х – расстояние от одного из таких элементов до оси, а dx – его длина. тогда момент инерции такого элемента dJc=x^2*dm=x^2DS*dx, где D – плотность материала цилиндра, S – площадь его поперечного сечения. интегрируя по ч от 0 до l/2 найдем момент инерции одной половинки цилиндра, а искомый момент будет в 2 раза больше Jc=2SD*int x^2*dx=2/3*DS(l/2)^3=ml^2/12, т. к. DSl=m. приведенный вами момент возможно получен после применения теоремы Гюйгенса-Штейнера, но о нём вы в вопросе ничего не говорите.

touch.otvet.mail.ru