Момент инерции тела, теория и примеры
Определение момента инерции
Это скалярная (в общем случае тензорная) физическая величина, которая равна произведению масс материальных точек () на которые следует провести разбиение рассматриваемого тела, на квадраты расстояний () от них до оси вращения:
В том случае, если тело можно считать непрерывным, то суммирование в формуле (1) заменяют на интегрирование, массы элементов тела обозначают как , тогда J тела, вращающегося около оси:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Для однородного тела выражение (2) можно представить как:
Момент инерции в международной системе единиц измеряется в :
Величина J входит в основные законы, при помощи которых описывают вращение твердого тела.
В общем случае величина момента инерции зависит от направления оси вращения, а так как в процессе движения вектор обычно изменяет свое направление относительно тела, то момент инерции следует рассматривать как функцию времени. Исключением является момент инерции тела, вращающегося вокруг неподвижной оси. В таком случае момент инерции остается постоянным.
Теорема Штейнера
Теорема Штейнера дает возможность вычислить момент инерции тела относительно произвольной оси вращения, когда является известным момент инерции рассматриваемого тела по отношению к оси, проходящей через центр масс этого тела и эти оси являются параллельными. В математическом виде теорема Штейнера представляется как:
где – момент инерции тела относительно оси вращения, проходящей через центр масс тела; m – масса, рассматриваемого тела; a- расстояние между осями. Обязательно следует помнить, что оси должны быть параллельны. Из выражения (4) следует, что:
Некоторые выражения для вычисления моментов инерции тела
При вращении вокруг оси материальная точка имеет момент инерции равный:
где m – масса точки; r – расстояние от точки до оси вращения.
Для однородного тонкого стержня массой m и длиной l J относительно оси, проходящей через его центр масс (ось перпендикулярна стержню), равен:
Тонкое кольцо, с массой вращающееся около оси, которая проходит через его центр, перпендикулярно плоскости кольца, то момент инерции вычисляется как:
где R – радиус кольца.
Круглый однородный диск, радиуса R и массы m имеет J относительно оси, проходящей через его центр и перпендикулярной плоскости диска, равный:
Для однородного шара
где m – масса шара; R – радиус шара. Шар вращается около оси, которая проходит через его центр.
Если осями вращения являются оси прямоугольной декартовой системы координат, то для непрерывного тела моменты инерции можно вычислить как:
где – координаты бесконечно малого элемента тела.
Примеры решения задач
ru.solverbook.com
Глава 3. Динамика вращательного движения
§ 3.1 Момент силы. Момент импульса.
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
М = Fp=Frsinα.
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
Направление М можно найти с помощью правила правого винта.
Моментом импульса частицы называется векторное произведение радиус-вектора частицы на её импульс:
или в скалярном виде L = гPsinα
Эта величины векторная и совпадает по направлению с векторами ω.
§ 3.2 Момент инерции. Теорема Штейнера
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая
Моментом инерции материальной точки относительно оси вращения называют произведение массы этой точки на квадрат расстояния её от оси:
Ii=miri2 (3.2)
Момент инерции тела относительно оси вращения называют сумму моментов инерции материальных точек, из которых состоит это тело:
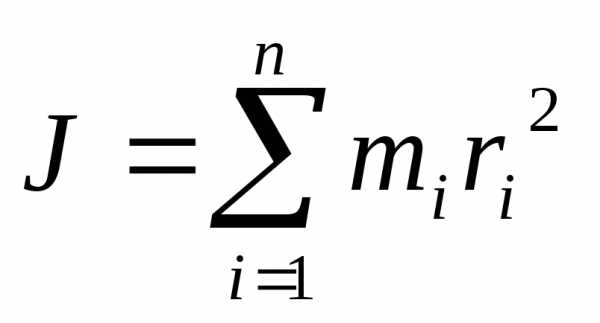 (3.3)
(3.3)
В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами dm, момент инерции определяется интегрированием:
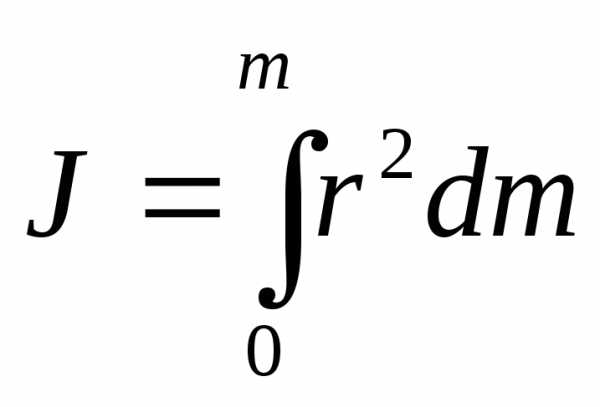 (3.4)
(3.4)
[r — расстояние от оси вращения до элемента массой dm].
Если
тело однородно и его плотность 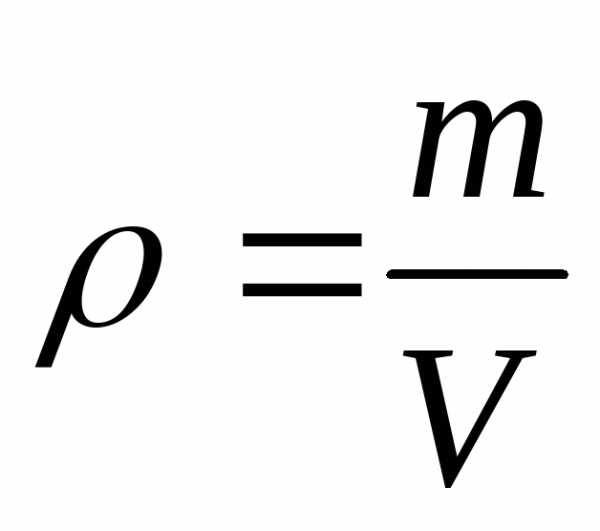 ,
то момент инерции тела
,
то момент инерции тела
 (3.5)
(3.5)
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.
Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню
 (3.6)
(3.6)
Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,

Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,
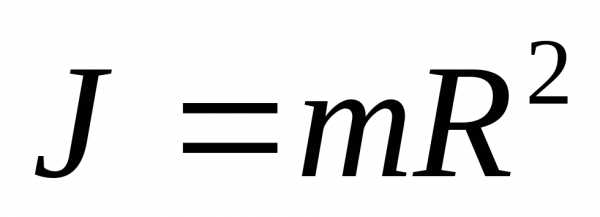 (3.8)
(3.8)
 (3.9)
(3.9)
Рассмотрим пример. Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоскости вращения. Масса диска — m, радиус — R.
Площадь кольца (рис. 3.2), заключенного между
r и r + dr, равна dS = 2πr·dr . Площадь диска S = πR2.
Следовательно,  .
Тогда
.
Тогда
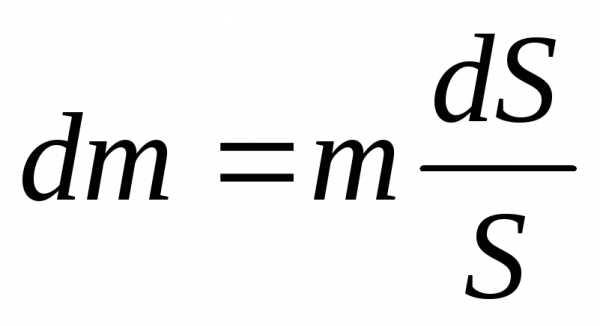 или
или 
Согласно
(3.10)
Приведенные формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться
(3.11)
[m — масса тела, d — расстояние от центра масс до выбранной оси вращения (расстояние между осями)].
Единица момента инерции — килограмм-метр в квадрате (кг· м2).
Так, момент инерции однородного стержня относительно оси, проходящей через его конец, по теореме Штейнера равен
(3.12)
8. Динамика твердого тела
В механике под твердым телом понимают систему материальных точек, расстояние между любыми двумя точками которого в процессе движения остается неизменным. Поэтому все результаты, полученные в предыдущих темах (“Динамика материальной точки”, “Закон сохранения импульса”, “Закон сохранения энергии” и “Закон сохранения момента импульса”) для системы материальных точек, применимы и к твердому телу.
Момент инерции твердого тела
Момент инерции – это величина, зависящая от распределения масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. При вращении твердого тела вокруг неподвижной оси момент инерции тела относительно этой оси определяется выражением
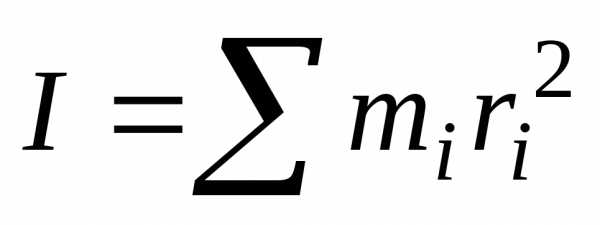 ,
,
где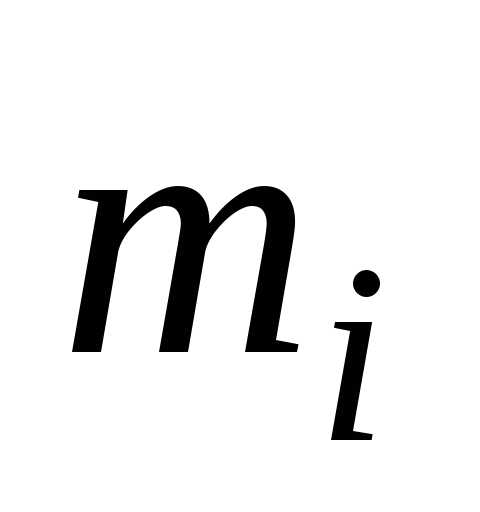 –
элементарные массы тела;
–
элементарные массы тела; –
их расстояния от оси вращения.
–
их расстояния от оси вращения.
Момент инерции тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции сводится к вычислению интеграла
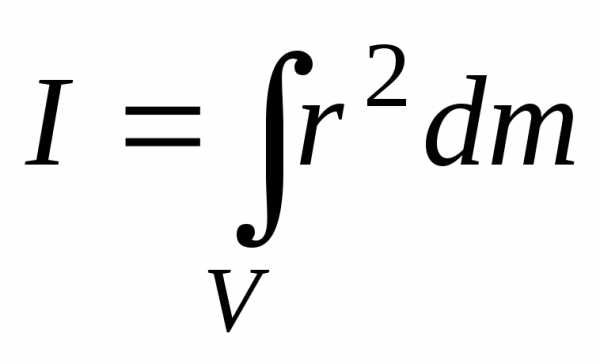 ,
(1)
,
(1)
где 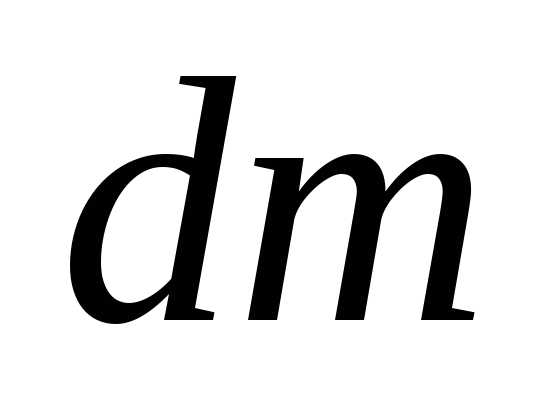 –
масса элемента тела, находящегося на
расстоянии
–
масса элемента тела, находящегося на
расстоянии от интересующей нас оси. Интегрирование
должно производиться по всему объему
тела.
от интересующей нас оси. Интегрирование
должно производиться по всему объему
тела.
Аналитическое вычисление таких интегралов возможно только в простейших случаях тел правильной геометрической формы.
Если
известен момент инерции тела относительно
какой-либо оси, можно найти момент
инерции относительно любой другой оси,
параллельной данной. Используя теорему
Штейнера, согласно которой момент
инерции тела 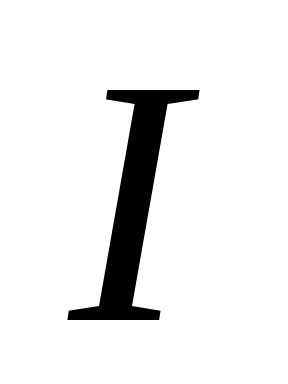 относительно произвольной оси равен
сумме момента инерции тела относительно
оси, проходящей через центр масс тела
относительно произвольной оси равен
сумме момента инерции тела относительно
оси, проходящей через центр масс тела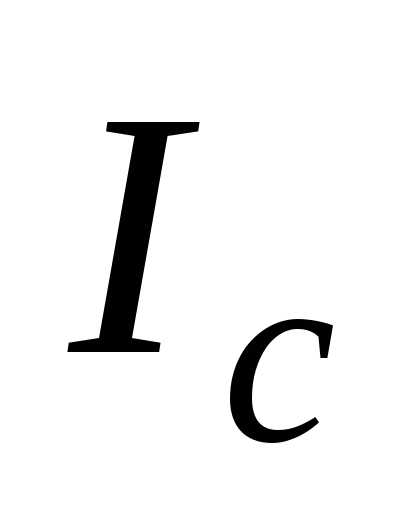 и параллельной данной оси, и произведения
массы телат на квадрат расстояния между осями
и параллельной данной оси, и произведения
массы телат на квадрат расстояния между осями  :
:
(2)
Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительномомент инерции относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений.
Рассмотрим
некоторую точку твердого тела массой  и с координатами
и с координатами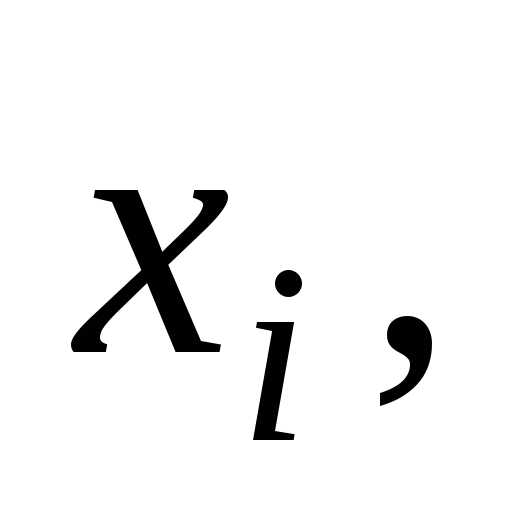
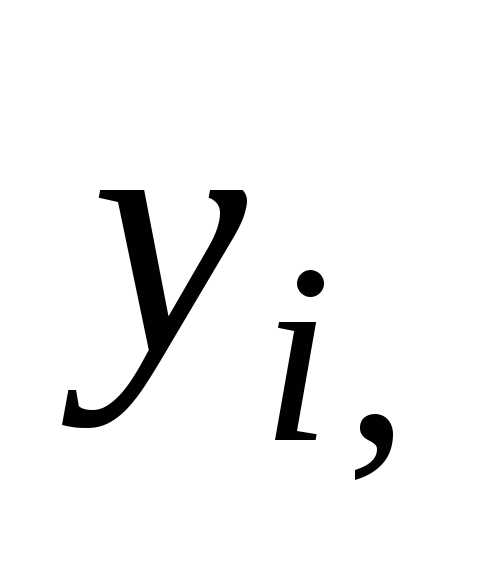
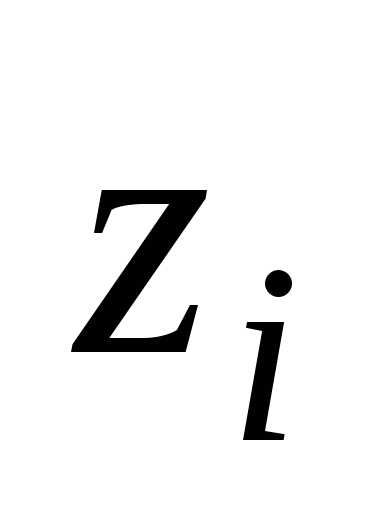 относительно прямоугольной системы
координат (рис. 1). Квадраты расстояний
ее до координатных осей
относительно прямоугольной системы
координат (рис. 1). Квадраты расстояний
ее до координатных осей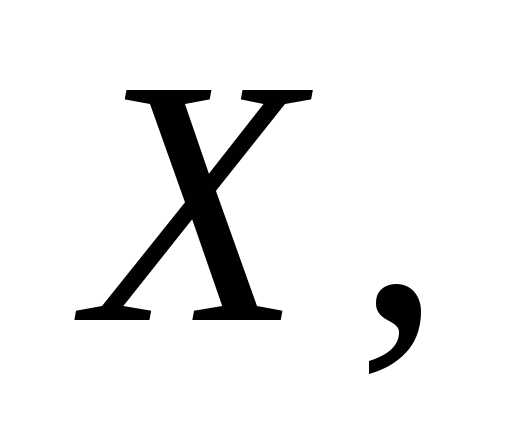
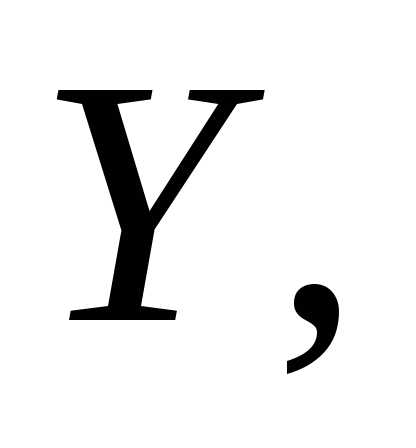
 равны соответственно
равны соответственно
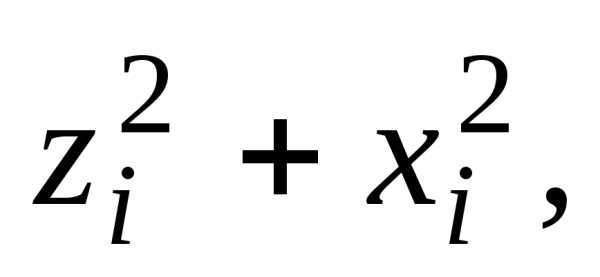
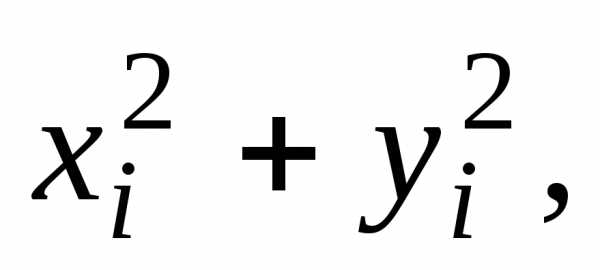 а
моменты инерции относительно тех же
осей
а
моменты инерции относительно тех же
осей
(3)
Сложив эти равенства и просуммировав по всему объему тела
(4)
получим
(5)
где – момент инерции телаотносительно точки.
Из
этого выражения можно получить связь
между моментами инерции плоского тела,
относительно осей 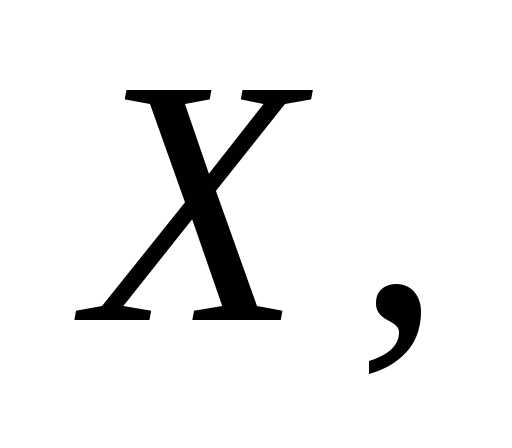
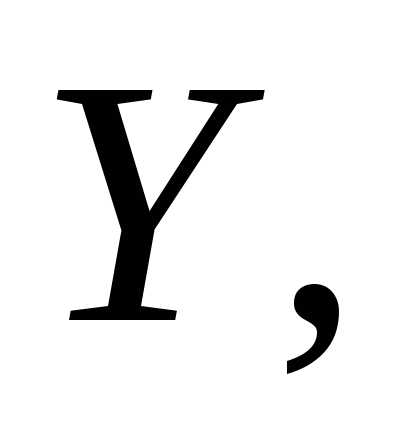
 .
Пусть масса плоского тела сосредоточена
в плоскости
.
Пусть масса плоского тела сосредоточена
в плоскости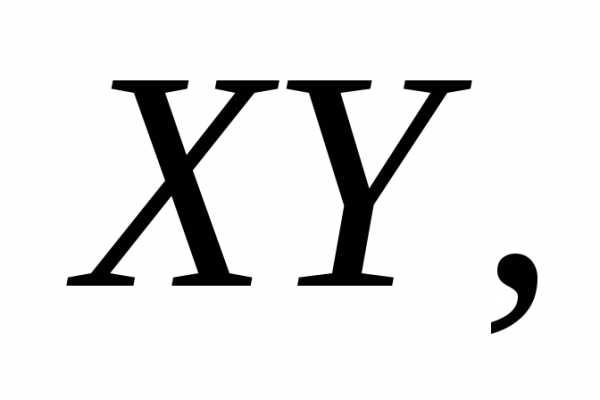 т.е. координата
т.е. координата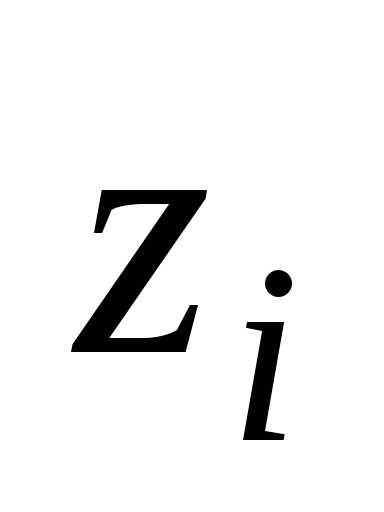 любой точки такого тел равна нулю,
тогда из
любой точки такого тел равна нулю,
тогда из
уравнений (3) и (4) следует, что
или
(6)
Вращение твердого тела вокруг неподвижной оси
Рассмотрим
твердое тело массой  ,
вращающееся вокруг неподвижной оси с
угловой скоростью
,
вращающееся вокруг неподвижной оси с
угловой скоростью .
Для того чтобы получить уравнение,
описывающее это движение, применим
уравнение моментов относительно оси,
полученное в разделе “ Закон сохранения
момента импульса”
.
Для того чтобы получить уравнение,
описывающее это движение, применим
уравнение моментов относительно оси,
полученное в разделе “ Закон сохранения
момента импульса”
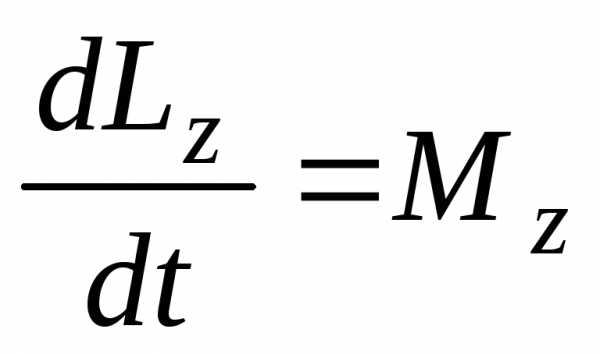 ,
(7)
,
(7)
напомним,
что в этом уравнении  и
и – момент импульса и момент силы
относительно оси, вокруг которой
вращается твердое тело.
– момент импульса и момент силы
относительно оси, вокруг которой
вращается твердое тело.
Момент
импульса некоторой точки тела массой 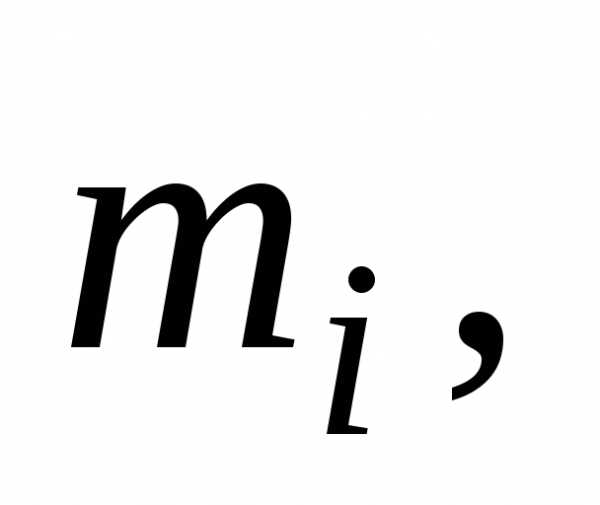 вращающейся
по окружности радиуса
вращающейся
по окружности радиуса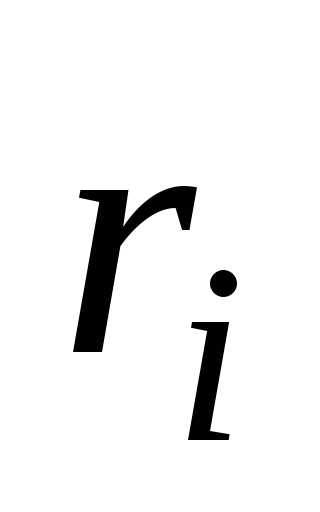 со скоростью
со скоростью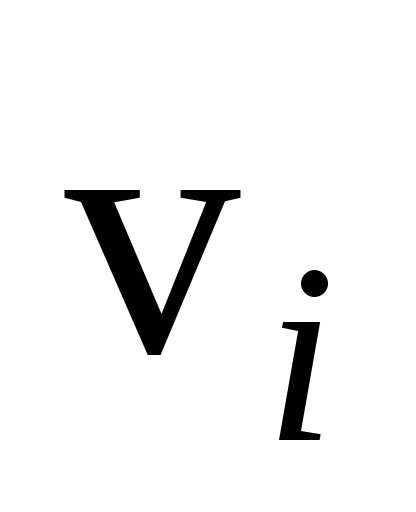 ,
равен
,
равен
Просуммировав
по всему объему тела, учитывая, что 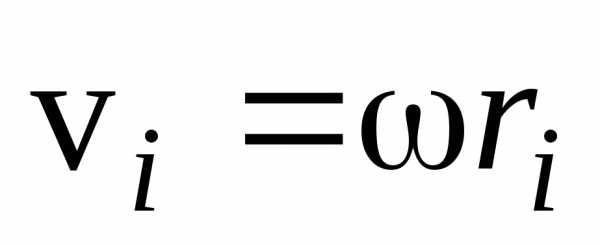 получим
получим
Таким образом, момент импульса твердого тела, вращающегося вокруг неподвижной оси, равен произведению момента инерции тела относительно этой оси на его угловую скорость.
Подставляя полученное выражение в (7), получим уравнение динамики твердого тела, вращающегося вокруг неподвижной оси,
 или
(8)
или
(8)
где  – угловое ускорение тела.
– угловое ускорение тела.
Найдем кинетическую энергию вращающегося тела. Для этого просуммируем по всему объему тела кинетические энергии отдельных его частей
или
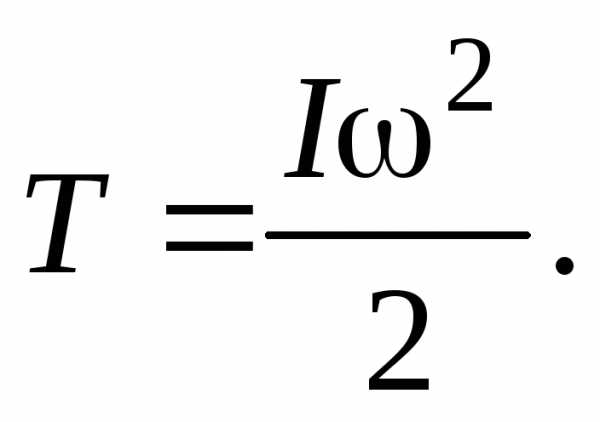 (9)
(9)
Зная
зависимость момента сил, действующих
на тело, от угла поворота, можно найти
работу этих сил при повороте тела на
конечный угол 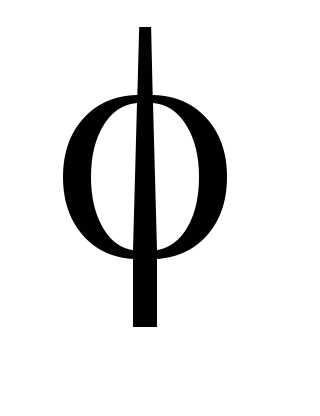
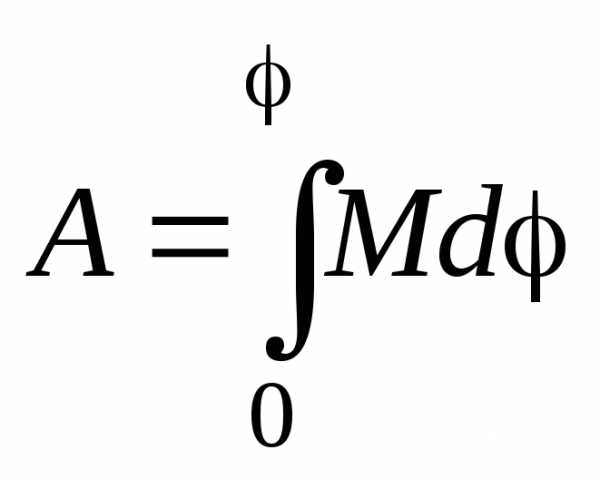 .
.
studfiles.net
Момент инерции – это… Что такое Момент инерции?
величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z называется величина, определяемая равенством:
где mi — массы точек тела, hi — их расстояния от оси z, ρ — массовая плотность, V — объём тела. Величина Iz является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой М. и. можно также выразить через линейную величину k, называемую радиусом инерции, по формуле Iz = Mk2, где М — масса тела. Размерность М. и. — L2M; единицы измерения — кг․м2 или г․см2.Центробежным М. и. относительно системы прямоугольных осей х, у, z, проведённых в точке О, называют величины, определяемые равенствами:
или же соответствующими объёмными интегралами. Эти величины являются характеристиками динамической неуравновешенности масс. Например, при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в которых закреплена ось.
М. и. относительно параллельных осей z и z’ связаны соотношением
Iz = Iz‘ + М d2 (3)
где z’ — ось, проходящая через центр масс тела, a d — расстояние между осями (теорема Гюйгенса).
М. и. относительно любой, проходящей через начало координат О оси Ol с направляющими косинусами α, β, γ находится по формуле:
lol = Ix α2 + Iy β2 + Iz γ2 — 2Ixy αβ — 2Iyz βγ — 2Izxγα. (4)
Зная шесть величин Ix, Iy, Iz, Ixy, Iyх, Izx, можно последовательно, используя формулы (4) и (3), вычислить всю совокупность М. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно-перпендикулярные оси, называемые главными осями инерции, для которых Ixy = Iyz = Izx = 0. Тогда М. и. тела относительно любой оси можно определить, зная главные оси инерции и М. и. относительно этих осей.
М. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о М. и. широко пользуются при решении многих задач механики и техники.
Лит.: Краткий физико-технический справочник, под общ. ред. К. П. Яковлева, т. 2, М., 1960, с. 94—101; Фаворин М. В., Моменты инерции тел. Справочник, М., 1970; Гернет М. М., Ратобыльский В. Ф., Определение моментов инерции, М., 1969; см. также лит. при ст. Механика.
С. М. Тарг.
dic.academic.ru
Момент инерции различных тел. Теорема Штейнера
Лабораторная работа 15
МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА.

Экспериментальная установка
Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.
Общие сведения
 Момент
инерции тела является мерой инертности тела при вращательном движении,
подобно тому, как масса тела является мерой инертности тела при поступательном
движении. Момент инерции тела зависит от размеров и формы тел и от
распределения массы тела относительно оси вращения. Для вычисления момента
инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на
большое число весьма малых элементов – материальных точек (рис.1). Тогда момент
инерции такой отдельной элементарной массы
Момент
инерции тела является мерой инертности тела при вращательном движении,
подобно тому, как масса тела является мерой инертности тела при поступательном
движении. Момент инерции тела зависит от размеров и формы тел и от
распределения массы тела относительно оси вращения. Для вычисления момента
инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на
большое число весьма малых элементов – материальных точек (рис.1). Тогда момент
инерции такой отдельной элементарной массы
где – расстояние от элемента объема до оси вращения, r – плотность вещества.
Момент инерции всего тела
,
Таким образом, момент инерции различных тел можно найти с помощью интегрирования.
Рассмотрим результаты расчета для некоторых частных случаев.
1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения
(1)
2. Момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Радиус диска R, его масса m.
(2)
.Эта же формула справедлива для момента инерции сплошного цилиндра относительно оси совпадающей с осью цилиндра..
3. Момент инерции полого цилиндра с внутренним радиусом R1 и внешним радиусом R2 относительно оси , совпадающей с осью цилиндра.
(3)
4. Момент инерции шара радиуса R относительно оси проходящей через его центр.
(4)
5. Момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину. Длина стержня l,
(5)
Эти формулы для моментов инерции относительно оси симметрии.
Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера:
Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния d между осями.
 Получим с помощью
этой теоремы формулу момента инерции стержня относительно оси перпендикулярной
к стержню и проходящей через его конец.
Получим с помощью
этой теоремы формулу момента инерции стержня относительно оси перпендикулярной
к стержню и проходящей через его конец.
(6)
В общем случае расчет момента инерции представляет собой достаточно сложную задачу, и часто он определяется экспериментально с помощью основного уравнения динамики вращательного движения, методом крутильных колебаний и др.
В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний.
Исследуемые тела насаживаются на ось спиральной пружины. Если зкрутить пружину на угол j, то в результате деформации пружины возникнет упругая сила. Она создает крутящий момент (момент силы) М
M=Dj (7)
Здесь D – модуль кручения пружины.
Этот крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания.
Из теории крутильных колебаний следует формула для периода колебаний
(8)
где J – момент инерции.
Отсюда
(9)
Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины.
Порядок выполнения работы.
Для определения модуля кручения D пружины возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру.
Поверните стержень на 90о (p/2 радиан). Прикрепите к стержню (у края грузов) динамометр и измерьте силу F. Необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню).
Вычислите момент силы М
М=Fl
Здесь l – плечо силы, то есть расстояние от оси вращения до места приложения силы (до места прикрепления динамометра).
vunivere.ru
Момент инерции твердого тела
Определение и общие сведения о моменте инерции твердого тела
Это скалярная (в общем случае тензорная) величина.
где – массы материальных точек, на которые разбивают тело; на квадраты расстояний от материальной точки до оси вращения.
Для непрерывного однородного тела, вращающегося около оси, момент инерции чаще определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Тензор инерции
Совокупность величин:
называют тензором инерции. Диагональные элементы тензора: . Тензор инерции является симметричным.
Пусть все недиагональные элементы тензора равны нулю, не равны нулю только диагональные составляющие. Тогда тензор запишем как:
В таком случае оси тела совпадают с осями координат и являются главными осями инерции. Величины:
называют главными моментами инерции. Тензор в виде (4) приведен у диагональному виду. Моменты инерции, находящиеся вне главной диагонали матрицы (3) называются центробежными. Если оси системы координат направлены вдоль главных осей инерции тела, то центробежные моменты инерции равны нулю.
Если главные оси проведены через центр масс тела, то они называются центральными главными осями, а тензор центральным тензором.
Главные оси не всегда для тела не всегда легко отыскать. Но иногда достаточно использовать соображения симметрии. Так, в шаре относительно любой точки главные оси можно найти так. Одна из главных осей проходит через центр шара, две другие ориентированы произвольно в плоскости, которая перпендикулярна первой оси.
Составляющие момента инерции сплошного тела относительно осей декартовой системы координат определены как:
где – координаты элемента массы тела (), которая обладает объемом .
Момент инерции твердого тела зависит от формы тела и распределения ассы в теле относительно оси вращения.
Величины, равные:
называют радиусами инерции тела по отношению к соответствующим осям системы координат.
Теорема Штейнера
В некоторых случаях вычисление момента инерции существенно облегчает знание теоремы Штейнера (иногда ее называют теоремой Гюйгенса): Момент инерции тела (J) относительно произвольной оси равен моменту инерции относительно оси, которая проведена через центр масс рассматриваемого тела (), плюс произведение массы тела (m) на расстояние между осями в квадрате, при условии, если оси параллельны:
Примеры решения задач
ru.solverbook.com
Момент инерции – это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
Осевые моменты инерции некоторых тел.Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
- Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
dic.academic.ru
