Осевые моменты инерции некоторых тел
Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения | |||
Тело | Описание | Положение оси a | Момент инерции Ja |
Материальная точка массы m | На расстоянии r от точки, неподвижная | ||
Ось цилиндра | |||
Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | ||
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | ||
Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
Прямой тонкий стержень длины | Ось перпендикулярна к стержню и проходит через его центр масс | ||
Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | ||
Шар радиуса r и массы m | Ось проходит через центр шара | ||
Конус радиуса r и массы m | Ось конуса | ||
Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину | ||
Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс | ||
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Тонкий стержень (ось проходит через центр)
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
studfiles.net
Моменты инерции некоторых тел — Мегаобучалка
Моменты инерции некоторых симметричных тел представлены на рис. 7.4.
Приблизительные значения моментов инерции туловища человека и его конечностей вычисляются по формулам для цилиндра или с помощью опытных данных. Для длинных звеньев конечностей моменты инерции приближенно равны 0,3 т/2(где т — масса звена, / — его длина). Моменты инерции элементов конечностей представлены в табл. 7.1.
На рис. 7.5 показаны моменты инерции тела относительно разных осей.
Момент инерции тела человека относительно заданной оси определяется как сумма моментов инерции всех звеньев тела относительно той же оси. Наименьший момент инерции тело человека имеет в выпрямленном состоянии относительно продольной оси
 |
тела, проходящей через его центр масс. Целенаправленное изменение момента инерции тела человека широко используется при управлении вращательными движениями в различных видах спорта.
Момент инерции относительно вертикальной оси вращения, проходящей через центр масс (центр масс человека находится в саггитальной плоскости несколько впереди второго крестцового
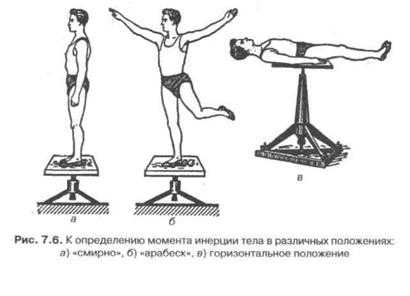
позвонка) в зависимости от положения человека, имеет следующие значения, рис. 7.6: а) 1,2 кгм2 — при стойке «смирно», б) 8 кгм2 — при стойке «арабеск», в) 17 кгм2 — в горизонтальном положении.
Пример
Вращательные движения без опоры.
В случае вращения вокруг свободных осей, внешнего удерживающего тела не существует. Звенья вращающегося тела спортсмена удерживаются на криволинейных траекториях внутренними связями. Ось вращения неизменно проходит через ОЦМтела, рис. 7.7.
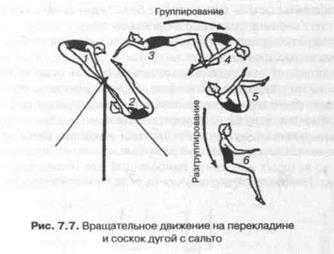
При соскоке дугой с сальто вперед из положения упора на перекладине стоя согнувшись, гимнаст под действием силы тяжести совершает движение вокруг оси перекладины назад. Из позы 2, резко разгибая ноги в тазобедренных суставах и сгибая в коленных, гимнаст отпускает перекладину и переходит в позу 3. Вращательное движение вокруг свободной оси, проходящей через
 |
инерции относительно поперечной оси. По закону сохранения момента инерции до позы 5 происходит нарастание скорости. Начиная с позы 5 гимнаст распрямляет тело, момент инерции относительно поперечной оси увеличивается, и вращение вокруг нее перед приземлением замедляется, поза 6.
Свободные оси
Тело может вращаться не только вокруг закрепленной оси, но и вокруг оси, которая не закреплена. В любом теле можно выбрать такие оси, направление которых при вращении вокруг них будет сохраняться без каких либо специальных устройств (например, подшипников). Такие оси называют свободными.
Свободные оси — оси, которые без специального закрепления сохраняют свое направление в пространстве.
Пример: ось вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела.
Очевидно, что для однородных тел свободной осью является ось полной геометрической симметрии. Можно доказать, что в любом теле имеется не менее трех взаимно перпендикулярных свободных осей вращения, эти оси называются главными осями инерции. При этом оказывается, что при отсутствии внешних воздействий устойчивым является вращение тела только вокруг двух осей, относительно которых оно имеет наибольший или наименьший момент инерции. Например, если, подбросив тело, привести его во вращение
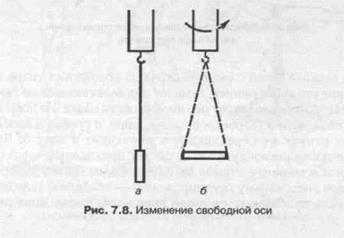
относительно произвольной оси, то, падая, оно само по себе перейдет к вращению вокруг оси, которой соответствует или наибольший, или наименьший момент инерции. В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно самопроизвольно изменяет эту ось на ось с наибольшим моментом. На рис. 7.8 показана иллюстрация этого явления.
К электродвигателю подвешено на нити цилиндрическое тело, которое может вращаться вокруг своей вертикальной геометрической оси (а) с моментом инерции </, =——. При достаточно боль-шой угловой скорости тело изменит свое положение (б). Момент
1-2
инерции относительно новой оси равен J2=—тг- • Если L2 > б/?2, то
/2 > /,. Вращение вокруг новой оси будет устойчивым.
Вращение человека в свободном полете и при различных прыжках происходит вокруг главной оси с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы, то при различных позах направления главных осей будут различны.
У человека из-за наличия многозвенных, большей частью открытых в ходе движения кинематических цепей, имеется большое число степеней свободы. Так, подвижность кончиков пальцев относительно грудной клетки определяется 12 степенями свободы;
| сил тяжести. Для этого разобьем тело на множество маленьких кусочков и нарисуем действующие на них силы тяжести (рис. 7.10). |
запястья относительно лопатки — 7; а общее число степеней свободы всего тела — трехзначное число.
Пример
На рис. 7.9. представлена упрощенная модель скелета руки. Кинематическая схема показывает подвижные звенья скелета и типы шарнирных соединений (два шаровых шарнира и один цилиндрический). Эта модель имеет семь степеней свободы: три степени свободы в плечевом поясе, одна степень свободы в локтевом суставе и три степени свободы у кисти. На динамической схеме стрелками показаны оси вращения, соответствующие этим степеням свободы.
megaobuchalka.ru
Моменты инерции некоторых простых однородных тел
1. Кольцо. Окружность. Вычислим момент инерции материальной окружности радиуса R и массы М относительно ее центра О (рис. 8.3). Для этого разобьем всю окружность на бесконечно малые элементы массой m. Все элементы находятся от точки О на одном расстоянии R, поэтому искомый момент равен:
. (8.13)
2. Тонкий диск. Момент инерции диска радиуса R и массы М относительно его центра О (рис. 8.4) вычислим следующим образом. Разобьем диск концентрическими окружностями на элементарные плоские кольца радиуса r, шириной – Dr. Массу кольца обозначим m. Искомый момент инерции равен сумме всех моментов инерции элементарных колец:
.
Обозначим поверхностную плотность через g, тогда
.
Площадь элементарного кольца представим в виде:
,
тогда
.
. (8.14)
3. Круглый цилиндр радиуса R, массой М. Разобьем весь цилиндр на тонкие диски. Момент инерции диска
,
где m – масса диска.
Искомый момент инерции цилиндра равен сумме моментов инерции всех дисков
. (8.15)
4. Шар. Вычислим момент инерции шара массой М и радиусом R относительно его центра. Обозначим плотность, приходящуюся на единицу объема r.
,
где V – объем шара.
,
тогда
.
Разобьем шар концентрическими сферами на бесконечно тонкие сферические слои радиуса r и толщиной Dr. Так как все частицы слоя находятся на одинаковом расстоянии от центра О, то момент инерции слоя равен
.
Объем сферы равен:
,
масса сферы:
,
тогда момент инерции шара равен:
.
Подставляя значение r, получим:
. (8.16)
Похожие статьи:
poznayka.org
Моменты инерции некоторых однородных тел — КиберПедия
Момент инерции тела, если известно распределение массы тела относительно оси вращения mi (R), может быть определён как
Теорема Штейнера.
Момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела Jc относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:
Jc— известный момент инерции относительно оси, проходящей через центр масс тела,
J — искомый момент инерции относительно параллельной оси,
m— масса тела,
d— расстояние между указанными осями.
Основной закон динамики вращательного движения.
Изменение момента количества движения твердого тела , равно импульсу момента всех внешних сил, действующих на это тело.
Согласно( )второй закон Ньютона для вращательного движения По определению угловое ускорение и тогда это уравнение можнопереписать следующим образом:
с учетом ( ):
или
1.8.
Момент импульса тела относительно оси.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что , получим
Выражение основного закона динамики вращательного движения через изменение момента импульса тела.
Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей Li, взятых относительно одной и той же точки выбранной системы отсчета.
L = ΣLi.
Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что
скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.
dL/dt = M.
Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.
Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением
.
Закон сохранения момента импульса. Примеры.
Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса):
.
Очень нагляден закон сохранения момента импульса в опытах с уравновешенным гироскопом – быстро вращающимся телом, имеющим три степени свободы (рис. 6.9).
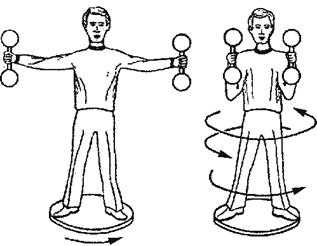Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского (рис. 6.11).
1.9.
Работа силы.
Работа силы-мера действия силы при превращении механического движения в другую форму движения.
Примеры формул работы сил.
работа силы тяжести; работа силы тяжести наклонной пов-ти
работа силы упругости
работа силы трения
cyberpedia.su
Моменты инерции тел простой геометрической формы
Момент инерции твердого тела относительно некоторой оси вращения определяется выражением (15):
.
Суммирование распространяется на элементы всего твердого тела. Если разбиение тела проводить на все более и более мелкие элементы, то тогда сумма в пределе трансформируется в интеграл, и в результате чего получим:
(16)
(интегрирование ведется по всему объему твердого тела).
Можно получить еще одну формулу полезную для расчета момента инерции. Для этого воспользуемся выражением для плотности вещества: . После подстановки dm = rdV в (16) получим:
. (17)
В качестве примера применения формулы (16) найдем момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину (рис.11). Длина стержня l, масса стержня т. Разобьем весь стержень на отрезки малой длины . Масса такого отрезка равна , а расстояние до оси вращения r = x. Момент инерции всего стержня найдем, воспользовавшись формулой (16):
Рис.12
|
.
Приведем, для справок, формулы для моментов инерции тел простейшей геометрической формы.
Момент инерции однородного диска (рис.12) относительно оси, перпендикулярной к плоскости диска и проходящей через его центр равен:
,
где радиус диска R, масса т.
Эта же формула справедлива и для момента инерции сплошного цилиндра относительно оси совпадающей с осью
цилиндра.
Момент инерции тонкого обруча относительно оси, перпендикулярной к плоскости обруча и проходящей через его центр будет (рис.13):
.
где радиус обруча – R, масса обруча – т.
Эта же формула справедлива для тонкостенного цилиндра.
Момент инерции шара относительно оси проходящей через его центр. Радиус шара R, масса т:
.
Момент инерции тонкого диска массы m и радиуса R, (толщина диска b << R), относительно оси совпадающей с диаметром диска:
:
,
Все приведенные формулы справедливы для моментов инерции относительно оси проходящей через центр масс (центр инерции) твердого тела. Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера:
Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела (центр масс тела) и произведения массы тела на квадрат расстояния между осями.
.
Рис.14
|
В качестве примера получим с помощью этой теоремы выражение для момента инерции стержня относительно оси перпендикулярной к стержню и проходящей через один из его концов (рис.14). Из рисунка ясно, что а = , кроме этого момент инерции относительно оси, проходящей через центр масс равен:
Поэтому по теореме Штейнера получим:
.
Главные оси инерции
Момент инерции твердого тела произвольной формы и распределения масс зависит от ориентации оси вращения. Допустим, что ось проходит через центр масс тела (центр инерции). Найдем такую ориентацию оси, для которой момент инерции максимален. Далее, как доказывается в теоретической механике, существует также ось перпендикулярная найденной, и проходящая через центр масс, для которой момент импульса твердого тела будет минимален. Для третьей оси, ортоганальной к первым двум, момент импульса в общем случае имеет величину промежуточную между максимальным и минимальным значениями. Введенные таким образом оси вращения называются главными осями инерции. Моменты инерции относительно этих осей не обязательно отличаются друг от друга по величине. Действительно, если однородное по плотности твердое тело обладает той или иной симметрией, то некоторые главные моменты инерции могут равняться друг другу. Так, например, однородный по плотности шар имеет три равных момента инерции относительно главных осей, каждый из которых равен: , где M, R – масса и радиус шара.
Однородный куб с массой М и длиной ребра имеет также три равных момента инерции относительно главных осей инерции . Главные оси инерции перпендикулярны граням куба и проходят через центр куба..
Тонкий однородный по плотности диск имеет максимальный по величине момент инерции относительно оси, проходящей через центр диска перпендикулярно его плоскости, а также два других главных момента инерции равных друг другу.
Приведем также пример тела, когда все три момента инерции относительно главных осей инерции различны – однородный по плотности параллелепипед с отличающимися по длине ребрами.
Рекомендуемые страницы:
lektsia.com
3.3. Моменты инерции некоторых тел
момент инерции является мерой инертности вращающегося тела (чем больше масса, тем труднее тело разогнать, а чем больше момент инерции, тем труднее тело раскрутить). Кроме того, из второго закона Ньютона видно, чем больше приложенная сила, тем больше ускорение тела (тело быстрее разгоняется), а из основного уравнения вращательного движения видно, чем больше приложенный момент, тем больше угловое ускорение тела (тело быстрее раскручивается).
Как уже говорилось, момент инерции зависит не только от массы, но и от формы и геометрических размеров тела, вычисляется по формуле (3.4) и измеряется в кг·м2. Приведем несколько примеров.
1) Момент инерции материальной точки массы m, находящейся на рас-
стоянии r от оси вращения,
J = mr2.
2) Момент инерции тонкого однородного стержня длины l относительно перпендикулярной оси, проходящей через его середину,
J = ml2 . 12
3) Момент инерции тонкостенного цилиндра (обруча) радиуса R относи-
тельно его оси
J = mR2.
4) Момент инерции сплошного однородного цилиндра (диска) радиуса R относительно его оси
dr
R r
Рис. 3.9
J = mR2 2 .
Выведем эту формулу. Для этого выделим в цилиндре трубку радиуса r со стенками бесконечно малой толщиныdr, как показано на рис. 3.9. Пусть высота цилиндраh, а
hплотность материала ρ. Тогда масса выделенной трубкиdm =ρdV = 2πρrh dr. Подставляя это выражение в интеграл
(3.4), получим
R
J = 2πρh∫r3dr= 12 πρhR4 = 12 (ρπR2h)R2 = 12 (ρV)R2 = 12 mR2 .
0
5) Момент инерции однородного шара радиуса R относительно оси, проходящей через его центр,
J= 52 mR2 .
Аеще момент инерции зависит от того, вокруг какой оси вращается тело.
22
Z0 Z
OC
d
Рис. 3.10
Этот факт отражает теорема Гюйгенса – Штейнера: если тело вращается вокруг осиZ0, не проходящей через центр масс (рис. 3.10), то момент инерцииJ0 относительно этой оси равен
где J – момент инерции относительно осиZ, проходящей через центр масс и параллельной оси вращения,d − расстояние между этими осями,m − масса тела.
Если, к примеру, шар радиуса R будет вращаться вокруг осиZ0, как показано на рис. 3.10, его момент инерции относительно этой оси будет
J0 = 52 mR2 + md2 .
Таким образом, момент инерции зависит от массы, формы и геометрических размеров тела, а также от оси, вокруг которой вращается тело.
3.4. Закон сохранения момента импульса. Энергия вращающегося тела
Еще раз запишем уравнение моментов для твердого тела (3.3) ddtL = Mr .
Если система замкнутая, то суммарный момент всех внешних сил относи-
тельно любой точки Mr = 0, поэтомуddtL = 0, следовательноLr = const , то есть
суммарный момент импульса не меняется.
Закон сохранения момента импульса: В замкнутой системе сумма момен-
тов импульса всех тел относительно какой-либоточки остается постоянной
L = const . (3.8)
Мы будем пользоваться только следствием из закона сохранения момента импульса.
Если тела в замкнутой системе вращаются вокруг одной оси, то их суммарный момент импульса относительно этой оси не меняется. Так, для двух взаимодействующих тел:
L1 +L2 =L1′ +L2′, | (3.8)′ |
где L1 иL2 – моменты импульса тел до взаимодействия,L1′ иL2′ – после взаимодействия. Моменты импульса берутся с учетом знаков.
23
Этот закон объясняет многие явления, происходящие с вращающимися телами. Например, крутящийся с раскинутыми руками фигурист, прижимая руки к туловищу, «автоматически» увеличивает свою угловую скорость. Закон сохранения момента импульса для фигуриста (одно тело):
L1= L2
J1ω1= J2ω2.
Откуда
ω2 = ω1 J1 .
J 2
Прижимая руки к туловищу, фигурист уменьшает свои размеры, а, значит, и свой момент инерции. Действительно, из определения и примеров моментов инерции мы видели, что, чем больше размеры тела, тем больше его момент инерции (J ~mr2). Поэтому, так какJ2 <J1, тоω2 >ω1.
Многие звезды вращаются вокруг своей оси и при этом сжимаются, например, Солнце. При сжатии размеры уменьшаются (из-заизлучения масса, как правило, тоже падает), и скорость вращения увеличивается в соответствии с законом сохранениямомента импульса.
Найдем теперь кинетическую энергию вращающегося тела. Метод такой же, как в п. 3.2. Выделим в теле бесконечно малую частицу массыdm, движущуюся со скоростьюυ по окружности радиусаr, рис. 3.7. Кинетическая энергия этой частицы
dK = υ2 dm = ω2r 2dm . 2 2
Чтобы найти кинетическую энергию тела нужно сложить энергии всех частиц, то есть взять интеграл от полученного выражения. Учитывая, что все частицы, составляющиетело, вращаютсясоднойугловой скоростьюω, получим
| ω2 | ∫r2dm= | ω2 |
| ||
K = | 2 | 2 J . |
| |||
Итак, кинетическая энергия вращающегося тела |
| |||||
| Kвр= | Jω2 | . | (3.9) | ||
| 2 |
| ||||
|
|
|
|
|
| |
Если тело движется поступательно и при этом вращается, например, катящееся колесо, то его полная кинетическая энергия складывается из энергии поступательного (2.10) и энергии вращательного (3.9) движений.
В заключение параграфа отметим, что формулы для основных динамических характеристик вращательного движения аналогичны соответствующим формулам для поступательного движения. Так, чтобы получить выражение для момента импульса в формуле для импульса вместо массы берем момент инерции, вместо скорости – угловую скорость. Те же самые замены делаются в выражении для кинетической энергии материальной точки, чтобы получить формулу для кинетической энергии вращающегося тела.
24
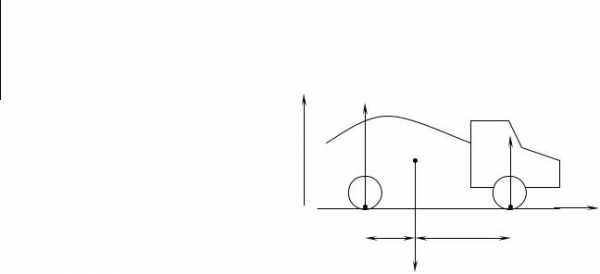
3.5. Статика
Из основного уравнения динамики вращательного движения твердого тела (3.6) вытекает одно простое, но важное следствие, что если полный момент сил, действующих на тело, равен нулю, то его угловое ускорение равно нулю, и тело либо не вращается, либо вращается с постоянной угловой скоростью. Это следствие аналогично следствию из второго закона Ньютона для поступательного движения (2.1): если суммарная сила, действующая на тело, равна нулю, то его ускорение равно нулю, и тело или покоится, или движется с постоянной скоростью.
Итак, чтобы тело находилось в равновесии (в покое), необходимо, чтобы векторная сумма всех сил (или сумма проекций всех сил на любое направление), действующих на тело, и сумма моментов этих сил относительно любой оси были равны нулю. На этих двух положениях основанастатика – наука о
равновесии тел. | Y | N1 |
|
|
| |
Например, для неподвижно- |
|
|
| |||
го грузового автомобиля (рис. 3.11) |
|
|
|
| N2 | |
эти условия имеют вид |
|
|
|
| ||
|
| C |
| |||
|
|
|
|
| ||
N1 +N2 –mg = 0, |
|
|
|
|
| |
|
|
|
|
|
| |
–N1l1+ N2l2= 0, |
|
|
|
|
|
|
где моменты сил брались относи- |
|
|
|
|
| X |
|
|
|
|
| ||
тельно оси Z, проходящей через |
|
| l1 | l2 | ||
|
|
| ||||
центр масс машины C и перпен- |
|
| mg |
|
| Рис. 3.11 |
дикулярной плоскости рисунка. |
|
|
|
| ||
Законы статики лежат в основе теории устойчивости различных сооружений и механических приспособлений (зданий, мостов, плотин, вышек, подъемных кранов и т.п.), а также в основе действия опорно-двигательногоаппарата человека и животных (членистоногих и позвоночных).
Вопросы к лекции 3
1.Что такое твердое тело, и почему это идеализация?
2.Дайте определения момента силы и момента импульса относительно точки.
3.Напишите уравнение моментов для твердого тела и поясните смысл входящих в него переменных. Где оно применяется?
4.Дайте определения момента силы и момента импульса относительно оси.
5.Выведите основное уравнение динамики вращательного движения твердого тела и дайте определение входящим в него физическим величинам.
6.Какой физический смысл имеет момент инерции?
7.Имеются две центрифуги одинаковой массы, но разного радиуса. Какую из них легче раскрутить?
8.Что такое момент импульса твердого тела?
9.Сформулируйте закон сохранения момента импульса и приведите примеры, где он выполняется.
10.Если вращающийся на льду фигурист хочет остановиться, он разводит руки в стороны, а если хочет вращаться быстрее, прижимает руки к туловищу. Как объяснить это явление?
11.В процессе горения солнце ежесекундно теряет огромную массу вещества. Как этот факт отражается на скорости вращения солнца вокруг своей оси?
12.Как найти кинетическую энергию катящегося без проскальзывания колеса?
13.Что изучает статика, и на каких принципах она основана?
25
studfiles.net
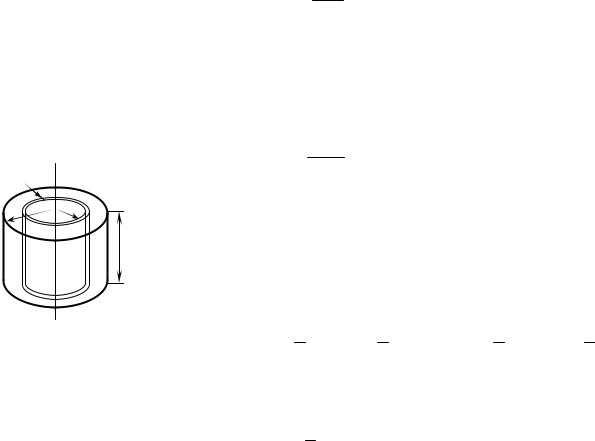
Расчёт моментов инерции некоторых тел
Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массы dm = dV. Тогда момент инерции тела относительно оси равен интегралу по объёму тела:
(1)
где r – расстояние элемента dm до оси.
Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его момент инерции относительно точки . Он вычисляется по формуле, аналогичной (1):
Рис. 1
(2)где r – расстояние элемента dm до выбранной точки (относительно которой вычисляется ). Пусть эта точка является началом системы координат X, Y, Z (рис. 1). Квадраты расстояний элемента dm до координатных осей X, Y, Z и до начала координат равны соответственно y2+z2, z2+x2, x2+y2, x2+y2+z2. Моменты инерции тела относительно осей X, Y, Z и относительно начала координат
Из этих соотношений следует, что
(3)
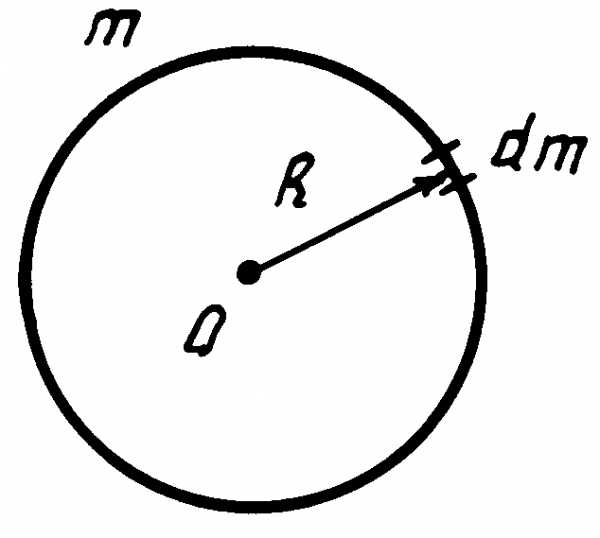
Рис. 2
Таким образом, сумма моментов инерции тела относительно трёх любых взаимно перпендикулярных осей , проходящих через одну точку, равна удвоенному моменту инерции тела относительно этой точки.Момент инерции тонкого кольца. Все элементы кольца dm (рис. 2) находятся на одинаковом расстоянии, равном радиусу кольца R, от его оси симметрии (ось Y) и от его центра. Момент инерции кольца относительно оси Y
(4)
Момент инерции тонкого диска. Пусть тонкий однородный диск массы m с концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусы R1 и R2. Мысленно разобьём диск на тонкие кольца радиуса r, толщины dr. Момент инерции такого кольца относительно оси Y (рис. 3, она перпендикулярна рисунку и не показана), в соответствии с (4):
(5)
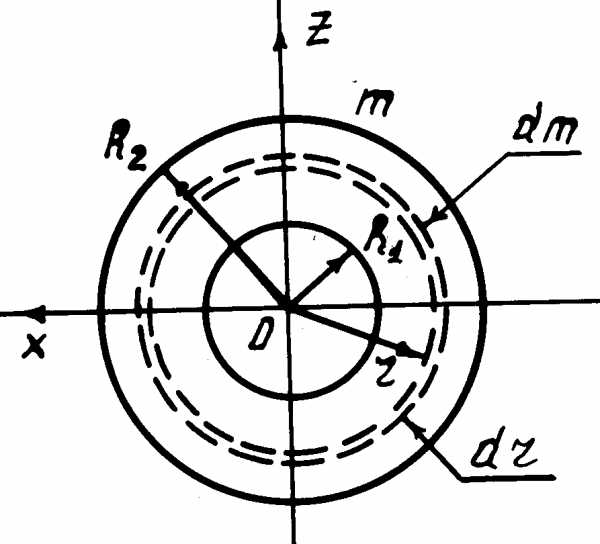
Рис. 3
Момент инерции диска:
(6)
В частности, полагая в (6) R1 = 0, R2 = R, получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси:
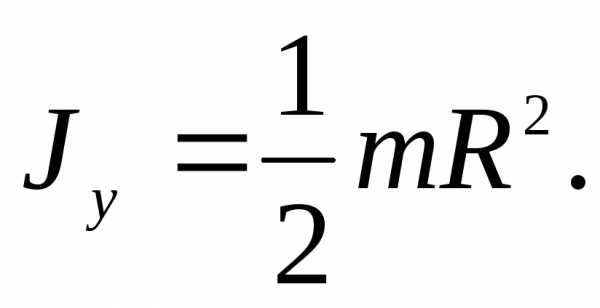(7)
Момент инерции диска относительно его оси симметрии не зависит от толщины диска. Поэтому по формулам (6) и (7) можно вычислять моменты инерции соответствующих цилиндров относительно их осей симметрии.
Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = Jy, а моменты инерции относительно осей X и Z равны между собой, Jx = Jz. Поэтому, в соответствии с (3): 2Jx +Jy = 2Jy, Jx = Jy/2, или
(8)
Рис. 4
Момент инерции цилиндра. Пусть имеется полый симметричный цилиндр массы m, длины l, внутренний и внешний радиусы которого равны R1 и R2. Найдём его момент инерции относительно оси X, проведенной через центр масс перпендикулярно оси цилиндра (рис. 4). Для этого мысленно разобьём его на диски бесконечно малой толщины dy. Один из таких дисков, массой dm = mdy/l, расположенный на расстоянии y от начала координат, показан на рис. 4. Его момент инерции относительно оси X, в соответствии с (8) и теоремой Гюйгенса – Штейнера(9)
Момент инерции всего цилиндра
(10)
Момент инерции цилиндра относительно оси X (оси вращения маятника Обербека) найдём по теореме Гюйгенса – Штейнера
где d – расстояние от центра масс цилиндра до оси X. В работе 13 этот момент инерции обозначен как Jц
(11)
12
studfiles.net