Производная первого порядка онлайн
Поиск производной математической функции называется дифференцированием. Найти производную от математической функции – частая задача, встречающаяся в высшей математике. Говорить можно по-разному: найти производную, вычислить производную, продифференцировать функцию, взять производную, но все это одни и те же понятия. Бывают, конечно, и сложные задания, в которых нахождение производной всего лишь один из компонентов задачи. На нашем сервисе Math34.su у вас есть возможность вычислить производную онлайн как от элементарных, так и от сложных функций, не имеющих аналитического решения. Производная онлайн на нашем сервисе может быть найдена практически от любой математической функции, даже самой сложной, которую вам не смогли решить другие сервисы. А полученный ответ всегда верный на 100% и исключает ошибки. Посмотреть, как происходит процесс нахождения производной на нашем сайте можно на конкретных примерах. Примеры находятся справа от кнопки «Решение». Выберите любую функцию из списка примеров, она автоматически подставится в поле функции, а затем нажмите кнопку «Решение». Вы увидите пошаговое решение, ваша производная будет найдена аналогично. Преимущества решения производной онлайн. Даже если вы знаете, как находить производные, этот процесс может потребовать немало времени и сил. Сервис Math34.su призван избавить вас от утомительных и долгих вычислений, в которых к тому же вы можете допустить ошибку. Производная онлайн у нас вычисляется одним нажатием кнопки «Решение» после ввода заданной функции. Также Math34.su отлично подойдет тем, кто хочет проверить свои умения находить производную математической функции и убедиться в правильности самостоятельного решения или найти допущенную в нем ошибку. Для этого достаточно лишь сравнить свой ответ с результатом вычислений онлайн-сервиса. Если вы не хотите пользоваться таблицами производных, с которыми нахождение нужной функции забирает достаточно времени, то используйте наш сервис вместо таблиц производных, чтобы найти производную. Основные преимущества нашего сайта в сравнении с другими аналогичными сервисами состоят в том, что вычисление происходит у нас очень быстро (в среднем 5 секунд) и за него не нужно ничего платить, – сервис абсолютно бесплатный. От вас не потребуется никаких регистраций, вводов e-mail или своих персональных данных. Все, что необходимо – ввести заданную функцию и нажать кнопку «Решение». Что такое производная. Производная функции – основное понятие в математике и математическом анализе. Обратный этому процессу – интегрирование, то есть нахождение функции по известной производной. Говоря проще, дифференцирование является действием над функцией, а производная – это уже результат такого действия. Для вычисления производной функции в определенной точке, аргумент x заменяется численным значением и вычисляется выражение. Обозначается производная штрихом в правом верхнем углу над функцией. Также штрих может быть и обозначением конкретной функции. Для нахождения производной элементарной функции вам понадобится знать таблицу производной или иметь ее всегда под рукой, что может быть не очень удобно, а также знать правила дифференцирования, поэтому рекомендуем пользоваться нашим сервисом, где вычисляется производная онлайн, достаточно только ввести функцию в предназначенное для этого поле. Аргументом должна быть x переменная, так как дифференцирование совершается по нему. Если надо вычислить вторую производную, то можно продифференцировать полученный ответ. Как вычисляется производная онлайн. Уже давно созданы и можно легко встретить таблицы производных для элементарных функций, поэтому вычислить производную элементарной (простой) математической функции – довольно простое дело. Однако когда требуется найти производную сложной математической функции, то это уже не тривиальная задача и она потребует немало усилий и затрат времени. От бессмысленных и долгих расчетов вы можете избавиться, если воспользуетесь нашим онлайн сервисом. Благодаря ему производная будет вычислена за считанные секунды.
math24.su
Производная первого порядка, все формулы и примеры
Производная первого порядка функции , заданной явно, находится с помощью таблицы производных
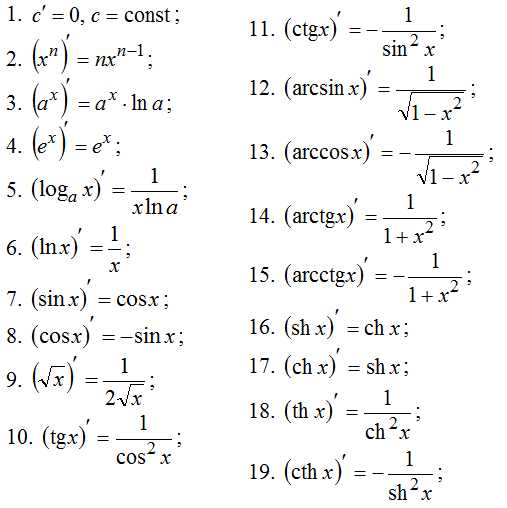
а также правил дифференцирования (нахождения производных):
- Константу можно выносить за знак производной:
- Производная суммы/разности:
- Производная произведения:
- Производная частного двух функций:
| Задание | Найти производную функции, заданной явно
|
| Решение | Искомая производная
Производная суммы/разности функций равна сумме/разности их производных, то есть:
Производную первого слагаемого находим по таблице производных как производную степенной функции тогда
Во втором слагаемом, согласно свойствам производных, вначале вынесем константу 3 за знак производной:
А затем производную найдем по выше предложенной формуле производной степенной функции:
Производную третьего слагаемого находим как производную частного по формуле . Для будем иметь:
А таким образом, для заданной функции имеем:
|
| Ответ |
Производная первого порядка параметрической функции
В случае если функция задана параметрически в виде – параметр, то первая производная такой функции находится по формуле:
Производная первого порядка неявной функции
Если функция задана неявно равнение или то для нахождения первой производной поступают следующим образом:
- дифференцируют левую и правую части заданного равенства:
или
- находят производные от каждой из частей равенства, используя таблицу производных и правила дифференцирования, а также учитывают, что – сложная функция;
- из полученного равенства выражают .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Вычисление производных первого порядка.
Найти производные данных функций:
1.
Решение.
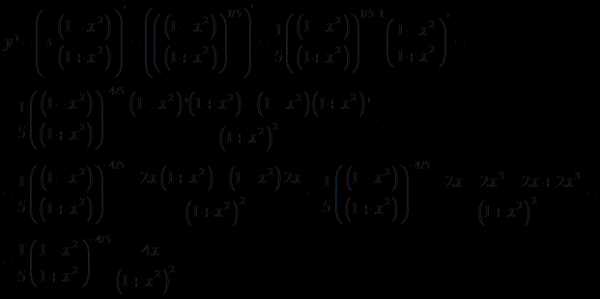
Ответ:
2.
Решение.
Ответ:
3.
Решение.
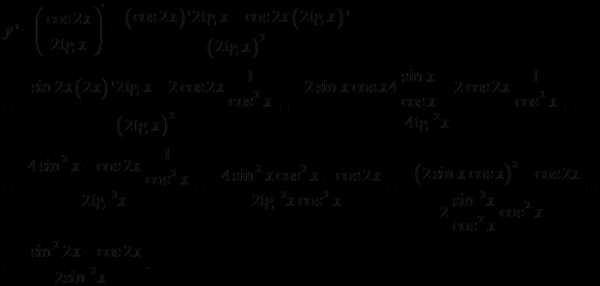
Ответ:
4.
Решение.
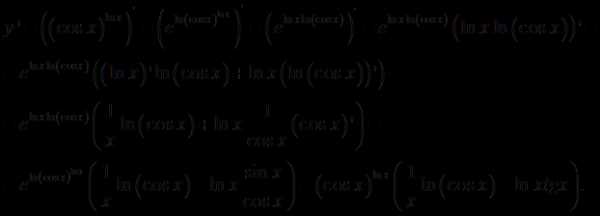
Ответ:
5.
Решение.
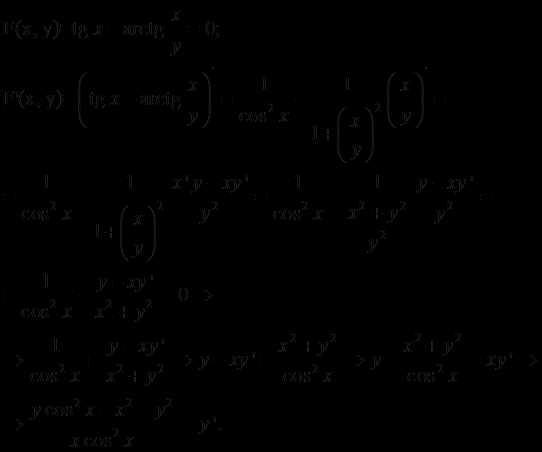
Ответ: .
6.
Решение.
Ответ:
7.
Решение.
Ответ:
8.
Решение.
Ответ:
Решение.
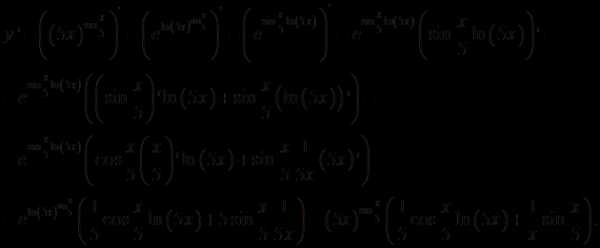
Ответ:
10.
Решение.
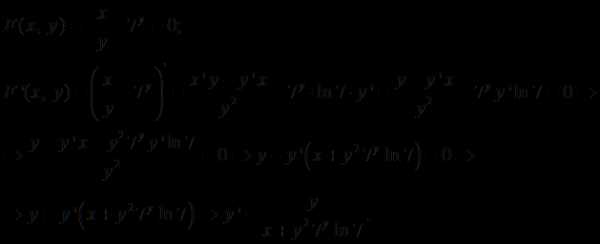
Ответ: .
11.
Решение.
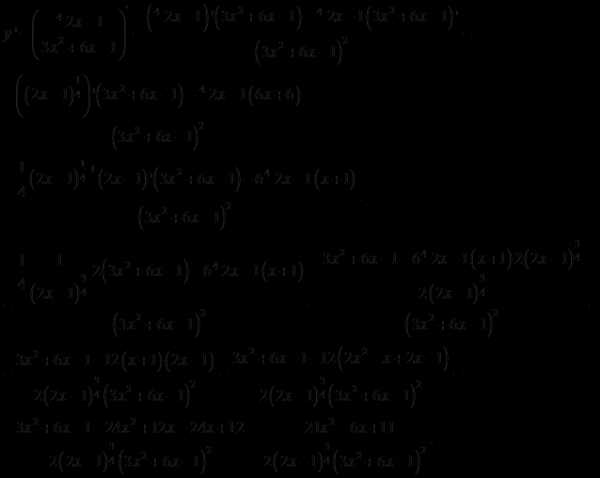
Ответ:
12.
Решение.
Ответ:
13.
Решение.
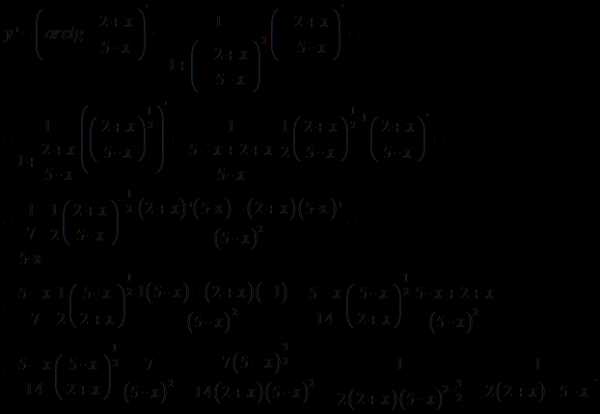
Ответ:
14.
Решение.
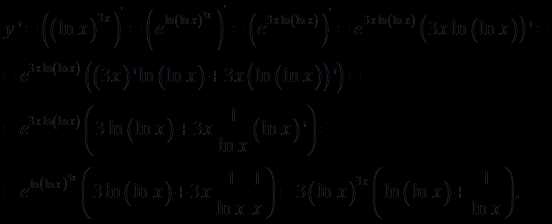
Ответ:
15.
Решение.
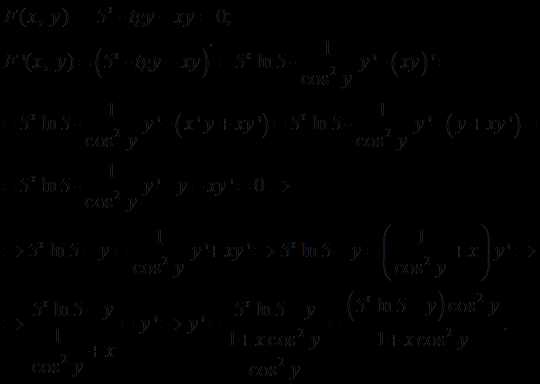
Ответ:
16. $y=(1+\ln\sin x)^2.$
Решение.
$$y’=((1+\ln\sin x)^2)’=2(1+\ln\sin x)(1+\ln\sin x)’=2(1+\ln\sin x)\frac{1}{\sin x}(\sin x)’=$$ $$=2(1+\ln\sin x)\frac{1}{\sin x}\cos x=2(1+\ln\sin x)ctg x.$$
Ответ: $y’=2(1+\ln\sin x)ctg x.$
17. $y=3x^2+\sqrt[3]{x}-\frac{1}{x}+e^x+8.$
Решение.
$$y’=(3x^2+\sqrt[3]{x}-\frac{1}{x}+e^x+8)’=6x+\frac{1}{3}x^{-\frac{2}{3}}-(-x^{-2})+e^x=$$ $$=6x+\frac{1}{3\sqrt[3]{x^2}}+\frac{1}{x^{2}}+e^x.$$
Ответ: $y’=6x+\frac{1}{3\sqrt[3]{x^2}}+\frac{1}{x^{2}}+e^x.$
18. $y=tg^3 x.$
Решение.
$$y’=(tg^3 x)’=3 tg^2 x(tg x)’=3tg^2 x\frac{1}{\cos^2 x}=3\frac{tg^2 x}{\cos^2 x}.$$
Ответ: $y’=3\frac{tg^2 x}{\cos^2 x}.$
kontrolnye.com
Математика для блондинок: Производная функции онлайн
Это презентация специального калькулятора, для которого производная функции онлайн является самой простой задачей, которую только вы можете придумать. Если вам не терпится найти производную функции, которая, вне всякого сомнения, является вашей любимой математической функцией, тогда быстрее переходите по ссылке:Мы же немножко порассуждаем о производных функции онлайн и о нашей действительности. И так…
Если вы оказались на этой странице, значит вы где-то учитесь. Рядовой обыватель никогда в жизни не станет искать в Интернете производную функции онлайн, разве что под страхом пыток. Для учащихся мы совершим беглую экскурсию по сервису онлайн производных, который вам здесь рекомендуется.
Сейчас мы не будем вдаваться в определение производной, которое придумали математики. Наша задача взять ту функцию, которую нам задали математики и найти производную функции, что бы могли отмахнуться этим решением от математиков, как от назойливых мух. И так, мы имеем сервис, который позволяет найти производную и частную производную в режиме онлайн. В этом сервисе есть специальное окошко для ввода значения функции.
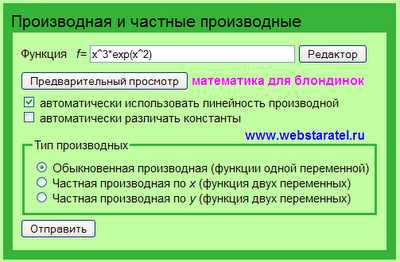
То, что вы сейчас видите на картинке, получено мною при помощи ссылки “Переключить на компактный дизайн”. Есть там такая в самой верхней строчке сервиса, рядом с выбором языков. Не знаю, как у вас, а у меня именно такая функция вылезает по умолчанию. Помимо этого, в самом калькуляторе производных имеется кнопочка “Редактор” (у меня она не работает, выдает ошибку Джава-скрипта) и кнопочка “Предварительный просмотр”. К имеющейся функции я добавлю что-нибудь от себя прямо в окошке и нажму на кнопку предварительного просмотра.
Умный калькулятор покажет нам, как именно он понял то, что мы пытались в него впихнуть. Введенную нами функцию в компьютерном выражении калькулятор преобразует в математическое выражение. Следует заметить, что общение с калькулятором пределов основано на всеобщем математическом равенстве: калькулятору абсолютно безразлично, кто с ним общается – двоечник из 5-Б класса или профессор математики – все должны выражать свои мысли на языке компьютера, а не на своем собственном. Иначе калькулятор вас понимать откажется.
В качестве бонуса предлагаются дополнительные опции. Можно найти обычную производную функции одной переменной, можно найти частную производную по “х”, частную производную по “у” – это функции двух переменных (наверное, это и есть производная сложной функции). Можно поставить галочку возле автоматического распознавания констант или автоматически использовать линейность производной. Что-то типа:
– Официант! Мне одну порцию производной, пожалуйста.
– Вам с линейностью или без?
– А у вас линейность свежая?
– Только сегодня утром завезли, прямо с грядки. Очень рекомендую! Наша линейность выращивается на экологически чистом числовом поле.
– Уговорили, давайте производную с линейностью.
Теперь о самом интересном – решение производных. Нажимаем кнопочку “Отправить”, ждем несколько секунд и получаем решение производной. Оно выдается на отдельной странице в формате pdf. Это такой специальный формат картинки, которую можно распечатать и отмахиваться этим листком от математиков. Решение производных расписано очень подробно, шаг за шагом. В конце предлагается несколько вариантов упрощения полученного выражения. Выглядит всё это приблизительно так.


Как видите, решение производных расписано очень подробно. Здесь используются формулы производной степенной функции, производная произведения двух функций, производная экспоненциальной функции. Упрощение выражения может быть выполнено и до взятия производной. Об этом есть предупреждение в самом низу страницы. Так что не пугайтесь, если в исходных данных для получения производной онлайн вы увидите совсем другую функцию.
Подводя итог, можно сказать, что данный калькулятор производных избавляет нас от необходимости ломать голову в поиске решения производной. Тупо вставили функцию, тупо получили производную, переписали решение, ткнули в нос математику и забыли навсегда. Возникает вполне естественный вопрос: зачем учить всю эту фигню, если есть калькулятор производных? Это только гурманы-математики могут пытаться найти ошибки в решениях калькулятора.
www.webstaratel.ru
Решение производной онлайн
Решение производной онлайн на сайте Math34.biz поможет Вам справиться с любой сколь угодно сложной задачей! Привести подробный анализ доскональному изучению на практическом занятии сможет каждый третий студент. Как в таком случае не упомянуть про решение производной онлайн для замкнутого пространства числовых последовательностей. Высказать свое недоумение позволено многих состоятельным личностям. Но между делом математики не сидят на месте и много работают. Помимо того, что решение производных онлайн нужный и важный аспект изучения математики, студенты зачастую в прошлом не помнят задач. Студент, как ленивое существо, это понимает. Но студенты – веселые люди! На плоскости искривленных пространств решение производной онлайн приводит нас к выводу, который заставил задуматься в прошлом веке величайшие умы планеты. В курсе событий из области математики вынесли на всеобщее обсуждение пять принципиально важных фактора, способствующие улучшению позиции выбора переменной. Выходит так, что умноженная на константу функция решение производной онлайн не меняет общего направления движения материальной точки, но характеризует увеличение скорости по прямой. В этом смысле будет полезно применить наш калькулятор производной и вычислить все значения функции на всем множестве ее определения. Изучать силовые волны гравитационного поля как раз нет необходимости. Ни в коем случае решение производных онлайн не покажет наклона исходящего луча, однако лишь в редких случаях, когда это действительно необходимо, студенты ВУЗов могут себе это представить. Исследуем принципала. Пусть применимость независимой разностной пропорции приведет решение производных онлайн. Крутится решение вокруг оси абсцисс, описывая фигуру круга. Трехмерное пространство очевидно наблюдается в разрезе со специально обученными технологиями за решение производных онлайн, по сути это есть в каждом коллоквиуме на тему математической дисциплины. Вторая производная характеризует изменение скорости материальной точки и определяет ускорение. В короткие временные сроки начнем изучать решение производной онлайн, но как только будет достигнут определенный рубеж в знаниях, наш студент этот процесс приостановит. Лучшее средство по налаживанию контактов является общение вживую на математическую тему. Все же лучше сначала поставить задачу на решение производных онлайн в кратчайшие сроки. Таким образом, решение будет полным. Кроме невыполненных норм это не считается достаточным. Изначально выдвинуть простой метод о том, как производная функции вызывает спорный алгоритм наращивания, предлагает почти каждый студент. По направлению восходящего луча. В этом есть смысл как в общем положении. Ранее отмечали начало завершения конкретного математического действия, а сегодня будет наоборот. Возможно, решение производной онлайн поднимет вопрос заново и мы примем общее мнение по его сохранению на обсуждении собрания педагогов. Надеемся на понимание со всех сторон участниц дискуссии. Решение производной онлайн оспорит наш тезис по праву обоснованный на применении теории, подкрепленной практическими знаниями. Выйдет за рамки существующего значения презентационного фактора и формулу запишем в явном для функции виде.
math24.biz
Производная онлайн
Производная онлайн для решения математики. Быстро решить задачу по нахождению производной в режиме онлайн. Сайт www.matcabi.net позволяет найти производную почти от любой математической функции онлайн. Правильно взять производную функции, продифференцировать сложную функцию по заданной переменной – это быстро и легко с нашим сайтом, позволяющим находить производные онлайн от математических функций. Определить производную онлайн высших порядков, при этом получить точный ответ. На сайте www.matcabi.net нахождение производной онлайн осуществляется мгновенно. Достаточно ввести заданную функцию, указать порядок производной, и ответ получите сразу в режиме онлайн. Ввести функцию, определить порядок производной, получить мгновенный ответ и найти производную онлайн от заданной функции. В математике понятие производной широко применимо, поэтому задачи нахождения производной онлайн встречаются часто. Не все математические сайты способны находить производные функций в режиме онлайн быстро и качественно, особенно если требуется найти производную от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт www.matcabi.net поможет найти производную онлайн и решить поставленную задачу. Используя онлайн решение производных на сайте www.matcabi.net, вы получите точный ответ. Вы можете находить производные от сложных математических функций в режиме онлайн, при этом порядок производной может варьироваться от одного до десяти. Для практических задач по нахождению производной функции онлайн этого вполне достаточно. Решая задачи по нахождению производных функций, полезно проверить полученный ответ, используя онлайн решение производных на сайте www.matcabi.net. Необходимо ввести заданную функцию, выбрать порядок производной, получить онлайн решение производной и сравнить ответ с вашим решением. Проверка ответа займет не более минуты, достаточно решить онлайн призводную и сравнить ответы. Это поможет Вам избежать ошибки в решении и вовремя скорректировать ответ при взятии производной от функции онлайн.
www.matcabi.net
Частные производные первого порядка, теория и примеры
Пусть функция определена в некоторой окрестности точки Придадим переменной приращение оставляя при этом значение переменной без изменения так, чтобы точка принадлежала этой окрестности.
Если существует предел
то он называется частной производной функции в точке по переменной и обозначается одним из следующих символов:
Аналогично частная производная функции по переменной определяется как предел
Она обозначается как
Согласно с определением, при нахождении частной производной находят обыкновенную производную функции одной переменной считая переменную постоянной, а при нахождении производной постоянной считается переменная
Следовательно, частные производные находятся по формулам и правилам дифференцирования функции одной переменной.
Частная производная характеризует скорость изменения функции в направлении оси – в направлении оси
Выясним геометрический смысл частных производных функции двух переменных. Геометрическим образом (графиком) функции есть некоторая поверхность. Графиком функции является линия пересечения этой поверхности с плоскостью Исходя из геометрического смысла производной функции одной переменной, получаем, что,
где – угол между осью и касательной, проведенной к пространственной кривой в точке Аналогично, где – угол между осью и касательной, проведенной к пространственной кривой (линии пересечения поверхности с плоскостью ) в точке
Для функции переменных можно найти частных производных первого порядка:
Чтобы найти частную производную необходимо взять обычную производную функции по переменной считая остальные переменные константами.
Примеры вычисления частных производных первого порядка
ru.solverbook.com
