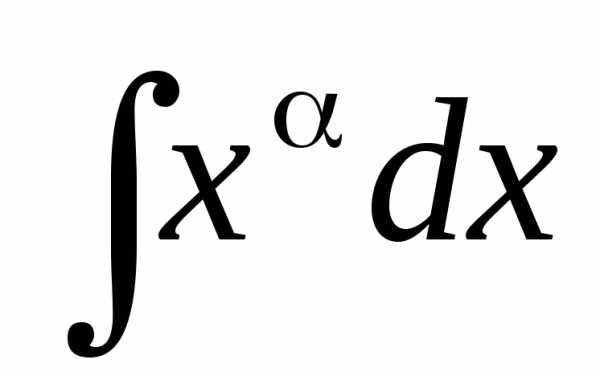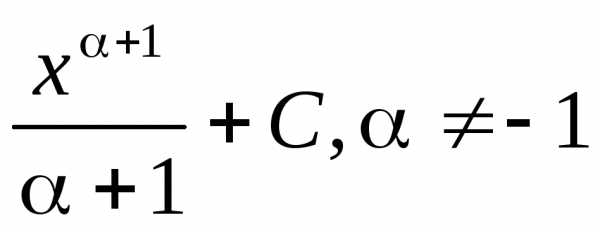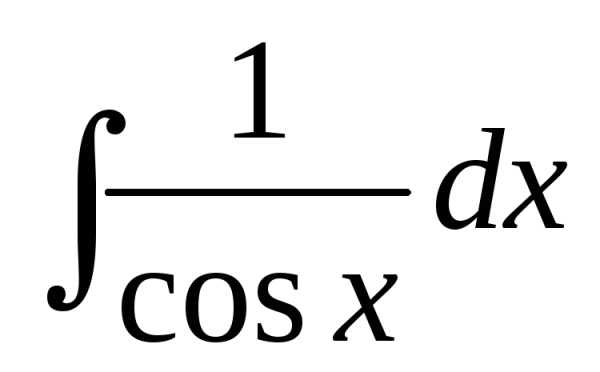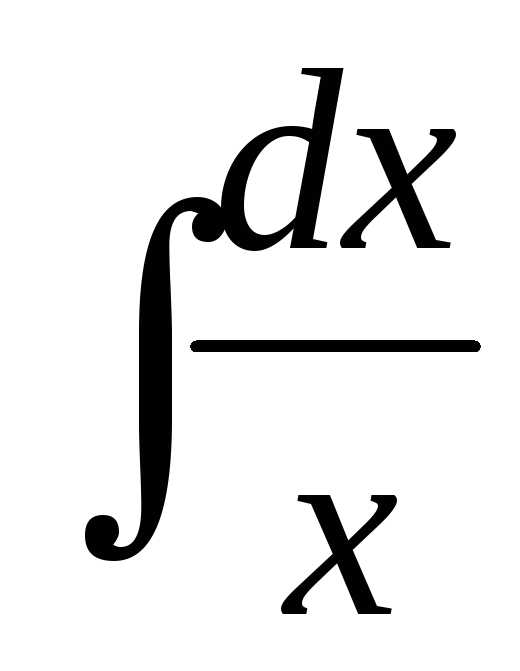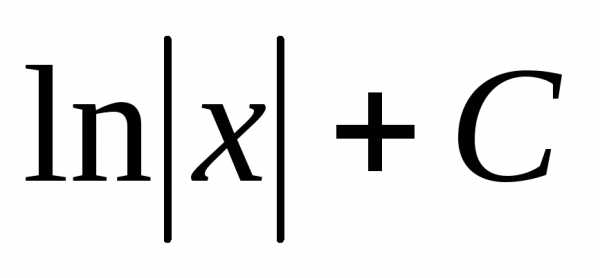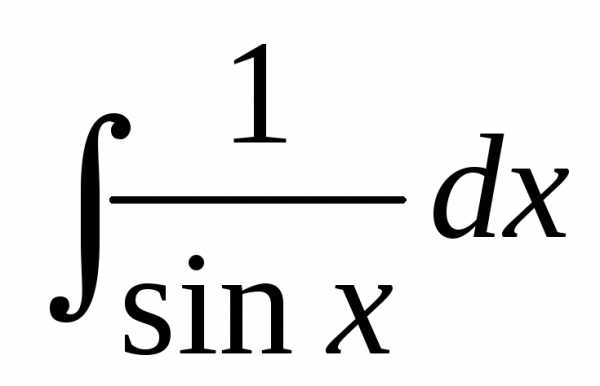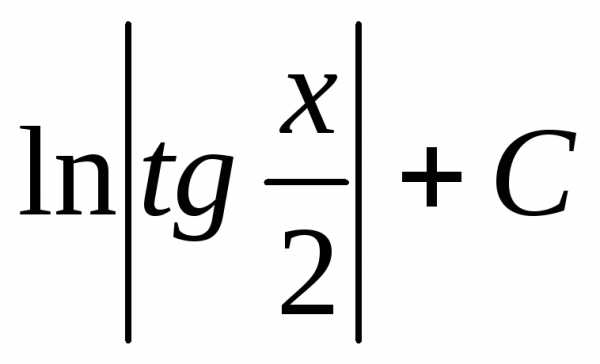Примеры решений неопределенных интегралов
- Попробуйте решить приведенные ниже неопределенные интегралы.
- Нажмите на изображение интеграла, и вы попадете на страницу с подробным решением.
Примеры на основные формулы и методы интегрирования
См раздел
Основные формулы и методы интегрирования > > >
Решение > > >
Решение > > >
Решение > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования рациональных функций (дробей)
См раздел
Интегрирование рациональных функций (дробей) > > >
> > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования иррациональных функций (корней)
См раздел
Методы интегрирования иррациональных функций (корней) > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования тригонометрических функций
См раздел
Методы интегрирования тригонометрических функций > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Неопределенный интеграл
Интегральное исчисление.
Первообразная функция.
Определение:ФункцияF(x) называетсяпервообразной функцией функцииf(x) на отрезке [a,b], если в любой точке этого отрезка верно равенство:
F(x) =f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) =F2(x) +C.
Неопределенный интеграл.
Определение:Неопределенным интегралом функцииf(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) +C.
Записывают:
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1.
2.
3.
4.
5. ,
6.
Пример:
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
Интеграл | Значение | Интеграл | Значение | ||
1 |
| -lncosx+C | 9 |
| ex + C |
2 |
| lnsinx+ C | 10 |
| sinx + C |
3 |
| |
| -cosx + C | |
4 |
| | 12 |
| tgx + C |
5 |
|
| 13 |
| -ctgx + C |
6 |
| ln | 14 |
| arcsin |
7 |
|
| 15 |
|
|
8 |
| | 16 |
| |
Методы интегрирования.
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти
значение интеграла  .
На основе известной формулы дифференцирования
.
На основе известной формулы дифференцирования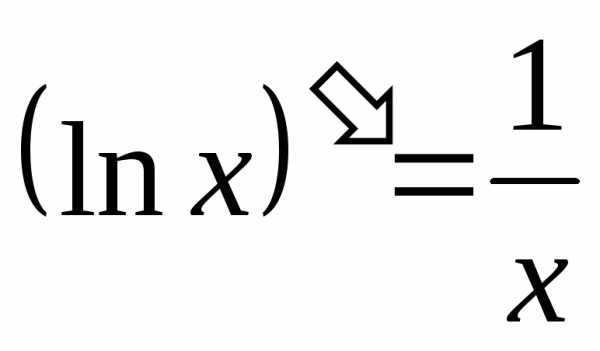
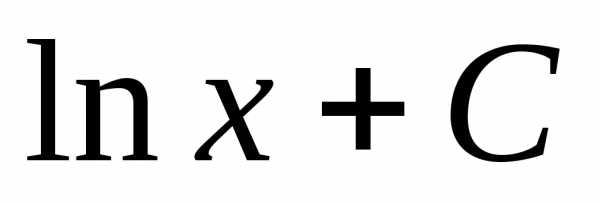 ,
где С – некоторое постоянное число.
Однако, с другой стороны.
Таким образом, окончательно можно
сделать вывод:
,
где С – некоторое постоянное число.
Однако, с другой стороны.
Таким образом, окончательно можно
сделать вывод: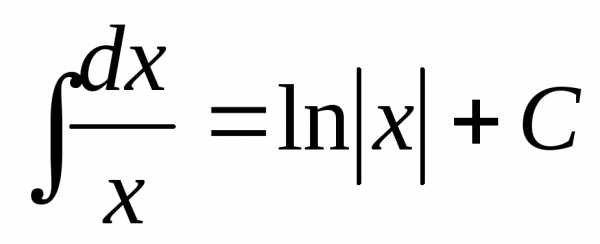
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема:Если
требуется найти интеграл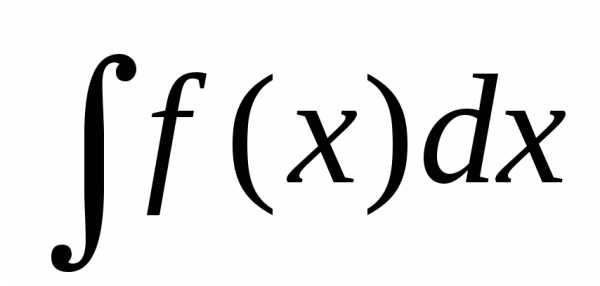 ,
но сложно отыскать первообразную, то с
помощью заменыx=(t)
иdx=(t)dtполучается:
,
но сложно отыскать первообразную, то с
помощью заменыx=(t)
иdx=(t)dtполучается:
Доказательство: Продифференцируем предлагаемое равенство:
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[(t)](t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример.Найти неопределенный интеграл.
Сделаем замену t = sinx, dt = cosxdt.
Пример.
Замена Получаем:
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)=uv+vu
где uиv– некоторые функции от х.
В дифференциальной форме: d(uv) =udv+vdu
Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:
или;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример.
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.
Пример.
Пример.
Пример.
Пример.

Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Интегрирование элементарных дробей.
Определение:Элементарными называются дроби следующих четырех типов:
I. 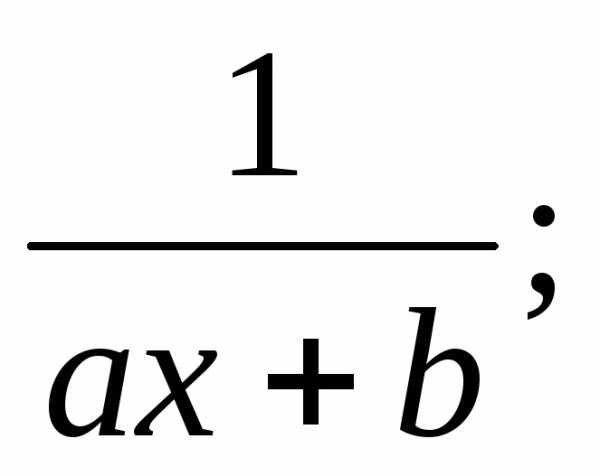 III.
III. 
II. 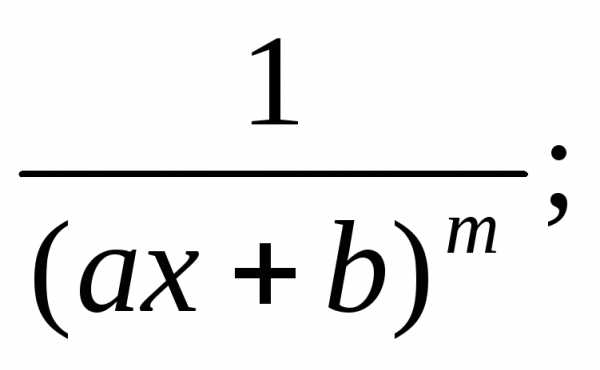 IV.
IV. 
m,n– натуральные числа (m2,n2) иb2– 4ac<0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t=ax+b.
II.
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида IIIможет быть представлен в виде:
Здесь в общем виде показано приведение интеграла дроби вида IIIк двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
Вообще говоря, если у трехчлена ax2+bx+cвыражениеb2– 4ac>0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.
Пример.
Рассмотрим теперь методы интегрирования простейших дробей IVтипа.
Сначала рассмотрим частный случай при М = 0, N= 1.
Тогда интеграл вида 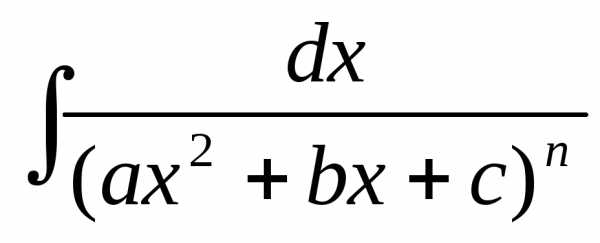 можно путем выделения в знаменателе
полного квадрата представить в виде
можно путем выделения в знаменателе
полного квадрата представить в виде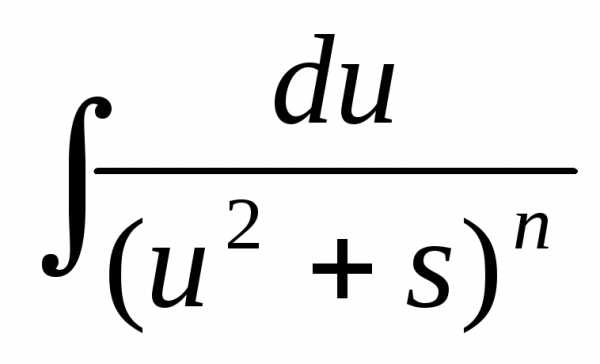 .
Сделаем следующее преобразование:
.
Сделаем следующее преобразование:
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 
Для исходного интеграла получаем:
Полученная формула называетсярекуррентной.Если применить ееn-1
раз, то получится табличный интеграл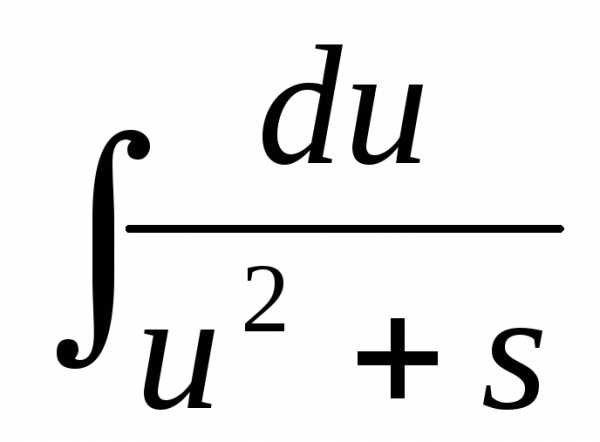 .
.
Вернемся теперь к интегралу от элементарной дроби вида IVв общем случае.
В
полученном равенстве первый интеграл
с помощью подстановки t = u2 + sприводится к табличному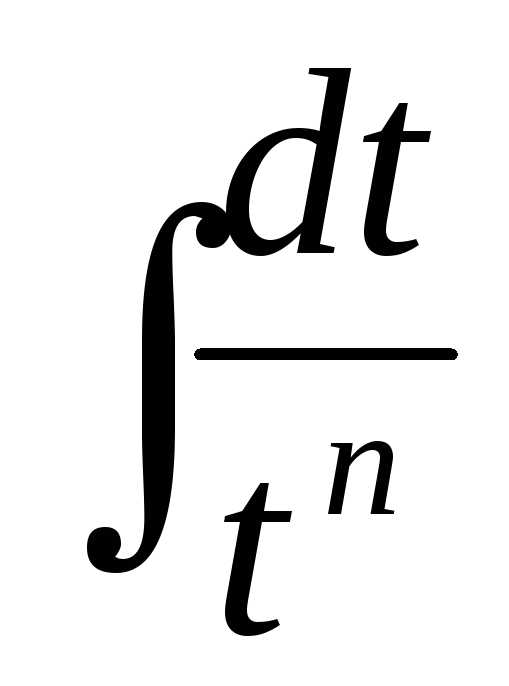 ,
а ко второму интегралу применяется
рассмотренная выше рекуррентная формула.
,
а ко второму интегралу применяется
рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степеньюn, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
Пример:
Интегрирование рациональных функций.
Интегрирование рациональных дробей.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема:Если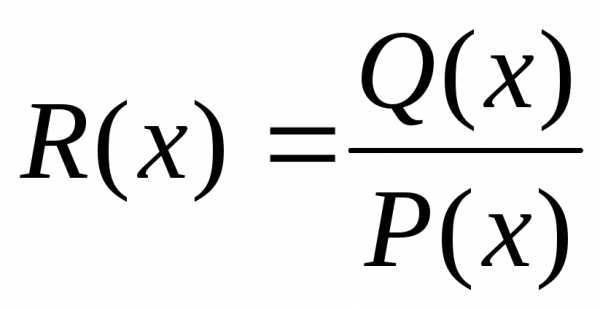 – правильная рациональная дробь,
знаменательP(x)
которой представлен в виде произведения
линейных и квадратичных множителей
(отметим, что любой многочлен с
действительными коэффициентами может
быть представлен в таком виде:P(x)
= (x – a)…(x – b)(x2 + px + q)…(x2 + rx + s)), то эта дробь может быть разложена
на элементарные по следующей схеме:
– правильная рациональная дробь,
знаменательP(x)
которой представлен в виде произведения
линейных и квадратичных множителей
(отметим, что любой многочлен с
действительными коэффициентами может
быть представлен в таком виде:P(x)
= (x – a)…(x – b)(x2 + px + q)…(x2 + rx + s)), то эта дробь может быть разложена
на элементарные по следующей схеме:
где Ai,Bi,Mi,Ni,Ri,Si– некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величинAi,Bi,Mi,Ni,Ri,Siприменяют так называемыйметод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
Т.к. (, то
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

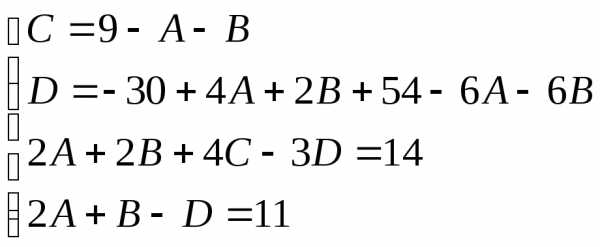
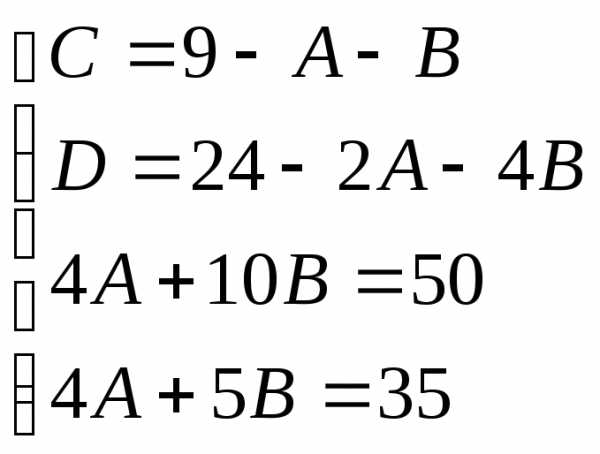


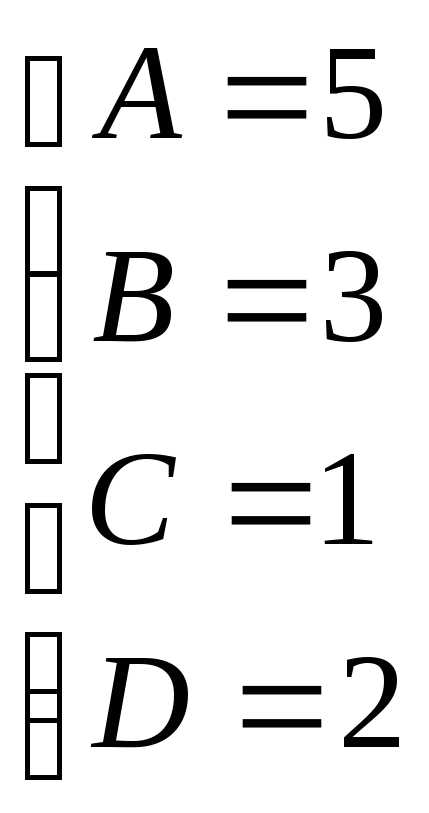
Итого:
Пример.
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
6x5– 8x4– 25x3+ 20x2– 76x– 7 3x3– 4x2– 17x+ 6
6x5– 8x4– 34x3+ 12x22x2+ 3
9x3 + 8x2 – 76x – 7
9x3 – 12x2 – 51x +18
20x2 – 25x – 25
Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:
3x3– 4x2– 17x+ 6x- 3
3x3– 9x23x2+ 5x- 2
5x2– 17x
5x2– 15x
– 2x+ 6
-2x+ 6
0
Таким образом 3x3– 4x2– 17x+ 6 = (x– 3)(3x2+ 5x– 2) = (x– 3)(x+ 2 )(3x– 1). Тогда:
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемыйметод произвольных значений. Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

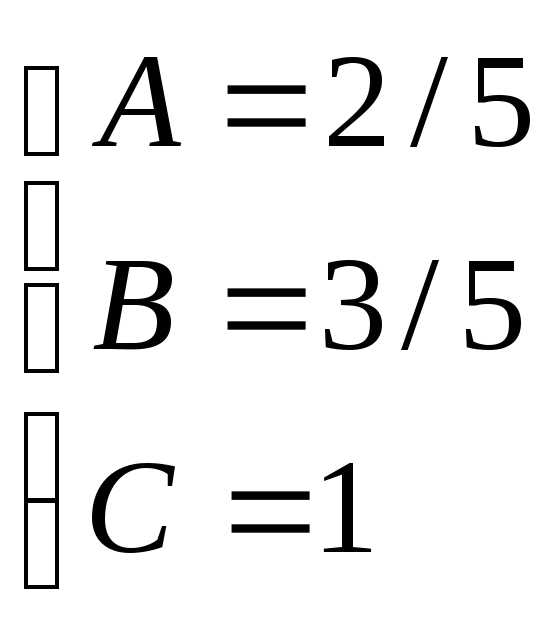
Окончательно получаем:
=
Пример.
Найдем неопределенные коэффициенты:
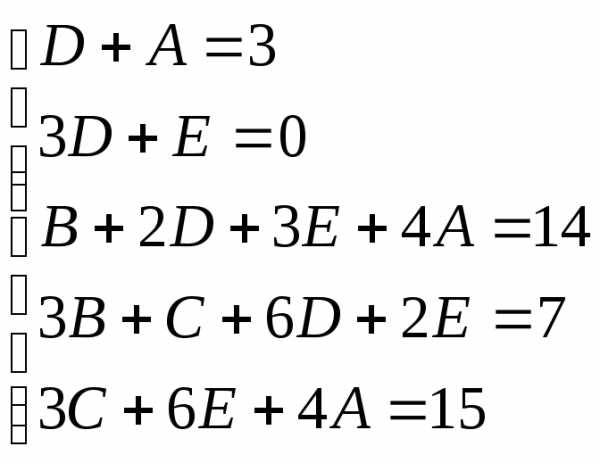

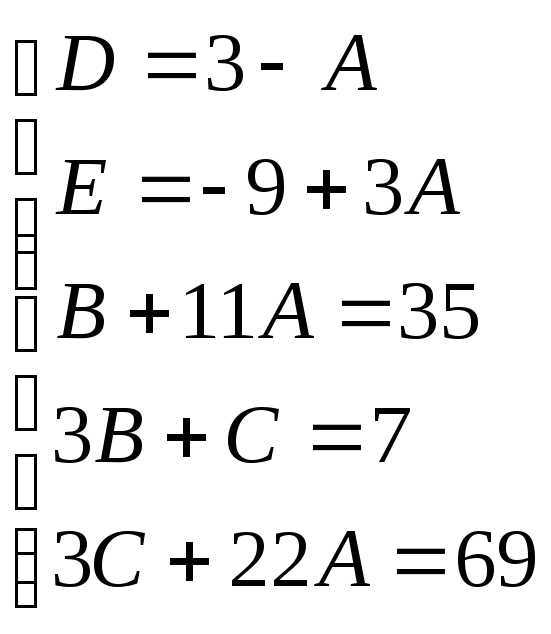
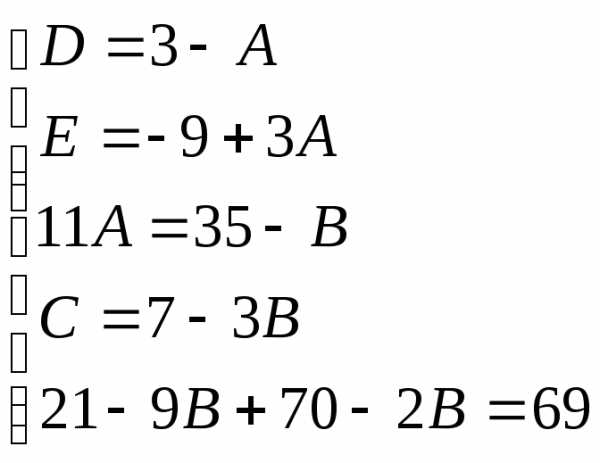
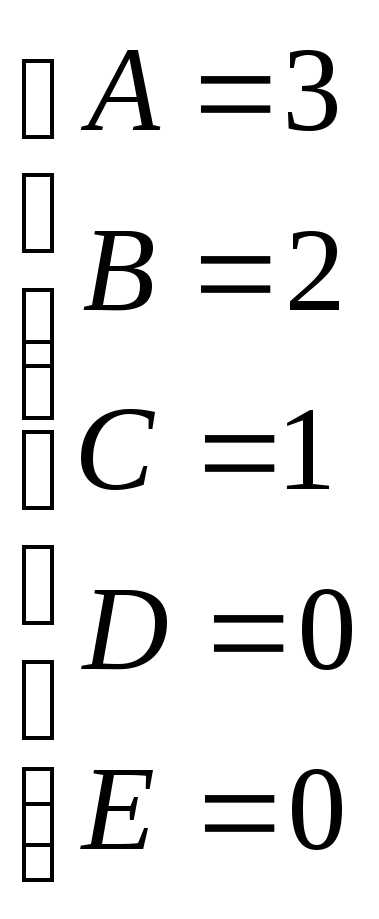
Тогда значение заданного интеграла:
Интегрирование некоторых тригонометрических
функций.
Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.
Интеграл вида .
Здесь R– обозначение некоторой рациональной функции от переменныхsinxиcosx.
Интегралы этого вида
вычисляются с помощью подстановки 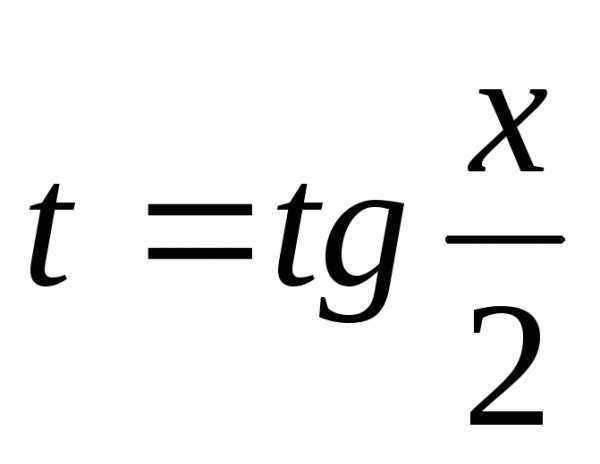 .
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
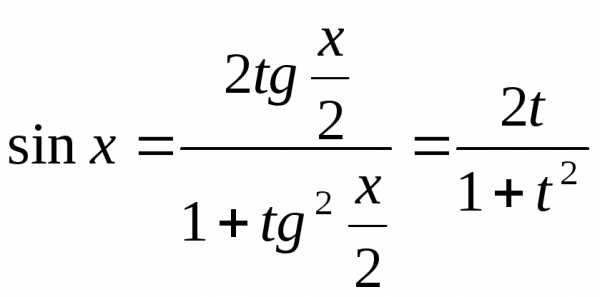 ,
,
Тогда
Таким образом:
Описанное выше преобразование называетсяуниверсальной тригонометрической подстановкой.
Пример.
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
Интеграл вида если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
Функция  может содержатьcosxтолько
в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительноsinx.
может содержатьcosxтолько
в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительноsinx.
Пример.
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл вида если
функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда
Пример.
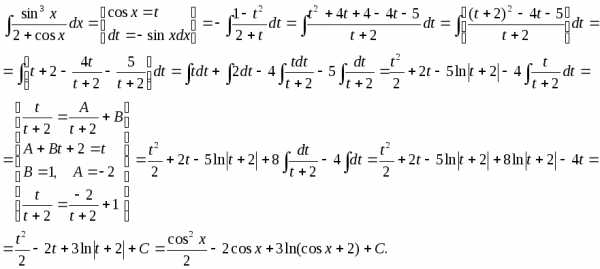
Интеграл вида
функция R четная относительно sinx и cosx.
Для преобразования функции Rв рациональную используется подстановка
t = tgx.
Тогда
Пример.
Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
Пример.
Пример.
Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.
Пример.
Пример.
Иногда применяются некоторые нестандартные приемы.
Пример.
Итого
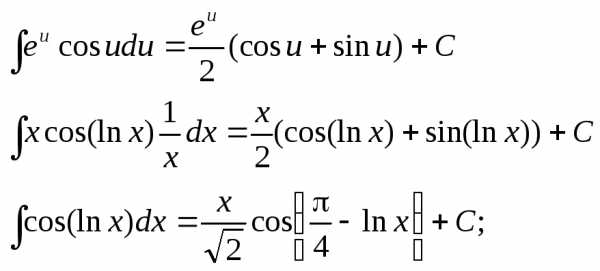
Интегрирование некоторых иррациональных функций.
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл
вида 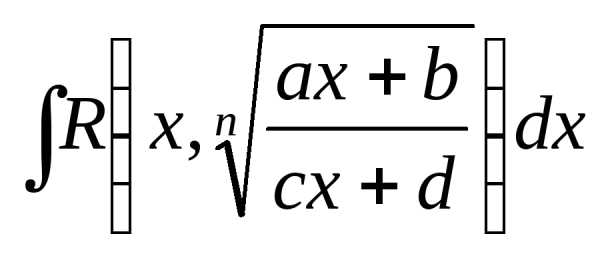 гдеn– натуральное
число.
гдеn– натуральное
число.
С помощью подстановки 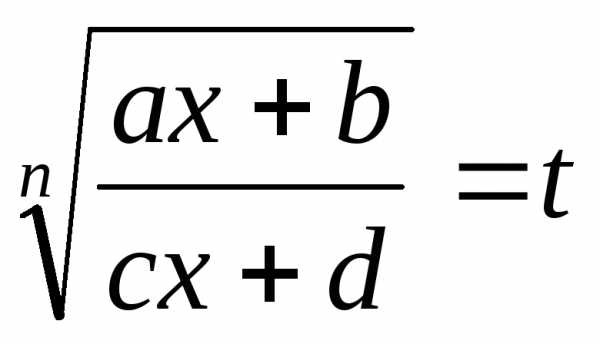 функция рационализируется.
функция рационализируется.
Тогда
Пример.
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример.
Интегрирование биноминальных дифференциалов.
Определение:Биноминальным дифференциалом называется выражение
xm(a + bxn)pdx
где m, n,иp– рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
Если р– целое число, то интеграл рационализируется с помощью подстановки
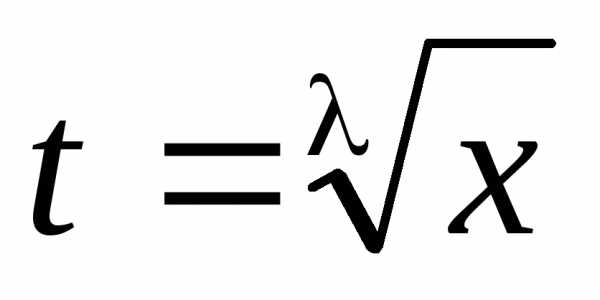 ,
где- общий знаменательmиn.
,
где- общий знаменательmиn.
Если
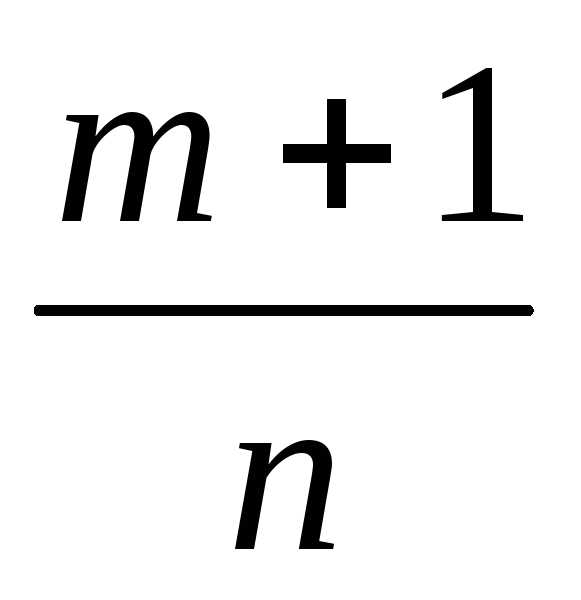 – целое число, то интеграл рационализируется
подстановкой
– целое число, то интеграл рационализируется
подстановкой
studfiles.net
∫ Решение неопределённых интегралов – Калькулятор Онлайн
Введите функцию, для которой необходимо вычислить интеграл
После вычисления неопределённого интеграла, вы сможете получить бесплатно ПОДРОБНОЕ решение введённого вами интеграла.
Найдем решение неопределенного интеграла от функции f(x)
(первообразную функции).
Примеры
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция – арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция – арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция – экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число – “Пи”, которое примерно равно 3.14
- sin(x)
- Функция – Синус от x
- cos(x)
- Функция – Косинус от x
- sinh(x)
- Функция – Синус гиперболический от x
- cosh(x)
- Функция – Косинус гиперболический от x
- sqrt(x)
- Функция – квадратный корень из x
- sqr(x) или x^2
- Функция – Квадрат x
- tg(x)
- Функция – Тангенс от x
- tgh(x)
- Функция – Тангенс гиперболический от x
- cbrt(x)
- Функция – кубический корень из x
- floor(x)
- Функция – округление x в меньшую сторону (пример floor(4.5)==4.0)
- sign(x)
- Функция – Знак x
- erf(x)
- Функция ошибок (Лапласа или интеграл вероятности)
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- – умножение
- 3/x
- – деление
- x^3
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
www.kontrolnaya-rabota.ru
Неопределенный интеграл. Свойства. Примеры.
Сегодня мы познакомимся с неопределенным интегралом, рассмотрим его свойства и порешаем несложные задачи. Для успешного изучения материала убедитесь, что у Вас нет проблем с производными 😉
Неопределенный интеграл функции — это совокупность всех первообразных данной функции.
— некоторая константа. является первообразной функции . Это значит, что если продифференцировать , мы получим , то есть .
Почему нужно писать «плюс константа»? Поскольку производная любой константы равна нулю, и производная суммы равна сумме производных, для функции можно записать бесконечное множество первообразных. Попробуйте, например, продифференцировать , , . Понятно, что везде будет получена функция . Таким образом, первообразной для функции будет множество функций вида .
Для решения базовых примеров необходимо знать свойства неопределенных интегралов и иметь перед глазами таблицу интегралов (которую, как и таблицу производных, стоит выучить наизусть).
Свойства:
Первое свойство говорит о том, что константу можно выносить за знак интеграла. Второе свойство: интеграл суммы (разности) двух функций равен сумме (разности) интегралов.
Таблица интегралов

[свернуть]
После решения конкретных задач на нахождение неопределенного интеграла рекомендую всегда делать проверку. Каким образом выполняется проверка? Положим, мы получили ответ . От этого выражения необходимо взять производную. Если производная оказалась в точности интегрируемой функцией , то интеграл вычислен верно.
Пример 1. Найти неопределенный интеграл. Результат проверить дифференцированием.
Решение: Понятно, что такой функции нет в таблице интегралов, поэтому нужно выполнить какие-то преобразования. Первым делом используем второе свойство интеграла:
Теперь каждый интеграл похож на табличный, но не совсем. Воспользуемся первым свойством — вынесем константы за знак интеграла. Отдельно нужно заметить, что не является функцией от , это самая обыкновенная константа.
Все полученные интегралы табличные. Глядя на таблицу интегралов, записываем ответ:
Ответ:
Выполним проверку — найдем производную от полученного выражения:
Итак, проверка выполнена, интеграл найден верно. Двигаемся дальше.
[свернуть]
Пример 2. Найти неопределенный интеграл. Результат проверить дифференцированием.
Решение: Подынтегральное выражение представляет собой дробь с весьма неприглядным числителем. Избавимся от дроби с помощью почленного деления числителя на знаменатель.
Используем свойство степеней .
Интеграл суммы равен сумме интегралов (2 свойство). Для каждого получившегося интеграла применяем третью формулу из таблицы.
Ответ:
И снова необходимо выполнить проверку. Дифференцируем полученное выражение:
[свернуть]
Как для нахождения производных, так и для вычисления интегралов существует множество программ. Особо удобны онлайн сервисы, например, Wolfram|Alpha. То есть необязательно выполнять (если того не требует задача) проверку вручную.
Пример 3. Найти интеграл. Выполнить проверку.
Решение: Преобразуем подынтегральное выражение. Применим формулу квадрата суммы, а затем раскроем скобки.
Интеграл суммы равен сумме интегралов. Для получившихся второго и третьего интегралов применяем первое свойство (выносим константу).
Ответ:
Интеграл найден. Выполним проверку — продифференцируем полученное выражение:
Итак, дифференцирование дало в точности подынтегральное выражение исходного интеграла. Таким образом, задача выполнена верно.
[свернуть]
Все разобранные примеры получились в основном на одну формулу из таблицы интегралов. Давайте это исправим 🙂
Пример 4. Найти интеграл.
Решение: Используем второе свойство — разбиваем интеграл на сумму нескольких.
Используем первое свойство — выносим константу за знак интеграла.
Теперь каждый интеграл является табличным. Аккуратно записываем ответ при помощи таблицы (первый — 10я формула, второй — 13я формула, третий — 12я формула, четвертый — 14я формула):
Ответ получен. Громоздкий? Ничего страшного! Главное, чтобы было правильно (сделайте проверку самостоятельно).
[свернуть]
Рассмотренный материал является первым маленьким шажком в освоении интегралов. Если здесь всё понятно, то предлагаю сразу перейти к следующей статье и научиться использовать замену при интегрировании.
Удачи! Желаю Вам никогда не забывать про константу в ответе 😉
higher-math.ru
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике – Элементы математического анализа
Первообразная
Определение 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого выполнено равенство
F’ (x) = f (x) .
Например, из справедливости равенства
(sin 2x)’ = 2 cos 2x
вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .
Замечание. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .
Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.
Теорема 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид
F (x) + с ,
где c – некоторое число.
Неопределенный интеграл
Определение 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
| (1) |
Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .
Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:
| (2) |
Однако для упрощения формулу (2) принято записывать в виде
| (3) |
подразумевая, но не указывая специально, что c – любое число.
В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования. Замена переменной в неопределенном интеграле
Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.
Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство
где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле
то есть интеграл от суммы функций равен сумме интегралов от этих функций.
Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле
то есть интеграл от разности функций равен разности интегралов от этих функций.
Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы
вытекает, что
| (4) |
если все входящие в формулу (4) функции f (φ (x)), φ’ (x), F (φ (x)) определены.
Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):
Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.
Замечание. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть
φ (x) = kx + b ,
что k и b – произвольные числа, .
В этом случае
φ’ (x) = k ,
и формула (4) принимает вид
| (5) |
Формула (5) часто используется при решении задач.
Таблица интегралов
Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций
| Основная формула | Обобщения |
, где k – любое число | |
где n – любое число, не равное – 1 | , где n, k, b – любые числа, , |
где n – любое число, | |
, x > 0 | , где k, b – любые числа, , |
где φ (x) > 0 | |
, где k, b – любые числа, | |
где a – любое положительное число, не равное 1 | , где a – любое положительное число, не равное 1, k, b – любые числа, |
, где a – любое положительное число, не равное 1 | |
, где k, b – любые числа, | |
, где k, b – любые числа, | |
, где k, b – любые числа, , | |
, | |
, где k, b – любые числа, , | |
, | |
| x | < 1 | где k, b – любые числа, , |
| φ (x) | < 1 | |
где a, b – любые числа, | |
, где k, b – любые числа, | |
где a, b – любые числа, |
Основная формула: Обобщения: , где k – любое число |
Основная формула: где n – любое число, не равное – 1 . Обобщения: , где n, k, b – любые числа, , _____ где n – любое число, |
Основная формула: , x > 0 Обобщения: , где k, b – любые числа, , kx + b > 0 _____ где φ (x) > 0 |
Основная формула: Обобщения: , где k, b – любые числа, _____ |
Основная формула: , где a – любое положительное число, не равное 1 . Обобщения: , где a – любое положительное число, не равное 1, k, b – любые числа, _____ , где a – любое положительное число, не равное 1 |
Основная формула: Обобщения: , где k, b – любые числа, _____ |
Основная формула: Обобщения: , где k, b – любые числа, _____ |
Основная формула: где Обобщения: , где k, b – любые числа, , _____ , где |
Основная формула: где Обобщения: , где k, b – любые числа, , _____ , |
Основная формула: | x | < 1 Обобщения: где k, b – любые числа, , | kx +b | < 1 _____ где | φ (x) | < 1 _____ где a, b – любые числа, |
Основная формула: Обобщения: , где k, b – любые числа, _____ _____ где a, b – любые числа, |
Примеры решения задач
Пример 1. Вычислить интеграл
Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов формулами из таблицы неопределенных интегралов, получаем


Ответ.
Пример 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти .
Решение. Поскольку Поскольку
то
Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c:
F (0) = 4 cos 0 + c = 9,
4 + c = 9, c = 5.
Следовательно,
F (x) = 4 cos x + 5
Поэтому
Ответ. 7
Пример 3. Найти первообразную F (x) функции
если F (2π) = 2e + 3.
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов
для функции φ (x) = cos x , получаем
Следовательно,
| (7) |
Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:
Итак,
c = 3e +3 .
Ответ.
Пример 4. Вычислить интеграл
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов
для функции φ (x) = ex, получаем
Ответ.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Метод интегрирования по частям
Формула интегрирования по частям
Формула интегрирования по частям имеет вид:
.
Метод интегрирования по частям состоит в применении этой формулы. При практическом применении стоит отметить, что u и v являются функциями от переменной интегрирования. Пусть переменная интегрирования обозначена как x (символ после знака дифференциала d в конце записи интеграла) . Тогда u и v являются функциями от x: u(x) и v(x).
Тогда
, .
И формула интегрирования по частям принимает вид:
.
То есть подынтегральная функция должна состоять из произведения двух функций:
,
одну из которых обозначаем как u: g(x) = u, а у другой должен вычисляться интеграл (точнее находиться первообразная):
, тогда dv = f(x) dx.
В некоторых случаях f(x) = 1. То есть в интеграле
,
можно положить g(x) = u, x = v.
Резюме
Итак, в данном методе, формулу интегрирования по частям стоит запомнить и применять в двух видах:
;
.
Интегралы, вычисляющиеся интегрированием по частям
Интегралы, содержащие логарифм и обратные тригонометрические (гиперболические) функции
По частям часто интегрируются интегралы, содержащие логарифм и обратные тригонометрические или гиперболические функции. При этом ту часть, которая содержит логарифм или обратные тригонометрические (гиперболические) функции обозначают через u, оставшуюся часть – через dv.
Вот примеры таких интегралов, которые вычисляются методом интегрирования по частям:
, , , , , , .
Подробное решение этих интегралов >>>
Интегралы, содержащие произведение многочлена и sin x, cos x или ex
По формуле интегрирования частям находятся интегралы вида:
, , ,
где P(x) – многочлен от x. При интегрировании, многочлен P(x) обозначают через u, а eax dx, cos ax dx или sin ax dx – через dv.
Вот примеры таких интегралов:
, , .
Подробное решение этих интегралов >>>
Примеры вычисления интегралов методом интегрирования по частям
Примеры интегралов, содержащих логарифм и обратные тригонометрические функции
Пример
Вычислить интеграл:
Подробное решение
Здесь подынтегральное выражение содержит логарифм. Делаем подстановки
u = ln x,
dv = x2 dx.
Тогда
,
.
.
Вычисляем оставшийся интеграл:
.
Тогда
.
В конце вычислений нужно обязательно добавить постоянную C, поскольку неопределенный интеграл – это множество всех первообразных. Также ее можно было добавлять и в промежуточных вычислениях, но это лишь загромождало бы выкладки.
Более короткое решение
Можно представить решение и в более коротком варианте. Для этого не нужно делать подстановки с u и v, а можно сгруппировать сомножители и применить формулу интегрирования по частям во втором виде.
.Ответ
Еще примеры решений подобных интегралов >>>
Примеры интегралов, содержащих произведение многочлена и sin x, cos x или ex
Пример
Вычислить интеграл:
.
Решение
Введем экспоненту под знак дифференциала:
e – x dx = – e – x d(–x) = – d(e – x).
Интегрируем по частям.
.
Также применяем метод интегрирования по частям.
.
.
.
Окончательно имеем:
.
Ответ
.
Еще примеры решений подобных интегралов >>>
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Решение неопределенных интегралов примеры – 1 Октября 2012 – Примеры решений задач
Пример 1. Вычислить интеграл
Решение:
На сайте имеется более 500 интегралов с подробным решением (для просмотра, нажмите по изображению правой кнопкой мышки )
Пример 2. Найти интеграл Решение.
Пример 3. Найти Решение.
Пример 4. Найти Решение.
Пример 5. Найти Решение.
Пример 6. Найти Решение.
Пример 7. Найти Решение.
Пример 8. Найти Решение.
Пример 9. Найти интеграл методом замены переменной (интегрирование подстановкой):
Решение:
Пример 10. Найти интеграл ( продолжение интегрирование подстановкой)
Решение:
Пример 11.Найти интеграл:
Решение:
Пример 12. Решение:
www.reshim.su



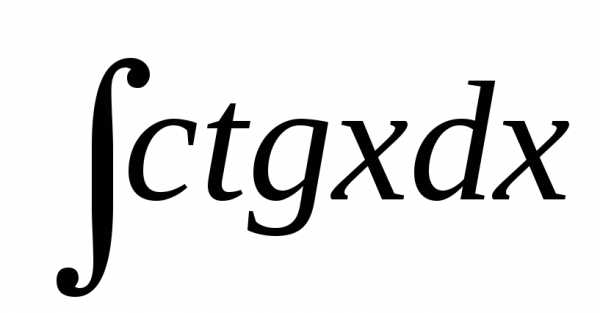
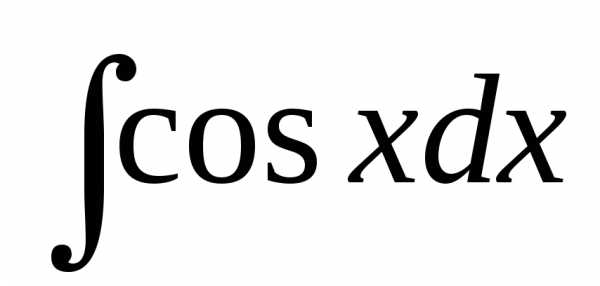
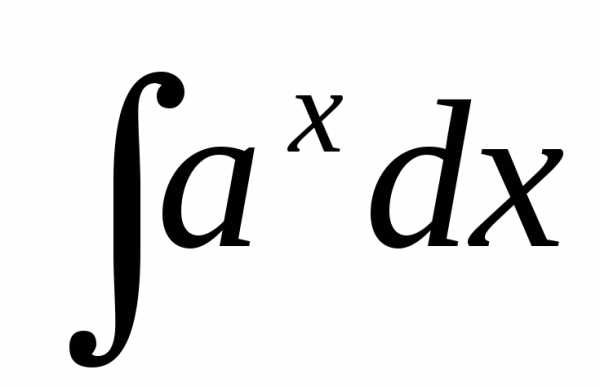

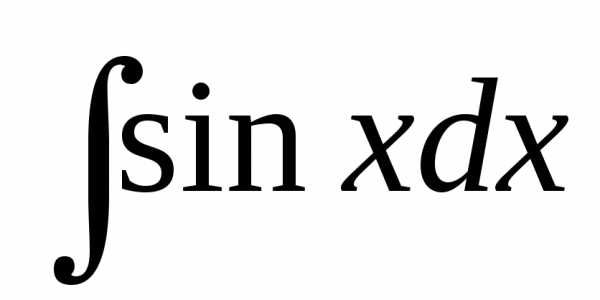

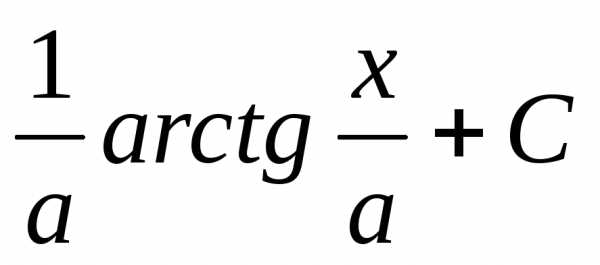
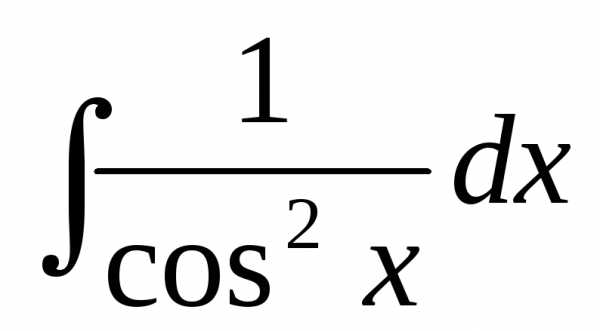

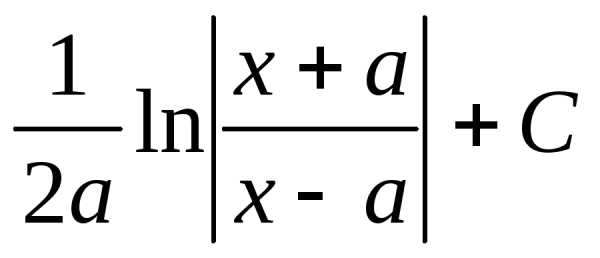
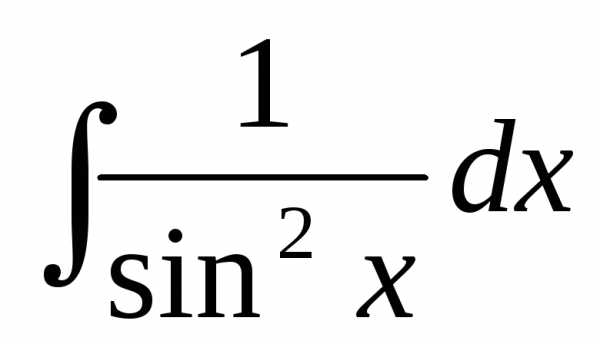
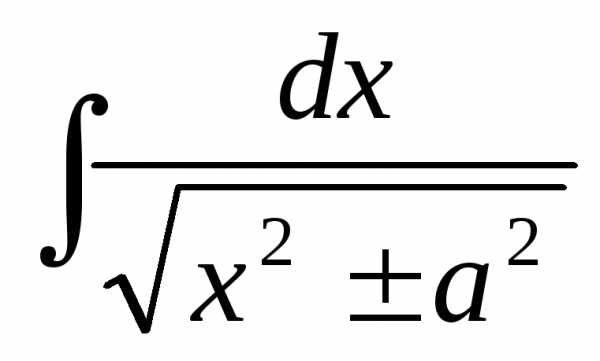
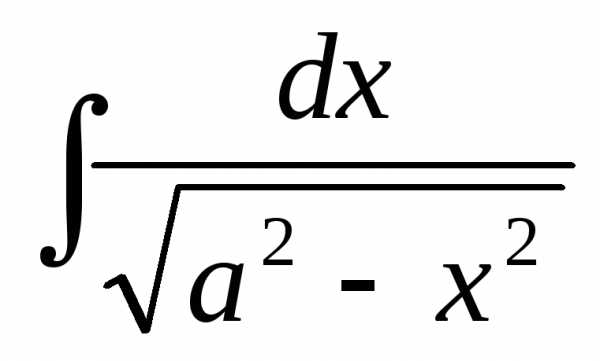
 + C
+ C