Найбільший спільний дільник та найменше спільне кратне
Означення: Найбільшим спільним дільником двох або декількох натуральних чисел називають найбільше натуральне число, на яке ділиться кожне з даних чисел.
Наприклад
НСД
Взаємно прості числа
Означення: Два натуральних числа називаються взаємно простими, якщо їхній НСД дорівнює одиниці.
Знаходження НСД за допомогою розкладання на прості множники
Щоб знайти НСД двох або кількох чисел, необхідно:
- Розкласти дані числа на прості множники.
- Скласти добуток зі спільних простих множників, взятих із найменшим показником степеня.
- Знайти значення добутку.
Алгоритм Евкліда
- Поділити на з остачею:
- Поділити дільник на :
- Поділити дільник на нову остачу :
Остання відмінна від нуля остача і є НСД.
Найменше спільне кратне (НСК)
Знаходження НСК двох натуральних чисел
Щоб знайти НСК двох або кількох чисел, необхідно:
HCK
Наприклад
НСК
Звязок між НСД і НСК двох чисел
HCД
cubens.com
НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ
Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ
§5. НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ
Знайдемо кратні числа 4. Для цього достатньо помножити число 4 на числа натурального ряду:
4; 8; 12; 16; 20; 24; 28; 32; 36; 40; 44…
Аналогічно знайдемо кратні числа 6:
6; 12; 18; 24; 30; 36; 42; 48; 54; 60; 66…
Серед кратних числа 4 і числа 6 є такі числа, які діляться на обидва ці числа:
12; 24; 36; 48…
Ці числа є спільними кратними чисел 4 і 6. Найменшим серед них є число 12. Це найменше спільне кратне чисел 4 і 6.
Записують: НСК (4; 6) = 12 і говорять: “Найменшим спільним кратним чисел 4 і 6 є число 12”.
Запам’ятайте!
Найменшим спілілим кратним двох чисел називається найменше число, яке ділиться на кожне з даних чисел.
Спільні кратні кількох чисел можна шукати за допомогою розкладів даних чисел на прості множники.
Задача 1. Знайдіть НСК чисел 18 і 45.
Розв’язання.
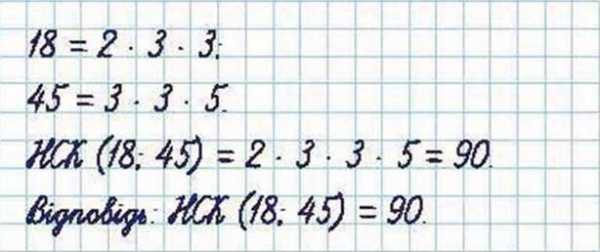
Запам’ятайте!
Правило знаходження НСК Щоб знайти НСК двох чисел:
1) розкладіть дані числа на прості множники;
2) запишіть розклад одного зданих чисел;
3) допишіть до цього розкладу такі множники із розкладу іншого числа, які ще не увійшли до добутку;
4) обчисліть отриманий добуток.
? Як знайти НСК двох взаємно простих чисел? кількох чисел?
Оскільки у взаємно простих чисел не має інших спільних дільників, крім 1, то НСК таких чисел дорівнює їх добутку. Наприклад,
НСК (8; 21) = 8 ∙ 21 = 168.
НСК кількох чисел шукають так само, як і двох чисел. Наприклад, знайдемо НСК (9; 12; 15). Маємо: 9 = 3 ∙ 3 = 32, 12=2 ∙ 2 ∙ 3 = 22 ∙ 3, 15 = 3∙ 5. Звідси НСК (9; 12; 15) = = З2 ∙ 22 ∙ 5 = 9 ∙ 4 ∙ 5 = 180.
Дізнайтеся більше
Виявляється, що між НСК та НСД чисел а і b існує зв’язок, який виражається такою формулою:
НСК (a; b) ∙ НСД (а; b) = а ∙ b.
Наприклад, для чисел 54 і 48 дістанемо:
54 = 2 ∙ З3,
48 = 24- 3.
Звідси НСД (54; 48) = 6, НСК (54; 48) = 432. А тепер скористаємося формулою. Маємо:
НСК (54; 48) ∙ НСД (54; 48) = 432 – 6 = 2592 = 54 – 48.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Яке число називається спільним кратним двох чисел?
2. Яке число називається найменшим спільним кратним двох чисел?
3. Як знайти найменше спільне кратне двох чисел?
4. Як знайти найменше спільне кратне двохвзаємно простих чисел?
162′. Назвіть будь-які три числа, які є спільними кратними чисел 4 і 10. Чи є серед них НСК (4; 10)?
163′. Чи правильно, що найменшим спільним кратним двох взаємно простих чисел є:
1) їх сума; 2) ‘їх різниця; 3) їх добуток; 4) їх частка?
164′. Чи правильно, що найменшим спільним кратним чисел 5 і 3 є число:
1) 8; 2) 15; 3) 15; 4) 30?
165°. Із чисел від десяти до тридцяти п’яти випишіть ті, які є спільними кратними чисел:
1) 2 і 5; 2) 4 і 8; 3)4 і 12.
166°. Із чисел від дванадцяти до сорока випишіть ті, які є спільними кратними чисел:
1) 3 і 5; 2) 3 і 6; 3) 3 і 12.
167°. На координатному промені позначте дві точки з координатами, які є спільними кратними чисел 2 і 3. (За одиничний відрізок візьміть клітинку зошита.)
168°. На координатному промені позначте три точки з координатами, які є спільними кратними чисел 3 і 4. (За одиничний відрізок візьміть півклітинки зошита.)
169°. Знайдіть НСК чисел а і b, якщо:
1)а = 2 ∙ 3 ∙ 7, b = 3 ∙ 5 ∙ 7;
2)а = 2 ∙ 2 ∙ 3 ∙ 5, b = 2 ∙ 3 ∙ 3 ∙ 5;
3)а =2 ∙ 3 ∙ 3 ∙ 7, b=3 ∙ 3 ∙ 5 ∙ 7.
170°. Знайдіть НСК чисел: 1) 12 і 18; 2) 15 і 18; 3) 14 і 21.
171°. Знайдіть НСК чисел: 1) 24 і 28; 2) 24 і 32; 3) 24 і 36.
172°. Знайдіть НСК чисельника і знаменника дробу:
173°. Знайдіть НСК знаменників дробів:
174°. Знайдіть НСК знаменників дробів:
175°. Відомо, що НСК(х; у) = ху. Що можна сказати про ці числа?
176. Відомо, що в ящику менше, ніж 80 яблук, і що їх кількість ділиться на 3, на 4, на 5 і на 6. Скільки яблук у ящику?
177. Мама спекла до свята деяку кількість пиріжків, яка менша, ніж 50. Відомо, що це число ділиться на 4, на 6 і на 9. Скільки пиріжків спекла мама?
178. Дідусеві Юрка ще немає 90 років, але його вік є числом, що ділиться на 6, 8, 9 і 12. Скільки років дідусеві?
179. Знайдіть НСК чисел:
1) 64 і 54; 3) 100 і 125; 5) 168 і 140; 7) 125 і 225;
2) 95 і 114; 4) 121 і 88; 6) 144 і 324; 8) 185 і 111.
180. Знайдіть НСК чисел:
1)162 і 243; 2) 192 і 256; 3)252 і 189; 4) 264 і 300.
181. Знайдіть НСК чисел:
1) 8, 12 і 18; 3) 33, 44 і 121; 5) 18, 24 і 32; 7) 21, 28 і 42;
2) 16, 32 і 48; 4) 35, 84 і 105; 6) 25, 45 і 60; 8) 11, 13 і 23.
182. Знайдіть НСК чисел:
1) 22, 33 і 55; 2) 16, 20 і 36; 3) 10, 25 і 35; 4) 11, 17 і 19.
183. Розв’яжіть дану пару рівнянь та знайдіть НСК (х; у):
1) 4,12х + 11,68 = 160 і 3,34у – 20,64 = 300;
2) 2,36x – 7,2 = 99 і 1,55y + 7,25= 170.
184. Дано числа від десяти до двадцяти. Випишіть усі можливі пари взаємно простих чисел та знайдіть їх НСК.
185*. Знайдіть найменше чотирицифрове число, яке ділиться і на 31, і на 3.
186*. Знайдіть найбільше трицифрове число, яке ділиться і на 28, і на 5.
187*. Два двоцифрові числа, що діляться на 9, записані тими самими цифрами. Знайдіть усі можливі пари таких чисел та їх НСК.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
188. Уздовж дороги від міста Достояли стовпи на відстані 30 м один від одного. Ці стовпи вирішили замінити новими і розташувати їх на відстані 45 м один від одного. Знайдіть відстань від міста N до найближчого стовпа, який буде стояти на місці старого, крім першого.
ЗАДАЧІ НА ПОВТОРЕННЯ
189. Довжина відрізка ВС дорівнює 24 см. Відрізок AD довший за відрізок ВС на 5 см і коротший від відрізка MN на 7 см. Знайдіть суму довжин відрізків BC, AD і MN.
190. Знайдіть три числа, якщо їх середнє арифметичне дорівнює 12, а друге число удвічі більше за перше і в тричі менше від третього.
predmety.in.ua
Урок 12. Найменше спільне кратне (НСК)
Спільним кратним кількох натуральних чисел є число, яке ділиться на всі ці числа без остачі. Найбільшим спільним дільником (НСД) кількох натуральних чисел називають найбільший дільник, на який діляться ці числа націло. Запишемо числа, кратні
– ці числа розкласти на прості множники;
– потім розклад одного числа доповнити простими множниками інших чисел, яких не вистачає;
– знайти добуток цих множників. Знайдемо найменше спільне кратне чисел 90 і 210. Якщо більше з даних чисел ділиться на всі інші, то воно і буде найменшим кратним для цих чисел. НСК (120; 60; 40) = 120. Найменшим спільним кратним двох взаємно простих чисел є добуток цих чисел. Найменше спільне кратне можна знайти не тільки для двох, але й для трьох і більше чисел. Для чисел 12, 18, 24 маємоНСК (11; 11; 15) =
Другий спосіб.Відомо, що
Найменше спільне кратне двох чисел дорівнює добутку цих чисел, поділеному на їх найбільший спільний дільник.
Використовуючи
цю залежність, можна визначити НСК.
Як знайти найменше спільне кратне чисел
Школярі часто зустрічають серед завдань з математики таку формулювання: “знайдіть найменше спільне кратне чисел”. Цього обов’язково потрібно навчитися робити, щоб виконувати різні дії з дробами з неоднаковими знаменниками.
Знаходження найменшого спільного кратного: основні поняття
Щоб зрозуміти, як обчислювати НОК, слід визначитися в першу чергу зі значенням терміна “кратне”.
Кратним числа А називають таке натуральне число, яке без остачі ділиться на А. Так, числами, кратними 5 можна вважати 15, 20, 25 і так далі.
Дільників конкретного числа може бути обмежена кількість, а ось кратних безліч.
Спільне кратне натуральних чисел – це таке число, яке ділиться на них без залишку.
Як знайти найменше спільне кратне чисел
Найменше спільне кратне (НСК) чисел (двох, трьох або більше) – це найменше натуральне число, яке ділиться на всі числа націло.
Щоб знайти НОК, можна використовувати кілька способів.
Для невеликих чисел зручно виписати в рядок усі кратні цих чисел до тих пір, поки серед них не знайдеться загальне. Кратні позначають запису заголовною буквою К.
Наприклад, кратні числа 4 можна записати так:
До (4) = {8,12, 16, 20, 24, …}
До (6) = {12, 18, 24, …}
Так, можна побачити, що найменшим спільним кратним чисел 4 і 6 є число 24. Цей запис виконують наступним чином:
НОК (4, 6) = 24
Якщо числа більші, або потрібно знайти найменше спільне кратне трьох і більше чисел, то краще використовувати інший спосіб обчислення НОК.
Для виконання завдання необхідно розкласти запропоновані числа на прості множники.
Спочатку потрібно виписати в рядок розкладання найбільшого числа, а під ним – інших.
В розкладанні числа кожного може бути різна кількість множників.
Наприклад, розкладемо на прості множники числа 50 і 20.
50 = 2 * 5 * 5
20 = 2 * 5 * 2
В розкладанні меншого числа слід підкреслити множники, які відсутні в розкладанні першого найбільшого числа, а потім додати до нього. У представленому прикладі не вистачає двійки.
Тепер можна обчислити найменше спільне кратне 20 і 50.
НОК (20, 50) = 2 * 5 * 5 * 2 = 100
Так, добуток простих множників більшого числа і множників другого числа, які не увійшли до розкладання більшого, буде найменшим спільним кратним.
Щоб знайти НОК трьох чисел і більше, слід їх все розкласти на прості множники, як і в попередньому випадку.
В якості прикладу можна знайти найменше спільне кратне чисел 16, 24, 36.
36 = 2 * 2 * 3 * 3
24 = 2 * 2 * 2 * 3
16 = 2 * 2 * 2 * 2
Так, розкладання більшого числа на множники не увійшли лише дві двійки з розкладання шістнадцяти (одна є в розкладанні двадцяти чотирьох).
Таким чином, їх потрібно додати до розкладання більшого числа.
НОК (12, 16, 36) = 2 * 2 * 3 * 3 * 2 * 2 = 9
Існують окремі випадки визначення найменшого спільного кратного. Так, якщо одне з чисел можна поділити без залишку на інше, то більше з цих чисел і буде найменшим спільним кратним.
Наприклад, НОК дванадцяти і двадцяти чотирьох буде двадцять чотири.
Якщо необхідно знайти найменше спільне кратне взаємно простих чисел, які не мають однакових дільників, то їх НОК буде дорівнювати їх добутку.
Наприклад, НОК (10, 11) = 110.
Відео по темі
adrian.com.ua
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ – ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ – Математика 6 класс – Н.А. Тарасенкова – Образование 2014
Раздел 1 ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
§5. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Найдем кратные числа 4. Для этого достаточно умножить число 4 на числа натурального ряда:
4; 8; 12; 16; 20; 24; 28; 32; 36; 40; 44…
Аналогично найдем кратные числа 6:
6; 12; 18; 24; 30; 36; 42; 48; 54; 60; 66…
Среди кратных числа 4 и числа 6 являются такие числа, которые делятся на оба эти числа:
12; 24; 36; 48…
Эти числа являются общими кратными чисел 4 и 6. Наименьшим среди них является число 12. Это наименьшее общее кратное чисел 4 и 6.
Записывают: НСК (4; 6) = 12 и говорят: «Наименьшим общим кратным чисел 4 и 6 является число 12».
Запомните!
Наименьшим спілілим кратным двух чисел называется наименьшее число, которое делится на каждое из данных чисел.
Общие кратные нескольких чисел можно искать с помощью разложений данных чисел на простые множители.
Задача 1. Найдите НСК чисел 18 и 45.
Решения.
Запомните!
Правило нахождения НСК Чтобы найти нок двух чисел:
1) разложите данные числа на простые множители;
2) запишите расписание одного сданных чисел;
3) допишите к этому раскладу такие множители из разложения другого числа, которые еще не вошли к произведению;
4) вычислите полученное произведение.
? Как найти нок двух взаимно простых чисел? нескольких чисел?
Поскольку у взаимно простых чисел нет иных общих делителей, кроме 1, то НСК таких чисел равна их произведению. Например, НСК (8; 21) = 8 ∙ 21 = 168.
НСК нескольких чисел ищут так же, как и двух чисел. Например, найдем НСК (9; 12; 15). Имеем: 9 = 3 ∙ 3 = 32, 12=2 ∙ 2 ∙ 3 = 22 ∙ 3, 15 = 3∙ 5. Отсюда НСК (9; 12; 15) = = С2 ∙ 22 ∙ 5 = 9 ∙ 4 ∙ 5 = 180.
Узнайте больше
Оказывается, что между НСК и НОД чисел а и b существует связь, которая выражается следующей формулой:
НСК (a; b) ∙ НОД (а; b) = а ∙ b.
Например, для чисел 54 и 48 получим:
54 = 2 ∙ С3,
48 = 24 – 3.
Отсюда НОД (54; 48) = 6, НОК (54; 48) = 432. А теперь воспользуемся формулой. Имеем:
НСК (54; 48) ∙ НОД (54; 48) = 432 – 6 = 2592 = 54 – 48.
ВСПОМНИТЕ ГЛАВНОЕ
1. Какое число называется общим кратным двух чисел?
2. Какое число называется наименьшим общим кратным двух чисел?
3. Как найти наименьшее общее кратное двух чисел?
4. Как найти наименьшее общее кратное двохвзаємно простых чисел?
162′. Назовите любые три числа, которые являются общими кратными чисел 4 и 10. Есть среди них НСК (4; 10)?
163′. Правильно, что наименьшим общим кратным двух взаимно простых чисел является:
1) сумма; 2) ‘их разница; 3) их произведение; 4) их доля?
164′. Правильно, что наименьшим общим кратным чисел 5 и 3 является число:
1) 8; 2) 15; 3) 15; 4) 30?
165°. Из чисел от десяти до тридцати пяти выпишите те, которые являются общими кратными чисел:
1) 2 и 5; 2) 4 и 8; 3)4 и 12.
166°. Из чисел от двенадцати до сорока выпишите те, которые являются общими кратными чисел:
1) 3 и 5; 2) 3 и 6; 3) 3 и 12.
167°. На координатном луче отметьте две точки с координатами, которые являются общими кратными чисел 2 и 3. (За единичный отрезок возьмите клеточку тетради.)
168°. На координатном луче отметьте три точки с координатами, которые являются общими кратными чисел 3 и 4. (За единичный отрезок возьмите півклітинки тетради.)
169°. Найдите НСК чисел а и b, если:
1)а = 2 ∙ 3 ∙ 7, b = 3 ∙ 5 ∙ 7;
2)а = 2 ∙ 2 ∙ 3 ∙ 5, b = 2 ∙ 3 ∙ 3 ∙ 5;
3)а =2 ∙ 3 ∙ 3 ∙ 7, b=3 ∙ 3 ∙ 5 ∙ 7.
170°. Найдите НСК чисел: 1) 12 и 18; 2) 15 и 18; 3) 14 и 21.
171°. Найдите НСК чисел: 1) 24 и 28; 2) 24 и 32; 3) 24 и 36.
172°. Найдите НСК числителя и знаменателя дроби:
173°. Найдите НСК знаменателей дробей:
174°. Найдите НСК знаменателей дробей:
175°. Известно, что НСК(х; у) = ху. Что можно сказать про эти числа?
176. Известно, что в ящике меньше, чем 80 яблок, и что их число делится на 3, на 4, на 5 и на 6. Сколько яблок в ящике?
177. Мама испекла к празднику некоторое количество пирожков, которая меньше, чем 50. Известно, что это число делится на 4, на 6 и на 9. Сколько пирожков испекла мама?
178. Дедушке Юры еще нет 90 лет, но его возраст является числом, которое делится на 6, 8, 9 и 12. Сколько лет дедушке?
179. Найдите НСК чисел:
1) 64 и 54; 3) 100 и 125; 5) 168 и 140; 7) 125 и 225;
2) 95 и 114; 4) 121 и 88; 6) 144 и 324; 8) 185 и 111.
180. Найдите НСК чисел:
1)162 и 243; 2) 192 и 256; 3)252 и 189; 4) 264 и 300.
181. Найдите НСК чисел:
1) 8, 12 и 18; 3) 33, 44 и 121; 5) 18, 24 и 32; 7) 21, 28 и 42;
2) 16, 32 и 48; 4) 35, 84 и 105; 6) 25, 45 и 60; 8) 11, 13 и 23.
182. Найдите НСК чисел:
1) 22, 33 и 55; 2) 16, 20 и 36; 3) 10, 25 и 35; 4) 11, 17 и 19.
183. Решите данную пару уравнений и найдите НСК (х; у):
1) 4,12 х + 11,68 = 160 и 3,34 в – 20,64 = 300;
2) 2,36x – 7,2 = 99 и 1,55y + 7,25= 170.
184. Даны числа от десяти до двадцати. Выпишите все возможные пары взаимно простых чисел и найдите их НСК.
185*. Найдите наименьшее четырехзначное число, которое делится и на 31, и на 3.
186*. Найдите наибольшее трицифрове число, которое делится и на 28, и на 5.
187*. Два двоцифрові числа, делящиеся на 9, записанные теми же цифрами. Найдите все возможные пары таких чисел и их НСК.
ПРИМЕНИТЕ НА ПРАКТИКЕ
188. Вдоль дороги от города Достояли столбы на расстоянии 30 м друг от друга. Эти столбы решили заменить новыми и расположить их на расстоянии 45 м друг от друга. Найдите расстояние от города N до ближайшего столба, который будет стоять на месте старого, кроме первого.
ЗАДАЧИ НА ПОВТОРЕНИЕ
189. Длина отрезка ВС равна 24 см. Отрезок AD длиннее отрезок ВС на 5 см и короче отрезка MN на 7 см. Найдите сумму длин отрезков BC,AD и MN.
190. Найдите три числа, если их среднее арифметическое равно 12, а второе число вдвое больше первого и в три раза меньше третьего.
schooled.ru
