Обратный ход метода Гаусса — Мегаобучалка
Учреждение образования «Белорусская государственная
Сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Метод Гаусса решения систем линейных
уравнений» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Метод Гаусса решения систем линейных уравнений
Эквивалентные системы уравнений
Две системы линейных уравнений называются эквивалентными, если каждое решение одной из них является решением другой. Процесс решения системы линейных уравнений состоит в последовательном преобразовании её в эквивалентную систему с помощью так называемых элементарных преобразований, которыми являются:
1) перестановка любых двух уравнений системы;
2) умножение обеих частей любого уравнения системы на отличное от нуля число;
3) прибавление к любому уравнению другого уравнения, умноженного на любое число;
4) вычёркивание уравнения, состоящего из нулей, т.е. уравнения вида .
Гауссовы исключения
Рассмотрим систему m линейных уравнений с n неизвестными:
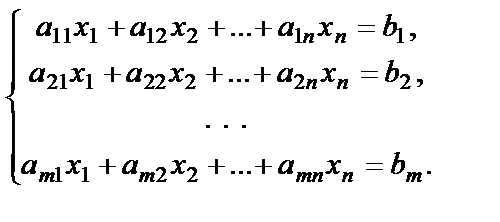
Суть метода Гаусса или метода последовательного исключения неизвестных состоит в следующем.
Вначале с помощью элементарных преобразований исключается неизвестная из всех уравнений системы, кроме первого. Такие преобразования системы называются
При выполнении одного шага гауссового исключения нужно пользоваться следующими правилами:
1) коэффициенты и свободный член разрешающего уравнения остаются неизменными;
2) коэффициенты разрешающего столбца, расположенные ниже разрешающего коэффициента, обращаются в нули;
3) все прочие коэффициенты и свободные члены при выполнении первого шага вычисляются по правилу прямоугольника:
, где i=2,3,…,m; j=2,3,…,n.
Аналогичные преобразования выполним и над вторым уравнением системы. Это приведёт к системе, у которой во всех уравнениях, кроме первых двух, будет исключена неизвестная . В результате таких преобразований над каждым из уравнений системы (прямой ход метода Гаусса) исходная система приводится к эквивалентной ей ступенчатой системе одного из следующих видов.
Обратный ход метода Гаусса
Ступенчатая система
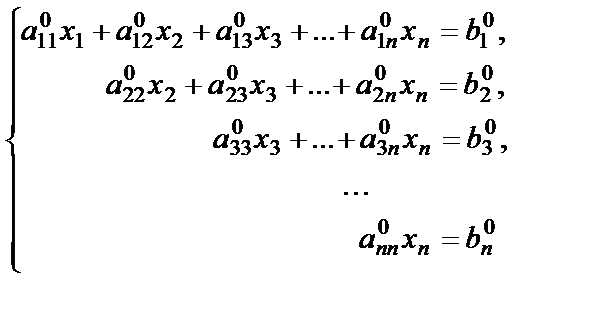
имеет треугольный вид и все (i=1,2,…,n). Такая система имеет единственное решение. Неизвестные определяются, начиная с последнего уравнения (обратный ход метода Гаусса).
Ступенчатая система имеет вид
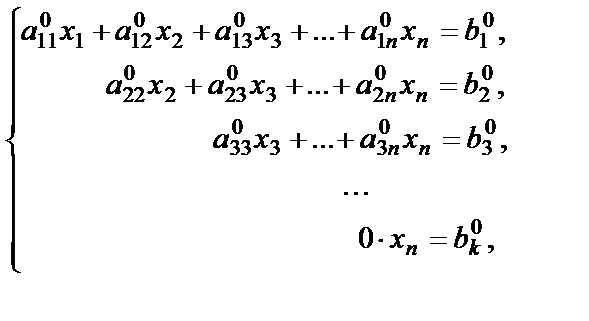
где , т.е. число уравнений системы меньше либо равно числу неизвестных. Эта система не имеет решений, так как последнее уравнение не будет выполняться ни при каких значениях переменной .
Ступенчатая система вида
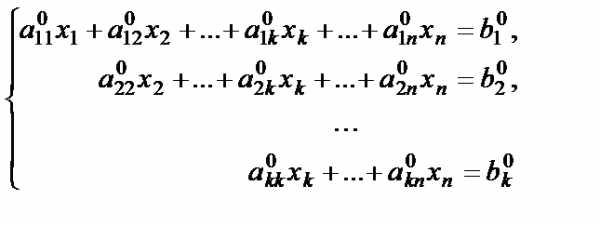
имеет бесчисленное множество решений. Из последнего уравнения неизвестная выражается через неизвестные . Затем в предпоследнее уравнение вместо неизвестной подставляется её выражение через неизвестные . Продолжая обратный ход метода Гаусса, неизвестные можно выразить через неизвестные . В этом случае неизвестные называются
При практическом решении систем удобно выполнять все преобразования не с системой уравнений, а с расширенной матрицей системы, состоящей из коэффициентов при неизвестных и столбца свободных членов.
Пример 1. Решить систему уравнений
Решение. Составим расширенную матрицу системы и выполним элементарные преобразования:
.
В расширенной матрице системы число 3 (оно выделено) является разрешающим коэффициентом, первая строка является разрешающей строкой, а первый столбец – разрешающим столбцом. При переходе к следующей матрице разрешающая строка не изменяется, все элементы разрешающего столбца ниже разрешающего элемента заменяются нулями. А все другие элементы матрицы пересчитываются по правилу четырёхугольника. Вместо элемента 4 во второй строке запишем , вместо элемента -3 во второй строке будет записано и т.д. Таким образом, будет получена вторая матрица. У этой матрицы разрешающим элементом будет число 18 во второй строке. Для формирования следующей (третьей матрицы) вторую строку оставляем без изменения, в столбце под разрешающим элементом запишем нуль и пересчитаем оставшиеся два элемента: вместо числа 1 запишем , а вместо числа 16 запишем .
В результате исходная система свелась к эквивалентной системе
Из третьего уравнения находим . Подставим это значение во второе уравнение: y=3. В первое уравнение подставим найденные значения y и z: , x=2.
Таким образом, решением данной системы уравнений является x=2, y=3, .
Пример 2. Решить систему уравнений 
Решение. Выполним элементарные преобразования над расширенной матрицей системы:


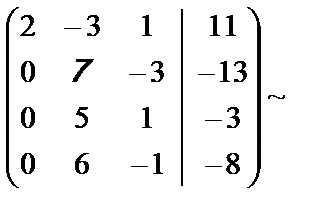
Во второй матрице каждый элемент третьей строки разделили на 2.
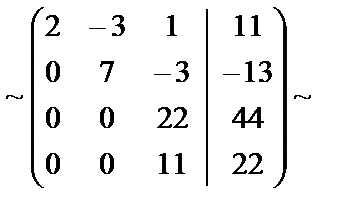
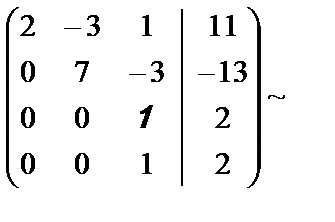
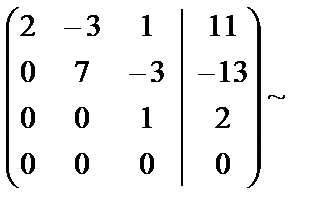
В четвёртой матрице каждый элемент третьей и четвёртой строки разделили на 11.
. Полученная матрица соответствует системе уравнений
Решая данную систему, найдём , , .
Пример 3. Решить систему уравнений

Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования:
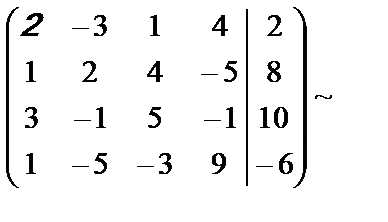

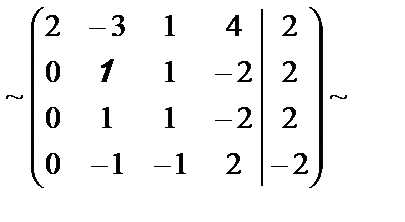
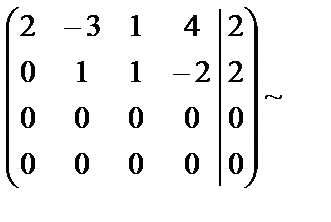 .
.
Во второй матрице каждый элемент второй, третьей и четвёртой строк разделили на 7.
В результате получена система уравнений
эквивалентная исходной.
Так как уравнений на два меньше, чем неизвестных, то из второго уравнения . Подставим выражение для в первое уравнение: , .
Таким образом, формулы дают общее решение данной системы уравнений. Неизвестные и являются свободными и могут принимать любые значения.
Пусть, например, Тогда и . Решение является одним из частных решений системы, которых бесчисленное множество.
Вопросы для самоконтроля знаний
1) Какие преобразования линейных систем называются элементарными?
2) Какие преобразования системы называются шагом гауссова исключения?
3) Что такое разрешающая переменная, разрешающий коэффициент, разрешающий столбец?
4) Какими правилами нужно пользоваться при выполнении одного шага гауссова исключения?
megaobuchalka.ru
Обратный ход метода Гаусса
Запишем линейную систему, получившуюся в результате прямого хода метода Гаусса, с расширенной матрицей, приведенной в табл. 3.3.:
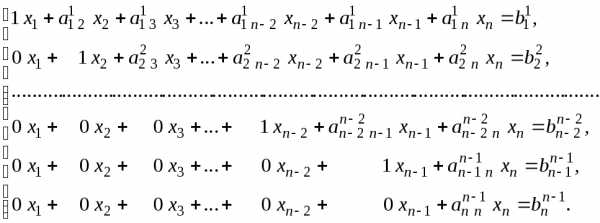 (3.2.10)
(3.2.10)
Система
(3.2.10) равносильна исходной системе
(3.2.1) и ее решение получить несложно. Из
последнего уравнения системы можно
сразу найти 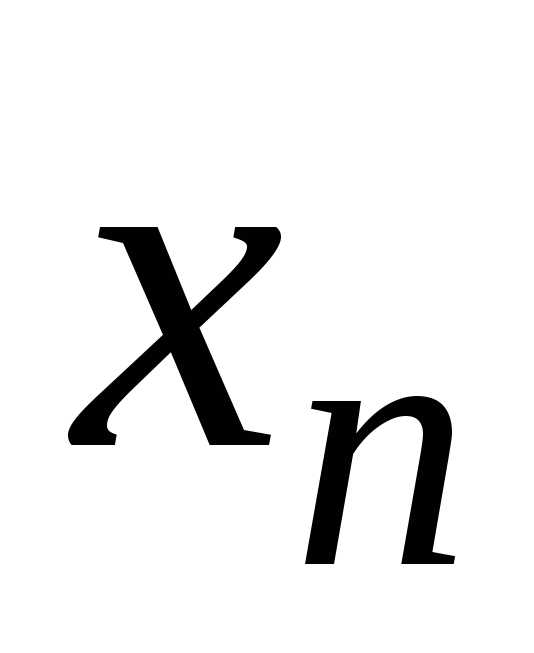 ,
из предпоследнего
,
из предпоследнего 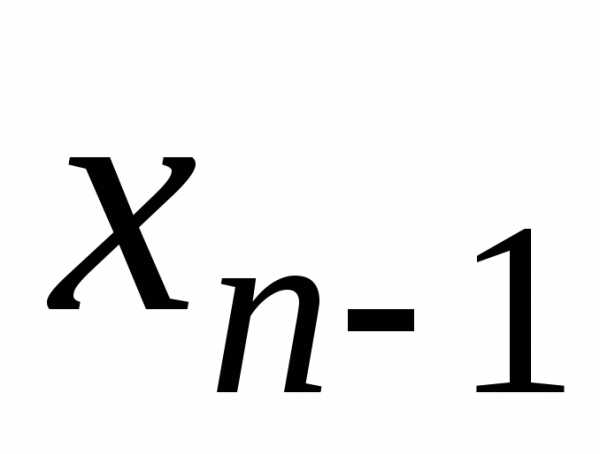
Алгоритм и расчетные формулы для обратного хода метода Гаусса
Приближенная проверка невырожденности матрицы системы. Если
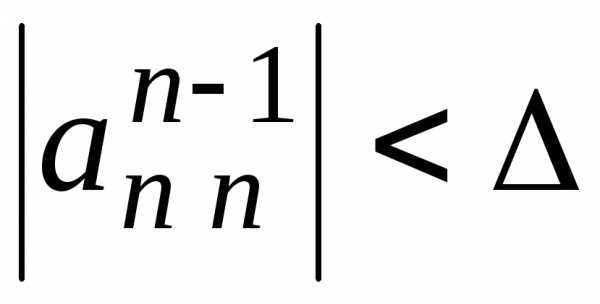 ,
то выдать сигнал о том, что матрица
системы близка к вырожденной и закончить
решение системы. При выполнении условия
,
то выдать сигнал о том, что матрица
системы близка к вырожденной и закончить
решение системы. При выполнении условия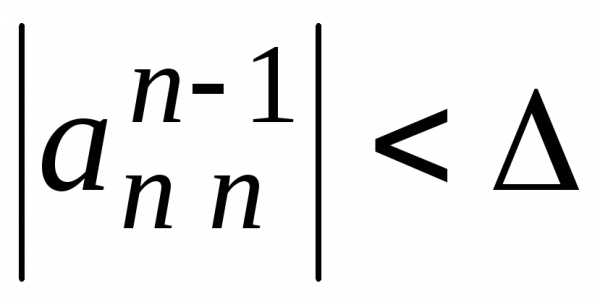 модуль определителя матрицы системы
будет меньше
модуль определителя матрицы системы
будет меньше и близок к нулю.
и близок к нулю.Вычисление решения по рекуррентным формулам
, (3.2.11)
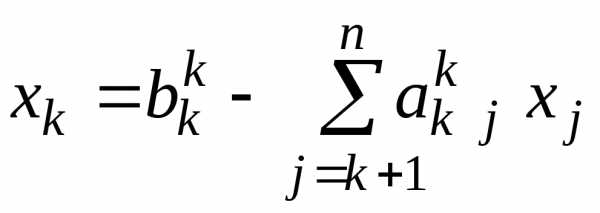 ,
.
(3.2.12)
,
.
(3.2.12)
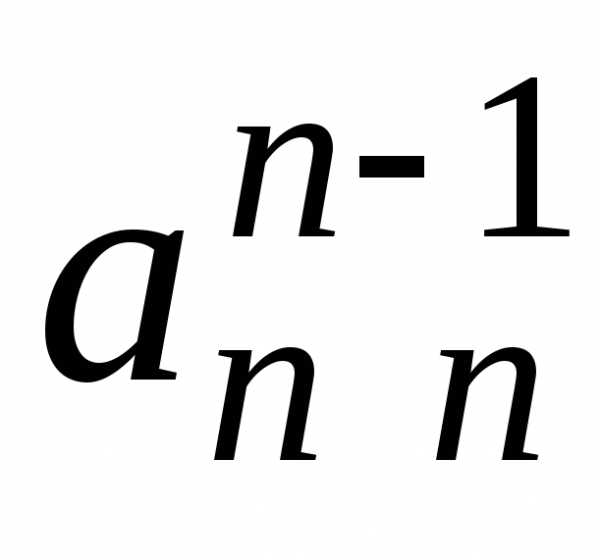 .
Нули, стоящие под главной диагональю,
и единицы, стоящие на главной диагонали,
для получения решения не нужны. Поэтому
их можно не вычислять. А для того чтобы
не делать эти лишние операции, можно исключить
из алгоритма прямого хода вычисления
по формулам (3.2.6), (3.2.8) при
.
Нули, стоящие под главной диагональю,
и единицы, стоящие на главной диагонали,
для получения решения не нужны. Поэтому
их можно не вычислять. А для того чтобы
не делать эти лишние операции, можно исключить
из алгоритма прямого хода вычисления
по формулам (3.2.6), (3.2.8) при  .
.Применение метода Гаусса для вычисления определителей Теоретические основы
При вычислении определителя квадратной матрицы А можно использовать прямой ход метода Гаусса. Применение метода Гаусса для вычисления определителей основано на их свойствах:
Если поменять местами две строки матрицы, то ее определитель поменяет свой знак, а абсолютная величина определителя не изменится .
Если какую-либо строку матрицы разделить на некоторую постоянную с, не равную нулю, то определитель матрицы уменьшится в с раз
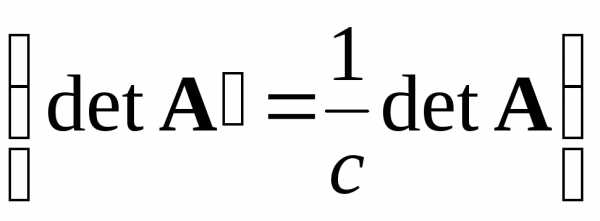 .
.Если из какой-либо строки матрицы вычесть другую строку, умноженную на некоторое число, не равное нулю, то определитель не изменится .
Если матрица является верхней треугольной (все ее элементы, лежащие ниже главной диагонали, равны 0), то её определитель будет равен произведению диагональных элементов этой матрицы.
В
результате преобразований прямого хода
метода Гаусса матрица А превратится в верхнюю треугольную
матрицу  .
На главной диагонали матрицы
.
На главной диагонали матрицы будут стоять единицы на всех строчках,
кроме последней. А в последней строке
на главной диагонали будет стоять
будут стоять единицы на всех строчках,
кроме последней. А в последней строке
на главной диагонали будет стоять 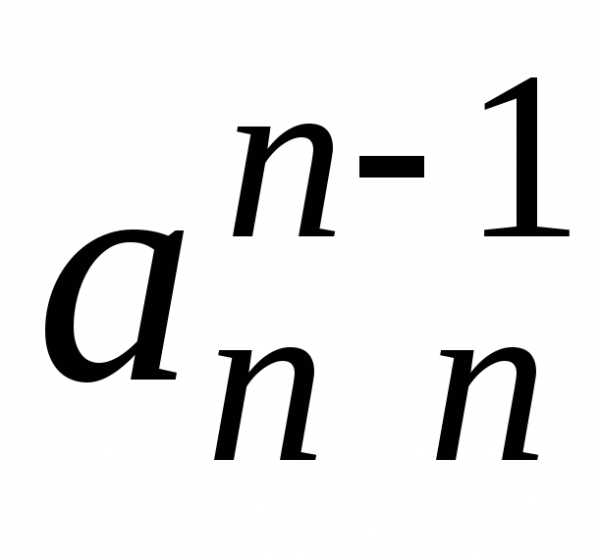 .
Поэтому определитель преобразованной
матрицы
.
Поэтому определитель преобразованной
матрицы  будет равен (произведению диагональных элементов).
В процессе прямого хода метода Гаусса
используются перестановки строк,
меняющие знак определителя, но не
меняющие его модуль. Обозначим через s число перестановок строк, совершаемых
в процессе прямого хода. Кроме того, в
процессе прямого хода производятся
деления строк матрицы на элементы
будет равен (произведению диагональных элементов).
В процессе прямого хода метода Гаусса
используются перестановки строк,
меняющие знак определителя, но не
меняющие его модуль. Обозначим через s число перестановок строк, совершаемых
в процессе прямого хода. Кроме того, в
процессе прямого хода производятся
деления строк матрицы на элементы  ,
которые приводят к тому, что величина
определителя будет разделена на
произведение.
Причемздесь
используются значения этих величин
после перестановки строк, если она
производится.
Таким образом,
.
Отсюда
,
которые приводят к тому, что величина
определителя будет разделена на
произведение.
Причемздесь
используются значения этих величин
после перестановки строк, если она
производится.
Таким образом,
.
Отсюда
. (3.2.13)
Все величины, входящие в эту формулу, кроме s, вычисляются в процессе прямого хода метода Гаусса, а вычислить величину s не составляет труда.
studfiles.net
Обратный ход метода Гаусса. 1. Приближенная проверка невырожденности матрицы системы. Если , то выдать сигнал о том, что матрица системы близка к вырожденной и закончить решение системы.
2. Вычисление решения по рекуррентным формулам
,
, ,.
3.3. Метод правой прогонки Алгоритм решения линейной системы методом правой прогонки
Метод правой прогонки применяется для решения систем с трёхдиагональными матрицами и представляет собой модификацию метода Гаусса. Трехдиагональная матрица отличается тем, что ненулевые элементы могут стоять только на главной диагонали матрицы и двух соседних диагоналях. Все остальные элементы матрицы должны быть равны нулю. Приведем в качестве примера систему с трехдиагональной матрицей пятого порядка
 .
(3.3.1)
.
(3.3.1)
При обозначении элементов матрицы системы применяется нестандартная система обозначений. Обозначения введены только для отличных от нуля коэффициентов, причем коэффициенты, стоящие на главной диагонали, обозначены буквой С со знаком минус, а коэффициенты, стоящие на двух соседних диагоналях обозначены буквами А и В. Это позволяет существенно экономить память ЭВМ, не забивая ее огромным количеством никому не нужных нулей. Знаки минус, поставленные перед коэффициентами С и правыми частями F, появились из-за того, что мы будем использовать метод прогонки в дальнейшем, при решении разных других задач, и нам будет удобнее, если матрица системы во всех случаях будет иметь одинаковый вид.
Запишем произвольную систему с трехдиагональной матрицей (М-1)-го порядка в общем виде, используя описанную систему обозначений:
(3.3.2)
Система (3.3.1) эквивалентна системе (3.3.2) при М=6.
Если применить к решению системы (3.3.2) процедуру прямого хода метода Гаусса, то в результате получится система, матрица которой будет иметь две диагоналями: главную и правую. Разделим каждое уравнение преобразованной системы на диагональный элемент, стоящий в этой строке. В результате получится система с двухдиагональной матрицей, на главной диагонали которой стоят единицы. Эта система будет иметь вид (при M=6)
 (3.3.3)
(3.3.3)
Тогда рекуррентные формулы обратного хода метода Гаусса примут вид
, (3.3.4)
причём
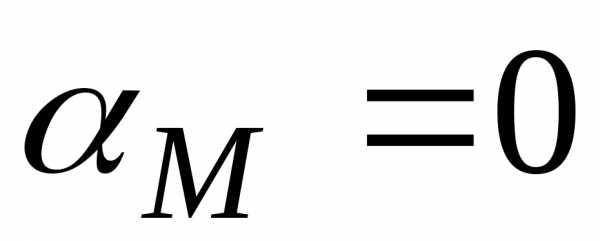 .
(3.3.5)
.
(3.3.5)
Для
определения коэффициентов 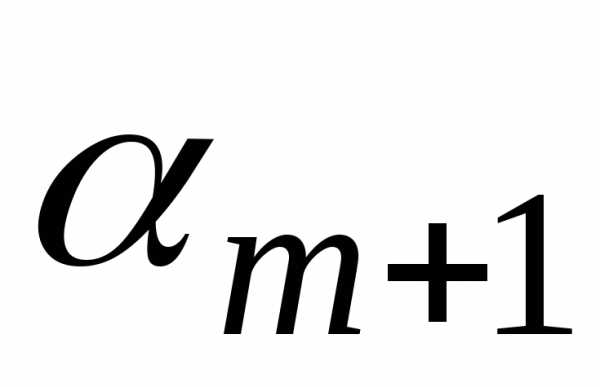 и
и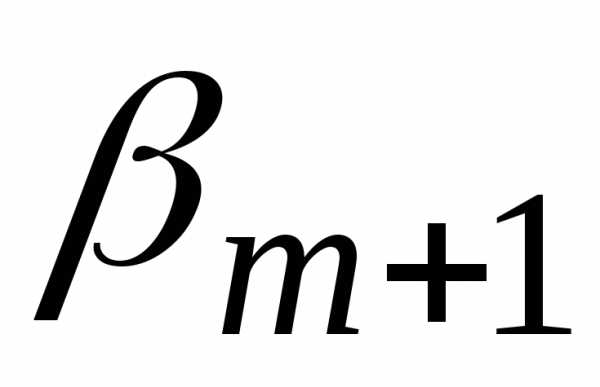 заменим в равенстве (3.2.4) величинуm на m-1:
заменим в равенстве (3.2.4) величинуm на m-1:
(3.3.6)
и подставим в исходную систему (3.3.2):
После элементарных преобразований получим
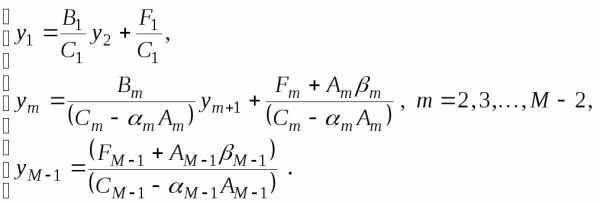
Сравнивая эти формулы с (3.3.4) получим
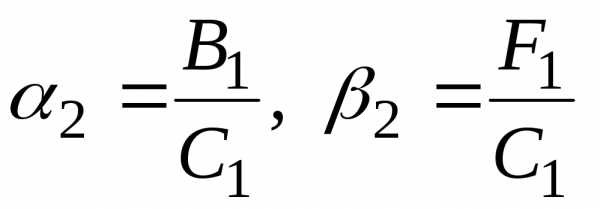
(3.3.7)
Введём
фиктивные величины 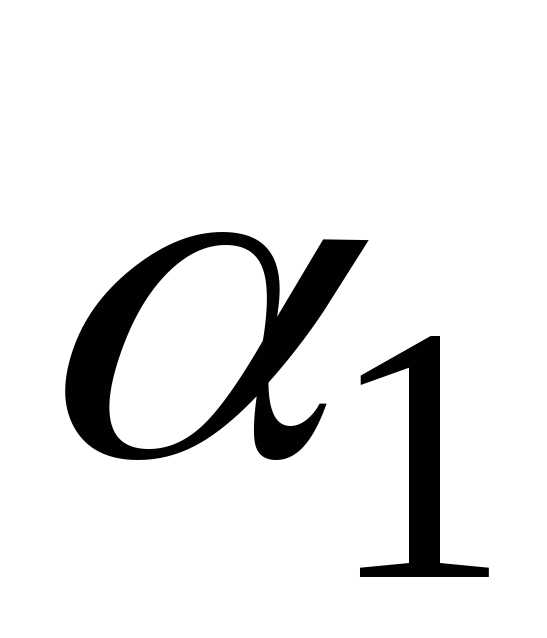 ,
, ,
, ,
,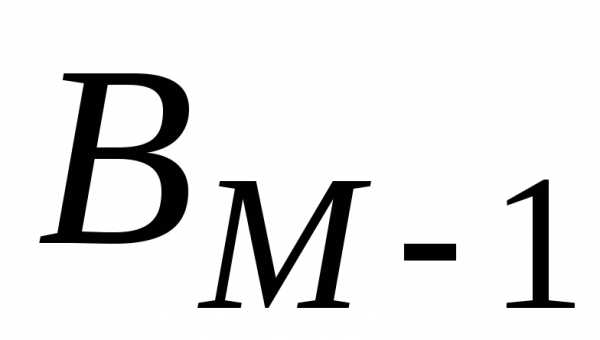 и
и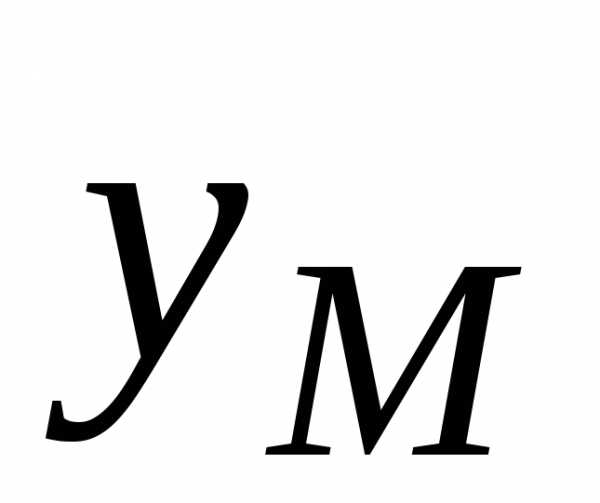 .
Положим
.
Положим
 ,,,
(3.3.8)
,,,
(3.3.8)
тогда формулы (3.3.7) можно будет записать одной строкой:
(3.3.9)
Рекуррентные
формулы (3.3.8) – (3.3.9) позволяют вычислить
все неизвестные коэффициенты 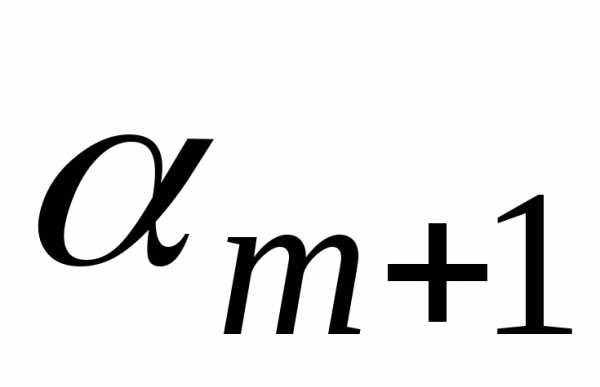 и
и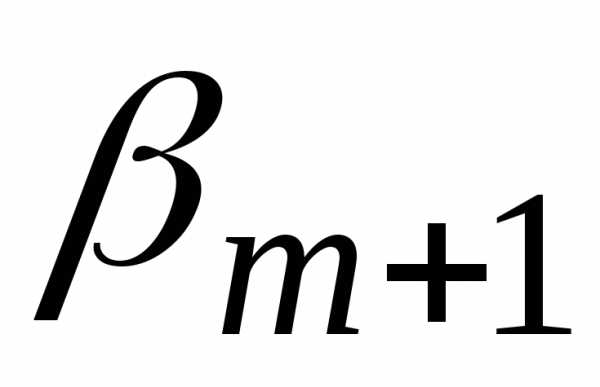 .
Для получения решения системы (3.3.2)
используем рекуррентную формулу (3.3.4),
но для начала счёта по ней необходимо
знать значение
.
Для получения решения системы (3.3.2)
используем рекуррентную формулу (3.3.4),
но для начала счёта по ней необходимо
знать значение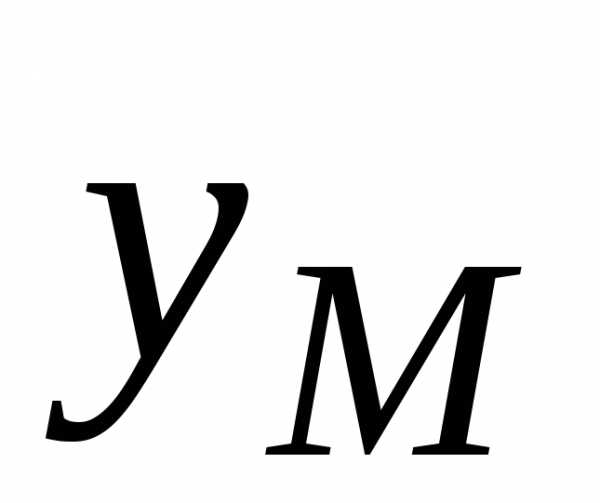 .
Поскольку
.
Поскольку (так как),
значение
(так как),
значение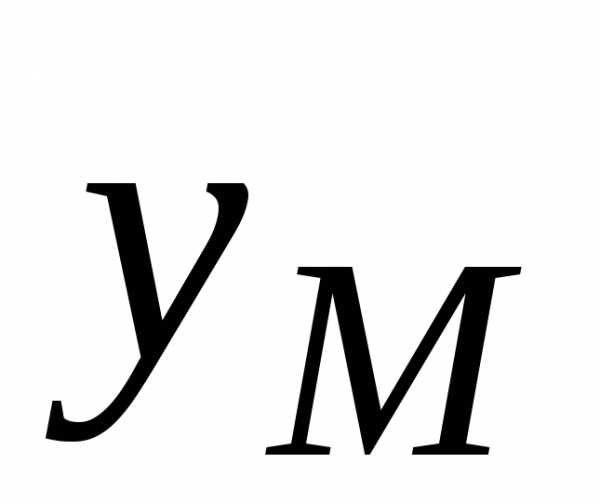 можно выбрать любое, например
можно выбрать любое, например
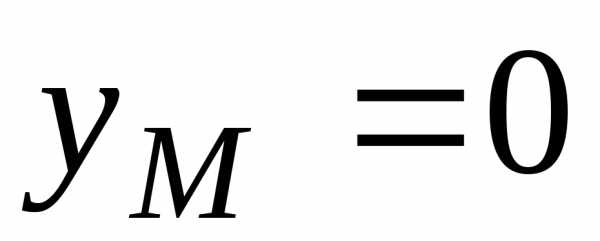 .
(3.3.10)
.
(3.3.10)
В
результате получим алгоритм решения
системы (3.3.2) методом прогонки: вначале
по рекуррентным формулам (3.3.9) с начальными
условиями (3.3.8) получим значения  ,
,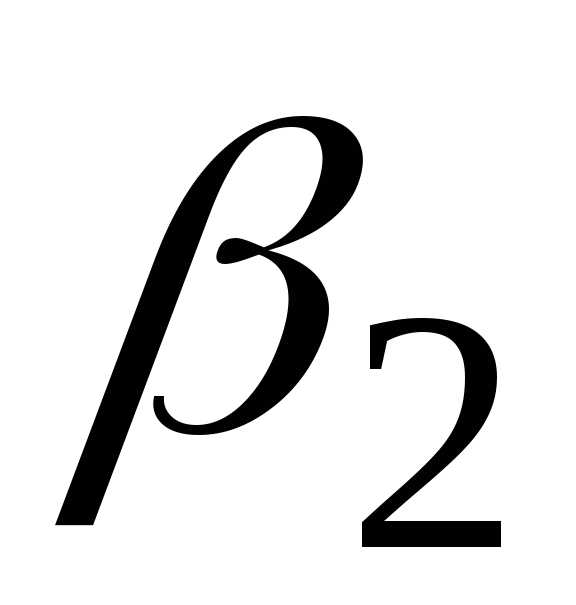 ,
, ,
, ,
… ,
,
… , ,
,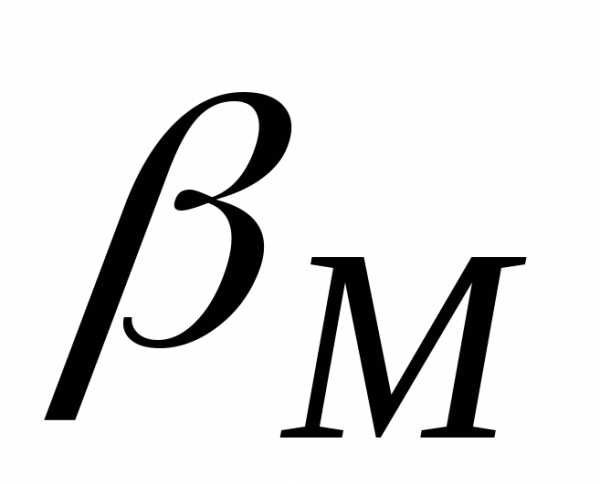 ,
затем по рекуррентной формуле (3.3.4) с
начальным условием (3.3.10) получим решение
системы:.
,
затем по рекуррентной формуле (3.3.4) с
начальным условием (3.3.10) получим решение
системы:.
studfiles.net
Обратный ход метода Гаусса | Бесплатные курсовые, рефераты и дипломные работы
Учреждение образования «Белорусская государственная
Сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Метод Гаусса решения систем линейных
уравнений» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Метод Гаусса решения систем линейных уравнений
Эквивалентные системы уравнений
Две системы линейных уравнений называются эквивалентными, если каждое решение одной из них является решением другой. Процесс решения системы линейных уравнений состоит в последовательном преобразовании её в эквивалентную систему с помощью так называемых элементарных преобразований, которыми являются:
1) перестановка любых двух уравнений системы;
…
2) умножение обеих частей любого уравнения системы на отличное от нуля число;
3) прибавление к любому уравнению другого уравнения, умноженного на любое число;
4) вычёркивание уравнения, состоящего из нулей, т.е. уравнения вида .
Гауссовы исключения
Рассмотрим систему m линейных уравнений с n неизвестными:
Суть метода Гаусса или метода последовательного исключения неизвестных состоит в следующем.
Вначале с помощью элементарных преобразований исключается неизвестная из всех уравнений системы, кроме первого. Такие преобразования системы называются шагом гауссового исключения. Неизвестная называется разрешающей переменной на первом шаге преобразований. Коэффициент называется разрешающим коэффициентом, первое уравнение называется разрешающим уравнением, а столбец коэффициентов при разрешающим столбцом.
При выполнении одного шага гауссового исключения нужно пользоваться следующими правилами:
1) коэффициенты и свободный член разрешающего уравнения остаются неизменными;
2) коэффициенты разрешающего столбца, расположенные ниже разрешающего коэффициента, обращаются в нули;
3) все прочие коэффициенты и свободные члены при выполнении первого шага вычисляются по правилу прямоугольника:
, где i=2,3,…,m; j=2,3,…,n.
Аналогичные преобразования выполним и над вторым уравнением системы. Это приведёт к системе, у которой во всех уравнениях, кроме первых двух, будет исключена неизвестная . В результате таких преобразований над каждым из уравнений системы (прямой ход метода Гаусса) исходная система приводится к эквивалентной ей ступенчатой системе одного из следующих видов.
Обратный ход метода Гаусса
Ступенчатая система
имеет треугольный вид и все (i=1,2,…,n). Такая система имеет единственное решение. Неизвестные определяются, начиная с последнего уравнения (обратный ход метода Гаусса).
Ступенчатая система имеет вид
где , т.е. число уравнений системы меньше либо равно числу неизвестных. Эта система не имеет решений, так как последнее уравнение не будет выполняться ни при каких значениях переменной .
Ступенчатая система вида
имеет бесчисленное множество решений. Из последнего уравнения неизвестная выражается через неизвестные . Затем в предпоследнее уравнение вместо неизвестной подставляется её выражение через неизвестные . Продолжая обратный ход метода Гаусса, неизвестные можно выразить через неизвестные . В этом случае неизвестные называются свободными и могут принимать любые значения, а неизвестные базисными.
При практическом решении систем удобно выполнять все преобразования не с системой уравнений, а с расширенной матрицей системы, состоящей из коэффициентов при неизвестных и столбца свободных членов.
Пример 1. Решить систему уравнений
Решение. Составим расширенную матрицу системы и выполним элементарные преобразования:
.
В расширенной матрице системы число 3 (оно выделено) является разрешающим коэффициентом, первая строка является разрешающей строкой, а первый столбец – разрешающим столбцом. При переходе к следующей матрице разрешающая строка не изменяется, все элементы разрешающего столбца ниже разрешающего элемента заменяются нулями. А все другие элементы матрицы пересчитываются по правилу четырёхугольника. Вместо элемента 4 во второй строке запишем , вместо элемента -3 во второй строке будет записано и т.д. Таким образом, будет получена вторая матрица. У этой матрицы разрешающим элементом будет число 18 во второй строке. Для формирования следующей (третьей матрицы) вторую строку оставляем без изменения, в столбце под разрешающим элементом запишем нуль и пересчитаем оставшиеся два элемента: вместо числа 1 запишем , а вместо числа 16 запишем .
В результате исходная система свелась к эквивалентной системе
Из третьего уравнения находим . Подставим это значение во второе уравнение: y=3. В первое уравнение подставим найденные значения y и z: , x=2.
Таким образом, решением данной системы уравнений является x=2, y=3, .
Пример 2. Решить систему уравнений
Решение. Выполним элементарные преобразования над расширенной матрицей системы:
Во второй матрице каждый элемент третьей строки разделили на 2.
В четвёртой матрице каждый элемент третьей и четвёртой строки разделили на 11.
. Полученная матрица соответствует системе уравнений
Решая данную систему, найдём , , .
Пример 3. Решить систему уравнений
Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования:
.
Во второй матрице каждый элемент второй, третьей и четвёртой строк разделили на 7.
В результате получена система уравнений
эквивалентная исходной.
Так как уравнений на два меньше, чем неизвестных, то из второго уравнения . Подставим выражение для в первое уравнение: , .
Таким образом, формулы дают общее решение данной системы уравнений. Неизвестные и являются свободными и могут принимать любые значения.
Пусть, например, Тогда и . Решение является одним из частных решений системы, которых бесчисленное множество.
Вопросы для самоконтроля знаний
1) Какие преобразования линейных систем называются элементарными?
2) Какие преобразования системы называются шагом гауссова исключения?
3) Что такое разрешающая переменная, разрешающий коэффициент, разрешающий столбец?
4) Какими правилами нужно пользоваться при выполнении одного шага гауссова исключения?
refac.ru
Обратный ход – метод – гаусс
Обратный ход – метод – гаусс
Cтраница 1
Обратный ход метода Гаусса также сопровождается вычислением контрольных элементов строк системы. [1]
Обратный ход метода Гаусса состоит в определении всех EJ из системы ( 10) с верхней треугольной матрицей. Нетрудно показать, что изложенный выше метод Гаусса можно применять в том случае, когда все главные миноры отличны от нуля. [2]
Прямой и часть обратного хода метода Гаусса можно выполнять только под ненулевыми элементами матриц А, В. [3]
Си ф соответствует обратному ходу метода Гаусса. [4]
Решение (3.5) называется прямым ходом метода Гаусса, решение (3.4) – обратным ходом метода Гаусса. [5]
Совокупность операций вычисления значений неизвестных хя, х2, х из уравнений (3.32) представляет обратный ход метода Гаусса. [6]
Метод оптимального исключения близок к методу Гаусса и отличается существенно лишь тем, что обратный ход метода Гаусса здесь видоизменен и соединен с прямым ходом. [7]
Определение значений неизвестных из системы ( 22) по формулам ( 23) называется обратным ходом метода Гаусса. [8]
Решение системы уравнений (1.46) можно прекратить, как только будут определены все неизвестные начальные параметры стержней, т.е. обратный ход метода Гаусса может быть сокращен. [9]
Решение системы уравнений (1.38) можно прекратить, как только будут определены все неизвестные начальные параметры стержней, т.е. обратный ход метода Гаусса может быть сокращен. [10]
Процесс приведения системы ( 1) к треугольному виду ( 9) называется прямым ходом, а нахождение неизвестных по формулам ( 10) – обратным ходом метода Гаусса. [11]
Совокупность операций, приводящую исходную систему к виду Dx d, называют обычно прямым ходом метода Гаусса, а совокупность операций по решению системы Dx d – обратным ходом метода Гаусса. [12]
На атом заканчивается прямой ход метода Гаусса. Эту часть процесса вычислений называют обратным ходом метода Гаусса. При этом следует отметить следующее. [13]
Обратный ход метода прогонки совпадает с обратным ходом метода Гаусса. [14]
Начиная с блока 2, осуществляется прямой ход метода Гаусса, в котором преобразуется п – 1 строка матрицы коэффициентов. Основные преобразования прямого хода выполняются в блоке 4 алгоритма. Блоки 5 и 6 определяют обратный ход метода Гаусса. [15]
Страницы: 1
www.ngpedia.ru
Прямой ход метода Гаусса (приведение матрицы системы к верхнетреугольному виду)
| (2) – <-ко второй строке раширенной матрице прибавляем первую | ||||
| умноженную на (-1), а третьей прибавляем первую умноженную на (-2) | ||||
| Цель получить два нуля под 1 Первую строку оставляем без. изм. |
| (4) | <- к третьей строке прибавляем вторую умноженную на (4,33) | ||||
| Цель получить 0 под 1. Первую, вторую строки оставляем без.изменений |
В результате прямого хода получили систему с верхнетреугольной матрицей с единицами на главной диагонали
Теперь в матричном виде система выглядит следующим образом:
Т.к. преобразования были эквивалентными, то мы получим решения исходной системы
Обратный ход:
Перейдём к скалярной форме записи:
Или
Из второго уравнения можем найти , а затем из первого
Ответ :
Частные случаи:
Первый частный случай:
если на 4 шаге получается, что третья строка вся состоит из нулей, то в этом случае наша система не имеет единственного решения, т.к.третье уравнение системы выглядит следующим образом:
(т.е в качестве его решения могут выступать произвольные числа )
В этом случае берем:
– произвольное число,
а и будут через него выражаться с помощью первых двух уравнений
Системы
– первое уравнение системы
– второе уравнение системы
Откуда:
, где – произвольное число (из второго ур.)
, где – произвольное число (из первого ур.)
Если , то получим базисное решение
Пример с числами:
Дано:
Найти решение этой системы методом Гаусса
Решение:
Наша система в матричном виде выглядит следующим образом
Решать методом обратной матрицы и методом Крамера данную систему нельзя, т.к.
– определитель матрицы системы равен 0
—————————————————————————————————–
———————————————————————————————————————
(формулу и пример расчета определителя см. в лекции№1)
Для решения нашей системы применим метод Гаусса
– расширенная матрица системы (к матрице системы A добавлен столбец свободных неизвестных B)
Прямой ход – приведение матрицы системы к верхнетреугольному виду с 1 на главной диагонали – все вычисления может провести компьютер (см. файл Excel для
6 задачи – выложен на стр. с вариантами)
Получили частный случай: последняя строка расширенной матрицы состоит из 0 =>решение системы не единственно
Обратный ход метода Гаусса:
studopedya.ru
Обратный ход метода Гаусса – Математика
Учреждение образования «Белорусская государственная
Сельскохозяйственная академия»
Кафедра высшей математики
Методические указания
по изучению темы «Метод Гаусса решения систем линейных
уравнений» студентами бухгалтерского факультета заочной формы получения образования (НИСПО)
Горки, 2013
Метод Гаусса решения систем линейных уравнений
Эквивалентные системы уравнений
Две системы линейных уравнений называются эквивалентными, если каждое решение одной из них является решением другой. Процесс решения системы линейных уравнений состоит в последовательном преобразовании её в эквивалентную систему с помощью так называемых элементарных преобразований, которыми являются:
1) перестановка любых двух уравнений системы;
2) умножение обеих частей любого уравнения системы на отличное от нуля число;
3) прибавление к любому уравнению другого уравнения, умноженного на любое число;
4) вычёркивание уравнения, состоящего из нулей, т.е. уравнения вида .
Гауссовы исключения
Рассмотрим систему m линейных уравнений с n неизвестными:
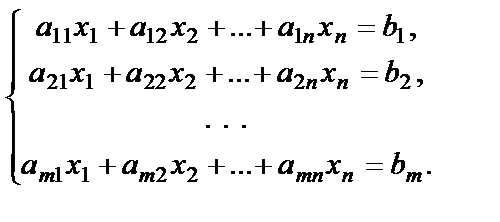
Суть метода Гаусса или метода последовательного исключения неизвестных состоит в следующем.
Вначале с помощью элементарных преобразований исключается неизвестная из всех уравнений системы, кроме первого. Такие преобразования системы называются шагом гауссового исключения. Неизвестная называется разрешающей переменной на первом шаге преобразований. Коэффициент называется разрешающим коэффициентом, первое уравнение называется разрешающим уравнением, а столбец коэффициентов при разрешающим столбцом.
При выполнении одного шага гауссового исключения нужно пользоваться следующими правилами:
1) коэффициенты и свободный член разрешающего уравнения остаются неизменными;
2) коэффициенты разрешающего столбца, расположенные ниже разрешающего коэффициента, обращаются в нули;
3) все прочие коэффициенты и свободные члены при выполнении первого шага вычисляются по правилу прямоугольника:
, где i=2,3,…,m; j=2,3,…,n.
Аналогичные преобразования выполним и над вторым уравнением системы. Это приведёт к системе, у которой во всех уравнениях, кроме первых двух, будет исключена неизвестная . В результате таких преобразований над каждым из уравнений системы (прямой ход метода Гаусса) исходная система приводится к эквивалентной ей ступенчатой системе одного из следующих видов.
Обратный ход метода Гаусса
Ступенчатая система
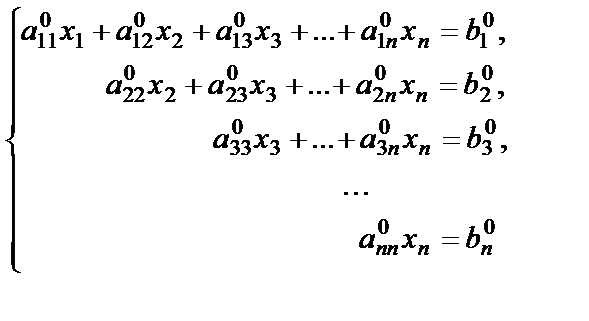
имеет треугольный вид и все (i=1,2,…,n). Такая система имеет единственное решение. Неизвестные определяются, начиная с последнего уравнения (обратный ход метода Гаусса).
Ступенчатая система имеет вид
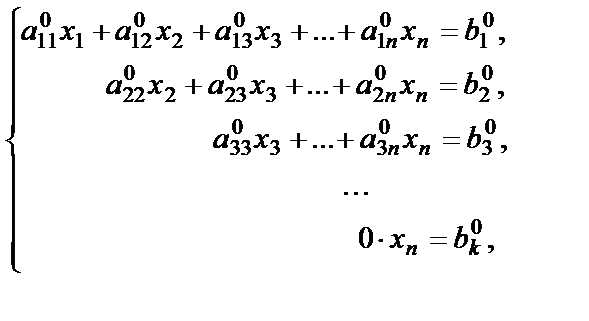
где , т.е. число уравнений системы меньше либо равно числу неизвестных. Эта система не имеет решений, так как последнее уравнение не будет выполняться ни при каких значениях переменной .
Ступенчатая система вида
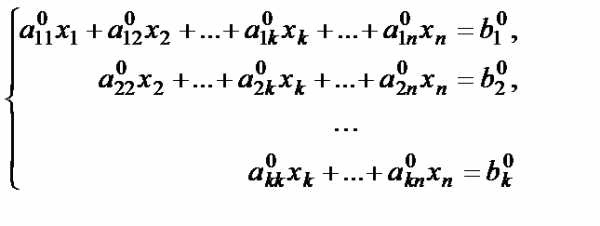
имеет бесчисленное множество решений. Из последнего уравнения неизвестная выражается через неизвестные . Затем в предпоследнее уравнение вместо неизвестной подставляется её выражение через неизвестные . Продолжая обратный ход метода Гаусса, неизвестные можно выразить через неизвестные . В этом случае неизвестные называются свободными и могут принимать любые значения, а неизвестные базисными.
При практическом решении систем удобно выполнять все преобразования не с системой уравнений, а с расширенной матрицей системы, состоящей из коэффициентов при неизвестных и столбца свободных членов.
Пример 1. Решить систему уравнений
Решение. Составим расширенную матрицу системы и выполним элементарные преобразования:
.
В расширенной матрице системы число 3 (оно выделено) является разрешающим коэффициентом, первая строка является разрешающей строкой, а первый столбец – разрешающим столбцом. При переходе к следующей матрице разрешающая строка не изменяется, все элементы разрешающего столбца ниже разрешающего элемента заменяются нулями. А все другие элементы матрицы пересчитываются по правилу четырёхугольника. Вместо элемента 4 во второй строке запишем , вместо элемента -3 во второй строке будет записано и т.д. Таким образом, будет получена вторая матрица. У этой матрицы разрешающим элементом будет число 18 во второй строке. Для формирования следующей (третьей матрицы) вторую строку оставляем без изменения, в столбце под разрешающим элементом запишем нуль и пересчитаем оставшиеся два элемента: вместо числа 1 запишем , а вместо числа 16 запишем .
В результате исходная система свелась к эквивалентной системе
Из третьего уравнения находим . Подставим это значение во второе уравнение: y=3. В первое уравнение подставим найденные значения y и z: , x=2.
Таким образом, решением данной системы уравнений является x=2, y=3, .
Пример 2. Решить систему уравнений 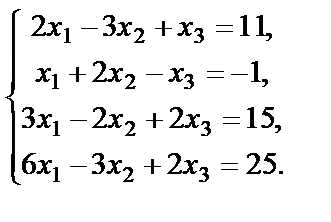
Решение. Выполним элементарные преобразования над расширенной матрицей системы:
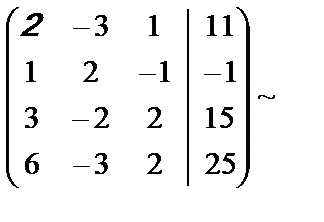
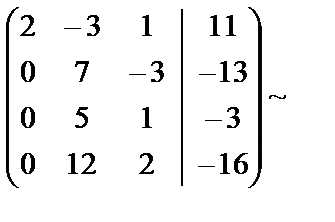
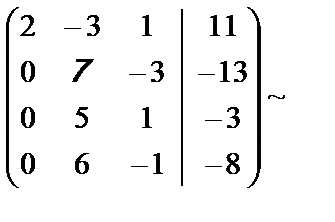
Во второй матрице каждый элемент третьей строки разделили на 2.
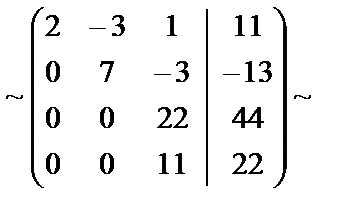
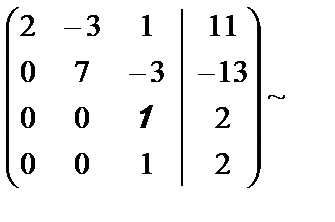
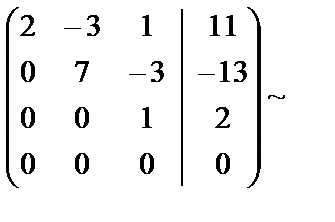
В четвёртой матрице каждый элемент третьей и четвёртой строки разделили на 11.
. Полученная матрица соответствует системе уравнений
Решая данную систему, найдём , , .
Пример 3. Решить систему уравнений
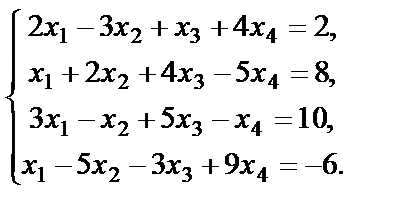
Решение. Запишем расширенную матрицу системы и выполним элементарные преобразования:
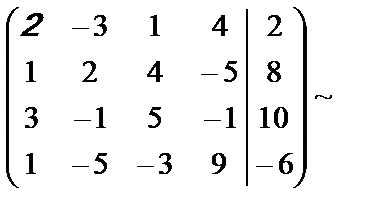
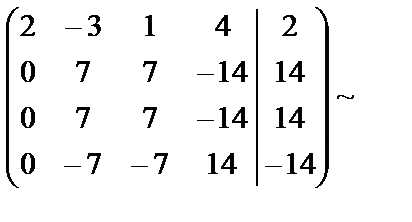
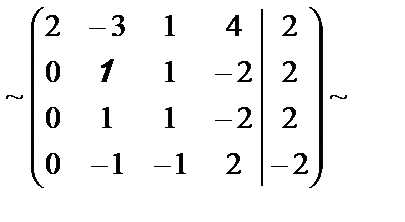
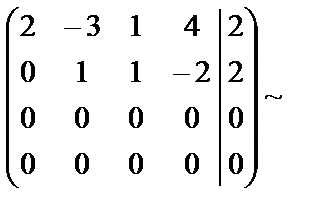 .
.
Во второй матрице каждый элемент второй, третьей и четвёртой строк разделили на 7.
В результате получена система уравнений
эквивалентная исходной.
Так как уравнений на два меньше, чем неизвестных, то из второго уравнения . Подставим выражение для в первое уравнение: , .
Таким образом, формулы дают общее решение данной системы уравнений. Неизвестные и являются свободными и могут принимать любые значения.
Пусть, например, Тогда и . Решение является одним из частных решений системы, которых бесчисленное множество.
Вопросы для самоконтроля знаний
1) Какие преобразования линейных систем называются элементарными?
2) Какие преобразования системы называются шагом гауссова исключения?
3) Что такое разрешающая переменная, разрешающий коэффициент, разрешающий столбец?
4) Какими правилами нужно пользоваться при выполнении одного шага гауссова исключения?
student2.ru
