Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
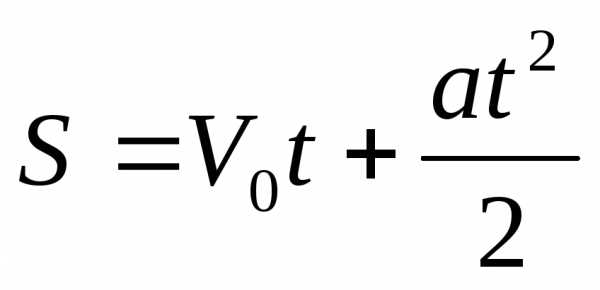
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения
Тогда получаем: – уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
– обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .
– обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается
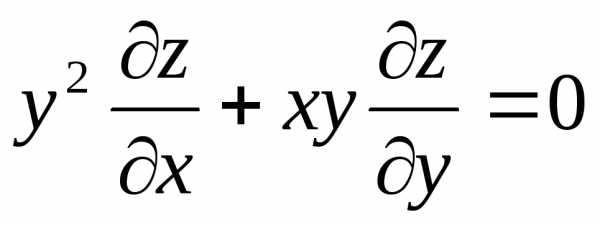 – дифференциальное
уравнение в частных производных первого
порядка.
– дифференциальное
уравнение в частных производных первого
порядка.
Определение. Общим решением
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = (х, С0).
Определение. Решение вида у = (х, С0) называется
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х
 уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения. Определение. Интегралом дифференциального
уравнения называется любое уравнение,
не содержащее производных, для которого
данное дифференциальное уравнение
является следствием.
Пример. Найти общее решение дифференциального уравнения .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

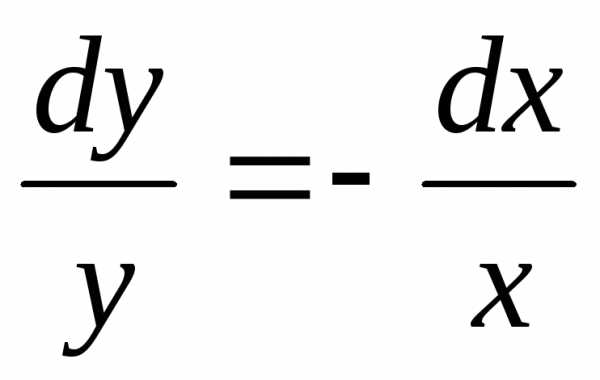
Теперь
интегрируем: 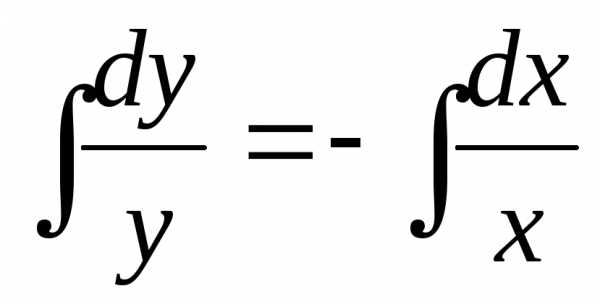
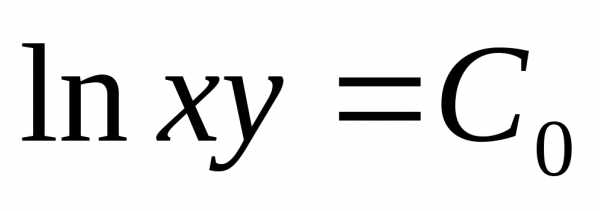
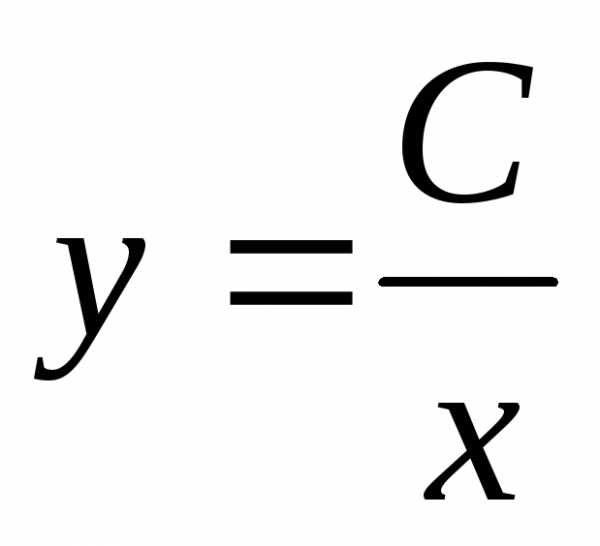 – это общее решение
исходного дифференциального уравнения.
– это общее решение
исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
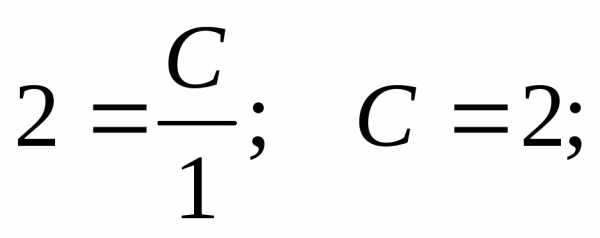
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
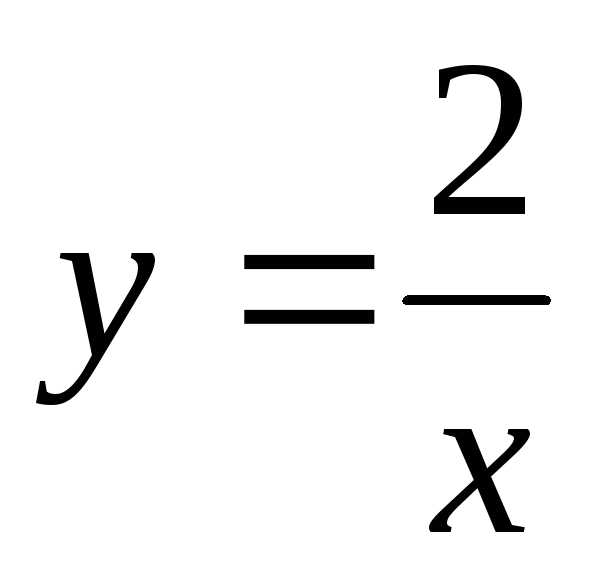
Определение. Интегральной кривой называется график y = (x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым
решением дифференциального
уравнения называется такое решение, во
всех точках которого условие единственности
Коши (см.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального уравнения: Найти особое решение, если оно существует.

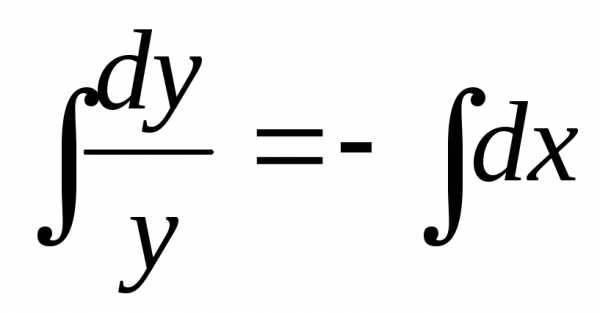
Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
studfiles.net
Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:

В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
Тогда получаем: – уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
– обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .
– обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается
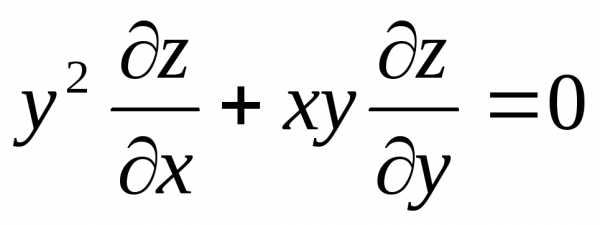 – дифференциальное
уравнение в частных производных первого
порядка.
– дифференциальное
уравнение в частных производных первого
порядка.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = (х, С0).
Определение. Решение вида у = (х, С0) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если
функция f(x, y)
непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную
частную производную
,
то какова бы не была точка (х0,
у0)
в области D,
существует единственное решение  уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
Определение. Интегралом дифференциального
уравнения называется любое уравнение,
не содержащее производных, для которого
данное дифференциальное уравнение
является следствием.
Пример. Найти общее решение дифференциального уравнения .
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
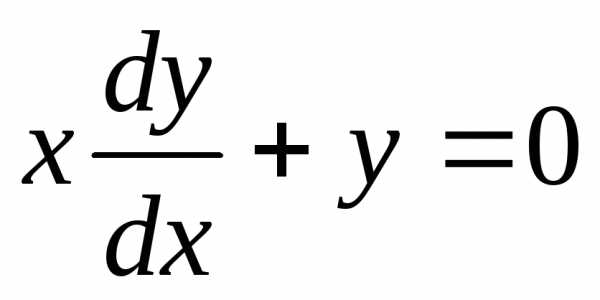
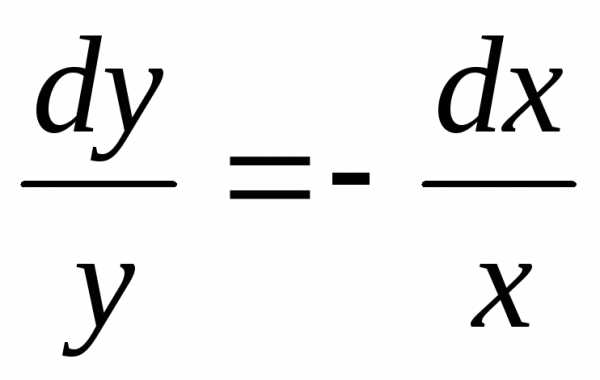
Теперь
интегрируем: 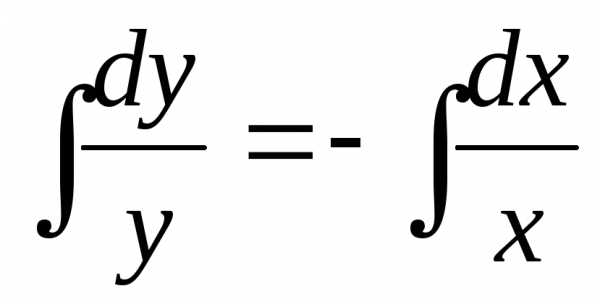

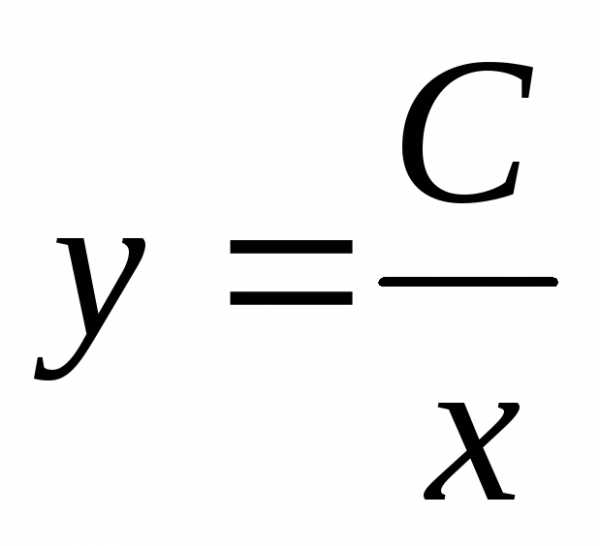 – это общее решение
исходного дифференциального уравнения.
– это общее решение
исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем

При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
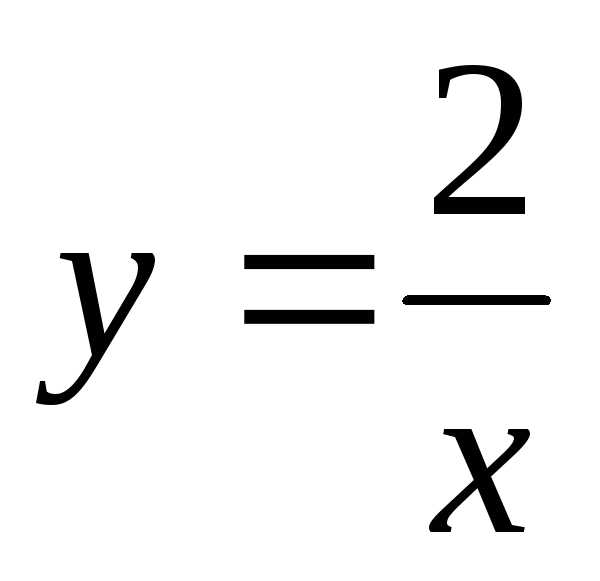
Определение. Интегральной кривой называется график y = (x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального уравнения: Найти особое решение, если оно существует.
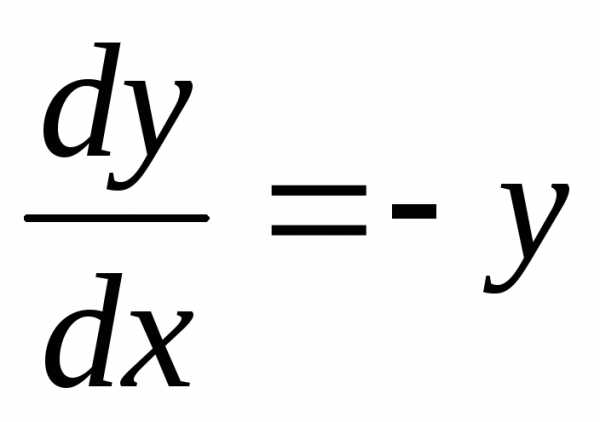
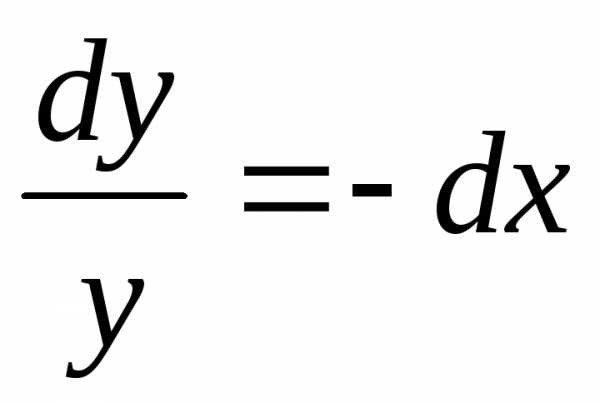
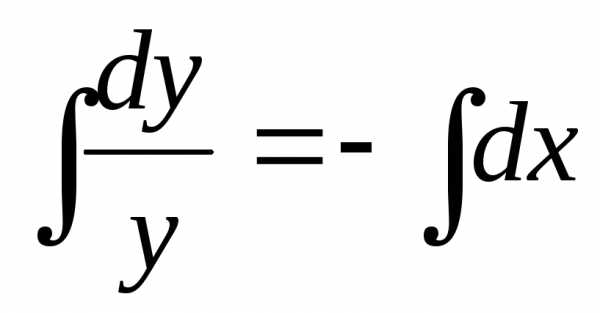
Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1 = eC 0.
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
studfiles.net
Обыкновенные дифференциальные уравнения 1-го порядка.
Обыкновенным дифференциальным уравнением 1-го порядка называется уравнение, связывающее независимую переменную, неизвестную искомую функцию, зависящую от этой переменной, и ее производную 1-го порядка.
В неявной форме записи дифференциальное уравнение 1-го порядка выглядит следующим образом: , (3)
где F – известная функция своих аргументов;
х – независимая переменная;
у – искомая неизвестная функция, зависящая от х;
или (в разрешенном относительно у/ виде): , (4)
где f – известная функция своих аргументов.
Заметим, что функция F в уравнении (3) может не содержать х или у (или оба этих аргумента), но непременно должна включать у/.
Дифференциальное уравнение 1-го порядка имеет бесчисленное множество решений. Так, например, решением уравнения будет являться не только функция , но и всякая функция вида (где С – произвольная постоянная), в чем можно убедиться непосредственной проверкой.
Одной из важных задач теории дифференциальных уравнений является задача Коши (Коши Огюстен Луи (1789-1857) – французский математик).
Для уравнения (4) (или (3)) задача Коши формулируется следующим образом: «среди всевозможных решений указанного уравнения найти такие, которые удовлетворяют заданному условию: , (5)
где х0, у0 – заданные действительные числа»
Условие (5) называется начальным условием.
Геометрическая интерпретация задачи Коши заключается в следующем: среди всех интегральных кривых уравнения (4) (или (3)) найти такие, которые проходят через наперед заданную точку с координатами (х0, у0) плоскости Оху.
Общим решением дифференциального уравнения 1-го порядка называется однопараметрическое семейство функций: , (6)
удовлетворяющее следующим условиям:
а) функция (6) является решением данного дифференциального уравнения при любом допустимом значении параметра С;
б) при любом допустимом начальном условии найдется такое значение С0 параметра С, при котором функция будет удовлетворять указанному начальному условию, т.е. будет иметь место равенство: .
Всякое решение дифференциального уравнения 1-го порядка, которое получается из общего решения (6) при конкретном, и вполне определенном значении С = С0, называется частным решением.
Таким
образом, общему решению (6) дифференциального
уравнения 1-го порядка на плоскости Оху
соответствует семейству интегральных
кривых; а частному решению, удовлетворяющую
начальному условию – кривая этого семейства
,
проходящая через точку 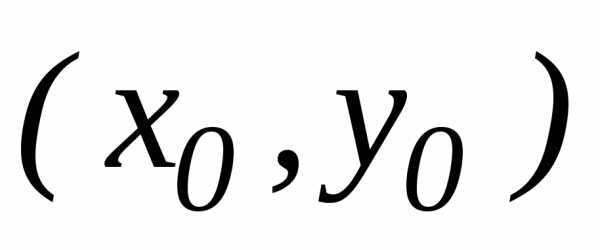 .
.
Общее решение дифференциального уравнения 1-го порядка, выраженное в неявной форме, т.е. в виде , называется общим интегралом.
Дифференциальные уравнения с разделяющимися переменными.
Простейшими дифференциальными уравнениями 1-го порядка являются дифференциальные уравнения с разделяющимися переменными.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: (7)
(или приводящееся к указанному виду).
Характерной особенностью уравнения (7) является то, что коэффициенты при дифференциалах dx, dy представляют собой произведение функций, зависящих только от х, или только от у.
Преобразуем дифференциальное уравнение (7) таким образом, чтобы при dx множителем была функция, зависящая только от х, а при dy – функция, зависящая только от у. С этой целью разделим обе части уравнения (7) на функцию (предполагая, что , в результате чего получаем:
(8)
При этом могли быть потеряны решения уравнения (7), которые одновременно являются и решениями уравнениями . Эти решения записываются в ответ в том случае, если их нельзя будет получить из общего решения ни при каком конкретном значении параметра С.
Почленное интегрирование уравнения (8) приводит к соотношению:
, (9)
(где С – произвольная постоянная, всегда возникающая при применении операции неопределенного интегрирования), которое и определяет общее решение исходного уравнения (7) в неявной форме (общий интеграл).
Пример
2. Для
дифференциального уравнения 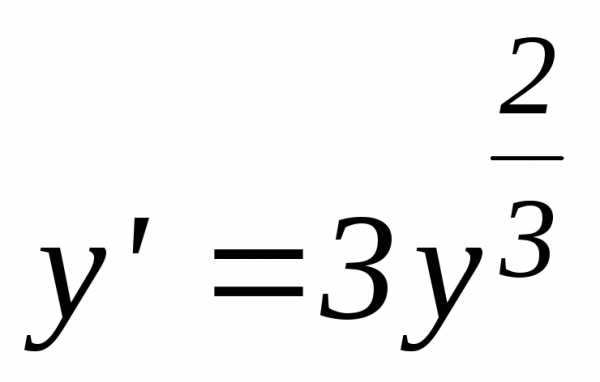 найти:
найти:
все его решения;
частное решение, удовлетворяющее условию .
Решение. 1) Заданное уравнение представляет собой дифференциальное уравнение 1-го порядка с разделяющимися переменными. Запишем его в виде:
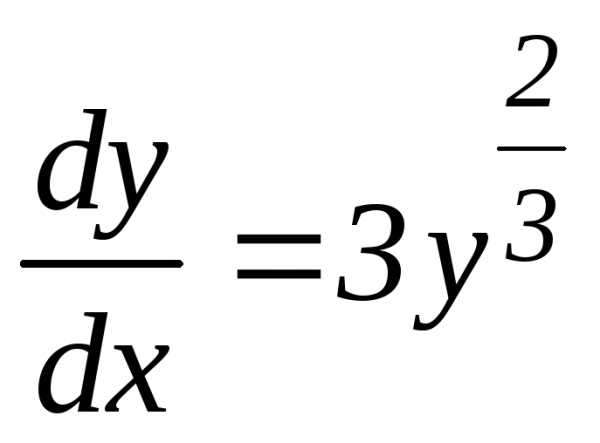 .
.
Умножив
обе части этого уравнения на dx,
получаем: 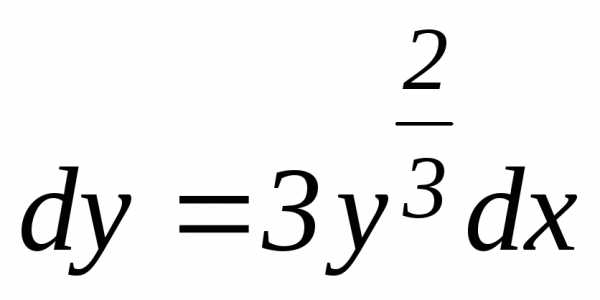 .
.
Разделив
обе части последнего уравнения на 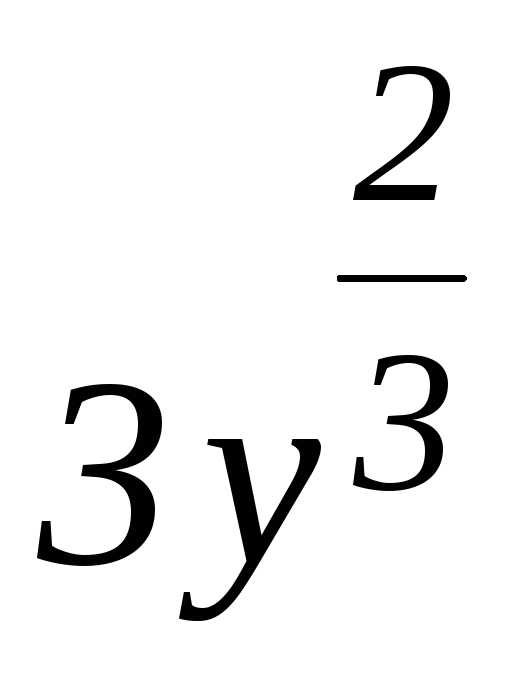 (предполагая, что
(предполагая, что 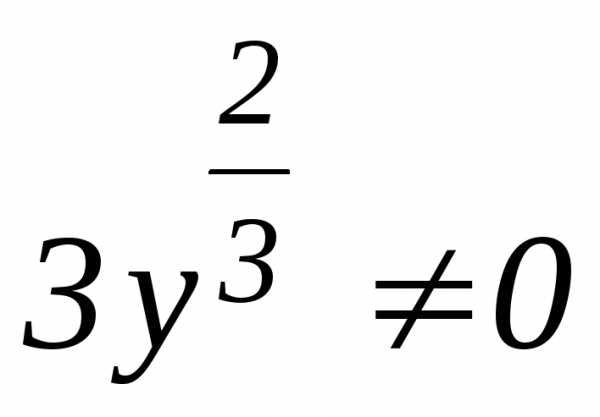 ),
имеем:
),
имеем:
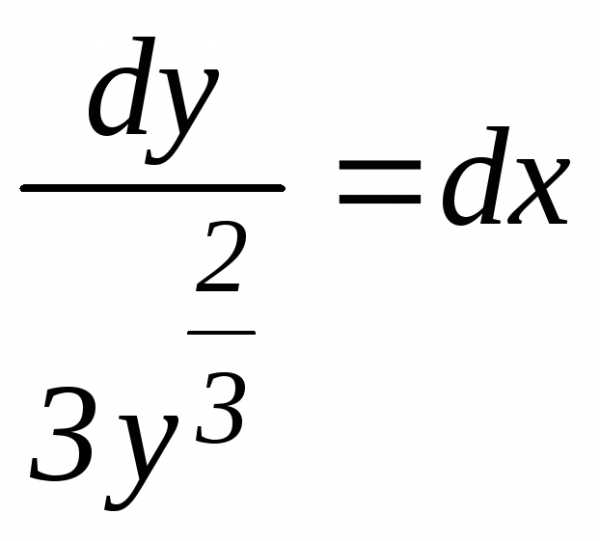 (10)
(10)
Проинтегрируем
обе части уравнения (10): 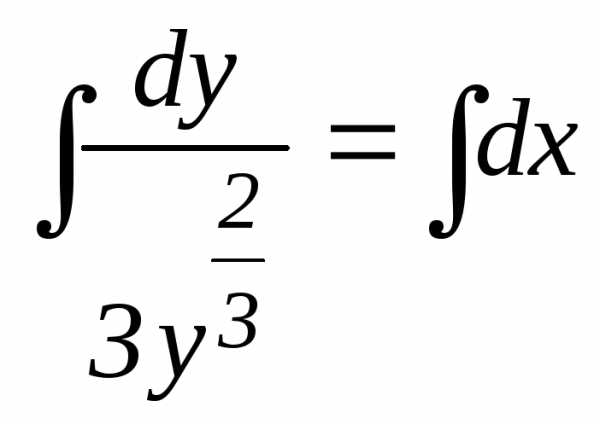 ;
;
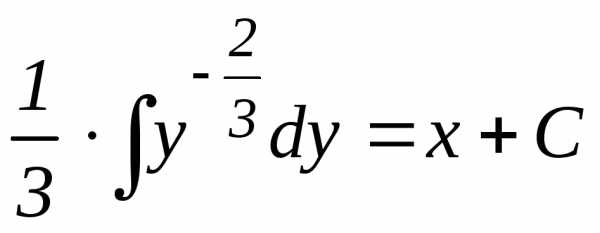 ,
где С =сonst;
,
где С =сonst;
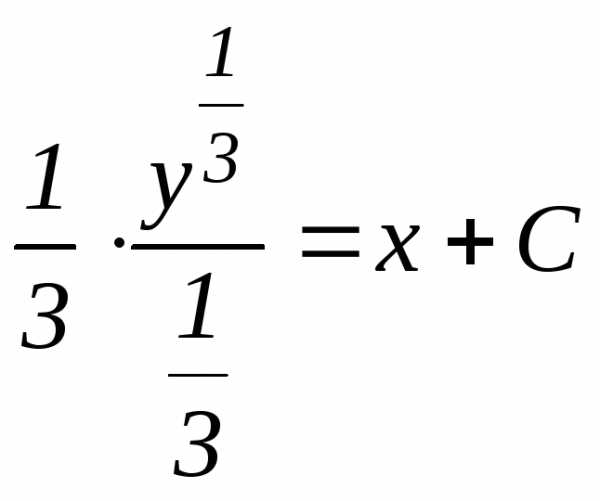 ;
;
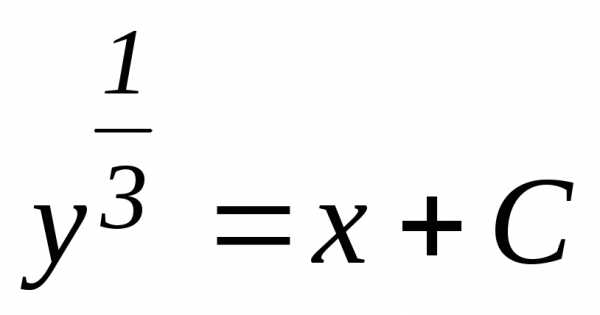 ;
;
Откуда (11)
Итак,
соотношение (11) определяет общее решение
исходного уравнения. В процессе перехода
к уравнению (10) при делении на функцию 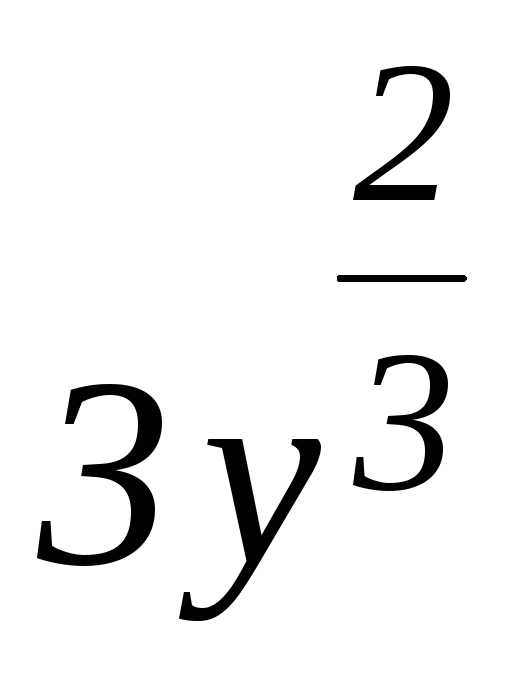 ,
могло быть потеряно решение заданного
уравнения, которое одновременно является
и решением уравнения
,
могло быть потеряно решение заданного
уравнения, которое одновременно является
и решением уравнения 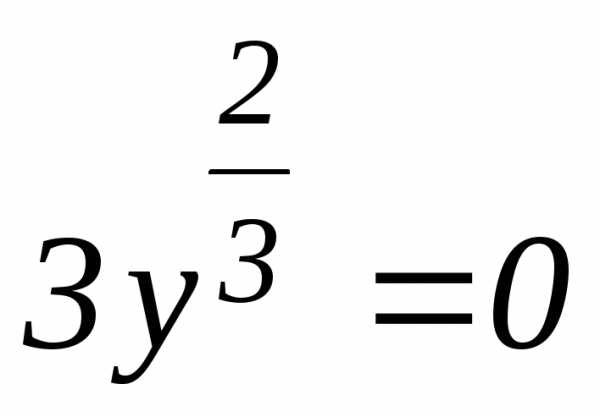 ,
т.е. у = 0. Непосредственной проверкой
убеждаемся, что функция у = 0 действительно
является решением заданного уравнения
(так как, если у = 0, то у/ = 0 и при их подстановки в исходное
уравнение
,
т.е. у = 0. Непосредственной проверкой
убеждаемся, что функция у = 0 действительно
является решением заданного уравнения
(так как, если у = 0, то у/ = 0 и при их подстановки в исходное
уравнение 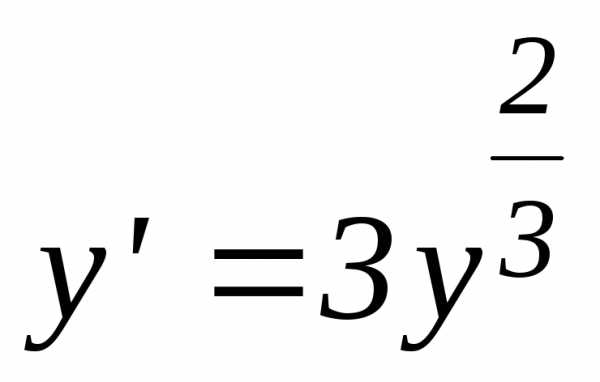 , получается тождество
, получается тождество 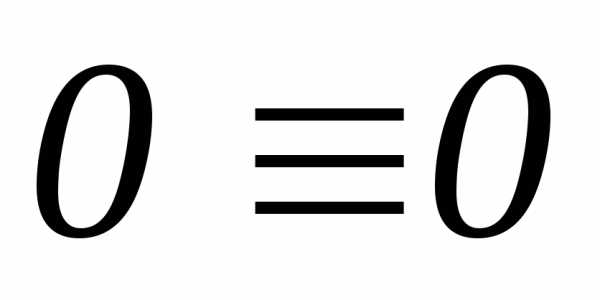 ).
Однако, решение у = 0 невозможно получить
из общего решения (11) ни при каком числовом
значении параметра С,
следовательно, оно утрачено.
).
Однако, решение у = 0 невозможно получить
из общего решения (11) ни при каком числовом
значении параметра С,
следовательно, оно утрачено.
Таким образом, совокупность всех решений заданного уравнения имеет вид:
2) Чтобы найти частное исходного уравнения, удовлетворяющее начальному условию у (-1) = 1, подставим х0 = -1 и у0 = 1 в общее решение (11):
1 = (-1 + С)-3;
(С – 1)3 = 1;
С – 1 = 1;
С = 2.
Подставив полученное выше значение параметра С в общее решение (11), находим частное решение, удовлетворяющее заданному начальному условию: у = (х +2)3.
С геометрической точки зрения, мы нашли ту интегральную кривую (кубическую параболу), которая на плоскости Оху проходит через точку М0 (-1; 1) (рис. 1).
Общему решению (11) на плоскости Оху соответствует семейство кубических парабол, смещающихся вдоль оси ОХ при изменении постоянной интегрирования С.
При С = 0 из (11) имеем: у = х3
С = 1 у = (х + 1)3;
С = 2 у = (х + 2)3;
С = 3 у = (х + 3)3;
С = -1 у = (х – 1)3;
С = -2,5 у = (х – 2,5)3.
Пример 3. Решить дифференциальное уравнение: у2 – 4 – 2хуу/ = 0 (12)
Решение. Уравнение (12) представляет собой дифференциальное уравнение с разделяющимися переменными. Запишем его в виде:
,
откуда 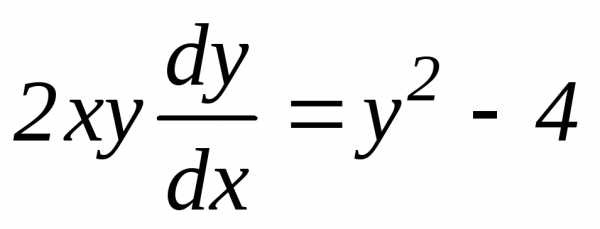 .
.
Умножив обе части последнего уравнения на dx, получим:
(13)
Преобразуем
уравнение (13) таким образом, чтобы
множителем при dx
являлась функция, зависящая только от
х, а при dy
– функция, зависящая только от у. С этой
целью, разделив обе части уравнения
(13) на 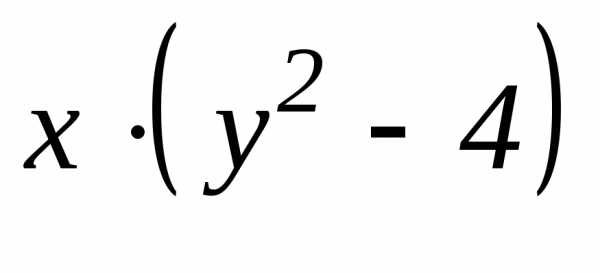 ,
будем иметь:
,
будем иметь:
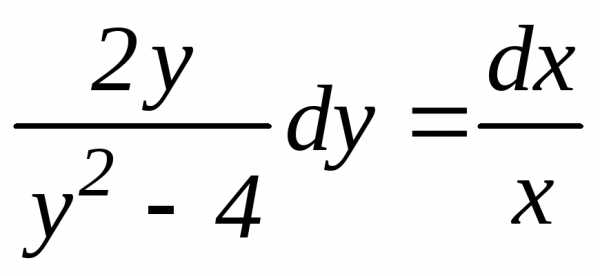 (14)
(14)
Проинтегрируем
обе части равенства (14). Имея в виду
дальнейшие преобразования, обозначим
произвольную постоянную через
,
что допустимо, так как, если С – константа,
то и 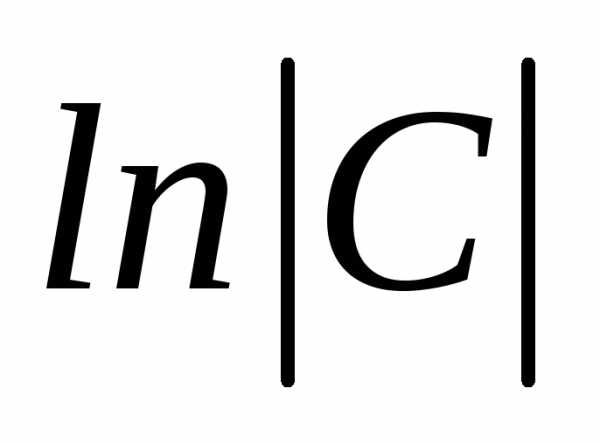 – тоже константа, принимающая любое
значение от
– тоже константа, принимающая любое
значение от 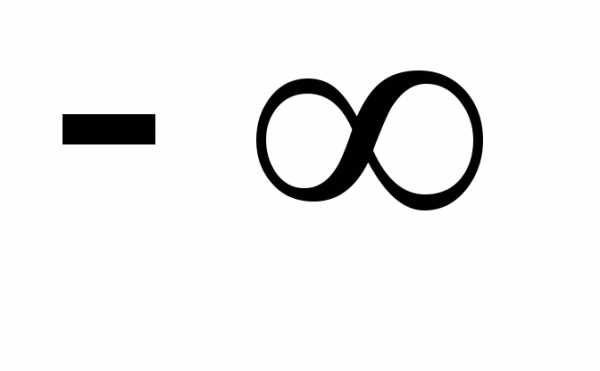 до
до 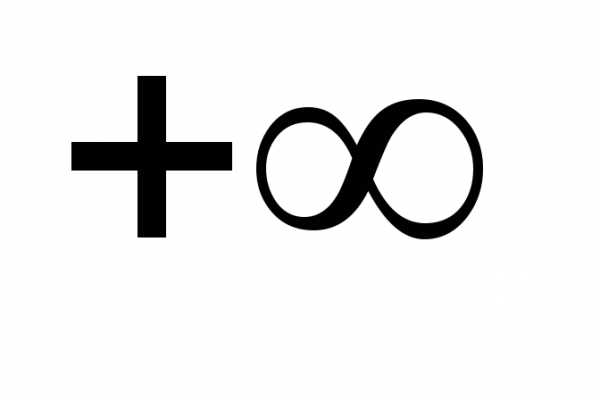
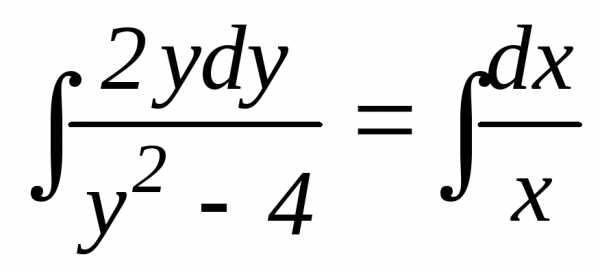
, где С – const; С ≠ 0
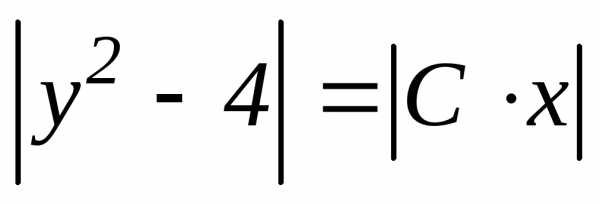
Положим С0 = ± С (где С0 = const, причем ), тогда
;
, где С0 = const; С ≠ 0 (15)
Таким образом, функция (15) определяет общее решение заданного уравнения (12).
В
процессе преобразований при переходе
от уравнения (13) к уравнению (14) могли
быть потеряны решения заданного уравнения
(12), которые одновременно являются и
решениями уравнения 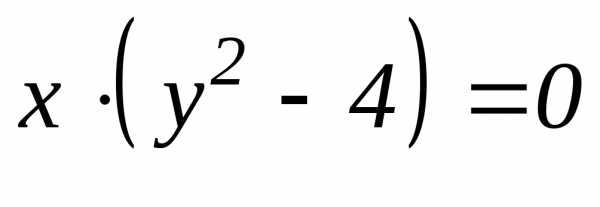 (т.е. х = 0, у =
(т.е. х = 0, у =  2)
2)
Непосредственной
проверкой убеждаемся, что х = 0 не является
решением уравнения (12), а у = ± 2 являются
его решениями (действительно при
подстановке у = ± 2 в уравнение (12) получаем
тождество 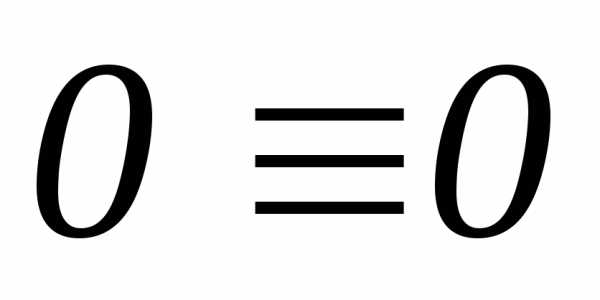 ).
).
Заметим, что решение у = ± 2 можно получить из общего решения (15), если допустить, что постоянна С0 в (15) может принимать значение равное нулю (т.е. С0 = 0).
Таким образом, все решения исходного уравнения (12) определяется формулой (15), в которой постоянная .
Ответ:
studfiles.net
Глава 1. Обыкновенные дифференциальные уравнения
Стр 1 из 2Следующая ⇒
Глава 1. Обыкновенные дифференциальные уравнения
Дифференциальные уравнения первого порядка
П.1.1.1. Основные понятия
Опр. Диф.уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции.
Если независимая переменная одна, то уравнение называется обыкновенным, если же независимых переменных две или более, то уравнение называется диф.уравнением в частных производных.
Обозначение: , (разрешенное относительно старшей производной), .
Опр. Наивысший порядок производной, входящей в уравнение, называется порядком ДУ.
Рассмотрим примеры ДУ:
1. ; ОДУ первого порядка
2. ; ОДУ второго порядка
3. ; ОДУ второго порядка
4. ; Уравнение в частных производных первого порядка
Данная глава посвящена только ОДУ, т.е. уравнение в частных производных рассматриваться здесь не будут, поэтому говоря ДУ, мы всюду далее будем понимать ОДУ.
В данном параграфе рассматриваются ДУ первого порядка.
Общий вид ДУ первого порядка: или в разрешенном виде относительно производной .
Опр. Решением ДУ называется такая дифференцируемая функция , которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.
Процесс нахождения решения ДУ называется интегрированием ДУ.
Опр. Общим решением ДУ первого порядка в области D называется функция , обладающая свойствами:
1) Она является решением данного уравнения при любых значениях постоянной ;
2) Для любого начального условия такого, что , существует единственное значение , при котором решение удовлетворяет заданному начальному условию.
Опр. Всякое решение , получающееся из общего решения при конкретном значении , называется частным решением.
Опр. Задача, в которой требуется найти частное решение уравнения , удовлетворяющее начальному условию , называется задачей Коши.
С геометрической точки зрения общее решение ДУ представляет собой семейство так называемых интегральных кривых на координатной плоскости, зависящее от одной произвольной постоянной С, а график частного решения, удовлетворяющего начальному условию , – есть кривая этого семейства, проходящая через точку .
Теорема о существовании и единственности решения ДУ (теорема Коши).
Если в уравнении функция и её частная производная по y непрерывны в некоторой области D на плоскости Оxy, то существует единственное решение этого уравнения, удовлетворяющее начальному условию .
С геометрической точки зрения: существует и притом единственная функция , график которой проходит через точку .
П.1.1.2. ДУ первого порядка с разделяющимися переменными
Рассмотрим ДУ следующих видов:
1. ;
2. ;
3. .
В первом случае, полагая, что и :
Мы получили соотношение, связывающее функцию y, независимую переменную x и произвольную постоянную С, т.е. мы получили общее решение ДУ.
Второй случай:
Третий случай:
Рассмотрим примеры:
1. Найти общее решение ДУ .
Решение: Преобразуем к виду .
есть общее решение ДУ.
2. Найти общее и частное решение ДУ , при
Решение:
есть общее решение ДУ. Найдем частное: С = 1, есть частное решение.
П.1.1.3. Однородные ДУ первого порядка
Опр. Функция называется однородной функцией n-ого измерения относительно переменных x, y, если при любом справедливо тождество:
.
Пример:
есть однородная функция второго измерения, т.к.
.
Опр. ДУ первого порядка называется однородным относительно x и y, если функция есть однородная функция нулевого измерения относительно x и y.
Опр. Уравнение вида называется однородным, если функции и – однородные функции одного измерения.
Однородное ДУ может быть приведено к виду .
Решение однородного ДУ первого порядка:
сделаем подстановку , где , при этом , тогда данное уравнение сводится к уравнению с разделяющимися переменными (с новой переменной t).
Пример:
Найти общее решение ДУ .
Решение:
есть общее решение ДУ.
Д.з.1. Разобрать самостоятельно тему: ДУ первого порядка, приводящиеся к однородным.
ДУ второго порядка
П.1.2.1. Основные понятия
Опр. Уравнение, связывающее независимую переменную x, неизвестную функцию y(x), а также её первые две производные , называется ДУ второго порядка.
Вид: или .
Задача Коши в случае ДУ второго порядка выглядит:
, .
Опр. Решением ДУ второго порядка называется всякая функция , которая при подстановке вместо в это уравнение обращает его в тождество.
Опр. Общим решением ДУ второго порядка называется функция , зависящая от двух произвольных постоянных и такая, что:
1) Она является решением этого уравнения при любых конкретных значениях ;
2) При любых допустимых начальных условиях можно подобрать такие значения постоянных, что функция будет удовлетворять этим начальным условиям.
Опр. Любая функция , получающаяся из общего решения при конкретных значениях , называется частным решением этого уравнения.
П.1.3.1. Основные понятия
Опр. Уравнение вида (1), где – независимая переменная, – искомая функция, – заданные функции, причем непрерывна на отрезке , называется линейным ДУ II порядка.
Если , то уравнение (1) называется однородным, если , то уравнение (1) называется неоднородным.
Выразим из уравнения (1):
(2)
(3)
(4)
Задача (2) – (4) есть задача Коши для линейного ДУ второго порядка.
Глава 1. Обыкновенные дифференциальные уравнения
Рекомендуемые страницы:
lektsia.com
Лекция 9. Обыкновенные дифференциальные уравнения первого порядка
Осн.лит. 12, глава 15, [383 –410]
Контрольные вопросы:
Что называется линией уровня и поверхностью уровня?
Что называется пределом функции двух переменных в точке, в области?
В чем состоит экономический смысл частной производной?
В направлении какого вектора скорость возрастания функции наибольшая?
Каковы достаточные условия экстремума функции двухпеременных?
Основные понятия
Определение. Дифференциальным
уравнением называется уравнение,
связывающее независимую переменную ,
искомую функцию
,
искомую функцию и ее производныет.е. уравнения вида(1)
и ее производныет.е. уравнения вида(1)
где 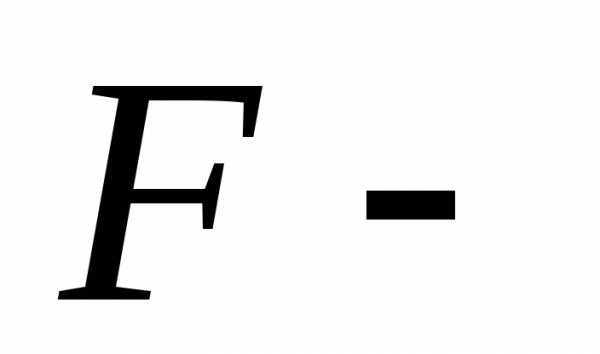 непрерывная функция
непрерывная функция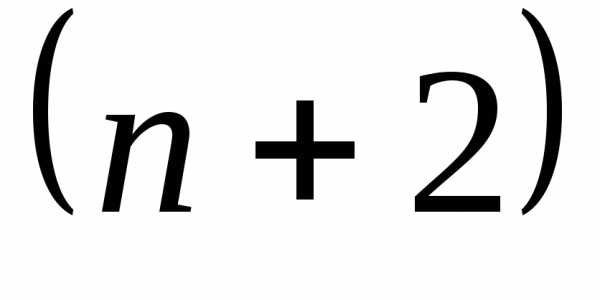 переменных.
переменных.
Если искомая функция  есть функция одной независимой переменной,
то дифференциальное уравнение называетсяобыкновенным.
есть функция одной независимой переменной,
то дифференциальное уравнение называетсяобыкновенным.
Если искомая функция зависит от нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.
Например, 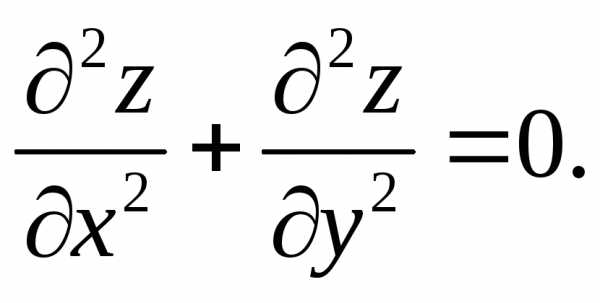 В дальнейшем будем рассматривать лишь
обыкновенные дифференциальные уравнения.Порядком дифференциального
уравнения называется порядок наивысшей
производной, явно входящей в уравнение.
В дальнейшем будем рассматривать лишь
обыкновенные дифференциальные уравнения.Порядком дифференциального
уравнения называется порядок наивысшей
производной, явно входящей в уравнение.
Например:
–
дифференциальное уравнение 2- го порядка.Решением дифференциального
уравнения (1) называется функция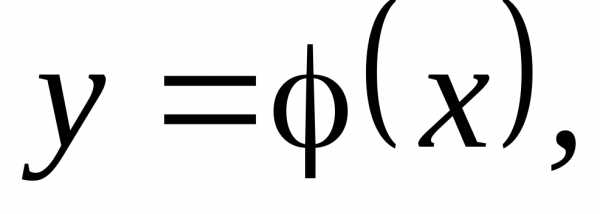 которая при подстановке в дифференциальное
уравнение обращает его в тождество.
Процесс отыскания решений
которая при подстановке в дифференциальное
уравнение обращает его в тождество.
Процесс отыскания решений
дифференциального уравнения называется интегрированием уравнения. График решения дифференциального уравнения называетсяинтегральной кривой этого уравнения.
2. Дифференциальные уравнения первого порядка
Общий вид уравнения первого порядка следующий: (2)
Если уравнение (2) удается разрешить
относительно  ,
то получим(3)
,
то получим(3)
Это уравнение называется уравнением
первого порядка, разрешенным
относительно производной. Условие, что
в уравнениипри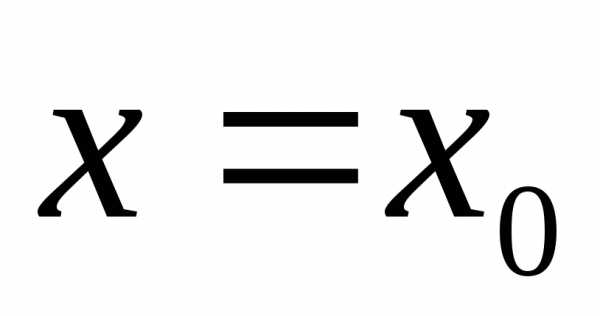 функция
функция должна равняться заданному числу
должна равняться заданному числу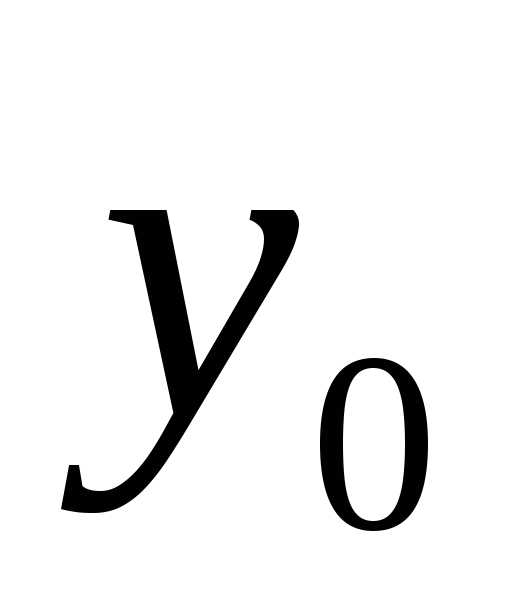 ,
называется начальным условием.Оно записывается в виде
,
называется начальным условием.Оно записывается в виде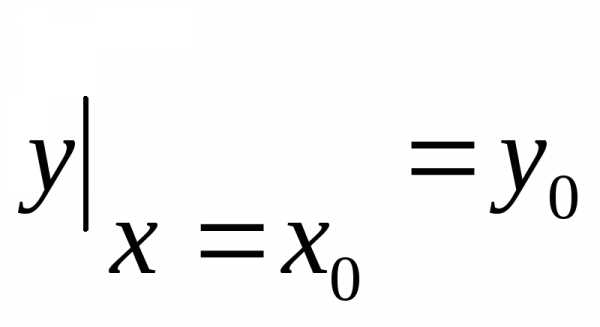 .
Задача отыскания решений уравнения,
удовлетворяющего начальным условиям,
носит названиезадачи Коши.
.
Задача отыскания решений уравнения,
удовлетворяющего начальным условиям,
носит названиезадачи Коши.
3. Уравнения с разделяющимися переменными Рассмотрим дифференциальное уравнение вида (4)
где правая часть есть произведение
функции, зависящей только от 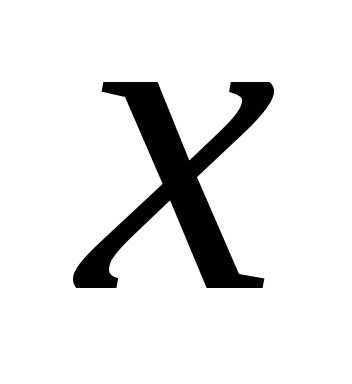 ,
на функцию, зависящую только от
,
на функцию, зависящую только от .
Предполагая, что
.
Предполагая, что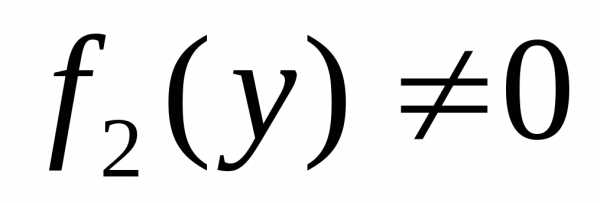 ,
преобразуем его следующим образом:
,
преобразуем его следующим образом:
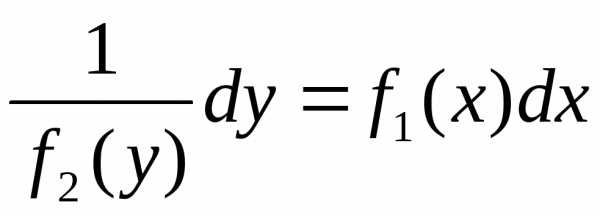 .
(5)
.
(5)
Считая  известной функцией от
известной функцией от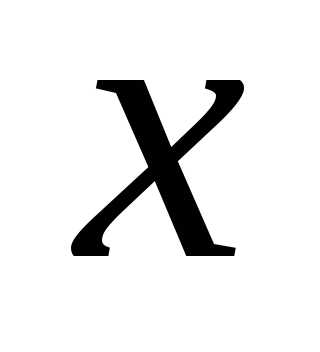 ,
равенство (5) можно рассматривать как
равенство двух дифференциалов, а
неопределенные интегралы от них будут
отличаться постоянным слагаемым.
,
равенство (5) можно рассматривать как
равенство двух дифференциалов, а
неопределенные интегралы от них будут
отличаться постоянным слагаемым.
Интегрируя левую часть по  ,
а правую по
,
а правую по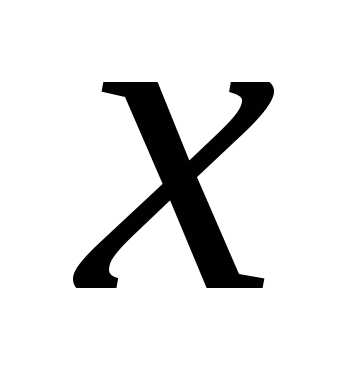 ,
получим.
,
получим.
Мы получили соотношение, связывающее
решение  ,
независимое переменное
,
независимое переменное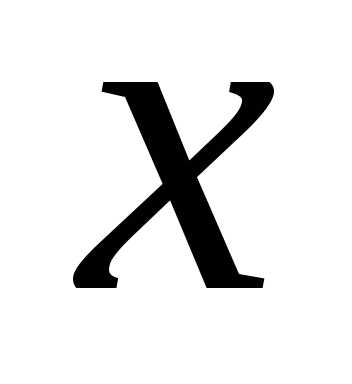 и произвольную постоянную
и произвольную постоянную ,
т.е. получили общий интеграл уравнения
(5).
,
т.е. получили общий интеграл уравнения
(5).
Дифференциальное уравнение типа (5) или вида (6) называютуравнением с разделенными переменными.
Общий интеграл его есть .
Уравнение вида , (7)
в которых коэффициенты при дифференциалах
распадаются на множители, зависящие
только от 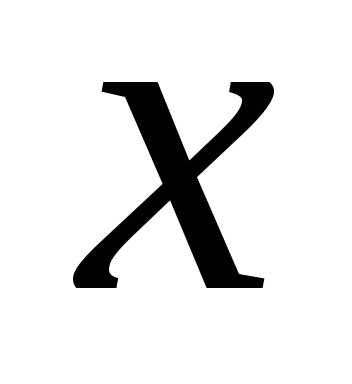 и только от
и только от ,
называется уравнениемс разделяющимися
переменными.
,
называется уравнениемс разделяющимися
переменными.
Путем деления обеих частей на произведение они приводятся к уравнениям с разделенными переменными:, т.е. к уравнению вида (6). Общий интеграл этого уравнения имеет вид.
Пример. Решить уравнение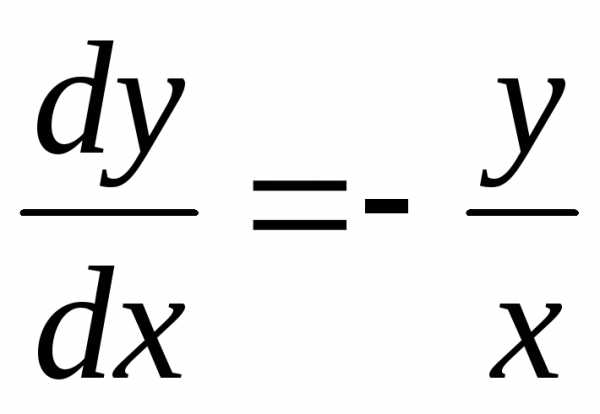 .
Разделяем переменные
.
Разделяем переменные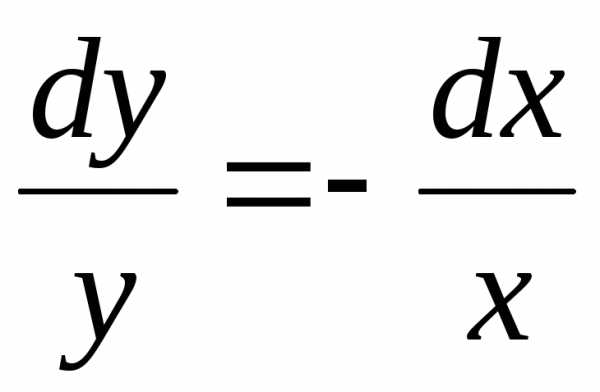 ;
;
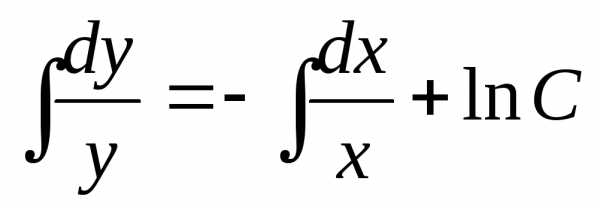 ;;
;;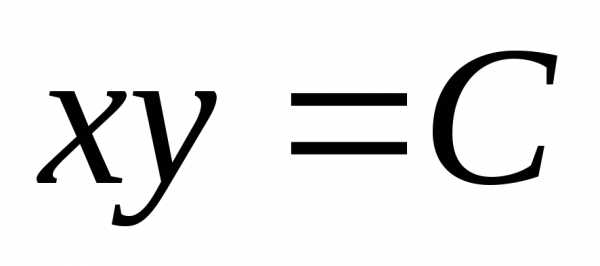 ;
;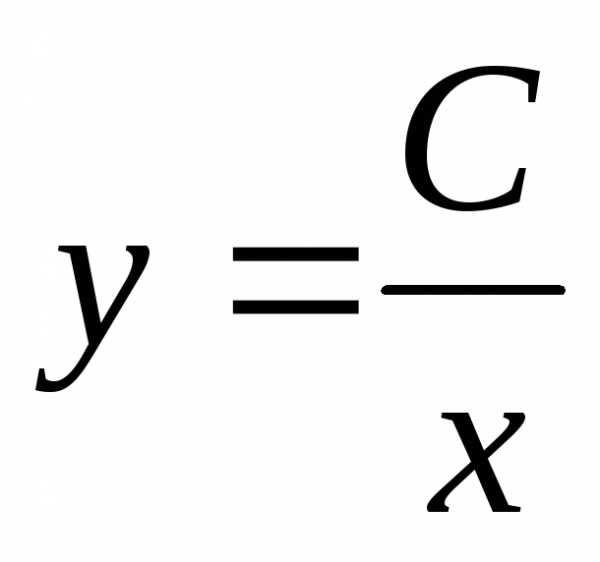 – общее решение.
– общее решение.
studfiles.net
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением,разрешенным относительно производной.
Преобразуем такое выражение далее:
Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x).
Пусть функция f(x) – определена и непрерывна на некотором интервале
a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х0 и у0, то можно определить постоянную С.
Уравнения с разделяющимися переменными
Определение. Дифференциальное уравнение называетсяуравнением с разделяющимися переменными, если его можно записать в виде
.
Такое уравнение можно представить также в виде:
Перейдем к новым обозначениям
Получаем:
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального
уравнения: 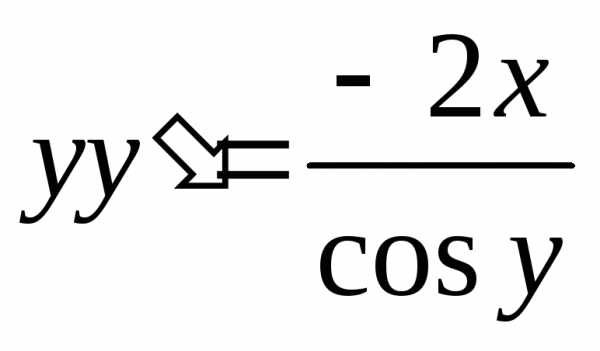

Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):

это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
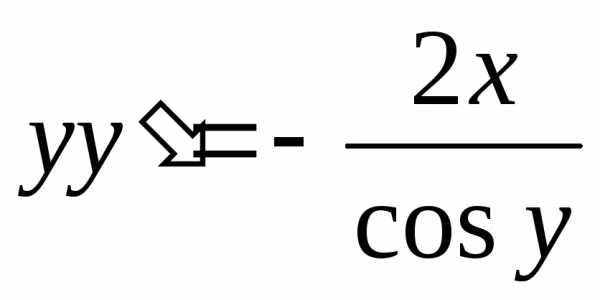 – верно
– верно
Пример. Найти решение дифференциального
уравнения  при условии у(2) = 1.
при условии у(2) = 1.
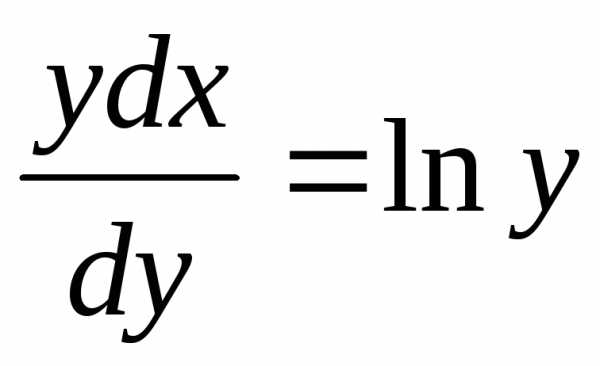
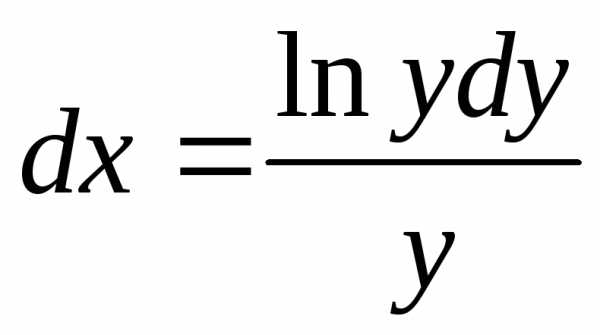
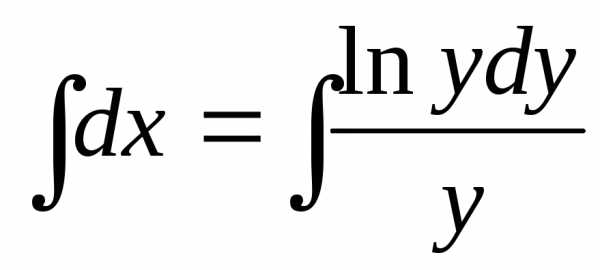

при у(2) = 1 получаем
Итого: или 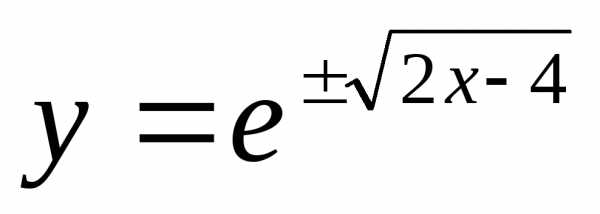 – частное решение;
– частное решение;
Проверка: , итого
– верно.
Пример. Решить уравнение 
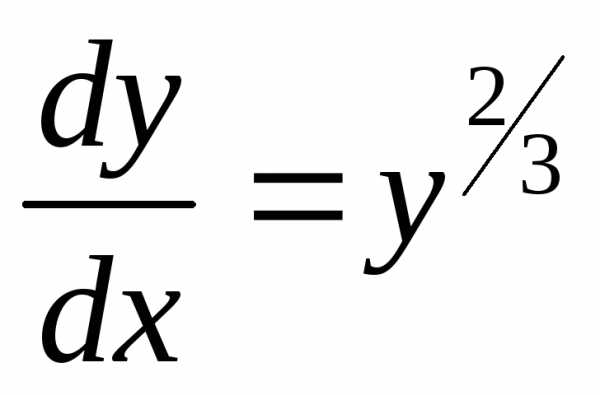
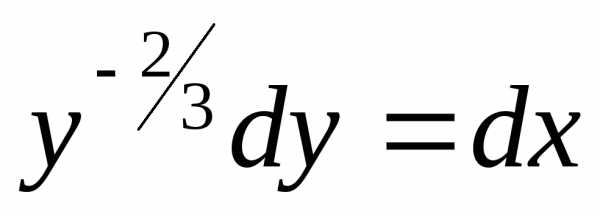
– общий интеграл
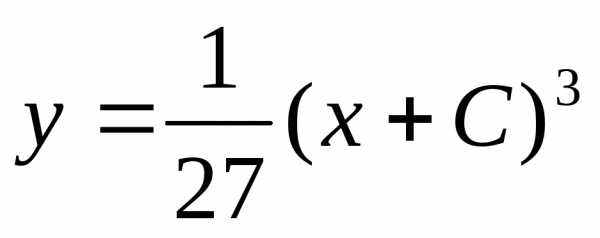 – общее решение
– общее решение
Пример. Решить уравнение
Пример. Решить уравнение 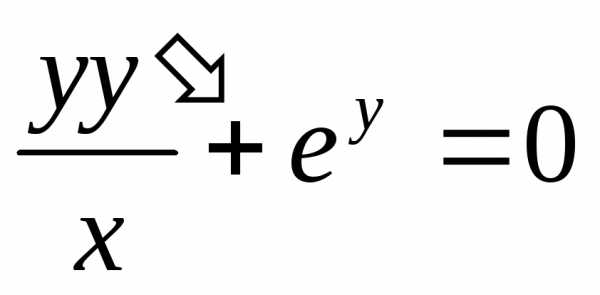 при
условии у(1) = 0.
при
условии у(1) = 0.

Интеграл, стоящий в левой части будем брать по частям (см. Интегрирование по частям. ).
Если у(1) = 0, то
Итого, частный интеграл: .
Пример. Решить уравнение .
Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. п.16. Получаем общий интеграл:
Пример. Решить уравнение 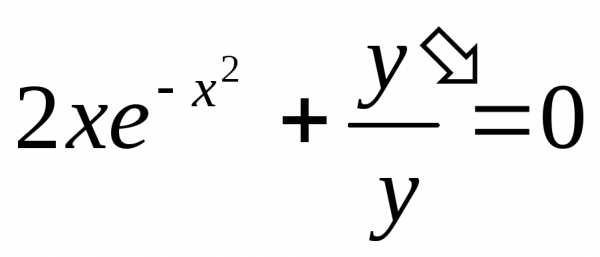
Преобразуем заданное уравнение:
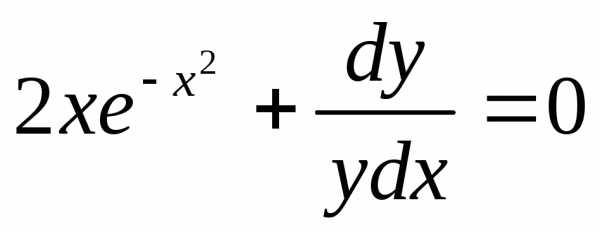
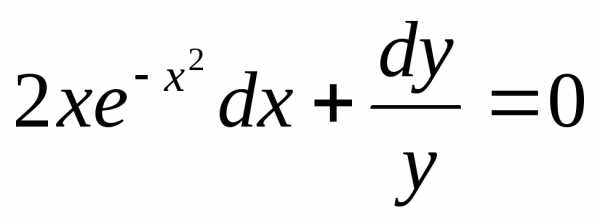
 Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Пример. Решить уравнение .
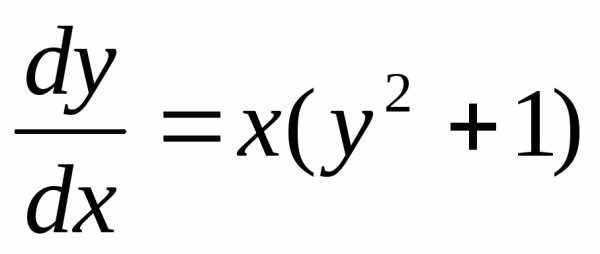
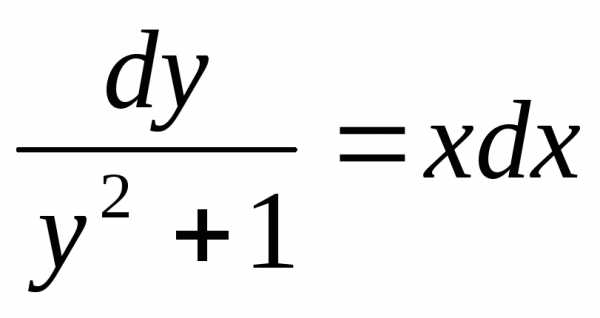
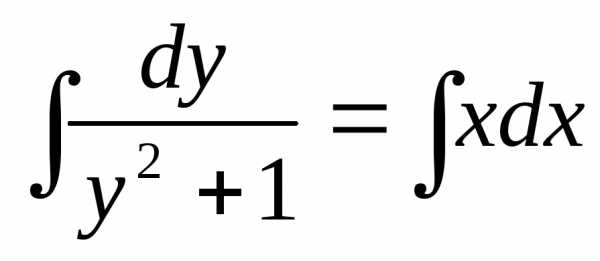 ;
; 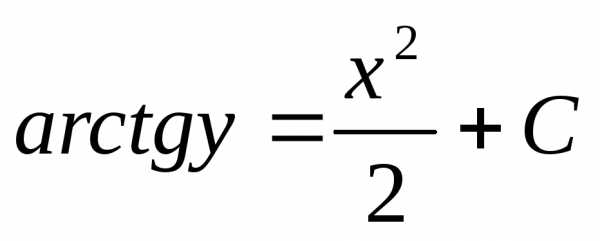 ;
;
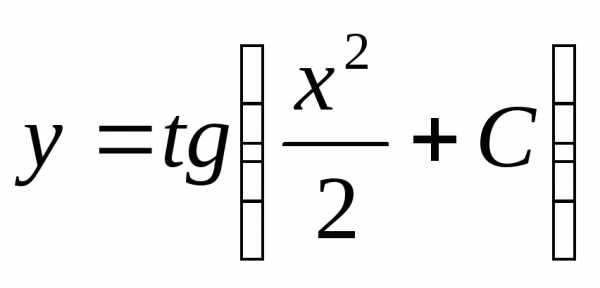
Допустим, заданы некоторые начальные условия х0 и у0. Тогда:
Получаем частное решение
studfiles.net
1.2. Обыкновенные дифференциальные уравнения 1-го порядка
Обыкновенное
дифференциальное уравнение 1-го порядка ( )
имеет вид:или (если его удаётся разрешить
относительно производной).
Общее решение или общий
интеграл
уравнения 1-го порядка содержат одну
произвольную постоянную. Единственное
начальное условие для уравнения 1-го
порядка
)
имеет вид:или (если его удаётся разрешить
относительно производной).
Общее решение или общий
интеграл
уравнения 1-го порядка содержат одну
произвольную постоянную. Единственное
начальное условие для уравнения 1-го
порядка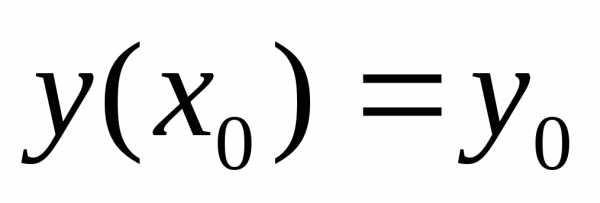 позволяет определить значение константы
из общего решения или из общего интеграла.
Таким образом можно найти частное
решение, то есть задача Коши будет
решена. Вопрос о существовании и
единственности решения задачи Коши
является одним из центральных в общей
теории обыкновенных дифференциальных
уравнений. Для уравнения 1-го порядка,
в частности, справедлива следующая
теорема, принимаемая здесь без
доказательства.
позволяет определить значение константы
из общего решения или из общего интеграла.
Таким образом можно найти частное
решение, то есть задача Коши будет
решена. Вопрос о существовании и
единственности решения задачи Коши
является одним из центральных в общей
теории обыкновенных дифференциальных
уравнений. Для уравнения 1-го порядка,
в частности, справедлива следующая
теорема, принимаемая здесь без
доказательства.
Теорема. Если в уравнении
функция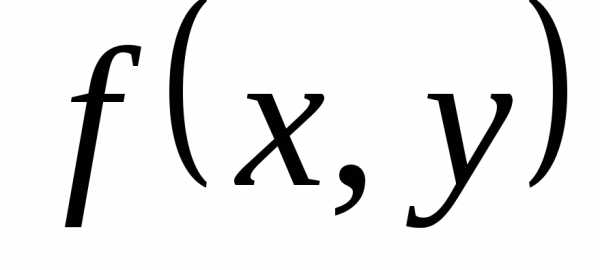 и её частная производная
и её частная производная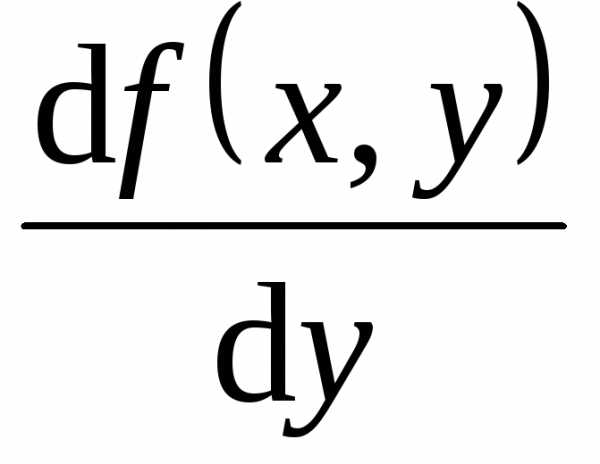 непрерывны в некоторой областиD плоскости XOY и в этой области задана точка
непрерывны в некоторой областиD плоскости XOY и в этой области задана точка 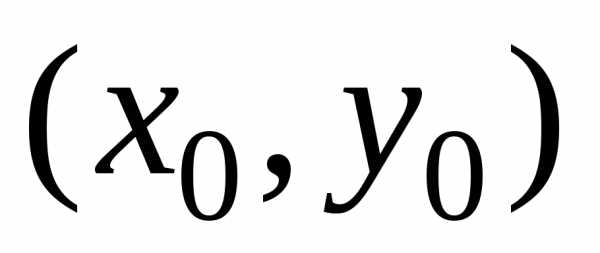 ,
то существует (и притом единственное)
решение
,
то существует (и притом единственное)
решение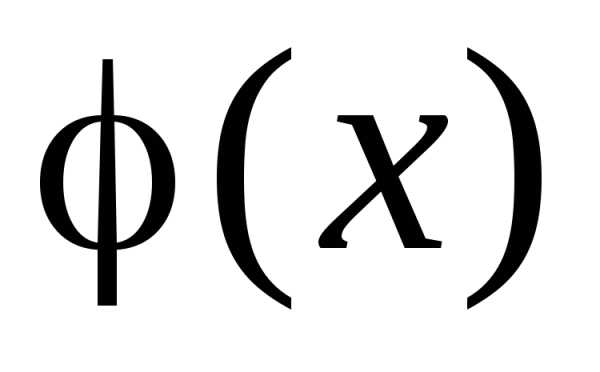 ,
удовлетворяющее как уравнению,
так и начальному условию.
,
удовлетворяющее как уравнению,
так и начальному условию.
Геометрически
общее решение уравнения 1-го порядка
представляет собой семейство кривых
на плоскости XOY,
не имеющих общих точек и отличающихся
друг от друга одним параметром –
значением константы C.
Эти кривые называются интегральными
кривыми для
данного уравнения. Интегральные кривые
уравнения
обладают очевидным геометрическим
свойством: в каждой точке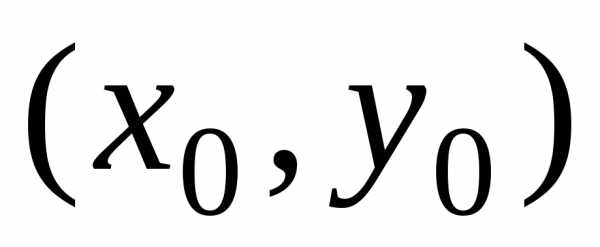 тангенс угла наклона касательной к
кривой равен значению правой части
уравнения в этой точке:.
Другими словами, уравнениезадаёт в плоскостиXOY поле направлений касательных к
интегральным кривым.
тангенс угла наклона касательной к
кривой равен значению правой части
уравнения в этой точке:.
Другими словами, уравнениезадаёт в плоскостиXOY поле направлений касательных к
интегральным кривым.
Замечание: Необходимо отметить, что к уравнению 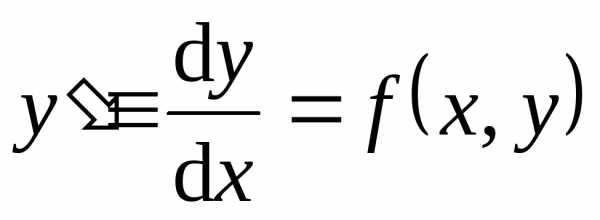 приводится уравнениеи так называемое уравнение в симметрической
форме
приводится уравнениеи так называемое уравнение в симметрической
форме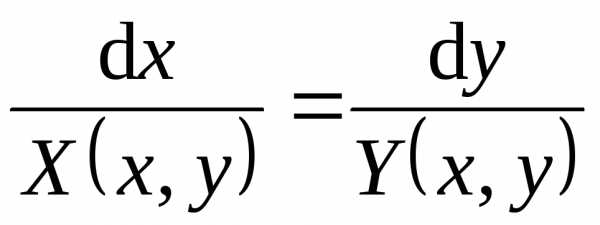 .
.
1.3. Дифференциальные уравнения 1-го порядка с разделяющимися переменными
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
(3.1)
или уравнение вида
(3.2)
Чтобы в уравнении (3.1) разделить переменные, то есть привести это уравнение к так называемому уравнению с разделёнными переменными, необходимо множители, содержащие переменную x перенести в одну сторону уравнения, а множители, содержащие переменную y, – в другую, а именно:
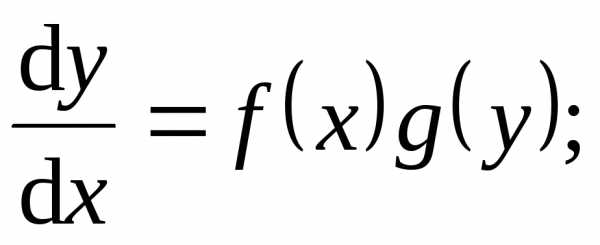
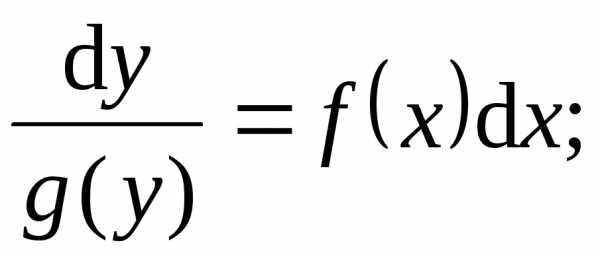
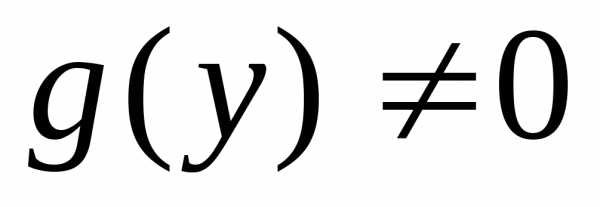
Остается проверить,
не потеряны ли решения при делении на
выражения, зависящие от переменных. Для
этого необходимо решить уравнение 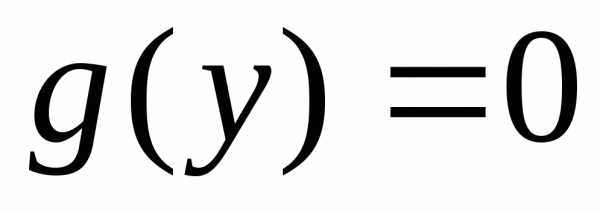 .
Если оно имеет вещественное решение
.
Если оно имеет вещественное решение 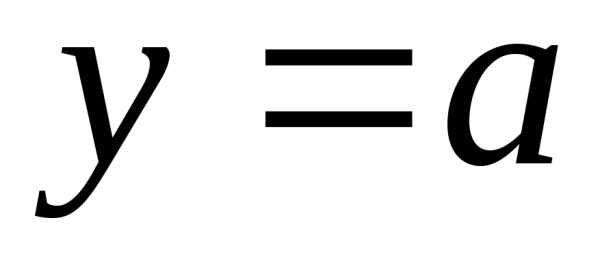 ,то тоже будет
решением уравнения (3.1).
,то тоже будет
решением уравнения (3.1).
Уравнение (3.2) приводится к уравнению с разделёнными переменными делением на произведение :
,
что позволяет получить общий интеграл уравнения (3.2):
(3.3)
Функции (3.3), определяющие интегральные кривые, будут дополнены решениями , если такие решения существуют.
Пример. Решить уравнение: .
Решение. Разделяем переменные:
; .
Интегрируя, получаем
.
Из уравнений 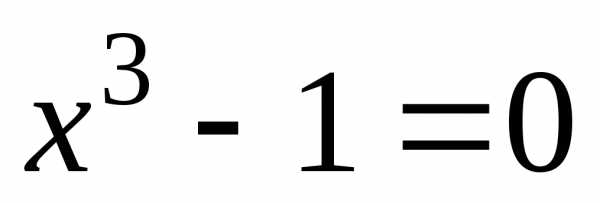 и
и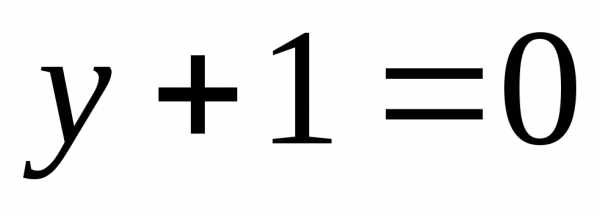 находим
находим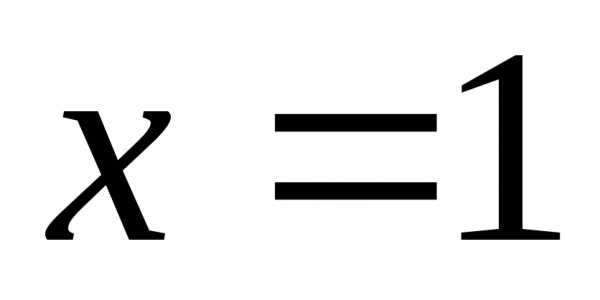 ,
,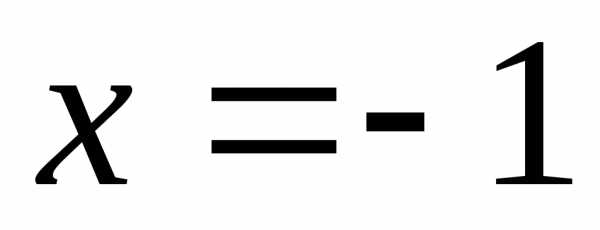 ,
,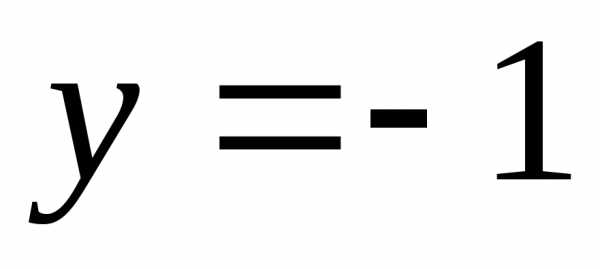 . Непосредственной подстановкой этих
функций в исходное уравнение убеждаемся,
что эти решения – частные решения.
. Непосредственной подстановкой этих
функций в исходное уравнение убеждаемся,
что эти решения – частные решения.
1.4. Однородные дифференциальные уравнения 1-го порядка
Определение 1. Уравнение
1-го порядка
называетсяоднородным,
если для его правой части при любых 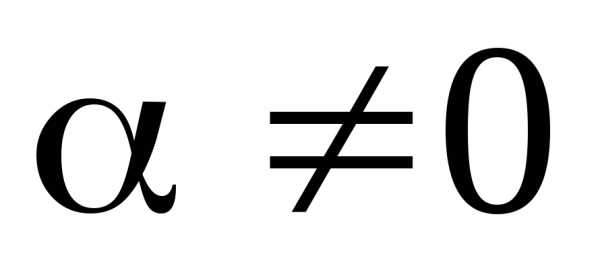 справедливо соотношение,
называемоеусловием
однородности функции двух переменных нулевого измерения.
справедливо соотношение,
называемоеусловием
однородности функции двух переменных нулевого измерения.
Пример 1. Показать,
что функция 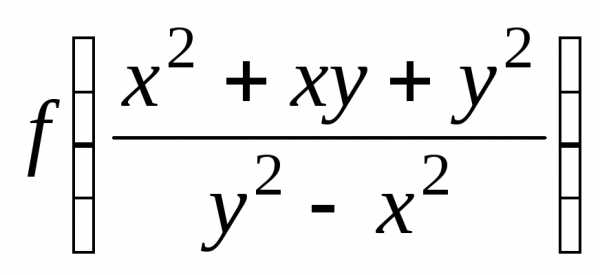 – однородная нулевого измерения.
– однородная нулевого измерения.
Решение.
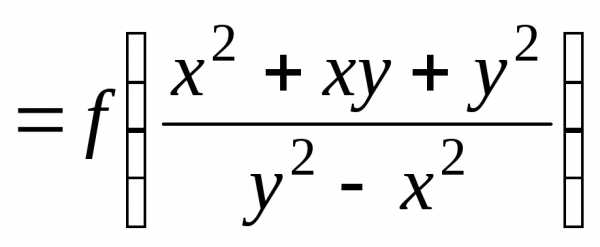 ,
,  ,
,
что и требовалось доказать.
Теорема. Любая функция  – однородна и, наоборот, любая однородная
функция
– однородна и, наоборот, любая однородная
функция нулевого измерения приводится к виду
нулевого измерения приводится к виду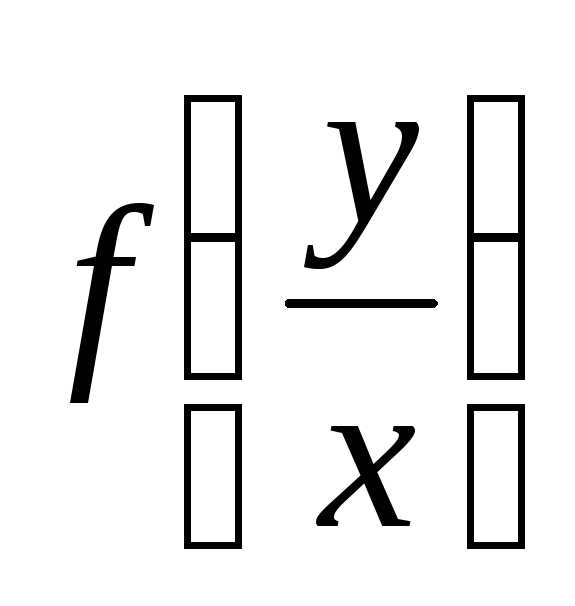 .
.
Доказательство. Первое
утверждение теоремы очевидно, так как 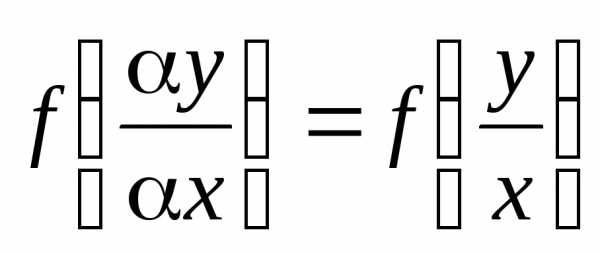 .
.
Докажем второе
утверждение. Положим 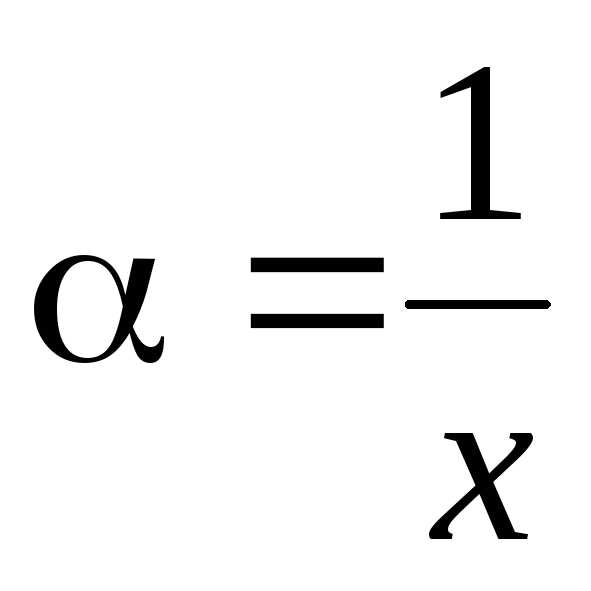 ,
тогда для однородной функции,
что и требовалось доказать.
,
тогда для однородной функции,
что и требовалось доказать.
Определение 2. Уравнение
, (4.1)
где M и N – однородные
функции одной и той же степени, то есть
обладают свойством
при всех ,
называетсяоднородным.
,
называетсяоднородным.
Очевидно, что уравнение (4.1) всегда может быть приведено к виду
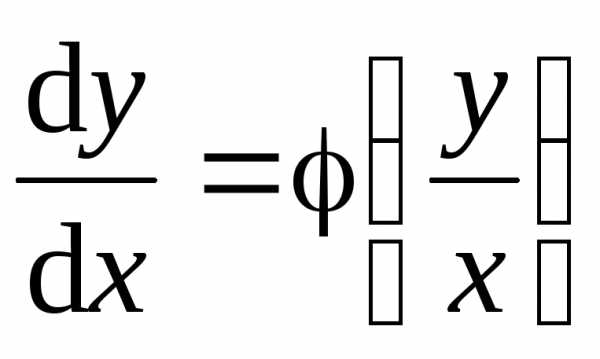 (4.2),
(4.2),
хотя для его решения можно этого и не делать.
Однородное уравнение
(4.1) приводится к уравнению с разделяющимися
переменными с помощью замены искомой
функции y по формуле , где 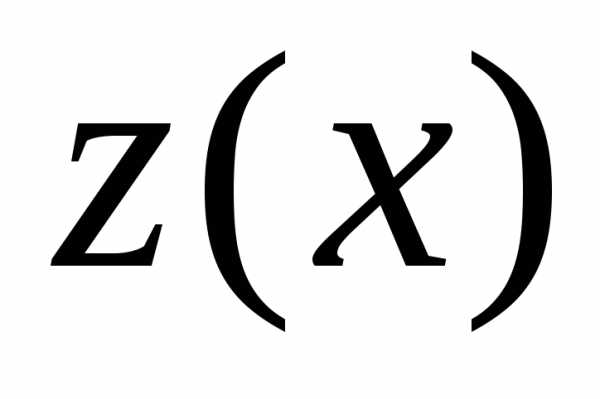 – новая
искомая функция. Выполнив эту замену в
уравнении (4.2), получим:
– новая
искомая функция. Выполнив эту замену в
уравнении (4.2), получим:
(4.3)
или
,
то есть
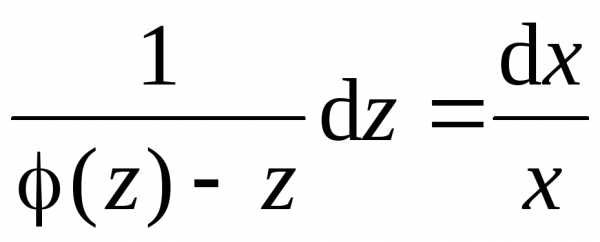 .
.
Интегрируя последнее
равенство, получаем общий интеграл
уравнения (4.3) относительно функции 
,
который после
повторной замены 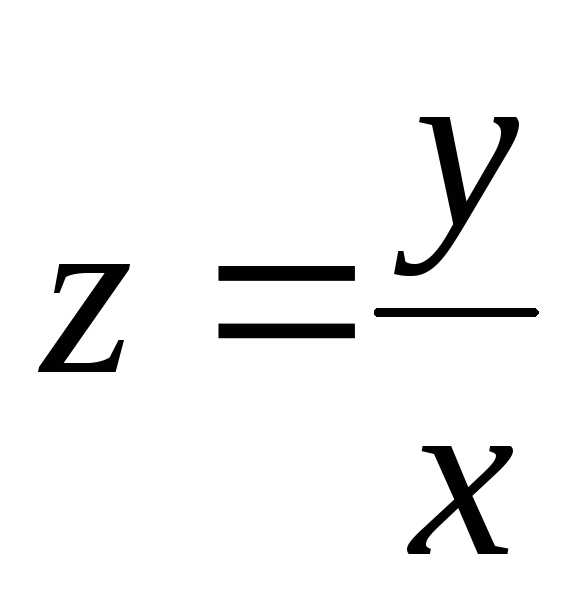 даёт общий интеграл исходного уравнения
(4.2). Кроме того, если
даёт общий интеграл исходного уравнения
(4.2). Кроме того, если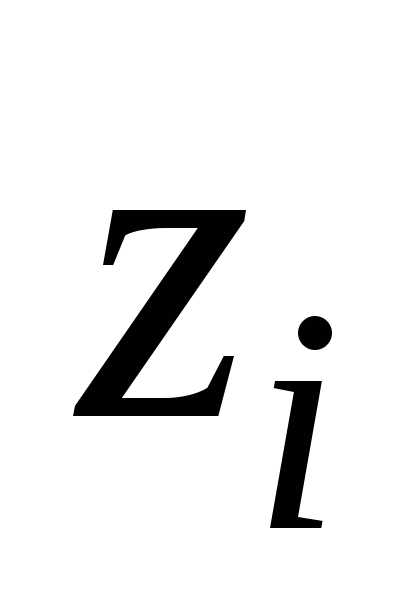 – корни уравнения,
то функции
– корни уравнения,
то функции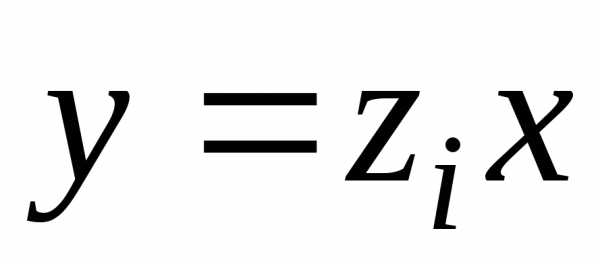 (где
(где )
– решения однородного уравнения (4.2).
Если же
)
– решения однородного уравнения (4.2).
Если же 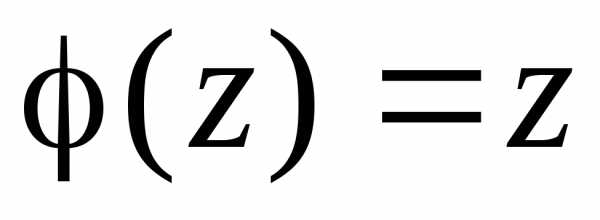 ,
то уравнение (4.2) принимает вид
,
то уравнение (4.2) принимает вид
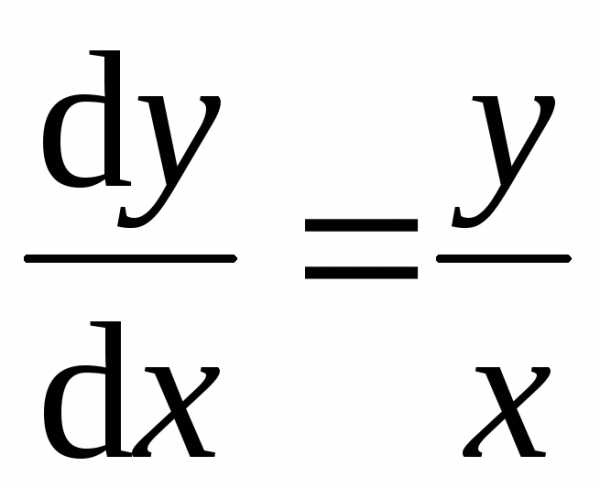
и становится уравнением с разделяющимися переменными. Его решениями являются функции, определяющие на плоскости полупрямые:
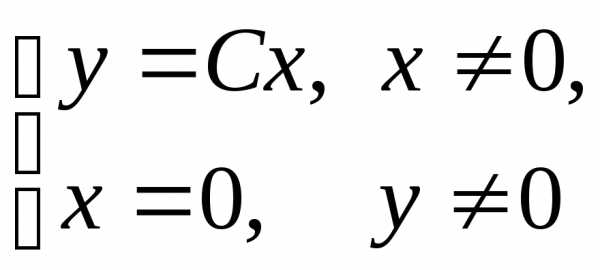 .
.
Замечание. Иногда целесообразно вместо указанной выше подстановки использовать замену .
studfiles.net
