2.2. Однородные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка
(9)
называется однородным относительно
переменных x и y,
если 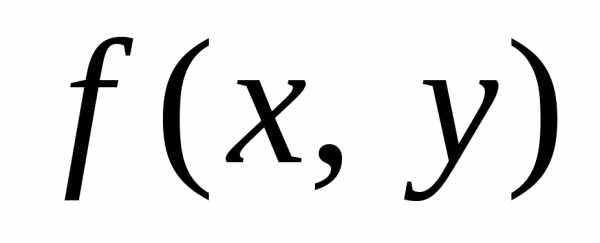 – однородная функция нулевой степени
относительно своих аргументов.
– однородная функция нулевой степени
относительно своих аргументов.
Дифференциальное уравнение первого порядка
(10)
называется однородным относительно
переменных x и y,
если  и
и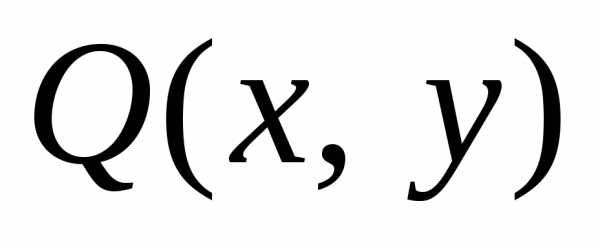 – однородные функции одной и той же
степениk относительно своих аргументов.
– однородные функции одной и той же
степениk относительно своих аргументов.
Функция 
.
Однородное дифференциальное уравнение первого порядка (как уравнение (9), так и уравнение (10)) может быть представлено в виде
 . (11)
. (11)
Метод
интегрирования однородных дифференциальных
уравнений состоит в следующем. Однородное
дифференциальное уравнение приводится
к виду (11). Вводится новая переменная 
 ,
где
,
где (),
и после подстановки в уравнение (11)
приходим к уравнению с разделяющимися
переменными относительно переменнойxи новой функцииt(x).
(),
и после подстановки в уравнение (11)
приходим к уравнению с разделяющимися
переменными относительно переменнойxи новой функцииt(x).В задании 2 необходимо решить однородное обыкновенное дифференциальное уравнение первого порядка.
Задание 2. Найти общий интеграл (общее решение) дифференциального уравнения. Сделать проверку.
a) 
c) , d).
Решение: Во всех случаях имеем однородные относительно переменных x и y обыкновенные дифференциальные уравнения первого порядка. Все они могут быть сведены к уравнению вида (11). В случаях a), c), d) предварительно необходимо показать, что эти уравнения являются однородными, а затем привести их к виду (11).
Задание
2a.  .
.
Данное
уравнением является уравнением первого
порядка. Рассмотрим функцию 
.
Таким образом, данное уравнением является однородным и его можно свести к уравнению (11). Для этого разделим числитель и знаменатель правой части на x:
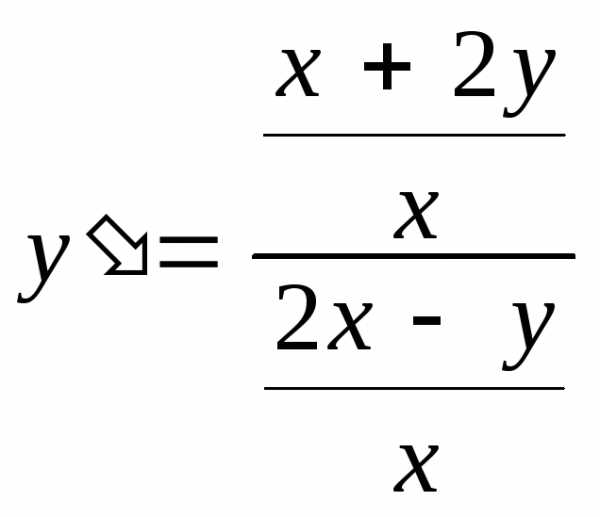 ;
;  .
.
Сделаем
замену переменной 
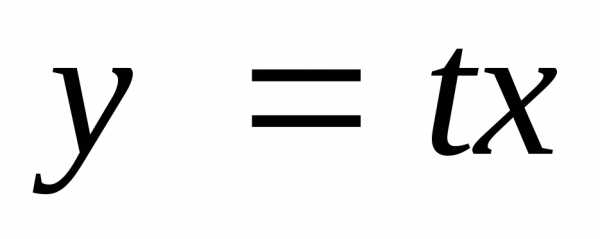 ,
где
,
где .
Найдеми подставим в преобразованное уравнение
.
Найдеми подставим в преобразованное уравнение ;
;  ;;
;;
; 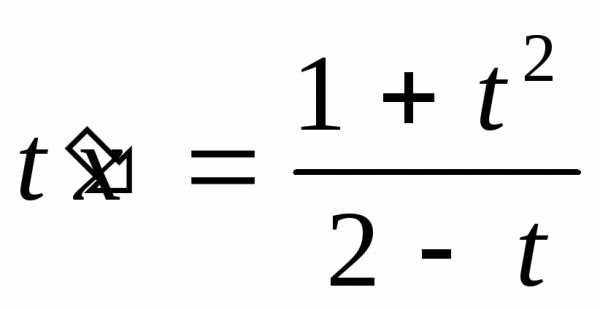 .
.
Пришли
к уравнению первого порядка с разделяющимися
переменными относительно переменной x и новой искомой функции t(x).
Заменяя 
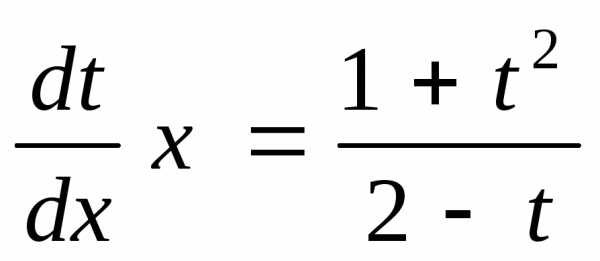 ;
; 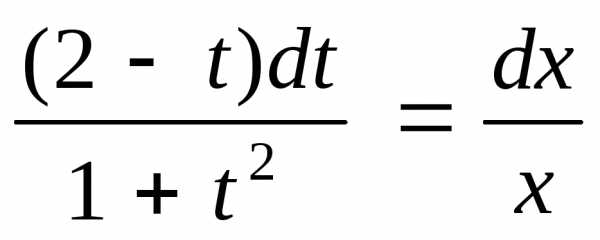 .
.
Проинтегрируем обе части полученного уравнения


Возвращаясь к исходному уравнению, получим
.
Умножив обе части равенства на два и уединяя произвольную постоянную, получим общий интеграл уравнения с разделяющимися переменными
.
Для
нахождения общего интеграла исходного
уравнения вернемся к старой переменной
через замену 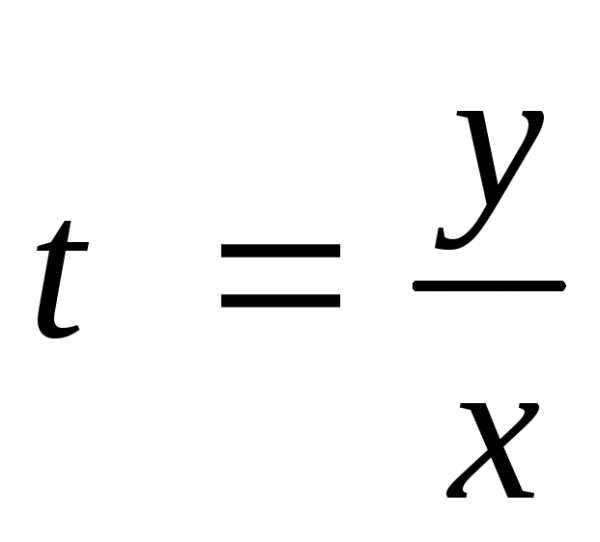 :
:
,
,
,
.
Таким образом, общий интеграл исходного уравнения примет вид:
.
Сделаем проверку. Вычислим производную искомой функции как функции, заданной неявно.
, ,
, ,
,
, .
.
Подставим найденное значение в искомое уравнение
и получим тождество (верное равенство).
Ответ: общий интеграл
Задание 2b. .
Имеем
обыкновенное дифференциальное уравнение
первого порядка, однородное относительно
переменных x и y. Сделаем замену переменной  или
или
 .
Найдеми подставим в исходное уравнение
.
Найдеми подставим в исходное уравнение; .
Пришли
к уравнению первого порядка с разделяющимися
переменными относительно переменной x и новой искомой функции t(x).
Заменяя  и разделяя переменные, получим
и разделяя переменные, получим
; .
Проинтегрируем обе части полученного уравнения
Интеграл,
стоящий в правой части является табличным 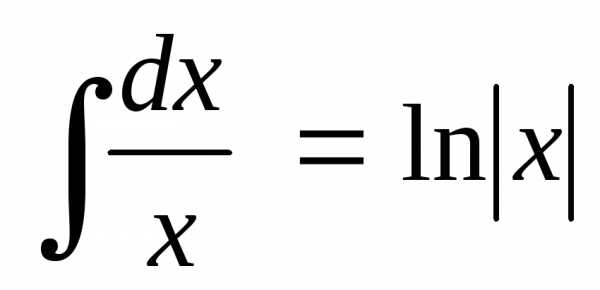
Найдем интеграл от дробно рациональной функции, стоящей слева. Для этого можно, например, разложить подынтегральную функцию на сумму простейших или, выделив в знаменателе полный квадрат и сделав замену переменной, прийти к табличному интегралу.
Тогда, возвращаясь к исходному уравнению, получим
, ,
 ,
,  .
.
 .
.
Откуда после преобразований записываем общий интеграл
 .
.
Проверка выполняется аналогично тому, как это делалось в предыдущих заданиях.
Ответ: общий интеграл  .
.
Задание 2c. .
Данное уравнением является уравнением первого порядка. Рассмотрим функцию . Эта функция является однородной функцией нулевой степени, так как для произвольного действительно числа
Таким
образом, данное уравнение является
однородным и его можно решить аналогично
тому, как это показано в пункте a),
предварительно разделив числитель и
знаменатель правой части на  .
.
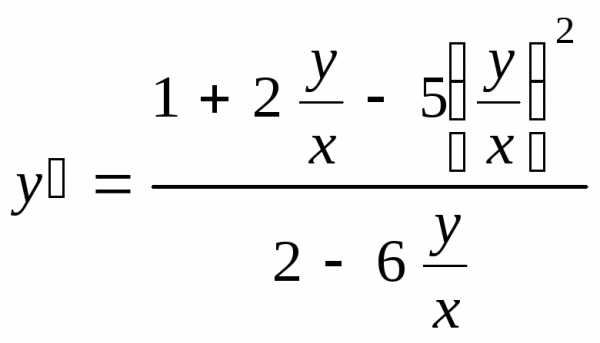 .
.
Сделаем замену переменной

 ,;
,;; 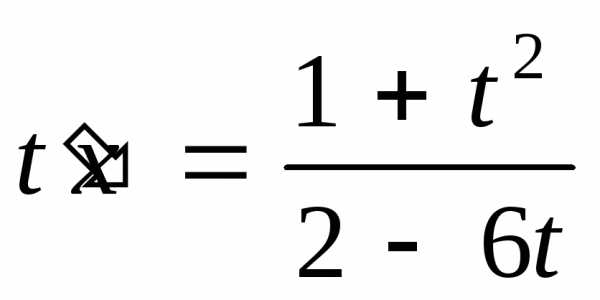 .
.
Пришли к уравнению первого порядка с разделяющимися переменными относительно переменной x и новой искомой функции t(x).
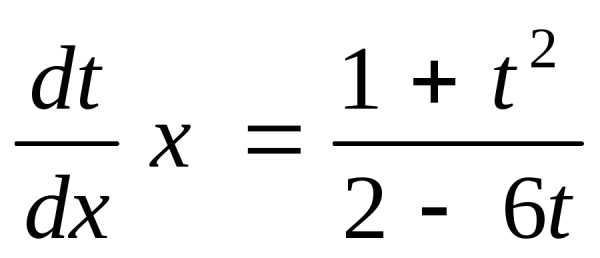 ;
;  ;.
;.
Тогда
,
,
,
,
,
.
Таким образом, общий интеграл исходного уравнения примет вид:
.
Проверку выполняется аналогично предыдущим примерам.
Ответ: общий интеграл .
Задание 2d. .
Рассмотрим функции ,. Эти функции являются однородными первой степени относительно переменныхx и y. Действительно:
,
.
Тогда исходное уравнение может быть сведено к уравнению вида (9), а затем к виду (11).
,
 ,
,
 .
.
Заметим, что полученное уравнение совпадает с уравнением из задания 2(a), то есть пришли к случаю, который уже рассмотрен.
studfiles.net
Однородные дифференциальные уравнения
Однородные уравнения
Функция [cbm]f(x,y)[/cbm] называется однородной функцией своих аргументов измерения [cbm]n[/cbm] , если справедливо тождество [cbm]f(tx,ty) \equiv t^nf(x,y)[/cbm] .
Например, функция [cbm]f(x,y)=x^2+y^2-xy[/cbm] есть однородная функция второго измерения, так как
[cbm]f(tx,ty)=(tx)^2+(ty)^2-(tx)(ty)=t^2(x^2+y^2-xy)=t^2f(x,y).[/cbm]
При [cbm]n=0[/cbm] имеем функцию нулевого измерения. Например, [cbm]\frac{x^2-y^2}{x^2+y^2}[/cbm] есть однородная функция нулевого измерения, так как
[cbm]{f(tx,ty)=\frac{(tx)^2-(ty)^2}{(tx)^2+(ty)^2}=\frac{t^2(x^2-y^2)}{t^2(x^2+y^2)}=\frac{x^2-y^2}{x^2+y^2}=f(x,y).}[/cbm]
Дифференциальное уравнение вида [cbm]\frac{dy}{dx}=f(x,y)[/cbm] называется однородным относительно [cbm]x[/cbm] и [cbm]y[/cbm] , если [cbm]f(x,y)[/cbm] есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде
[cbm]\frac{dy}{dx}=\varphi\!\left(\frac{y}{x}\right).[/cbm](1)
Вводя новую искомую функцию [cbm]u=\frac{y}{x}[/cbm] , уравнение (1) можно привести к уравнению с разделяющими переменными:
[cbm]x\frac{du}{dx}=\varphi(u)-u.[/cbm]
Если [cbm]u=u_0[/cbm] есть корень уравнения [cbm]\varphi(u)-u=0[/cbm] , то решение однородного уравнения будет [cbm]u=u_0[/cbm] или [cbm]y=u_0x[/cbm] (прямая, проходящая через начало координат).
Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку [cbm]y=ux[/cbm] .
Пример 1. Решить однородное уравнение [cbm]xy’=\sqrt{x^2-y^2}+y[/cbm] .
Решение. Запишем уравнение в виде [cbm]y’=\sqrt{1-{\left(\frac{y}{x}\right)\!}^2}+\frac{y}{x}[/cbm] так что данное уравнение оказывается однородным относительно [cbm]x[/cbm] и [cbm]y[/cbm] . Положим [cbm]u=\frac{y}{x}[/cbm] , или [cbm]y=ux[/cbm] . Тогда [cbm]y’=xu’+u[/cbm] . Подставляя в уравнение выражения для [cbm]y[/cbm] и [cbm]y'[/cbm] , получаем [cbm]x\frac{du}{dx}=\sqrt{1-u^2}[/cbm] . Разделяем переменные: [cbm]\frac{du}{1-u^2}=\frac{dx}{x}[/cbm] . Отсюда интегрированием находим
[cbm]\arcsin{u}=\ln|x|+\ln{C_1}~(C_1>0)[/cbm] , или [cbm]\arcsin{u}=\ln{C_1|x|}[/cbm] .
Так как [cbm]C_1|x|=\pm{C_1x}[/cbm] , то, обозначая [cbm]\pm{C_1}=C[/cbm] , получаем [cbm]\arcsin{u}=\ln{Cx}[/cbm] , где [cbm]|\ln{Cx}|\leqslant\frac{\pi}{2}[/cbm] или [cbm]e^{-\pi/2}\leqslant{Cx}\leqslant{e^{\pi/2}}[/cbm] . Заменяя [cbm]u[/cbm] на [cbm]\frac{y}{x}[/cbm] , будем иметь общий интеграл [cbm]\arcsin{y}{x}=\ln{Cx}[/cbm] .
Отсюда общее решение: [cbm]y=x\sin\ln{Cx}[/cbm] .
При разделении переменных мы делили обе части уравнения на произведение [cbm]x\sqrt{1-u^2}[/cbm] , поэтому могли потерять решение, которые обращают в ноль это произведение.
Положим теперь [cbm]x=0[/cbm] и [cbm]\sqrt{1-u^2}=0[/cbm] . Но [cbm]x\ne0[/cbm] в силу подстановки [cbm]u=\frac{y}{x}[/cbm] , а из соотношения [cbm]\sqrt{1-u^2}=0[/cbm] получаем, что [cbm]1-\frac{y^2}{x^2}=0[/cbm] , откуда [cbm]y=\pm{x}[/cbm] . Непосредственной проверкой убеждаемся, что функции [cbm]y=-x[/cbm] и [cbm]y=x[/cbm] также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых [cbm]C_\alpha[/cbm] однородного уравнения [cbm]y’=\varphi\!\left(\frac{y}{x}\right)[/cbm] . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.
Примечание: Будем называть соответственными те точки на кривых [cbm]C_\alpha[/cbm] , которые лежат на одном луче, выходящем из начала координат.
Решение. По определению соответственных точек имеем [cbm]\frac{y}{x}=\frac{y_1}{x_1}[/cbm] , так что в силу самого уравнения [cbm]y’=y’_1[/cbm] , где [cbm]y'[/cbm] и [cbm]y’_1[/cbm] — угловые коэффициенты касательных к интегральным кривым [cbm]C_\alpha[/cbm] и [cbm]C_{\alpha_1}[/cbm] , в точках [cbm]M[/cbm] и [cbm]M_1[/cbm] соответственно (рис. 12).
Уравнения, приводящиеся к однородным
А. Рассмотрим дифференциальное уравнение вида
[cbm]\frac{dy}{dx}=f\!\left(\frac{ax+by+c}{a_1x+b_1y+c_1}\right).[/cbm](3)
где [cbm]a,b,c,a_1,b_1,c_1[/cbm] — постоянные, а [cbm]f(u)[/cbm] — непрерывная функция своего аргумента [cbm]u[/cbm] .
Если [cbm]c=c_1=0[/cbm] , то уравнение (3) является однородным и оно интегрируется, как указано выше.
Если хотя бы одно из чисел [cbm]c,c_1[/cbm] отлично от нуля, то следует различать два случая.
1) Определитель [cbm]\Delta=\begin{vmatrix}a&b\\a_1&b_1\end{vmatrix}\ne0[/cbm] . Вводя новые переменные [cbm]\xi[/cbm] и [cbm]\eta[/cbm] по формулам [cbm]x=\xi+h,~y=\eta+k[/cbm] , где [cbm]h[/cbm] и [cbm]k[/cbm] — пока неопределенные постоянные, приведем уравнение (3) к виду
[cbm]\frac{d\eta}{d\xi}=f\!\left(\frac{a\xi+b\eta+ah+bk+c}{a_1\xi+b_2\eta+a_1h+b_1k+c_1}\right).[/cbm]
Выбирая [cbm]h[/cbm] и [cbm]k[/cbm] как решение системы линейных уравнений
[cbm]\begin{cases}ah+bk+c=0,\\a_1h+b_1k+c_1=0\end{cases}~(\Delta\ne0),[/cbm](4)
получаем однородное уравнение [cbm]\frac{d\eta}{d\xi}=f\!\left(\frac{a\xi+b\eta}{a_1\xi+b_1\eta}\right)[/cbm] . Найдя его общий интеграл и заменив в нем [cbm]\xi[/cbm] на [cbm]x-h[/cbm] , a [cbm]\eta[/cbm] на [cbm]y-k[/cbm] , получаем общий интеграл уравнения (3).
2) Определитель [cbm]\Delta=\begin{vmatrix}a&b\\a_1&b_1\end{vmatrix}=0[/cbm] . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае [cbm]\frac{a_1}{a}=\frac{b_1}{b}=\lambda[/cbm] , и, следовательно, уравнение (3) имеет вид [cbm]\frac{dy}{dx}=f\!\left(\frac{ax+by+c}{\lambda(ax+by)+c_1}\right)[/cbm] . Подстановка [cbm]z=ax+by[/cbm] приводит его к уравнению с разделяющимися переменными.
Пример 3. Решить уравнение [cbm](x+y-2)\,dx+(x-y+4)\,dy=0[/cbm] .
Решение. Рассмотрим систему линейных алгебраических уравнений [cbm]\begin{cases}x+y-2=0,\\x-y+4=0.\end{cases}[/cbm]
Определитель этой системы [cbm]\Delta=\begin{vmatrix}\hfill1&\hfill1\\\hfill1&\hfill-1\end{vmatrix}=-2\ne0[/cbm] .
Система имеет единственное решение [cbm]x_0=-1,~y_0=3[/cbm] . Делаем замену [cbm]x=\xi-1,~y=\eta+3[/cbm] . Тогда уравнение (5) примет вид
[cbm](\xi+\eta)\,d\xi+(\xi-\eta)\,d\eta=0.[/cbm]
Это уравнение является однородным уравнением. Полагая [cbm]\eta=u\xi[/cbm] , получаем
[cbm](\xi+\xi{u})\,d\xi+(\xi-\xi{u})(\xi\,du+u\,d\xi)=0[/cbm] , откуда [cbm](1+2u-u^2)\,d\xi+\xi(1-u)\,du=0[/cbm] .
Разделяем переменные [cbm]\frac{d\xi}{\xi}+\frac{1-u}{1+2u-u^2}\,du=0.[/cbm]
Интегрируя, найдем [cbm]\ln|\xi|+\frac{1}{2}\ln|1+2u-u^2|=\ln{C}[/cbm] или [cbm]\xi^2(1+2u-u^2)=C[/cbm] .
Возвращаемся к переменным [cbm]x,~y[/cbm] :
[cbm](x+1)^2\left[1+2\frac{y-3}{x+1}-\frac{(y-3)^2}{(x+1)^2}\right]=C_1[/cbm] или [cbm]x^2+2xy-y^2-4x+8y=C~~(C=C_1+14).[/cbm]
Пример 4. Решить уравнение [cbm](x+y+1)\,dx+(2x+2y-1)\,dy=0[/cbm] .
Решение. Система линейных алгебраических уравнений [cbm]\begin{cases}x+y+1=0,\\2x+2y-1=0\end{cases}[/cbm] несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку [cbm]x+y=z[/cbm] , [cbm]dy=dz-dx[/cbm] . Уравнение примет вид
[cbm](2-z)\,dx+(2z-1)\,dz=0.[/cbm]
Разделяя переменные, получаем
[cbm]dx-\frac{2z-1}{z-2}\,dz=0[/cbm] отсюда [cbm]x-2z-3\ln|z-2|=C.[/cbm]
Возвращаясь к переменным [cbm]x,~y[/cbm] , получаем общий интеграл данного уравнения
[cbm]x+2y+3\ln|x+y-2|=C.[/cbm]
Б. Иногда уравнение можно привести к однородному заменой переменного [cbm]y=z^\alpha[/cbm] . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному [cbm]x[/cbm] приписать измерение 1, переменному [cbm]y[/cbm] — измерение [cbm]\alpha[/cbm] и производной [cbm]\frac{dy}{dx}[/cbm] — измерение [cbm]\alpha-1[/cbm] .
Пример 5. Решить уравнение [cbm](x^2y^2-1)\,dy+2xy^3\,dx=0[/cbm] .
Решение. Делаем подстановку [cbm]y=z^\alpha,~dy=\alpha{z^{\alpha-1}}\,dz[/cbm] , где [cbm]\alpha[/cbm] пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для [cbm]y[/cbm] и [cbm]dy[/cbm] , получим
[cbm]\alpha(x^2x^{2\alpha}-1)z^{\alpha-1}\,dz+2xz^{3\alpha}\,dx=0[/cbm] или [cbm]\alpha(x^2z^{3\alpha-1}-z^{\alpha-1})\,dz+2xz^{3\alpha}\,dx=0,[/cbm]
Заметим, что [cbm]x^2z^{3\alpha-1}[/cbm] имеет измерение [cbm]2+3\alpha-1=3\alpha+1,[/cbm] [cbm]z^{\alpha-1}[/cbm] имеет измерение [cbm]\alpha-1[/cbm] , [cbm]xz^{3\alpha}[/cbm] имеет измерение [cbm]1+3\alpha[/cbm] . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие [cbm]3\alpha+1=\alpha-1[/cbm] , или [cbm]\alpha-1[/cbm] .
Положим [cbm]y=\frac{1}{z}[/cbm] ; исходное уравнение принимает вид
[cbm]\left(\frac{1}{z^2}-\frac{x^2}{z^4}\right)dz+\frac{2x}{z^3}\,dx=0[/cbm] или [cbm](z^2-x^2)\,dz+2xz\,dx=0.[/cbm]
Положим теперь [cbm]z=ux,~dz=u\,dx+x\,du[/cbm] . Тогда это уравнение примет вид [cbm](u^2-1)(u\,dx+x\,du)+2u\,dx=0[/cbm] , откуда [cbm]u(u^2+1)\,dx+x(u^2-1)\,du=0[/cbm] .
Разделяем переменные в этом уравнении [cbm]\frac{dx}{x}+\frac{u^2-1}{u^3+u}\,du=0[/cbm] . Интегрируя, найдем
[cbm]\ln|x|+\ln(u^2+1)-\ln|u|=\ln{C}[/cbm] или [cbm]\frac{x(u^2+1)}{u}=C.[/cbm]
Заменяя [cbm]u[/cbm] через [cbm]\frac{1}{xy}[/cbm] , получаем общий интеграл данного уравнения [cbm]1+x^2y^2=Cy.[/cbm]
Уравнение имеет еще очевидное решение [cbm]y=0[/cbm] , которое получается из общего интеграла при [cbm]C\to\infty[/cbm] , если интеграл записать в виде [cbm]y=\frac{1+x^2y^2}{C}[/cbm] , а затем перейти к пределу при [cbm]C\to\infty[/cbm] . Таким образом, функция [cbm]y=0[/cbm] является частным решением исходного уравнения.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
calcsbox.com
Однородные дифференциальные уравнения первого порядка
Легко можно убедиться в том, что дифференциальные уравнения
не являются уравнениями с разделяющимися переменными. Они являются однородными уравнениями.
Определение. Дифференциальное уравнение
называетсяоднородным
дифференциальным уравнением первого
порядка, если  – однородная функция нулевого измерения.
– однородная функция нулевого измерения.
Дадим понятие однородной функции нулевого измерения.
Определение. Функция 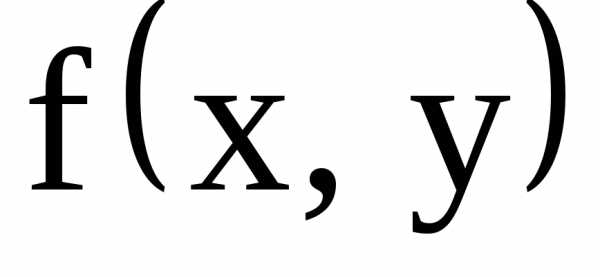 называетсяоднородной
функцией нулевого измерения, если при любом t
справедливо тождество
называетсяоднородной
функцией нулевого измерения, если при любом t
справедливо тождество
Так, функции  – однородные функции нулевого измерения,
т. к.
– однородные функции нулевого измерения,
т. к.
Чтобы проверить, является ли д. у.1 однородным уравнением, нужно в этом уравнении заменить Если после этогоt всюду сократится и получится первоначальное уравнение, то данное уравнение – однородное.
Поэтому уравнение является однородным. Действительно,
сократив уравнение на t, получим исходное уравнение.
Решение однородного дифференциального уравнения первого порядка
Так как функция  в правой части уравненияявляется однородной функцией нулевого
измерения, то, по определению,Положим в этом тождестве
в правой части уравненияявляется однородной функцией нулевого
измерения, то, по определению,Положим в этом тождестве получим
получим  т. е. однородная функция нулевого
измерения зависит только от отношения у/х. Д.у.1 в этом случае примет вид
т. е. однородная функция нулевого
измерения зависит только от отношения у/х. Д.у.1 в этом случае примет вид

Сделаем подстановку y/x=u, т. е.
где неизвестная функция.
Тогда
Уравнение  примет видилиили
примет видилиили – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.

Интегрируя, находим
Найдя отсюда выражение u как функции от x, подставим его в равенство получим искомое общее решение однородного д.у.1. Чаще всего не уда-
ется найти явное
выражение функции  Тогда после интегрирования следует
Тогда после интегрирования следует
в левую часть
вместо u
подставить  В результате получим общий интеграл
(т. е. общее решение в неявном виде).
В результате получим общий интеграл
(т. е. общее решение в неявном виде).
Решим уравнения.
Пример 1. Найти общее решение дифференциального уравнения
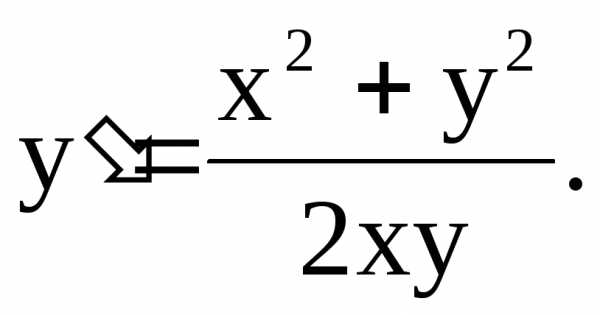
Решаем уравнение
подстановкой Подставив  в данное уравнение, получим
в данное уравнение, получим
или 
Получили
дифференциальное уравнение с разделяющимися
переменными относительно вспомогательной
функции  Упростим правую часть:
Упростим правую часть:
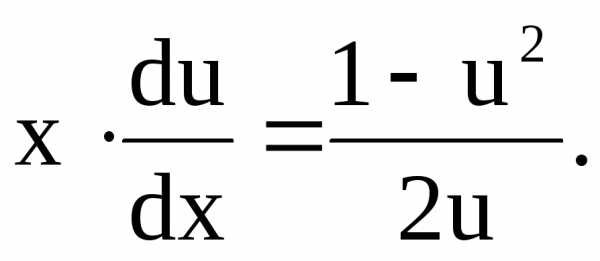 Умножив на
Умножив на  ,
получим уравнение с разделенными
переменными
,
получим уравнение с разделенными
переменными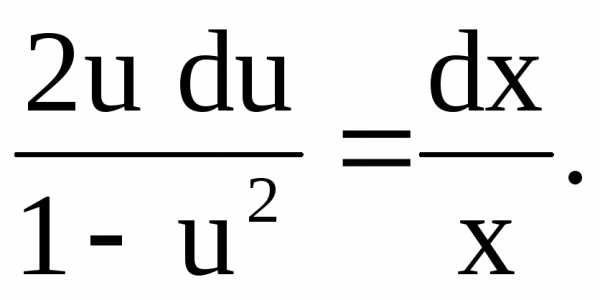
Интегрируя, получим
или
или 
Потенцируем
Подставив 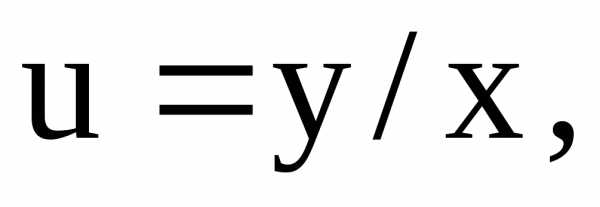 получим общий интеграл данного
дифференциального уравнения.
получим общий интеграл данного
дифференциального уравнения.
Проверка: 
или – искомое уравнение.
Пример 2. Найти частное решение дифференциального уравнения
при начальных
условиях 
Убедимся, что
данное дифференциальное уравнение
является однородным. Подставим в
уравнение вместо  соответственно
Получим
соответственно
Получим
Разделив на t обе части уравнения, получим данное уравнение. Решаем уравнение подстановкой
Поставим  в уравнение, получим
в уравнение, получим
Сгруппируем слагаемые с .
–это уравнение с разделяющимися переменными. Разделив обе части на получим
–уравнение с разделенными переменными. Интегрируя левую и правую части уравнения, получим
Подставив 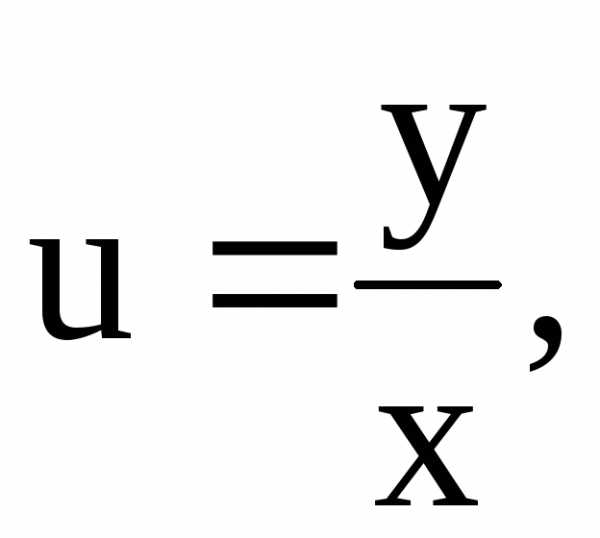 получим общий интеграл данного
дифференциального уравнения:
получим общий интеграл данного
дифференциального уравнения:
Найдем частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям
Подставим в формулу общего интеграла
отсюда  и частный интеграл
и частный интеграл

studfiles.net
Приводящиеся к однородным дифференциальные уравнения первого порядка
К однородным уравнениям первого порядка приводится уравнение вида:
(1) ,
где f – функция.
Как определить, что дифференциальное уравнение приводится к однородному
Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:
a1x + b1y + c1, a2x + b2y + c2,
и выполнить замену:
a1x + b1y + c1 → t (a1x + b1y + c1);
a2x + b2y + c2 → t (a2x + b2y + c2).
Если, после преобразований, t сократится, то это уравнение приводится к однородному.
Пример
Определить, приводится ли данное дифференциальное уравнение к однородному:
.
Решение
Выделяем две линейные формы:
x + 2y + 1 и x + 4y + 3.
Первую заменим на t (x + 2y + 1), вторую – на t (x + 4y + 3):
.
По свойству логарифма:
.
t сокращается:
.
Следовательно, это уравнение приводится к однородному.
Решение дифференциального уравнения, приводящегося к однородному уравнению
Решаем систему уравнений:
(2)
Здесь возможны три случая.
1) Система (2) имеет бесконечное множество решений (прямые a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0 совпадают). В этом случае
;
.
Тогда
.
Это простейший вид уравнения с разделяющимися переменными:
.
Его решение:
y = Ax + C .
2) Система (2) не имеет решений (прямые a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0 параллельны). В этом случае a1b2 = a2b1.
Применим это соотношение.
.
Это означает, что a2x + b2y + c2 является функцией от a1x + b1y + c1. Поэтому является функцией от a1x + b1y + c1. То есть f является функцией от a1x + b1y + c1. Обозначим такую функциею как g. Тогда исходное уравнение (1) имеет вид:
.
Это уравнение приводится к уравнению с разделяющимися переменными подстановкой
z = a1x + b1y + c1.
3) Система (2) имеет одно решение (прямые a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0 пересекаются в одной точке). Обозначим это решение как x0, y0. Тогда
(3)
Делаем подстановку x = t + x0, y = u + y0, где u – это функция от t. Тогда
dx = dt, dy = du;
.
Или
.
Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой u = z t, где z – это функция от t.
Пример решения дифференциального уравнения, приводящегося к однородному уравнению первого порядка
Решить уравнение
(П.1) .
Решение
1) Проверим, приводится ли это дифференциальное уравнение к однородному. Для этого выделяем две линейные формы:
2x – y + 4 и x – 2y + 5.
Первую заменим на t (2x – y + 4), вторую – на t (x – 2y + 5):
.
Делим на t:
.
t сократилось, поэтому это уравнение приводится к однородному.
2) Решаем систему
Из первого уравнения y = 2x + 4. Подставляем во второе:
x – 2(2x + 4) + 5 = 0;
x – 4x – 8 + 5 = 0;
– 3x = 3;
x = –1;
y = 2x + 4 = 2·(–1) + 4 = 2.
Итак, мы нашли решение системы:
x0 = –1, y0 = 2.
3) Делаем подстановку:
x = t + x0 = t – 1;
y = u + y0 = u + 2,
где u – функция от t. dx = dt, dy = du, ;
;
.
Подставляем в (П.1):
(П.2) .
Это – однородное уравнение.
4) Решаем однородное уравнение (П.2). Делаем подстановку:
u = z · t, где z – функция от t.
u′ = (z · t)′ = z′t + z t′ = z′t + z.
Подставляем в (П.2):
.
Сокращаем на t и выполняем преобразования:
;
;
.
Разделяем переменные – умножаем на dt и делим на t (z2 – 1). При z2 ≠ 1 получаем:
.
Интегрируем:
(П.3) .
Вычисляем интегралы:
;
.
Подставляем в (П.3):
.
Умножим на 2 и потенцируем:
;
.
Заменим постоянную e2C → C. Раскроем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C. Умножим на (z + 1)2 и применим формулу: z2 – 1 = (z – 1)(z + 1).
.
Сократим на (z – 1):
.
Возвращаемся к переменным u и t, используя формулу: u = z t. Для этого умножим на t:
;
;
.
Возвращаемся к переменным x и y, используя формулы: t = x + 1, u = y – 2.
;
(П.4) .
Теперь рассмотрим случай z2 = 1 или z = ±1.
;
.
Для верхнего знака «+» имеем:
;
.
Это решение входит в общий интеграл (П.4) при значении постоянной C = 0.
Для нижнего знака «–»:
;
.
Эта зависимость также является решением исходного дифференциального уравнения, но не входит в общий интеграл (П.4). Поэтому к общему интегралу добавим решение
.
Ответ
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Обобщенные однородные дифференциальные уравнения первого порядка
Обобщенное однородное дифференциальное уравнение первого порядка это уравнение вида:
, где α ≠ 0, α ≠ 1, f – функция.
Как определить, является ли дифференциальное уравнение обобщенным однородным
Для того, чтобы определить, является ли дифференциальное уравнение обобщенным однородным, нужно ввести постоянную t и сделать замену:
y → t α· y, x → t·x.
Если удастся выбрать такое значение α, при котором постоянная t сократится, то это – обобщенное однородное дифференциальное уравнение. Изменение производной y′ при такой замене имеет вид:
.
Пример
Определить, является ли данное уравнение обобщенным однородным:
.
Решение
Делаем замену y → t α· y, x → t·x, y′ → t α–1 y′:
;
.
Разделим на t α+5:
;
.
Уравнение не будет содержать t, если
4α – 6 = 0, α = 3/2.
Поскольку при α = 3/2, t сократилось, то это обобщенное однородное уравнение.
Решение обобщенного однородного дифференциального уравнения
Рассмотрим обобщенное однородное дифференциальное уравнение первого порядка:
(1) .
Покажем, что оно приводится к однородному уравнению с помощью подстановки:
t = x α.
Действительно,
.
Отсюда
; .
Подставляем в исходное уравнение (1):
;
.
Это – однородное уравнение. Оно решается подстановкой:
y = z · t,
где z – функция от t.
При решении задач, проще сразу применять подстановку:
y = z x α,
где z – функция от x.
Пример решения обобщенного однородного дифференциального уравнения первого порядка
Решить дифференциальное уравнение
(П.1) .
Решение
Проверим, является ли данное уравнение обобщенным однородным. Для этого в (П.1) делаем замену:
y → t α· y, x → t·x, y′ → t α–1 y′.
.
Разделим на t α:
.
t сократится, если положить α = –1. Значит – это обобщенное однородное уравнение.
Делаем подстановку:
y = z x α = z x –1,
где z – функция от x.
.
Подставляем в исходное уравнение (П.1):
(П.1) ;
;
.
Умножим на x и раскрываем скобки:
;
;
.
Разделяем переменные – умножим на dx и разделим на x z 2. При z ≠ 0 имеем:
.
Интегрируем, пользуясь таблицей интегралов:
;
;
;
.
Потенцируем:
.
Заменим постоянную e C → C и уберем знак модуля, поскольку выбор нужного знака определяется выбором знака постоянной С:
.
Возвращаемся к переменной y. Подставляем z = xy:
.
Делим на x:
(П.2) .
Когда мы делили на z2, мы предполагали, что z ≠ 0. Теперь рассмотрим решение z = xy = 0, или y = 0.
Поскольку при y = 0, левая часть выражения (П.2) не определена, то к полученному общему интегралу, добавим решение y = 0.
Ответ
;
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
3. Однородные дифференциальные уравнения первого порядка
Понятие однородного дифференциального уравнения первого порядка связано с однородными функциями.
Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
. | (3.1) |
Например, функция – однородная функция первого измерения, так как
;
– однородная функция третьего измерения , так как
;
 – однородная функция нулевого измерения,
так как
– однородная функция нулевого измерения,
так как
, т.е..
Определение 2.Дифференциальное уравнение первого порядкаy‘ = f(x,y) называется однородным, если функцияf(x,y) есть однородная функция нулевого измерения относительноx иy, или, как говорят,f(x,y) – однородная функция степени нуль.
Его можно представить в виде
P (x, y) dx + Q (x, y) dy = 0, | (3.2) |
где P(x,y) иQ(x,y) – однородные функции одинакового измерения: отношение двух однородных функций одного и того же измерения является однородной функцией нулевого измерения (см. третий из приведенных выше примеров).
Возможна следующая форма записи уравнения (3.2):
| (3.3) |
что позволяет определить однородное уравнение как такое дифференциальное, которое можно преобразовать к виду (3.3).
Замена  приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим
приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим ,
,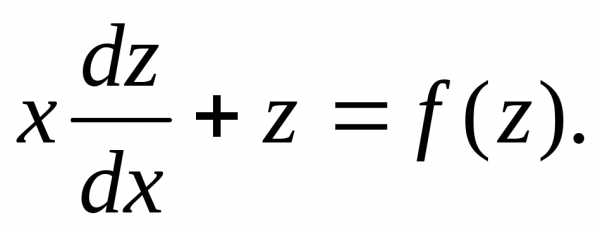 Разделяя переменные и интегрируя,
найдем:
Разделяя переменные и интегрируя,
найдем:
 ,
,

Пример 1.Решить уравнение .
Δ Полагаем у = zx,  Подставляем
эти выраженияy иdyв данное уравнение:
Подставляем
эти выраженияy иdyв данное уравнение: или
или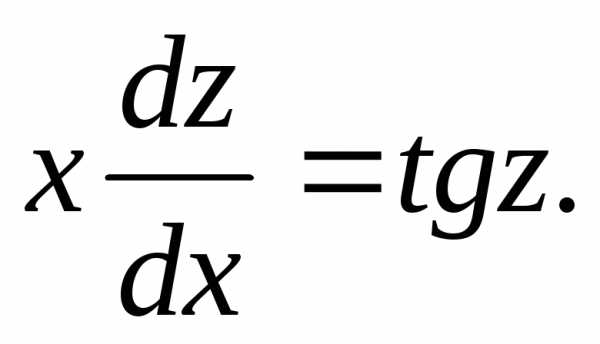 Разделяем переменные:
Разделяем переменные: и интегрируем:
и интегрируем: ,
,
Заменяя zна ,
получим
,
получим .
.
Пример 2. Найти общее решение уравнения.
Δ В данном уравнении P (x,y)
=x2-2y2,Q(x,y)
=2xy– однородные
функции второго измерения, следовательно,
данное уравнение является однородным.
Его можно представить в виде и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx + xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx + xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
,
то есть

или
dx+2zxdz = 0.
Разделяем переменные, считая 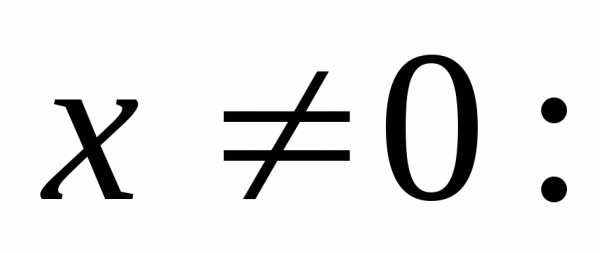
 .
.
Интегрируем почленно это уравнение
 ,
откуда
,
откуда
то есть  .
Возвращаясь к прежней функции
.
Возвращаясь к прежней функции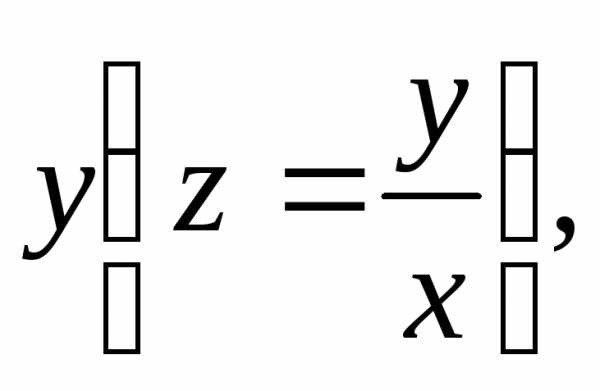 находим общее решение
находим общее решение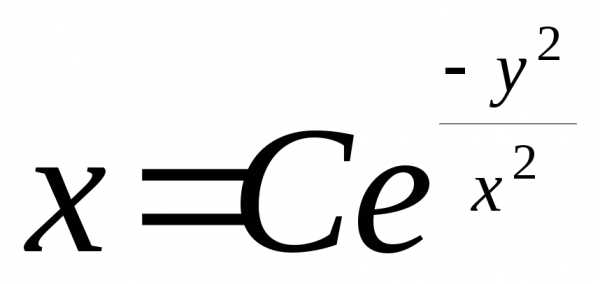
Пример 3. Найти общее
решение уравнения .
.
Δ
Цепочка преобразований:  ,y = zx,,
,y = zx,,  ,
,  ,
,  ,
, 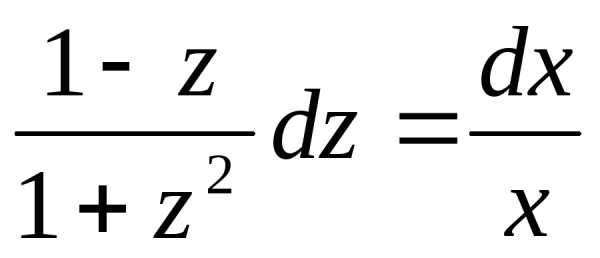 ,
,
, , , .
,
,
, , , .
Лекция 8.
4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
, | (4.1) |
где  ,
, ,c(x) –
непрерывные функции.
,c(x) –
непрерывные функции.
Если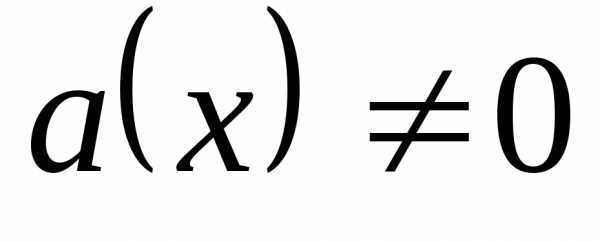 ,
то уравнение (4.1) можно записать в
приведённом виде
,
то уравнение (4.1) можно записать в
приведённом виде
(4.1a) |
Здесь – свободный член, называемый также правой частью уравнения. В этом виде будем рассматривать линейное уравнение в дальнейшем.
Если  0,
то уравнение (4.1а) называется линейным
неоднородным. Если же
0,
то уравнение (4.1а) называется линейным
неоднородным. Если же 0, то уравнение принимает вид
0, то уравнение принимает вид
(4.2) |
и называется линейным однородным.
Название уравнения (4.1а) объясняется
тем, что неизвестная функция y и её производная входят в него линейно, т.е. в первой
степени.
входят в него линейно, т.е. в первой
степени.
В линейном однородном уравнении
переменные разделяются. Переписав его
в виде  откуда
откуда и интегрируя, получаем:,т.е.
и интегрируя, получаем:,т.е.
| (4.3) |
При делении на  теряем решение
теряем решение .
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
.
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
Существует несколько методов решения уравнения (4.1а). Согласно методу Бернулли, решение ищется в виде произведения двух функций отх:
(4.4) |
Одна из этих функций может быть выбрана произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, другая определяется на основании уравнения (4.1а).
Дифференцируя обе части равенства (4.4), находим .
Подставляя полученное выражение
производной  ,
а также значениеу в уравнение (4.1а), получаем,
или
,
а также значениеу в уравнение (4.1а), получаем,
или
. | (4.5) |
Так как одну из неизвестных функций можем выбрать произвольно, выберем функцию u так, чтобы
| (4.6) |
т.е. в качестве функции vвозьмём решение однородного линейного уравнения (4.6):
. | (4.3а) |
Ввиду произвольности в выборе v,мы можем не учитывать произвольную постояннуюС (точнее – можем приравнять её нулю). Подставляя найденное значениеv(x) в уравнение (4.5), получим, учитывая (4.6):
| (4.7) |
откуда
(4.8) |
(Здесь Cписать обязательно, иначе получится не общее, а частное решение).
Таким образом, видим, что в результате используемой подстановки (4.4) уравнение (4.1а) сводится к двум уравнениям с разделяющимися переменными (4.6) и (4.7).
Подставляя  иv(x) в
формулу (4.4), окончательно получаем
иv(x) в
формулу (4.4), окончательно получаем
,
или
. | (4.9) |
Пример 1.Найти общее решение
уравнения
Положим  ,
тогда
,
тогда .
Подставляя выражения
.
Подставляя выражения и
и в
исходное уравнение, получимили(*)
в
исходное уравнение, получимили(*)
Приравняем нулю коэффициент при  :
: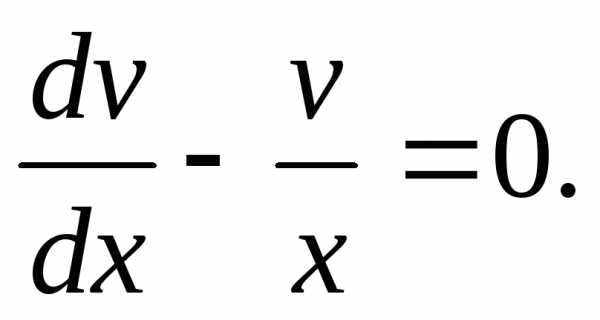
Разделяя переменные в полученном
уравнении, имеем 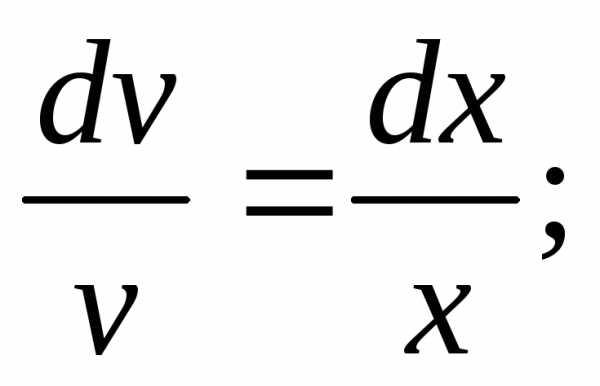

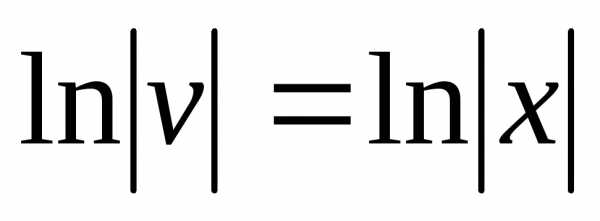 (произвольную постояннуюC не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
(произвольную постояннуюC не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
 ,,
,,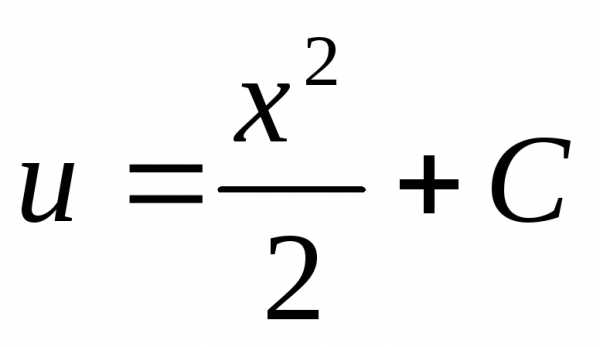 .
.
Следовательно,  общее
решение исходного уравнения.
общее
решение исходного уравнения.
Отметим, что уравнение (*) можно было записать в эквивалентном виде:
.
Произвольно выбирая функцию u,
а неv, мы могли полагать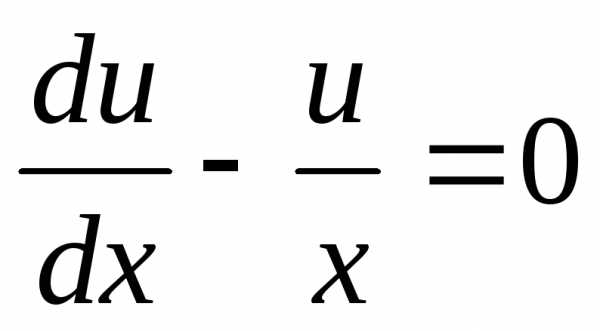 .
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
.
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
На основании изложенного выше получаем алгоритм решения линейного дифференциального уравнения первого порядка.
Приводим рассматриваемое уравнение к виду.
Используя подстановку
 ,
находими
подставляем эти выражения в уравнение.
,
находими
подставляем эти выражения в уравнение.Группируем члены уравнения, выносим одну из функций uилиvза скобки. Находим вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.
Подставляем найденную функцию в оставшееся выражение и находим вторую функцию.
Записываем общее решение, подставив выражения для найденных функций u иvв равенство
 .
.Если требуется найти частное решение, то определяем Сиз начальных условий и подставляем в общее решение.
Отметим далее, что иногда уравнение первого порядка становится линейным, если усчитать независимой переменной, аx– зависимой, т.е. поменять ролиx иy. Это можно сделать при условии, чтоxиdxвходят в уравнение линейно.
Пример 2. Решить уравнение .
Однако если рассматривать xкак функцию оту, то, учитывая, что ,его
можно привести к виду
,его
можно привести к виду
| (4.1 б) |
Заменив  на
на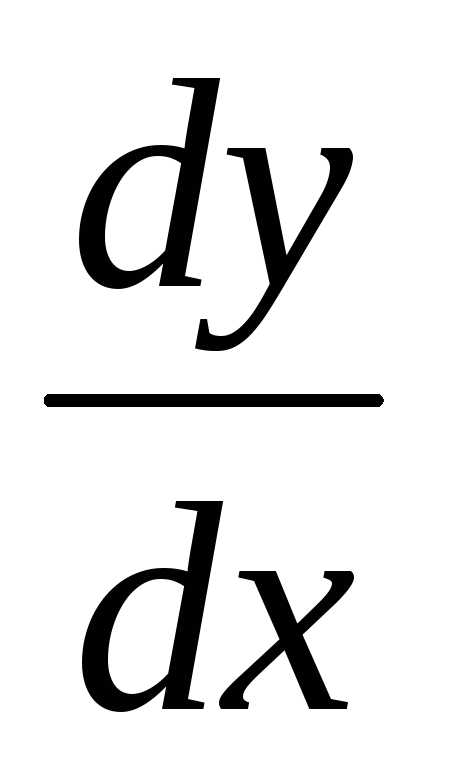 ,получим
,получим или.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
или.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
 , или
, или .
(**)
.
(**)
Здесь P(y)= ,
, .
Это линейное уравнение относительноx. Полагаем,.
Подставляя эти выражения в (**), получаем
.
Это линейное уравнение относительноx. Полагаем,.
Подставляя эти выражения в (**), получаем
или.
Выберем vтак, чтобы ,
, ,
откуда
,
откуда ;
; .
Далее имеем
.
Далее имеем ,
, ,
, .
.
Т.к. , то приходим к общему решению данного уравнения в виде
 .
.
Отметим, что в уравнение (4.1а) P(x) иQ (x) могут входить не только в виде функций от x, но и констант:P=a,Q=b. Линейное уравнение
(4.10) |
можно решать и с помощью подстановки y=uv и разделением переменных:
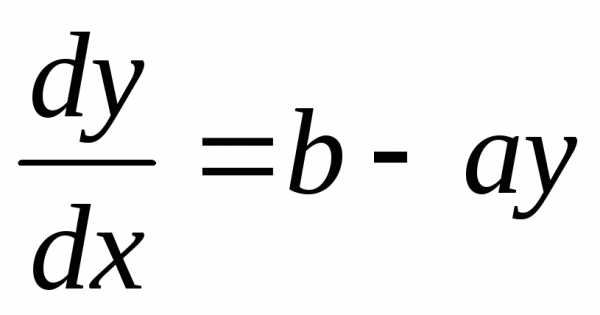 ;
; .
.
Отсюда  ;;;
где
;;;
где .
Освобождаясь от логарифма, получаем
общее решение уравнения
.
Освобождаясь от логарифма, получаем
общее решение уравнения
 (здесь
(здесь ).
).
При b=0 приходим к решению уравнения
| (4.10а) |
в виде
| (4.11) |
(см. уравнение показательного роста
(2.4) при  ).
).
Применим далее для интегрирования неоднородного линейного уравнения (4.1а) метод вариации произвольной постоянной (метод Лагранжа).
Сначала интегрируем соответствующее однородное уравнение (4.2). Как указано выше, его решение имеет вид (4.3). Будем считать сомножитель Св (4.3) функцией отх, т.е. по существу делаем замену переменной
, | (4.3а) |
где C(x)-новая
неизвестная функцияx.
Подставляя производнуюв исходное неоднородное уравнение
(4.1а), получим: ,
или
,
или
, | (4.12) |
откуда, интегрируя, находим
dx+C1, | (4.13) |
где С1-постоянная. Следовательно,
. | (4.14) |
Отметим, что согласно (4.14) (см. также (4.9)), общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения (4.3) и частного решения неоднородного уравнения, определяемого вторым слагаемым, входящим в (4.14) (и в (4.9)).
При решении конкретных уравнений следует повторять приведённые выше выкладки, а не использовать громоздкую формулу (4.14).
Применим метод Лагранжа к уравнению, рассмотренному в примере 1:
 .
.
Интегрируем соответствующее однородное
уравнение  .
.
Разделяя переменные, получаем  и далее.
Решение выражения формулойy = Cx. Решение исходного
уравнения ищем в видеy = C(x)x.
Подставив это выражение в заданное
уравнение, получим;
и далее.
Решение выражения формулойy = Cx. Решение исходного
уравнения ищем в видеy = C(x)x.
Подставив это выражение в заданное
уравнение, получим; ;,
;, .
Общее решение исходного уравнения имеет
вид
.
Общее решение исходного уравнения имеет
вид
.
В заключение отметим, что к линейному уравнению приводится уравнение Бернулли
,
( | (4.15) |
которое можно записать в виде
. | (4.15а) |
Заменой  оно приводится к линейному уравнению:
оно приводится к линейному уравнению:
 ,
,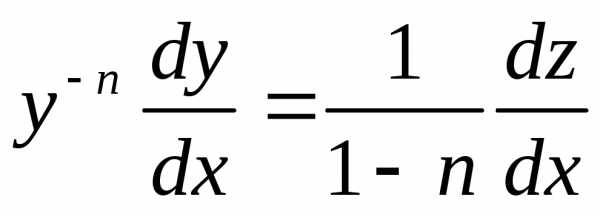 ,.
,.
Уравнения Бернулли также решаются изложенными выше методами.
Пример 3. Найти общее решения уравнения.
Цепочка преобразований:  ,,,,
,,,,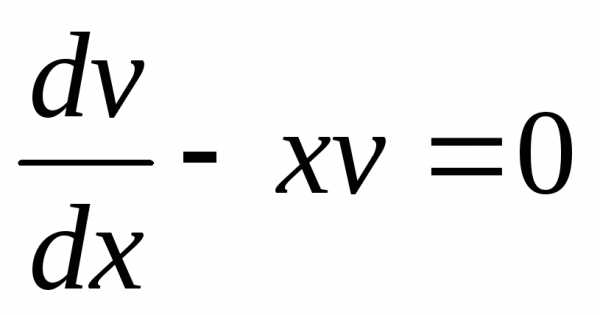 ,
, ,
,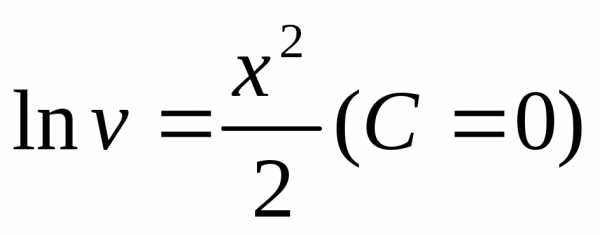 ,
,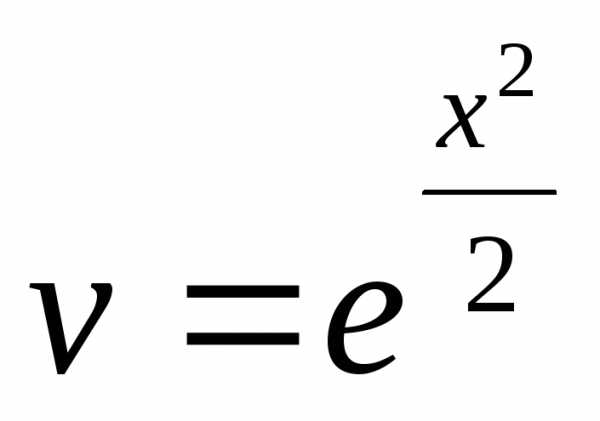 ,
,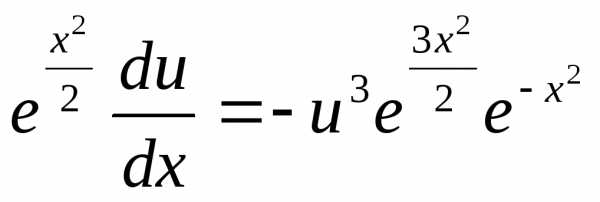 ,
, ,
, ,
, ,
,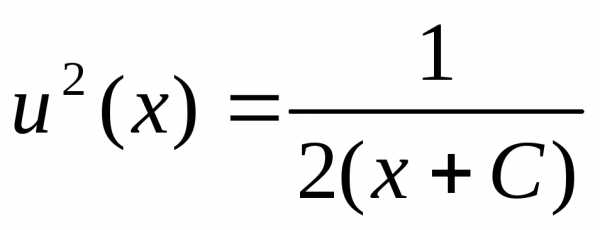 ,,
,,
studfiles.net
Однородные дифференциальные уравнения [wiki.eduVdom.com]
Функция f(x,y) называется однородной функцией своих аргументов измерения n, если справедливо тождество
$$ f(tx,ty)=t^{n}f(x,y) $$
При n=0 имеем функцию нулевого измерения.
Дифференциальное уравнение вида ${y}’=\frac{dy}{dx}=f(x,y)$ называется однородным относительно x и y, если f(x,y) есть однородная функция своих аргументов нулевого измерения.
Однородное уравнение всегда можно представить в виде $\frac{dy}{dx}=\varphi\left (\frac{y}{x} \right )$
Вводим новую переменную $u=\frac{y}{x}$ , тогда $y=u\cdot x \;;\; \frac{dy}{dx}=\frac{du}{dx}\cdot x+u\cdot 1$
В результате, получаем уравнение с разделяющимися переменными $$ x\frac{du}{dx} = \varphi(u)-u $$
Пример 1
Найти общее решение дифференциального уравнения: ${xy}’=x+2y$
Решение дифференциального уравнения:
Пример 2. Решить уравнение (найти общее решение дифференциального уравнения) $$ {xy}’ = \sqrt{x^{2} – y^{2}} + y $$
Решение. Запишем уравнение в виде
$$ {y}’ = \sqrt{ 1 – \left ( \frac{y}{x} \right )^{2} } + \frac{y}{x} $$
так что данное уравнение оказывается однородным относительно x и y.
Положим $u=\frac{y}{x}$ или $y=u\cdot x$ , тогда ${y}’ = {xu}’ +u$ . Подставляя в уравнение выражение для $y$ и ${y}’$ , получаем $$ x\frac{du}{dx} = \sqrt{1-u^{2}} $$
Разделяем переменные: $$ \frac{du}{ \sqrt{1-u^{2}} } = \frac{dx}{x} ;\;\; \int \frac{du}{ \sqrt{1-u^{2}} } = \int \frac{dx}{x} \\ \arcsin{u} = \ln{|x|} + \ln{C_1} ;\;\; \arcsin{u} = \ln{C_{1}|x|} $$
, т.к. $C_{1}|x| = \pm C_{1}x$ , то, обозначая $\pm C_{1} = C$ , получаем $\arcsin{u} = \ln{Cx}$ Заменяя $u$ на $\frac{y}{x}$ , будем иметь общий интеграл $\arcsin{\frac{y}{x}} = \ln{Cx} ,\;\; y = x\sin{\ln{Cx}}$
Пример 3 $$(x^{2}+2xy)\;dx+xy\;dy=0$$
Решение:
wiki.eduvdom.com

 ,
,

 ,
,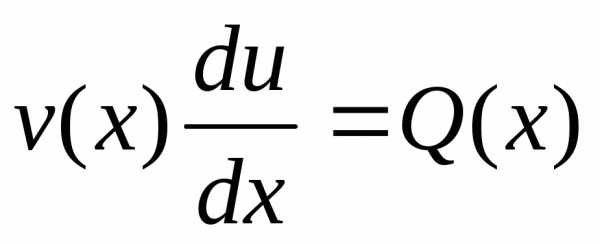 ,
,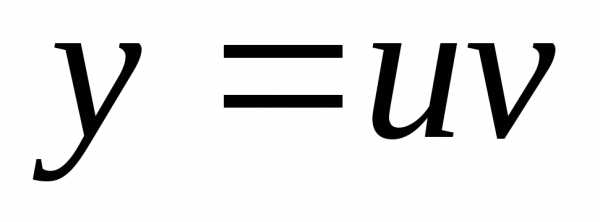 ,
находими
подставляем эти выражения в уравнение.
,
находими
подставляем эти выражения в уравнение.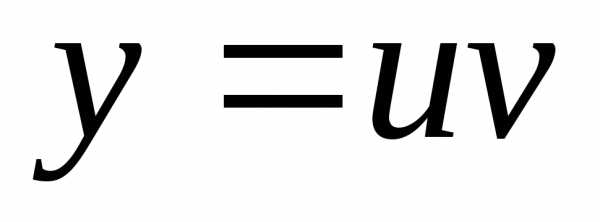 .
.

 )
)