Односторонние пределы
Пусть
Х – область определения функции,
которая, быть может, не содержит точку  ,
но для любого
,
но для любого правая полуокрестность точки
правая полуокрестность точки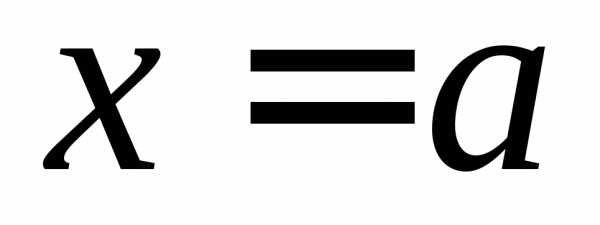 (интервал)
содержит точки множества Х.
(интервал)
содержит точки множества Х.
ОПРЕДЕЛЕНИЕ 7 (правый предел функции в точке 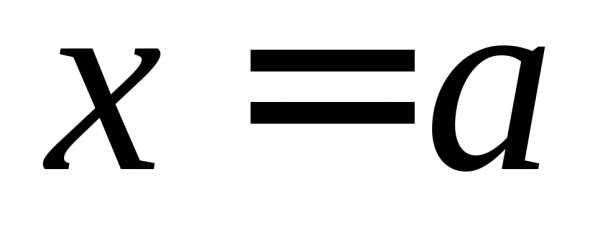 по Гейне). Число
по Гейне). Число называется правым пределом функции
называется правым пределом функции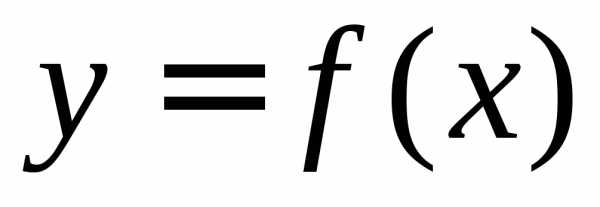 в точке
в точке ,
если для любой последовательности
значений ее аргумента
,
если для любой последовательности
значений ее аргумента
 и состоящей их чисел, больших
и состоящей их чисел, больших соответствующая последовательность
значений функций
соответствующая последовательность
значений функций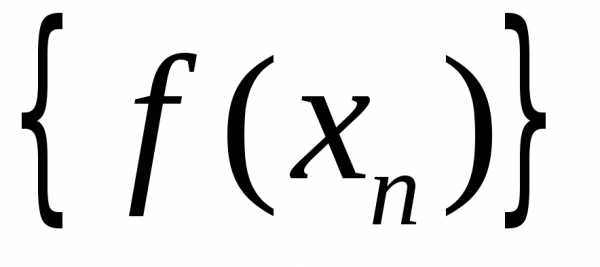 сходится к
сходится к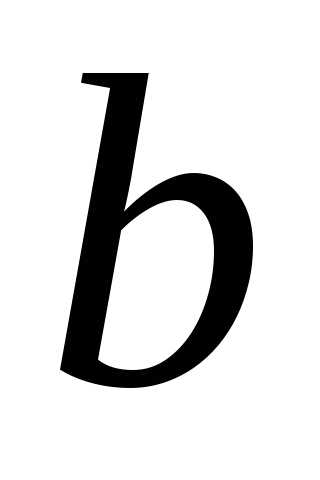 .
Обозначение:
.
Обозначение: ОПРЕДЕЛЕНИЕ 8 (правый предел функции в точке  по Коши). Число
по Коши). Число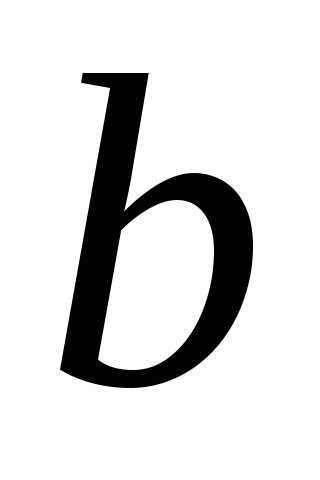 называется правым пределом функции
называется правым пределом функции
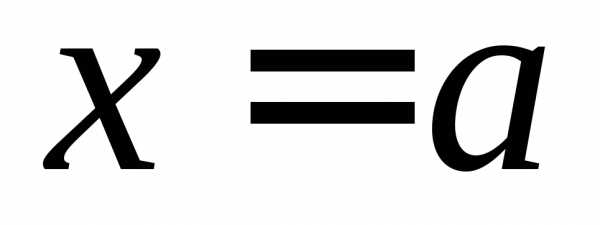 ,
если,
,
если, Для определения
левого предела будем считать, что любая
левая полуокрестность точки  ,
интервал,
содержит точки Х.
,
интервал,
содержит точки Х.
ОПРЕДЕЛЕНИЕ 9 (левый предел функции в точке  по Гейне). Число
по Гейне). Число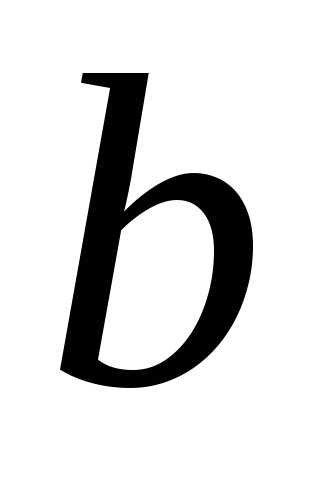 называется левым пределом функции
называется левым пределом функции
 ,
если для любой последовательности
значений ее аргумента
,
если для любой последовательности
значений ее аргумента ,
сходящейся к
,
сходящейся к и состоящей их чисел, меньших
и состоящей их чисел, меньших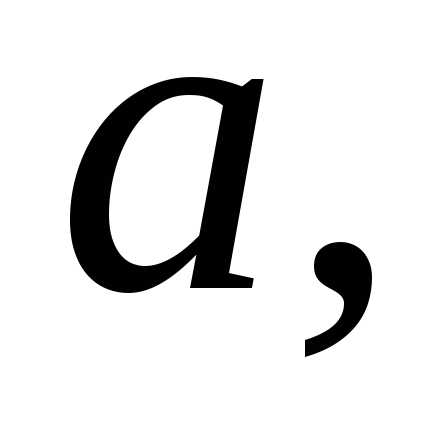 соответствующая последовательность
значений функций
соответствующая последовательность
значений функций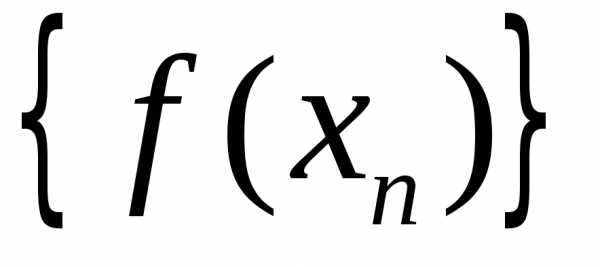 сходится к
сходится к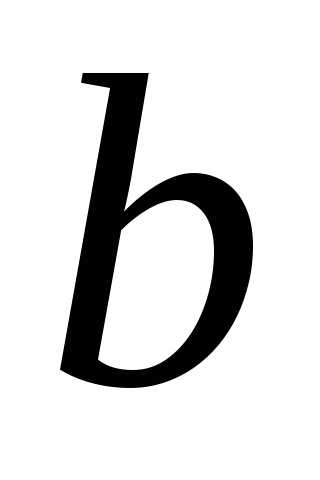 .
Обозначение:
.
Обозначение: ОПРЕДЕЛЕНИЕ 10 (левый предел функции в точке 
 называется левым пределом функции
называется левым пределом функции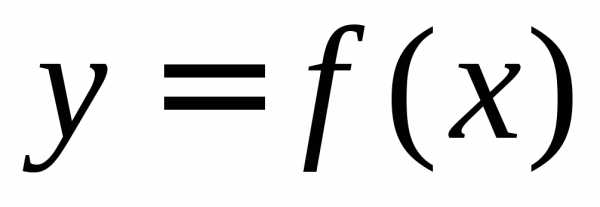 в
точке
в
точке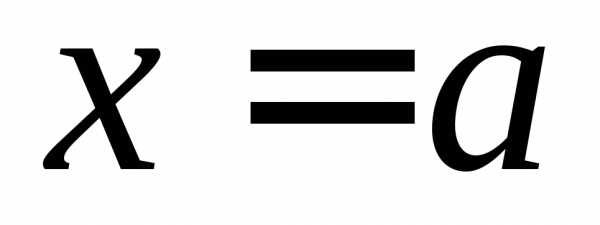 ,
если,
,
если,ПРИМЕР. Найти односторонние пределы (правый и левый) функции

в точках  и
и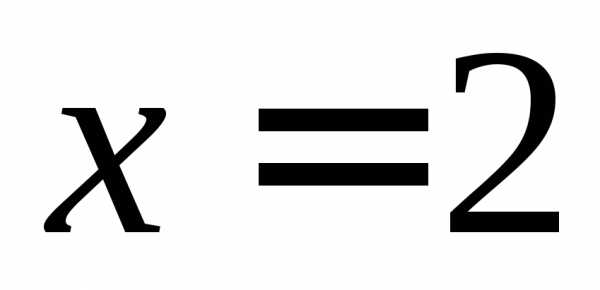
Так как справа от
0 и близко к нему  тоОчевидно,
тоОчевидно,
что хорошо видно на графике функции (рис. 5):
y 1 -1 О 2 4 x Рис. 5 |
Существуют
ли 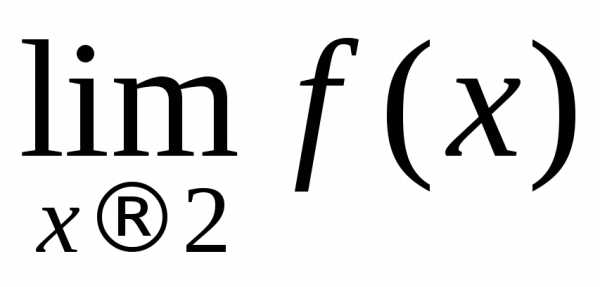 ? Не существуют, так как левый предел
не равен правому пределу в этих точках.
Имеет место утверждение: ? Не существуют, так как левый предел
не равен правому пределу в этих точках.
Имеет место утверждение: |
для того, чтобы функция имела в точке предел , необходимо и достаточно, чтобы в этой точке существовали равные односторонние пределы.
ПРИМЕР.
Найти односторонние пределы функции  в точке
в точке
ПРИМЕР.
Найти односторонние пределы функции 
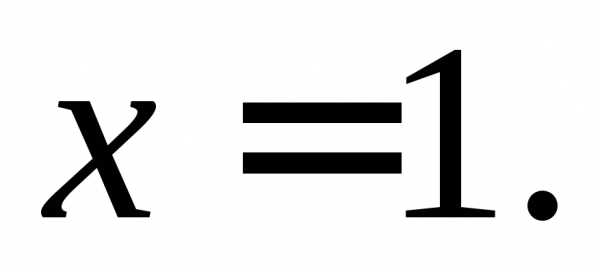
y 1 О 1 2 x Рис. 6 | Предел функции в этой точке существует, так как односторонние пределы равны (рис.6). |
Сравнение бесконечно малых
ОПРЕДЕЛЕНИЕ.
Функция  называетсябесконечно
малой (б.м.)
в точке
называетсябесконечно
малой (б.м.)
в точке  если
если
ПРИМЕРЫ.  – б.м. в точках
– б.м. в точках
 – б.м. в точках
– б.м. в точках – б.м. в точке
– б.м. в точке
 и
и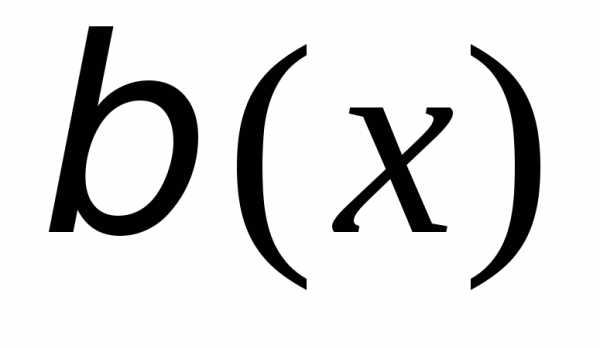 – б.м. в точке
– б.м. в точке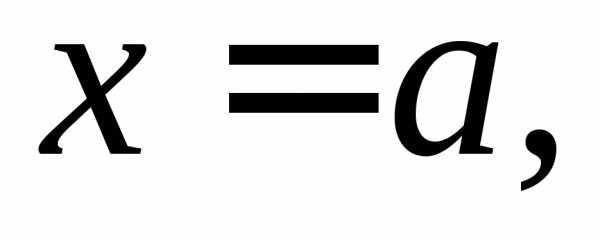 то естьПредел отношения б.м. функций
то естьПредел отношения б.м. функций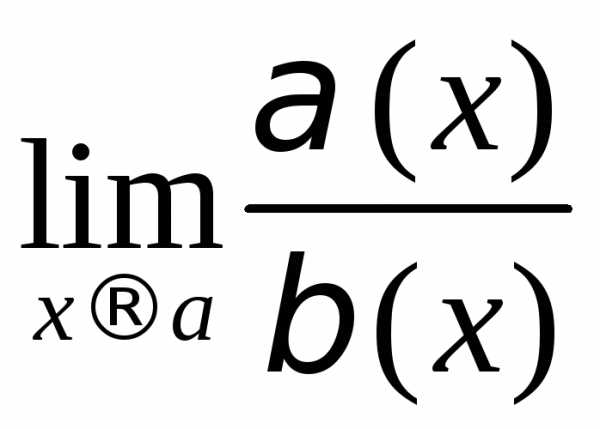 называетсянеопределенностью
вида
называетсянеопределенностью
вида 
ПРИМЕР.
– б.м. в точке

ОПРЕДЕЛЕНИЕ
 функция
функция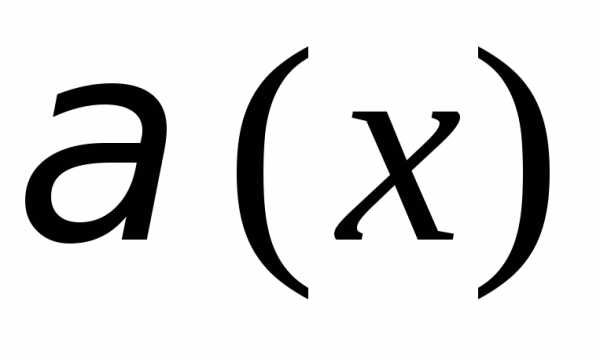 имеетболее
высокий порядок малости,
чем
имеетболее
высокий порядок малости,
чем 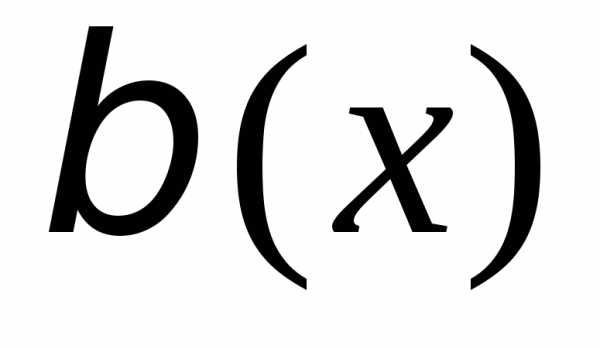 ,
если
,
если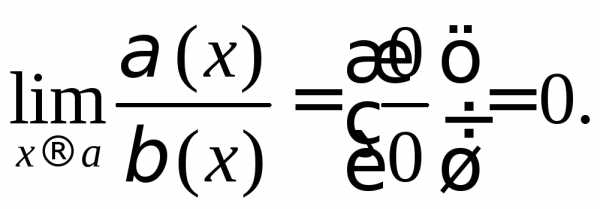
2) Б.м. в точке 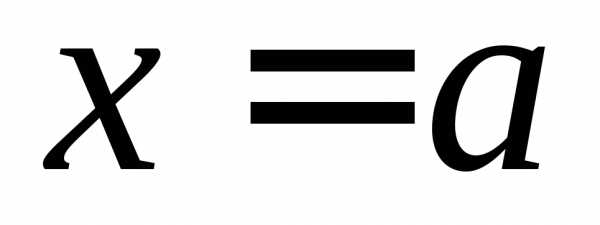 функции
функции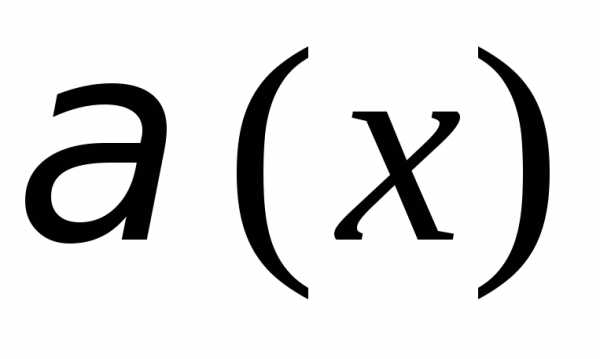 и
и одного порядка
малости,
если
одного порядка
малости,
если
3) Б.м. в точке 
 .
.
Эквивалентные б.м. обозначаются так:
ПРИМЕР.  имеет более высокий порядок малости в
точке
имеет более высокий порядок малости в
точке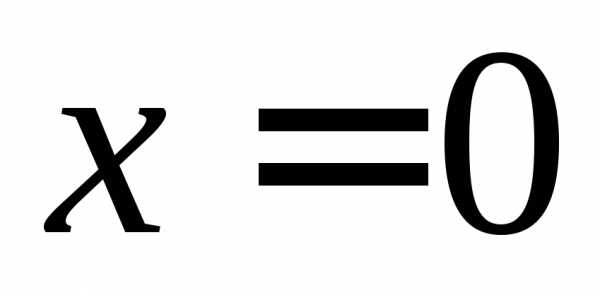 ,
чем
,
чем и
и
 и
одного порядка малости.
и
одного порядка малости.
ПРИМЕР.
Сравнить функции 

Вычислим предел отношения:
в точке 
ТЕОРЕМА (принцип замены эквивалентных бесконечно
малых). Пусть
б.м.
функции в точке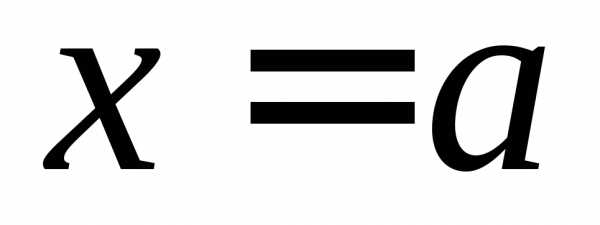 иТогда
иТогда
ДОКАЗАТЕЛЬСТВО. Так как то
Что и требовалось доказать.
studfiles.net
Односторонние пределы функций
Предел функции.
Определение 1(Гейне). Пусть функция определена на некотором интервале , кроме, быть может, точки . Число A называется пределом функции при , если для любой последовательности значений аргумента , сходящейся к и такой, что , соответствующая последовательность значений функции сходится к числу :
.
Тот факт, что есть предел функции при (в точке ), будем записывать следующим образом:
.
Из определения следует, что значения функции в точках , лежащих вне некоторой окрестности точки , и значение функции в точке не влияют ни на существование, ни на величину предела функции в точке .
Пример 1. Покажем, что функция имеет предельное значение в каждой точке бесконечной прямой. В самом деле, для любой сходящейся к последовательности значений аргумента соответствующая последовательность значений функции имеет вид , т.е. сходится к . Значит, предельное значение функции в любой точке равно .▲
Пример 2. Функция в каждой точке бесконечной прямой имеет предельное значение . Действительно, пусть – любая сходящаяся к последовательность значений аргумента. Соответствующая последовательность значений функции имеет вид , т.е. сходится к . Значит, предельное значение функции в любой точке равно .▲
Пример 3. Найти предел функции (рис.1) в точке .
Решение.  Будем рассматривать данную функцию в некоторой окрестности точки , например, на интервале . Функция определена всюду на указанном интервале, в том числе и в точке . Возьмем какую-нибудь последовательность значений аргумента , и рассмотрим соответствующую последовательность значений функции . На основании теорем о пределе последовательности имеем
Будем рассматривать данную функцию в некоторой окрестности точки , например, на интервале . Функция определена всюду на указанном интервале, в том числе и в точке . Возьмем какую-нибудь последовательность значений аргумента , и рассмотрим соответствующую последовательность значений функции . На основании теорем о пределе последовательности имеем
.
Ввиду произвольности выбранной последовательности согласно определению предела функции в точке .▲
Пример 4. Найти предел функции (рис.2) в точке .
Решение. В точке функция не определена. Будем рассматривать функцию в некоторой окрестности точки , например, на интервале . Возьмем какую-нибудь последовательность значений аргумента сходящуюся к точке : и рассмотрим соответствующую последовательность значений функции :
.
На основании теорем о пределах последовательностей имеем
.
Ввиду произвольности выбранной последовательности согласно определению предела функции в точке получаем .
Заметим, что функции и тождественны всюду, кроме точки , где функция не определена.▲
Для того чтобы доказать, что функция не имеет предела в точке , достаточно указать какую-нибудь сходящуюся к последовательность значений аргумента чтобы соответствующая последовательность значений функции не имела предела (или указать такие две сходящиеся к последовательности и , что и имеют разные пределы).
Пример 5. Пусть (рис.3). Выяснить, существует ли .
 Решение. Возьмем две последовательности значений аргумента и : и . Очевидно, , . В точках последовательности заданная функция принимает значение , а в точках последовательности – значение . Поэтому , , то есть . Значит, не существует. ▲
Решение. Возьмем две последовательности значений аргумента и : и . Очевидно, , . В точках последовательности заданная функция принимает значение , а в точках последовательности – значение . Поэтому , , то есть . Значит, не существует. ▲
Определение 2(Коши). Пусть функция определена на некотором интервале , кроме, быть может, точки . Число A называется пределом функции при , если для любого найдется такое , что для всех , удовлетворяющих неравенству , выполняется неравенство .
Это определение коротко можно записать с помощью кванторов:
.
Пример 6. Показать, что .
Решение. Зададим произвольное . Мы должны найти такое , чтобы из неравенства вытекало неравенство . Преобразуем последнее неравенство:
Решая это неравенство относительно , находим . Значит, в качестве можно взять (или любое меньшее число). В самом деле,
,
а это согласно определению и означает, что .▲
Пример 7. Самостоятельно показать, что .▲
Односторонние пределы функций.
Определение.Пусть функция определена на интервале . Число называется пределом слева функции в точке (при ), если для любого существует такое , что для всех , удовлетворяющих неравенству , выполняется неравенство . Предел слева обозначают .
Аналогично, в случае, когда функция определена на интервале , вводится понятие предела справа. Предел справа обозначают так:
.
Теорема. Функция имеет предел в точке тогда и только тогда, когда в этой точке существуют пределы слева и справа и они равны, то есть
= .
Пример 1. Покажем, что функция
имеет в точке и правое, и левое
предельные значения.
Решение. Действительно, пусть – любая сходящаяся к нулю последовательность значений аргумента, элементы которой . Соответствующая последовательность значений функции имеет вид , т. е. сходится к 1. Если элементы сходящейся к нулю последовательности отрицательны, то им соответствует последовательность значений функции , сходящаяся к -1. А это в силу определения и означает, что
Таким образом, функция имеет в точке и правое, и левое предельные значения, но они не совпадают: . Поэтому в точке не имеет предельного значения. ▲
Для функций, область определения которых – интервал или , вводится понятие предела при или при .
Определение.Число называют пределом функции при , если для любого существует такое , что для всех , удовлетворяющих неравенству , выполняется неравенство .
Этот предел обозначают .
Определение.Число называют пределом функции при , если для любого существует такое , что для всех , удовлетворяющих неравенству , выполняется неравенство .
Этот предел обозначают .
Для односторонних пределов справедливы теоремы о пределе суммы, разности, произведения, частного.
Пример 2.Записать на языке кванторов, дать геометрическую интерпретацию
1. при , 2. при ,
3. при , 4. при .
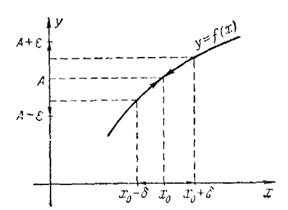
Решение. 1. а) Сначала запишем на языке « » утверждение: «предел функции равен 3 при стремлении аргумента к 1»:
.
Раскроем модули: ; .
б) По условию, аргумент стремится к точке 1 справа, оставаясь больше 1; при этом функция стремится к своему предельному значению 3, оставаясь меньше этого значения. Другими словами, попадание аргумента в правую -окрестность точки 1 гарантирует попадание значений функции в левую (нижнюю) -окрестность точки 3:
Эскиз графика функции расположен в прямоугольнике .
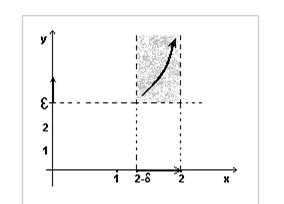
2. а) Запишем на языке « » утверждение: «функция стремится
к бесконечности при стремлении аргумента к 2»:
и раскроем модули в неравенствах:
;
.
б) По условию, аргумент стремится к точке 2, оставаясь меньше 2; при этом функция , оставаясь положительной, неограниченно возрастает. Это значит, что попадание аргумента в левую -окрестность точки 2 гарантирует выполнение неравенства
.
Эскиз графика функции расположен в полуполосе .
Прямая – вертикальная асимптота графика функции.
3. а) .
 Раскроем модули в неравенствах:
Раскроем модули в неравенствах:
.
б) По условию, аргумент стремится к отрицательной бесконечности, при этом функция стремится к своему предельному значению 3, оставаясь больше 3. Иначе, если для аргумента выполняется неравенство , это гарантирует попадание значений функции в правую (верхнюю) -окрестность точки 3:
.
Эскиз графика функции расположен в полуполосе ,
прямая – горизонтальная асимптота графика функции.
4. ,
поэтому
.
Эскиз графика функции расположен внутри угла .
studopedya.ru
3. Односторонние пределы.
бозначение предела
Предел функции обозначается как или через символ предела:. Всюду ниже предполагается, что пределы функцийсуществуют.
Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
Расширенное правило суммы
Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
Предел произведения функции на постоянную величину
Постоянный коэффициент можно выносить за знак предела:
Предел произведения
Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):
Расширенное правило произведения
Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Предел степенной функции
где степень p – действительное число. В частности,
Если f ( x ) = x, то
Предел показательной функции
где основание a > 0.
Предел логарифмической функции
где основание a > 0.
Теорема “о двух милиционерах”
Предположим, что для всехx близких к a, за исключением, быть может, самой точкиx = a. Тогда, если
то
То есть функция f (x) остается “зажатой” между двумя другими функциями, стремящимися к одному и тому же пределу L.
studfiles.net
5.07.2 Односторонние пределы и их связь с пределом
Когда мы формулировали определение предела функции в точке , то не делали никакого ограничения на способ стремления значений к , т. е. точка могла стремиться к точке и справа, и слева. Если в определении предела функции потребовать, чтобы стремилось к не любым способом, а только слева (оставаясь все время меньше ) или только справа (оставаясь больше ), то получим определение предела слева и справа в точке .
Определение. Число называется пределом функции при , стремящемся к слева, если для любого , найдется такое , что для всех , удовлетворяющих неравенству , выполняется неравенство .
Определение предела функции при , стремящемся к справа, формулируется аналогично, с той лишь разницей, что выполнение неравенства требуется для из правой полуокрестности : .
Пределы слева и справа иначе называются односторонними пределами и соответственно обозначаются так:
, .
Из определения предела следует, что если функция имеет в какой–либо внутренней точке промежутка предел, то она имеет в этой точке и односторонние пределы, причем
.
Но функция может иметь односторонние пределы и при отсутствии предела в точке, например, пусть
Таким образом , , следовательно в точке эта функция не имеет предела.
Если же функция в некоторой точке имеет односторонние пределы, причем , то их общее значение будет пределом функции в этой точке.
Все сформулированные выше теоремы о пределах и все изложенное в пункте 5.6 относительно неопределенностей легко переносятся на случай функций, если воспользоваться определением предела функции на языке последовательностей.
Понятия бесконечно малой и бесконечно большой переменной можно перенести на функцию.
Определение. Функция называется бесконечно малой при , если . Функция называется бесконечно большой при , если .
Например, функция является бесконечно малой при (так как ) и бесконечно большой при (так как ).
| < Предыдущая | Следующая > |
|---|
matica.org.ua
3.Понятие предела функции при , . Примеры. Односторонние пределы.
1)Предел при по Гейне:
Число А называется пределом функции в точке , если для любой последовательности допустимых значений аргумента , сходящейся к , последовательность соответствующих значений функции сходится к A.
2)Предел при по Коши:
Число A называется пределом функции в точке , если для любого положительного числа найдется такое положительное число , что для всех , удовлетворяющих неравенству , выполняется неравенство .
2)Предел при :
Число A называется пределом функции при , если для любого положительного числа существует такое число , что для всех , удовлетворяющих неравенству , выполняется неравенство .
Односторонние пределы:
1)Предел слева
Число A называется пределом функции слева в точке , если для любого положительного числа существует такое число , что при , выполняется неравенство .
Записывается так:
2)Предел справа
Число A называется пределом функции слева в точке , если для любого положительного числа существует такое число , что при , выполняется неравенство .
Записывается так:
Пример:
Вычислить.
Решение:
itm-x18.narod.ru




