Главная
Онлайн матрицы гаусса – Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса — «Шпаргалка ЕГЭ»

Онлайн матрицы гаусса – Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса — «Шпаргалка ЕГЭ»

Содержание

Решение системы линейных уравнений (метод Гаусса)

Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений (СЛУ) методом Гаусса.

Для того чтобы решить систему линейных уравнений методом Гаусса, выберите количество неизвестных величин: 2345

Заполните систему линейных уравнений

Для изменения в уравнении знаков с “+” на “-” вводите отрицательные числа. Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.

Решить систему

Воспользуйтесь также:
Решение системы линейных уравнений (метод подстановки)
Решение системы линейных уравнений (метод Крамера)
Решение системы линейных уравнений (матричный метод)

Решение системы линейных уравнений методом Гаусса

Метод Гаусса

Это классический метод решения системы линейных уравнений, в основе которого лежат элементарные преобразования системы (сложение, вычитание уравнений, умножение на коэффмцменты) для приведения к равносильной системе уравнений треугольного типа, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные неизвестные. Решение системы линейных уравнений методом Гаусса осуществляется в два этапа.

На нашем сайте решение происходит в режиме онлайн, каждый шаг решения имеет подробное описание, поэтому вы с легкость сможете освоить метод Гаусса решения систем линейных уравнений. Также мы применяем наиболее полную форму метода Гаусса, когда матрица приводится не к диагональному виду, а к единичной форме. В этом случае правая колонка и будет представлять значения неизвестных переменных. При этом нет необходимости вычислять новые неизвестные через ранее рассчитанные.

matematikam.ru

Матричный метод онлайн

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку “Вычислить”.

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

где

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы

A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A−1. Тогда

Учитывая определение обратной матрицы, имеем A−1A=E, где E– единичная матрица. Следовательно (4) можно записать так:

или, учитывая, что Ex=x:

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

.

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

.

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

.

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

.

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

.

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

.

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

.

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

.

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

.

Ответ:

Пример 2. Решить следующую систему линейных уравнений матричным методом:

.

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

.

Вычислим все алгебраические дополнения матрицы A:

,
,
,
,
,
,
,
,
.

Обратная матрица вычисляется из следующего выражения:

где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

Ответ:

matworld.ru

Решение матриц методом Гаусса, с примерами

Метод Гаусса используется для решения систем линейных уравнений и для нахождения обратной матрицы. Начнем с нахождения обратной матрицы.

Алгоритм нахождения обратной матрицы методом Гаусса

1. Пусть задана квадратная матрица

   

припишем к столбцам матрицы справа столбцы единичной матрицы того же порядка. Получим матрицу

   

2. С помощью элементарных преобразований строк приведем матрицу к матрице, в левой части которой будет стоять единичная матрица:

   

3. Полученная таким образом матрица, стоящая в правой части матрицы , и будет обратной матрицей к матрице

   

Алгоритм применения метода Гаусса для решения СЛУ

Пусть задана система линейных уравнений

   

Записывается матрица – расширенная матрица этой системы:

   

Над строками матрицы производятся элементарные преобразования: разрешается изменять порядок строк, умножать строки на любые отличные от нуля числа и прибавлять к любой строке матрицы любую другую её строку, умноженное на произвольное число. В результате таких элементарных преобразований основная матрица системы должна быть приведена к нижнему треугольному виду

   

Эта матрица эквивалентна системе линейных уравнений

   

Из этой системы последовательно снизу вверх выражаются все неизвестные переменные.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Ранг матрицы методом Гаусса | Мозган калькулятор онлайн

Для того что бы вычислить ранг матрицы можно применить метод окаймляющих миноров или метод Гаусса. Рассмотрим метод Гаусса или метод элементарных преобразований.

Рангом матрицы называют максимальный порядок её миноров, среди которых есть хотя бы один, не равный нулю.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Метод Гаусса использует элементарные преобразования, которые не изменяют ее ранг:

  1. Транспонирование.
  2. Перестановка местами строк или столбцов.
  3. Прибавление одной строки/столбца к другой строке/столбцу умноженного на ненулевое число.
  4. Умножение строки или столбца на ненулевое число.

С помощью данного метода нужно привести матрицу к ступенчатому виду и посчитать количество строк, в которых есть хоть один не нулевой элемент.

Пример

Рассмотрим данный метод на примере. Дана матрицы:

Для облегчения дальнейших расчетов поменяем местами строку №1 со строкой №2.

Сделаем элемент a3,1 равный нулю.

Из строки №3 вычтем строку №1, умноженную на 3/2.

Сделаем элемент a4,1 равный нулю.

Из строки №4 вычитаем строку №1, умноженную на 2.

Сделаем элемент a3,2 равный нулю.

Из строки №3 вычтем строку №2, умноженную на -1/4. Мы его получили разделив элимент a3,2 = -0.5 на элимент a2,2 = 2.

Сделаем элемент a4,2 равный нулю.

Из строки №4 вычтем строку №2, умноженную на -1/2.

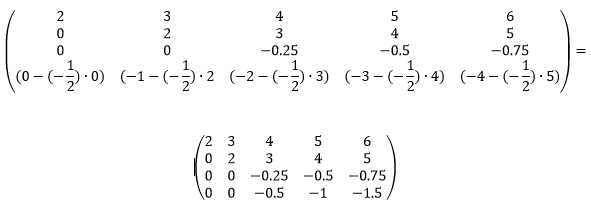
Сделаем элемент a4,3 равный нулю.

Из строки №4 вычитаем строку №3, умноженную на 2.

В получившейся матрице одна строка содержит нулевые элементы, а три строки имеют не нулевые элементы. Ответ: Ранг=3.

mozgan.ru

Решение системы линейных алгебраических уравнений методом Гаусса

Система линейных уравнений вида:

может быть решена методом Гаусса при помощи нашего калькулятора.

Система уравнений задается в виде расширенной матрицы, т. е. матрицы коэффициентов и свободных членов размерности [n : n+1] вида:

Описание метода Гаусса следует сразу за калькулятором.

8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51СЛАУ в матричном видеТочность вычисления

Знаков после запятой: 2

Количество решений

 

Вектор решения системы уравнений

 

Детали вычислений

Сохранить share extension

Метод Гаусса

Метод был назван в честь гениального немецкого математика XIX века Карла Фридриха Гаусса. Сам Гаусс не был первооткрывателем метода (метод был известен и ранее (еще в I-II веке до н. э. метод упоминался в китайском труде «Математика в девяти книгах»).

Приведение матрицы к ступенчатому виду

На первом шаге решения системы уравнений методом Гаусса матрица коэффициентов и свободных членов приводится к ступенчатому виду:

Матрица превращается в ступенчатую форму путем элементарных преобразований — перемена строк местами, умножение строки на коэффициент, сложение строк.
В нашем калькуляторе для перехода к ступенчатому виду осуществляется последовательное вычитание из нижних строк матрицы, помноженных на , верхних строк , помноженных на коэффициент , где i — индекс текущей строки (индекс строки, которую вычитают из нижних строк).
При осуществлении этой операции требуется, чтобы коэффициент главной переменной был не нулевым. В случае нулевого коэффициента, строка меняется местами с любой другой нижней строкой, в которой в текущем столбце значение отлично от нуля.

Выражение базисных переменных

Получив ступенчатую матрицу, мы переходим к выражению базисных переменных, для этого сначала выполняется деление текущей строки на коэффициент , затем производится обратное вычитание из верхних строк , этой строки , помноженных на коэффициент , где j — индекс текущей строки (индекс строки, которую вычитают из верхних строк). Операция повторяется с каждой строкой, начиная от n-й до 1-й.
В результате матрица приобретает диагональный вид:
,
далее, поделив строки матрицы на коэффициент , в столбце свободных членов получаем вектор решений системы уравнений.

planetcalc.ru

Решение матрицы методом гаусса онлайн — Все о ремонте и строительстве

Математика без Ху%!ни. Метод Гаусса. Метод Жордано-Гаусса.


Математика без Ху%!ни. Метод Гаусса. Система линейных уравнений. Объясняем просто и со вкусом 😉 vk.com/sergejkuts…

Метод Гаусса и метод Жордана-Гаусса


Метод Гаусса решения систем линейных уравнений. Поддержать Проект: http://donationalerts.ru/r/valeryvolkov Мои занятия в…

Метод Гаусса решения линейных уравнений


использован для решения любой совместной системы. Суть метода Гаусса состоит в следующем: исходная система…

Метод Жордана-Гаусса (метод прямоугольников). Видеоурок


Видеоурок по высшей математике. Линейная алгебра. Метод решения систем линейных уравнений методом Жордана-…

Метод Крамера за 3 минуты. Решение системы линейных уравнений – bezbotvy


Это один из самых простых способов решения систем уравнений. Я его очень-очень КУ. Чего и вам советую. Решает…

Метод Гаусса онлайн с решением. Самый легкий способ.


http://calc-lab.com/ Решение систем линейных алгебраических уравнений в Вычислительной лаборатории онлайн с решен…

Высшая математика. Решение совместных определенных систем методом Гаусса


Решение совместных определенных систем методом Гаусса.

Метод Гаусса (01)


Рассмотрена суть метода Гаусса. Для системы двух линейных уравнений с двумя неизвестными данный метод…

Система линейных уравнений. Метод обратной матрицы. Матричный метод.


Математика Без Ху%!ни. Система линейных уравнений. Метод Крамера. Матричный метод. vk.com/sergejkuts vkcom/matematikaprosto…

arenda095.ru

Матричный калькулятор онлайн

Инструкция матричного онлайн калькулятора

С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень, умножить матрицу на число, сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.

Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a/b, где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.

Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы или очищать содержимое ячеек ).

Рис.1

При вычислениях пустая ячейка воспринимается как нуль.

Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .

Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.

Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.

Рис.2

Вычисление суммы, разности, произведения матриц онлайн

Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.

Для вычисления суммы, разности или произведения матриц:

  1. Введите размерности матриц и .
  2. Введите элементы матриц.
  3. Нажмите на кнопку “A+B “,”A-B” или “A×B”.

Вычисление обратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.

Для вычисления обратной матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Введите размерность матрицы .
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “обратное “.

Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.

Вычисление определителя матрицы онлайн

Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.

Для вычисления определителя матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Введите размерность матрицы .
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “определитель “.

Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.

Вычисление ранга матрицы онлайн

Матричным онлайн калькулятором можно вычислить ранг матрицы.

Для вычисления ранга матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Введите размерность матрицы .
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “ранг “.

Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.

Вычисление псевдообратной матрицы онлайн

Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.

Для вычисления псевдообратной матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Введите размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “псевдообратное “.

Удаление линейно зависимых строк или столбцов матрицы онлайн

Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.

Для удаления линейно зависимых строк или столбцов матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Введите размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “полный ранг строк ” или “полный ранг столбцов”.

Скелетное разложение матрицы онлайн

Для проведения скелетного разложения матрицы онлайн

  1. Выберите матрицу или с помощью радиокнопки .
  2. Введите размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “скелетное разложение “.

Решение матричного уравнения или системы линейных уравнений AX=B онлайн

Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.

Для решения матричного уравнения:

  1. Введите размерности матриц и .
  2. Введите элементы матриц.
  3. Нажмите на кнопку “решение AX=B”.

Учтите, что матрицы и должны иметь равное количество строк .

Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн

Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.

Для исключения Гаусса или приведения матрицы к треугольному виду

  1. Выберите матрицу или с помощью радиокнопки .
  2. Задайте размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “Треугольный вид”.

LU-разложение или LUP-разложение матрицы онлайн

Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.

Для LU(LUP)-разложения:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Задайте размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “LU-разложение”.

Построение ядра (нуль-пространства) матрицы онлайн

С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.

Для построения нуль-пространства (ядра) матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Задайте размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “ядро (·)”.

Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн

С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.

Для ортогонализации или ортонормализации матрицы:

  1. Выберите матрицу или с помощью радиокнопки .
  2. Задайте размерность матрицы.
  3. Введите элементы матрицы.
  4. Нажмите на кнопку “Ортогонализация Г.-Ш. (·)” или “Ортонормализация Г.-Ш. (·)”.

matworld.ru

Оставить комментарий