Определитель метод крамера – Метод Крамера для решения СЛАУ: алгоритм, примеры задач

метод крамера

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.

При изучении материала Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.

Навигация по странице.

• Метод Крамера – вывод формул.

• Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

• Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера – вывод формул.

Пусть нам требуется решить систему линейных уравнений вида где x₁, x₂, …, x_n – неизвестные переменные, a_{i j} , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b₁, b₂, …, b_n – свободные члены. Решением СЛАУ называется такой набор значений x₁, x₂, …, x_n при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B, где  – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных,  – матрица – столбец свободных членов, а  – матрица – столбец неизвестных переменных. После нахождения неизвестных переменных 

x₁, x₂, …, x_n, матрица  становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделе решение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

1. Определитель квадратной матрицы  равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

2. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:

Итак, приступим к нахождению неизвестной переменной x₁. Для этого умножим обе части первого уравнения системы на А_{1 1} , обе части второго уравнения – на А_{2 1} , и так далее, обе части n-ого

 уравнения – на А_{n 1} (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):

Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x₁, x₂, …, x_n, и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем   и предыдущее равенство примет вид   откуда

Аналогично находим x₂. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы 

А:

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x₁, x₂, …, x_n и применяем свойства определителя: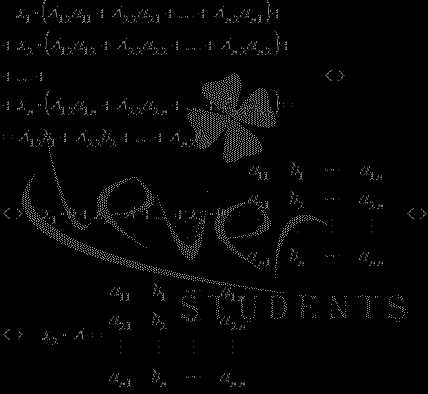

Откуда .

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить   то получаем формулы для нахождения неизвестных переменных по методу Крамера .

Замечание.

Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение  (при ). Действительно, при нулевых свободных членах все определители  будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы  дадут .

К началу страницы

Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера.

1. Вычисляем определитель основной матрицы системы  и убеждаемся, что он отличен от нуля.

2. Находим определители   которые являются определителями матриц, полученных из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.

3. Вычисляем искомые неизвестные переменные 

   x₁, x₂, …, x_n по формулам .

4. Выполняем проверку результатов, подставляя x₁, x₂, …, x_n в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.

К началу страницы

Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.

Пример.

Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель по формуле :

Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители  и . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем.

Вычисляем эти определители:

Находим неизвестные переменные 

x₁ и x₂ по формулам :

Выполним проверку. Подставим полученные значения x₁ и x₂ в исходную систему уравнений:

Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.

Пример.

Найдите решение системы линейных уравнений методом Крамера .

Решение.

Перепишем систему в виде , чтобы стало видно основную матрицу системы . Найдем ее определитель по формуле

Имеем

Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :

Таким образом,

Ответ:

.

Обозначения неизвестных переменных в уравнениях системы могут отличаться от x₁, x₂, …, x_n. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.

Пример.

Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .

Решение.

В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместоx₁, x₂ и x₃). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как . Теперь основную матрицу системы хорошо видно . Вычислим ее определитель:

Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители  (обратите внимание на обозначения) и вычислим их:

Осталось найти неизвестные переменные по формулам :

Выполним проверку. Для этого умножим основную матрицу на полученное решение  (при необходимости смотрите раздел операции над матрицами):

В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.

Ответ:

x = 0, y = -2, z = 3.

Пример.

Решите методом Крамера систему линейных уравнений , гдеa

 и b – некоторые действительные числа.

Решение.

Вычислим определитель основной матрицы системы:

Определитель отличен от нуля, следовательно, можно применить метод Крамера.

Находим неизвестные переменные

Рекомендуем проверить полученные результаты.

Ответ:

.

Пример.

Найдите решение системы уравнений  методом Крамера,  – некоторое действительное число.

Решение.

Вычислим определитель основной матрицы системы: . Область значений выражения  есть интервал , поэтому  при любых действительных значениях . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем  и :

Таким образом, .

Выполним проверку:

Уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

Пример.

Решите систему линейных алгебраических уравнений методом Крамера .

Решение.

Вычислим определитель основной матрицы системы уравнений:

Определитель основной матрицы равен нулю, следовательно, метод Крамера не подходит для решения такой системы уравнений.

Пример.

Методом Крамера найдите решение СЛАУ .

Решение.

Эта система однородная, так как все свободные члены равны нулю. Определитель основной матрицы отличен от нуля , поэтому ее единственным решением является x₁ = 0, x₂ = 0. О таких СЛАУ мы уже упоминали вышев замечании.

Ответ:

x₁ = 0, x₂ = 0.

Пример.

Найдите решение системы четырех линейных алгебраических уравнений  содержащую четыре неизвестных переменных.

Решение.

Сразу скажем, что не будем подробно описывать вычисление определителей матриц, так как это выходит за рамки данной статьи.

Вычислим определитель основной матрицы системы, разложив его по элементам второй строки:

Определитель основной матрицы системы отличен от нуля, поэтому можно воспользоваться методом Крамера для решения системы.

Найдем :  аналогично вычисляются

Таким образом,

Ответ:

.

К началу страницы

Подведем итог.

Метод Крамера позволяет находить решение систем линейных алгебраических уравнений, если определитель основной матрицы отличен от нуля. По сути метод сводится к вычислению определителей матриц порядка n на n и применению соответствующих формул для нахождения неизвестных переменных.

Если число уравнений в системе велико (больше трех), то целесообразно искать решениеметодом Гаусса.

studfiles.net

Метод Крамера

Метод Крамера.

Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.

При изучении материала Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.

Навигация по странице.

• Метод Крамера – вывод формул.

• Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

• Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера – вывод формул.

Пусть нам требуется решить систему линейных уравнений вида гдеx₁, x₂, …, x_n – неизвестные переменные, a_{i j} , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b₁, b₂, …, b_n – свободные члены. Решением СЛАУ называется такой набор значений x₁, x₂, …, x_n при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B, где – основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных,- матрица – столбец свободных членов, а- матрица – столбец неизвестных переменных. После нахождения неизвестных переменныхx₁, x₂, …, x_n, матрица становится решением системы уравнений и равенствоA ⋅ X = B обращается в тождество .

Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при разобраны в разделерешение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

1. Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:

2. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:

Итак, приступим к нахождению неизвестной переменной x₁. Для этого умножим обе части первого уравнения системы на А_{1 1} , обе части второго уравнения – на А_{2 1} , и так далее, обе части n-ого уравнения – на А_{n 1} (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):

Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x₁, x₂, …, x_n, и приравняем эту сумму к сумме всех правых частей уравнений:

Если обратиться к озвученным ранее свойствам определителя, то имеем и предыдущее равенство примет видоткуда

Аналогично находим x₂. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:

Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x₁, x₂, …, x_n и применяем свойства определителя: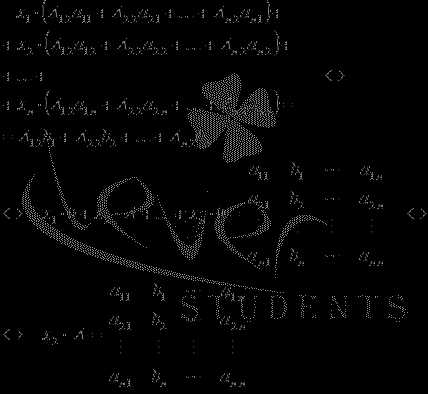

Откуда .

Аналогично находятся оставшиеся неизвестные переменные.

Если обозначить то получаемформулы для нахождения неизвестных переменных по методу Крамера .

Замечание.

Если система линейных алгебраических уравнений однородная, то есть , то она имеет лишь тривиальное решение(при). Действительно, при нулевых свободных членах все определителибудут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулыдадут.

К началу страницы

Алгоритм решения систем линейных алгебраических уравнений методом Крамера.

Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера.

1. Вычисляем определитель основной матрицы системы и убеждаемся, что он отличен от нуля.

2. Находим определители которые являются определителями матриц, полученных из матрицыА заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.

3. Вычисляем искомые неизвестные переменные x₁, x₂, …, x_n по формулам .

4. Выполняем проверку результатов, подставляя x₁, x₂, …, x_n в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.

К началу страницы

Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения нескольких примеров.

Пример.

Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера .

Решение.

Основная матрица системы имеет вид . Вычислим ее определитель по формуле:

Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители и. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель. Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем.

Вычисляем эти определители:

Находим неизвестные переменные x₁ и x₂ по формулам :

Выполним проверку. Подставим полученные значения x₁ и x₂ в исходную систему уравнений:

Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.

Пример.

Найдите решение системы линейных уравнений методом Крамера .

Решение.

Перепишем систему в виде , чтобы стало видно основную матрицу системы. Найдем ее определитель по формуле

Имеем

Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители :

Таким образом,

Ответ:

.

Обозначения неизвестных переменных в уравнениях системы могут отличаться от x₁, x₂, …, x_n. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.

Пример.

Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными .

Решение.

В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместоx₁, x₂ и x₃). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как. Теперь основную матрицу системы хорошо видно. Вычислим ее определитель:

Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители (обратите внимание на обозначения) и вычислим их:

Осталось найти неизвестные переменные по формулам :

Выполним проверку. Для этого умножим основную матрицу на полученное решение (при необходимости смотрите разделоперации над матрицами):

В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.

Ответ:

x = 0, y = -2, z = 3.

Пример.

Решите методом Крамера систему линейных уравнений , гдеa и b – некоторые действительные числа.

Решение.

Вычислим определитель основной матрицы системы:

Определитель отличен от нуля, следовательно, можно применить метод Крамера.

Находим неизвестные переменные

Рекомендуем проверить полученные результаты.

Ответ:

.

Пример.

Найдите решение системы уравнений методом Крамера,- некоторое действительное число.

Решение.

Вычислим определитель основной матрицы системы: .Область значений выражения есть интервал, поэтомупри любых действительных значениях. Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляеми:

Таким образом, .

Выполним проверку:

Уравнения системы обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

Пример.

Решите систему линейных алгебраических уравнений методом Крамера .

Решение.

Вычислим определитель основной матрицы системы уравнений:

Определитель основной матрицы равен нулю, следовательно, метод Крамера не подходит для решения такой системы уравнений.

Пример.

Методом Крамера найдите решение СЛАУ .

Решение.

Эта система однородная, так как все свободные члены равны нулю. Определитель основной матрицы отличен от нуля , поэтому ее единственным решением являетсяx₁ = 0, x₂ = 0. О таких СЛАУ мы уже упоминали вышев замечании.

Ответ:

x₁ = 0, x₂ = 0.

Пример.

Найдите решение системы четырех линейных алгебраических уравнений содержащую четыре неизвестных переменных.

Решение.

Сразу скажем, что не будем подробно описывать вычисление определителей матриц, так как это выходит за рамки данной статьи.

Вычислим определитель основной матрицы системы, разложив его по элементам второй строки:

Определитель основной матрицы системы отличен от нуля, поэтому можно воспользоваться методом Крамера для решения системы.

Найдем :аналогично вычисляются

Таким образом,

Ответ:

.

К началу страницы

Подведем итог.

Метод Крамера позволяет находить решение систем линейных алгебраических уравнений, если определитель основной матрицы отличен от нуля. По сути метод сводится к вычислению определителей матриц порядка n на n и применению соответствующих формул для нахождения неизвестных переменных.

studfiles.net

Теория определителей. Метод Крамера.(знать устно)

а) Определители второго и третьего порядка.

б) Свойства определителей.

в) Разложение определителя по элементам строки или столбца.

г) Формулы Крамера с помощью определителей.

( уметь решать системы уравнений методом Крамера, находить миноры и алгебраические дополнения)

Аналитическая геометрия.( знать определения и формулы)

а) Понятие вектора в пространстве.

б) Формула длины вектора.

в) Действия над векторами.

г) Скалярное произведение векторов. Угол между векторами

( уметь решать: угол между двумя векторами , находить длину отрезка, скалярное произведение)

 

Теория пределов функции.( свойства и формулы)

а) Понятие предела функции.

б) Основные свойства пределов.

в) Методы нахождения пределов функций.

( уметь решать: неопределенности вида 0\0,∞\∞, ∞―∞)

 

Дифференциальное исчисление.(определения и таблицу производных, геометрический и механический смысл производной)

а) Понятие производной функции.

б) Правила дифференцирования.

в) Таблица производных функций.

г) Производная сложной функции.

( уметь решать: находить производные с помощью таблиц)

 

Исследование функций с помощью производной.( определения и формулы)

а) Схема исследования функции.

б) Возрастание и убывание функции.

в) Экстремумы функции.

г) Точки перегиба графика функции.

д) Направление выпуклости графика функции.

е) Асимптоты графика функции.

( уметь решать ; строить графики элементарных функций по алгоритму)

 

Интегральное исчисление.( таблицу интегралов и определения)

а) Понятие определенного интеграла.

б) Свойства определенного интеграла.

в) Таблица основных интегралов.

г) Формула Ньютона — Лейбница.

д) Методы интегрирования.

( уметь решать: находить интегралы по таблице )

 

Методические указания

К выполнению контрольной работы.

I. Теория определителей

Определители второго и третьего порядка

 

Определителем второго порядка называется число .

Определителем третьего порядка называется число

Основные свойства определителей:

1. Если строки определителя поменять местами с соответственными столбцами, то значение определителя не изменится.

2. Если переставить две строки (столбца) определителя местами, то значение определителя изменится на противоположное.

3. Если элементы строки (столбца) определителя содержат общий множитель, то его можно вынести за знак определителя.

4. Если две строки (столбца) определителя содержат соответственно пропорциональные элементы, то значение определителя равно нулю.

5. Если к элементам какой-либо строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число, то значение определителя не изменится.

Пример.

Вычислить определитель:

Упростив определитель согласно перечисленным свойствам, найдем его значение:

1) вынесем множитель 3 из второй строки за знак определителя;

2) сложим соответственные элементы первой и второй строки;

3) сложим соответственно элементы второго и третьего столбца;

4) вынесем множитель 2 из второго столбца за знак определителя;

5) вынесем множитель 3 из первой строки за знак определителя;

6) вычислим определитель по правилу.

 

 

studopedya.ru

Реферат Метод Крамера

скачать

Реферат на тему:

План:

Введение

• 1 Описание метода
• 2 Пример
• 3 Вычислительная сложность
Примечания

Введение

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

1. Описание метода

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b₁,b₂,…,b_n и x₁,x₂,…,x_n, либо набор c₁,c₂,…,c_n состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

2. Пример

Система линейных уравнений:

Определители:

Решение:

Пример:

Определители:

3. Вычислительная сложность

Метод Крамера требует вычисления n + 1 определителей размерности . При использовании метода Гаусса для вычисления определителей, метод имеет временную сложность порядка O(n⁴), что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n³), сравнимой со сложностью метода Гаусса.^[1]

Примечания

1. Ken Habgood and Itamar Arel. 2010. Revisiting Cramer’s rule for solving dense linear systems. In Proceedings of the 2010 Spring Simulation Multiconference (SpringSim ’10).

wreferat.baza-referat.ru

Метод Крамера Википедия

Ме́тод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно).^[1]

Описание метода

Для системы n{\displaystyle n} линейных уравнений с n{\displaystyle n} неизвестными (над произвольным полем)

{a11x1+a12x2+…+a1nxn=b1a21x1+a22x2+…+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+…+annxn=bn{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}}

с определителем матрицы системы Δ{\displaystyle \Delta }, отличным от нуля, решение записывается в виде

xi=1Δ|a11…a1,i−1b1a1,i+1…a1na21…a2,i−1b2a2,i+1…a2n…………………an−1,1…an−1,i−1bn−1an−1,i+1…an−1,nan1…an,i−1bnan,i+1…ann|{\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&\ldots &a_{1,i-1}&b_{1}&a_{1,i+1}&\ldots &a_{1n}\\a_{21}&\ldots &a_{2,i-1}&b_{2}&a_{2,i+1}&\ldots &a_{2n}\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n-1,1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}}

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

(c1x1+c2x2+⋯+cnxn)⋅Δ=−|a11a12…a1nb1a21a22…a2nb2……………an1an2…annbnc1c2…cn0|{\displaystyle (c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n})\cdot \Delta =-{\begin{vmatrix}a_{11}&a_{12}&\ldots &a_{1n}&b_{1}\\a_{21}&a_{22}&\ldots &a_{2n}&b_{2}\\\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n1}&a_{n2}&\ldots &a_{nn}&b_{n}\\c_{1}&c_{2}&\ldots &c_{n}&0\\\end{vmatrix}}}

В этой форме метод Крамера справедлив без предположения, что Δ{\displaystyle \Delta } отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,…,bn{\displaystyle b_{1},b_{2},…,b_{n}} и x1,x2,…,xn{\displaystyle x_{1},x_{2},…,x_{n}}, либо набор c1,c2,…,cn{\displaystyle c_{1},c_{2},…,c_{n}} состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений с вещественными коэффициентами:

{a11x1+a12x2+a13x3=b1a21x1+a22x2+a23x3=b2a31x1+a32x2+a33x3=b3{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}=b_{2}\\a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}=b_{3}\\\end{cases}}}

Определители:

Δ=|a11a12a13a21a22a23a31a32a33|,  Δ1=|b1a12a13b2a22a23b3a32a33|,  {\displaystyle \Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}},\ \ \Delta _{1}={\begin{vmatrix}b_{1}&a_{12}&a_{13}\\b_{2}&a_{22}&a_{23}\\b_{3}&a_{32}&a_{33}\\\end{vmatrix}},\ \ }

Δ2=|a11b1a13a21b2a23a31b3a33|,  Δ3=|a11a12b1a21a22b2a31a32b3|{\displaystyle \Delta _{2}={\begin{vmatrix}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\\\end{vmatrix}},\ \ \Delta _{3}={\begin{vmatrix}a_{11}&a_{12}&b_{1}\\a_{21}&a_{22}&b_{2}\\a_{31}&a_{32}&b_{3}\\\end{vmatrix}}}

В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы.

Решение:

x1=Δ1Δ,  x2=Δ2Δ,  x3=Δ3Δ{\displaystyle x_{1}={\frac {\Delta _{1}}{\Delta }},\ \ x_{2}={\frac {\Delta _{2}}{\Delta }},\ \ x_{3}={\frac {\Delta _{3}}{\Delta }}}

Пример:

{2×1+5×2+4×3=30×1+3×2+2×3=1502×1+10×2+9×3=110{\displaystyle {\begin{cases}2x_{1}+5x_{2}+4x_{3}=30\\x_{1}+3x_{2}+2x_{3}=150\\2x_{1}+10x_{2}+9x_{3}=110\\\end{cases}}}

Определители:

Δ=|2541322109|=5,  Δ1=|305415032110109|=−760,  {\displaystyle \Delta ={\begin{vmatrix}2&5&4\\1&3&2\\2&10&9\\\end{vmatrix}}=5,\ \ \Delta _{1}={\begin{vmatrix}30&5&4\\150&3&2\\110&10&9\\\end{vmatrix}}=-760,\ \ }

Δ2=|23041150221109|=1350,  Δ3=|253013150210110|=−1270.{\displaystyle \Delta _{2}={\begin{vmatrix}2&30&4\\1&150&2\\2&110&9\\\end{vmatrix}}=1350,\ \ \Delta _{3}={\begin{vmatrix}2&5&30\\1&3&150\\2&10&110\\\end{vmatrix}}=-1270.}

x1=−7605=−152,  x2=13505=270,  x3=−12705=−254{\displaystyle x_{1}=-{\frac {760}{5}}=-152,\ \ x_{2}={\frac {1350}{5}}=270,\ \ x_{3}=-{\frac {1270}{5}}=-254}

Вычислительная сложность

Метод Крамера требует вычисления n+1{\displaystyle n+1} определителей размерности n×n{\displaystyle n\times n}. При использовании метода Гаусса для вычисления определителей метод имеет сложность по элементарным операциям сложения-умножения порядка O(n4){\displaystyle O(n^{4})}, что сложнее, чем метод Гаусса при прямом решении системы. Поэтому метод, с точки зрения затрат времени на вычисления, считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n3){\displaystyle O(n^{3})}, сравнимой со сложностью метода Гаусса^[2].

Литература

• Мальцев А. И. Основы линейной алгебры. — Изд. 3-е, перераб., М.: «Наука», 1970. — 400 c.

Примечания

1. ↑ Cramer, Gabriel. Introduction à l’Analyse des lignes Courbes algébriques (фр.) 656–659. Geneva: Europeana (1750). Проверено 18 мая 2012.
2. ↑ Ken Habgood and Itamar Arel. 2010. Revisiting Cramer’s rule for solving dense linear systems. In Proceedings of the 2010 Spring Simulation Multiconference (SpringSim ’10)

См. также

wikiredia.ru

Метод Крамера — Википедия

Материал из Википедии — свободной энциклопедии

Ме́тод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно).^[1]

Описание метода

Для системы n{\displaystyle n} линейных уравнений с n{\displaystyle n} неизвестными (над произвольным полем)

{a11x1+a12x2+…+a1nxn=b1a21x1+a22x2+…+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+…+annxn=bn{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}}

с определителем матрицы системы Δ{\displaystyle \Delta }, отличным от нуля, решение записывается в виде

xi=1Δ|a11…a1,i−1b1a1,i+1…a1na21…a2,i−1b2a2,i+1…a2n…………………an−1,1…an−1,i−1bn−1an−1,i+1…an−1,nan1…an,i−1bnan,i+1…ann|{\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&\ldots &a_{1,i-1}&b_{1}&a_{1,i+1}&\ldots &a_{1n}\\a_{21}&\ldots &a_{2,i-1}&b_{2}&a_{2,i+1}&\ldots &a_{2n}\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n-1,1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}}

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

(c1x1+c2x2+⋯+cnxn)⋅Δ=−|a11a12…a1nb1a21a22…a2nb2……………an1an2…annbnc1c2…cn0|{\displaystyle (c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n})\cdot \Delta =-{\begin{vmatrix}a_{11}&a_{12}&\ldots &a_{1n}&b_{1}\\a_{21}&a_{22}&\ldots &a_{2n}&b_{2}\\\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n1}&a_{n2}&\ldots &a_{nn}&b_{n}\\c_{1}&c_{2}&\ldots &c_{n}&0\\\end{vmatrix}}}

В этой форме метод Крамера справедлив без предположения, что Δ{\displaystyle \Delta } отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,…,bn{\displaystyle b_{1},b_{2},…,b_{n}} и x1,x2,…,xn{\displaystyle x_{1},x_{2},…,x_{n}}, либо набор c1,c2,…,cn{\displaystyle c_{1},c_{2},…,c_{n}} состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Видео по теме

Пример

Система линейных уравнений с вещественными коэффициентами:

{a11x1+a12x2+a13x3=b1a21x1+a22x2+a23x3=b2a31x1+a32x2+a33x3=b3{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}=b_{2}\\a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}=b_{3}\\\end{cases}}}

Определители:

Δ=|a11a12a13a21a22a23a31a32a33|,  Δ1=|b1a12a13b2a22a23b3a32a33|,  {\displaystyle \Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}},\ \ \Delta _{1}={\begin{vmatrix}b_{1}&a_{12}&a_{13}\\b_{2}&a_{22}&a_{23}\\b_{3}&a_{32}&a_{33}\\\end{vmatrix}},\ \ }

Δ2=|a11b1a13a21b2a23a31b3a33|,  Δ3=|a11a12b1a21a22b2a31a32b3|{\displaystyle \Delta _{2}={\begin{vmatrix}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\\\end{vmatrix}},\ \ \Delta _{3}={\begin{vmatrix}a_{11}&a_{12}&b_{1}\\a_{21}&a_{22}&b_{2}\\a_{31}&a_{32}&b_{3}\\\end{vmatrix}}}

В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы.

Решение:

x1=Δ1Δ,  x2=Δ2Δ,  x3=Δ3Δ{\displaystyle x_{1}={\frac {\Delta _{1}}{\Delta }},\ \ x_{2}={\frac {\Delta _{2}}{\Delta }},\ \ x_{3}={\frac {\Delta _{3}}{\Delta }}}

Пример:

{2×1+5×2+4×3=30×1+3×2+2×3=1502×1+10×2+9×3=110{\displaystyle {\begin{cases}2x_{1}+5x_{2}+4x_{3}=30\\x_{1}+3x_{2}+2x_{3}=150\\2x_{1}+10x_{2}+9x_{3}=110\\\end{cases}}}

Определители:

Δ=|2541322109|=5,  Δ1=|305415032110109|=−760,  {\displaystyle \Delta ={\begin{vmatrix}2&5&4\\1&3&2\\2&10&9\\\end{vmatrix}}=5,\ \ \Delta _{1}={\begin{vmatrix}30&5&4\\150&3&2\\110&10&9\\\end{vmatrix}}=-760,\ \ }

Δ2=|23041150221109|=1350,  Δ3=|253013150210110|=−1270.{\displaystyle \Delta _{2}={\begin{vmatrix}2&30&4\\1&150&2\\2&110&9\\\end{vmatrix}}=1350,\ \ \Delta _{3}={\begin{vmatrix}2&5&30\\1&3&150\\2&10&110\\\end{vmatrix}}=-1270.}

x1=−7605=−152,  x2=13505=270,  x3=−12705=−254{\displaystyle x_{1}=-{\frac {760}{5}}=-152,\ \ x_{2}={\frac {1350}{5}}=270,\ \ x_{3}=-{\frac {1270}{5}}=-254}

Вычислительная сложность

Метод Крамера требует вычисления n+1{\displaystyle n+1} определителей размерности n×n{\displaystyle n\times n}. При использовании метода Гаусса для вычисления определителей метод имеет сложность по элементарным операциям сложения-умножения порядка O(n4){\displaystyle O(n^{4})}, что сложнее, чем метод Гаусса при прямом решении системы. Поэтому метод, с точки зрения затрат времени на вычисления, считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n3){\displaystyle O(n^{3})}, сравнимой со сложностью метода Гаусса^[2].

Литература

• Мальцев А. И. Основы линейной алгебры. — Изд. 3-е, перераб., М.: «Наука», 1970. — 400 c.

Примечания

1. ↑ Cramer, Gabriel. Introduction à l’Analyse des lignes Courbes algébriques (фр.) 656–659. Geneva: Europeana (1750). Проверено 18 мая 2012.
2. ↑ Ken Habgood and Itamar Arel. 2010. Revisiting Cramer’s rule for solving dense linear systems. In Proceedings of the 2010 Spring Simulation Multiconference (SpringSim ’10)

См. также

wikipedia.green

Метод Крамера — WiKi

Для системы n{\displaystyle n}  линейных уравнений с n{\displaystyle n}  неизвестными (над произвольным полем)

{a11x1+a12x2+…+a1nxn=b1a21x1+a22x2+…+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯an1x1+an2x2+…+annxn=bn{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+\ldots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\ldots +a_{2n}x_{n}=b_{2}\\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\a_{n1}x_{1}+a_{n2}x_{2}+\ldots +a_{nn}x_{n}=b_{n}\\\end{cases}}} 

с определителем матрицы системы Δ{\displaystyle \Delta } , отличным от нуля, решение записывается в виде

xi=1Δ|a11…a1,i−1b1a1,i+1…a1na21…a2,i−1b2a2,i+1…a2n…………………an−1,1…an−1,i−1bn−1an−1,i+1…an−1,nan1…an,i−1bnan,i+1…ann|{\displaystyle x_{i}={\frac {1}{\Delta }}{\begin{vmatrix}a_{11}&\ldots &a_{1,i-1}&b_{1}&a_{1,i+1}&\ldots &a_{1n}\\a_{21}&\ldots &a_{2,i-1}&b_{2}&a_{2,i+1}&\ldots &a_{2n}\\\ldots &\ldots &\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n-1,1}&\ldots &a_{n-1,i-1}&b_{n-1}&a_{n-1,i+1}&\ldots &a_{n-1,n}\\a_{n1}&\ldots &a_{n,i-1}&b_{n}&a_{n,i+1}&\ldots &a_{nn}\\\end{vmatrix}}} 

(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

(c1x1+c2x2+⋯+cnxn)⋅Δ=−|a11a12…a1nb1a21a22…a2nb2……………an1an2…annbnc1c2…cn0|{\displaystyle (c_{1}x_{1}+c_{2}x_{2}+\dots +c_{n}x_{n})\cdot \Delta =-{\begin{vmatrix}a_{11}&a_{12}&\ldots &a_{1n}&b_{1}\\a_{21}&a_{22}&\ldots &a_{2n}&b_{2}\\\ldots &\ldots &\ldots &\ldots &\ldots \\a_{n1}&a_{n2}&\ldots &a_{nn}&b_{n}\\c_{1}&c_{2}&\ldots &c_{n}&0\\\end{vmatrix}}} 

В этой форме метод Крамера справедлив без предположения, что Δ{\displaystyle \Delta }  отличен от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,…,bn{\displaystyle b_{1},b_{2},…,b_{n}}  и x1,x2,…,xn{\displaystyle x_{1},x_{2},…,x_{n}} , либо набор c1,c2,…,cn{\displaystyle c_{1},c_{2},…,c_{n}}  состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Система линейных уравнений с вещественными коэффициентами:

{a11x1+a12x2+a13x3=b1a21x1+a22x2+a23x3=b2a31x1+a32x2+a33x3=b3{\displaystyle {\begin{cases}a_{11}x_{1}+a_{12}x_{2}+a_{13}x_{3}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+a_{23}x_{3}=b_{2}\\a_{31}x_{1}+a_{32}x_{2}+a_{33}x_{3}=b_{3}\\\end{cases}}} 

Определители:

Δ=|a11a12a13a21a22a23a31a32a33|,  Δ1=|b1a12a13b2a22a23b3a32a33|,  {\displaystyle \Delta ={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}},\ \ \Delta _{1}={\begin{vmatrix}b_{1}&a_{12}&a_{13}\\b_{2}&a_{22}&a_{23}\\b_{3}&a_{32}&a_{33}\\\end{vmatrix}},\ \ } 

Δ2=|a11b1a13a21b2a23a31b3a33|,  Δ3=|a11a12b1a21a22b2a31a32b3|{\displaystyle \Delta _{2}={\begin{vmatrix}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\\\end{vmatrix}},\ \ \Delta _{3}={\begin{vmatrix}a_{11}&a_{12}&b_{1}\\a_{21}&a_{22}&b_{2}\\a_{31}&a_{32}&b_{3}\\\end{vmatrix}}} 

В определителях столбец коэффициентов при соответствующей неизвестной заменяется столбцом свободных членов системы.

Решение:

x1=Δ1Δ,  x2=Δ2Δ,  x3=Δ3Δ{\displaystyle x_{1}={\frac {\Delta _{1}}{\Delta }},\ \ x_{2}={\frac {\Delta _{2}}{\Delta }},\ \ x_{3}={\frac {\Delta _{3}}{\Delta }}} 

Пример:

{2×1+5×2+4×3=30×1+3×2+2×3=1502×1+10×2+9×3=110{\displaystyle {\begin{cases}2x_{1}+5x_{2}+4x_{3}=30\\x_{1}+3x_{2}+2x_{3}=150\\2x_{1}+10x_{2}+9x_{3}=110\\\end{cases}}} 

Определители:

Δ=|2541322109|=5,  Δ1=|305415032110109|=−760,  {\displaystyle \Delta ={\begin{vmatrix}2&5&4\\1&3&2\\2&10&9\\\end{vmatrix}}=5,\ \ \Delta _{1}={\begin{vmatrix}30&5&4\\150&3&2\\110&10&9\\\end{vmatrix}}=-760,\ \ } 

Δ2=|23041150221109|=1350,  Δ3=|253013150210110|=−1270.{\displaystyle \Delta _{2}={\begin{vmatrix}2&30&4\\1&150&2\\2&110&9\\\end{vmatrix}}=1350,\ \ \Delta _{3}={\begin{vmatrix}2&5&30\\1&3&150\\2&10&110\\\end{vmatrix}}=-1270.} 

x1=−7605=−152,  x2=13505=270,  x3=−12705=−254{\displaystyle x_{1}=-{\frac {760}{5}}=-152,\ \ x_{2}={\frac {1350}{5}}=270,\ \ x_{3}=-{\frac {1270}{5}}=-254} 

Метод Крамера требует вычисления n+1{\displaystyle n+1}  определителей размерности n×n{\displaystyle n\times n} . При использовании метода Гаусса для вычисления определителей метод имеет сложность по элементарным операциям сложения-умножения порядка O(n4){\displaystyle O(n^{4})} , что сложнее, чем метод Гаусса при прямом решении системы. Поэтому метод, с точки зрения затрат времени на вычисления, считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью O(n3){\displaystyle O(n^{3})} , сравнимой со сложностью метода Гаусса^[2].

ru-wiki.org