Основы динамики – Основы динамики для чайников в физике. Решение задач, законы

Основы динамики

34. Динамика – это раздел механики, в котором изучаются связи между различными видами движений и причинами их вызывающими.

35. Первый закон Ньютона: существуют такие системы отсчёта, относительно которых тела движутся равномерно и прямолинейно, если на них не действуют другие тела или действие этих тел скомпенсировано.

36. Инерция – это свойство тела сохранять скорость своего движения неизменной по величине и направлению.

37. Инерциальная система отсчета – система отсчета, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно (по инерции).

38. Масса – это физическая величина, характеризующая инерционные и гравитационные свойства тел. Масса численно равна отношению ускорения a

0 эталона массы m₀=1 кг к ускорению a тела при их взаимодействии.

39. Плотность тела – это физическая величина, равная отношению массы тела к его объёму.

Измеряется в кг/м³.

40. Сила – это физическая величина, характеризующая действие на тело других тел или полей, в результате которого тело изменяет скорость своего движения или подвергается деформации. Сила измеряется в ньютонах. 1 Н= кг^.м/с². Сила – величина векторная. Она характеризуется числовым значением, направлением в пространстве и точкой приложения.

41. Второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально силе, приложенной к телу, и обратно пропорционально массе тела.

42. 1 ньютон – это сила, под действием которой тело массой 1 кг движется с ускорением 1 м/с².

43. Третий закон Ньютона: Тела действуют друг на друга с силами равными по модулю, противоположными по направлению и одинаковыми по природе.

44. Закон всемирного тяготения: тела притягиваются друг к другу с силой прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

где G – гравитационная постоянная.

45. Гравитационная постоянная G численно равна силе, с которой притягиваются тела массами по 1 кг на расстоянии 1 м друг от друга.

46. Сила тяжести – это сила, с которой тело притягивается Землёй.

47. Вес тела – это сила, с которой тело давит на опору или растягивает подвес.

48. Силы трения – это силы, препятствующие перемещению одного тела по поверхности другого. Они возникают в результате зацепления друг за друга мелких выступов, находящихся на поверхностях тел. При шлифовке выступы и впадины уменьшаются, что приводит к уменьшению сил трения. Но, если поверхности отшлифовать очень хорошо, силы трения вновь начинают увеличиваться из-за действия межмолекулярных сил трущихся поверхностей. Для уменьшения сил трения кроме шлифовки применяют смазку и замену трения скольжения трением качения, которое обычно на порядок меньше сил трения скольжения.

49. Сила трения покоя – это сила, возникающая на границе соприкосновения тел при отсутствии относительного движения тел. Она численно равна силе, приложенной к телу, и может изменяться от нуля до максимального значения внешней силы, при котором тело начинает перемещаться. Сила трения покоя в некоторых случаях может быть больше силы трения скольжения.

50. Коэффициент трения – это число, показывающее долю силы трения от силы, прижимающей поверхности друг к другу.

Коэффициент трения зависит от рода трущихся поверхностей и от чистоты обработки поверхностей.

studfiles.net

Лекция 5 Основы динамики

ПЛАН

1. Классическая механика. Границы ее применимости.

2. Первый закон Ньютона. Инерциальные системы отсчета.

3. Масса и импульс тела. Второй закон Ньютона.

4. Третий закон Ньютона.

1. Как уже говорилось, кинематика изучает движение тел, не рассматривал причин, обуславливающих это движение. Динамика же рассматривает законы движения тел и те причины, которые его вызывают или изменяют.

В основе так называемой классической или ньютоновской механики лежат три закона динамики, сформулированные Ньютоном в 1687 году.

Законы Ньютона (как и все остальные физические законы) возникли в результате обобщения большого количества опытных фактов. Правильность их (хотя и для обширного, но все же ограниченного круга явлений) подтверждается согласием с опытом тех следствий, которые из них вытекают.

Ньютоновская механика достигла в течений двух столетий та­ких огромных успехов; что многие физики XIX столетия были убеж­дены в ее всемогуществе. Однако с развитием науки обнаружились новые факты, которые не укладывались в рамки классической механики. Эти факты подучили свое объяснение в новых теориях – специальной теории относительности и квантовой механики. В специальной теории относительности, созданной Эйнштейном в 1905 году; подверглись радикальному пересмотру ньютоновские представления о пространстве и времени. Это привело к созданию «механики больших скоростей» или; как ее называют, релятивистской механики. Новая механика не привела, однако, к полному отрицанию старой ньютоновской механики. Уравнения релятивистской ме­ханики в пределе (для скоростей, малых по сравнению со скоростью света) переходят в уравнения классической механики. Та­ким образом, классическая механика вошла в релятивистскую меха­нику как ее частный случай и сохранила свое прежнее значение для описания движений, происходящими со скоростями, значительно меньшими скорости света. Аналогично обстоит дело и о соотноше­нием между классической и квантовой механикой, возникшей в 20-х годах нашего века в результате развития физики атома. Уравнения квантовой механики также дают в пределе (для масс, больших по сравнению с массами атомов) уравнения классической механики. Классическая механика вошла и в квантовую механику в качестве ее предельного случая. Таким образом, развитие науки не перечеркнуло классическую механику, я лишь показало ее ограниченную применимость. Классическая механика, основывающаяся на законах Ньютона, является механикой тел больших (по сравнению с массой атомов) масс, движущихся с малыми скоростями (по сравнению со скоростью света).

2. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит изменить ее это состояние.

Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии воздействия на него дру­гих тел называется

инерцией. Поэтому I закон называется такжезаконом инерции.Непосредственно проверить I закон Ньютона, строго говоря, невозможно, однако обобщение ряда экспериментальных фактов; а также совпадение вытекающих из закона следствий с опытными данными доказывает его справедливость. Часто наблюдаемое состояние покоя окружающих нас тел обусловлено тем, что воздействия различных тел компенсируют друг друга. При движении тело тем дольше сохраняет свою скорость, чем слабее на него действуют другие тела: например, скользящий по поверхности камень тем дольше движется, чем ровнее поверхность, то есть, чем меньше на него воздействие этой поверхности. Механическое движение относительно, ^ его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета. Те системы отсчета, по отношению к которым он выполняется, называютсяинерциальными системами отсчета.

Инерциальной системой отсчета является такая, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы.

С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звездную) систему отсчета. В этой системе тело отсчета – Солнце, координатные оси, представляющие собой три взаимоперпендикулярных направления, ориентированные на три произвольно выбранные звезды. Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако эффекты, обусловленные ее неинерциальностыо (Земля вращается вокруг собственной оси и вокруг Солнца), пренебрежимо малы, поэтому при решении многих задач ее можно считать инерциальной.

Никакими механическими опытами и наблюдениями, производимыми внутри инерциальной системы отсчета, нельзя установить, движется эта система отсчета равномерно и прямолинейно или покоится. Это заключение называется принципом относительности Галилея-Ньютона в механике. Теория относительности Эйнштейна обобщает этот результат и распространяет его на все явления природы.

3. Из опыта известно, что при одинаковых воздействиях различные тела неодинаково изменяют скорость своего движения, иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его массы). Всякое тело противится попыткам изменить состояние его движения. Это свойство тел называется инертностыо. В качестве количественной характеристики инертности используется величина, навиваемая массой тела. Масса тела– физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гра­витационная масса) свойства. С помощью точных экспериментов ус­тановлено, что инертная и гравитационная массы пропорциональны друг другу. Выбирая единицы таким образом, чтобы коэффициент пропорциональности стал равным единице, получим,m_ин=m_гр. Поэтому в дальнейшем будем говорить просто о массе тела.

Чтобы описать воздействия, упоминаемые в I законе Ньютона, вводят понятие силы.Под действием сил тела либо изменяют скорость, то есть приобретают ускорения (динамическое проявление сил), либо деформируются, то есть изменяют свою форму и размеры (статическое проявление сил). В каждый момент времени сила характеризуется числовым значением, направлением в пространстве и точкой приложения. Итак, сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело получает ускорение или изменяет свою форму и размеры (обозначим силу буквойF).

Второй закон Ньютона

Второй закон Ньютона – основной закон динамики поступатель­ного движения – отвечает на вопрос; как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил. Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение всегда прямо пропорционально равнодействующей приложенных сил a ~ F (m=const)[1] (равнодействующая сила – сила, равная геометрической сумме всех приложенных к телу сил). При действии одной и той же силы на различные тела их ускорения оказываются различными. Чем больше масса тела, то есть чем больше его инертность, тем меньшее ускорение под действием данной силы оно приобретает, то естьa~ 1/m(F=const) [2]. Используя выражения (1) и (2) и учитывая, что сила и ускорение- величины векторные, можем записать а = kF/m [ 3]. Полученное соотношение выражаетII закон Ньютона:ускорение, приобретаемое материальной точкой (телом) совпадает по направлению с действующей на нее силой и равно отношению этой силы к массе материальной точки (тела). В системе единиц СИ К=1, тогда

a=F/mF=ma=mdv/dt[ 4 ]

Учитывая, что масса тела (материальной точки) в классической механике есть величина постоянная, в выражении (4) ее можно внести под знак производной: F= d(mv)/dt [5]. Векторная ве­личина P=mV[ 6 ], численно равная произведению массы тела на его скорость и имеющая направление скорости; называетcяимпульсом этого тела(материальной точки). Подставив (6) в (5) получим F=dP/dt [ 7 ]. Выражение (7) – более общая формулировкаIi закона Ньютона: производная импульса материальной точки (тела) по времени равна действующей на нее силе. Из формулы (4) следует определение: за единицу силы принимают силу, которая единице массы сообщает ускорение, равное единице. Единица силы – ньютон (Н) : 1Н – сила, которая массе в 1 кг сообщает ускорение 1м/с², в направлении действия силы: 1Н= 1кг м/с².

В механике большое значение имеет принцип независимости сил: если на материальную точку действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласноII-му закону Ньютона, как будто других сил не было.

Согласно этому принципу, силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения за

дач. Например, на рис.1 действующая сила F=mаразложена на два компонента наF_(направлена по касательной к траектории) иF_n(направлена по нормали к центру кривизны).

Используя выражение a_=dv/dt и a_n=V²/R и V=R, можно записать:

F_ = m a_ = m dv/dt; F_n = ma_n = mV²/R = m  R²

4. Третий закон Ньютона.

Характер взаимодействия между материальными точками (телами) определяется третьим законом Ньютона: всякое действие тел друг на друга носит характер взаимодействия; силы с которыми действуют друг на друга тела (материальные точки), всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти тела: F₁=-F₂[ 8 ]. Рассмотрим например, два тела массамиm₁иm₂, которые действуют друг на друга с силамиF₁иF₂. Под действием силF₁иF₂тела приобретают ускоренияa₁иa₂.

Согласно второму закону Ньютона, можно записать :

F₁=m₁a₁иF₂=m₂a₂[ 9 ].

Используя выражения (8) и (9), получим m₁a₁ = -m₂a₂илиa₁ = -m₂a₂/m₁, т.е. ускорения двух взаимодействующих тел обратно-пропор-циональны их массам и направлены в противоположные стороны.

При использовании законов динамики иногда допускают следующую ошибку: если действующая сила всегда вызывает равную по модулю и противоположную по направлению силу противодействия, то, следовательно; их равнодействующая должна быть равна нулю и тела вообще не могут приобрести ускорения. Однако надо помнить, что во втором законе Ньютона речь идет об ускорении, приобретаемом телом под воздействием приложенных к нему сил. Равенство нулю ускорения означает равенство нулю равнодействующей сил, приложенных к одному и тому же телу. Третий закон Ньютона говорит о равенстве сил, приложенных к различным телам. На каждое из двух взаимодействующих тел действует только одна сила, которая и сообщает данному телу ускорение. Третий закон Ньютона так же как и первый, и второй законы динамики, выполняется только в инерциальных системах отсчета.

studfiles.net

Глава 1. Механика Основы динамики

1.7. Первый закон Ньютона. Масса. Сила

При движении тела по траектории его скорость может изменяться по модулю и направлению. Это означает, что тело двигается с некоторым ускорением. Вкинематике не ставится вопрос о физической причине, вызвавшей ускорение движения тела. Как показывает опыт, любое изменение скорости тела возникает под влиянием других тел. Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел.

Взаимодействием тел принято называть взаимное влияние тел на движение каждого из них.

Раздел механики, изучающий законы взаимодействия тел, называется динамикой.

Законы динамики были открыты великим ученым И. Ньютоном (1687 г.). Три закона динамики, сформулированные Ньютоном, лежат в основе так называемой классической механики. Законы Ньютона следует рассматривать как обобщение опытных фактов. Выводы классической механики справедливы только при движении тел с малыми скоростями, значительно меньшими скорости света c.

Самой простой механической системой является изолированное тело, на которое не действуют никакие тела. Так как движение и покой относительны, в различных системах отсчета движение изолированного тела будет разным. В одной системе отсчета тело может находиться в покое или двигаться с постоянной скоростью, в другой системе это же тело может двигаться с ускорением.

Первый закон Ньютона (или закон инерции) из всего многообразия систем отсчета выделяет класс так называемых инерциальных систем.

Существуют такие системы отсчета, относительно которых изолированные поступательно движущиеся тела сохраняют свою скорость неизменной по модулю и направлению.

Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Поэтому первый закон Ньютона называют законом инерции.

Впервые закон инерции был сформулирован Г. Галилеем (1632 г.). Ньютон обобщил выводы Галилея и включил их в число основных законов движения.

В механике Ньютона законы взаимодействия тел формулируются для класса инерциальных систем отсчета.

При описании движения тел вблизи поверхности Земли системы отсчета, связанные с Землей, приближенно можно считать инерциальными. Однако, при повышении точности экспериментов, обнаруживаются отклонения от закона инерции, обусловленные вращением Земли вокруг своей оси.

Примером тонкого механического эксперимента, в котором проявляется неинерциальность системы, связанной с Землей, служит поведение маятника Фуко. Так называется массивный шар, подвешенный на достаточно длинной нити и совершающий малые колебания около положения равновесия. Если бы система, связанная с Землей, была инерциальной, плоскость качаний маятника Фуко оставалась бы неизменной относительно Земли. На самом деле плоскость качаний маятника вследствие вращения Земли поворачивается, и проекция траектории маятника на поверхность Земли имеет вид розетки (рис. 1.7.1).

Рисунок 1.7.1. Поворот плоскости качаний маятника Фуко.

С высокой степенью точности инерциальной является гелиоцентрическая система отсчета (или система Коперника), начало которой помещено в центр Солнца, а оси направлены на далекие звезды. Эту систему использовал Ньютон при открытии закона всемирного тяготения (1682 г.).

Инерциальных систем существует бесконечное множество. Система отсчета, связанная с поездом, идущим с постоянной скоростью по прямолинейному участку пути, – тоже инерциальная система (приближенно), как и система, связанная с Землей. Все инерциальные системы отсчета образуют класс систем, которые движутся друг относительно друга равномерно и прямолинейно. Ускорения какого-либо тела в разных инерциальных системах одинаковы (

см. §1.2).

Итак, причиной изменения скорости движения тела в инерциальной системе отсчета всегда является его взаимодействие с другими телами. Для количественного описания движения тела под воздействием других тел необходимо ввести две новые физические величины – инертную массу тела и силу.

Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.

Если два тела взаимодействуют друг с другом, то в результате изменяется скорость обоих тел, т. е. в процессе взаимодействия оба тела приобретают ускорения. Отношение ускорений двух данных тел оказывается постоянным при любых воздействиях. В физике принято, что массы взаимодействующих тел обратно пропорциональны ускорениям:

В этом соотношении величины иследует рассматривать как проекции векторовина осьOX (рис. 1.7.2). Знак «минус» в правой части формулы означает, что ускорения взаимодействующих тел направлены в противоположные стороны.

В Международной системе единиц (СИ) масса тела измеряется в килограммах (кг).

Масса любого тела может быть определена на опыте путем сравнения с массой эталона (m_эт = 1 кг). Пусть m₁ = m_эт= 1 кг. Тогда

Масса тела – скалярная величина. Опыт показывает, что если два тела с массами m₁ и m₂ соединить в одно, то масса m составного тела оказывается равной сумме масс m₁ и m₂этих тел:

Это свойство масс называют аддитивностью.

Рисунок 1.7.2. Сравнение масс двух тел.

Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую причину: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.

Для измерения сил необходимо установить эталон силы и способ сравнения других тел с этим эталоном.

В качестве эталона силы можно взять пружину, растянутую до некоторой заданной длины. Модуль силы F₀, с которой эта пружина при фиксированном растяжении действует на прикрепленное к ее концу тело, называют эталоном силы. Способ сравнения других тел с эталоном состоит в следующем: если тело под действием измеряемой силы и эталонной силыостается в покое (или движется равномерно и прямолинейно), то силы равны по модулюF = F₀ (рис. 1.7.3).

Рисунок 1.7.3. Сравнение силы с эталоном..

Если измеряемая сила F больше (по модулю) эталонной силы, то можно соединить две эталонные пружины параллельно (рис. 1.7.4). В этом случае измеряемая сила равна 2F₀. Аналогично могут быть измерены силы 3F₀, 4F₀ и т. д.

Рисунок 1.7.4. Сравнение силы с эталоном..

Измерение сил, меньших 2F₀, может быть выполнено по схеме, показанной на рис. 1.7.5.

Рисунок 1.7.5. Сравнение силы с эталоном..

Эталонная сила в Международной системе единиц называется ньютон (Н).

На практике нет необходимости все измеряемые силы сравнивать с эталоном силы. Для измерения сил используют пружины, откалиброванные описанным выше способом. Такие откалиброванные пружины называются динамометрами. Сила измеряется по растяжению динамометра (рис. 1.7.6).

Рисунок 1.7.6. Измерение силы по растяжению пружины. При равновесии

studfiles.net

Основы Динамики

Основы Динамики

При решении задач кинематики системы отсчета выбирались произвольно, а причины изменения скорости, то есть возникновения ускорения, не рассматривались.

Раздел механики, в котором решаются задачи, связанные со взаимодействием тел и соответственно с возникновением ускорений, называется динамикой. Основные законы динамики были открыты Исааком Ньютоном и носят его имя.

Первый закон Ньютона позволяет ввести новое понятие – “инерциальная система отсчета”. В этих системах явления природы описываются наиболее просто.

За инерциалъную систему отсчета принимается такая система, в которой тело движется равномерно и прямолинейно, если на него не действуют другие тела или их действия скомпенсированы.

Итак, первый закон Ньютона является постулатом существования инерциальных систем отсчета.

Если можно с достаточной степенью приближенности выделить инерциальную систему отсчета (например, связанную с Землей), то можно указать и другие инерциальные системы отсчета. Примером служит равномерно и прямолинейно движущийся относительно Земли поезд.

Если свободное тело относительно поезда будет двигаться с постоянной скоростью, то относительно Земли оно будет двигаться так же, хотя величина скорости будет другой. Это вытекает из закона сложения скоростей Галилея.

В инерциальных системах отсчета изменение скорости (и возникновение ускорения) может быть вызвано только взаимодействием тел. Физическая природа взаимодействий может быть различной. Однако все они характеризуются абстрактной физической величиной – силой. Сила измеряется в ньютонах.

Второй закон Ньютона гласит, что ускорение, которое возникает у тела, прямо пропорционально действующей на него силе и обратно пропорционально массе тела:

Отсюда можно сделать вывод, что сила есть причина возникновения ускорения:

В Международной системе единиц (СИ) за единицу силы принимается 1 Н. 1 Н – это такая сила, которая телу массой 1 кг сообщает ускорение 1 м/с².

Если на тело действует несколько сил, то необходимо искать равнодействующую. А поскольку сила – векторная величина, в общем случае получаем:

Это уравнение носит название основного уравнения динамики (ОУД). Из него следует, что именно равнодействующая сила обусловливает величину и направление ускорения.

Третий закон Ньютона показывает, что при взаимодействии двух тел возникают сразу две силы, равные по модулю, противоположно направленные и действующие по линии, соединяющей два тела.

Эти силы приложены к разным телам, поэтому не подлежат сложению. Эти силы равноправны, результатом их действия являются ускорения взаимодействующих тел.

В итоге следует отметить, что второй и третий законы Ньютона выполняются только в инерциальных системах отсчета и только для тел, которые могут быть приняты за материальные точки.

Все задачи по динамике решаются с применением основного уравнения динамики (ОУД). Сначала предстоит выделить тело, которое мы примем за материальную точку (или систему материальных точек).

Далее следует рассмотреть поочередно все взаимодействия, в которых участвует выделенная материальная точка.

При составлении чертежа следует анализировать действие каждой из двух сил, возникающих по третьему закону Ньютона при взаимодействии, причем на основной чертеж проставлять только ту силу, которая приложена к выделенной нами материальной точке. Рассмотрим действия, которые следует произвести, на примере простой задачи.

Задача. Человек массой 50 кг поднимается в лифте с ускорением 1,5 м/с². Найти давление, создаваемое человеком на пол лифта.

Дано: m = 50 кг а = 1,5 м/с²
F – ?
Решение
Для составления чертежа следует решить вопрос: человека или лифт целесообразно принять за материальную точку? Так как все взаимодействия человека с другими телами известны, целесообразно именно человека принять за материальную точку. Изобразив на основном чертеже лифт и человека, укажем оси проецирования и направление ускорения.

Проанализируем взаимодействие человека с Землей. В результате этого взаимодействия возникают две силы: одна из них приложена к человеку (mg), другая по третьему закону Ньютона – к Земле.

Из этих двух сил на основной чертеж проставляем только силу тяжести (mg), поскольку она приложена к интересующей нас материальной точке (рис. 21). Если бы действовала только эта сила, человек начал бы свободно падать. Однако ситуация иная: он поднимается вверх с ускорением. Следовательно, выделенная нами материальная точка участвует во втором взаимодействии – человека и пола лифта.

Укажем на дополнительном чертеже расстановку сил (рис. 22). Человек оказывает давление на пол лифта (F_д), пол лифта действует на человека с силой упругости N.

Эти силы возникают соответственно третьему закону Ньютона. Нас интересует при этом только сила N, поскольку она приложена к выделенной материальной точке, и ее мы проставляем на основной чертеж. Других взаимодействий нет.

Поскольку на материальную точку действуют 2 силы, применяем ОУД:

Проецируем векторы на ось Оу и получаем:

Отсюда находим N:

Ответ: человек давит на пол лифта с силой 575 Н.

sfiz.ru

1.2 Основы динамики

Законы Ньютона. Масса. Импульс. Закон сохранения импульса. Реактивное движение. Силы в механике − гравитационные, упругости, трения. Невесомость и перегрузки. Неинерциальные системы отсчета. Физические и биологические вопросы, связанные с неинерциальными системами отсчета. Абсолютно твердое тело. Момент силы. Центр тяжести. Рычаг. Суставы и рычаги в опорно-двигательном аппарате человека. Момент инерции.

Литература: [1, с. 9–14; 23–27]; [2, с. 25–46; 66–74];

Основные законы динамики были сформулированы в 80-х годах XVII столетия Ньютоном. Они представляют собой обобщение ре­зультатов многовекового человеческого опыта. Приведем современные формулировки трех законов Ньютона.

Первый закон Ньютона (закон инерции): всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не выведет его из этого состояния.

Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инерцией (от латинского inertia − бездеятельность). Опыт показывает, что при одинаковом воздействии различные тела по-разному изменяют свою скорость. Иными словами, одинаковые воздействия вызывают у различных тел различные ускорения. Следовательно, величина ускорения, приобретаемого телом, зависит не только от величины воздействия, но и от некоторого собственного свойства тела. Это свойство тела характеризуют физической величиной, называемой массой. В этом смысле можно сказать, что масса есть мера инерции тела. Обозначают массу − m. Единица измерения массы в системе СИ − кг (килограмм).

Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. В этих системах отсчета движение тела выглядит особенно простым. Тела, не подверженные воздействию других тел, движутся относительно таких систем без ускорения, т.е. прямолинейно и равномерно.

Второй закон Ньютона: ускорение 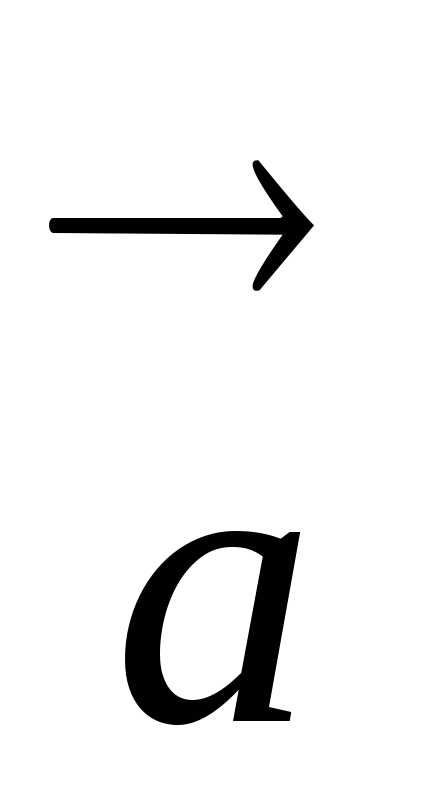, приобретаемое телом под действием силы 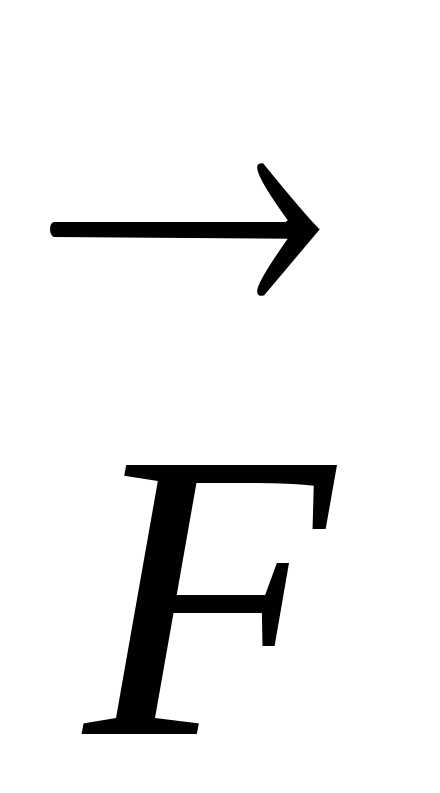, направлено так же, как сила, а по величине пропорционально силе и обратно пропорционально массе тела:

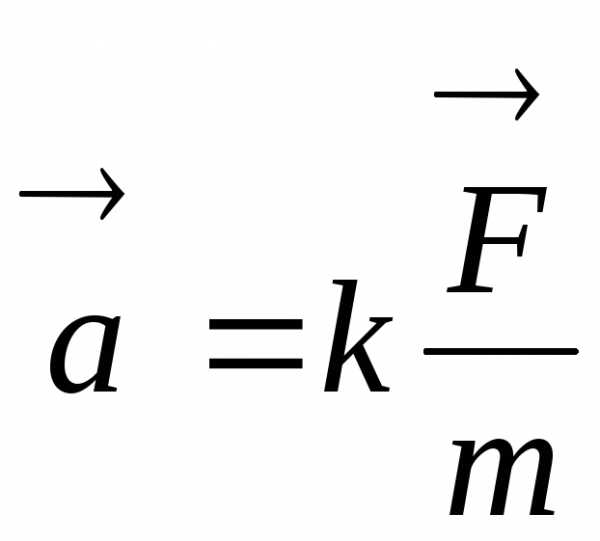(1.2.1)

где k − коэффициент пропорциональности, зависящий от выбора единиц измерения. Единицы измерения силы можно, выбрать так, чтобы k=1. Тогда:

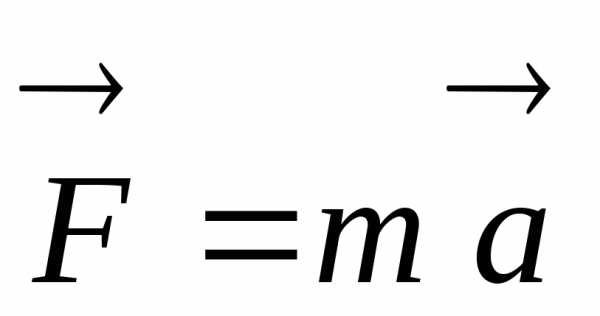(1.2.2)

В таком математическом виде принято выражать второй закон Ньютона (основной закон динамики поступательного движения). Подчеркнем, что под 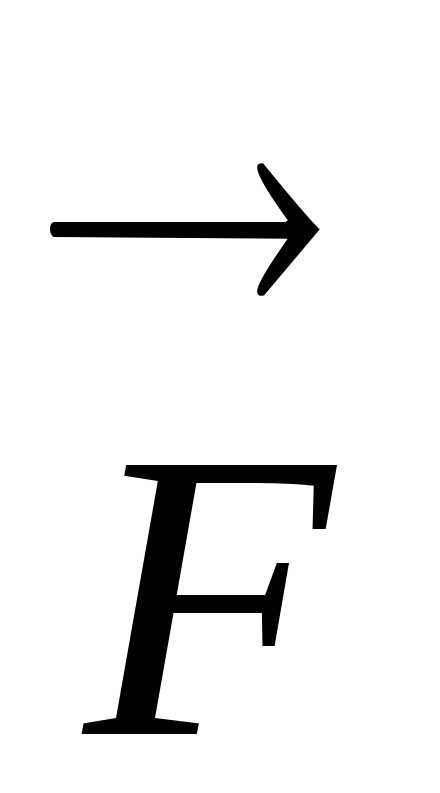подразумевается векторная сумма (равнодействующая) всех сил, действующих на тело.

Если одно тело действует на второе, то в свою очередь второе тело действует на первое. Например, груз, давящий на опору, испытывает давление со стороны этой опоры. Соотношение между силами, приложенными к взаимодействующим телам, описывается третьим законом Ньютона (закон действия и противодействия): два взаимодействующих тела действуют друг на друга с силами, равными по величине и противоположными по направлению

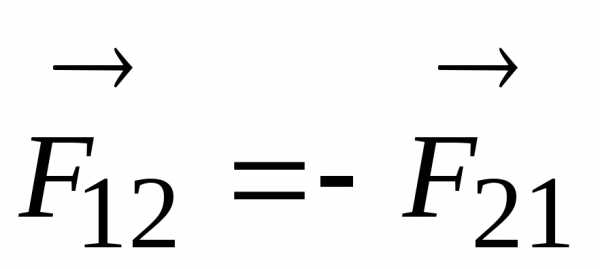(1.2.3)

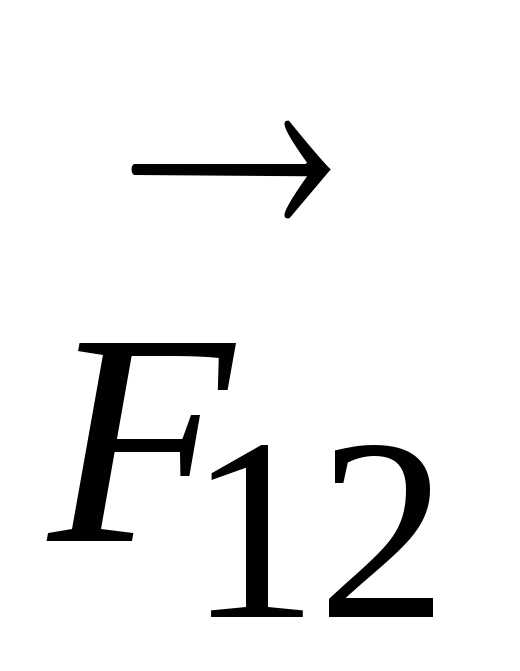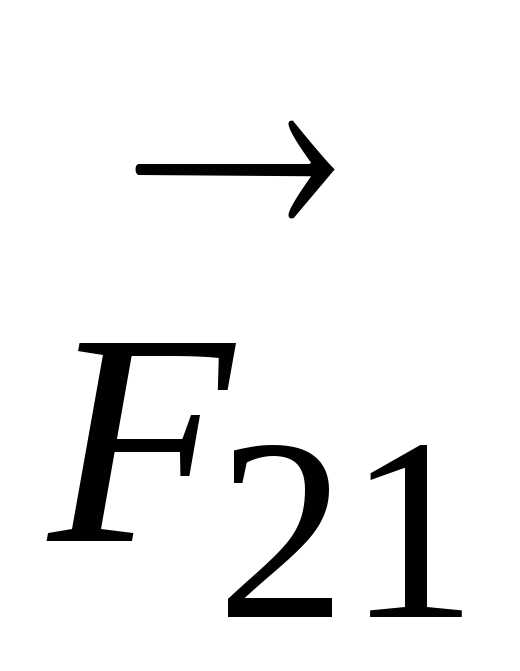где − сила действия первого тела на второе, — сила действия второго тела на первое.

На основании законов Ньютона можно уточнить формулировку понятия силы: сила − физическая величина, характеризующая взаимодействие тел, в результате которого они приобретают ускорение. На основе второго закона Ньютона можно установить единицу измерения силы. Она получила название ньютон (Н):

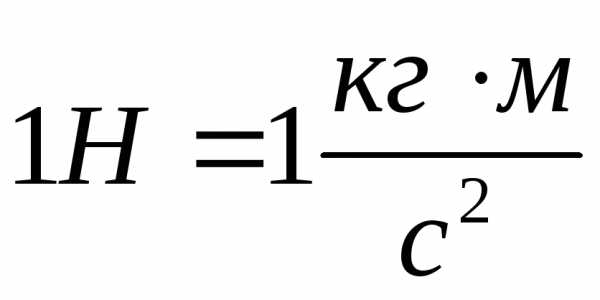
Второй закон Ньютона можно записать в другой форме. На основании формулы (1.1.12) следует, что:

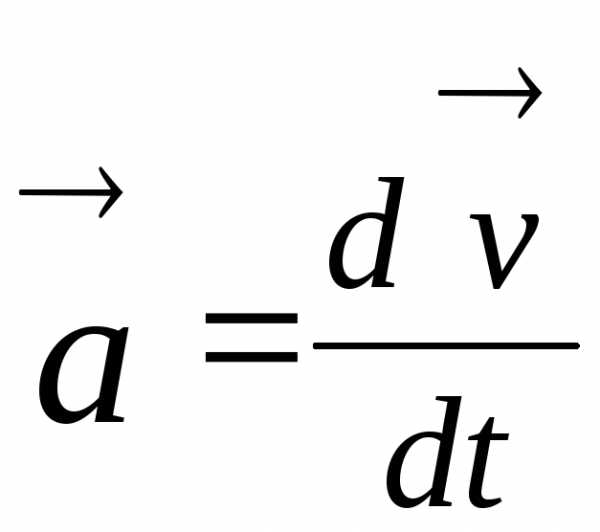(1.2.4)

тогда

(1.2.5)

Физическая величина:

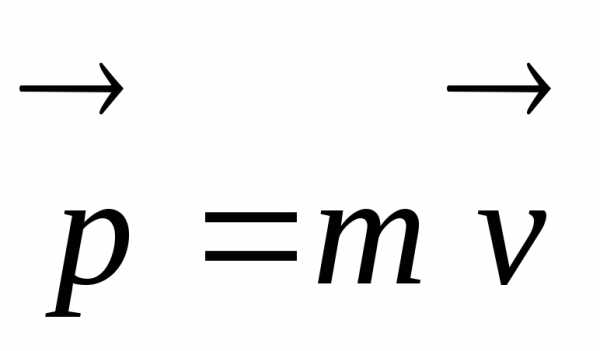(1.2.6)

равная произведению массы тела на его скорость называется импульсом тела. Совокупность тел, выделенных для рассмотрения, называется механической системой. Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соответствии с этим силы, действующие на тела системы, подразделяются на внутренние и внешние. Внутренними называют силы, с которыми тела системы действуют друг на друга, внешними − силы, обусловленные воздействием тел, не принадлежащих системе. Система, в которой внешние силы отсутствуют, называется замкнутой (или изолированной). Представим себе некую механическую изолированную систему, состоящую из n тел. Пусть, взаимодействуя друг с другом, тела данной системы изменяют свой импульс. Используя для каждого из тел системы второй закон Ньютона изменение его импульса за время dt можно представить следующим образом:

,

,

…………………..,

,

…………………..,

.

где 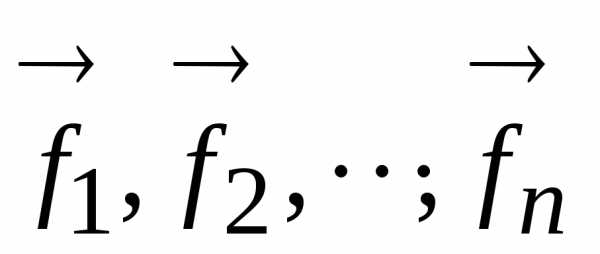− равнодействующие внутренних, а− равнодействующие внешних сил действующих на каждое из тел. Сложим вышеприведенныеn равенств почленно. Так как согласно третьему закону Ньютона, каждой силе соответствует равная по величине противодействующая сила, то при сложении все внутренние силы взаимно уничтожаются, поэтому 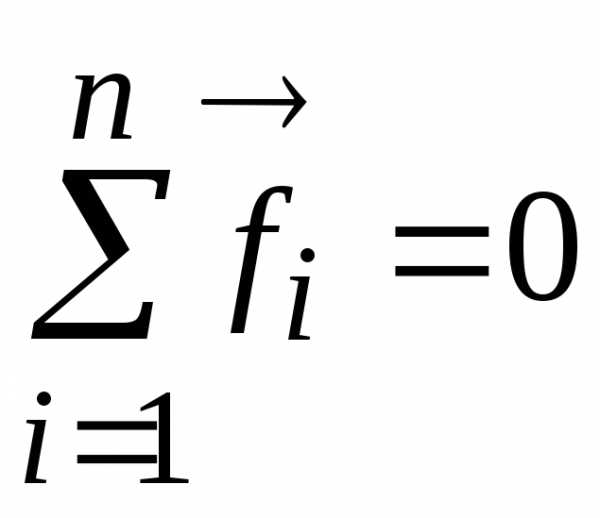. Тогда:

.

Для изолированной системы: . Поэтому:

(1.2.7)

Формула (1.2.1.7) выражает закон сохранения импульса: в изолированной системе векторная сумма импульсов всех тел остается величиной постоянной при любых взаимодействиях тел этой системы. Закон сохранения импульса находит широкое отражение в технике и природе. Именно выполнением закона сохранения импульса объясняется реактивное движение − движение тела, возникающее при отделении от него с некоторой относительной скоростью какой то части тела (движение ракет, явление отдачи при выстреле и т.д.). Тело (ракета, ружье) приобретает импульс, равный по величине импульсу отделившегося тела (газ, пуля). Данный вид движения используется некоторыми живыми организмами, которые передвигаются посредством отдачи воды, выбрасываемой ими из особых полостей тела (кальмары, спруты, медузы, некоторые моллюски).

До сих пор мы рассматривали силы вообще, не интересуясь их происхождением. Рассмотрим некоторые разновидности сил, широко представленных в механических процессах, происходящих в живых организмах. Классическая механика рассматривает силы, имеющие гравитационную и электромагнитную природу.

Силы тяготения (гравитационные силы (от латинского слова gravitas − тяжесть)) − силы с которыми притягиваются друг к другу все материальные тела во Вселенной. Данное взаимодействие тел осуществляется посредством гравитационного поля (поля тяготения). Гравитационные силы подчиняются закону всемирного тяготения, открытому Ньютоном в 1667 году. Согласно этому закону любые две материальные точки притягиваются друг к другу с силой F_гр, пропорциональной произведению их масс (m₁ и m₂) и обратно пропорциональной квадрату расстояния r между ними:

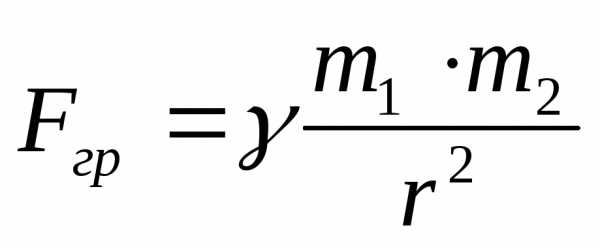(1.2.8).

Коэффициент пропорциональности γ называется гравитационной постоянной. На данный момент времени опытным путем установлено, что численное значение . Если тела нельзя считать материальными точками, их представляют как совокупность материальных точек и, геометрически суммируя силы взаимодействия отдельных точек, находят результирующую силу тяготения между ними.

Из закона всемирного тяготения следует, что масса характеризует не только инерцию тел, но и их гравитационные свойства.

Вблизи поверхности Земли все тела падают с одинаковым ускорением, которое называют ускорение свободного падения и обозначают 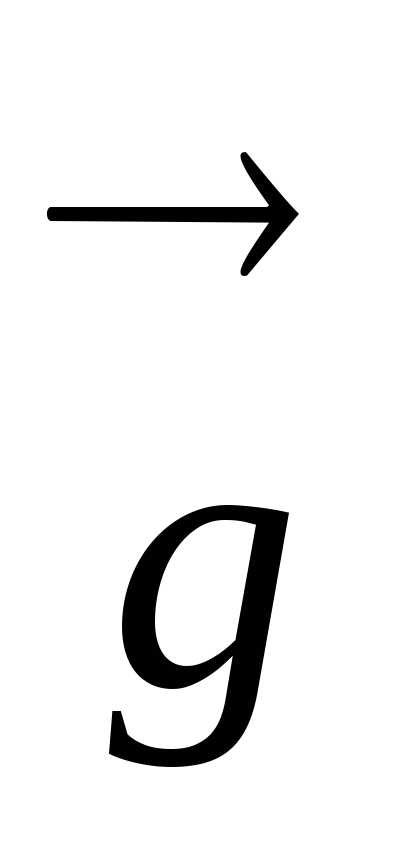. Значение ускорения свободного падения определяется выражением:

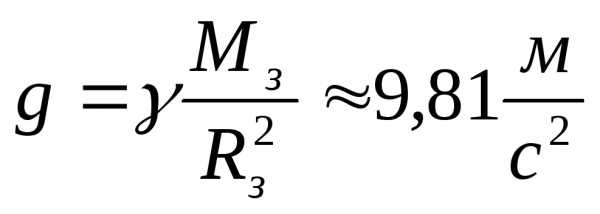(1.2.9)

где М_з − масса Земли, R_з − радиус Земли. Отсюда вытекает, что в системе отсчета связанной с Землей, на всякое тело действует сила:

(1.2.10).

Эта сила называется силой тяжести. По величине она приблизительно равна (отличие не превышает 0,36%) силе гравитационного притяжения тела к Земле. Данное различие обусловлено тем, что строго говоря, система отсчета связанная с Землей не является инерциальной (вращается с нормальным ускорением ). Силу тяжести не следует путать с весом тела. Вес тела это сила, с которой тело действует на подвес или опору вследствие гравитационного притяжения к Земле.

Сила тяжести 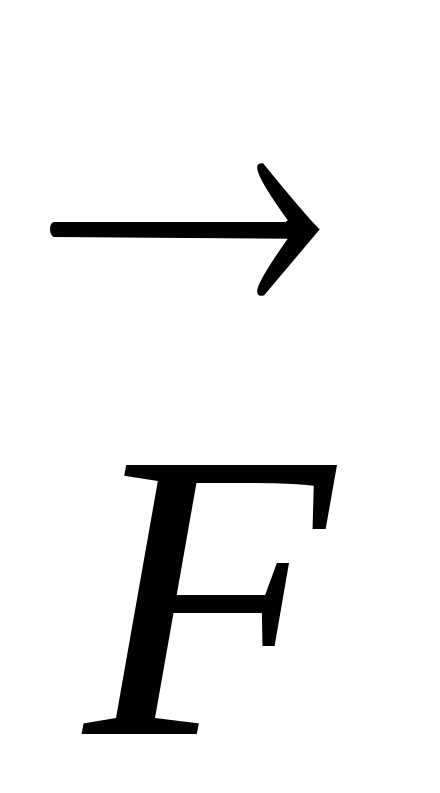это сила, действующая на тело вблизи поверхности Земли вследствие гравитационного притяжения к Земле.

Сила тяжести имеет гравитационную природу, вес тела электромагнитную. У данных сил разные точки приложения: вес приложен к опоре или подвесу, сила тяжести к самому телу (рисунок 1.10).

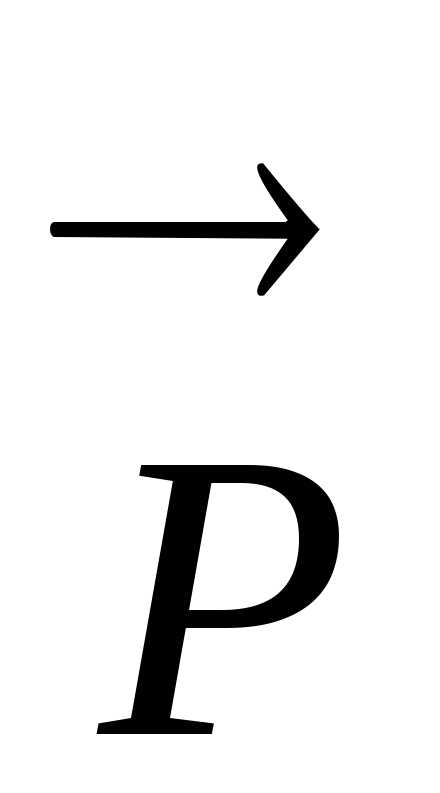
рисунок 1.10

Если опора или подвес покоятся относительно Земли или движутся без ускорения, то сила тяжести равна весу тела:

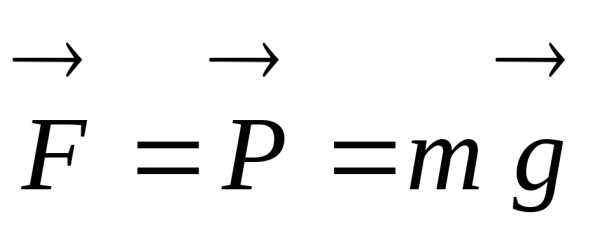(1.2.11)

Если опора или подвес движется с ускорением 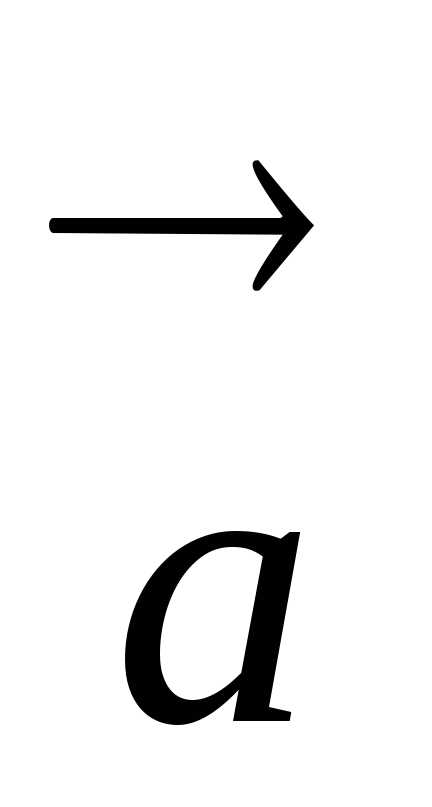, вес тела перестает быть равным силе тяжести. Используя второй закон Ньютона можно получить, что в данном случае:

(1.2.12)

При движении опоры или подвеса с ускорением равным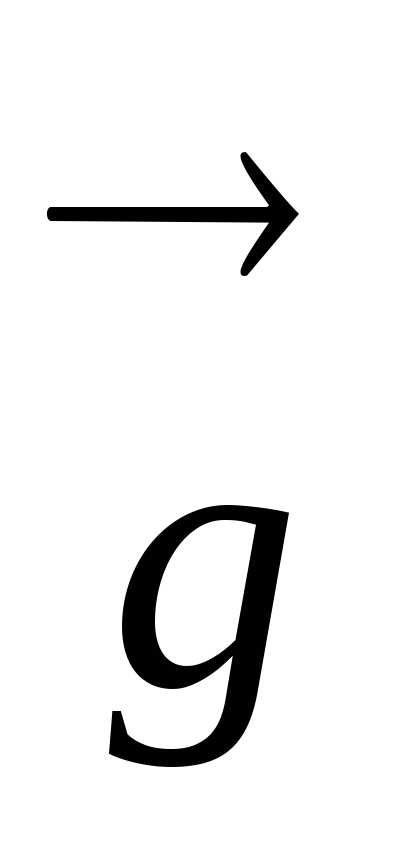вес тела становится равным нулю. Тело не будет оказывать давление на опору и наступает так называемое состояниеневесомости. В состоянии невесомости нарушается течение многих биологических процессов, так как внутренние органы перестают давить на внутренние органы расположенные ниже, а все тело в целом перестает давить на кости скелета в целом. Формула (1.2.12) объясняет возникновение перегрузки − увеличение веса тела, вызванное его ускоренным движением относительно инерциальной системы отсчета. Например, при старте космического корабля ускорение 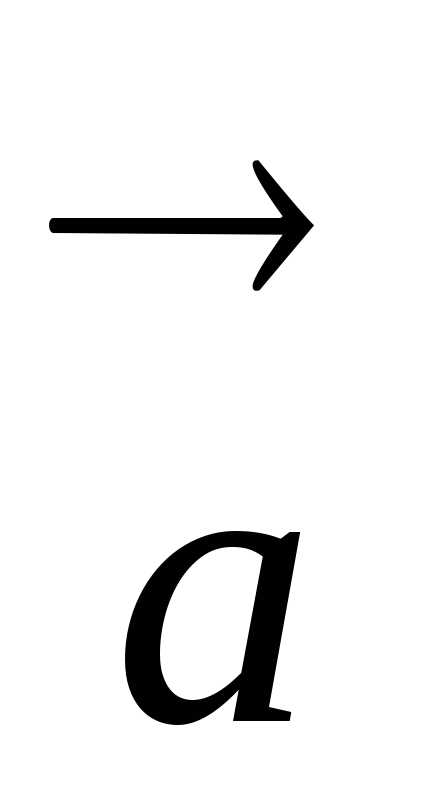направленно верх и вес космонавта определяется выражением:P = m (g+a). Численно перегрузка n (коэффициент перегрузки) равна:

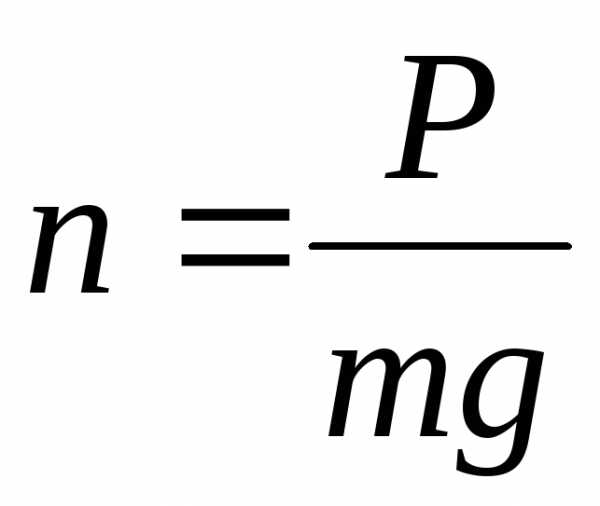(1.2.13)

Сила может деформировать тело − сместить составляющие его частицы относительно друг друга. В соответствии с третьим законом Ньютона внутри тела возникает противодействующая сила равная по величине деформирующей силе и противоположная ей по направлению. Данную силу называют силой упругости. Силы упругости обусловлены взаимодействием между молекулами и атомами тела и имеют электромагнитную природу. Величина силы упругости возникающей при малых деформациях определяется законом Гука:

(1.2.14)

где k − коэффициент пропорциональности, называемый жесткостью или коэффициентом жесткости; Δx − величина деформации (смещение). Знак минус указывает на противоположность направления силы упругости и смещения.

Очень распространенным взаимодействием тел является трение. Трение подразделяется на внешнее и внутреннее. Внешнее трение возникает при соприкосновении поверхностей разных тел движущихся относительно друг друга. Внутреннее возникает между слоями одного и того же тела (жидкость, газ). Различают также сухое и жидкое (вязкое) трение. Сухое возникает между поверхностями твердых тел в отсутствии жидкой или газообразной прослойки. Жидкое трение это трение между твердым телом и жидкостью (газом) или слоями жидкости (газа). Помимо этого выделяют трение покоя, трение скольжения и трение качения (возникает между цилиндрическим или шарообразным телом и поверхностью). Опыт показывает, что возникающая при этом сила трения покоя, скольжения и качения не зависит от площади соприкасающихся тел и приблизительно прямо пропорциональна силе нормального давления 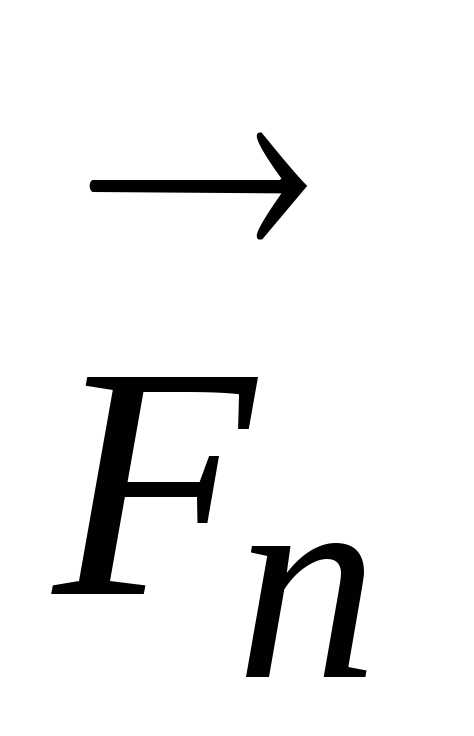, прижимающей трущиеся поверхности друг к другу:

(1.2.15)

где k − коэффициент трения. Он зависит от рода вещества и качества обработки трущихся поверхностей. Силы трения обусловлены взаимодействием частиц соприкасающихся тел и имеют электромагнитную природу. Трение играет большую роль в природе. Действие органов передвижения и хватательных органов живых существ основано на трении скольжения, трение удерживает корни растений в почве, шарообразность семян некоторых растений (трение качения) способствует их откатыванию на большие расстояния и т д.

Рассмотренные нами законы Ньютона справедливы только для инерциальных систем отсчета. В неинерциальных системах отсчета (движущихся относительно инерциальных систем с ускорением) они несоблюдаются. Невыполнение данных законов в неинерциальных системах можно обнаружить на примере тела, покоящегося в некоторой инерциальной системе. В этом случае векторная сумма всех сил действующих на тело равна 0 (). Однако для наблюдателя, находящегося в неинерциальной системе отсчета, движущейся относительно инерциальной с ускорением а, тело будет иметь ускорение -а, приобретаемое без воздействия каких либо тел. Применяя второй закон Ньютона наблюдатель получит: 0=-ma, что невозможно.

Для того, чтобы законы Ньютона были применимы к неинерциальным системам отсчета вводят в рассмотрение силы особого рода – силы инерции. В нашем примере наблюдатель, связанный с неинерциальной системой отсчета может считать, что тело пришло в движение под действием силы инерции . Сила инерции обусловлена неинерциальностью той системы отсчета, в которой рассматриваются механические явления. Не существует тел, воздействием которых была бы обусловлена эта сила. Тогда в общем случае второй закон Ньютона в неинерциальных системах отсчета принимает следующий вид:

(1.2.16)

Таким образом, введение сил инерции позволяет описывать движение тел в любых системах отсчета (как инерциальных так и не инерциальных) с помощью одних и тех же уравнений. Примером действия сил инерции является действие сил на пассажиров при резком торможении транспорта. Силы инерции возникают не только в прямолинейно движущихся, но и во вращающихся неинерциальных системах. Такие силы называют центробежными силами инерции. Если тело еще и движется относительно вращающейся системы отсчета с некой скоростью v, кроме центробежной возникает еще одна сила инерции – сила Кориолиса (Гюстав Кориолис французский механик).

Данная сила перпендикулярна к скорости v. Именно эта сила при свободном падении отклоняет тела к востоку. Благодаря ее действию у рек подмывается всегда правый берег в северном полушарии и левый в южном, поворачивает плоскость колебания маятника с течением времени (доказательство суточного вращения Земли).

Под абсолютно твердым телом понимают физическое тело, неподверженное деформации, составные части которого не смещаются относительно друг друга. Пусть твердое тело произвольной формы вращается под действием силы вокруг неподвижной оси ОО^‘.

Моментом силы называется вектор , модуль которого равен произведению вращающей силы на ее плечо. Плечом силы называют длину перпендикуляра от данной оси, до прямой вдоль которой действует сила (в нашем случае это радиус окружности описываемой точкой приложения силы, т.е. точкой А). Таким образом:

(1.2.17)

Центр тяжести тела это точка приложения равнодействующей сил тяжести действующих на все элементарные (очень малые) части тела, которая не изменяет своего положения при любых поворотах тела. Центр тяжести однородных симметричных тел (шар, квадрат, цилиндр и т.п.) находится в их геометрическом центре. Центр тяжести может находиться вне тела (например, центр тяжести однородного кольца).

Простые механизмы – это приспособления, которые изменяют величину или направление приложенных к телу сил. Одним из самых распространенных механизмов является рычаг.

Рычаг – тело, которое может поворачиваться вокруг неподвижной оси, проходящей через это тело, или вокруг неподвижной точки опоры. Различают рычаги первого или второго рода.

Рисунок 1.11

Действие рычага основано на том, что при вращательном движении справедлив закон, аналогичный третьему закону Ньютона для поступательного движения. При взаимодействии двух вращающихся тел вращающий момент М₁, с которым первое тело действует на второе, равен вращающему моменту М₂с которым второе тело действует на первое, и противоположен ему по направлению.

(1.2.18)

Из рисунка 1.11 видно, что согласно (1.2.18) и (1.2.17) F₁L₁= F₂L₂ и поэтому рычаг дает выигрыш в силе.

В скелете животных и человека все кости, имеющие некоторую свободу движения, являются рычагами. Например, у человека – кости рук и ног, нижняя челюсть, череп, пальцы. У кошек рычагами являются подвижные когти; у многих рыб – шипы спинного плавника; у членистоногих – большинство сегментов их наружного скелета; у двустворчатых моллюсков – створки раковины.

Рычажные механизмы скелета в основном рассчитаны на выигрыш в скорости при потере в силе. Особенно большие выигрыши в скорости получаются у насекомых.

Рассмотрим условия равновесия рычага на примере черепа (рисунок 1.13). Здесь ось вращения рычага О проходит через сочленение черепа и первого позвонка. Спереди от точки опоры на относительно коротком плече действует сила тяжести головы R, позади – сила F тяги мышц и связок, прикреплённых к затылочной кости.

Другим примером работы рычага является действие свода стопы при подъёме на полупальцы. Опорой О рычага, через которую проходит ось вращения, служат головки плюсневых костей. Преодолеваемая сила R – вес всего тела – приложена к таранной кости.

Действующая мышечная сила F, осуществляющая подъём тела, передаётся через ахиллово сухожилие и приложена к выступу пяточной кости.

Интересные рычажные механизмы можно найти в некоторых цветках (например, тычинки шалфея), а также в некоторых раскрывающихся плодах.

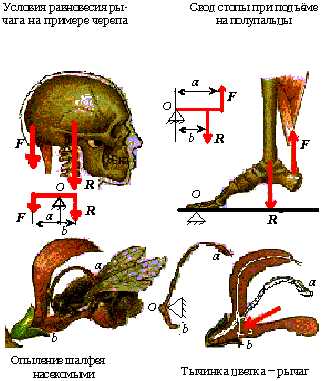
Рисунок 1.12

Мысленно разобьем наше вращающееся тело (см. рис.1.12) на очень малые частицы – элементарные массы Δm_i. Тогда к каждой элементарной массе Δm_i будет приложена элементарная вращающая сила ΔF_i. Согласно второму закону Ньютона:

(1.2.19)

где a_i – линейное ускорение, сообщаемое элементарной массе. Умножив обе части этого равенства на радиус r_i окружности, описываемой элементарной массой и воспользовавшись связью между угловым ускорением ε и линейным ускорением а, получим:

(1.2.20)

Очевидно, что ΔF_ir_i= ΔM_i – вращающий момент силы ΔF_i, приложенный к элементарной массе. Физическая величина:

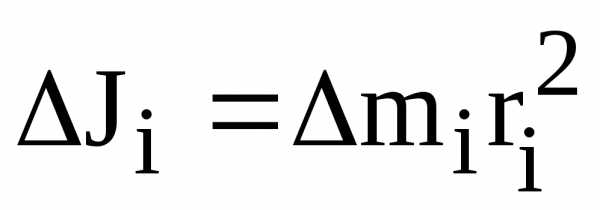(1.2.21)

равная произведению массы материальной точки на квадрат расстояния до оси вращения называется моментом инерции материальной точки. Учитывая введенное обозначение, получим:

ΔM_i=ΔJ_iε (1.2.22)

Cсуммируя вращающие моменты ΔM_i, приложенные ко всем элементарным массам, составляющим тело, получим:

ΣΔM_i=εΣΔJ_i (1.2.23)

где ΣΔM_i = М – вращающий момент, приложенный к телу, т.е. момент силы F. ΣΔJ_i = J – момент инерции тела. Следовательно, моментом инерции тела называется сумма моментов инерции всех материальных точек, составляющих тело. Тогда формула (1.2.22) примет следующий вид:

M=Jε (1.2.24)

Формула (1.2.23) выражает второй закон Ньютона для вращательного движения: момент вращающей силы, приложенный к телу, равен произведению момента инерции тела на угловое ускорение. Момент инерции характеризует инерционные свойства тел при вращательном движении подобно тому, как масса характеризует инерционные свойства тел при поступательном движении. Однако в отличие от массы момент инерции тела может иметь множество значений в зависимости от выбора оси вращения. Из формулы (1.2.20) следует, что единицей измерения момента инерции является ().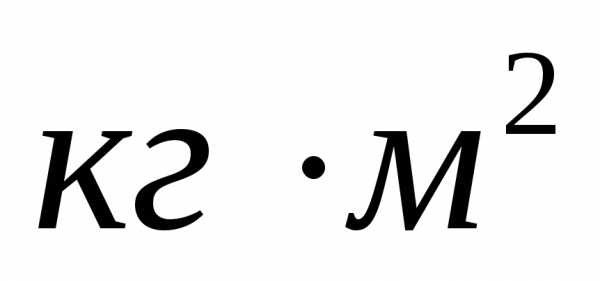

Так как: (см. формулу 1.1.22) формулу (1.2.23) можно представить в виде:

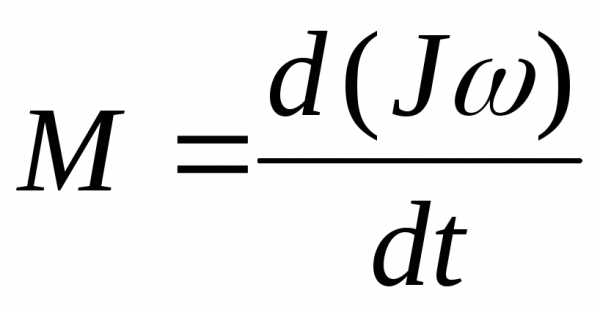(1.2.25)

Векторная величина называется моментом импульса.

studfiles.net

Глава 1. Механика Основы динамики

1.8. Второй закон Ньютона

Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.

Приступая к формулировке второго закона, следует вспомнить, что в динамике (см. §1.7) вводятся две новые физические величины – масса тела m и сила а также способы их измерения. Первая из этих величин – массаm – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила – является количественной мерой действия одного тела на другое.

Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:

1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:

2. Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам:

Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:

Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила :

В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с². Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы (см. §1.7):

Если на тело одновременно действуют несколько сил (например, ито под силойв формуле, выражающей второй закон Ньютона, нужно пониматьравнодействующую всех сил:

Если равнодействующая сила то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

Глава 1. Механика Основы динамики

1.9. Третий закон Ньютона

В §1.7 понятие массытела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений

В векторной форме это соотношение принимает вид

Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами ивозникающими при взаимодействии тел. Отсюда следует:

Это равенство называется третьим законом Ньютона.

Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.

Рис. 1.9.1 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.

Рисунок 1.9.1. Третий закон Ньютона.

Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю. В качестве примера рассмотрим рис. 1.9.2, на котором изображены два тела с массами m₁ и m₂, жестко связанные между собой невесомой нерастяжимой нитью и двигающиеся с одинаковым ускорением как единое целое под действием внешней силыМежду телами действуют внутренние силы, подчиняющиеся третьему закону Ньютона:Движение каждого тела зависит от сил взаимодействия между ними. Второй закон Ньютона, примененный к каждому телу в отдельности, дает:

Складывая левые и правые части этих уравнений и принимая во внимание, что иполучим:

Внутренние силы исключились из уравнения движения системы двух связанных тел.

Рисунок 1.9.2. Исключение внутренних сил.

studfiles.net

Глава 1. Механика Основы динамики

1.8. Второй закон Ньютона

Второй закон Ньютона – основной закон динамики. Этот закон выполняется только в инерциальных системах отсчета.

Приступая к формулировке второго закона, следует вспомнить, что в динамике (см. §1.7) вводятся две новые физические величины – масса тела m и сила а также способы их измерения. Первая из этих величин – массаm – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие. Вторая – сила – является количественной мерой действия одного тела на другое.

Второй закон Ньютона – это фундаментальный закон природы; он является обобщением опытных фактов, которые можно разделить на две категории:

1. Если на тела разной массы подействовать одинаковой силой, то ускорения, приобретаемые телами, оказываются обратно пропорциональны массам:

2. Если силами разной величины подействовать на одно и то же тело, то ускорения тела оказываются прямо пропорциональными приложенн силам:

Обобщая подобные наблюдения, Ньютон сформулировал основной закон динамики:

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение:

Это и есть второй закон Ньютона. Он позволяет вычислить ускорение тела, если известна его масса m и действующая на тело сила :

В Международной системе единиц (СИ) за единицу силы принимается сила, которая сообщает телу массой 1 кг ускорение 1 м/с². Эта единица называется ньютоном (Н). Ее принимают в СИ за эталон силы (см. §1.7):

Если на тело одновременно действуют несколько сил (например, ито под силойв формуле, выражающей второй закон Ньютона, нужно пониматьравнодействующую всех сил:

Если равнодействующая сила то тело будет оставаться в состоянии покоя или равномерного прямолинейного движения. Таким образом, формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

Глава 1. Механика Основы динамики

1.9. Третий закон Ньютона

В §1.7 понятие массытела было введено на основе опытов по измерению ускорений двух взаимодействующих тел: массы взаимодействующих тел обратно пропорциональны численным значениям ускорений

В векторной форме это соотношение принимает вид

Знак «минус» выражает здесь тот опытный факт, что ускорения взаимодействующих тел всегда направлены в противоположные стороны. Согласно второму закону Ньютона, ускорения тел вызваны силами ивозникающими при взаимодействии тел. Отсюда следует:

Это равенство называется третьим законом Ньютона.

Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.

Силы, возникающие при взаимодействии тел, всегда имеют одинаковую природу. Они приложены к разным телам и поэтому не могут уравновешивать друг друга. Складывать по правилам векторного сложения можно только силы, приложенные к одному телу.

Рис. 1.9.1 иллюстрирует третий закон Ньютона. Человек действует на груз с такой же по модулю силой, с какой груз действует на человека. Эти силы направлены в противоположные стороны. Они имеют одну и ту же физическую природу – это упругие силы каната. Сообщаемые обоим телам ускорения обратно пропорциональны массам тел.

Рисунок 1.9.1. Третий закон Ньютона.

Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю. В качестве примера рассмотрим рис. 1.9.2, на котором изображены два тела с массами m₁ и m₂, жестко связанные между собой невесомой нерастяжимой нитью и двигающиеся с одинаковым ускорением как единое целое под действием внешней силыМежду телами действуют внутренние силы, подчиняющиеся третьему закону Ньютона:Движение каждого тела зависит от сил взаимодействия между ними. Второй закон Ньютона, примененный к каждому телу в отдельности, дает:

Складывая левые и правые части этих уравнений и принимая во внимание, что иполучим:

Внутренние силы исключились из уравнения движения системы двух связанных тел.

Рисунок 1.9.2. Исключение внутренних сил.

studfiles.net