Уравнение состояния идеального газа Менделеева-Клапейрона с выводом
Уравнение состояния идеального газа показывает корреляцию его основных макропараметров, а именно: объема V, давления P, а также температуры T.
P – давление [Па]
V- объем [м3]
ν – количество вещества [моль]
R – универсальная газовая постоянная, 8,31 [Дж/(моль · К)]
T – температура [K]
Данную формулу также называют уравнением Менделеева-Клапейрона для идеального газа в честь двух ученых впервые получившего (Бенуа Клапейрон (1799 – 1864)) и применившего (Дмитрий Иванович Менделеев (1834 – 1907)) его.
Вывод уравнения Менделеева-Клапейрона
Давление идеального газа зависит от концентрации частиц и температуры тела:
n – концентрация частиц [м-3]
k – константа Больцмана k = 1,38 · 10-23 [Дж/К]
Т – абсолютная температура, в кельвинах [К]
Возьмем основное уравнение МКТ, выведенное через кинетическую энергию:
Подставим nkT вместо давления и выразим кинетическую энергию:
Концентрация частиц газа n равна:
N – число молекул газа в емкости объемом V [м3]. N также можно представить как произведение количества вещества ν и числа Авогадро NA:
Подставим эти величины в уравнение давления идеального газа (p=nkT):
Произведение числа Авогадро NA и константы Больцмана k дает универсальную газовую постоянную R, которая равна 8,31 [Дж/(моль · К)]. Используя это, упростим уравнение давления и получим искомое уравнение состояния идеального газа:
Учитывая, что количество вещества
можно привести уравнение к следующему виду:
Частными случаями уравнения являются газовые законы, описывающие изопроцессы в идеальных газах, т.е. процессы, при которых один из макропараметров (T, P, V) в закрытой изолированной системе постоянный. Всего этих частных случаев 3.
Закон Бойля-Мариотта – изотермический процесс
Проходит при постоянной температуре: T= const.
P·V = const, то есть для конкретного вещества произведение давления на объем остается постоянным:
P1·V1 = P2·V2.
Закон Гей-Люссака – изобарный процесс
Проходит при постоянном давлении: P = const.
V/T = const, то есть для конкретного вещества отношение объема и температуры остается постоянным:
V1/T1 = V2/T2.
Закон Шарля – изобарный процесс
Проходит при постоянном объеме: V = const.
P/T = const, то есть для конкретного вещества отношение давления и температуры остается постоянным:
P1/T1 = P2/T2.
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
Идеальный газ и его определение :: SYL.ru
Наука физика играет значимую роль в изучении окружающего мира. Поэтому ее понятия и законы начинают проходить еще в школе. Свойства вещества измеряются в разных аспектах. Если рассматривать его агрегатное состояние, то здесь существует особая методика. Идеальный газ – это физическая концепция, которая позволяет оценить свойства и характеристики материала, из которого состоит весь наш мир.
Общее определение
Идеальным газом названа модель, в которой взаимодействием между молекулами принято пренебрегать. Процесс взаимодействия частиц любого вещества друг с другом довольно сложный.  Когда они подлетают друг к другу вплотную и находятся на очень малом расстоянии, они сильно взаимоотталкиваются. Но на большой удаленности между молекулами действуют относительно небольшие силы притяжения. Если же среднее расстояние, на котором они находятся друг от друга, большое, это положение вещества называют разреженным газом. Взаимодействие таких частиц проявляется как редкие удары молекул. Это происходит, лишь когда они подлетают вплотную друг к другу. В идеальном же газе взаимодействие молекул не учитывается вообще. В идеальном газе количество молекул очень большое. Поэтому вычисления происходят только при помощи статистического метода. Причем следует отметить, что частички вещества в таком случае распределяются в пространстве равномерно. Это самое часто встречающееся состояние идеального газа.
Когда они подлетают друг к другу вплотную и находятся на очень малом расстоянии, они сильно взаимоотталкиваются. Но на большой удаленности между молекулами действуют относительно небольшие силы притяжения. Если же среднее расстояние, на котором они находятся друг от друга, большое, это положение вещества называют разреженным газом. Взаимодействие таких частиц проявляется как редкие удары молекул. Это происходит, лишь когда они подлетают вплотную друг к другу. В идеальном же газе взаимодействие молекул не учитывается вообще. В идеальном газе количество молекул очень большое. Поэтому вычисления происходят только при помощи статистического метода. Причем следует отметить, что частички вещества в таком случае распределяются в пространстве равномерно. Это самое часто встречающееся состояние идеального газа.
Когда газ можно считать идеальным
Существует несколько факторов, благодаря которым газ называется идеальным. Первым признаком является поведение молекул как абсолютно упругих тел, между ними отсутствуют силы притяжения. При этом газ будет очень разряжен. Расстояние между мельчайшими составляющими вещества будет гораздо больше размеров их самих. В таком случае тепловое равновесие будет достигаться мгновенно по всему объему. Чтобы достичь положения идеального газа в лабораторных условиях, реальный его тип разрежается соответствующим образом. Некоторые вещества в газообразном состоянии даже при комнатной температуре и нормальном атмосферном давлении практически не отличаются от идеального состояния.
Границы применения модели
Иеальный газ рассматривается в зависимости от поставленных задач. Если перед исследователем поставлена задача определить зависимость между температурой, объемом и давлением, то идеальным можно считать такое состояние вещества, при котором у газа наблюдается высокая точность до давлений, измеряемых несколькими десятками атмосфер. Но в случае изучения фазового перехода, например, испарения и конденсации, процесса достижения равновесия в газе, рассматриваемую модель нельзя применять даже при очень маленьком давлении. Давление газа на стенку пробирки происходит при хаотическом ударении молекул о стекло. Когда такие удары часты, организм человека может уловить эти изменения как непрерывное воздействие.
Уравнение идеального газа
Основываясь на главных принципах молекулярно-кинетической теории, было выведено главное уравнение идеального газа. Работа идеального газа имеет следующее выражение: p = 1/3m0nv2, где p – давление газа идеального, m0 – молекулярная масса, v2 – среднее значение концентрации частиц, квадрат скорости молекул. Если обозначить средний показатель кинетического движения частиц вещества, как Ек = m0n/2, то уравнение будет иметь такой вид: p = 2/3nEk. Молекулы газа, ударяясь о стенки сосуда, вступают с ними во взаимодействие как упругие тела по законам механики. Импульс от таких ударов передается стенкам сосуда.
Работа идеального газа имеет следующее выражение: p = 1/3m0nv2, где p – давление газа идеального, m0 – молекулярная масса, v2 – среднее значение концентрации частиц, квадрат скорости молекул. Если обозначить средний показатель кинетического движения частиц вещества, как Ек = m0n/2, то уравнение будет иметь такой вид: p = 2/3nEk. Молекулы газа, ударяясь о стенки сосуда, вступают с ними во взаимодействие как упругие тела по законам механики. Импульс от таких ударов передается стенкам сосуда.
Температура
Вычислив только давление газа на стенки сосуда, нельзя определить средний показатель кинетической энергии его частиц.

Причем этого нельзя сделать ни для отдельной молекулы, ни для их концентрации. Поэтому для измерения параметров газа необходимо определять еще одну величину. Ею выступает температура, которая также связана с кинетической энергией молекул. Такой показатель выступает скалярной физической величиной. Температура описывает термодинамическое равновесие. В таком состоянии не происходит изменение параметров на микроуровне. Температура измеряется как отклонение от нулевого значения. Она характеризует насыщенность хаотического движения наименьших частиц газа. Она измеряется средним значением их кинетической энергии. Определяется этот показатель при помощи термометров в градусах различных отметок. Существует термодинамическая абсолютная шкала (Кельвина) и эмпирические ее разновидности. Они отличаются начальными точками.
Уравнение положения идеального газа с учетом температуры
Физик Больцман утверждает, что средний показатель кинетической энергии частицы пропорционален абсолютному показателю температуры. Ек = 3/2 кТ, где к = 1,38∙10-23, Т – температура. Работа идеального газа будет равна: Р = NkT/V, где N – количество молекул, V – объем сосуда. Если к этому показателю добавить концентрацию n = N/V, то вышеприведенная формула будет иметь такой вид: p = nkT. Эти два уравнения имеют различные формы записи, но они связывают для идеального газа давление, объем и температуру. Эти вычисления можно применять как к чистым газам, так и к их смесям. В последнем варианте под n нужно понимать все число молекул веществ, их суммарную концентрацию или полное количество молей в веществе.
Три газовых закона
Идеальный газ и его частные законы были открыты экспериментально и лишь потом подтверждены теоретически.  Первый частный закон гласит, что идеальный газ при постоянной массе и температуре будет иметь обратно пропорциональное давление его объему. Процесс, при котором показатель температуры постоянный, был назван изотермическим. Если же при исследовании постоянным является давление, то объем пропорционален значению абсолютной температуры. Этот закон носит имя Гей-Люссака. Изохорный же процесс происходит при постоянном объеме. При этом давление будет пропорционально абсолютным температуре. Его название – закон Шарля. Это три частных закона поведения идеального газа. Их удалось подтвердить лишь при овладении знаниями о молекулах.
Первый частный закон гласит, что идеальный газ при постоянной массе и температуре будет иметь обратно пропорциональное давление его объему. Процесс, при котором показатель температуры постоянный, был назван изотермическим. Если же при исследовании постоянным является давление, то объем пропорционален значению абсолютной температуры. Этот закон носит имя Гей-Люссака. Изохорный же процесс происходит при постоянном объеме. При этом давление будет пропорционально абсолютным температуре. Его название – закон Шарля. Это три частных закона поведения идеального газа. Их удалось подтвердить лишь при овладении знаниями о молекулах.
Абсолютная шкала измерения
В абсолютной шкале измерения принято единицей называть Кельвин. Она выбрана исходя из популярной шкалы Цельсия. Один Кельвин соответствует одному градусу по Цельсию. Но в шкале абсолютной за ноль принято значение, при котором давление идеального газа при постоянном объеме будет равно нулю.
 Это общепринятая система. Такое значение температуры названо абсолютным нулем. Произведя соответствующие вычисления, можно получить ответ, что значение этого показателя будет составлять -273 градуса по Цельсию. Это подтверждает, что между абсолютной и шкалой Цельсия существует связь. Ее можно выразить в таком уравнении: Т = t + 237. Следует отметить, что достичь абсолютного нуля невозможно. Любой охладительный процесс основан на испарении с поверхности вещества молекул. Приближаясь к абсолютному нулю, поступательное движение частиц так сильно замедляется, что испарение прекращается практически совсем. Но чисто с теоретической точки зрения если бы было реально достичь точки абсолютного нуля, то скорость движения молекул уменьшилась бы настолько, что ее можно было бы назвать отсутствующей вовсе. Тепловое движение молекул прекратилось бы.
Это общепринятая система. Такое значение температуры названо абсолютным нулем. Произведя соответствующие вычисления, можно получить ответ, что значение этого показателя будет составлять -273 градуса по Цельсию. Это подтверждает, что между абсолютной и шкалой Цельсия существует связь. Ее можно выразить в таком уравнении: Т = t + 237. Следует отметить, что достичь абсолютного нуля невозможно. Любой охладительный процесс основан на испарении с поверхности вещества молекул. Приближаясь к абсолютному нулю, поступательное движение частиц так сильно замедляется, что испарение прекращается практически совсем. Но чисто с теоретической точки зрения если бы было реально достичь точки абсолютного нуля, то скорость движения молекул уменьшилась бы настолько, что ее можно было бы назвать отсутствующей вовсе. Тепловое движение молекул прекратилось бы.
Изучив такое понятие, как идеальный газ, можно понять принцип работы любого вещества. Расширив знания в этой области, можно понять свойства и поведение любого газообразного вещества.
www.syl.ru
Идеальный газ. Уравнение состояния идеального газа. Изопроцессы.
Идеальный газ, уравнение состояния идеального газа, его температура и давление, объем… список параметров и определений, которыми оперируют в соответствующем разделе физики, можно продолжать достаточно долго. Сегодня мы поговорим как раз на эту тему.
Что рассматривается в молекулярной физике?

Основным объектом, который рассматривается в этом разделе, является идеальный газ. Уравнение состояния идеального газа было получено с учетом нормальных условий окружающей среды, и об этом мы поговорим немного позднее. Сейчас давайте подойдем к этой “проблеме” издалека.
Допустим, у нас есть некоторая масса газа. Ее состояние можно определить при помощи трех параметров термодинамического характера. Это, конечно же, давление, объем и температура. Уравнением состояния системы в этом случае будет формула связи между соответствующими параметрами. Она выглядит таким образом: F (p, V, T) = 0.
Вот здесь мы впервые потихоньку подбираемся к появлению такого понятия, как идеальный газ. Им называется газ, в котором взаимодействия между молекулами пренебрежимо малы. Вообще в природе такого не существует. Однако любой сильно разреженный газ близок к нему. От идеального мало чем отличаются азот, кислород и воздух, находящиеся в нормальных условиях. Чтобы записать уравнение состояния идеального газа, мы можем использовать объединенный газовый закон. Получим: pV/T = const.
Связанное понятие № 1: закон Авогадро
Он может рассказать нам о том, что если мы возьмем одинаковое количество молей абсолютно любого случайного газа и поставим их в одинаковые условия, среди которых температура и давление, то газы займут одинаковый объем. В частности, опыт проводился при нормальных условиях. Это означает, что температура была равна 273,15 Кельвинам, давление – одной атмосфере (760 миллиметров ртутного столба или же 101325 Паскалей). При таких параметрах газ занял объем равный 22,4 литра. Следовательно, мы можем говорить о том, что для одного моля любого газа соотношение числовых параметров будет величиной постоянной. Именно поэтому было принято решение этой цифре дать обозначение буквой R и назвать ее универсальной газовой постоянной. Таким образом, она равняется 8,31. Размерность Дж/моль*К.
Идеальный газ. Уравнение состояния идеального газа и манипуляции с ним
Давайте попробуем переписать формулу. Для этого запишем его в таком виде: pV = RT. Далее совершим нехитрое действие, умножим обе части уравнения на произвольное количество молей. Получим pVu = uRT. Примем во внимание тот факт, что произведение молярного объема на количество вещества есть просто объем. Но ведь количество молей одновременно будет равняться частному массы и молярной массы. Именно так выглядит уравнение Менделеева-Клапейрона. Оно дает четкое понятие о том, какую систему образует идеальный газ. Уравнение состояния идеального газа примет вид: pV = mRT/M.
Выведем формулу для давления
Давайте проведем еще некоторые манипуляции с полученными выражениями. Для этого правую часть уравнения Менделеева-Клапейрона умножим и разделим на число Авогадро. Теперь внимательно смотрим на произведение количества вещества на число Авогадро. Это есть не что иное, как общее число молекул в газе. Но в то же время отношение универсальной газовой постоянной к числу Авогадро будет равно постоянной Больцмана. Следовательно, формулы для давления можно записать таким образом: p = NkT/V или p = nkT. Здесь обозначение n это концентрация частиц.
Процессы идеального газа
В молекулярной физике существует такое понятие, как изопроцессы. Это термодинамические процессы, которые имеют место в системе при одном из постоянных параметров. При этом масса вещества также должна оставаться постоянной. Давайте рассмотрим их более конкретно. Итак, законы идеального газа.
Постоянным остается давление
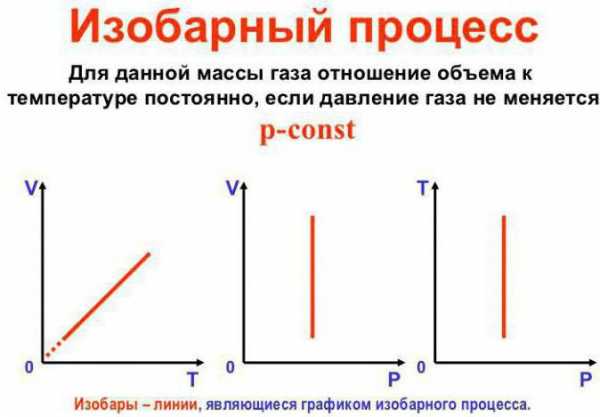
Это закон Гей-Люссака. Выглядит он так: V/T = const. Его можно переписать и по-другому: V = Vo (1+at). Здесь a равняется 1/273,15 К^-1 и носит название “коэффициент объемного расширения”. Мы можем подставить температуру как по шкале Цельсия, так и по шкале Кельвина. В последнем случае получим формулу V = Voat.
Постоянным остается объем

Это второй закон Гей-Люссака, более часто называемый законом Шарля. Выглядит он так: p/T = const. Есть и другая формулировка: p = po (1 + at). Преобразования могут быть проведены в соответствии с предыдущим примером. Как можно видеть, законы идеального газа иногда бывают достаточно похожими друг на друга.
Постоянным остается температура

Если температура идеального газа остается величиной постоянной, то мы можем получить закон Бойля-Мариотта. Он может быть записан таким образом: pV = const.
Связанное понятие № 2: парциальное давление
Допустим, у нас имеется сосуд с газами. Это будет смесь. Система находится в состоянии теплового равновесия, а сами газы между собой не реагируют. Здесь N будет обозначать общее количество молекул. N1, N2 и так далее, соответственно, количество молекул в каждом из компонентов имеющейся смеси. Возьмем формулу давления p = nkT = NkT/V. Ее можно раскрыть для конкретного случая. Для двухкомпонентной смеси формула примет вид: p = (N1 + N2) kT/V. Но тогда получится, что общее давление будет суммироваться из частных давлений каждой смеси. А значит, оно будет иметь вид p1 + p2 и так далее. Это и будут парциальные давления.
Для чего это нужно?
Полученная нами формула указывает на то, что давление в системе оказывается со стороны каждой группы молекул. Оно, кстати, не зависит от других. Этим воспользовался Дальтон при формулировании закона, названного впоследствии в его честь: в смеси, где газы не реагируют между собой химически, общее давление будет равно сумме парциальных давлений.
fb.ru
Уравнение состояния идеального газа. Изопроцессы
Соотношение
связывающее давление газа с его температурой и концентрацией молекул, получено в 3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
Здесь N – число молекул в сосуде,
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:
R = 8,31 Дж/моль·К. |
Соотношение
(*) |
называется уравнением состояния идеального газа.
Для одного моля любого газа это соотношение принимает вид:
Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный
V0 = 0,0224 м3 |
Это утверждение называется законом Авогадро.
Для смеси невзаимодействующих газов уравнение состояния принимает вид
pV = (ν1 + ν2 + ν3 + …)RT, |
где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Бенуа Клайпероном, в форме (*) оно было впервые записано Дмитрием Ивановичем Менделеевым. Поэтому уравнение состояния газа называется
Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.
Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются
Интерес представляют процессы, в которых один из параметров (p,
Изотермический процесс (T = const)
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:
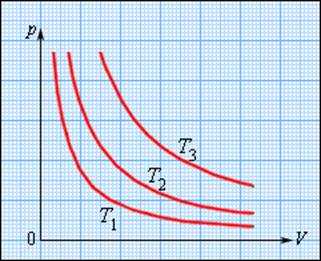
На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p ~ 1 / V, которые называются
|
Рисунок 3.3.1. |
Изохорный процесс (V = const)
Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.
Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или
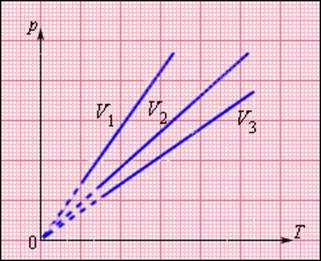
На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).
|
Рисунок 3.3.2. Семейство изохор на плоскости (p, T). V3 > V2 > V1 |
Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.
Уравнение изохорного процесса может быть записано в виде:
где p0 – давление газа при T = T0 = 273,15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273,15) К–1, называют температурным коэффициентом давления.
Изобарный процесс (p = const)
Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.
Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:
где V0 – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К–1. Его называют температурным коэффициентом объемного расширения газов.
На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.
|
Рисунок 3.3.3. Семейство изобар на плоскости (V, T). p3 > p2 > p1 |
Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Жозефом Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.
Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.
www.its-physics.org
Идеальный газ — Мегаэнциклопедия Кирилла и Мефодия — статья
Идеа́льный газ — теоретическая математическая модель газа; в которой пренебрегают размерами частиц газа, не учитывают силы взаимодействия между частицами газа, предполагая, что средняя кинетическая энергия частиц много больше энергии их взаимодействия, и считают, что столкновения частиц газа между собой и со стенками сосуда абсолютно упругие.Существуют модель классического идеального газа, свойства которого описываются законами классической физики, и модель квантового идеального газа, подчиняющегося законам квантовой механики. Обе модели идеального газа справедливы для реальных классических и квантовых газов при достаточно высоких температурах и разряжениях.
В модели классического идеального газа газ рассматривают как совокупность огромного числа одинаковых частиц (молекул), размеры которых пренебрежимо малы. Газ заключен в сосуд, и в состоянии теплового равновесия никаких макроскопических движений в нем не происходит. Т. е. это газ, энергия взаимодействия между молекулами которого значительно меньше их кинетической энергии, а суммарный объем всех молекул значительно меньше объема сосуда. Молекулы движутся по законам классической механики независимо друг от друга, и взаимодействуют между собой только во время столкновений, которые носят характер упругого удара. Давление идеального газа на стенку сосуда равно сумме импульсов, переданных за единицу времени отдельными частицами при столкновениях со стенкой, а энергия — сумме энергий отдельных частиц.
Установленная опытным путем связь между давлением, объемом и температурой газа приближенно описывается уравнением Клапейрона, которое выполняется тем точнее, чем ближе газ по свойствам к идеальному. Классический идеальный газ подчиняется уравнению состояния Клапейрона p = nkT, где р — давление, n – число частиц в единице объема, k — постоянная Больцмана, Т — абсолютная температура. Уравнение состояния и закон Авогадро впервые связали макрохарактеристики газа — давление, температуру, массу — с массой его молекулы.В идеальном газе, где молекулы не взаимодействуют между собой, энергия всего газа является суммой энергий отдельных молекул и для одного моля одноатомного газа эта энергия U =3/2(RT), где R — универсальная газовая постоянная. Эта величина не связана с движением газа как целого и является внутренней энергией газа. Для неидеального газа внутренняя энергия представляет сбой сумму энергий отдельных молекул и энергии их взаимодействия.Частицы классического идеального газа распределены по энергиям согласно распределению Больцмана (см. Больцмана статистика).Модель идеального газа можно использовать при изучении реальных газов, так как в условиях, близких к нормальным, а также при низких давлениях и высоких температурах реальные газы близки по свойствам к идеальному газу.
В современной физике понятие идеальный газ применяют для описания любых слабовзаимодействующих частиц и квазичастиц, бозонов и фермионов. Внеся поправки, учитывающие собственный объем молекул газа и действующие межмолекулярные силы, можно перейти к теории реальных газов.При понижении температуры Т газа или увеличении его плотности n до определенного значения становятся существенными волновые (квантовые) свойства частиц идеального газа. Переход от классического идеального газа к квантовому происходит при таких значениях Т и n, при которых длины Волн де Бройля частиц, движущихся со скоростями порядка тепловых, сравнимы с расстоянием между частицами.В квантовом случае различают два вида идеального газа: если частицы газа одного вида имеют спин, равный единице, то к ним применяют статистику Бозе — Эйнштейна, если частицы имеют спин, равный Ѕ, то применяют статистику Ферми — Дирака. Применение теории идеального газа Ферми — Дирака к электронам в металлах позволяет объяснить многие свойства металлического состояния.megabook.ru
Богданов К.Ю. – учебник по физике для 10 класса
§ 24. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ЗАКОН АВОГАДРО
Уравнение состояния идеального газа связывает между собой три его макроскопические характеристики – занимаемый газом объём, его давление и температуру.
В §23 мы вывели формулу, связывающую давление идеального газа, p, концентрацию молекул в нём, n, и его абсолютную температуру, Т:
p = nkT , (24.1)
где k – постоянная Больцмана. Однако в большинстве случаев пользоваться формулой (24.1) неудобно, т.к. величина n, как правило, неизвестна, а мы лишь знаем, какой это газ и какой объём он занимает. Чтобы в этих случаях формулой (24.1) было пользоваться проще, преобразуем её следующим образом. Пусть газ, состоящий из N молекул, находится в сосуде объёмом V. Тогда концентрация, n молекул равна:
где m и n – масса и количество вещества, содержащееся в газе с молярной массой M и объёмом V, а NA – число Авогадро (см. 19.1 и 19.2). Подставляя (24.2) в (24.1), получаем:
Произведение kNA обозначают буквой R и называют универсальной (молярной) газовой постоянной, которая равна 8,31 Дж/(моль.К). Заменяя kNA на R в формуле (24.3), получаем:
Уравнение (24.4) называют уравнением состояния идеального газа или уравнением Менделеева-Клапейрона, названным в честь русского учёного Д.И. Менделеева и французского физика Б. Клапейрона. Формула (24.4) определяет взаимозависимость трёх макроскопических характеристик данной массы газа, определяющих его состояние, – давления, объёма и температуры.
Уравнение Менделеева-Клапейрона позволяет вычислить одну из пяти переменных (p, V, m, M и T), если значения остальных четырёх известны. Можно, например, найти молярную массу, М газа, т.е. определить его относительную молекулярную массу, если измерить его давление, объём, массу и температуру.
Из уравнения (24.4) следует, что если данная масса газа находится в состоянии 1, в котором её давление, объём и температуры равны p1, V1 и T1, соответственно, а потом переходит в состояние 2 (см. рис. 24а), в котором её давление, объём и температуры становятся равными p2, V2 и T2, то:
Уравнение (24.5), называемое уравнением Клапейрона, позволяет вычислить значение одной из макроскопических характеристик газа в состоянии 2, если остальные две известны.
Возьмём одинаковое число молей n двух разных газов (А и Б). Пусть эти газы имеют одинаковую температуру T0 и давление p0. Тогда из уравнения (24.4) следует, что объёмы этих газов, VА и VБ, тоже равны:
Таким образом, при одинаковых давлении и температуре равные объёмы различных газов содержат одинаковое количество вещества, т.е. молекул. Этот вывод называют законом Авогадро. Из закона Авогадро и формулы (24.6) следует, что при нормальных условиях, т.е. при температуре 0оС (Т0=273 К) и нормальном атмосферном давлении (p0=101325 Па), газ, взятый в количестве 1 моль, занимает объём 0,0224 м3 или 22,4 литра (см. рис. 24б).
Вопросы для повторения:
· Сформулируйте уравнение Менделеева-Клапейрона. Для каких газов оно справедливо?
· Как связана универсальная газовая постоянная с постоянными Больцмана и Авогадро?
· Сформулируйте закон Авогадро.
· Какие объёмы занимает один, два и три моля идеального газа при нормальных условиях?
Рис. 24. (а) – связь между параметрами газа в двух его состояниях; (б) – связь между параметрами одного моля газа при нормальных условиях.
kaf-fiz-1586.narod.ru