Перевод из одной системы в другую информатика – Системы счисления. Перевод из одной системы в другую. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):


0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):


0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

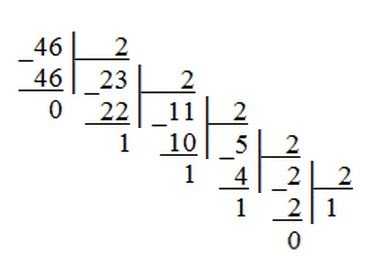
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

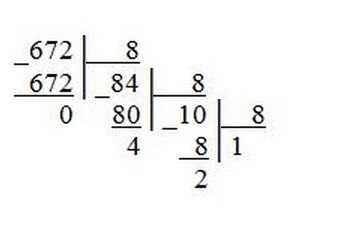
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.


0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6.

Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.


0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27

(бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Правила перевода чисел из одной системы в другую » СтудИзба

Правила перевода чисел из одной системы счисления в другую

Поскольку одно и то же число может быть записано в различных системах счисления (например, ), то встает вопрос о переводе представления числа из одной системы в другую. Правила перевода для целых и дробных чисел отличаются.

Для перевода чисел из любой системы счисления в десятичную можно воспользоваться формулой (1).

Пример. Перевести в десятичную систему счисления числа

Решение:

Перевод целых чисел из одной системы счисления в другую

1. Делить заданное число на новое основание, записанное в виде числа со старым основанием до получения остатка.

2. Полученное частное следует вновь делить на новое основание, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя.

3. Полученные остатки от деления и последнее частное записываются в порядке обратном полученному при делении.

Пример. Перевести число в двоичную, восьмеричную, шестнадцатеричную системы счисления.

Решение:

Перевод дробных чисел из одной системы счисления в другую

Умножить заданное число на новое основание, записанное в виде числа со старым основанием. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата.

Пример. Перевести число в двоичную, восьмеричную, шестнадцатеричную системы счисления.

Решение:

Пример. Перевести число в двоичную систему счисления.

Решение: Переведем отдельно целую и дробную части числа в двоичную систему счисления.

Соединяя целую и дробную части, получим

Так как двоичная, восьмеричная и шестнадцатеричная системы счисления связаны друг с другом через степени 2, то преобразования между ними можно выполнять более простым способом.

1. Для перевода из шестнадцатеричной (восьмеричной) системы счисления в двоичную достаточно двоичным кодом записать шестнадцатеричные (восьмеричные) коды цифр тетрадами (триадами).

2. Обратный перевод из двоичного кода производится в обратном порядке: двоичное число разбивается влево и вправо от запятой на тетрады для последующей записи цифр в шестнадцатеричном представлении и на триады – для записи их значений восьмеричными цифрами.

3. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно используется вспомогательный, двоичный код числа.

Пример. Перевести число в восьмеричную, шестнадцатеричную системы счисления.

Решение:

Пример. Перевести число в двоичную систему счисления.

Решение:

studizba.com

3.3. Правила перевода чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2,

и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней двойки:

Таблица 4. Степени числа 2

n (степень)

128

256

512

1024

Пример . Число перевести в десятичную систему счисления.

2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней восьмерки:

Таблица 5. Степени числа 8

n (степень)	0	1	2	3	4	5	6
	1	8	64	512	4096	32768	262144

Пример . Число перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

При переводе удобно пользоваться таблицей степеней числа 16:

Таблица 6. Степени числа 16

n (степень)	0	1	2	3	4	5	6
	1	16	256	4096	65536	1048576	16777216

Пример . Число перевести в десятичную систему счисления.

4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в двоичную систему счисления.

5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в восьмеричную систему счисления.

6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в шестнадцатеричную систему счисления.

7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример. Число перевести в восьмеричную систему счисления.

8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример. Число перевести в шестнадцатеричную систему счисления.

9. Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.

Пример. Число перевести в двоичную систему счисления.

10. Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.

Пример. Число перевести в двоичную систему счисления.

11. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Пример 1. Число перевести в восьмеричную систему счисления.

Пример 2. Число перевести в шестнадцатеричную систему счисления.

3.6. Контрольные вопросы. Системы счисления

1. Что называется системой счисления?

2. На какие два типа можно разделить все системы счисления?

3. Какие системы счисления называются непозиционными? Почему? Приведите пример такой системы счисления и записи чисел в ней?

4. Какие системы счисления применяются в вычислительной технике: позиционные или непозиционные? Почему?

5. Какие системы счисления называются позиционными?

6. Как изображается число в позиционной системе счисления?

7. Что называется основанием системы счисления?

8. Что называется разрядом в изображении числа?

9. Как можно представить целое положительное число в позиционной системе счисления?

10. Приведите пример позиционной системы счисления.

11. Опишите правила записи чисел в десятичной системе счисления: а) какие символы образуют алфавит десятичной системы счисления? б) что является основанием десятичной системы счисления? в) как изменяется вес символа в записи числа в зависимости от занимаемой позиции?

12. Какие числа можно использовать в качестве основания системы счисления?

13. Какие системы счисления применяются в компьютере для представления информации?

14. Охарактеризуйте двоичную систему счисления: алфавит, основание системы счисления, запись числа.

15. Почему двоичная система счисления используется в информатике?

16. Дайте характеристику шестнадцатеричной системе счисления: алфавит, основание, запись чисел. Приведите примеры записи чисел.

17. По каким правилам выполняется сложение двух положительных целых чисел?

18. Каковы правила выполнения арифметических операций в двоичной системе счисления?

19. Для чего используется перевод чисел из одной системы счисления в другую?

20. Сформулируйте правила перевода чисел из системы счисления с основанием р в десятичную систему счисления и обратного перевода: из десятичной системы счисления в систему счисления с основанием S. Приведите примеры.

21. В каком случае для перевода чисел из одной системы счисления (СС) в другую может быть использована схема Горнера вычисления значения многочлена в точке? Каковы преимущества ее использования перед другими методами? Приведите пример.

22. Как выполнить перевод чисел из двоичной СС в восьмеричную и обратный перевод? Из двоичной СС в шестнадцатеричную и обратно? Приведите примеры. Почему эти правила так просты?

23. По каким правилам выполняется перевод из восьмеричной в шестнадцатеричную СС и наоборот? Приведите примеры.

studfiles.net

Задание №1. Перевод из одной системы счисления в другую

Автор материалов – Лада Борисовна Есакова.

Системы счисления и их разновидности.

Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.

Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.

1. Непозиционные системы счисления.

В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.

Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.

Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.

Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:

Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число

Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.

2. Позиционные системы счисления.

В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.

Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.

Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).

Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.

Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».

2.1. Однородные системы счисления.

В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.

2.2. Смешанные системы счисления.

В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.


0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30


0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Таблицу соответствия мы научились строить в п.1.


0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.


0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Десятичные дроби и смешанные числа в разных системах счисления.

Автор – Лада Борисовна Есакова.

Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.

1. Перевод смешанного числа в десятичную систему счисления из любой другой.

Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.

Пример 1.

Переведите число 105,4 из восьмеричной системы в десятичную.

Решение:

Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :

Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:

Ответ:

2. Перевод десятичных дробей из десятичной системы счисления в любую другую.

Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.

Пример 2

Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.

Решение:

Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:

Ответ:

Пример 3.

Переведите десятичное число 0,8125 в восьмеричную систему.

Решение:

Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:

Ответ:

3. Перевод смешанных чисел из десятичной системы счисления в любую другую

Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.

Пример 4.

Сколько единиц в двоичной записи десятичного числа 14,125?

Решение:

Переведем целую часть числа в двоичную систему:

Переведем дробную часть числа в двоичную систему:

Соединим целую и дробную части:

14,12510 = 1110,0012

Количество единиц равно 4.

Ответ: 4

Ты нашел то, что искал? Поделись с друзьями!

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Перевод чисел из одной системы счисления в другую

Разделы: Информатика

Цели урока:

повторить изученный материал по теме система счисления ;

научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот;

освоить принципы перевода чисел из одной системы в другую;

развивать логическое мышление.

Ход урока

Вначале урока краткое повторение и проверка домашнего задания..

Вопросы:

– В каком виде представлена числовая информация в памяти компьютера?

– Для чего используются системы счисления?

– Какие виды систем счисления вы знаете? Привести свои примеры.

– Чем отличаются позиционные системы от непозиционных?.

Цель нашего урока научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот. Но в начале мы рассмотрим, как можно

представить любое целое неотрицательное чисело:

В позиционных системах значение записи целого числа определяется по следующему правилу: пусть a _na _n-1a _n-2…a ₁a ₀— запись числа A, а _i – цифры, тогда

A = a _n·pⁿ+a _n-1·p^n-1 +a _n-2·p^n-2+…+a ₁·p¹+ a₀·p⁰       (1),

где p — целое число большее 1, которое называется основанием системы счисления

Для того, чтобы при заданном p любое неотрицательное целое число можно было бы записать по формуле (1) и притом единственным образом, числовые значения различных цифр должны быть различными целыми числами, принадлежащими отрезку от 0 до p-1.

Пример:

1) Десятичная система

p = 10

цифры: 0,1,2,3,4,5,6,7,8,9

число 5735 = 5·10³+7·10²+3·10¹+8·10⁰

2) Троичная система

p = 3

цифры: 0,1,2

число 201₃ = 2·3²+0·3¹+1·3⁰

Замечание: нижним индексом в записи числа обозначается основание системы счисления, в которой записано число. Для десятичной системы счисления индекс можно не писать.

Представление отрицательных и дробных чисел:

Во всех позиционных системах для записи отрицательных чисел так же как и в десятичной системе используется знак ‘–‘. Для отделения целой части числа от дробной используется запятая. Значение записи a _na _n-1a _n-2…a ₁a ₀, a _-1 a_-2…a _m-2a _m-1a _mчисла A определяется по формуле, являющейся обобщением формулы (1):

A = a_n·pⁿ+a _n-1·p^n-1+a _n-2·p ^n-2+…+a₁·p¹+a₀·p⁰+a_-1·p^-1+a_-2·p^-2+…+a_m-2·p^–(m–2)+a_m–1·p^–(m–1)+a_mp^–m     (2),

Пример:

75,6 = 7·10¹+5·10⁰+6·10^–1

–2,314₅ = –(2·5⁰+3·5^–1+1·5^–2+4·5^–3)

Перевод чисел из произвольной системы счисления в десятичную:

Следует понимать, что при переводе числа из одной системы счисления в другую количественное значение числа не изменяется, а меняется только форма записи числа, так же как при переводе названия числа, например, с русского языка на английский.

Перевод чисел из произвольной системы счисления в десятичную выполняется непосредственным вычислением по формуле (1) для целых и формуле (2) для дробных чисел.

Перевод чисел из десятичной системы счисления в произвольную.

Перевести число из десятичной системы в систему с основанием p – значит найти коэффициенты в формуле (2). Иногда это легко сделать простым подбором. Например, пусть нужно перевести число 23,5 в восьмеричную систему. Нетрудно заметить, что 23,5 = 16+7+0,5 = 2·8+7+4/8 = 2·8¹+7·8⁰+4·8^–1 =27,48. Понятно, что не всегда ответ столь очевиден. В общем случае применяется способ перевода отдельно целой и дробной частей числа.

Для перевода целых чисел применяется следующий алгоритм (полученный на основании формулы (1)):

1. Найдем частное и остаток от деления числа на p. Остаток будет очередной цифрой ai (j=0,1,2 …) записи числа в новой системе счисления.

2. Если частное равно нулю, то перевод числа закончен, иначе применяем к частному пункт 1.

Замечание 1. Цифры ai в записи числа нумеруются справа налево.

Замечание 2. Если p>10, то необходимо ввести обозначения для цифр с числовыми значениями, большими или равными 10.

Пример:

Перевести число 165 в семеричную систему счисления.

165:7 = 23 (остаток 4) => a₀ = 4

23:7 = 3 (остаток 2) => a₁ = 2

3:7 = 0 (остаток 3) => a₂= 3

Выпишем результат: a₂a₁a₀, т.е. 3247.

Выполнив проверку по формуле (1), убедимся в правильности перевода:

3247=3·7²+2·7¹+4·7⁰=3·49+2·7+4 = 147+14+4 = 165.

Для перевода дробных частей чисел применяется алгоритм, полученный на основании формулы (2):

1. Умножим дробную часть числа на p.

2. Целая часть результата будет очередной цифрой am (m = –1,–2, –3 …) записи числа в новой системе счисления. Если дробная часть результата равна нулю, то перевод числа закончен, иначе применяем к ней пункт 1.

Замечание 1. Цифры a_mв записи числа располагаются слева направо в порядке возрастания абсолютного значения m.

Замечание 2. Обычно количество дробных разрядов в новой записи числа ограничивается заранее. Это позволяет выполнить приближенный перевод с заданной точностью. В случае бесконечных дробей такое ограничение обеспечивает конечность алгоритма.

Пример 1:

Перевести число 0,625 в двоичную систему счисления.

0,625·2 = 1,25 (целая часть 1) => a_-1 =1

0,25·2 = 0,5 (целая часть 0) => a-₂= 0

0,5·2 = 1,00 (целая часть 1) => a-₃= 1

Итак, 0,62510 = 0,1012

Выполнив проверку по формуле (2), убедимся в правильности перевода:

0,1012=1·2^-1+0·2-²+1·2^-3=1/2+1/8 = 0,5+0,125 = 0,625.

Пример 2:

Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.

0,165·4 = 0,66 (целая часть 0) => a_-1=0

0,66·4 = 2,64 (целая часть 2) => a_-2= 2

0,64·4 = 2,56 (целая часть 2) => a_-3= 2

0,56·4 = 2,24 (целая часть 2) => a_-4= 2

Итак, 0,16510 ” 0,02224

Выполним обратный перевод, чтобы убедиться, что абсолютная погрешность не превышает 4–4:

0,02224 = 0·4^-1+2·4^-2+2·4^-3+2·4^-4= 2/16+2/64+2/256 = 1/8+1/32+1/128 = 21/128 = 0,1640625

|0,1640625–0,165| = 0,00094 < 4–4 = 0,00390625

Перевод чисел из одной произвольной системы в другую

В этом случае сначала следует выполнить перевод числа в десятичную систему, а затем из десятичной в требуемую.

Особым способом выполняется перевод чисел для систем с кратными основаниями.

Пусть p и q – основания двух систем счисления. Будем называть эти системы системами счисления с кратными основаниями, если p = qn или q = pn, где n – натуральное число. Так, например, системы счисления с основаниями 2 и 8 являются системами счисления с кратными основаниями.

Пусть p = qn и требуется перевести число из системы счисления с основанием q в систему счисления с основанием p. Разобьем целую и дробную части записи числа на группы по n последовательно записанных цифр влево и вправо от запятой. Если количество цифр в записи целой части числа не кратно n, то надо дописать слева соответствующее количество нулей. Если количество цифр в записи дробной части числа не кратно n, то нули дописываются справа. Каждая такая группа цифр числа в старой системе счисления будет соответствовать одной цифре числа в новой системе счисления.

Пример:

Переведем 1100001,111₂ в четверичную систему счисления.

Дописав нули и выделив пары цифр, получим 01100001,11102.

Теперь выполним перевод отдельно каждой пары цифр, пользуясь пунктом Перевод чисел из одной произвольной системы в другую.

01₂=1₁₀=1₄

10₂=2₁₀=2₄

00₂=0₁₀=0₄

01₂=1₁₀=1₄

11₂=3₁₀=3₄

10₂=2₁₀=2₄

Итак, 1100001,1112 = 01100001,11102 = 1201,324.

Пусть теперь требуется выполнить перевод из системы с большим основанием q, в систему с меньшим основанием p, т.е. q = p_n. В этом случае одной цифре числа в старой системе счисления соответствует n цифр числа в новой системе счисления.

Пример: Выполним проверку предыдущего перевода числа.

1201,324 = 1100001,11102=1100001,1112

В шестнадцатеричной системе есть цифры с числовыми значениями 10,11,12, 13,14,15. Для их обозначения используют первые шесть букв латинского алфавита A, B, C, D, E, F.

Приведем таблицу чисел от 0 до 16, записанных в системах счисления с основаниями 10, 2, 8 и 16.

Число в десятичной системе счисления 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
В восьмеричной 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 20
В двоичной 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000
В шестнадцатеричной 0 1 2 3 4 5 6 7 8 9 A B C D E F 10
Для записи шестнадцатеричных цифр можно использовать также строчные латинские буквы a-f.

Пример: Переведем число 110101001010101010100,11₂ в шестнадцатеричную систему счисления.

Воспользуемся кратностью оснований систем счисления (16=2⁴). Сгруппируем цифры по четыре, дописав, слева и справа нужное количество нулей

000110101001010101010100,1100₂

и, сверяясь с таблицей, получим: 1A9554,C₁₆

Вывод:

В какой системе счисления лучше записывать числа – это вопрос удобства и традиций. С технической точки зрения, в ЭВМ удобно использовать двоичную систему, так как в ней для записи числа используются только две цифры 0 и 1, которые можно представить двумя легко различимыми состояниями “нет сигнала ” и “есть сигнал”.

А человеку, напротив, неудобно иметь дело с двоичными записями чисел из-за того, что они более длинные, чем десятичные и в них много повторяющихся цифр. Поэтому, при необходимости работать с машинными представлениями чисел используют восьмеричную или шестнадцатеричную системы счисления. Основания этих систем – целые степени двойки, и поэтому числа легко переводятся из этих систем в двоичную и обратно.

Записываем задание на дом:

а) Запишите дату рождения всех членов вашей семьи в различных системах счисления.

б) Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 1001111110111,011₂;

б) 1110101011,1011101₂
1.03.2007
xn--i1abbnckbmcl9fb.xn--p1ai
1. Перевод дробных чисел из одной системы счисления в другую
Каждый знает, что дроби бывают обыкновенные и десятичные. Обыкновенная дробь представляет собой отношение целого числа к натуральному. Поэтому ее перевод в другую систему счисления трудности не представляет: надо отдельно перевести в новую систему счисления числитель и знаменатель, затем записать их отношение. Запись числа десятичной дробью — это распространение позиционного принципа вправо от разряда единиц. Вспомните: при переходе на один разряд влево «вклад» цифры увеличивается в \(10\) раз, а при переходе на один разряд вправо уменьшается в \(10\) раз. Так что запись \(1,38054\) обозначает число: 1⋅100+3⋅10−1+8⋅10−2+0⋅10−3+5⋅10−4+4⋅10−5.
Легко понять, что и здесь вместо числа \(10\) можно использовать любое другое натуральное число \(b\), большее \(1\). Скажем, 1,38054b=1⋅b0+3⋅b−1+8⋅b−2+0⋅b−3+5⋅b−4+4⋅b−5.
По аналогии с десятичными дробями будем называть такую запись дробного числа b-ичной дробью. Так же как и для целых чисел, каждая цифра, используемая в записи b-ичной дроби, должна быть меньше \(b\). Как же переводить десятичную дробь в b-ичную? Для того что-бы найти алгоритм, запишем b-ичную дробь c=0,a1a2…an в виде суммы разрядных слагаемых: c=a1⋅b−1+a2⋅b−2+…+an−1⋅bn−1+an⋅b−n.

Из этой записи видно, что целая часть числа bc=a1,a2…an дает первую цифру после запятой в указанном представлении числа \(c\). Выделив в \(bc\) дробную часть, поступим с ней точно так же   умножим на \(b\). Таким образом мы получим еще одну цифру — a2. И так далее. Вот пример перевода десятичной дроби \(0,36\) в пятеричную систему:

Ответ: 0,145.

А теперь попытаемся перевести ту же дробь в семеричную систему счисления:

Обратите внимание: после четвертого умножения мы снова получили дробь \(0,36\). Это значит, что дальше процесс будет повторяться и никогда не закончится! Тем самым после перевода числа \(0,36\) в семеричную систему счисления получается бесконечная периодическая дробь: 0,23432343…7= 0,(2343)7. При переводе конечной b-ичной дроби в десятичную систему тоже может получиться бесконечная дробь. К примеру, запись 0,13 представляет одну треть и, следовательно, в десятичной системе будет выглядеть как бесконечная десятичная дробь 0,33333…=0,(3).
Как вы знаете, бесконечные дроби нередко округляют, оставляя такое количество разрядов, которое обеспечивает необходимую точность.
Напомним, что в десятичной системе правило округления таково: если цифра в разряде, с которого производится округление, меньше \(5\), то цифра в предшествующем разряде не меняется, в противном случае она увеличивается на \(1\).
Для b-ичной дроби правило нужно модифицировать: если цифра в разряде, с которого производится округление, меньше \(b/2\), то цифра в предшествующем разряде не меняется, в противном случае она увеличивается на \(1\).
Например, дробь 0,23432343…7 при округлении до третьего разряда после запятой дает 0,2347, а при округлении до шестого разряда после запятой даёт 0,2343247.
Источники:
Гейн А. Г., Ливчак А. Б., Сенокосов А. И. Информатика и ИКТ.  11 класс. М. : Просвещение, 56 с.
www.yaklass.ru
Перевод из одной системы счисления в другую
«Перевод чисел из одной системы счисления в другую»
Цель урока: Научит выполнять перевод чисел из десятичной в двоичную, восьмеричную, шестнадцатеричную
Научить выполнять перевод чисел из восьмерично, шестнадцатеричной в двоичную систему счисления
Развить познавательный интерес, логическое мышление
Развить алгоритмическое мышление, память, внимательность.
Тип урока: комбинированный.
Результат:учащие должны знать правила перевода чисел из одной системы счисления в другую.
Развить творческий подход по представлению информации, умение делать выводы
Этапы урока/ Стратегия, форма, время
Содержание
Результат
Оценивание.
Орг. Момент/ «импульс» 1,5 мин
Учащиеся делятся на две группы и становятся по обе стороны от учителя. Кто уловит импульс тот и победил.
эмоциональный настрой.
Создание коллоборативной среды.
Сообщение темы и постановка целей урока
Мы продолжаем тему предыдущего урока. Сегодня мы научимся переводить числа из 10 в 2,8,16-ю, переводить десятичные дроби, переводить из 2-й в 8,16-ю, и из 8,16-й в ю систему счисления.
Озвучиваю сама
Групповая работа/ представитель
Группы созданы по желанию учащихся.
Конверты с заданиями выбираются учащимися (приложение 1)
1группа: перевод чисел из десятичной системы в двоичную, восьмеричную, шестнадцатеричную системы счисления.
2группа: перевод десятичной дроби.
3группа: перевод целых чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную.
4группа: перевод целых чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную.
Разбирают задания в группе (приложение 2)
Выбирают представителя, который будет объяснять свою тему другой группе.
Выбирают конверты
Делают конспект своей темы
Объясняет свою тему другой группе, делают конспект.
Взаимооценивание.
Физминутка (приложение 3)
Закрепление/ индивидуальная работа,
Задание для самостоятельной работы: (приложение 4)
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=101000010₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=1014₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=87₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=16753₈ и 1DEB₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=100011110₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=10100011011₂
Рассчитать детей, для обмена при взаимопроверки.
Взаимооценивание
Сравнение с образцом
Подведение итога /Рефлексия. «стикер»
1 мин
Дети садятся на свои места. Берут стикеры и наклеиваю на доску, отвечая на вопрос «Понравился урок или нет?»
Наклеивают стикеры.
Самооценивание.
д/з 2 мин
Пар 3, задание стр 15-16 письменно.
Приложение 1
1группа: перевод чисел из десятичной системы в двоичную, восьмеричную, шестнадцатеричную системы счисления.
2группа: перевод десятичной дроби.
3группа: перевод целых чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную.
4группа: перевод целых чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную.
1 группа: перевод чисел из десятичной системы в двоичную, восьмеричную, шестнадцатеричную системы счисления.
Алгоритм перевода:
Десятичное число делится с остатком на основание системы, полученное частное делится с остатком. Так продолжается до тех пор, пока частное не станет меньше делителя.
Полученные остатки записываются в обратной последовательности.
125
2
124
62
2
1
62
31
2
0
30
15
2
1
14
7
2
1
6
3
2

1
2
1
1
125
8
120
15
8
1
8
1

0
125
16
112
7
13
2группа: перевод десятичной дроби.
Алгоритм перевода десятичной дроби
Десятичная дробь последовательно умножается на основание системы, а полученная дробная часть снова умножается на основание системы. Так продолжается до сих пор, пока не получится нулевая дробная часть или не будет достигнута требуемая точность вычисления.
Полученные целые части произведения записываются в прямой последовательности.
0
125

х2
0
250

х2
0
500

х2
1
000
0
125

х8
1
000
0
125

х16
2
000
3группа: перевод целых чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную
Что бы перевести целое двоичное число в восьмеричное, необходимо его разбить по три цифры справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями
101111₂=1*2²+0*2¹+1*2⁰1*2²+1*2¹+1*2⁰=57₈
А также для перевода можно использовать таблицу: стр 14 учебника.
Чтобы перевести целое двоичное число в шестнадцатеричное, необходимо его разбить по четыре цифры справа налево, а затем преобразовать каждую группу в шестнадцатеричную цифру. Если в последней, левой группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями
00101111₂=0*2³+0*2²+1*2¹+0*2⁰ 1+2³+1*2²+1*2¹+1*2⁰=2F₁₆
А также для перевода можно использовать таблицу: стр15 учебника.
4группа: перевод целых чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную
Чтобы перевести целое число из восьмеричной и шестнадцатеричной систем счисления, необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр, а при преобразовании шестнадцатеричного числа – в группу из четырех цифр. Для помощи воспользоваться таблицами на стр 14-15.
127₈=001010111=001010111₂
1 2 7
127₁₆=000100100111=000100100111₂
1 2 7
Приложение 4
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
Перевести целое десятичное число в двоичную систему счисления: 322₁₀=________________₂
Перевести десятичное число в восьмеричную систему счисления: 254₁₀=______________₈
Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=__________₁₆
Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=______________₈ и ______________₁₆
Перевести восьмеричное число в двоичную систему счисления: 436₈=_______________₂
Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=__________________₂
kopilkaurokov.ru

Число в десятичной системе счисления	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
В восьмеричной	1	2	3	4	5	6	7	10	11	12	13	14	15	16	17	20
В двоичной	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111	10000
В шестнадцатеричной	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10

Этапы урока/ Стратегия, форма, время	Содержание	Результат	Оценивание.
Орг. Момент/ «импульс» 1,5 мин	Учащиеся делятся на две группы и становятся по обе стороны от учителя. Кто уловит импульс тот и победил.	эмоциональный настрой. Создание коллоборативной среды.
Сообщение темы и постановка целей урока	Мы продолжаем тему предыдущего урока. Сегодня мы научимся переводить числа из 10 в 2,8,16-ю, переводить десятичные дроби, переводить из 2-й в 8,16-ю, и из 8,16-й в ю систему счисления.	Озвучиваю сама
Групповая работа/ представитель	Группы созданы по желанию учащихся. Конверты с заданиями выбираются учащимися (приложение 1) 1группа: перевод чисел из десятичной системы в двоичную, восьмеричную, шестнадцатеричную системы счисления. 2группа: перевод десятичной дроби. 3группа: перевод целых чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную. 4группа: перевод целых чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную. Разбирают задания в группе (приложение 2) Выбирают представителя, который будет объяснять свою тему другой группе.	Выбирают конверты Делают конспект своей темы Объясняет свою тему другой группе, делают конспект.	Взаимооценивание.
	Физминутка (приложение 3)
Закрепление/ индивидуальная работа,	Задание для самостоятельной работы: (приложение 4) Перевести целое десятичное число в двоичную систему счисления: 322₁₀=101000010₂ Перевести десятичное число в восьмеричную систему счисления: 254₁₀=1014₈ Перевести десятичное число в шестнадцатеричную систему счисления:135₁₀=87₁₆ Перевести двоичное число в восьмеричную и шестнадцатеричную систему счисления: 1110111101011₂=16753₈ и 1DEB₁₆ Перевести восьмеричное число в двоичную систему счисления: 436₈=100011110₂ Перевести шестнадцатеричное число в двоичную систему счисления:А36₁₆=10100011011₂	Рассчитать детей, для обмена при взаимопроверки.	Взаимооценивание Сравнение с образцом
Подведение итога /Рефлексия. «стикер» 1 мин	Дети садятся на свои места. Берут стикеры и наклеиваю на доску, отвечая на вопрос «Понравился урок или нет?»	Наклеивают стикеры.	Самооценивание.
д/з 2 мин	Пар 3, задание стр 15-16 письменно.

Системы счисления. Перевод из одной системы в другую.

Правила перевода чисел из одной системы в другую » СтудИзба

3.3. Правила перевода чисел из одной системы счисления в другую

Задание №1. Перевод из одной системы счисления в другую

Системы счисления и их разновидности.

Системы счисления. Перевод из одной системы в другую.

Десятичные дроби и смешанные числа в разных системах счисления.

Перевод чисел из одной системы счисления в другую

1. Перевод дробных чисел из одной системы счисления в другую

Перевод из одной системы счисления в другую

Оставить комментарий Отменить ответ