кратко и понятно о формулах и формулировках на конкретных примерах
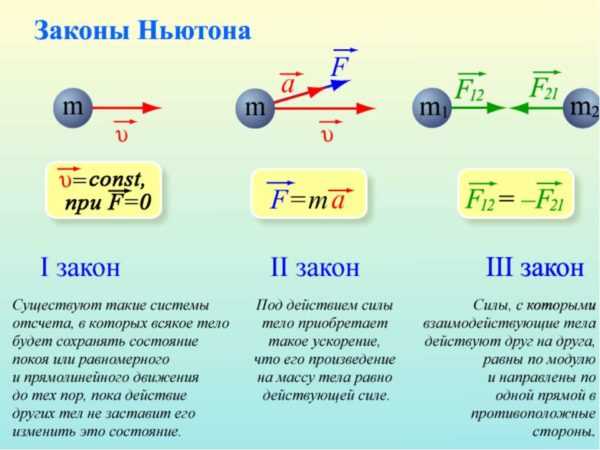
В школьном курсе физики изучаются три закона Ньютона, являющиеся основой классической механики. Сегодня с ними знаком каждый школьник, но во времена великого ученого подобные открытия считались революционными. Законы Ньютона, кратко и понятно будут описаны ниже, они помогают не только понять основу механики и взаимодействия объектов, но и помогают записать данные в качестве уравнения.
Содержание статьи
Вводная информация
Впервые три закона Иссак Ньютон описал в труде «Математические начала натуральной философии» (1867 год), в котором были подробно изложены не только собственные выводы ученого, но все знания по этой теме открытые другими философами и математиками. Таким образом, труд стал фундаментальным в истории механики, а позднее и физики. В нем рассмотрены перемещение и взаимодействие массивных тел.
Интересно знать! Исаак Ньютон был не только талантливым физиком, математиком и астрономом, но и считался гением в механике. Занимал должность президента королевского общества Лондона.
 Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).
Каждое утверждение освещает одну из сфер взаимодействия и перемещения предметов в природе, правда обращение к ним было несколько упразднено Ньютоном, и они были приняты как точки без определенного размера (математические).
Именно это упрощение позволило проигнорировать естественные физические явления: воздушное сопротивление, трение, температуру или другие физические показатели объекта.
Полученные данные могли быть описаны только по времени, массе или длине. Именно из-за этого формулировки Ньютона обеспечивают лишь подходящие, но приближенные значения, которые нельзя использовать для описания точной реакции крупных или изменяемых по форме объектов.
Перемещение массивных предметов, которые участвуют в определениях, принято исчислять в инерциальной системе отсчета, представленной в виде системы координат из трех измерений, и при этом она не увеличивает свою скорость и не оборачивается вокруг своей оси.
Ее часто называют системой отсчета Ньютона, но при этом ученый никогда не создавал и не использовал подобной системы, а использовал нерациональную. Именно в этой системе тела могут двигаться так, как описывает это Ньютон.
Первый закон
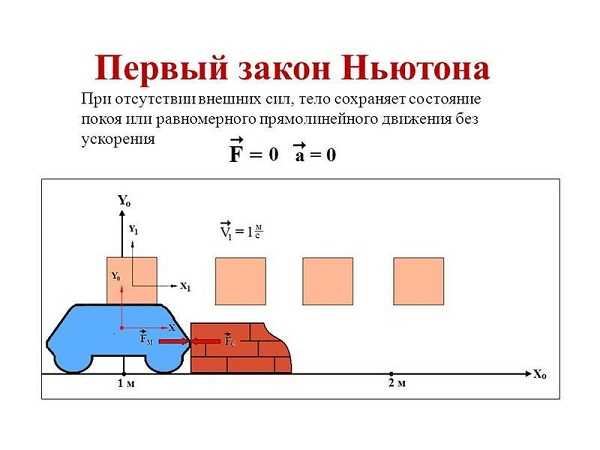
Называется законом инерции. Не существует его практической формулы, зато есть несколько формулировок. В учебниках по физике предлагается следующая формулировка первого закона Ньютона: есть инерциальные системы отсчета, в отношении которых объект, если он свободен от воздействия любых сил (или же они моментально компенсируется), находиться в полном покое или же двигается по прямой и с одинаковой скоростью. Что означает данное определение и как его понять?
Простыми словами первый закон Ньютона объясняется так: любое тело, если его не трогать и никоим образом не воздействовать на него, будет оставаться постоянно в состоянии покоя, то есть бесконечно стоять на месте. То же самое происходит и при его движении: оно будет равномерно двигаться по заданной траектории бесконечно, пока на него не воздействует что-либо.
Подобное утверждение озвучивал Галилео Галилей, но не смог уточнить и точно описать это явление. В этой формулировке важно правильно понять, что такое инерциальные системы отсчета. Если сказать совсем простыми словами, то это система, в которой выполняется действие данного определения.
Первый закон Ньютона
В мире можно увидеть огромное множество подобных систем, если понаблюдать за движением:
- поезда на заданном участке с одинаковой скоростью;
- Луны вокруг Земли;
- колеса обозрения в парке.
В качестве примера рассмотрим некоего парашютиста, который уже раскрыл парашют и движется прямолинейно и при этом равномерно по отношению к поверхности Земли. Движение человека не прекратиться до тех пор, пока земное притяжение будет компенсироваться движением и сопротивлением воздуха. Как только это сопротивление уменьшится, то притяжение увеличится, что приведет к изменению скорости парашютиста – его движение станет прямолинейным и равноускоренным.
Именно в отношении этой формулировки существует яблочная легенда: Исаак отдыхал в саду под яблоней и размышлял о физических явлениях, когда с дерева сорвалось спелое яблоко и упало в траву. Именно ровное падение заставило ученого изучить этот вопрос и выдать в итоге научное объяснение движению предмета в некой системе отсчета.
Интересно знать! Помимо трех явлений в механике, Исаак Ньютон также объяснил движение Луны как спутника Земли, создал корпускулярную теорию света и разложил радугу на 7 цветов.
Второй закон
 Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.
Данное научное обоснование касается не просто движения предметов в пространстве, а взаимодействия их с другими объектами и результатов этого процесса.
Закон гласит: увеличение скорости объекта с некоторой постоянной массой в инерциальной системе отсчета прямо пропорционально силе воздействия и обратно пропорционально постоянной массе движущегося предмета.
Проще говоря, если существует некое движущиеся тело, масса которого не изменяется, и на него вдруг начнет воздействовать посторонняя сила, то оно начнет ускоряться. А вот скорость ускорения будет прямо зависеть от воздействия и обратно пропорционально зависеть от массы движущегося предмета.
Для примера можно рассмотреть снеговой шар, который катиться с горы. Если шар толкать по ходу движения, то ускорения шара будет зависеть от мощности воздействия: чем она больше, тем больше ускорение. Но, чем больше масса данного шара, тем меньше будет ускорение. Данное явление описывается формулой, в которой учитывается ускорение, или «a», равнодействующая масса всех воздействующих сил, или «F», а также масса самого предмета, или «m»:
а = F/m
Следует уточнить, что данная формула может существовать только в том случае, если равнодействующая всех сил не меньше и не равна нулю. Применяется закон только относительно тел, которые двигаются со скоростью меньше световой.
Полезное видео: первый и второй законы Ньютона
Третий закон
 Многие слышали выражение: «На каждое действие есть свое противодействие». Его часто используют не только в общеобразовательных целях, но и воспитательных, объясняя, что на каждую силу найдется большая.
Многие слышали выражение: «На каждое действие есть свое противодействие». Его часто используют не только в общеобразовательных целях, но и воспитательных, объясняя, что на каждую силу найдется большая.
Эта формулировка пошла от очередного научного утверждения Исаака Ньютона, а точнее его третьего закона, который объясняет взаимодействие различных сил в природе относительно какого-либо тела.
Третий закон Ньютона определение имеет такое: предметы оказывают воздействие друг на друга с силами одинаковой природы (соединяющей массы предметов и направлены вдоль прямой), которые равны по своим модулям и при этом направлены в разные стороны. Данная формулировка звучит достаточно сложно, но простыми словами объяснить закон легко: каждая сила имеет свое противодействие или равную силу, направленную в обратную сторону.
Гораздо проще будет понять смысл закона, если в качестве примера взять пушку, из которой стреляют ядрами. Пушка воздействует на снаряд с той же силой, с которой снаряд воздействует на пушку. Подтверждением этого будет небольшое движение пушки назад во время выстрела, что подтвердит воздействие ядра на орудие. Если взять как пример тоже самое яблоко, которое падает на землю, то станет понятно, что яблоко и земля воздействуют друг на друга с равной силой.
Закон имеет также математическое определение, в котором используется сила первого тела (F1) и второго (F2):
F1 = -F2
Знак минуса сообщает о том, что векторы сил двух разных тел направлены в противоположные стороны. При этом важно помнить, что данные силы не компенсируют друг друга, поскольку направлены относительно двух тел, а не одного.
Полезное видео: 3 закона Ньютона на примере велосипеда
Вывод
Данные законы Ньютона кратко и четко необходимо знать каждому взрослому человеку, поскольку они являются основой механики и действуют в повседневной жизни, несмотря на то, что не при всех условиях данные закономерности соблюдаются. Они стали аксиомами в классической механике, и на основе их были созданы уравнения движения и энергии (сохранение импульса и сохранение механической энергии).
Вконтакте
Google+
Законы Ньютона — Википедия РУ
Первый закон Ньютона
Первый закон Ньютона постулирует существование инерциальных систем отсчета. Поэтому он также известен как закон инерции. Инерция (она же инертность) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой.
Современная формулировка
В современной физике первый закон Ньютона принято формулировать в следующем виде
Историческая формулировка
Ньютон сформулировал первый закон механики так:
Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние. |
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» следует заменить термином «материальная точка», так как тело конечных размеров в отсутствие внешних сил может совершать и вращательное движение. Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и абсолютного времени, а это представление современная физика отвергает. С другой стороны, в произвольной (например, вращающейся) системе отсчёта закон инерции неверен, поэтому ньютоновская формулировка была заменена постулатом существования инерциальных систем отсчета.
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО).
Масса материальной точки при этом полагается величиной постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами[4][5][6][7].
Современная формулировка
В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. |
При подходящем выборе единиц измерения, этот закон можно записать в виде формулы:
a→=F→m,{\displaystyle {\vec {a}}={\frac {\vec {F}}{m}},}где a→{\displaystyle {\vec {a}}} — ускорение материальной точки;
F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к материальной точке;
m{\displaystyle m} — масса материальной точки.
Второй закон Ньютона может быть также сформулирован в эквивалентной форме с использованием понятия импульс:
В инерциальной системе отсчета скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней внешних сил. dp→dt=F→,{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}},} |
где p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} — импульс точки, v→{\displaystyle {\vec {v}}} — её скорость, а t{\displaystyle t} — время. При такой формулировке, как и при предшествующей, полагают, что масса материальной точки неизменна во времени[8][9][10].
Иногда предпринимаются попытки распространить сферу применения уравнения dp→dt=F→{\displaystyle {\frac {d{\vec {p}}}{dt}}={\vec {F}}} и на случай тел переменной массы. Однако, вместе с таким расширительным толкованием уравнения приходится существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила[11][12].
Замечания
Когда на материальную точку действуют несколько сил, с учётом принципа суперпозиции, второй закон Ньютона записывается в виде:
ma→=∑i=1nFi→{\displaystyle m{\vec {a}}=\sum _{i=1}^{n}{\vec {F_{i}}}}или
dp→dt=∑i=1nFi→.{\displaystyle {\frac {d{\vec {p}}}{dt}}=\sum _{i=1}^{n}{\vec {F_{i}}}.}Второй закон Ньютона, как и вся классическая механика, справедлив только для движения тел со скоростями, много меньшими скорости света. При движении тел со скоростями, близкими к скорости света, используется релятивистское обобщение второго закона, получаемое в рамках специальной теории относительности.
Следует учитывать, что нельзя рассматривать частный случай (при F→=0{\displaystyle {\vec {F}}=0} ) второго закона как эквивалент первого, так как первый закон постулирует существование ИСО, а второй формулируется уже в ИСО.
Историческая формулировка
Исходная формулировка Ньютона:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. |
Интересно, что если добавить требование инерциальности для системы отсчёта, то в такой формулировке этот закон справедлив даже в релятивистской механике.
Третий закон Ньютона
Этот закон описывает, как взаимодействуют две материальные точки. Возьмём для примера замкнутую систему, состоящую из двух материальных точек. Первая точка может действовать на вторую с некоторой силой F→1→2{\displaystyle {\vec {F}}_{1\to 2}} , а вторая — на первую с силой F→2→1{\displaystyle {\vec {F}}_{2\to 1}} . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия F→1→2{\displaystyle {\vec {F}}_{1\to 2}} равна по модулю и противоположна по направлению силе противодействия F→2→1{\displaystyle {\vec {F}}_{2\to 1}} .
Современная формулировка
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению: F→2→1=−F→1→2.{\displaystyle {\vec {F}}_{2\to 1}=-{\vec {F}}_{1\to 2}.} |
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно[13].
Историческая формулировка
Ньютон дал следующую формулировку закона[1]:
Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны. |
Для силы Лоренца третий закон Ньютона не выполняется. Лишь переформулировав его как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость[14].
Следствия законов Ньютона
Законы Ньютона являются аксиомами классической ньютоновской механики. Из них, как следствия, выводятся уравнения движения механических систем, а также «законы сохранения», указанные ниже. Разумеется, есть и законы (например, всемирного тяготения или Гука), не вытекающие из трёх постулатов Ньютона.
Уравнения движения
Уравнение F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}} является дифференциальным уравнением: ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию (перемещение) механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости.
Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
Закон сохранения импульса
Закон сохранения импульса утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю[15].
Закон сохранения механической энергии
Если все силы консервативны, то возникает закон сохранения механической энергии взаимодействующих тел: полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной[16].
Законы Ньютона и силы инерции
Использование законов Ньютона предполагает задание некой ИСО. Однако, на практике приходится иметь дело и с неинерциальными системами отсчёта. В этих случаях, помимо сил, о которых идёт речь во втором и третьем законах Ньютона, в механике вводятся в рассмотрение так называемые силы инерции.
Обычно речь идёт о силах инерции двух различных типов[13][17]. Сила первого типа (даламберова сила инерции[18]) представляет собой векторную величину, равную произведению массы материальной точки на её ускорение, взятое со знаком минус. Силы второго типа (эйлеровы силы инерции[18]) используются для получения формальной возможности записи уравнений движения тел в неинерциальных системах отсчёта в виде, совпадающем с видом второго закона Ньютона. По определению, эйлерова сила инерции равна произведению массы материальной точки на разность между значениями её ускорения в той неинерциальной системе отсчёта, для которой эта сила вводится, с одной стороны, и в какой-либо инерциальной системе отсчёта, с другой[13][17]. Определяемые таким образом силы инерции силами в истинном смысле слова не являются[19][13], их называют фиктивными[20], кажущимися[21] или псевдосилами[22].
Законы Ньютона в логике курса механики
Существуют методологически различные способы формулирования классической механики, то есть выбора её фундаментальных постулатов, на основе которых затем выводятся законы-следствия и уравнения движения. Придание законам Ньютона статуса аксиом, опирающихся на эмпирический материал, — только один из таких способов («ньютонова механика»). Этот подход принят в средней школе, а также в большинстве вузовских курсов общей физики.
Альтернативным подходом, использующимся преимущественно в курсах теоретической физики, выступает лагранжева механика. В рамках лагранжева формализма имеются одна-единственная формула (запись действия) и один-единственный постулат (тела движутся так, чтобы действие было стационарным), являющийся теоретической концепцией. Из этого можно вывести все законы Ньютона, правда, только для лагранжевых систем (в частности, для консервативных систем). Следует, однако, отметить, что все известные фундаментальные взаимодействия описываются именно лагранжевыми системами. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима.
Исторический очерк
Практика применения машин в мануфактурной промышленности, строительство зданий, кораблестроение, использование артиллерии позволили ко времени Ньютона накопиться большому числу наблюдений над механическими процессами. Понятия инерции, силы, ускорения всё более прояснялись в течение XVII столетия. Работы Галилея, Борелли, Декарта, Гюйгенса по механике уже содержали все необходимые теоретические предпосылки для создания Ньютоном в механике логичной и последовательной системы определений и теорем[23].
 Страница «Начал» Ньютона с аксиомами механики
Страница «Начал» Ньютона с аксиомами механикиОсновные законы механики Исаак Ньютон сформулировал в своей книге «Математические начала натуральной философии»[1]:
Оригинальный текст (лат.)
LEX I
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quantenus a viribus impressis cogitur statum illum mutare.LEX II
Mutationem motus proportionalem esse vi motrici impressae et fieri secundum lineam rectam qua vis illa imprimitur.LEX III
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Русский перевод этих формулировок законов см. в предыдущих разделах.
Первый закон (закон инерции), в менее чёткой форме, опубликовал ещё Галилей, допускавший свободное движение не только по прямой, но и по окружности (видимо, из астрономических соображений)[24]. Галилей также сформулировал важнейший принцип относительности, который Ньютон не включил в свою аксиоматику, потому что для механических процессов данный принцип является следствием уравнений динамики. Кроме того, Ньютон считал пространство и время абсолютными понятиями, едиными для всей Вселенной, и явно указал на это в своих «Началах».
Ньютон также дал строгие определения таких физических понятий, как количество движения (не вполне ясно использованное у Декарта[24]) и сила. Он ввёл в физику понятие массы как меры инертности тела и, одновременно, его гравитационных свойств (ранее физики пользовались понятием вес).
В середине XVII века ещё не существовало современной техники дифференциального и интегрального исчисления. Соответствующий математический аппарат в 1680-е годы параллельно создавался самим Ньютоном (1642—1727), а также Лейбницем (1646—1716). Завершили математизацию основ механики Эйлер (1707—1783) и Лагранж (1736—1813).
Примечания
- ↑ 1 2 3 Исаак Ньютон. Математические начала натуральной философии. Перевод с латинского и примечания А. Н. Крылова / под ред. Полака Л. С.. — М.: Наука, 1989. — С. 40—41. — 690 с. — (Классики науки). — 5 000 экз. — ISBN 5-02-000747-1.
- ↑ Тарг С. М. Ньютона законы механики // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 370. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Инерциальная система отсчёта // Физическая энциклопедия (в 5 томах) / Под редакцией акад. А. М. Прохорова. — М.: Советская Энциклопедия, 1988. — Т. 2. — С. 145. — ISBN 5-85270-034-7.
- ↑ «Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.» стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
- ↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
- ↑ Журавлёв В. Ф. Основы теоретической механики. — М.: Физматлит, 2001. — С. 9. — 319 с. — ISBN 5-95052-041-3. «Масса [материальной точки] полагается постоянной, независящей ни от положения точки в пространстве, ни от времени».
- ↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
- ↑ «В ньютоновской механике… m=const и dp/dt=ma». Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с..
- ↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
- ↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
- ↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
- ↑ 1 2 3 4 Ишлинский А. Ю. Классическая механика и силы инерции. — М.: «Наука», 1987. — 320 с.
- ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.
- ↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 282. — 416 с. — ISBN 5-06-003117-9.
- ↑ Савельев И. В. Глава 3. Работа и энергия // Курс общей физики. Механика. — 4-е изд. — М.: Наука, 1970. — С. 89—99. — ISBN 5-17-002963-2.
- ↑ 1 2 Тарг С. М. Сила инерции // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 494-495. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ 1 2 Ишлинский А. Ю. К вопросу об абсолютных силах и силах инерции в классической механике // Теоретическая механика. Сборник научно-методических статей. — 2000. — № 23. — С. 3-8.
- ↑ «”Силы инерции” — не силы». Журавлёв В. Ф. Основания механики. Методические аспекты. — М.: ИПМ АН СССР, 1985. — С. 21. — 46 с.
- ↑ Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 82. — 368 с. — ISBN 5-93972-051-X.
- ↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Выпуск 1. Современная наука о природе. Законы механики // Фейнмановские лекции по физике. — М.: «Мир», 1965. — С. 225.
- ↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 186-197;
- ↑ 1 2 Кузнецов Б. Г. Генезис механического объяснения физических явлений и идеи картезианской физики // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — С. 160-161, 169-170, 177;
Литература
- Лич Дж. У. Классическая механика. М.: Иностр. литература, 1961.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
- Том 1. Часть 1-я; Часть 2-я
- Том 2. Часть 1-я; Часть 2-я
- Кудрявцев П. С. Курс истории физики. — М.: Просвещение, 1974.
- Crowell, Benjamin (2011), Light and Matter (2011, Light and Matter), especially at Section 4.2, Newton’s First Law, Section 4.3, Newton’s Second Law, and Section 5.1, Newton’s Third Law.
- Feynman, R. P. The Feynman Lectures on Physics / R. P. Feynman, Leighton, Sands. — 2nd. — Pearson/Addison-Wesley, 2005. — Vol. Vol. 1. — ISBN 0-8053-9049-9.
- Fowles, G. R. Analytical Mechanics / G. R. Fowles, Cassiday. — 6th. — Saunders College Publishing, 1999. — ISBN 0-03-022317-2.
- Likins, Peter W. Elements of Engineering Mechanics. — McGraw-Hill Book Company, 1973. — ISBN 0-07-037852-5.
- Marion, Jerry. Classical Dynamics of Particles and Systems / Jerry Marion, Thornton. — Harcourt College Publishers, 1995. — ISBN 0-03-097302-3.
- NMJ Woodhouse. Special Relativity. — London/Berlin : Springer, 2003. — P. 6. — ISBN 1-85233-426-6.
- Newton, Isaac, “Mathematical Principles of Natural Philosophy”, 1729 English translation based on 3rd Latin edition (1726), volume 1, containing Book 1, especially at the section Axioms or Laws of Motion, starting page 19.
- Newton, Isaac, “Mathematical Principles of Natural Philosophy”, 1729 English translation based on 3rd Latin edition (1726), volume 2, containing Books 2 & 3.
- Thomson, W (Lord Kelvin), and Tait, P G, (1867), Treatise on natural philosophy, volume 1, especially at Section 242, Newton’s laws of motion.
Ссылки
http-wikipediya.ru
Законы Ньютона – Физика – Справочник – Каталог статей
Формулировка законов Ньютона
Первый закон Ньютона
- Первый закон Ньютона гласит: существуют системы отсчёта (называемые инерциальными), в которых замкнутая система продолжает оставаться в состоянии покоя или прямолинейного равномерного движения. По сути, этот закон постулирует инертность тел. Это может казаться очевидным сейчас, но это не было очевидно на заре исследований природы. Так, например, Аристотель утверждал, что причиной всякого движения является сила, т. е. у него не было движения по инерции.
Инерциальная система отсчёта – это система отсчёта, связанная со свободным невращающимся телом. Свободное тело — тело, не взаимодействующее с другими телами.
Второй закон Ньютона
Второй закон Ньютона — дифференциальный закон движения, описывающий взаимосвязь между приложенной к телу силой и ускорением этого тела. Один из трех законов Ньютона.
Второй закон Ньютона утверждает, что ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела.
Этот закон записывается в виде формулы:
=
где — ускорение тела, — сила, приложенная к телу, а m — масса тела.
Или, в более известном виде:
=
Если на тело действуют несколько сил, то во втором законе Ньютона под подразумевается равнодействующая всех сил.
В случае, если масса тела меняется со временем, то второй закон Ньютона записывается в более общем виде:
где — импульс (количество движения) тела, t — время, а — производная по времени. Второй закон Ньютона действителен только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. →
В данном законе как частный случай заключен первый закон Ньютона. Это можно видеть если = 0 (т.е. если на тело не действуют силы или равнодействующая сил равна нулю) при этом соответственно получаем что и = 0, а значит, тело сохраняет состояние покоя или равномерного прямолинейного движения.
Третий закон Ньютона
- Третий закон Ньютона объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F12, а второе — на первое с силой F21. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия, F21 = −F12. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Сам закон: Тела действуют друг на друга с силами, направленными вдоль одной и той же прямой, равными по модулю и противоположными по направлению.
Выводы
Из законов Ньютона сразу же следуют некоторые интересные выводы. Так, третий закон Ньютона говорит, что, как бы тела ни взаимодействовали, они не могут изменить свой суммарный импульс: возникает закон сохранения импульса. Далее, надо потребовать, чтобы потенциал взаимодействия двух тел зависел только от модуля разности координат этих тел U(|r1–r2|). Тогда возникает закон сохранения суммарной механической энергии взаимодействующих тел:
Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики.
Комментарии к законам Ньютона
Силы инерции
Законы Ньютона, строго говоря, справедливы только в инерциальных системах отсчета. Если мы честно запишем уравнение движения тела в неинерциальной системе отсчета, то оно будет по виду отличаться от второго закона Ньютона. Однако часто, для упрощения рассмотрения, вводят некую фиктивную «силу инерции», и тогда эти уравнения движения переписываются в виде, очень похожем на второй закон Ньютона. Математически здесь все корректно, но с точки зрения физики новую фиктивную силу нельзя рассматривать как нечто реальное, как результат некоторого реального взаимодействия. Ещё раз подчеркнем: «сила инерции» — это лишь удобная параметризация того, как отличаются законы движения в инерциальной и неинерциальной системах отсчета.
Законы Ньютона и лагранжева механика
Законы Ньютона — не самый глубокий уровень формулирования классической механики. В рамках лагранжевой механики имеется одна-единственная формула (запись механического действия) и один-единственный постулат (тела движутся так, чтобы действие было минимальным), и из этого можно вывести все законы Ньютона. Более того, в рамках лагранжева формализма можно легко рассмотреть гипотетические ситуации, в которых действие имеет какой-либо другой вид. При этом уравнения движения станут уже непохожими на законы Ньютона, но сама классическая механика будет по-прежнему применима…
Решение уравнений движения
Уравнение F = ma (то есть второй закон Ньютона) является дифференциальным уравнением второго порядка, поскольку ускорение есть вторая производная от координаты по времени. Это значит, что эволюцию механической системы во времени можно однозначно определить, если задать её начальные координаты и начальные скорости. Заметим, что если бы уравнения, описывающие наш мир, были бы уравнениями первого порядка, то из нашего мира исчезли бы такие явления, как инерция, колебания, волны.
24-school.3dn.ru
1 закон ньютона формулировка и формулы — Гильдия юристов и риэлторов
1 закон ньютона формулировка и формулы
Формула второго закона Ньютона (жирным шрифтом указаны векторы):
Сила, действующая на тело создаёт ускорение a . Это важный момент, который представлен вторым законом Ньютона:
Из этой записи формулы второго закона Ньютона видно, что чем больше масса тела, тем меньшее ускорение оно получит от действия данной силы:
Рассмотрим подробнее формулу второго закона Ньютона.
Ускорение – это вектор, его направление совпадает с направлением силы F .
На это тело действует внешняя сила F , т.е. сила во втором законе Ньютона – это вектор внешней силы, сила действует на данное тело массы m.
1, 2, 3 Законы Ньютона
В механической системе тел, по 3-му закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направлены, т.е. геометрическая сумма внутренних сил равна 0.
Третий закон Ньютона. Всякое действие мт (тел) друг на друга, носит характер взаимодействия; силы, с которыми действуют друг на друга мт, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки.
Масса тела – физ.величина, являющаяся одной из основных характеристик материи, определяющая её инерционные (инертная масса) и гравитационные (гравитационная масса) св-ва.
; , т.е. импульс системы равен произведению массы системы на скорость её центра масс.
В основе Динамики мат.точки лежат три закона Ньютона.
Центр масс (центр инерции) системы мт называется воображаемая точка С, положение которой характеризует распределение массы этой системы.
Масса и сила Законы Ньютона
дистанционные лекции НИЯУ МИФИ на сайте МИФИ () или на сайте «Школа Росатома» (http://www.rosatomschool.ru)
Определять центростремительное ускорение шарика при его равномерном движении по окружности.
Закон Гука: формулировка, формула, экспериментальное подтверждение, следствия, границы применимости.
Утверждение, что материальная точка покоится или движется равномерно и прямолинейно, если на нее не действуют другие тела или воздействие на него других тел взаимно уравновешено,
Материал для самоподготовки по теме «Законы Ньютона. Силы в природе»
1) движется равномерно по прямолинейному участку шоссе
Первый закон Ньютона
Следует помнить, что в первом законе Ньютона речь идет о телах, которые могут быть приняты за материальные точки.
Первый закон Ньютона выполняется только в инерциальных системах отсчета. Например, тела, находящиеся в покое в салоне самолета, который движется равномерно, могут прийти в движение без всякого воздействия на них других тел, если самолет начнет маневрировать. В транспорте при резком торможении пассажиры падают, хотя никто их не толкает.
Например, шарик на нитке висит в покое, потому что сила тяжести компенсируется силой натяжения нити.
Первый закон Ньютона показывает, что состояние покоя и состояние равномерного прямолинейного движения не требуют для своего поддержания внешних воздействий. Свойство свободного тела сохранять скорость неизменной называется инерцией. Поэтому первый закон Ньютона называют ещё законом инерции. Равномерное прямолинейное движение свободного тела называется движением по инерции.
Закон инерции отнюдь не очевиден, как это может показаться на первый взгляд. С его открытием было покончено с одним давним заблуждением. До этого на протяжении веков считалось, что при отсутствии внешних воздействий на тело оно может находиться только в состоянии покоя, что покой – это как бы естественное состояние тела. Для движения же тела с постоянной скоростью необходимо, чтобы на него действовало другое тело. Казалось, что это подтверждал повседневный опыт: для того чтобы повозка двигалась с постоянной скоростью, ее должна все время тянуть лошадь; чтобы стол двигался по полу, его нужно непрерывно тянуть или толкать и т. д. Галилео Галилей был первым, кто указал, что это неверно, что при отсутствии внешнего воздействия тело может не только покоиться, но и двигаться прямолинейно и равномерно. Прямолинейное и равномерное движение является, следовательно, таким же «естественным» состоянием тел, как и покой. Фактически первый закон Ньютона говорит о том, что нет разницы между покоем тела и равномерным прямолинейным движением.
Проверить опытным путем закон инерции невозможно, потому что невозможно создать такие условия, при которых бы тело было свободным от внешних воздействий. Однако, всегда можно проследить обратное. В любом случае. когда тело изменяет скорость или направление своего движения, всегда можно найти причину – силу, которая вызвала это изменение.
1 закон ньютона формулировка и формулы
Сила, действующая на тело создаёт ускорение a . Это важный момент, который представлен вторым законом Ньютона:
Рассмотрим подробнее формулу второго закона Ньютона.
Формула второго закона Ньютона (жирным шрифтом указаны векторы):
Дано физическое тело массой m, т.е. масса во втором законе Ньютона – это масса данного тела.
Из этой записи формулы второго закона Ньютона видно, что чем больше масса тела, тем меньшее ускорение оно получит от действия данной силы:
На это тело действует внешняя сила F , т.е. сила во втором законе Ньютона – это вектор внешней силы, сила действует на данное тело массы m.
Три закона Ньютона
Повторим один из опытов, которые поставил итальянский ученый Галилео Галилей.
10. Брусок массой 0,5 кг соскальзывает с наклонной плоскости с углом наклона 30º. Скорость бруска увеличивается. Ускорение бруска равно 2 м/с2. Изобразите на чертеже равнодействующую приложенных к бруску сил. Чему она равна? Есть ли в задаче лишние данные?
Как вы уже знаете из курса физики основной школы, силы – векторные величины: каждая сила характеризуется числовым значением (модулем) и направлением. Силы измеряют с помощью динамометров. Единицей силы в СИ является 1 ньютон (Н). Определение ньютона мы дадим позже.
Единицу силы в СИ определяют на основе второго закона Ньютона: сила в 1 ньютон сообщает телу массой 1 кг ускорение 1 м/с 2 . Поэтому 1 Н = 1 кг * м/с 2 .
Инерциальных систем отсчета бесконечно много. Ведь если некоторая система отсчета является инерциальной, то инерциальной будет любая другая система отсчета, движущаяся относительно нее прямолинейно и равномерно.
Если на тело, которое можно считать материальной точкой, действуют несколько сил, то их можно заменить одной силой, которая является векторной суммой этих сил. Ее называют равнодействующей.
Еще по теме:
- Социальный закон социализации Механизмы социализации Социализация человека во взаимодействии с различными факторами и агентами происходит с помощью ряда, условно говоря, «механизмов». Также выделяют следующие группы механизмов социализации: По Г. Тарду(1843-1904) […]
- Предмет преступления по ст228 ук рф Предмет преступления по ст228 ук рф Уголовная ответственность по п. «в» ч. 3 ст. 228.1 УК РФ наступает лишь в тех случаях, когда лицо совершает деяния, предусмотренные ч. 1 или ч. 2 указанной статьи УК РФ, в отношении лица, не достигшего […]
- Правила рубок главного пользования 2 Проект рубок главного пользования Табл. 2. Сводная ведомость рубок главного пользования Согласно “Правил рубок . ” и других отраслевых и нормативных документов, осуществляется обоснование способов рубок главного пользования. Для […]
- Закон о договоре комиссии Договор комиссии Одна из основных отличительных черт договора комиссии проявляется в его предмете: совершение комиссионером только сделок, а не любых юридических действий. По договору комиссии нельзя доверить лицу быть представителем в […]
- Правило на умножение свойства Умножение отрицательных чисел, правило, примеры Умножение отрицательных рациональных чисел с помощью разобранного правила можно свести к умножению обыкновенных дробей, умножению смешанных чисел или умножению десятичных дробей. Запишем это […]
grb03.ru
Первый закон ньютона и формула
Первый закон ньютона и формула
В биомеханике также рассматривают взаимодействие между телом человека и внешним окружением, между звеньями тела, между двумя людьми (например, в единоборствах). В результате возникают силы, которые и являются количественной мерой этих взаимодействий.
При изучении величин, которые характеризуются не только величиной, но и направлением (например, скорость, ускорение. сила и т. п.) применяют их векторное изображение.
Формулировка первого закона Ньютона. Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или состояние равномерного прямолинейного движения, если на него не действуют другие или действие других тел компенсируется.
Первый закон Ньютона выполняется только в инерциальных системах отсчета. Например, тела, находящиеся в покое в салоне самолета, который движется равномерно, могут прийти в движение без всякого воздействия на них других тел, если самолет начнет маневрировать.
Сейчас вы окончательно убедитесь в том, что движение есть столь же естественное состояние любого тела, как и покой, а потому не требует никакой причины. Первый закон механики, или закон инерции, как его часто называют, был установлен еще Галилеем.
Но строгую формулировку этого закона дал и включил его в число основных законов механики Ньютон. Закон инерции относится к самому простому случаю движения — движению тела, на которое не оказывают воздействия другие.
Производя опыты с действием сил на тела, мы установили пропорциональность между модулем силы , действующей на тело, и модулем ускорения , которое эта сила сообщает, а также ввели новую величину — массу тела .
Опыты показали также, что направление ускорения совпадает с направлением силы, вызвавшей ускорение (§ 42), т. е. что векторы и совпадают по направлению. Следовательно, формулу (43.
Законы Ньютона
Фундамент динамики заложили законы движения Ньютона .
Классическая динамика базируется на трех основных законах Ньютона. К ним относится и закон независимости действия сил .
который гласит: при одновременном действии на материальную точку нескольких сил каждая из них сообщает точке такое ускорение, какое она сообщила бы, если бы действовала одна. 1) зная закон движения тела (т.е. уравнения, определяющие положение тела в пространстве в любой момент времени)
«Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».
С современной точки зрения, такая формулировка неудовлетворительна.
Во-первых, термин «тело» надо заменить на «материальная точка», так как тело в отсутствие внешних сил может совершать и вращательное движение.
Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает.
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка сохраняет свою скорость неизменной, если на нее не действуют другие тела.
Первый закон Ньютона. Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Масса тела – количественная мера его инертности.
В СИ она измеряется в килограммах.
Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными.
Системы отсчета, движущиеся относительно инерциальных с ускорением, называются неинерциальными .
Сила – количественная мера взаимодействия тел.
Сила – векторная величина и измеряется в ньютонах (Н). Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.
Сегодняшний урок физики будет посвящен рассмотрению темы о первом законе Ньютона.
Давайте вначале озвучим определение этого закона.
Итак, первый закон Ньютона гласит: То есть, можно сказать, что первый закон Ньютона, является законом инерции и с многообразных систем отсчета, акцентирует внимание на инерциальных системах.Конечно, вы можете сказать, что инерциальных систем отсчета может быть очень и очень много, но реально на самом деле, мы можем говорить, что такая система немного идеализирована, поскольку при ближайшем рассмотрении таких систем отсчета все таки, нет.
При движении тела его скорость может изменяться по модулю и направлению. Это означает, что тело двигается с некоторым ускорением .
В кинематике не ставится вопрос о физической причине, вызвавшей ускорение движения тела.
Как показывает опыт, любое изменение скорости тела возникает под влиянием других тел. Динамика рассматривает действие одних тел на другие как причину, определяющую характер движения тел.
Законы динамики были открыты в 1687 г.
advokat-boyko.ru
Первый закон ньютона формулы | vigor24.ru
Первый закон Ньютона
Формулировка первого закона Ньютона. Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или состояние равномерного прямолинейного движения, если на него не действуют другие тела или действие других тел компенсируется. Первый закон Ньютона выполняется только в инерциальных системах отсчета. Например, тела, находящиеся в покое в салоне самолета, который движется равномерно, могут прийти в движение без всякого воздействия на них других тел, если самолет начнет маневрировать.
Первый закон ньютона формулы
«Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».
С современной точки зрения, такая формулировка неудовлетворительна. Во-первых, термин «тело» надо заменить на «материальная точка», так как тело в отсутствие внешних сил может совершать и вращательное движение.
Во-вторых, и это главное, Ньютон в своём труде опирался на существование абсолютной неподвижной системы отсчёта, то есть абсолютного пространства и времени, а это представление современная физика отвергает.
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка сохраняет свою скорость неизменной, если на нее не действуют другие тела.
Мы ознакомились с тремя законами движения — законами Ньютона.
Значение законов Ньютона состоит в том, что они позволяют решать основную задачу механики. Первый закон Ньютона утверждает, что существуют инерциальные системы отсчета. Второй закон, справедливый для инерциальных систем отсчета, связывает силу, действующую на тело, с вызванным ею ускорением.
И если сила известна, то можно найти ускорение тела в любой точке траектории.
В биомеханике также рассматривают взаимодействие между телом человека и внешним окружением, между звеньями тела, между двумя людьми (например, в единоборствах). В результате возникают силы, которые и являются количественной мерой этих взаимодействий.
При изучении величин, которые характеризуются не только величиной, но и направлением (например, скорость, ускорение. сила и т. п.) применяют их векторное изображение.
Ньютон сформулировал закон инерции, включив его в основу механики в качестве первого из трех законов.
Поэтому этот закон называют первым законом Ньютона . В окружении любого тела, покоится оно или движется, есть другие тела, некоторые из которых или все как-то действуют на тело, влияют на состояние его движения. Чтобы выяснить влияние окружающих тел, надо исследовать каждый отдельный случай.
Второй закон Ньютона
Второй закон Ньютона связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Хотите легко и быстро, на примерах понять, как это происходит?
Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать.
Начнем с практической части. Нагрузите чем-нибудь две сумки или два пакета. Один чуть-чуть, а второй очень сильно.
Галилей исследовал законы движения самых обычных предметов, которые были у него под рукой.
Изучая эти законы, производя различные опыты, чтобы выяснить, как скатываются шарики по наклонной плоскости, как качаются маятники и т. д. Галилей открыл великий принцип, который называется принципом инерции и состоит вот в чем: если на предмет ничто не действует и он движется с определенной скоростью по прямой линии, то он будет двигаться с той же самой скоростью и по той же самой прямой линии вечно.
Вот такое удивительное свойство нашего мира.
Законы Ньютона (выполняются в ИСО)Первый закон
Существуют такие системы отсчета, называющиеся инерциальными, в которых свободные тела движутся поступательно, равномерно и прямолинейно или покоятся, если действия всех внешних сил скомпенсированы.
Второй закон (2) Ускорение прямо пропорционально внешней силе и обратно пропорционально массе.
Масса: · Мера инертности тела, т.е. способности тела приобретать ускорение · Количество вещества в теле и в классической механике масса – величина постоянная · Выполняется закон сохранения массы · В релятивистском случае Где mo – масса покоя, v – скорость движения тела, с – скорость распространения света в вакууме Основное уравнение динамики, (4), Где — импульс – количество движения материальной точки, величина относительная.
Классическая механика Ньютона сыграла и играет до сих пор огромную роль в развитии естествознания. Она объясняет множество физических явлений и процессов в земных и внеземных условиях, составляет основу для многих технических достижений в течение длительного времени.
На ее фундаменте формировались многие методы научных исследований в различных отраслях естествознания. Во многом она определяла мышление и мировоззрение.
vigor24.ru
Первый закон ньютона формула | Консультация юриста в Москве, компания jursait.ru
Первый закон ньютона формула
ГЛАВА 2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Как уже отмечалось, динамика – это раздел классической механики, изучающий движение материальных тел под действием приложенных к ним сил, т.е. дающий связь между взаимодействиями тел и изменениями в их движении. Она является основным разделом механики и базируется на трех законах Ньютона (1687 г.) Первый Ньютона (закон инерции) формулируется следующим образом: всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние . Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии или взаимном уравновешивании внешних воздействий называется инертностью.
Первый закон Ньютона
Формулировка первого закона Ньютона. Существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или состояние равномерного прямолинейного движения, если на него не действуют другие тела или действие других тел компенсируется.
Например, шарик на нитке висит в покое, потому что сила тяжести компенсируется силой натяжения нити.
Первый закон выполняется только в инерциальных системах отсчета.
Законы Ньютона
Три Ньютона лежат в основе классической механики и позволяют вывести уравнения движения. С момента формулировки законов Ньютона пошел отчет в истории не только
Английский физик, математик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии»
современной физики, но и естественных наук.
Первый закон Ньютона часто еще называется инерциальным.
Первый закон ньютона формула
Первый закон Ньютона. существуют системы отсчета, в которых любое изолированное не подвергающееся действию внешних сил тело сохраняет свое состояние покоя или равномерного прямолинейного движения. Такие системы отсчета называются инерциальными.Первый часто называют инерции, поскольку движение, не поддерживаемое никаким воздействием, — это движение по инерции.
Второй закон Ньютона
Главная  >  Wiki-учебник  >  Физика  > 9 класс  > : формула и определение + маленький опыт
связывает вместе три, на первый взгляд, совершенно не связанные друг с другом величины: ускорение, массу и силу. Хотите легко и быстро, на примерах понять, как это происходит? Запросто. Надо будет проделать пару элементарных опытов и немного порассуждать.
Начнем с практической части.
Инерциальные системы отсчета: первый закон Ньютона
Главная  >  Wiki-учебник  >  Физика  > 9 класс  > Инерциальные системы отсчета: первый
С древнейших времен движение материальных тел не переставало волновать умы ученых. Так, например, сам Аристотель считал, что если на тело не действуют никакие силы, то такое тело всегда будет находиться в покое.
И лишь только спустя 2000 лет итальянский ученый Галилео Галилей смог исключить из формулировки Аристотеля слово «всегда».
Первый закон ньютона формула
2. Взаимодействие тел. Сила. Законы динамики Ньютона
Простые наблюдения и опыты, например с тележками (рис. 3), приводят к следующим качественным заключениям: а) тело, на которое другие тела не действуют, сохраняет свою скорость неизменной; б) ускорение тела возникает под действием других тел, но зависит и от самого тела; в) действия тел друг на друга всегда носят характер взаимодействия.
jursait.ru
