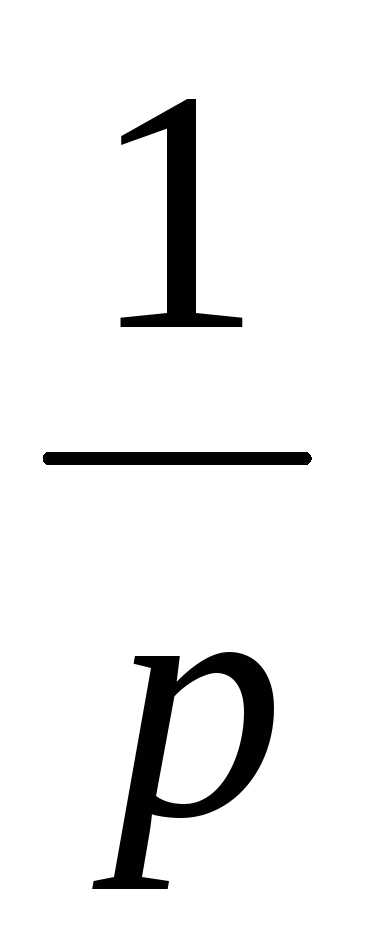
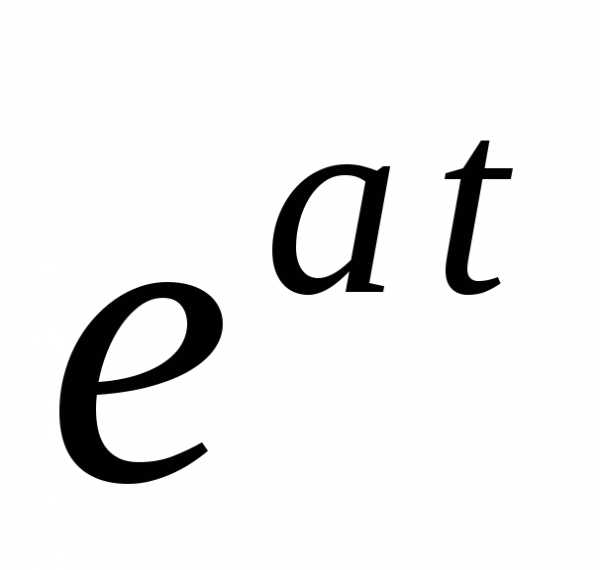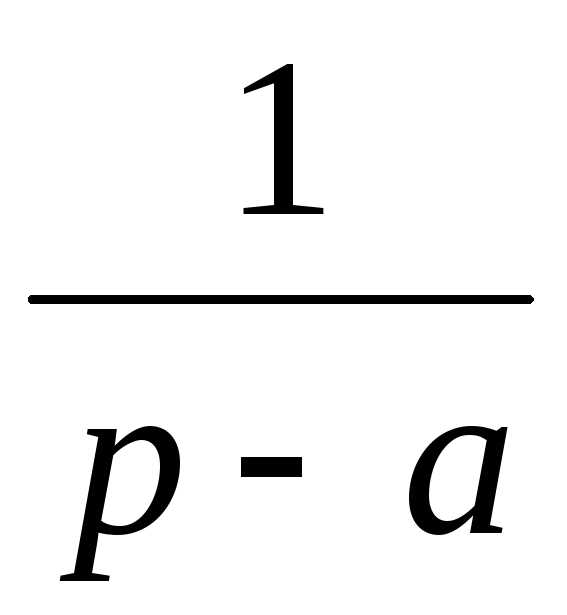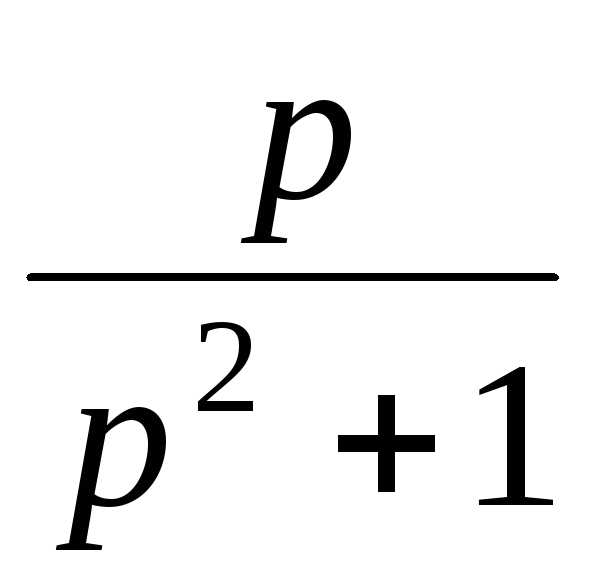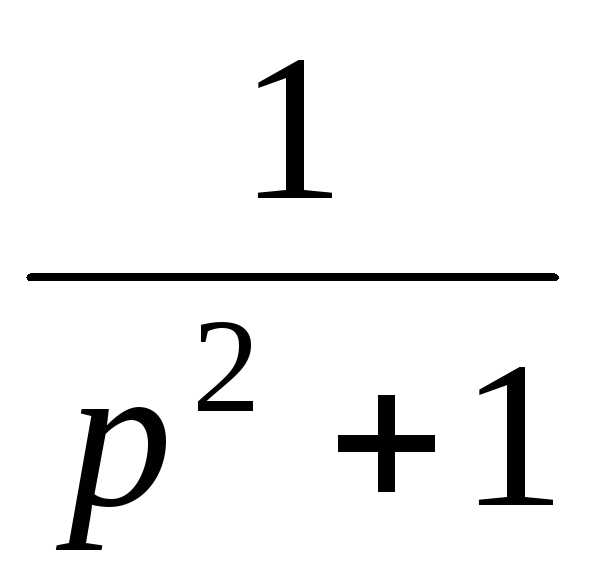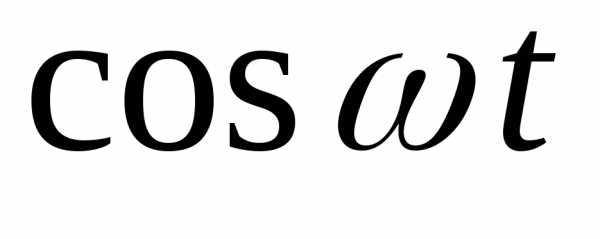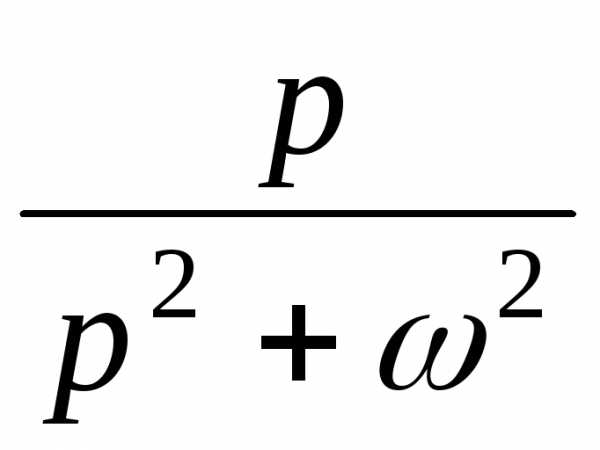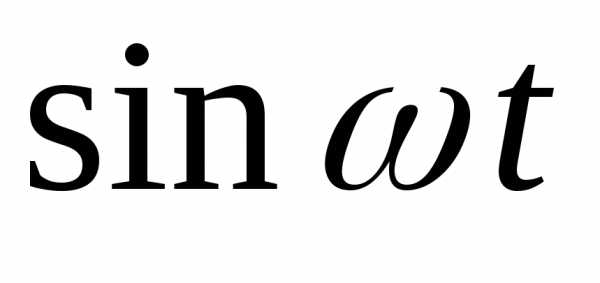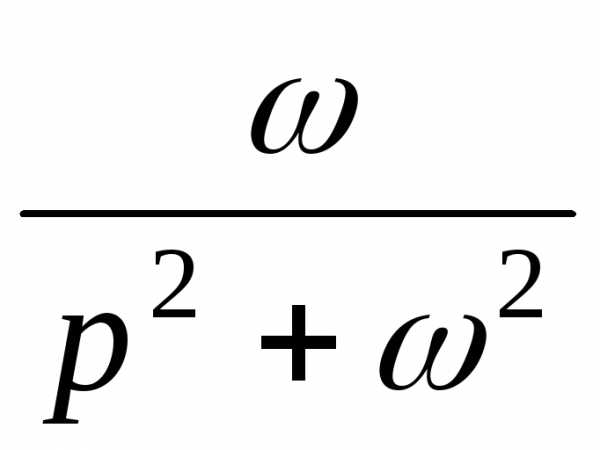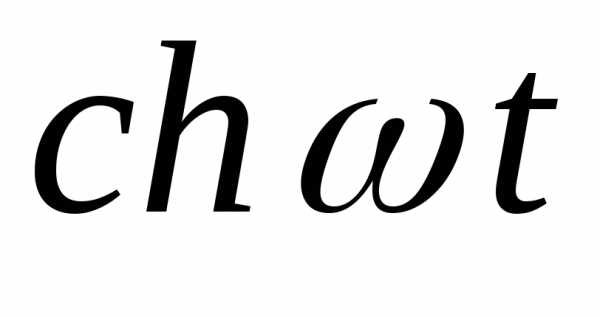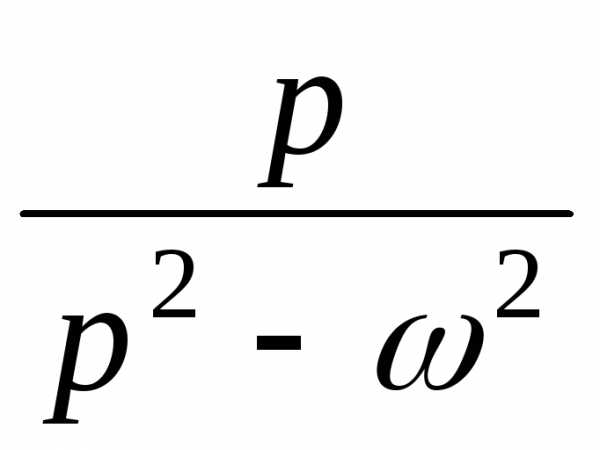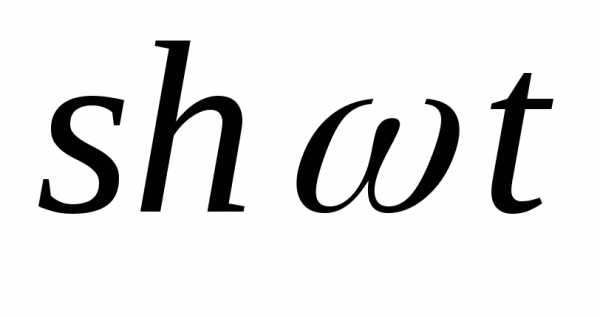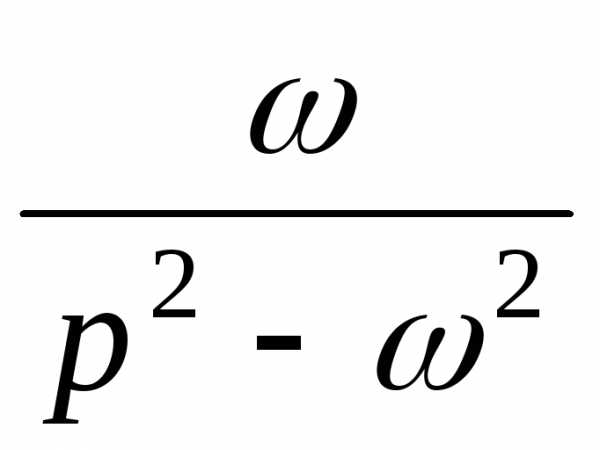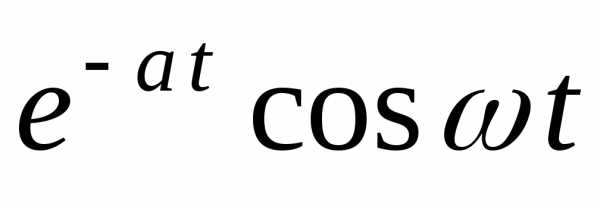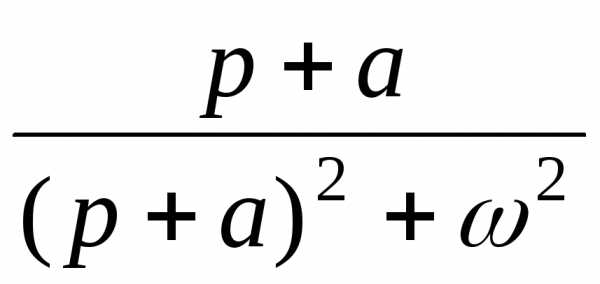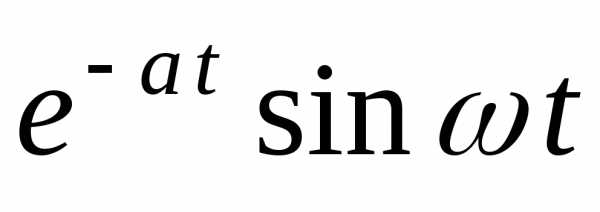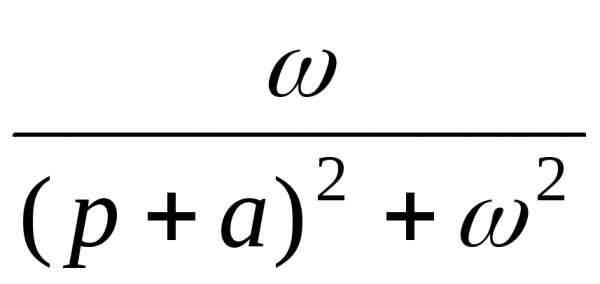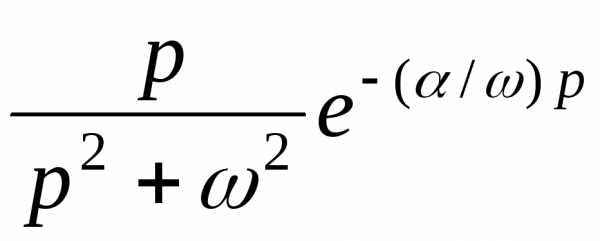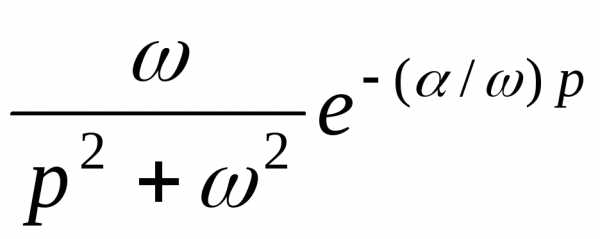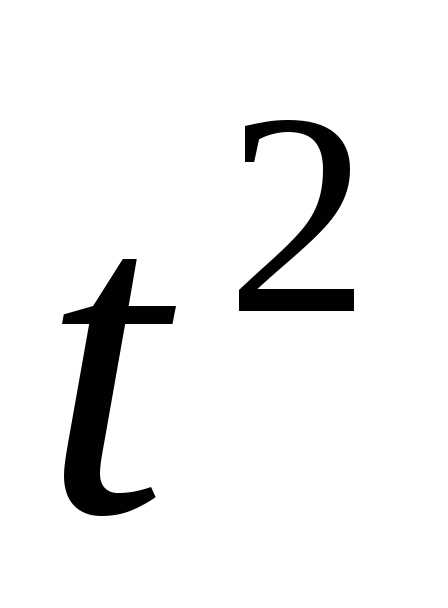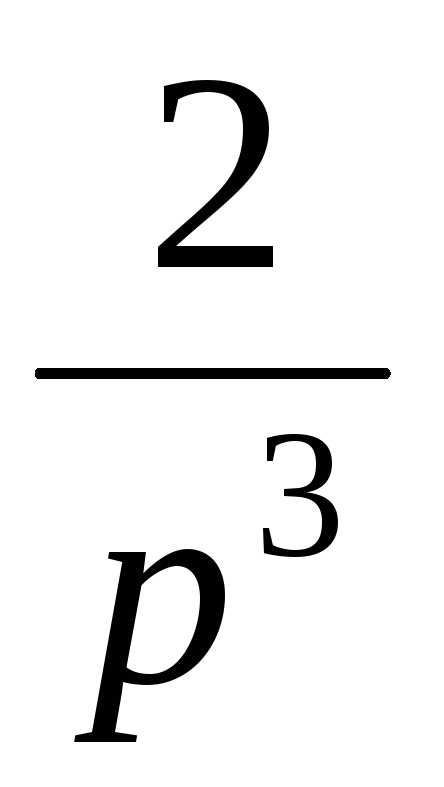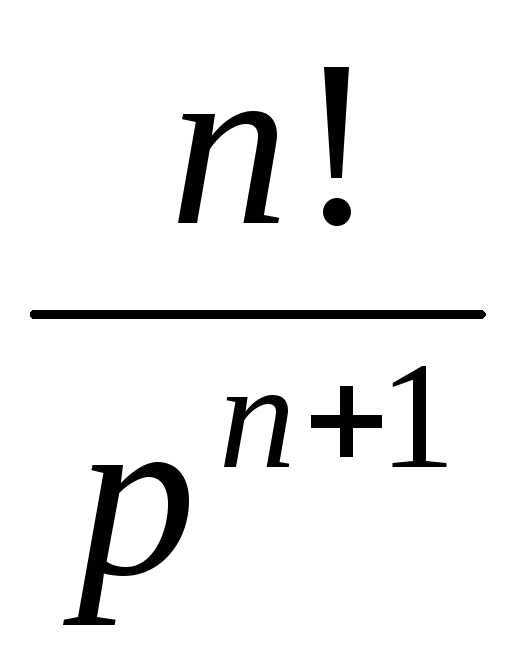Восстановление оригиналов по изображению. — МегаЛекции
Заключительный шаг схемы применения операционного исчисления состоит в нахождении оригинала по полученному изображению, этот шаг или эту операцию называют обратным преобразованием Лапласа и символически записывают следующим образом: .
Раcсмотрим основные способы восстановления оригиналов по изображениям.
П.1 Восстановление оригиналов с помощью таблиц.
Этот способ является самым простым, но удобен в применении только, если изображение легко сводится к табличному виду элементарными преобразованиями.
Пример1. Найти оригинал изображения .
Решение.
Приведем к табличному виду
Пример 2. Найти оригинал изображения
Решение.
Приведем к табличному виду
По таблице получаем, что .
Пример 3. Найти оригинал изображения
Решение. Приведем к табличному виду:
Примеры для самостоятельного решения.
Найти оригинал изображения.
Ответы :
П.2 Восстановление оригиналов с помощью свертки.
Этот вопрос подробно был рассмотрен в § 9, поэтому сразу перейдем к примерам.
Пример 1. Восстановить оригинал следующего изображения : .
Решение.
Преобразуем изображение к виду удобному для применения теоремы о свертке.
.
По таблице сверток находим, что оригинал для этого изображения имеет вид :
.
Пример 2.
Решение.
Преобразуем изображение к виду удобному для применения теоремы о свертке:
.
По таблице сверток находим, что оригинал для этого изображения имеет вид: .
Примеры для самостоятельного решения можно взять из §7.
П.3 Нахождение оригиналов с помощью разложения дроби на сумму простейших.
Если изображение является правильной дробью, то методом неопределенных коэффициентов эту дробь можно представить в виде суммы простейших дробей I-IV типов так, как это делалось при интегрировании рациональных дробей. При этом дробь 1-го типа соответствуют оригиналу , дробь 2-го типа соответствует оригиналу , дробь 3-го типа сначала преобразовывается к виду:
, а затем по таблице определяется оригинал: .
Выполнив аналогичные преобразования для дробей 4-го типа, можно найти для них оригиналы или по таблицам, или с помощью свертки.
Пример 1. Найти оригинал следующего изображения:
Решение.
Представим эту дробь в виде суммы простейших дробей:
.
Найдем A , B, C, D методом неопределенных коэффициентов.
2p²-4p+8=A(p-2)(p²+4)+B(p²+4)+(p-2)²(Cp+D)
При
p=2 8=8B , т.е. B=1
: 0=A+C
: 2=-2A+B+D-4C
: -4=4A+4C-4D D=1(A+C=0)
A=0, C=0
Получили, что F(p)= . Применяя теоремы линейности и затухания, находим оригинал: .
Пример 2.
Найти оригинал следующего изображения:
Решение.
Представим в виде суммы простейших дробей:
,т.е.
.
Приравниваем коэффициенты при равных степенях:
: 14=9B+4D
: 0=9A+4C
1=B+D
0=A+C. Решая соответствующие системы, получаем, что
A=0; C=0; B=2; D=-1 .
,т.е. .
При решении этих задач использовались теоремы единственности, линейности, затухания, таблица оригиналов и изображений.
Примеры для самостоятельного решения.
Найти оригинал изображения
Ответы.
П.4. Нахождение оригиналов с помощью теоремы запаздывания.
Пример1. Найти оригинал следующего изображения:
Найдем сначала оригинал для дроби .
Разложим эту дробь на простейшие и найдем коэффициенты методом неопределенных коэффициентов
При получим
При получим
При получим
,
оригинал равен , а оригинал данного .
Примеры для самостоятельного решения.
Найти оригиналы следующих изображений:
1) ; 2) ; 3) ;
4)
Ответы:
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Между основными оригиналами и изображениями
Функция – оригинал (f(t) | Изображение F(p) |
1 |
|
|
|
cos t |
|
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
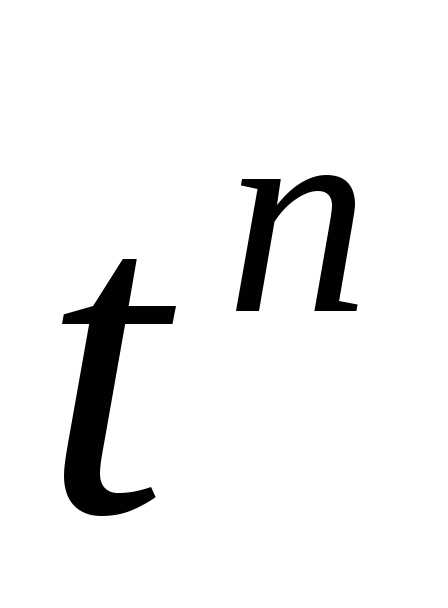 |
|
Примеры нахождения изображений сложных функций
1. .
Так как
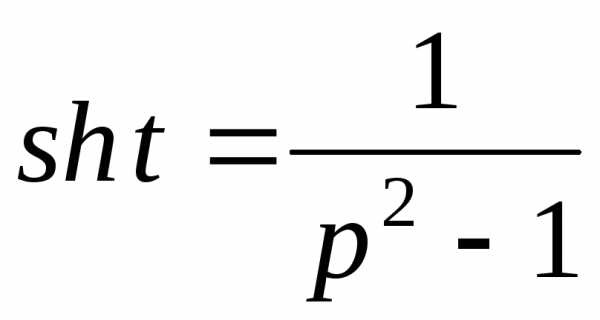 ,
то применяя теорему дифференцирования,
,
то применяя теорему дифференцирования,
найдем
Следовательно,
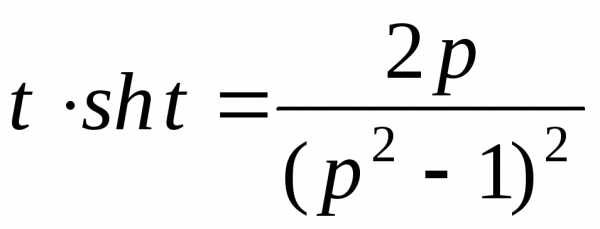
2.
Применять
теорему дифференцирования пять раз,
конечно, неудобно. Представим  в виде
в виде
Так как
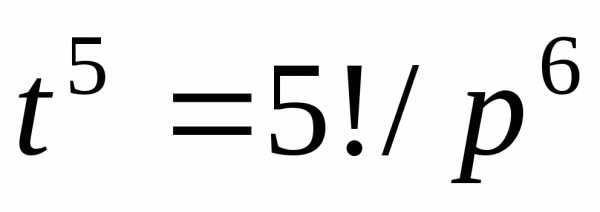 ,
то по теореме смещения изображения
,
то по теореме смещения изображения
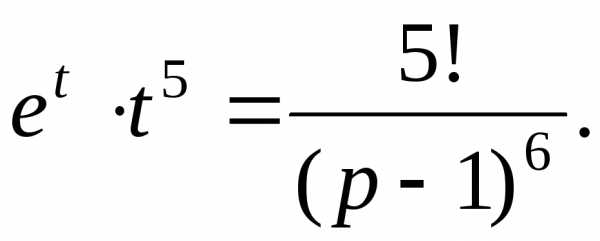
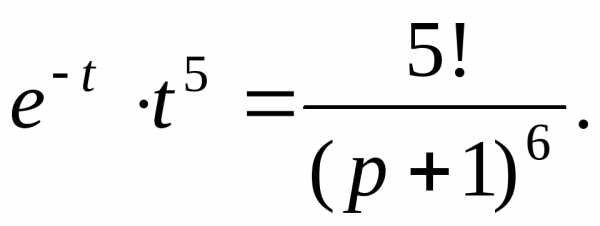
Теперь по теореме линейности находим
3.
Представим 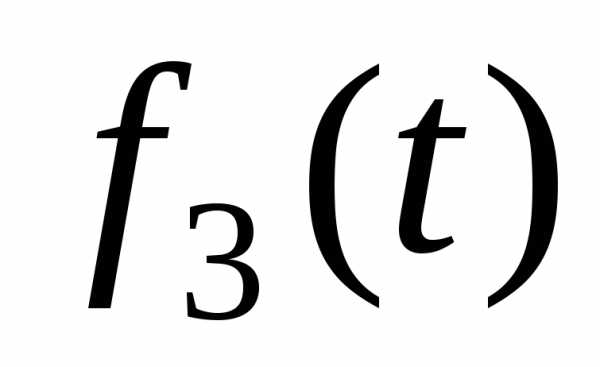 в видеДля функции
изображение известно:
в видеДля функции
изображение известно:
По теореме дифференцирования изображения – . Следовательно,
4.
Так как
то
5.
Так как то
Учитывая,
что 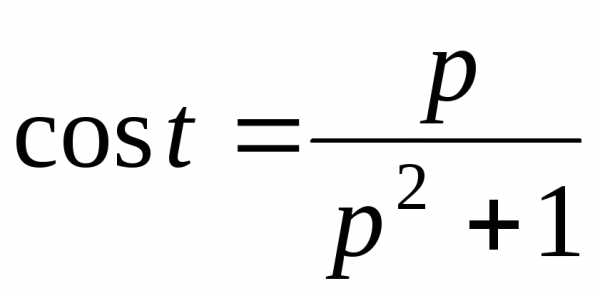 ,
по теоремам подобия и линейности
получим
,
по теоремам подобия и линейности
получим
Замечания.
1. Грубой ошибкой будет представление изображения заданных функций в виде произведения изображений, соответствующих каждому из сомножителей, так как умножению оригиналов в пространстве оригиналов соответствует другая операция в пространстве изображений [4,5].
2. Решение приведенных задач возможно различными способами. В пособии указан лишь один из возможных способов решения.
3.2. Обратное преобразование Лапласа
При практическом применении преобразования Лапласа всегда приходится решать обратную задачу – построение оригинала по его изображению. Общий метод построения оригинала f(t) по заданному изображению F(p) базируется на теореме обращения ( формуле Меллина ):
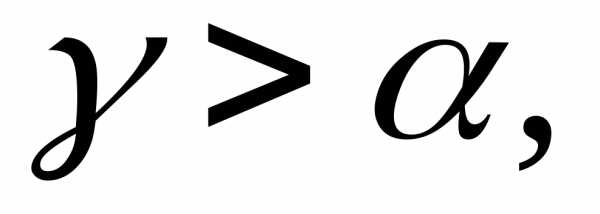
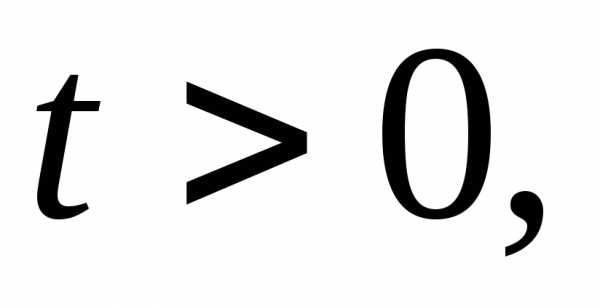 (3.22)
(3.22)
где интегрирование проводится по любой бесконечной прямой 7 0Re p = 7g 0, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа [7,8]. Непосредственно формулой (3.22) для нахождения оригинала по известному изображению пользуютя редко. При нахождении оригинала по его изображению обычно применяют таблицы соответствия между оригиналами и их изображениями [5] и свойства преобразования Лапласа.
В самом распространенном случае, когда изображение F(p) является дробно – рациональной функцией вида
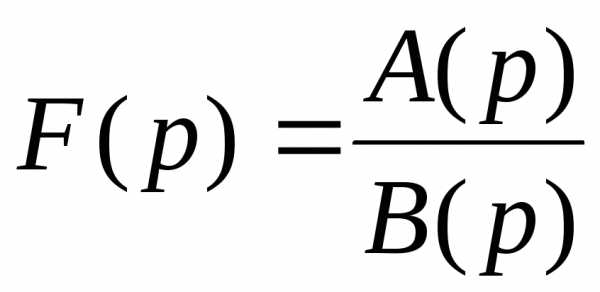 ,
,
где A(p) и B(p) – многочлены, причем степень многочлена B(p) больше степени многочлена A(p), оригинал может быть найден разложением дроби A(p) /B(p) на простейшие.
Пример. Дано изображение

Найти оригинал f(t) = F(p).
Разложим заданную дробь на простейшие:
Приводя к общему знаменателю, получим
.
При p = 0 1 = -8A,
При p = 2 5 = 16B,
следовательно, A = -1/8, B = 5/16.
Приравнивая
далее коэффициенты, например, при 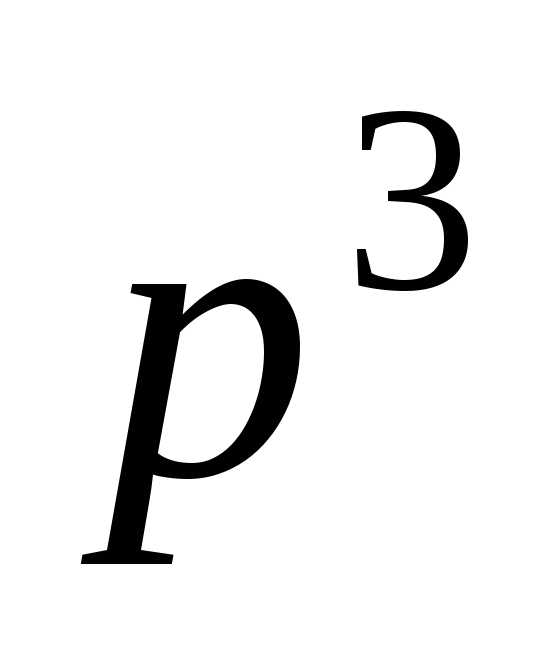 и
и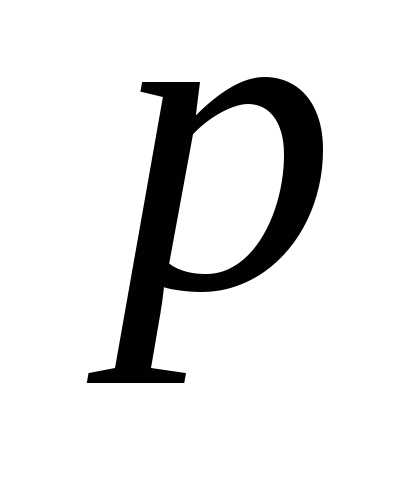 в левой и правой частях равенства,
получим
в левой и правой частях равенства,
получим
Поэтому
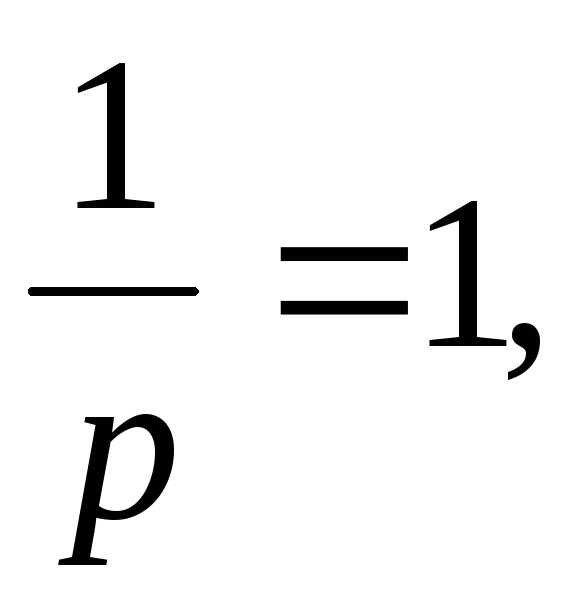
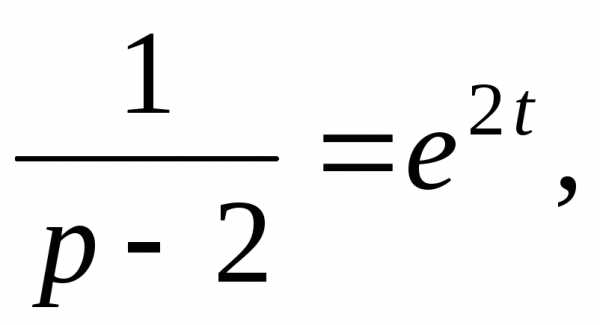
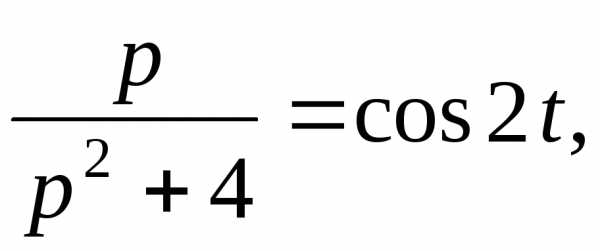
Применяя теорему линейности, окончательно найдем
Пример. Найти оригинал по его изображению
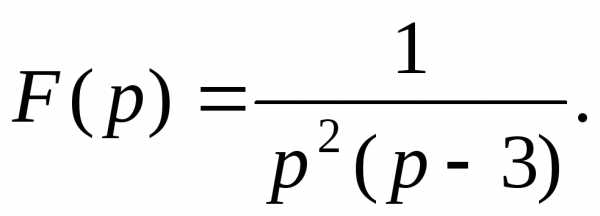
Разложение данной дроби на простейшие имеет вид
После приведения к общему знаменателю получим
При p = 0 1 = -3A, откуда A = – 1/3;
при p = 3 1 = 9C, откуда C = 1/9.
Приравнивая
далее коэффициенты при 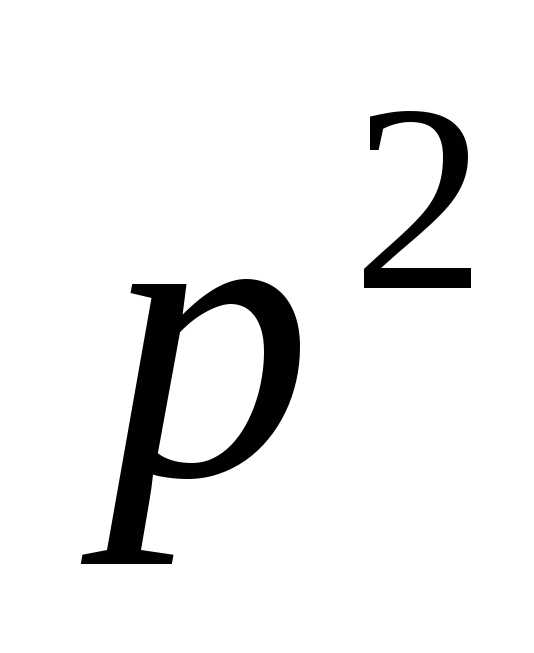 в правой и левой частях равенства,
получим уравнение 0 = B + C, из которого
следует B = – 1/9.
в правой и левой частях равенства,
получим уравнение 0 = B + C, из которого
следует B = – 1/9.
Итак,
Если знаменатель рациональной дроби B(p) имеет простые не-
нулевые корни , то есть если
то оригинал функции F(p) может быть найден по формуле
(3.23)
Пример. Найти оригинал по его изображению
Здесь,
Корни
знаменателя 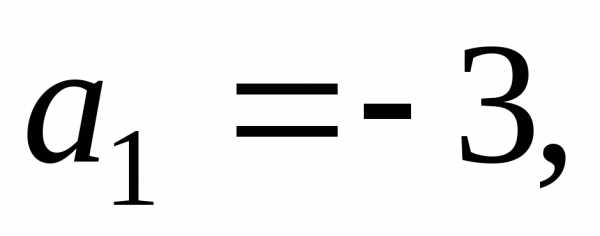
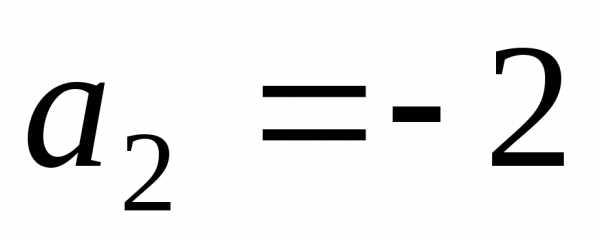 .
Следовательно,
.
Следовательно,
Поэтому
Если
один из простых корней знаменателя B(p)
равен нулю, то есть B(p) можно представить
в виде
,
где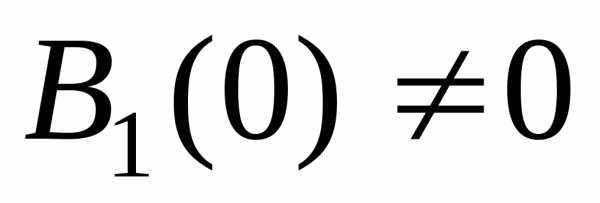 ,
то оригинал находится по формуле
,
то оригинал находится по формуле
(3.24)
Здесь суммирование распространяется на все ненулевые корни
многочлена 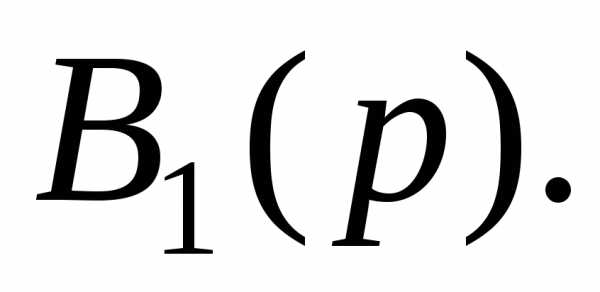
Пример. Найти оригинал по его изображению
.
Здесь
Корни
знаменателя 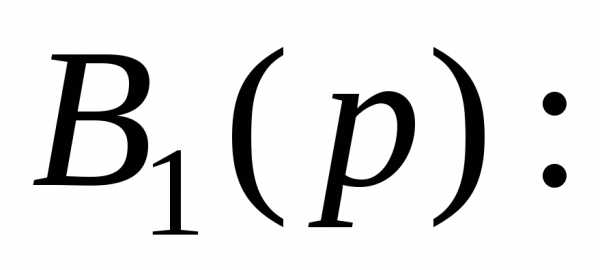
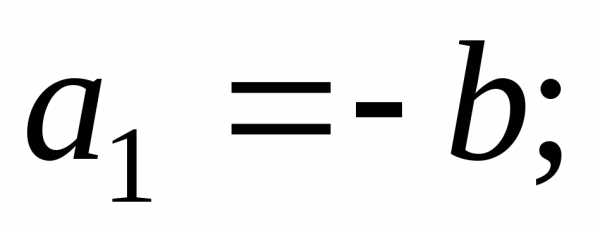
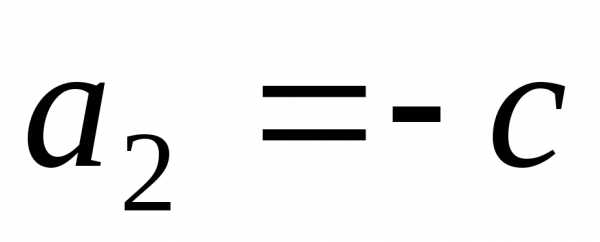 .
Поэтому
.
Поэтому
Применяя формулу (3.24), находим
Если знаменатель рациональной дроби представляет собой квадратный трехчлен, корни которого комплексные, удобно представить его в виде суммы квадратов слагаемых и применить теорему смещения изображения.
Пример. Найти оригинал по его изображению
studfiles.net
3. Нахождение оригинала по изображению.
Задача 1.Найти оригинал для изображения
при помощи разложения на простейшие дроби.
Решение.Разложим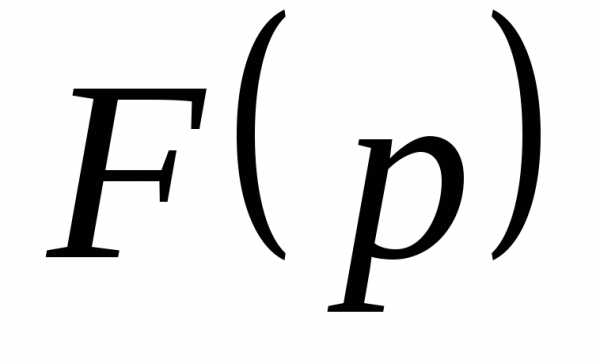 на сумму простейших дробей
на сумму простейших дробей
.
Найдем неопределенные коэффициенты A, B, C, D. Так как
,
то, приравнивая коэффициенты при
одинаковых степенях 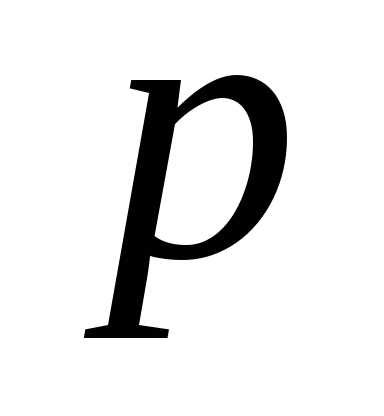 ,
получаем
,
получаем
 ,
, 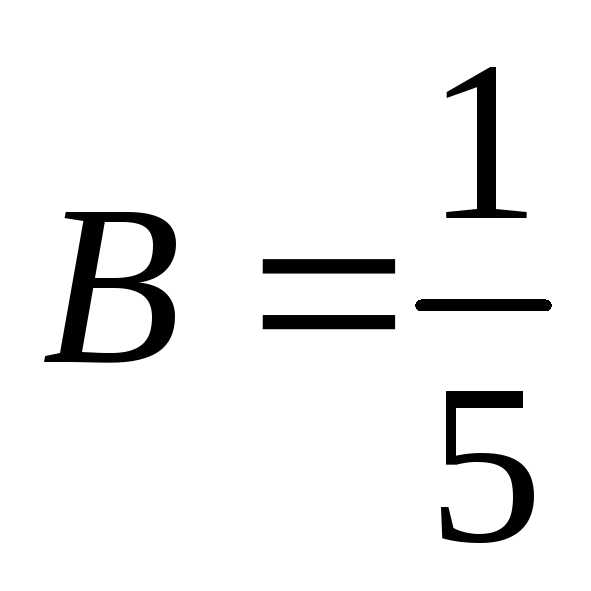 ,
, 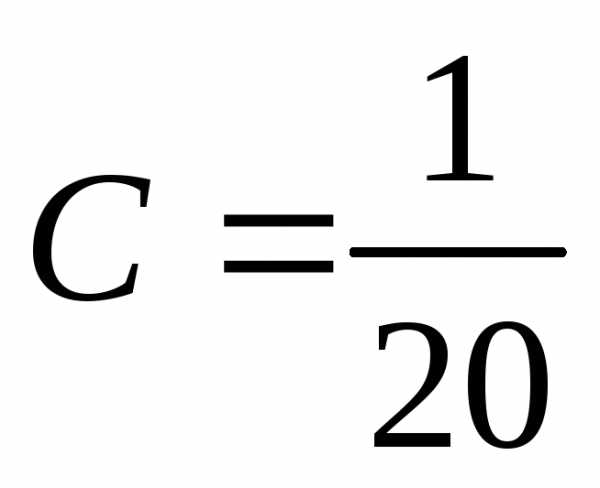 ,
, 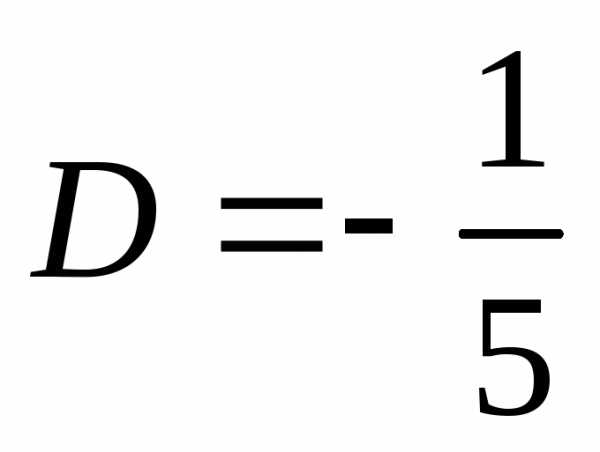 .
.
Таким образом,
.
Свертка оригиналов.Пусть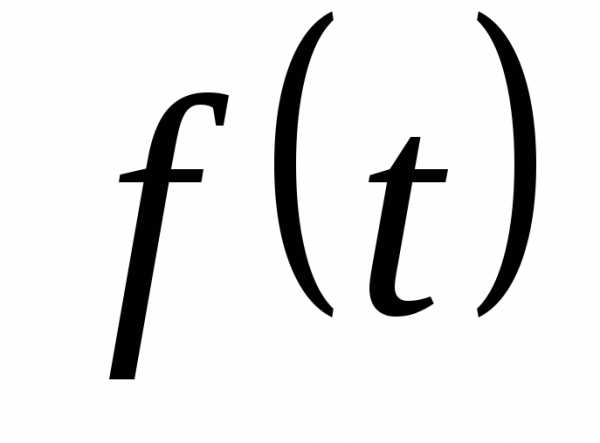 и
и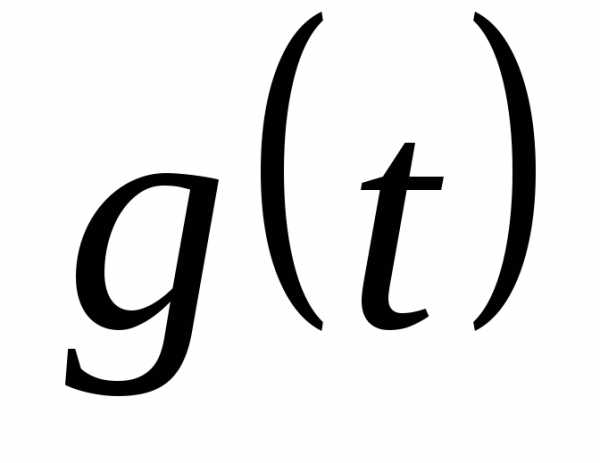 – функции-ориентиры и,
.
По определению, сверткой оригиналов
– функции-ориентиры и,
.
По определению, сверткой оригиналов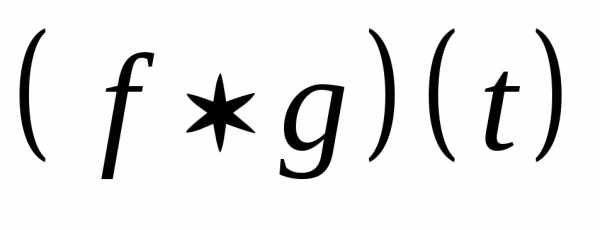 называется интеграл(3.1)
называется интеграл(3.1)
По теореме сложения изображений свертки
оригиналов 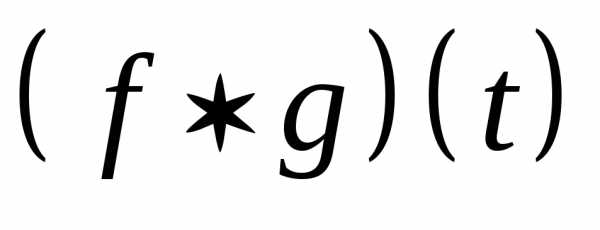 соответствует произведение изображений
соответствует произведение изображений
.
Задача 2.Найти свертку функций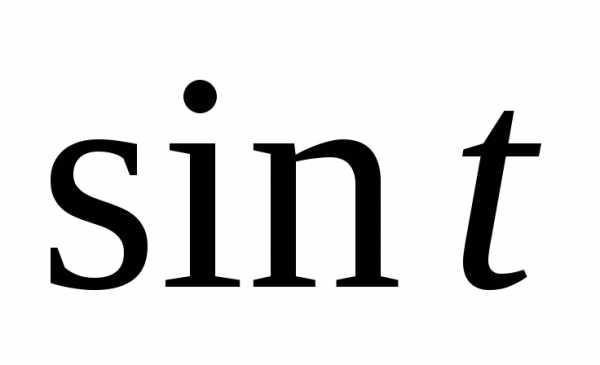 и
и .
.
Решение.Имеем
Задача 3.Восстановить оригинал по
изображению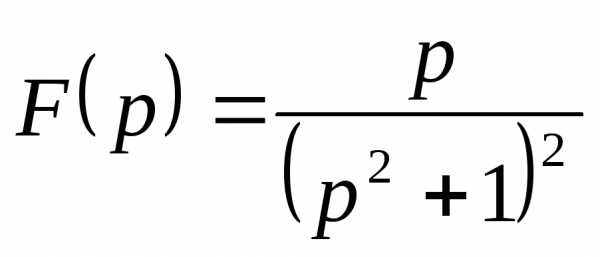 при помощи свертки.
при помощи свертки.
Решение.Представим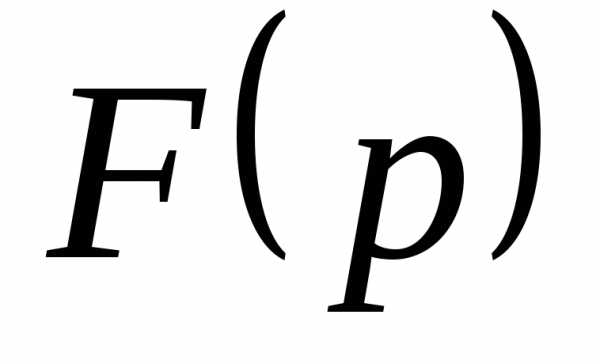 как произведение двух функций и используя
теорему умножения, запишем
как произведение двух функций и используя
теорему умножения, запишем
. (см. задачу 2)
4. Решение линейных дифференциальных уравнений и систем.
Рассмотрим применение правил и теорем операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами и их систем при заданных начальных условиях. Предлагаем, что искомое решение, его производные и правая часть дифференциального уравнения являются оригиналами.
Схема решения дифференциального уравнения.
Искомая функция, ее производные, входящие в данное уравнение, правая часть уравнения заменяются их изображениями. В результате получается так называемое операторное уравнение.
Решаем операторное уравнение относительно изображения искомой функции.
Переходим от изображения искомой функции к оригиналу.
Схема решения систем дифференциальных уравнений такая же.
Задача 1.Решить дифференциальное уравнение
,
если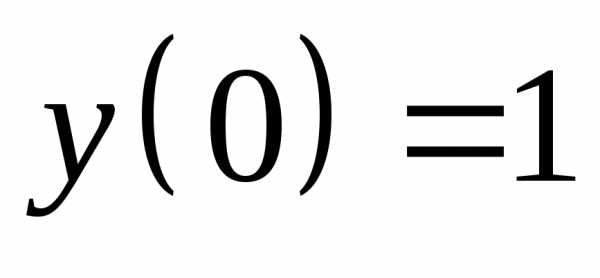 ,
, 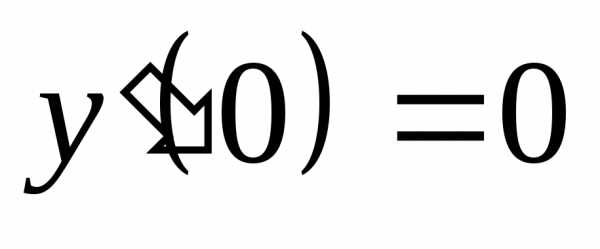
Решение.Пусть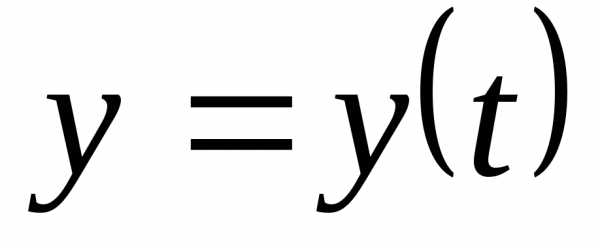 – искомое решение.
– искомое решение.
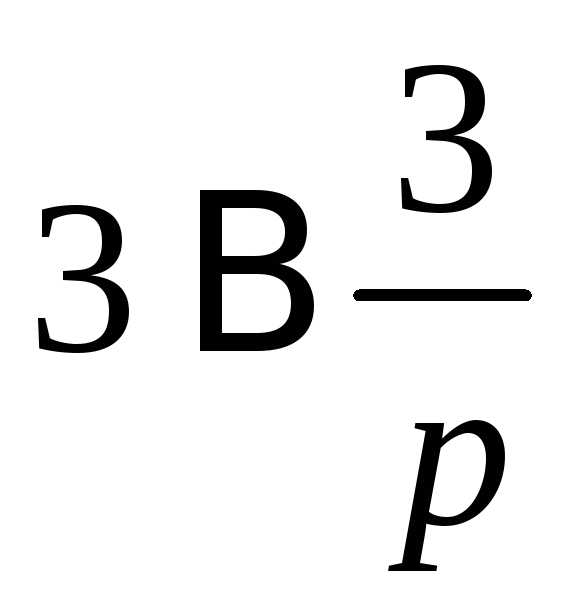 .
.
Запишем операторное уравнение
или
.
Находим A, B, C. 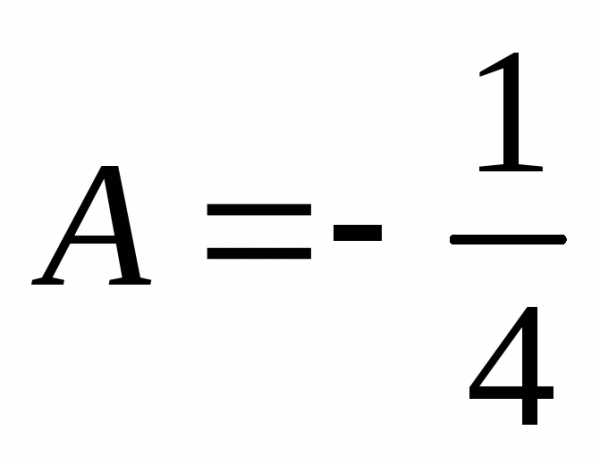 ,
,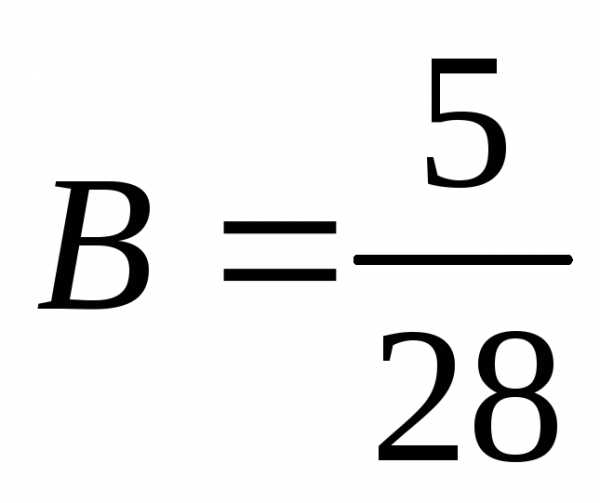 ,
,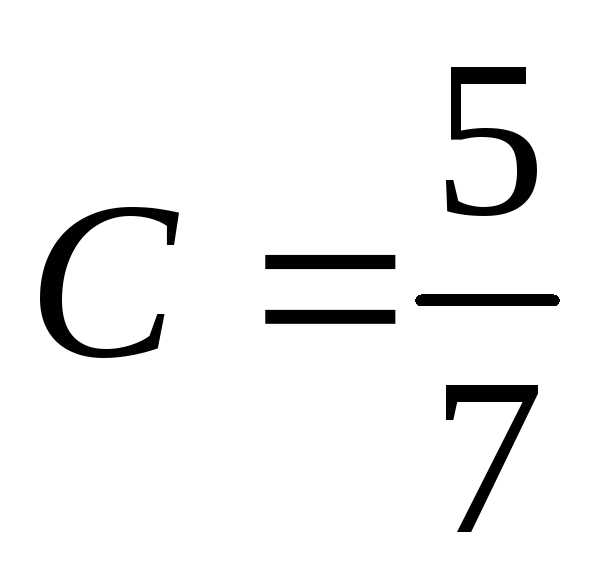 .
.
Итак,
.
Задача 2.Найти решение системы дифференциальных уравнений
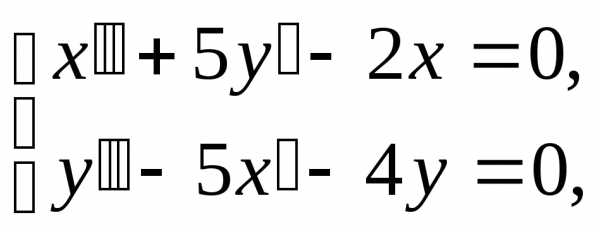
удовлетворяющее начальным условиям 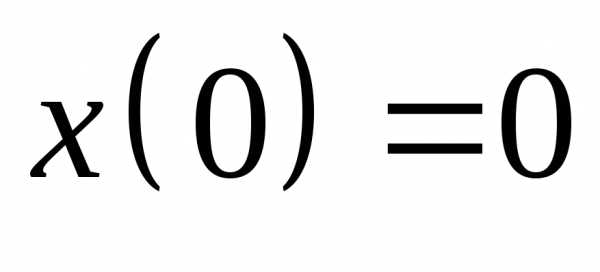 ,
, 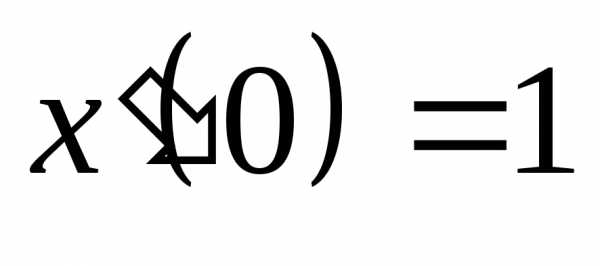 ,
, 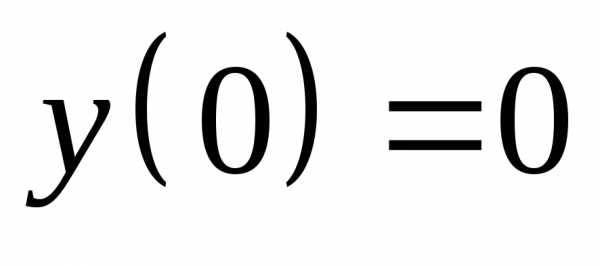 ,
, 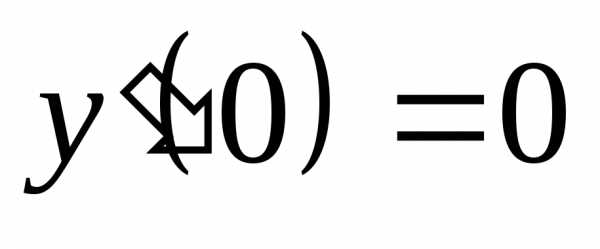
Решение.Пусть, . Тогда
; ;;.
Преобразованная система имеет вид
Определяем 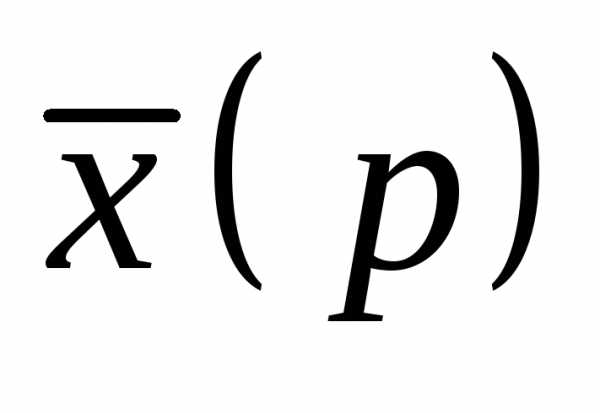 ,
, 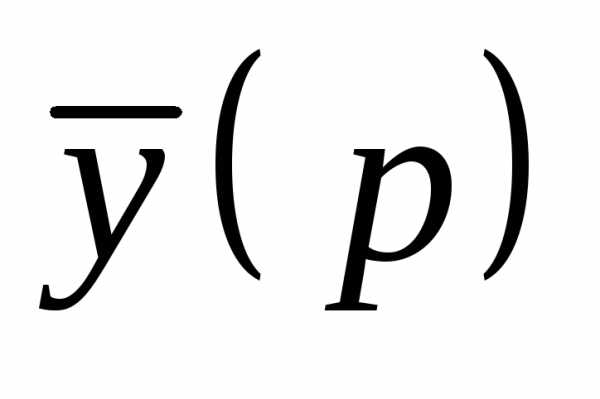 по правилу Крамера
по правилу Крамера
;
Вычислим получим
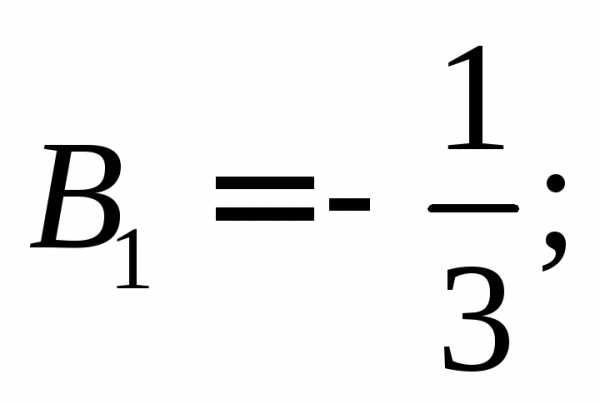
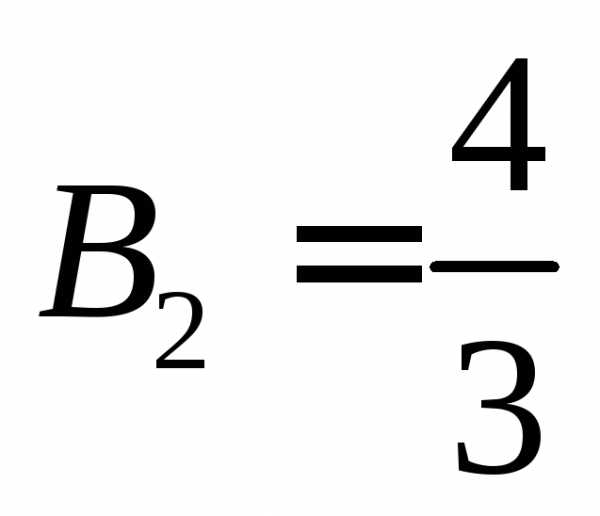
Итак,
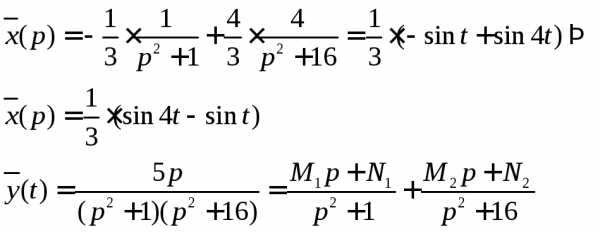
Вычислим получим
Тогда
Итак,
Рассмотрим решение дифференциальных уравнений при нулевых начальных условиях с использованием интеграла Дюамеля.
Интеграл Дюамеля.
Если и, то
(4.1)
или
(4.1’)
Рассмотрим линейное дифференциальное уравнение с постоянными коэффицентами
при Если
,
то получим
или
,
где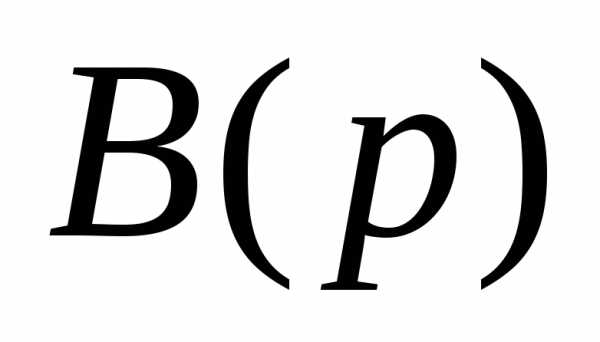 –
многочленn-ой степени;
–
многочленn-ой степени;
отсюда
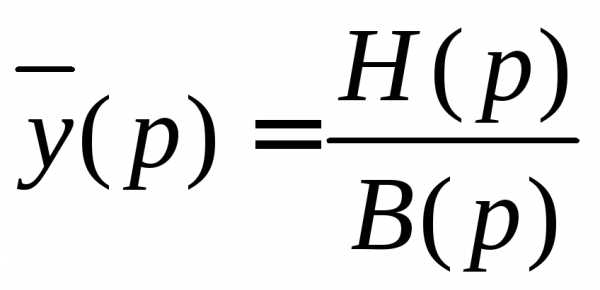 (4.2)
(4.2)
Если рассмотреть ещё одно дифференциальное уравнение, у которого правая часть равна единице,
то при тех же нулевых начальных условиях в изображениях получим уравнение
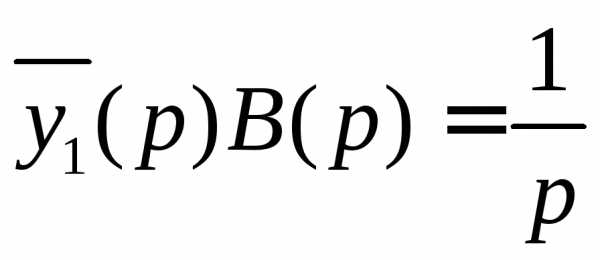
Отсюда 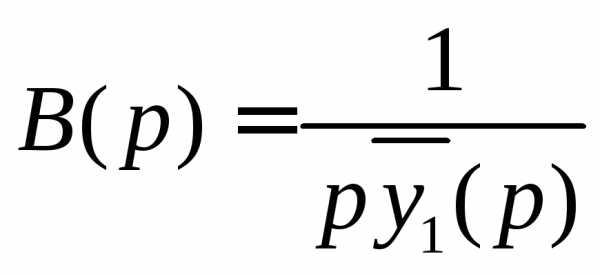 (4.3)
(4.3)
Подставим (4.3) в (4.2), получим
(4.4)
Используя интеграл Дюамеля (4.1’) для и учитывая, что, получаем
(4.5)
Итак, достаточно решить уравнение с правой частью равной единице, чтобы при помощи интеграла (4.5) получить решения при различных правых частях.
Задача 3.
Найти частное решение дифференциального уравнения, используя интеграл Дюамеля:
(4.7)
Пусть , тогда
Получим уравнение для изображения 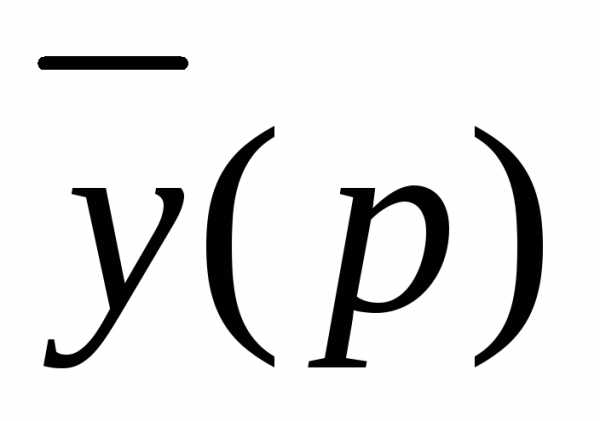
Отсюда
Возвращаясь к первоначальному уравнению
для 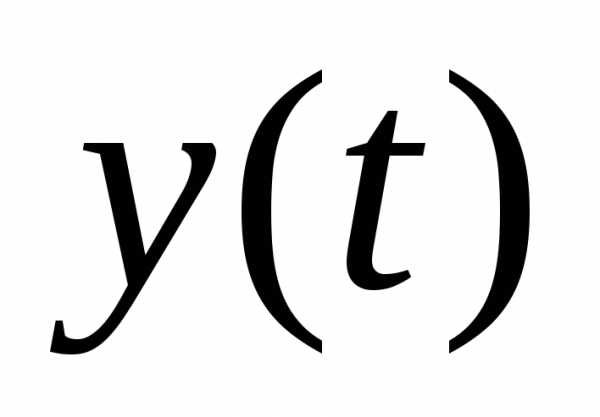 ,
Запишем
,
Запишем
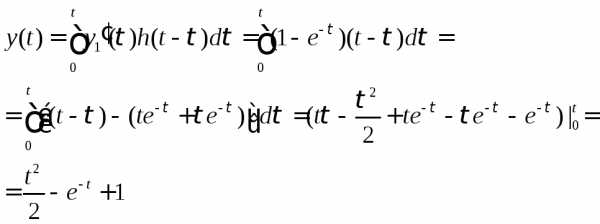
Следует отметить, что преимущество операционного метода решения дифференциальных уравнений состоит в том, что благодаря этому методу мы заменяем решение дифференциального уравнения на решение алгебраического уравнения, что сильно упрощает вычисление.
Применение методов операционного исчисления в
задачах электротехники.
Методы операционного исчисления широко используются в решениях специальных задач электротехники.
Задача1.
Включение дополнительного источника ЭДС в цепь с ненулевыми начальными условиями.
Рассмотрим электрическую цепь с ненулевыми начальными условиями (рис. 5.1), где r- сопротивление;L- индуктивность;C– ёмкость конденсатора;k– выключатель.
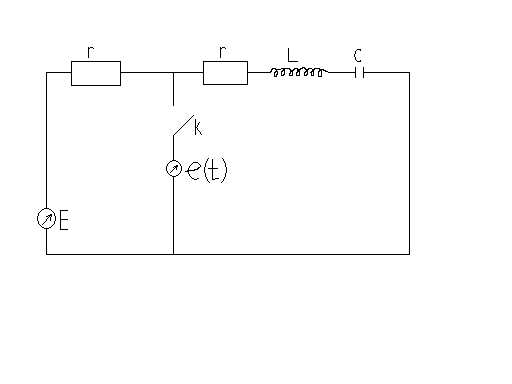
рис 5.1
Эта цепь характеризуется тем, что при отключении ЭДС Е в цепи происходит арядка конденсатора. После зарядки конденсатора ток в цепи становится равным нулю. Требуется найти ток i(t) после подключения к цепи дополнительной ЭДС е(t).
По второму закону Кирхгофа (алгебраическая
сумма падения напряжения на сопротивлениях
равна алгебраической сумме действующих
в цепи ЭДС) для момента времени 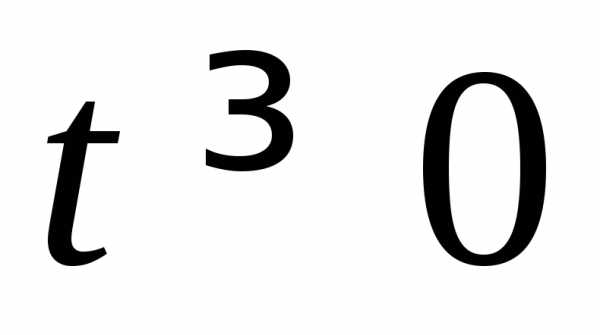 имеем
имеем
, (5.1)
где 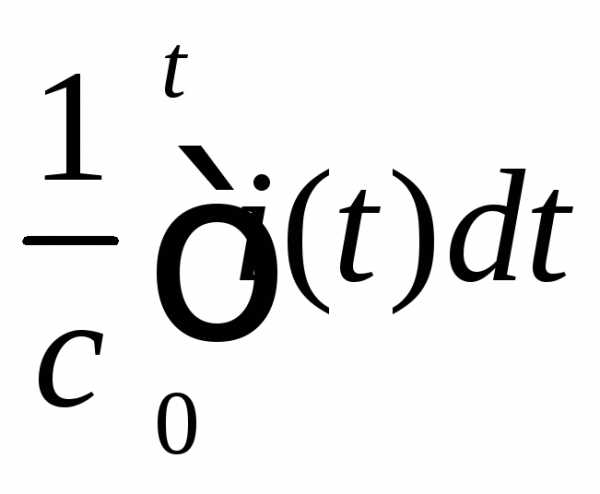 – напряжение на конденсаторе;
– напряжение на конденсаторе;
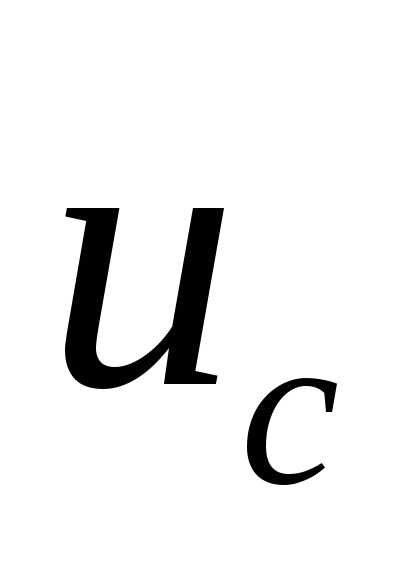 (0)
– начальное напряжение на конденсаторе,
обусловленное тем, что конденсатор уже
был ранее заряжен.
(0)
– начальное напряжение на конденсаторе,
обусловленное тем, что конденсатор уже
был ранее заряжен.
Решение.
Применяя к интегро-дифяфференциальному уравнению (5.1) преобразование Лапласа, запишем
где 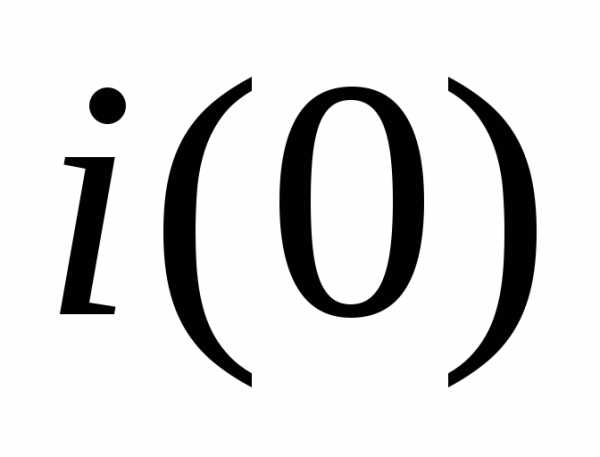 –
начальный ток в цепи. Используя указанные
соотношения, получаем алгебраическое
уравнение в изобржениях
–
начальный ток в цепи. Используя указанные
соотношения, получаем алгебраическое
уравнение в изобржениях
где неизвестной величиной является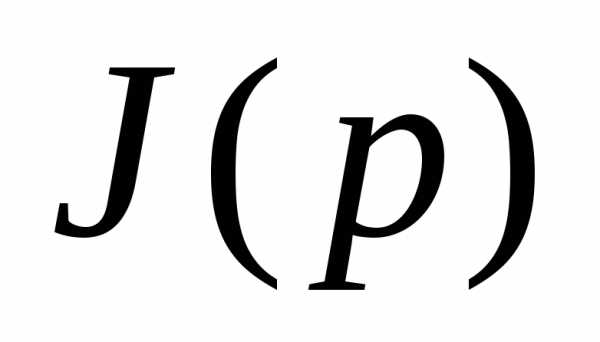 .
Остальные величины известныИз (5.2) получаем
.
Остальные величины известныИз (5.2) получаем
(5.3)
Рассмотрим конкретный пример. Пусть
Применяя преобразование Лапласа,
получаем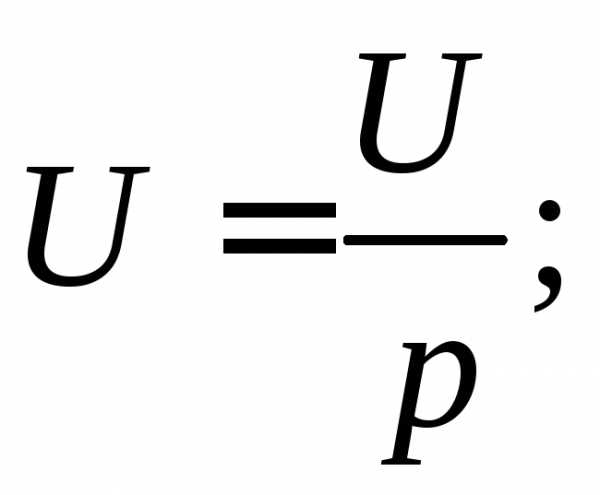 следовательно,
следовательно,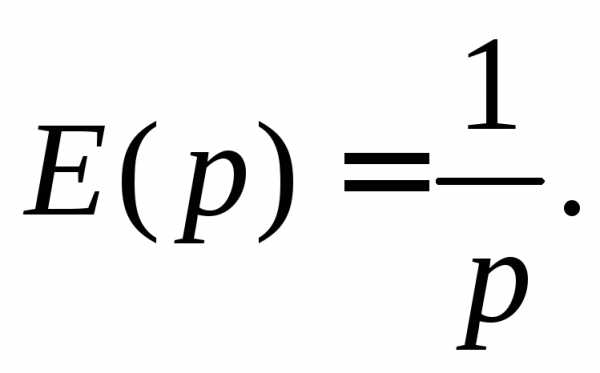 С учётом этих условий из (5.3) получаем
С учётом этих условий из (5.3) получаем
(5.4)
Замечание.Из полученного решения
(5.4) следует, что ,
при,
т.е.Это означает что за некоторое время
конденсатор дополнительно зарядится
и ток станет равным нулю.
,
при,
т.е.Это означает что за некоторое время
конденсатор дополнительно зарядится
и ток станет равным нулю.
Задача 2.
Определить ток в цепи, состоящей из последовательно соединённых сопротивления rи конденсатора С, если в моментt=0 цепь подсоединяется к источнику ЭДС (рис 5.2) в виде треугольного импульса (рис 5.3).
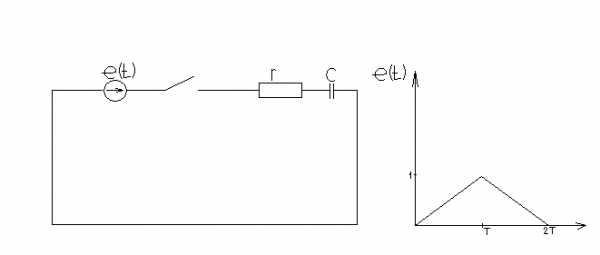
рис 5.2 рис 5.3
В задаче задано
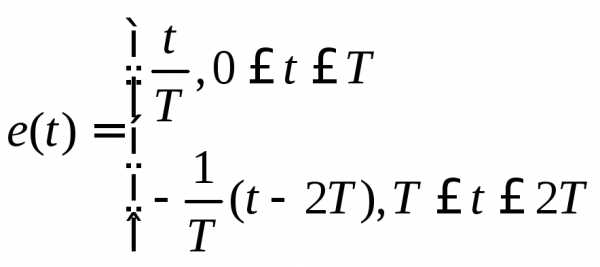
Решение.
Используя второй закон Кирхгофа, получим интегральное уравнение для рассматриваемого контура
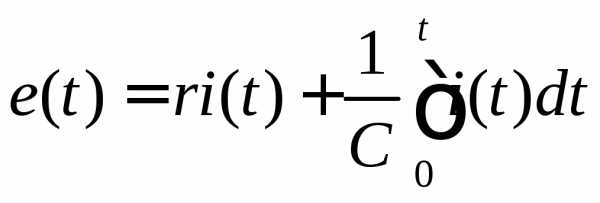 (5.5)
(5.5)
Решение уравнения (5.5) выразим при помощи интеграла Дюамеля (4.1)
(5.6)
где 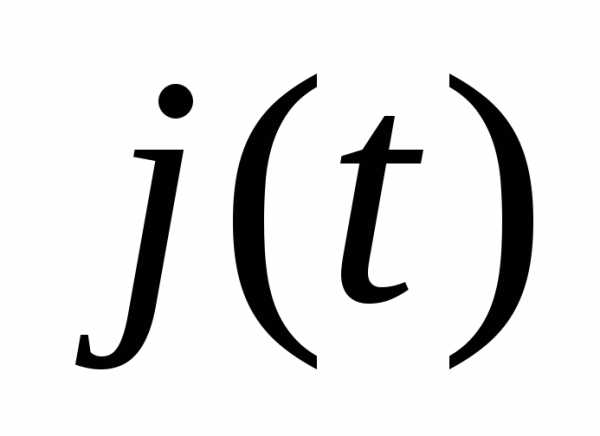 – решение вспомогательного уравнения
– решение вспомогательного уравнения
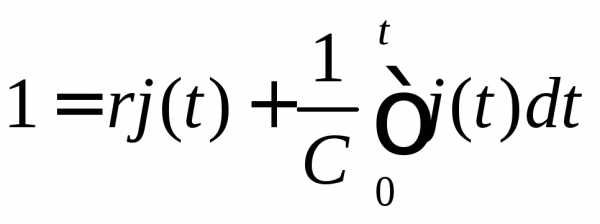 (5.7)
(5.7)
Применяя преобразование Лапласа, имеем
Уравнение (5.7) преобразуется к алгебраическому уравнению для нахождения J(p)
откуда(5.8)
Подставляя найденное решение (5.8) вспомогательного уравнения (5.7) в интеграл Дюамеля (5.6) получаем решение исходного уравнения (5.5)
.
Пример контрольной работы по операционному исчислению
и комплексным числам.
Вариант 1.
1. Восстановить оригинал по изображению:
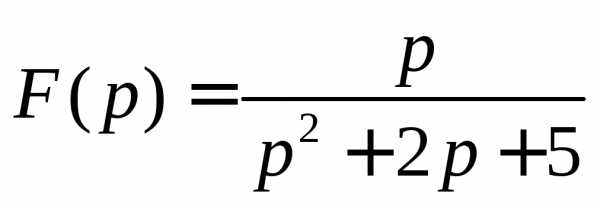
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
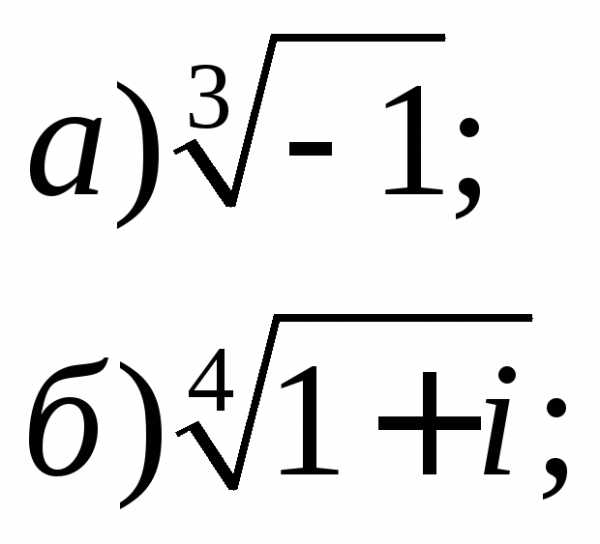
4. Представить в алгебраической форме:
5. Найти изображение оригинала, заданного графически
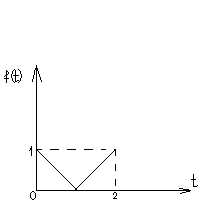
6. Решить систему
Вариант 2.
Найти изображение функции:
Решить задачу Коши операторным методом:
3. Найти все значения корней
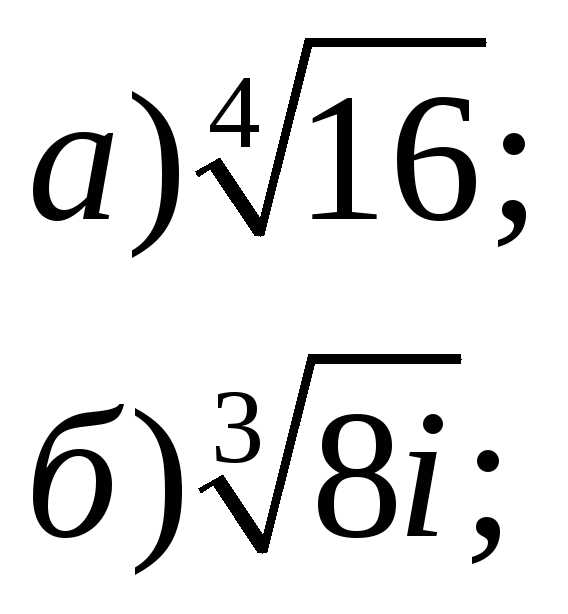
4. Представить в алгебраической форме:
Восстановить оригинал по изображению
6. Решить систему
Вариант 3.
1. Восстановить оригинал по изображению:
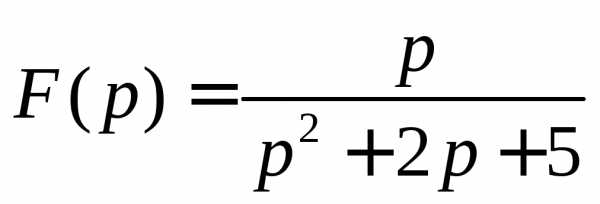
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
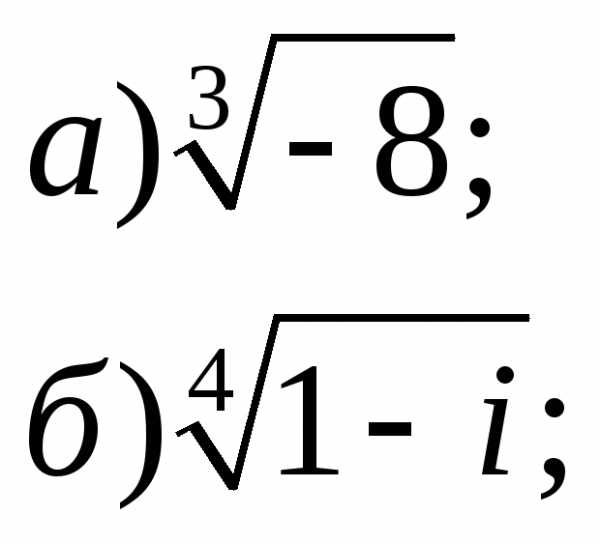
4. Представить в алгебраической форме:
5. Найти изображение оригинала, заданного графически:
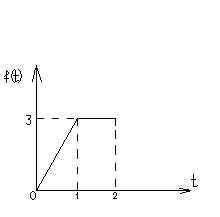
6. Решить систему
Вариант 4.
Найти изображение функции:
Решить задачу Коши операторным методом:
3. Найти все значения корней
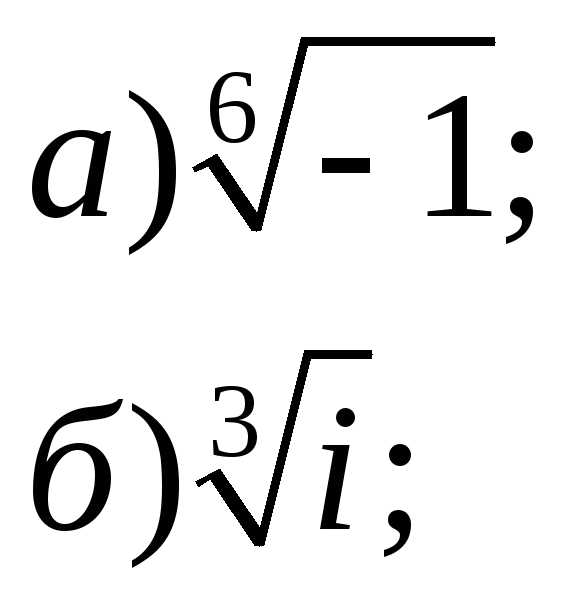
4. Представить в алгебраической форме:
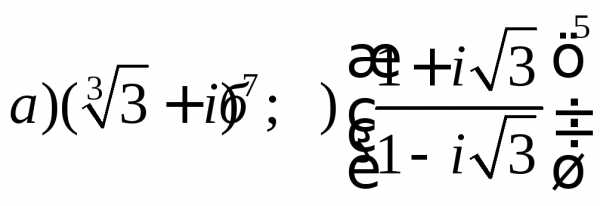
Восстановить оригинал по изображению
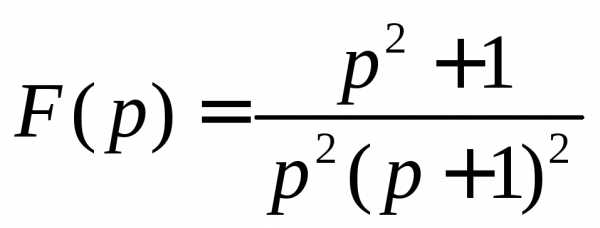
6. Решить систему
Вариант 5.
1. Восстановить оригинал по изображению:
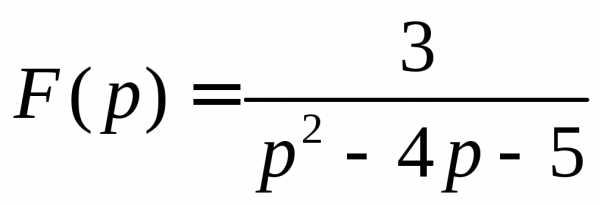
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) 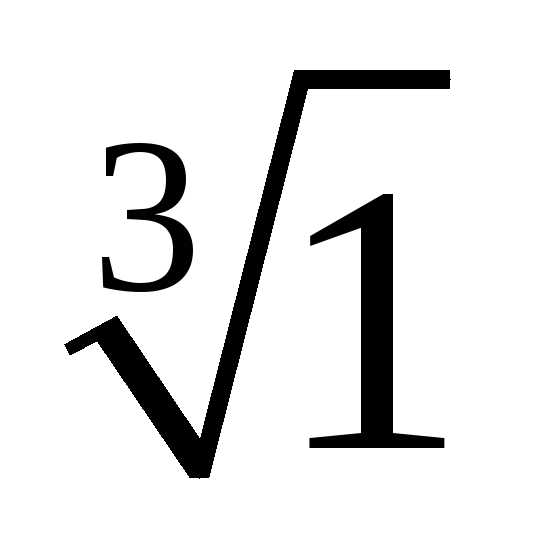 ;
;
б)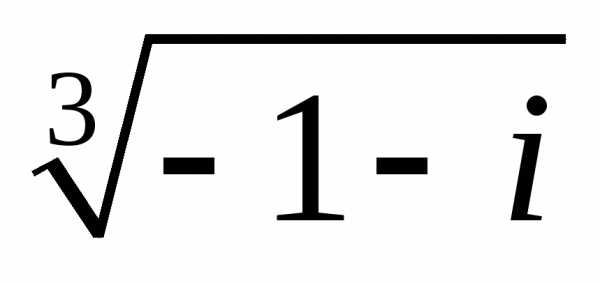
4. Представить в алгебраической форме:
а)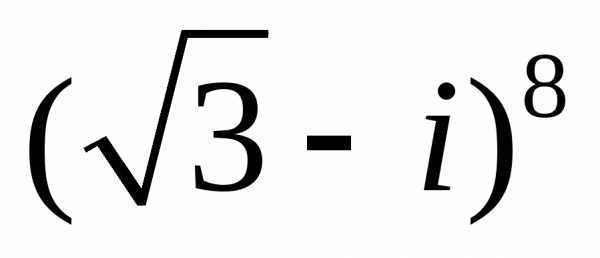 ;
б)
;
б)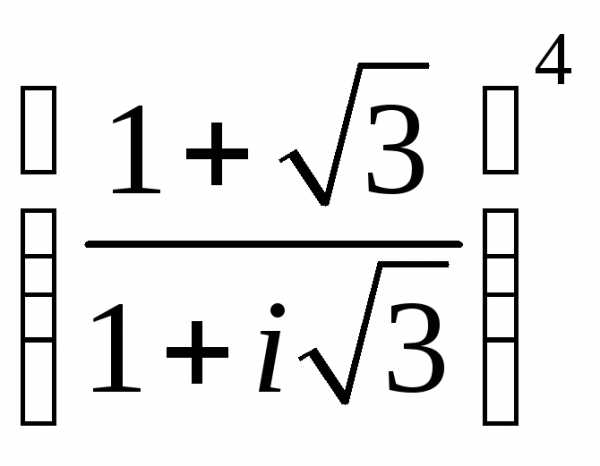
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 6.
Найти изображение функции:
Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 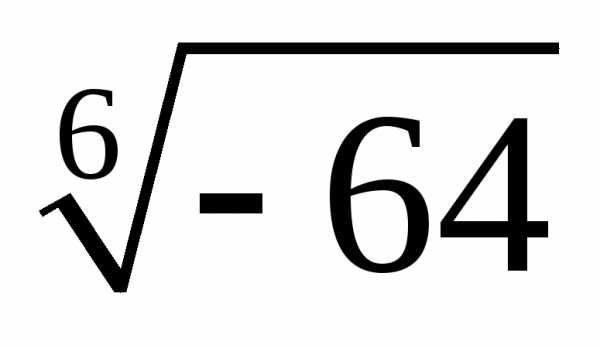 ;
;
б)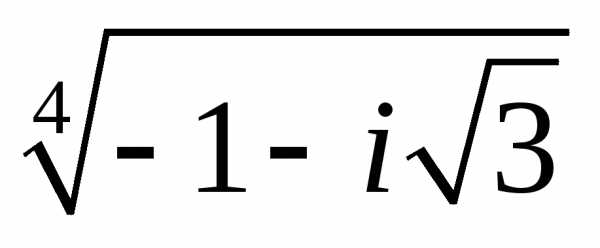
4. Представить в алгебраической форме:
а) 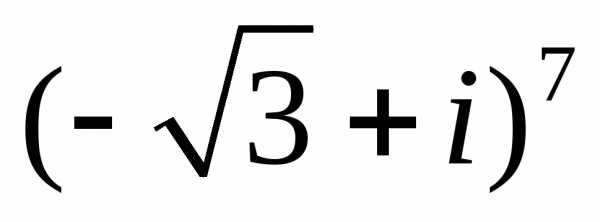 ;
б)
;
б)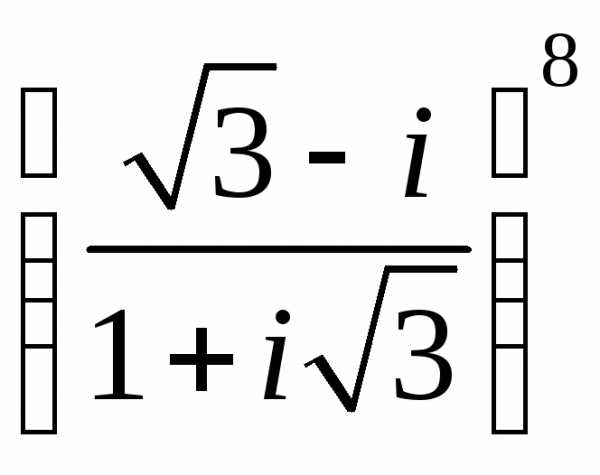
Восстановить оригинал по изображению
6. Решить систему
Вариант 7.
1. Восстановить оригинал по изображению:
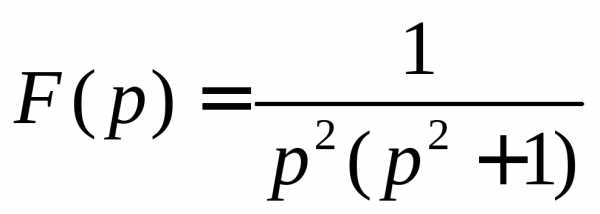
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) 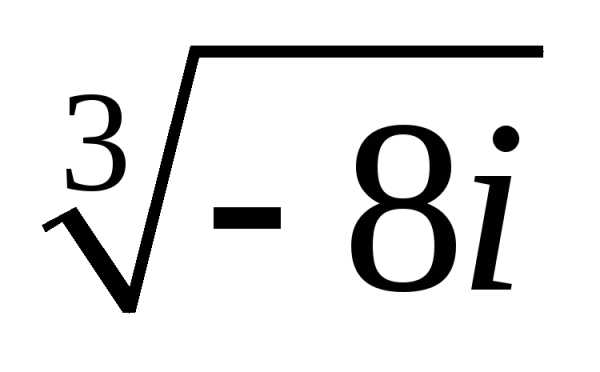 ;
;
б) 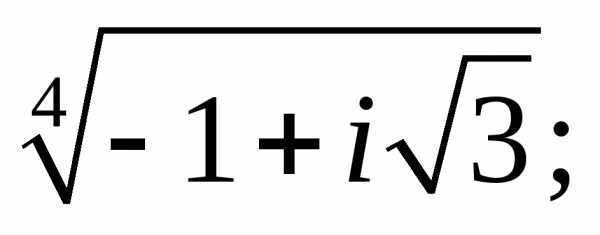
4. Представить в алгебраической форме:
а) 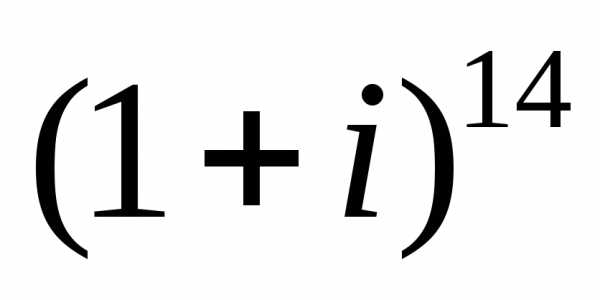 ;
б)
;
б)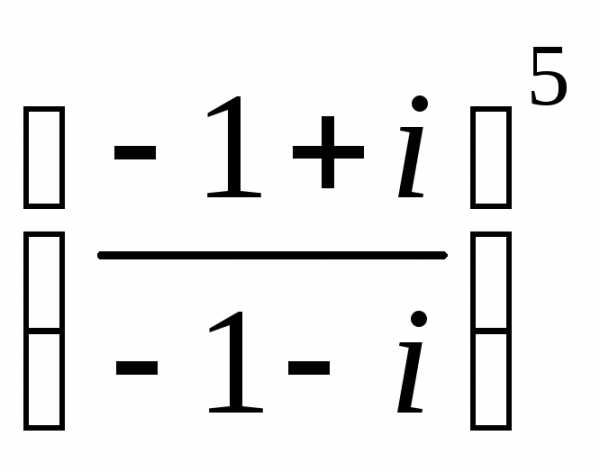
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 8.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 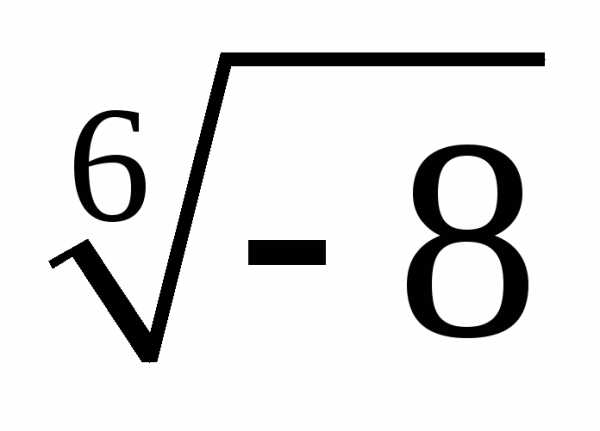 ;
;
б)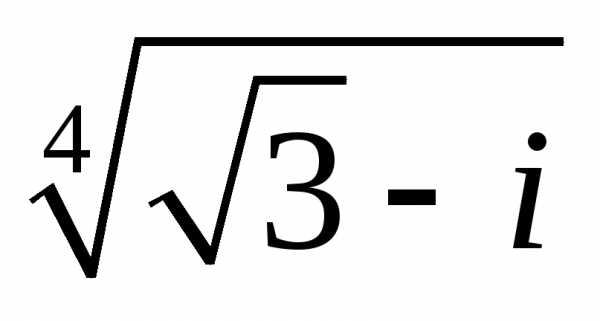
4. Представить в алгебраической форме:
а) 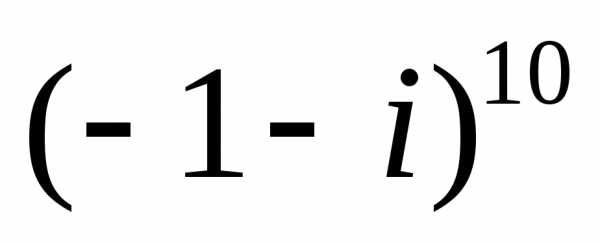 ;
;
б) 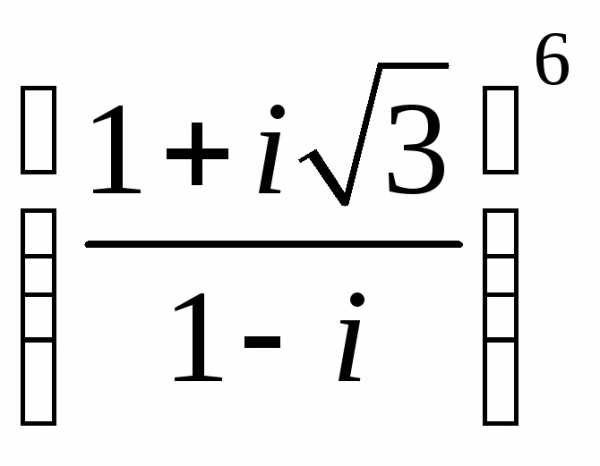
Восстановить оригинал по изображению
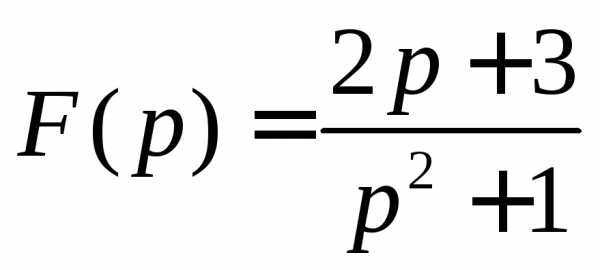
6. Решить систему
Вариант 9.
1. Восстановить оригинал по изображению:
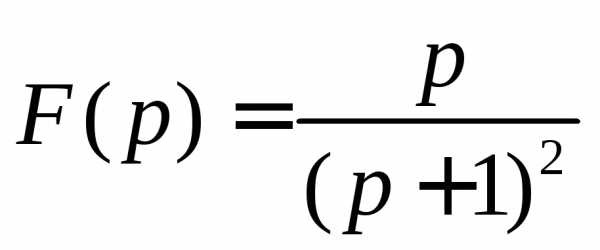
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) 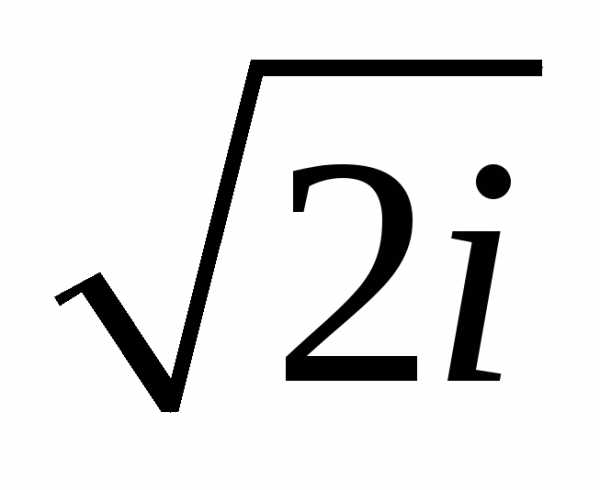 ;
;
б) 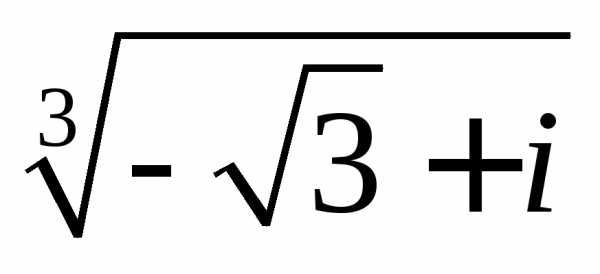
4. Представить в алгебраической форме:
а) 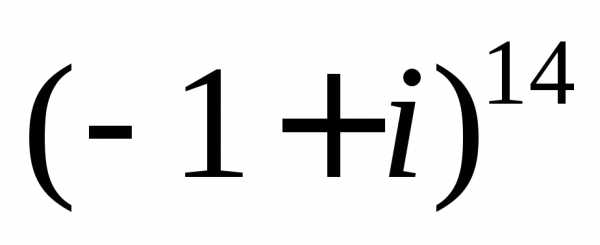 ;
б)
;
б)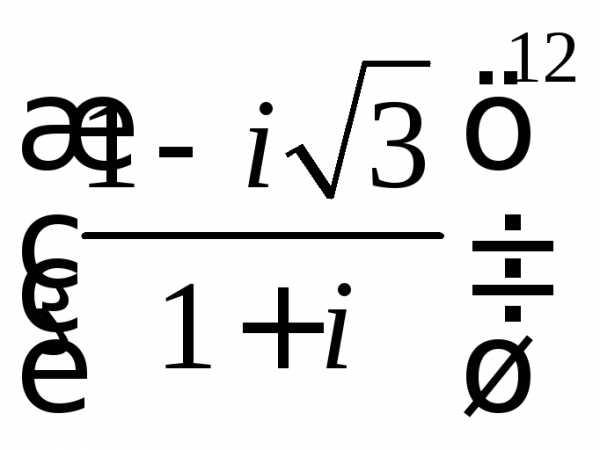
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 10.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 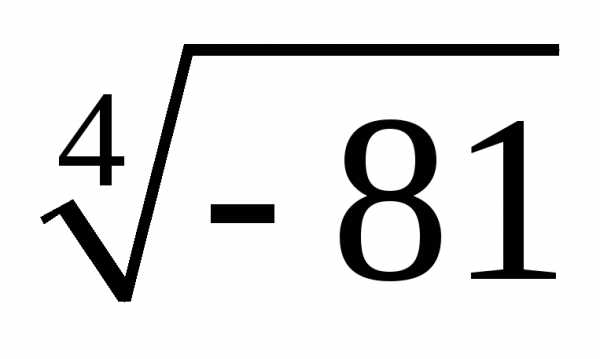 ;
;
б)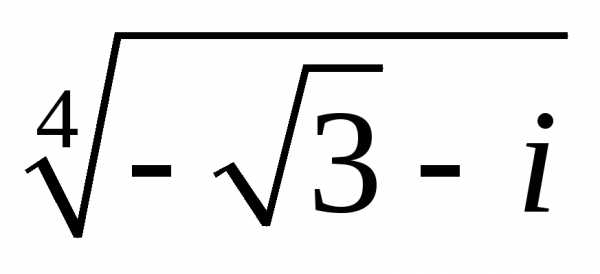
4. Представить в алгебраической форме:
а) 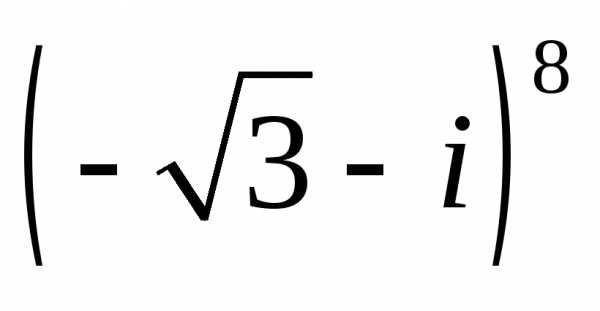 ;
б)
;
б)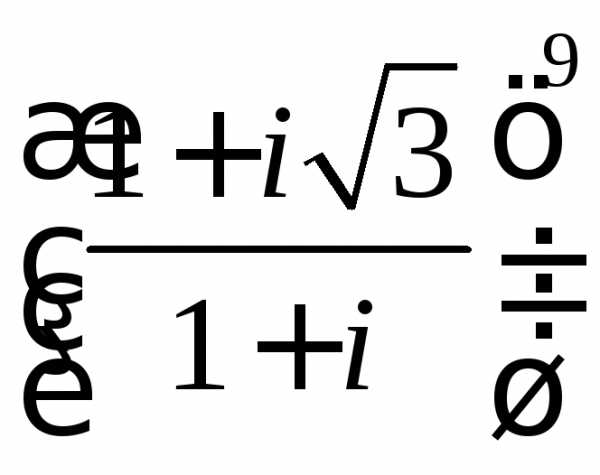
5. Восстановить оригинал по изображению
6. Решить систему
Вариант 11.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а)  ;
;
б)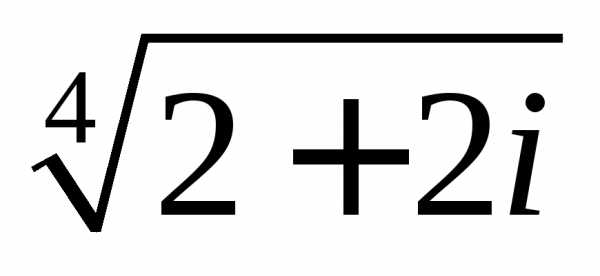
4. Представить в алгебраической форме:
а) 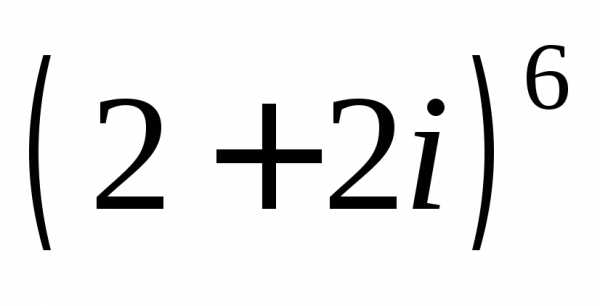 ;
б)
;
б)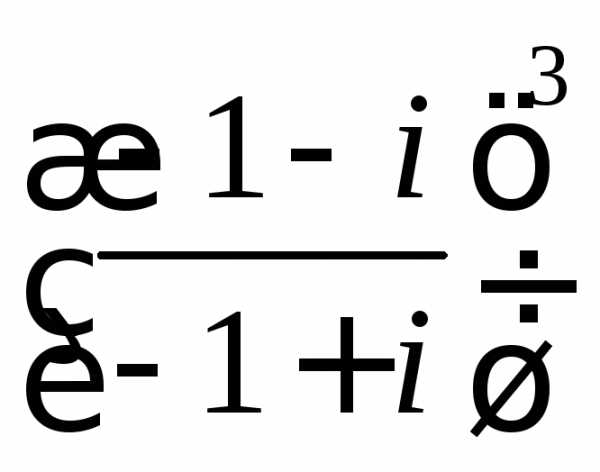
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 12.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 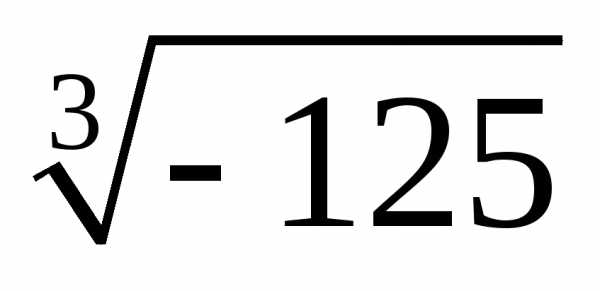 ;
;
б) 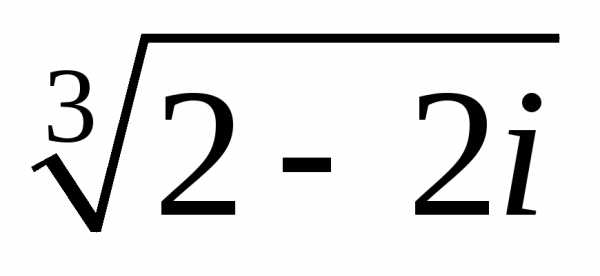
4. Представить в алгебраической форме:
а) 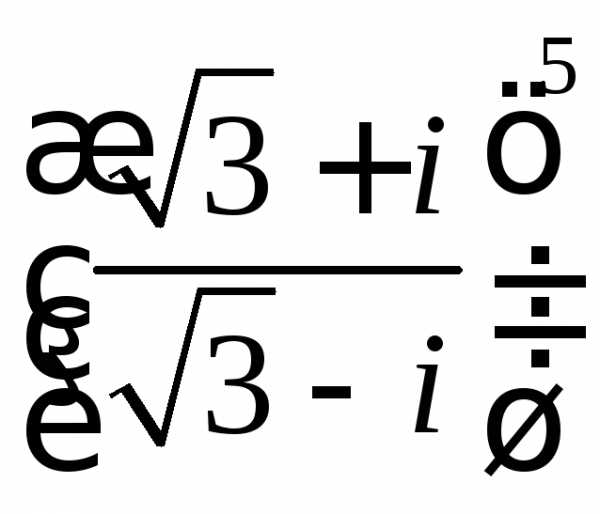 ;
б)
;
б)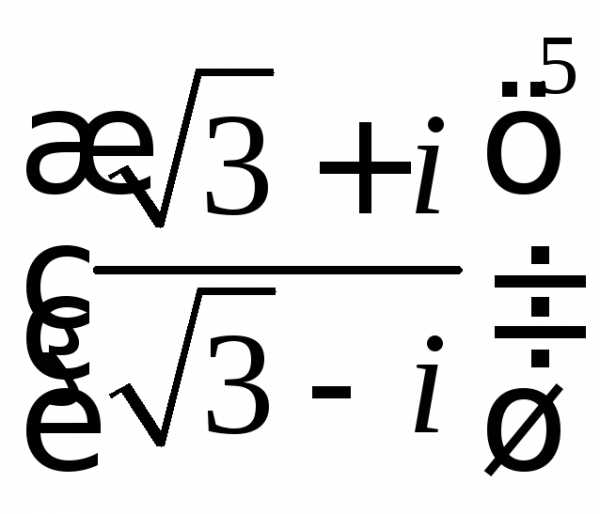
5. Восстановить оригинал по изображению
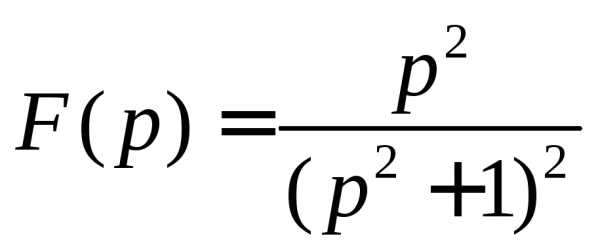
6. Решить систему
Вариант 13.
1. Восстановить оригинал по изображению:
2. Решить задачу Коши операторным методом:
.
3. Найти все значения корней
а) 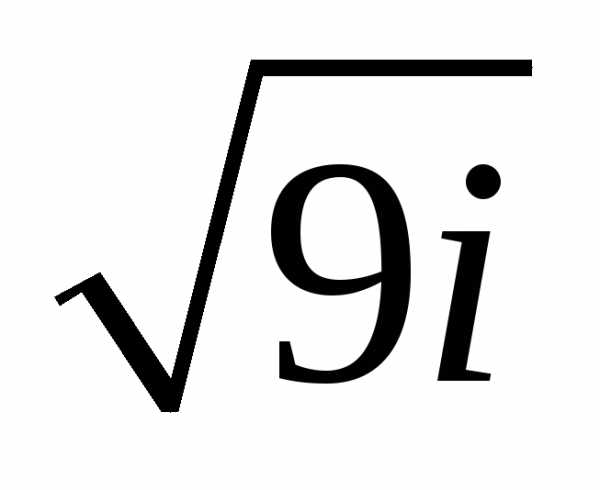 ;
;
б) 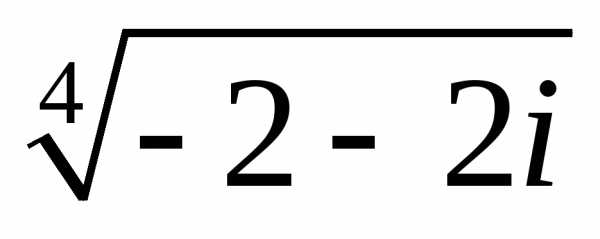
4. Представить в алгебраической форме:
а) 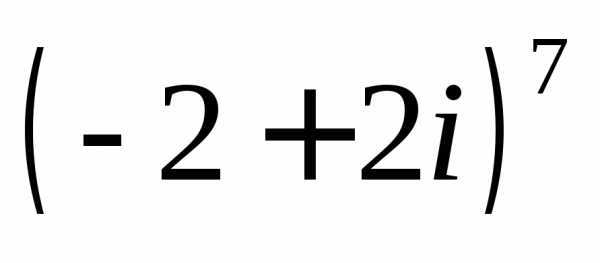 ;
б)
;
б)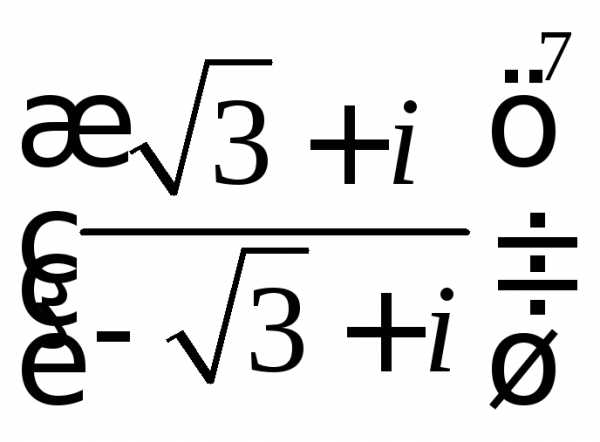
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 14.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 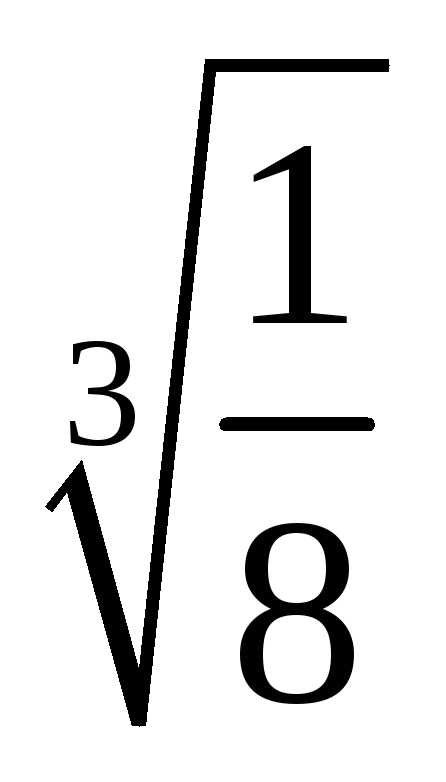 ;
;
б) 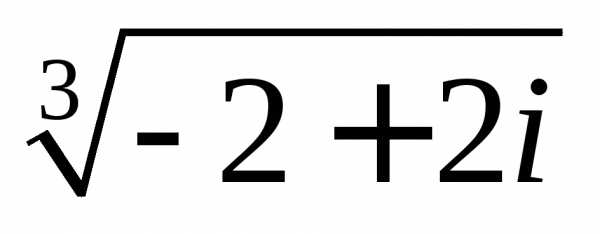
4. Представить в алгебраической форме:
а) 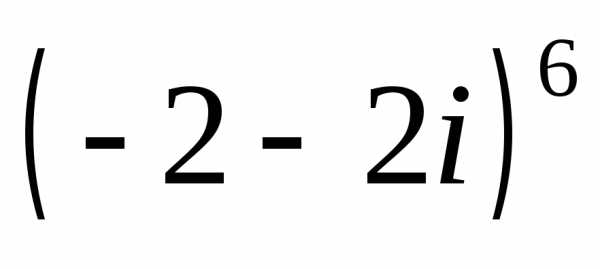 ;
б)
;
б)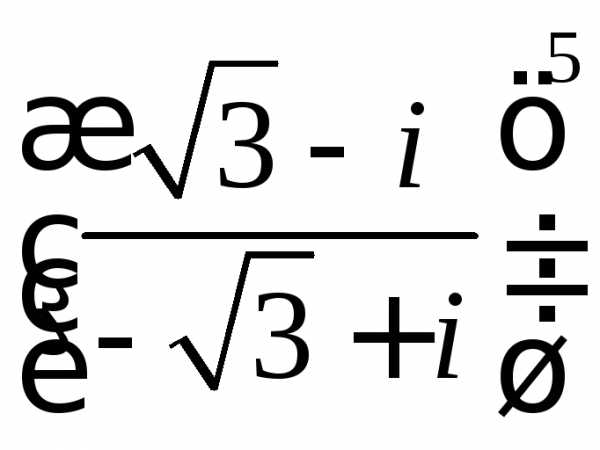
5. Восстановить оригинал по изображению
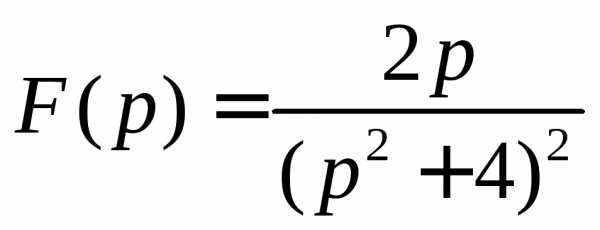
6. Решить систему
Вариант 15.
1. Восстановить оригинал по изображению
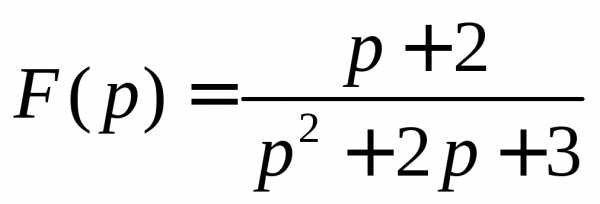
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 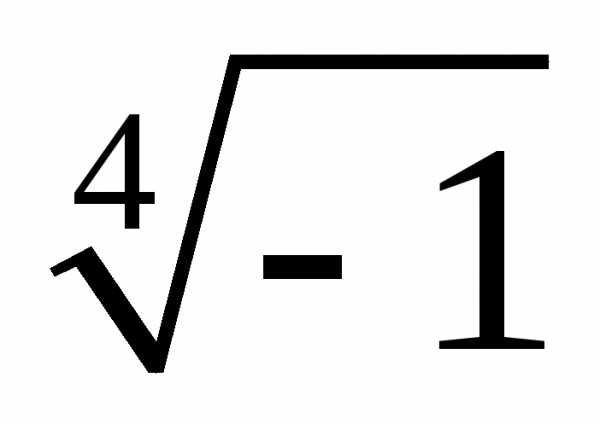 ;
;
б) 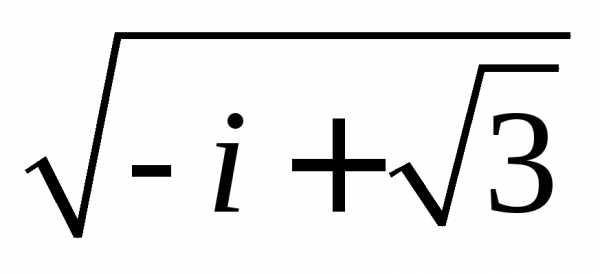
4. Представить в алгебраической форме:
а) 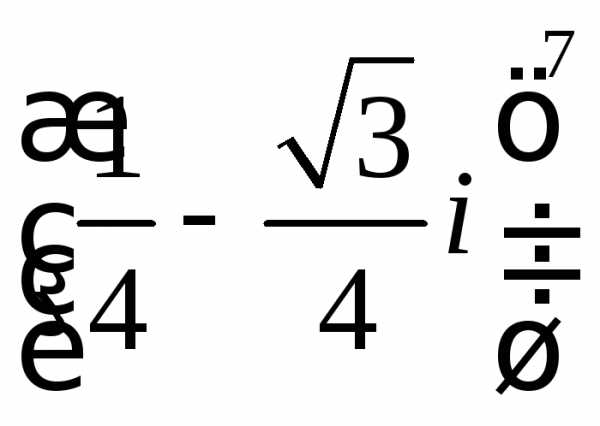 ;
б)
;
б)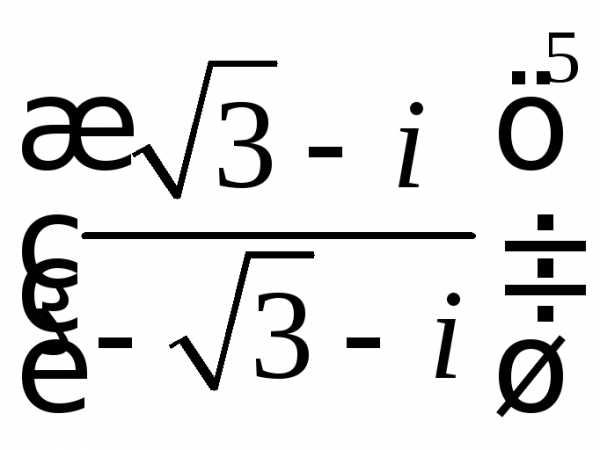
5. Найти изображение оригинала, заданного графически:
6. Решить систему
Вариант 16.
1. Найти изображение функции:
2. Решить задачу Коши операторным методом:
3. Найти все значения корней
а) 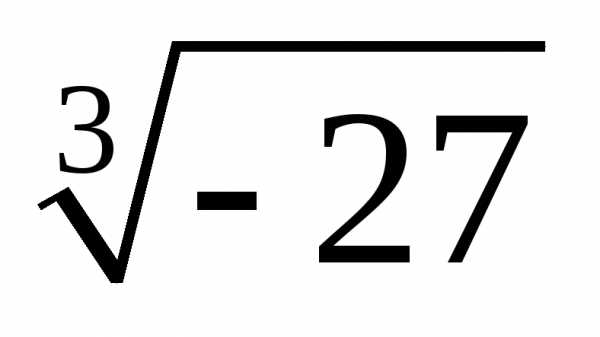 ;
;
б) 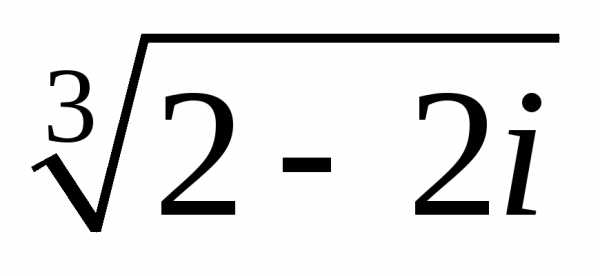
4. Представить в алгебраической форме:
а) 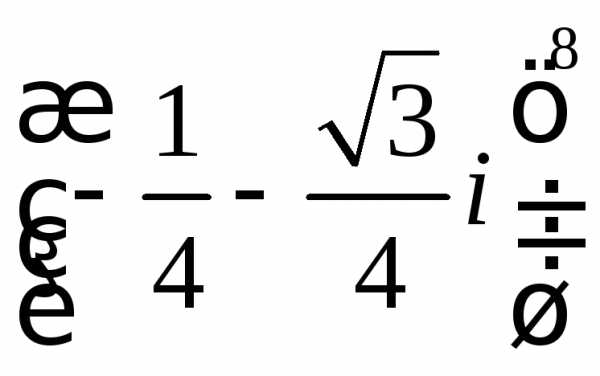 ;
б)
;
б)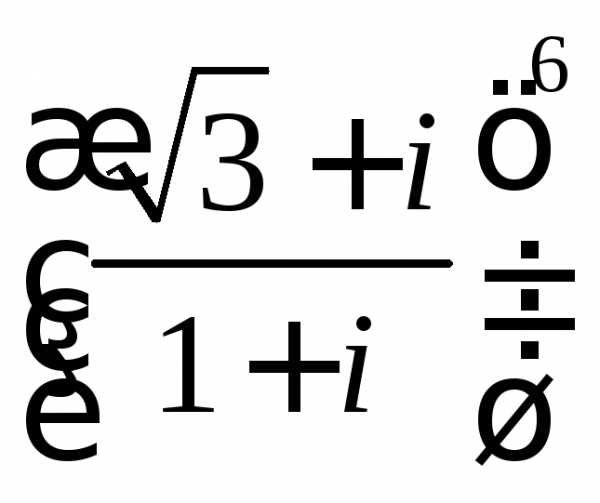
5. Восстановить оригинал по изображению
6. Решить систему
Оглавление.
Введение.
Комплексные числа.
Преобразование Лапласа. Оригинал и изображение.
Нахождение оригинала по изображению.
Решение линейных дифференциальных уравнений и систем.
Применение методов операционного исчисления в задачах электротехники.
Пример контрольной работы по операционному исчислению и комплексным числам.
Литература.
Литература.
Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 1981, 448с.
Сборник задач по математике для втузов. Ч.З. Под ред. А.В. Ефимова, А.С. Поспелова. М.: издательства физико-математической литературы, 2002. 576с.
Краснов М.Л., Киселев А.Н., Макаренко Г.Н. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. М.: Наука, 1981. 304с.
Глатенок И.В., Заварзина И.Ф. Теория функций комплексного переменного и операционное исчисление. М.: Московский энергетический институт, 1989. 48с.
31
studfiles.net
Свертка функций. Отыскание оригинала по изображению.
Поиск ЛекцийТаблица изображений некоторых элементарных оригиналов.
Приведем примеры использования определения и результатов утверждений для нахождения изображений.
Найти изображение функции , используя преобразование Лапласа.
Подчеркнем, что является оригиналом. Так как для всех , то изображение этой функции будет определено и аналитично в полуплоскости . Далее находим:
.
Используя таблицу изображений и свойство линейности преобразования Лапласа найти изображения оригинала:
По таблице изображений найдем: .
.
Найти изображение функции , воспользовавшись свойством дифференцирования изображений.
Воспользовавшись таблицей изображений, запишем:
.
Тогда по теореме о дифференцировании получим:
.
Последовательно вычисляя производные, находим:
и далее .
Окончательно запишем: .
Найти изображение функции .
Можно, вычислив интеграл, найти изображение по таблице изображений. Однако в данном случае проще воспользоваться теоремой об интегрировании оригинала. Действительно, имеем: . Тогда по теореме об интегрировании оригинала имеем право, записать:
.
Свертка функций. Отыскание оригинала по изображению.
Сверткой функций будем называть функцию .
Отметим, что операция свертывания обладает свойством коммутативности: , то есть .
Утверждение 10 (об умножении изображений, или теорема о свертке). Пусть ; . Тогда .
Таким образом, изображением свертки двух оригиналов является произведение их изображений.
Найти свертку функций и :
Приведем два способа решения этой задачи.
Первый способ. Воспользуемся таблицей изображений: и .
Воспользовавшись теоремой о свертке, запишем: .
Итак, изображение свертки найдено. Найдем саму свертку. Для этого, как и в предыдущей задаче, с помощью метода неопределенных коэффициентов представим дробь в виде суммы простейших дробей: . Тогда по таблице изображений запишем: .
Второй способ. Вычислим свертку функций, воспользовавшись определением: .
Интегрируем по частям: . Следовательно, .
Теперь по таблице изображений находим изображение свертки: .
Итак, нами получен тот же результат.
Пользуясь теоремой о свертке, найти оригинал изображения: .
Представим изображение в виде произведения . По теореме о свертке имеем: . Найдем теперь свертку функций и :
.
Таким образом, .
Заметим, что в данном случае оригинал можно было найти и по таблице изображений.
При нахождении оригиналов по заданным изображениям можно использовать несколько приемов.
Первый состоит в том, что изображение представляется в виде суммы элементарных дробей, каждая из которых является изображением простых оригиналов. Далее, используя таблицу оригиналов и свойство линейности преобразования Лапласа, находят оригинал, соответствующий исходной дроби.
Второй способ состоит в том, чтобы представить дробь в виде произведения дробей, каждая из которых является изображением некоторой функции, и применить теорему о свертке.
Третий способ основан на следующем утверждении:
Утверждение 11 (о разложении). Пусть функция представляет собой правильную рациональную дробь, имеющую полюсы в точках , где . Тогда оригиналом для неё служит функция , где сумма берется по всем полюсам.
Отметим, что данное утверждение допускает некоторое упрощение в случае, когда
а) все корни многочлена, стоящего в знаменателе изображения имеют кратность единица: ,
б) корни многочлена, стоящего в знаменателе изображения кратные:
, .
Приведем примеры использования вышеперечисленных идей при решении задач.
Найти оригинал изображения: .
При работе с первым слагаемым по таблице изображений находим: . Поэтому, по свойству линейности преобразования Лапласа, находим соответствующий оригинал: .
Аналогично преобразуем второе слагаемое в выражении: .
Для нахождения оригинала, соответствующего третьему слагаемому выделим полный квадрат в знаменателе: . С учетом этого запишем: . Окончательно для этого слагаемого получим: .
Для нахождения оригинала, соответствующего последнему слагаемому , воспользуемся утверждением запаздывания оригинала. Так как оригинал для функции : , то, применив теперь теорему запаздывания оригинала, имеем
Итак, оригинал, соответствующий нашему изображению имеет вид:
.
Найти оригинал изображения: .
Представим дробь в виде суммы простейших дробей .
Воспользуемся стандартной техникой нахождения неопределенных коэффициентов . Приведем правую часть равенства к общему знаменателю. Тогда дроби равны, знаменатели равны, а значит, и числители равны: .
Слева и справа у нас многочлены. По теореме о равенстве двух многочленов два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях неизвестного. Тогда запишем соответствующую систему и вычислим коэффициенты разложения:
.
Таким образом, исходную дробь представим в виде .
Следовательно, .
Проиллюстрируем теперь использование теоремы о разложении для нахождения оригиналов, соответствующих изображениям.
Пользуясь теоремой о разложении, найти оригинал изображения: .
Функция имеет полюсы второго порядка: , и полюс первого порядка . Тогда по тереме о разложении оригиналом для служит функция . Вычислим соответствующие вычеты .
,
,
.
Следовательно, имеем право, записать
.
Найти оригинал изображения: .
Заметим, что все корни знаменателя действительные и простые.
При этом , а и .
Итак, корни многочлена знаменателя: .
Найдем соответствующие коэффициенты: , , , .
Следовательно, .
Приведем также пример ситуации с кратными корнями.
Найти оригинал изображения: .
Разложение изображения на простые дроби имеет вид: .
Найдем коэффициенты этого разложения
;
;
;
;
??????????
Методы операционного исчисления удобно использовать при решении некоторых дифференциальных и интегро-дифференциальных уравнений, а также систем таких уравнений. При этом предполагают, что в правой части такого уравнения стоит оригинал некоторой функции. Приведем примеры использования утверждений, касающихся свойств оригиналов и изображений.
Найти частное решение дифференциального уравнения
.
Пусть функция , удовлетворяющая данному уравнению имеет изображение: . Тогда воспользовавшись утверждением о дифференцируемости оригинала запишем:
, а .
Правая часть уравнения преобразуется следующим образом:
.
Приходим к операторному уравнению: .
Выразим из полученного уравнения изображение частного решения дифференциального уравнения:
.
Найдем разложение получившейся дроби на сумму дробей, представляющих собой оригиналы элементарных функций.
.
Следовательно, решение исходной задачи Коши.
Найти общее решение дифференциального уравнения .
Выберем произвольные начальные условия задачи Коши. Пусть . И пусть . Тогда
и , кроме того . И соответствующее операторное уравнение имеет вид: .
Выразим отсюда :
.
И значит решением исходного уравнения будет функция
. (здесь ).
Решить интегральное уравнение .
Выпишем уравнение для изображений, воспользовавшись утверждением 8 об интегрировании оригинала. (Полагая, что ).
. Выразим функцию изображения . Найдем оригинал, соответствующий данному изображению .
Решить интегральное уравнение .
Отметим, что левая часть уравнения представляет собой свертку функций и . Переходя к соответствующим изображениям запишем
. Выражая из последнего уравнения убедимся . И, значит, этому изображению соответствует оригинал .
Решить систему уравнений
Пусть и .Выпишем соответствующую операторную систему линейных уравнений
.
Выразим из получившейся операторной системы и :
, .
Отметим, что для нахождения соответствующих оригиналов удобно воспользоваться теоремой разложения, учтя при этом, что корни знаменателя имеют первую кратность.
Таким образом , и .
Найти изображение функции Хевисайда: (см. рис.)
Ранее было получено, что изображением для оригинала является функция ,тогда, воспользовавшись теоремой запаздывания, получим: .
Найти изображение функции, заданной следующим графиком:
Аналитически запись этой функции будет выглядеть следующим образом:
Поэтому ее изображение можно найти, используя формулу преобразования Лапласа, учитывая области определения кусочно-заданного оригинала:
.
Найти изображение ступенчатой функции, изображенной на рисунке.
Аналитически запись этой функции будет выглядеть следующим образом:
. Это легко проверяется графическим сложением функций , , и т.д., изображенных на одном и том же чертеже. По теореме запаздывания получаем: . Второй сомножитель из правой части равенства представляет собой геометрическую прогрессию, со знаменателем . Так как, , то геометрическая прогрессия сходится, и получаем: .
poisk-ru.ru
Свертка функций. Отыскание оригинала по изображению.
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса – ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший “Салат из свеклы с чесноком”
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека – Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков – Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) – В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Таблица изображений некоторых элементарных оригиналов.
Приведем примеры использования определения и результатов утверждений для нахождения изображений.
Найти изображение функции , используя преобразование Лапласа.
Подчеркнем, что является оригиналом. Так как для всех , то изображение этой функции будет определено и аналитично в полуплоскости . Далее находим:
.
Используя таблицу изображений и свойство линейности преобразования Лапласа найти изображения оригинала:
По таблице изображений найдем: .
.
Найти изображение функции , воспользовавшись свойством дифференцирования изображений.
Воспользовавшись таблицей изображений, запишем:
.
Тогда по теореме о дифференцировании получим:
.
Последовательно вычисляя производные, находим:
и далее .
Окончательно запишем: .
Найти изображение функции .
Можно, вычислив интеграл, найти изображение по таблице изображений. Однако в данном случае проще воспользоваться теоремой об интегрировании оригинала. Действительно, имеем: . Тогда по теореме об интегрировании оригинала имеем право, записать:
.
Свертка функций. Отыскание оригинала по изображению.
Сверткой функций будем называть функцию .
Отметим, что операция свертывания обладает свойством коммутативности: , то есть .
Утверждение 10 (об умножении изображений, или теорема о свертке). Пусть ; . Тогда .
Таким образом, изображением свертки двух оригиналов является произведение их изображений.
Найти свертку функций и :
Приведем два способа решения этой задачи.
Первый способ. Воспользуемся таблицей изображений: и .
Воспользовавшись теоремой о свертке, запишем: .
Итак, изображение свертки найдено. Найдем саму свертку. Для этого, как и в предыдущей задаче, с помощью метода неопределенных коэффициентов представим дробь в виде суммы простейших дробей: . Тогда по таблице изображений запишем: .
Второй способ. Вычислим свертку функций, воспользовавшись определением: .
Интегрируем по частям: . Следовательно, .
Теперь по таблице изображений находим изображение свертки: .
Итак, нами получен тот же результат.
Пользуясь теоремой о свертке, найти оригинал изображения: .
Представим изображение в виде произведения . По теореме о свертке имеем: . Найдем теперь свертку функций и :
.
Таким образом, .
Заметим, что в данном случае оригинал можно было найти и по таблице изображений.
При нахождении оригиналов по заданным изображениям можно использовать несколько приемов.
Первый состоит в том, что изображение представляется в виде суммы элементарных дробей, каждая из которых является изображением простых оригиналов. Далее, используя таблицу оригиналов и свойство линейности преобразования Лапласа, находят оригинал, соответствующий исходной дроби.
Второй способ состоит в том, чтобы представить дробь в виде произведения дробей, каждая из которых является изображением некоторой функции, и применить теорему о свертке.
Третий способ основан на следующем утверждении:
Утверждение 11 (о разложении). Пусть функция представляет собой правильную рациональную дробь, имеющую полюсы в точках , где . Тогда оригиналом для неё служит функция , где сумма берется по всем полюсам.
Отметим, что данное утверждение допускает некоторое упрощение в случае, когда
а) все корни многочлена, стоящего в знаменателе изображения имеют кратность единица: ,
б) корни многочлена, стоящего в знаменателе изображения кратные:
, .
Приведем примеры использования вышеперечисленных идей при решении задач.
Найти оригинал изображения: .
При работе с первым слагаемым по таблице изображений находим: . Поэтому, по свойству линейности преобразования Лапласа, находим соответствующий оригинал: .
Аналогично преобразуем второе слагаемое в выражении: .
Для нахождения оригинала, соответствующего третьему слагаемому выделим полный квадрат в знаменателе: . С учетом этого запишем: . Окончательно для этого слагаемого получим: .
Для нахождения оригинала, соответствующего последнему слагаемому , воспользуемся утверждением запаздывания оригинала. Так как оригинал для функции : , то, применив теперь теорему запаздывания оригинала, имеем
Итак, оригинал, соответствующий нашему изображению имеет вид:
.
Найти оригинал изображения: .
Представим дробь в виде суммы простейших дробей .
Воспользуемся стандартной техникой нахождения неопределенных коэффициентов . Приведем правую часть равенства к общему знаменателю. Тогда дроби равны, знаменатели равны, а значит, и числители равны: .
Слева и справа у нас многочлены. По теореме о равенстве двух многочленов два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях неизвестного. Тогда запишем соответствующую систему и вычислим коэффициенты разложения:
.
Таким образом, исходную дробь представим в виде .
Следовательно, .
Проиллюстрируем теперь использование теоремы о разложении для нахождения оригиналов, соответствующих изображениям.
Пользуясь теоремой о разложении, найти оригинал изображения: .
Функция имеет полюсы второго порядка: , и полюс первого порядка . Тогда по тереме о разложении оригиналом для служит функция . Вычислим соответствующие вычеты .
,
,
.
Следовательно, имеем право, записать
.
Найти оригинал изображения: .
Заметим, что все корни знаменателя действительные и простые.
При этом , а и .
Итак, корни многочлена знаменателя: .
Найдем соответствующие коэффициенты: , , , .
Следовательно, .
Приведем также пример ситуации с кратными корнями.
Найти оригинал изображения: .
Разложение изображения на простые дроби имеет вид: .
Найдем коэффициенты этого разложения
;
;
;
;
??????????
Методы операционного исчисления удобно использовать при решении некоторых дифференциальных и интегро-дифференциальных уравнений, а также систем таких уравнений. При этом предполагают, что в правой части такого уравнения стоит оригинал некоторой функции. Приведем примеры использования утверждений, касающихся свойств оригиналов и изображений.
Найти частное решение дифференциального уравнения
.
Пусть функция , удовлетворяющая данному уравнению имеет изображение: . Тогда воспользовавшись утверждением о дифференцируемости оригинала запишем:
, а .
Правая часть уравнения преобразуется следующим образом:
.
Приходим к операторному уравнению: .
Выразим из полученного уравнения изображение частного решения дифференциального уравнения:
.
Найдем разложение получившейся дроби на сумму дробей, представляющих собой оригиналы элементарных функций.
.
Следовательно, решение исходной задачи Коши.
Найти общее решение дифференциального уравнения .
Выберем произвольные начальные условия задачи Коши. Пусть . И пусть . Тогда
и , кроме того . И соответствующее операторное уравнение имеет вид: .
Выразим отсюда :
.
И значит решением исходного уравнения будет функция
. (здесь ).
Решить интегральное уравнение .
Выпишем уравнение для изображений, воспользовавшись утверждением 8 об интегрировании оригинала. (Полагая, что ).
. Выразим функцию изображения . Найдем оригинал, соответствующий данному изображению .
Решить интегральное уравнение .
Отметим, что левая часть уравнения представляет собой свертку функций и . Переходя к соответствующим изображениям запишем
. Выражая из последнего уравнения убедимся . И, значит, этому изображению соответствует оригинал .
Решить систему уравнений
Пусть и .Выпишем соответствующую операторную систему линейных уравнений
.
Выразим из получившейся операторной системы и :
, .
Отметим, что для нахождения соответствующих оригиналов удобно воспользоваться теоремой разложения, учтя при этом, что корни знаменателя имеют первую кратность.
Таким образом , и .
Найти изображение функции Хевисайда: (см. рис.)
Ранее было получено, что изображением для оригинала является функция ,тогда, воспользовавшись теоремой запаздывания, получим: .
Найти изображение функции, заданной следующим графиком:
Аналитически запись этой функции будет выглядеть следующим образом:
Поэтому ее изображение можно найти, используя формулу преобразования Лапласа, учитывая области определения кусочно-заданного оригинала:
.
Найти изображение ступенчатой функции, изображенной на рисунке.
Аналитически запись этой функции будет выглядеть следующим образом:
. Это легко проверяется графическим сложением функций , , и т.д., изображенных на одном и том же чертеже. По теореме запаздывания получаем: . Второй сомножитель из правой части равенства представляет собой геометрическую прогрессию, со знаменателем . Так как, , то геометрическая прогрессия сходится, и получаем: .
megapredmet.ru
§ 9.4.2 Восстановление оригинала по изображению.
Пример. Восстановить оригинал по изображению:
а) ; б) .
Решение. а) по табл. 2 находим и . По табл. 1 учитываем запаздывание аргумента оригинала, а именно и
. Окончательно получаем оригинал , или
б) аналогично имеем последовательно , .
ПРИМЕР 26. Найти оригинал по его изображению .
Решение. Сначала пытаемся найти оригинал сразу по табл. 2, но в данном примере это не удается. Поэтому сведем к табличным выражениям, преобразуя следующим образом:
.
По табл. 2 находим и или .
Окончательно оригинал запишется так:
.
Таким образом, для отыскания оригинала по известному изображению иногда можно представить изображение в виде суммы табличных изображений, затем найти оригинал каждого слагаемого, а результаты сложить. Обращение преобразования Лапласа в общем виде рассмотрено далее.
Задание. Восстановить оригинал по изображению:
а) ; б) .
Ответы: а) ;
б) .
Следствие 1
А= В=
Если $ n1: n³n1 => an=bn, тогда A~B (либо оба сходящиеся либо оба расходящиеся)
Доказательство: n0³n1 | am+1+…+an |=| bm+1+…+bn |
Следствие 2
A= B=, Если bn = kan, n ³1, k¹0, тогда A~B.
Если сходится, то сходится.
Доказательство: По критерию Коши:
| am+1+…+an |≤|am+1|+|am+2|+…+|an|<e
Достаточные признаки сходимости знакопостоянных рядов.
В задании IV требуется проинтегрировать некоторую тригонометрическую функцию. Рассмотрим основные приемы вычисления подобных интегралов.
1. Интеграл вида , где – рациональная функция, можно привести к интегралу от рациональной дроби универсальной тригонометрической подстановкой . Используя формулы тригонометрии, получим . Кроме того , откуда .
Применение этой подстановки доказывает, что каждый интеграл сводится к интегралу от рациональной функции и, следовательно, первообразная функции , стоящей под интегралом, выражается через элементарные функции.
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
it-iatu.ru
ВОССТАНОВЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ С ПОМОЩЬЮ СВОЙСТВ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Авторы: Г.А.Батырбаева- старший преподаватель, магистр математики (г.Алматы, Казахский государственный женский педагогический университет)
Дополнительное применение свойств изображений позволяет существенно расширить возможности восстановления оригинала по заданному изображению. Для восстановления оригинала по заданному изображению в простейших случаях используется таблица изображений.
Непосредственное применение формулы обращения для восстановления оригинала по изображению затруднительно. Для нахождения оригинала обычно пользуются теоремами разложения.
Класс оригиналов можно расширить, включив в него функции, которые могут быть неограничены в окрестности конечного множества точек, но такие, что интеграл Лапласа от них тем не менее в некоторой полуплоскости сходится абсолютно. К числу таких обобщенных оригиналов относится степенная функция при , функция lnt и некоторые другие. В частности, к такому классу относится всякая функция , которая в некоторых точках является бесконечно большой порядка, меньшего единицы, т.е. такая что при некотором и если вне некоторых окрестностей точек она удовлетворяет условиям, при которых функцию можно считать оригиналом.
Пример. Найти изображение функции .
Решение. или, после подстановки , . Итак, .
Элементарный метод. Во многих случаях заданное изображение можно преобразовать к такому виду, когда оригинал легко восстанавливается непосредственно с помощью свойств преобразования Лапласа и таблицы изображений.
Для преобразования изображения широко используется в этом случае метод разложения рациональной дроби в сумму простейших.
Пример1. Найти оригинал по изображению .
Решение. Найдем оригинал непосредственно с помощью свойств преобразования Лапласа и таблицы изображений. Поскольку
, ,
то на основании формулы Дюамеля имеем
Пример 2. Найти оригинал по изображению
Решение. Из таблицы изображений имеем . Используя свойства линейности и интегрирования оригинала, находим:
Пример3. Найти оригинал, соответствующий изображению
Решение. Представим в виде суммы элементарных дробей:
Тогда по теореме разложения найдем оригинал:
Пример 4. Найти оригинал по изображению
Решение. Функция правильная рациональная несократимая дробь, для которой точки , являются простыми полюсами. Так как
для
для
для
то по 2-й теореме разложения получим:
Пример 5. Найти оригинал для функции F(p)=.
Решение. Первый способ. Выделяя полный квадрат в знаменателе и далее, используя табличное изображение для и теорема смещения, получаем:
=.
Второй способ. Раскладывая дробь в сумму простейших и используя изображение для получаем
=.
Пример 6. Найти оригинал для функции F(p)=.
Решение. Первый способ. Раскладывая дробь в сумму простейших , получаем
== =
Второй способ. Заметим, что
причем согласно теореме о дифференцировании изображения
Применяя теперь теорему об интегрировании оригинала, находим
Третий способ. Используя теорему Бореля об изображении свертки, получаем
=
group-global.org