Постоянная r в термодинамике – Универсальная газовая постоянная — Википедия

Универсальная газовая постоянная, формула и примеры

Уравнение состояния идеального газа

Для неизменной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная:

   

Выясним, чему равна эта постоянная величина. Рассмотрим 1 моль идеального газа. При нормальных условиях газ имеет температуру =273 K и давление =101325 Па. При таких условиях 1 моль этого газа занимает объем .

Подставив эти значения в уравнение состояния, получим:

   

Универсальная газовая постоянная

Таким образом, для 1 моля идеального газа произведение давления на объем, отнесенное к абсолютной температуре есть величина постоянная для всех газов. Эта величина называется универсальной газовой постоянной:

   

Уравнение состояния идеального газа было получено французским физиком Б. Клапейроном в 1834 г. Это уравнение полностью определяет параметры состояния термодинамической системы при переходе из одного состояния в другое.

При переходе системы из состояния 1 в состояние 2 уравнение состояния записывают в виде:

   

Знание уравнения состояния очень важно при исследовании тепловых процессов. Это уравнение позволяет полностью или частично ответить на ряд вопросов:

1. уравнение состояния позволяет определить одну из величин, характеризующих состояние, например температуру, если известны две другие величины.
2. уравнение состояния позволяет определить, как протекают в системе различные процессы при определенных внешних условиях: например, как будет меняться давление газа, если увеличивать его объем при неизменной температуре, и т. д.
3. зная уравнение состояния, можно определить, как меняется состояние системы, если она совершает работу или получает теплоту от окружающих тел.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Второй закон термодинамики

В общем случае второй закон термодинамики обобщает особенности теплоты, проявляющиеся при ее передаче и преобразовании.

Эквивалентные формулировки второго закона термодинамики:

«Энергия в форме теплоты самопроизвольно переходит от теплых тел к холодным; для обратного перехода надо затратить работу (Р.Клаузиус, 1850 г.).

«В периодически действующем двигателе невозможно всю подведенную теплоту без компенсации превратить в работу» (В.Томсон, 1851 г.).

«Все естественные процессы являются переходом от менее вероятных к более вероятным состояниям» (Л.Больцман, 1870 – 1876 г.г.).

Математической записью второго закона термодинамики является выражение:

dS ,

здесь знак равенства относится к обратимым процессам, а неравенства – к необратимым.

Эксергия

В термодинамике максимально возможную техническую работу

системы называют эксергией.

Обозначают эксергию системы E_x. За единицу эксергию в СИ принят джоуль (Дж). Ее приведенное значение (e

x = Е_x/m) имеет единицу измерения Дж/кг.

Цикл

Циклом или круговым процессом называют совокупность термодинамических процессов, в результате осуществления которых рабочее тело возвращается в свое первоначальное состояние.

Рабочее тело

Рабочим телом термодинамической системы называют материальное тело, посредством которого в термодинамическом процессе осуществляется преобразование теплоты в работу или работы в теплоту.

Рабочими телами, как правило, являются газообразные вещества – газы и пары, которые способны значительно изменять свой объем при изменении внешних условий.

Термический КПД

Под термическим КПД понимают отношение теплоты, преобразо-

ванной в полезную работу цикла, ко всей подведенной теплоте.

Обозначают η _t и вычисляют с помощью выражения η _t = .

Удельная газовая постоянная

Удельная газовая постоянная – физическая величина, равная отношению произведения давления на удельный объем газа к абсолютной температуре.

Обозначают удельную газовую постоянную R , единица измерения джоуль на килограмм-кельвин (Дж/(кгИз определения:

R =. При известной молярной массе газа R = .

Универсальная газовая постоянная

Газовую постоянную одного моля газа называют универсальной, так как для любого газа при одинаковых состояниях ее числовое значение одно и то же.

Универсальная газовая постоянная обозначается и имеет единицу измерения джоуль на моль-кельвин (Дж/(мольК)). Числовое значение

= 8314 Дж/(мольК).

Политропный процесс

Обратимый процесс перехода рабочего тела из начального равновесного состояния в конечное равновесное состояние при условии неизменной теплоемкости называют политропным процессом.

Удельную массовую теплоемкость политропного процесса обознача-ют c_n . Характер изменения состояния рабочего тела определяется численным значением c _n , которое может быть .

Уравнение политропного процесса имеет вид:

p v ⁿ = const.

Показатель степени у удельного объема n называют показателем политропы. Его можно определить, используя выражения

studfiles.net

Уравнение состояния идеальных газов. Газовая постоянная.

Как было отмечено ранее, в термодинамических системах в качестве рабочего тела часто рассматривается идеальный газ, являющийся теоретической моделью газа, в которой не учитываются взаимодействия частиц газа – молекул, представляющих собой материальные точки, не имеющие объема и сил межмолекулярного сцепления.

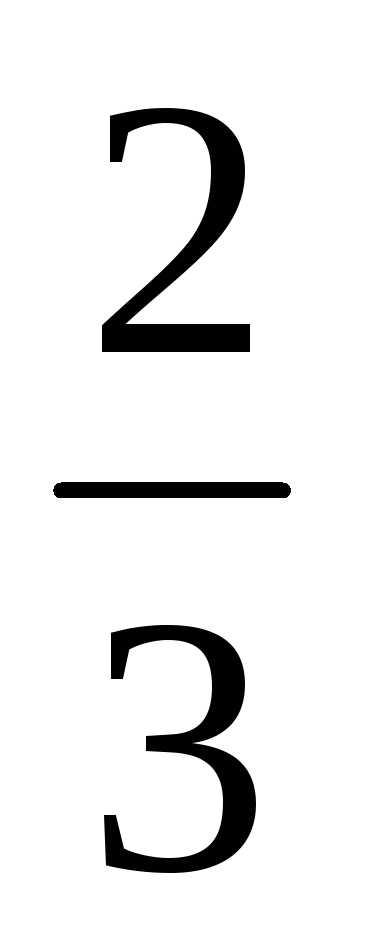Основные параметры состояния (абсолютное давление, удельный объем и абсолютная температура) однородного тела зависят один от другого и взаимно связаны уравнением состояния F(P, v, T) = 0. Из молекулярно-кинетической теории следует, что абсолютное давление газа численно равно средней кинетической энергии поступательного движения молекул, заключенных в единице объема:

(2.4)

где n

– число молекул в удельном объеме; v – удельный объем газа; m – масса молекулы;  – средняя квадратичная скорость поступательного движения молекул; – средняя кинетическая энергия молекулы.

Молекулярно-кинетическая теория газов устанавливает прямо пропорциональную зависимость между средней кинетической энергией молекулы и абсолютной температурой:

(2.5)

где Т – абсолютная температура; В – коэффициент пропорциональности.

С учетом (2.2) уравнение (2.1) можно представить в виде

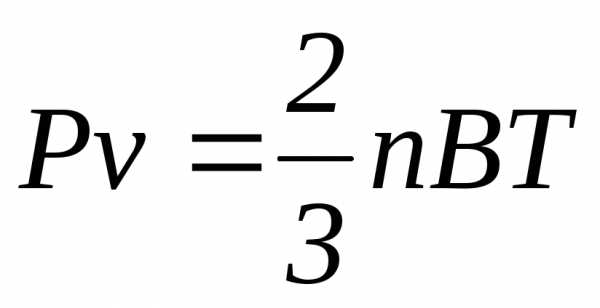(2.6)

Если уравнение (2.3) отнести к двум состояниям газа, то для каждого из них получаем:

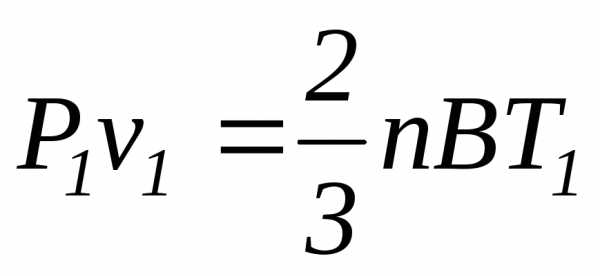
Почленное деление этих уравнений приводит к следующему соотношению:

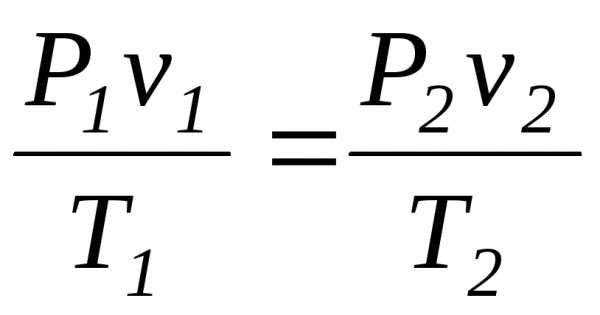(2.7)

Это соотношение между параметрами состояния может быть получено из совместного рассмотрения законов Бойля-Мариотта и Гей-Люссака, поэтому часто это соотношение называют объединенным законом Бойля-Мариотта и Гей-Люссака.

Выражение (2.8) показывает, что произведение абсолютного давления идеального газа и удельного объема, деленное на абсолютную температуру, для любого равновесного состояния есть величина постоянная:

. (2.8)

Постоянную величину обозначают R и называют удельной газовой постоянной:

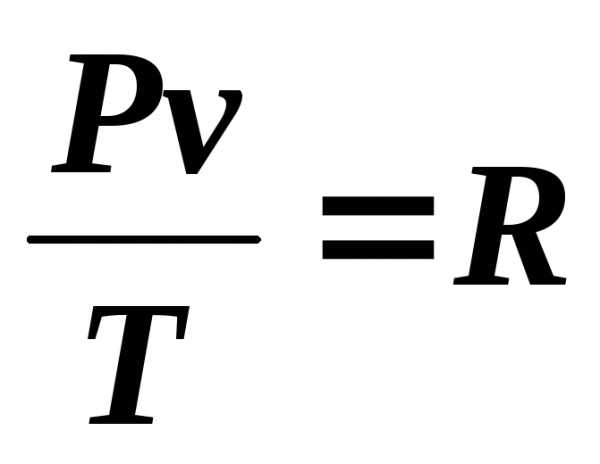или (2.9)

Уравнение (2.9) называют термическим уравнением состояния идеальных газов или характеристическим уравнением, однозначно связывающим между собой параметры P, v, T. Это уравнение было выведено французским физиком Клапейроном в 1834 году и поэтому названо его именем.

Для произвольного количества газа массой m [кг] уравнение состояния имеет вид:

Pv = mRT, (2.10)

где P – абсолютное давление газа в Па; v – объем рассматриваемого количества газа в м³;

m – масса газа в кг; T – абсолютная температура газа в К.

Выясним физический смысл удельной газовой постоянной. Запишем уравнение Клапейрона для двух состояний газа при одном и том же давлении:

Вычитая из второго уравнения первое, получим:

P(V₂-V₁) = mR(T₂-T₁), (2.11)

откуда

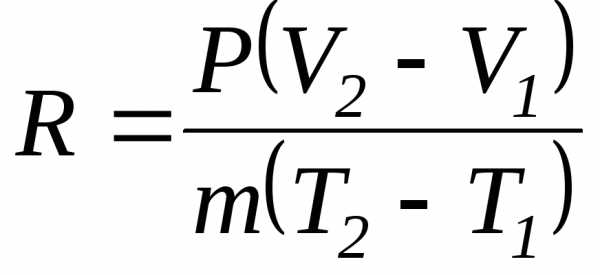. (2.12)

Числитель правой части представляет собой работу газа в процессе при постоянном давлении. Если разность температур равна 1К, а масса газа равна 1кг, то удельная газовая постоянная есть работа в Дж 1кг газа в процессе при постоянном давлении и при изменении температуры на 1К.

Удельная газовая постоянная имеет следующую размерность:

Удельная газовая постоянная представляет собой физическую постоянную, которая для каждого газа имеет вполне определенное значение, зависящее от природы газа и не зависящее от его состояния.

Уравнение Клапейрона в рассмотренном виде может применяться не только для идеальных газов, но и для реальных газов, имеющих низкое давление и высокую температуру.

Если  – молярная масса газа, то умножив на  обе части уравнения (2.9), получим уравнение Клапейрона-Менделеева:

Pv = RT; Pv_ = R_T, (2.13)

где v_ = v – молярный объем рабочего тела [м³/моль] при нормальных физических условиях (давлении 101325 Па и температуре 273,15К), объем 1 кмоль газа равен 22,4143 м³/кмоль;

R_ = R – универсальная газовая постоянная, равная

Дж/(кмольК)

Уравнение (2.13) впервые было предложено Менделеевым в 1874 году и является наиболее общим для идеальных газов.

studfiles.net

Постоянная Больцмана — Традиция

Для постоянной, связанной с энергией излучения чёрного тела, смотри Постоянная Стефана-Больцмана

Постоянная Больцмана (\(k\) или \(k_{\rm B}\)) — физическая постоянная, определяющая связь между температурой вещества и энергией теплового движения частиц этого вещества. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её экспериментальное значение в системе СИ равно $$k=1{,}380\,650\,4(24)\times 10^{-23}$$Дж/К.

В таблице последние цифры в круглых скобках указывают стандартную погрешность значения постоянной. В принципе, постоянная Больцмана может быть получена из определения абсолютной температуры и других физических постоянных. Однако точное вычисление постоянной Больцмана с помощью основных принципов слишком сложно и невыполнимо при современном уровне знаний.

Экспериментально постоянную Больцмана можно определить с помощью закона теплового излучения Планка, описывающего распределение энергии в спектре равновесного излучения при определённой температуре излучающего тела, а также другими методами.

Существует связь между универсальной газовой постоянной \(~R\) и числом Авогадро \(~ N_{\rm A}\), из которой следует значение постоянной Больцмана: $$~k = \frac{R}{N_{\rm A}}.$$

Размерность постоянной Больцмана такая же, как и у энтропии.

В 1877 г. Больцман впервые связал между собой энтропию и вероятность, однако достаточно точное значение постоянной k как коэффициента связи в формуле для энтропии появилось лишь в трудах М. Планка. При выводе закона излучения чёрного тела Планк в 1900–1901 гг. для постоянной Больцмана нашёл значение 1,346 • 10⁻²³ Дж/K, почти на 2,5% меньше принятого в настоящее время.^[2]

До 1900 г. соотношения, которые сейчас записываются с постоянной Больцмана, писались с помощью газовой постоянной R, а вместо средней энергии на одну молекулу использовалась общая энергия вещества. Лаконичная формула вида S = k log W на бюсте Больцмана стала таковой благодаря Планку. В своей нобелевской лекции в 1920 г. Планк писал: ^[3]

Эта константа часто называется постоянной Больцмана, хотя, насколько я знаю, сам Больцман никогда не вводил её — странное состояние дел, при том, что в высказываниях Больцмана не было речи о точном измерении этой константы.

Такая ситуация может быть объяснена проведением в то время научных дебатов по выяснению сущности атомного строения вещества. Во второй половине 19 века существовали значительные разногласия в отношении того, являются ли атомы и молекулы реальными, либо они лишь удобный способ описания явлений. Не было единства и в том, являются ли “химические молекулы”, различаемые по их атомной массе, теми же самыми молекулами, что и в кинетической теории. Далее в нобелевской лекции Планка можно найти следующее:^[3]

Ничто не может лучше продемонстрировать положительную и ускоряющуюся скорость прогресса, чем искусство эксперимента за последние двадцать лет, когда было открыто сразу множество методов измерения массы молекул практически с той же точностью, что и измерение массы какой-нибудь планеты.

Уравнение состояния идеального газа[править]

Для идеального газа справедлив объединённый газовый закон, связывающий давление P, объём V, количество вещества n в молях, газовую постоянную R и абсолютную температуру T: $$~\ PV = nRT.$$

В данном равенстве можно сделать замену \(~R = k N_{\rm A}\). Тогда газовый закон будет выражаться через постоянную Больцмана и количество молекул N в объёме газа V: $$~P V = N k T .$$

Связь между температурой и энергией[править]

В однородном идеальном газе, находящемся при абсолютной температуре \(T\), энергия, приходящаяся на каждую поступательную степень свободы, равна, как следует из распределения Максвелла, \(kT/2\). При комнатной температуре (≈ 300 K) эта энергия составляет \(2{,}07\times 10^{-21}\) Дж, или 0,013 эВ.

Соотношения газовой термодинамики[править]

В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия \(3 kT /2\). Это хорошо согласуется с экспериментальными данными. Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню из атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона.

Кинетическая теория даёт формулу для среднего давления P идеального газа: $$ ~P = \frac{1}{3}\frac{N}{V} m {\overline{v^2}}.$$ Учитывая, что средняя кинетическая энергия прямолинейного движения равна: $$~ \frac{1}{2}m \overline{v^2} = \frac{3}{2} k T,$$ находим уравнение состояния идеального газа: $$~ P = \frac{N k T}{V}.$$

Это соотношение неплохо выполняется и для молекулярных газов; однако зависимость теплоёмкости изменяется, так как молекулы могут иметь дополнительные внутренние степени свободы по отношению к тем степеням свободы, которые связаны с движением молекул в пространстве. Например, двухатомный газ имеет уже приблизительно пять степеней свободы.

Множитель Больцмана[править]

В общем случае система в равновесии с тепловым резервуаром при температуре T имеет вероятность p занять состояние с энергией E, что может быть записано с помощью соответствующего экспоненциального множителя Больцмана: $$~p \propto \exp\left(-\frac{E}{kT}\right).$$ В данном выражении фигурирует величина kT с размерностью энергии.

Вычисление вероятности используется не только для расчётов в кинетической теории идеальных газов, но и в других областях, например в химической кинетике в уравнении Аррениуса.

Роль в статистическом определении энтропии[править]

Вена, Zentralfriedhof, изображение Больцмана и формулы для энтропии на бюсте.

Энтропия S изолированной термодинамической системы в термодинамическом равновесии определяется через натуральный логарифм от числа различных микросостояний \(W\), соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией E): $$~S=k \ln W.$$ Коэффициент пропорциональности \(k\) является постоянной Больцмана. Это выражение, определяющее связь между микроскопическими и макроскопическими состояниями (через \(W\) и энтропию \(S\) соответственно), выражает центральную идею статистической механики и является главным открытием Больцмана.

В классической термодинамике используется выражение Клаузиуса для энтропии: $$~\Delta S = \int \frac{{\rm d}Q}{T}.$$

Таким образом, появление постоянной Больцмана k можно рассматривать как следствие связи между термодинамическим и статистическим определениями энтропии.

Энтропию можно выразить в единицах k , что даёт следующее: $$~{S^{\,’} = \frac {S}{k}= \ln W} \; ; \; \; \; \Delta S^{\,’} = \int \frac{\mathrm{d}Q}{kT}.$$

В таких единицах энтропия точно соответствует информационной энтропии.

Характерная энергия kT равна количеству теплоты, необходимому для увеличения энтропии \(S^{‘}\) на один нат.

Роль в физике полупроводников: тепловое напряжение[править]

В отличие от других веществ, в полупроводниках существует сильная зависимость электропроводности от температуры: $$~ \sigma= \sigma_0 \exp (-E_A /kT),$$

где множитель \( \sigma_0 \) достаточно слабо зависит от температуры по сравнению с экспонентой, \( E_A \) – энергия активации проводимости. Плотность электронов проводимости также экспоненциально зависит от температуры. Для тока через полупроводниковый p — n-переход вместо энергии активации рассматривают характерную энергию данного p-n перехода при температуре T как характерную энергию электрона в электрическом поле: $$~ q V_T = kT,$$

где \( q \) – элементарный электрический заряд, а \( V_T \) есть тепловое напряжение, зависящее от температуры.

Данное соотношение является основой для выражения постоянной Больцмана в единицах эВ•К⁻¹. При комнатной температуре (≈ 300 K) значение теплового напряжения порядка 25,85 милливольт ≈ 26 мВ.

В классической теории часто используют формулу, согласно которой эффективная скорость носителей заряда в веществе равна произведению подвижности носителей \( \mu \) на напряженность электрического поля. В другой формуле плотность потока носителей связывается с коэффициентом диффузии \( D \) и с градиентом концентрации носителей \( n \): $$~ j_D =-D \nabla n.$$

Согласно соотношению Эйнштейна-Смолуховского, коэффициент диффузии связан с подвижностью: $$~ D =kT \mu /q.$$

Постоянная Больцмана k входит также в закон Видемана-Франца, по которому отношение коэффициента теплопроводности к коэффициенту электропроводности в металлах пропорционально температуре и квадрату отношения постоянной Больцмана к электрическому заряду.

Применения в других областях[править]

Для разграничения температурных областей, в которых поведение вещества описывается квантовыми или классическими методами, служит температура Дебая: $$~ Q_D = \hbar \omega_D /k,$$ где \( \hbar \) – постоянная Дирака, \( \omega_D =u \sqrt[3]{6\pi^2 n } \) есть предельная частота упругих колебаний кристаллической решётки, \( u \) – скорость звука в твёрдом теле, \( n \) – концентрация атомов.

При температурах ниже \( Q_D \) требуется использовать квантовую статистику. Если же температуры выше \( Q_D \), то тепловая энергия (порядка kT) превышает характерную энергию колебаний решётки и система может быть описана формулами классической статистической механики.

Постоянная Больцмана входит в формулу Найквиста, определяющую средний квадрат шумового напряжения в электрической цепи с сопротивлением R в полосе частот \( \Delta \nu\) при температуре T. В классическом приближении формула для теплового шума имеет вид: $$~ \bar {V^2} = 4 R k T \Delta \nu .$$

Постоянная Больцмана в планковских единицах[править]

В планковской системе естественных единиц постоянная Больцмана равна 1. Это даёт $$ ~E = \frac{T}{2} $$ как среднюю кинетическую энергию газовой молекулы на одну степень свободы; при этом определение термодинамической энтропии совпадает с определением информационной энтропии: $$~ S = – \sum p_i \ln p_i.$$

Планковская единица температуры равна 1,416 785(71) • 10³² К, соответствуя энергии покоя планковской массы.

Постоянная Больцмана в теории бесконечной вложенности материи[править]

С точки зрения теории бесконечной вложенности материи, постоянная Больцмана является характеристикой лишь одного, а именно атомного уровня материи. Как показывает анализ естественных единиц измерения физических величин, при использовании вместо температурной шкалы шкалы тепловой энергии, содержащейся в единице количества вещества, постоянная Больцмана становится излишней. Отсюда следует, что при использовании температуры как физической величины на некотором масштабном уровне материи необходимо пересчитывать значение постоянной Больцмана для этого уровня материи с помощью соответствующих коэффициентов подобия. Теоретической основой для этой процедуры является SPФ-симметрия.

Для уровня звёзд аналогично звёздной постоянной Планка, задающей характерный момент импульса типичных звёздных объектов, появляется звёздная постоянная Больцмана. Eё значение равно K_ps = k ∙ Ф = 9,187∙10³² Дж/К, где Ф – коэффициент подобия по массе. ^[4] Звёздная постоянная Больцмана определяет связь между эффективной температурой совокупности типичных звёздных объектов как меры тепловой энергии, и средней кинетической энергией движения в расчёте на один звёздный объект. Кроме этого, она связывает внутреннюю температуру звёздных объектов с внутренней энергий вещества этих объектов. Аналогичные постоянные могут быть вычислены для каждого масштабного уровня материи. Следовательно, обычная постоянная Больцмана не только позволяет оценить кинетическую температуру частиц вещества по известной энергии этого вещества, но и даёт возможность найти температуру вещества внутри самих частиц, например, внутри нуклона.

Значения в различных единицах[править]

Значение k	Размерность	Примечание
1,380 6504(24) • 10−23	Дж / К	единицы СИ, значение CODATA 2006[1]
8,617 343(15) • 10−5	эВ/K	1  эВ= 1,602 176 53(14) • 10−19 Дж 1/k = 11 604,51(2)  K/эВ
2,303 6644(36) • 1010	Гц/K	1 Гц = 6,626 068 96(33) • 10−34 Дж
3,166 815(36) • 10−6	EH/K	EH = 2R∞hc = 4,359 743 94(22) • 10−18 Дж
1,380 6504(24) • 10−16	эрг/K	1 эрг = 1• 10−7 Дж
3,297 6268(56) • 10−24	кал/K	1 калория = 4,1868 Дж
1,832 0149(31) • 10−24	кал/R	1 градус Ранкина = 4/9 K
1,039 9503(18) • 10−23	Фут фунт/R	1 Фут-фунт сила = 1,355 817 948 331 4004 Дж
0,695 0356(12)	см−1/K	1 см−1 = 1,986 445 501(99) • 10−23 Дж

Поскольку k есть константа пропорциональности между температурой и энергией, численное значение k зависит от выбора единиц изменения температуры и энергии. Шкала температур Кельвина выбиралась из того условия, чтобы интервал температур, в котором существует жидкая вода, равнялся 100 градусов. Малое численное значение k является отражением малости энергии в джоулях, необходимой для увеличения энергии частицы на 1 К. Как правило, в физических выражениях используется произведение kT как характерная энергия при температуре T. Если измерять температуру в энергетических единицах, подобно планковским единицам, тогда постоянная Больцмана будет не нужна вообще, равняясь точно 1. ^[5]

1. ↑ ^{а б} CODATA, 2006
2. ↑ Max Planck «Ueber das Gesetz der Energieverteilung im Normalspectrum» // Annalen der Physik. — 1901. — Т. 309. — № 3. — С. 553–63.. English translation: “On the Law of Distribution of Energy in the Normal Spectrum”.
3. ↑ ^{а б} Max Planck «The Genesis and Present State of Development of the Quantum Theory (Nobel Lecture)». — 2 June 1920.
4. ↑ Федосин С. Г. Физика и философия подобия от преонов до метагалактик, Пермь: Стиль-МГ, 1999, 544 стр., Табл.66, Ил.93, Библ. 377 назв. ISBN 5-8131-0012-1.
5. ↑ Kalinin, M; Kononogov, S «Boltzmann’s Constant, the Energy Meaning of Temperature, and Thermodynamic Irreversibility» // Measurement Techniques. — 2005. — Т. 48. — № 7. — С. 632–36.

traditio.wiki

Постоянная Больцмана

Больцман Людвиг (1844—1906) — великий австрийский физик, один из основоположников молекулярно-кинетической теории. В трудах Больцмана молекулярно-кинетическая теория впервые предстала как логически стройная, последовательная физическая теория. Больцман дал статистическое истолкование второго закона термодинамики. Им много сделано для развития и популяризации теории электромагнитного поля Максвелла. Борец по натуре, Больцман страстно отстаивал необходимость молекулярного истолкования тепловых явлений и принял на себя основную тяжесть борьбы с учеными, отрицавшими существование молекул.

В уравнение (4.5.3) входит отношение универсальной газовой постоянной R к постоянной Авогадро N_A. Это отношение одинаково для всех веществ. Оно называется постоянной Больцмана, в честь Л. Больцмана, одного из основателей молекулярно-кинетической теории.

Постоянная Больцмана равна:

(4.5.4)

Уравнение (4.5.3) с учетом постоянной Больцмана записывается так:

(4.5.5)

Физический смысл постоянной Больцмана

Исторически температура была впервые введена как термодинамическая величина, и для нее была установлена единица измерения — градус (см. § 3.2). После установления связи температуры со средней кинетической энергией молекул стало очевидным, что температуру можно определять как среднюю кинетическую энергию молекул и выражать ее в джоулях или эргах, т. е. вместо величины Т ввести величину Т* так, чтобы

Определенная таким образом температура связана с температурой, выражаемой в градусах, следующим образом:

Поэтому постоянную Больцмана можно рассматривать как величину, связывающую температуру, выражаемую в энергетических единицах, с температурой, выраженной в градусах.

Зависимость давления газа от концентрации его молекул и температуры

Выразив Е из соотношения (4.5.5) и подставив в формулу (4.4.10), получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:

(4.5.6)

Из формулы (4.5.6) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же.

Отсюда следует закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.

Средняя кинетическая энергия поступательного движения молекул прямо пропорциональна абсолютной температуре. Коэффициент пропорциональности — постоянную Больцмана k = 10^-23Дж/К — надо запомнить.

§ 4.6. Распределение максвелла

В большом числе случаев знание одних средних значений физических величин недостаточно. Например, знание среднего роста людей не позволяет планировать выпуск одежды различных размеров. Надо знать приблизительное число людей, рост которых лежит в определенном интервале. Точно так же важно знать числа молекул, имеющих скорости, отличные от среднего значения. Максвелл первым нашел, как эти числа можно определять.

Вероятность случайного события

В §4.1 мы уже упоминали, что для описания поведения большой совокупности молекул Дж. Максвелл ввел понятие вероятности.

Как неоднократно подчеркивалось, в принципе невозможно проследить за изменением скорости (или импульса) одной молекулы на протяжении большого интервала времени. Нельзя также точно определить скорости всех молекул газа в данный момент времени. Из макроскопических условий, в которых находится газ (определенный объем и температура), не вытекают с необходимостью определенные значения скоростей молекул. Скорость молекулы можно рассматривать как случайную величину, которая в данных макроскопических условиях может принимать различные значения, подобно тому как при бросании игральной кости может выпасть любое число очков от 1 до 6 (число граней кости равно шести). Предсказать, какое число очков выпадет при данном бросании кости, нельзя. Но вероятность того, что выпадет, скажем, пять очков, поддается определению.

Что же такое вероятность наступления случайного события? Пусть произведено очень большое число N испытаний (N — число бросаний кости). При этом в N‘ случаях имел место благоприятный исход испытаний (т. е. выпадение пятерки). Тогда вероятность данного события равна отношению числа случаев с благоприятным исходом к полному числу испытаний при условии, что это число сколько угодно велико:

(4.6.1)

Для симметричной кости вероятность любого выбранного числа очков от 1 до 6 равна .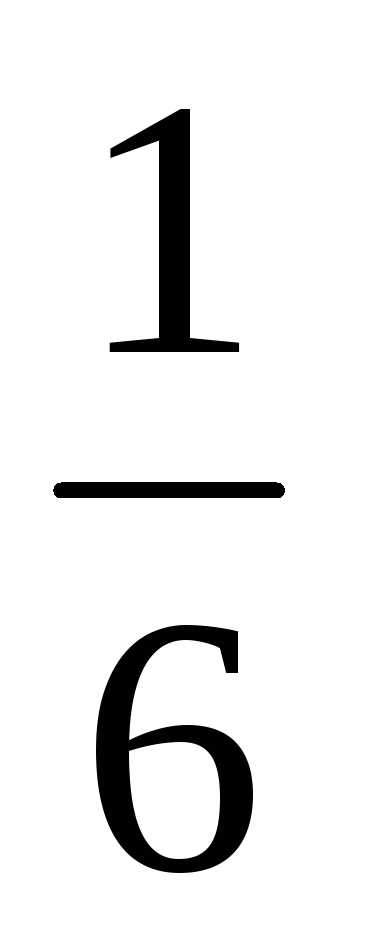

Мы видим, что на фоне множества случайных событий обнаруживается определенная количественная закономерность, появляется число. Это число — вероятность — позволяет вычислять средние значения. Так, если произвести 300 бросаний кости, то среднее число выпаданий пятерки, как это следует из формулы (4.6.1), будет равно: 300 ·= 50, причем совершенно безразлично, бросать 300 раз одну и ту же кость или одновременно 300 одинаковых костей.

Несомненно, что поведение молекул газа в сосуде гораздо сложнее движения брошенной игральной кости. Но и здесь можно надеяться обнаружить определенные количественные закономерности, позволяющие вычислять статистические средние, если только ставить задачу так же, как в теории игр, а не как в классической механике. Нужно отказаться от неразрешимой задачи определения точного значения скорости молекулы в данный момент и попытаться найти вероятность того, что скорость имеет определенное значение.

studfiles.net

Теплотехника

1. Предмет и методы термодинамики. Основные понятия и определения термодинамики.

Термодинамика — раздел, изучающий соотношения и превращения теплоты и других форм энергии. Термодинамика — это феноменологическая наука, опирающаяся на обобщения опытных фактов. Она изучает макроскопические системы, состоящие из огромного числа частиц —термодинамические системы. Процессы, происходящие в таких системах, описываются макроскопическими величинами, такими как давление или температура, которые не применимы к отдельным молекулам и атомам.

Термодинамические системы

В термодинамике изучаются физические системы, состоящие из большого числа частиц и находящиеся в состоянии термодинамического равновесия или близком к нему. Такие системы называются термодинамическими системами.

Термодинамическое равновесие

 Утверждается, что любая замкнутая термодинамическая система, для которой внешние условия остаются неизменными, с течением времени переходит в равновесное состояние, в котором прекращаются все макроскопические процессы.

Термодинамические параметры

Термодинамика не рассматривает особенности строения тел на молекулярном уровне. Равновесные состояния термодинамических систем могут быть описаны с помощью небольшого числа макроскопических параметров, таких как температура, давление, плотность, концентрации компонентов и т. д., которые могут быть измерены макроскопическими приборами. Описанное таким образом состояние называется макроскопическим состоянием, и законы термодинамики позволяют установить связь между макроскопическими параметрами.

Термодинамические процессы

При изменении внешних параметров или при передаче энергии в систему в ней могут возникать сложные процессы на макроскопическом и молекулярном уровне, в результате которых система переходит в другое состояние.

Нулевое начало термодинамики

названо так потому, что оно было сформулировано уже после того, как первое и второе начало вошли в число устоявшихся научных понятий. Оно утверждает, что изолированная термодинамическая система с течением времени самопроизвольно переходит в состояние термодинамического равновесия и остаётся в нём сколь угодно долго, если внешние условия сохраняются неизменными.

Первое начало термодинамики

Выражает универсальный закон сохранения энергии применительно к задачам термодинамики и исключает возможность создания вечного двигателя первого рода, то есть устройства, способного совершать работу без соответствующих затрат энергии.

Внутреннюю энергию U термодинамической системы можно изменить двумя способами, совершая над ней работу или посредством теплообмена с окружающей средой. Первое начало термодинамики утверждает, что теплота, полученная системой, идёт на увеличение внутренней энергии системы и на совершение этой системой работы, что можно записать как δQ = δA + dU. Здесь dU — полный дифференциал внутренней энергии системы, δQ — элементарное количество теплоты, переданное системе, аδA — бесконечно малая или элементарная работа, совершённая системой.

Второе начало термодинамики

Второе начало термодинамики задаёт ограничения на направление процессов, которые могут происходить в изолированной системе, и исключает возможность создания вечного двигателя второго рода.

Постулат Кельвина: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара». Такой круговой процесс называется процессом Томсона-Планка, и постулируется, что такой процесс невозможен.

Постулат Клаузиуса: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому»

 функция термодинамического состояния S=S(T,x,N), называется энтропией

2. Параметры и состояние системы.

Все макроскопические признаки, характеризующие систему и ее

отношение к окружающей среде, называются макроскопическими

параметрами или параметрами системы. Термодинамические параметры

– физические величины, характеризующие состояние термодинамической

системы (температура, объем, плотность, давление, масса, намагниченность,

электрическая поляризация, теплоемкость при постоянном объеме и другие),

т.е. любые признаки, имеющие количественную меру и относящиеся к

системе в целом или к ее макроскопическим частям (кроме характеристик

потоков энергии и массы, в размерность которых входит время). Свойства,

заимствованные термодинамикой у физики, химии, техники

рассматриваются в зависимости от типичной термодинамической

характеристики – температуры.

Величины, количественно выражающие термодинамические

параметры (свойства), называют также термодинамическими переменными.

Поскольку все они взаимосвязаны, их разделяют на независимые переменные

и функции, что эквивалентно делению математических величин на аргументы

и функции. Параметры, поддающиеся прямому измерению, считаются

основными (температура, давление, плотность, объем, концентрация).

Внутренняя энергия, энтропия, энтальпия и другие аналогичные параметры

считаются функциями основных параметров. Так как параметры

взаимосвязаны, то для характеристики состояния системы достаточно

задать только определенное число переменных. Эти переменные называют

независимыми, остальные рассматриваются как функции независимых

переменных. Таким образом, одна и та же характеристика в зависимости

от контекста может называться термодинамической величиной,

переменной, параметром, функцией или просто свойством.

Параметры разделяют на внешние и внутренние.

Внешние параметры – это величины, определяемые положением не входящих в систему тел – (объем, магнитная индукция, напряженность электрического поля)

Внешние параметры являются функциями координат внешних тел.

Внутренние параметры – это величины, определяемые совокупным

движением и распределением в пространстве входящих в систему частиц

(температура, давление, внутренняя энергия, плотность, поляризованность,

намагниченность)

Равновесные и неравновесные состояния:

Термодинамически равновесное состояние тела или системы это такое состояние теплового и механического равновесия элементов тела или системы, которое без внешнего воздействия может сохраняться сколь угодно долго.

Равновесная система это система тел, находящихся в термодинамическом равновесии, в противном случае она будет называться неравновесной системой. Так, без учета гравитационных сил, равновесное состояние тела или системы есть такое их состояние, при котором по всему их объему давления и температуры имеют одинаковые значения. Равенство только давления во всех точках обусловливает механическое равновесие, равенство температур – термическое равновесие.

3. Тепловой процесс и его свойства

Тепловой процесс (термодинамический процесс) — изменение макроскопического состояния термодинамической системы.

Система, в которой идёт тепловой процесс, называется рабочим телом.

Тепловые процессы можно разделить на равновесные и неравновесные.

Прямой и обратимый процессы:

Обратимый – процесс, при котором система проходит все те же состояния что и в прямом направлении, но в обратном порядке, при этом остаточных изменений в окружающей среде не наблюдается.

Круговые процессы– при которых система из начального состояния проходит ряд последовательных состояний и в него же возвращается.

4. Внутренняя энергия термодинамической системы.

Внутренняя энергия термодинамической системы (обозначается как E или U) — это сумма энергий теплового движения молекул и межмолекулярных взаимодействий.

Изменение внутренней энергии системы при переходе её из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе, то есть, оно зависит только от начального и конечного состояния системы.

5. Теплота и работа термодинамического процесса. Физическая сущность, выражение теплоты и работы через параметры состояния системы. Графическое определение теплоты и работы по диаграммам в координатах P–V и T-S.

Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется количеством теплоты или просто теплотой.

Термодинамическая работа — способ передачи энергии, связанный с изменением внешних параметров системы. Определяется, как:

Теплота и работа определяются для разных видов процессов по первому закону термодинамики

Q = Δu + l

Для изохорного:

Q=Cv ΔT

Cv – изохорная теплоемкость

L=0

Δu=Cv ΔТ

Для изобарного:

Q=Cp ΔТ = Δi

i – Энтальпия

L=p ΔV

Δu=qV

Для изотермического:

Δu=Cv ΔТ

Q=L

L=RTln(p1/p2)

Для адиабатного

Q=0

L=- Δu

Δu=Cv ΔТ

6. Идеальный газ- газ, молекулы которого представляют собой материальную точку ,а силы взаимодействия между молекулами отсутствуют.

Основные законы идеального газа

1)Бойль-Мариотта

Т=const p1v1=p2v2 pv=const

2)Гей-Люсака

P=const T1/v1=T2/v2 T/v=const

3)Шарль

V=const p1/T1=p2/T2 p/T=const

4)Клапейрон

P1v1/T1=p2v2/T2 pv/T=const

Pv/T=R

R-газовая постоянная

Ro-универсальная газовая постоянная =8,314 Дж/моль К

PV=RT – уравнение состояния идеального газа,уравнение Клапейрона

PV=(m/(мю)) Ro T – основное уравнение состояния идеального газа , уравнение Менделеева- Клапейрона.

7 вопрос

Теплоемкость тела — это физическая  величина, определяемая отношением количества теплоты, поглощенной телом при нагревании, к изменению его температуры:  

Физический смысл  теплоемкости тела:  теплоемкость тела  равна количеству теплоты, поглощенному телом при нагревании или  выделенному при его охлаждении  на 1К.

Так как теплоемкости переменные величины, то различают среднюю и истинную теплоемкости.  Под средней теплоемкостью понимают отношение количества теплоты q, подведенной к единице количества вещества (газа), к изменению его температуры от t1 до t2при условии, что разность температур t2 – t1 является величиной конечной.  Средние массовая, объемная и мольная теплоемкости соответственно обозначаются через cm, cm’ и m. Из определения средней теплоемкости следует, что если температура газа повышается от t1 до t2 то его средняя теплоемкость [кДж/(кг*К)]

Под истинной теплоемкостью понимают теплоемкость газа, соответствующую бесконечно малому изменению температуры газа, соответствующую бесконечно малому изменению температуры dt, т. е.

c = dq/dt,

откуда dq = cdt.

Удельная   теплоемкость  —  это   способность  разных   веществ к поглощению теплоты при их нагревании. Удельная  теплоемкость вещества  определяется  отношением количества теплоты, полученной им при нагревании, к массе вещества и изменению его температуры, если :

8 вопрос

соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера) :  Cp = CV + R. ИЛИ БОЛЕЕРАЗВЕРНУТО Теплоёмкость идеального газа Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются. Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.  c = Q / (mΔT).  Во многих случаях удобно использовать молярную теплоемкость C:  C = M · c,  где M – молярная масса вещества. Определенная таким образом теплоемкость не является однозначной характеристикой вещества. Согласно первому закону термодинамики изменение внутренней энергии тела зависит не только от полученного количества теплоты, но и от работы, совершенной телом. В зависимости от условий, при которых осуществлялся процесс теплопередачи, тело могло совершать различную работу. Поэтому одинаковое количество теплоты, переданное телу, могло вызвать различные изменения его внутренней энергии и, следовательно, температуры. Такая неоднозначность определения теплоемкости характерна только для газообразного вещества. При нагревании жидких и твердых тел их объем практически не изменяется, и работа расширения оказывается равной нулю. Поэтому все количество теплоты, полученное телом, идет на изменение его внутренней энергии. В отличие от жидкостей и твердых тел, газ в процессе теплопередачи может сильно изменять свой объем и совершать работу. Поэтому теплоемкость газообразного вещества зависит от характера термодинамического процесса. Обычно рассматриваются два значения теплоемкости газов: CV – молярная теплоемкость в изохорном процессе (V = const) и Cp – молярная теплоемкость в изобарном процессе (p = const). В процессе при постоянном объеме газ работы не совершает: A = 0. Из первого закона термодинамики для 1 моля газа следует  QV = CVΔT = ΔU.  Изменение ΔU внутренней энергии газа прямо пропорционально изменению ΔT его температуры. Для процесса при постоянном давлении первый закон термодинамики дает:  Qp = ΔU + p(V2 – V1) = CVΔT + pΔV,  где ΔV – изменение объема 1 моля идеального газа при изменении его температуры на ΔT. Отсюда следует:  Отношение ΔV / ΔT может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:  pV = RT,  где R – универсальная газовая постоянная. При p = const Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера) :  Cp = CV + R.

Газовая постоянная численно равна работе расширения 1 моля идеального газа под постоянным давлением при нагревании на 1 K.  R = pV/T = 1.01•10⁵•22.4•10-3/273[Па•м³/моль]/K =8.31(44) Dж/(моль•K) 

Универсальная газовая постоянная — универсальная, фундаментальная физическая константа R, равная произведению постоянной Больцмана k на постоянную Авогадро

  

Физический смысл: Газовая постоянная численно равна работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К

В системе СГС Газовая постоянная равна :

Удельная Газовая постоянная равна :

Показатель адиабаты (иногда называемый коэффициентом Пуассона) — отношение теплоёмкости при постоянном давлении () к теплоёмкости при постоянном объёме (). Иногда его ещё называют фактором изоэнтропийного расширения. Обозначается греческой буквой (гамма) или (каппа). Буквенный символ в основном используется в химических инженерных дисциплинах. В теплотехнике используется латинскаябуква ^[1].

9 вопрос

Смесью газов называется совокупность нескольких разнородных газов, которые при рассматриваемых условиях не вступают друг с другом в химические реакции.

Смесь газов – гомогенная термодинамическая система (внутри которой нет поверхностей раздела, отделяющих друг от друга макроскопические части системы, различающиеся по своим свойствам и составу).

Парциальным давлением P_i i-го газа в смеси называется давление, под которым находился бы этот газ, если бы из смеси были удалены все остальные газы, а V и T остались прежними.

Закон Дальтона — Давление смеси газов, не взаимодействующих друг с другом химически, равно сумме парциальных давлений этих газов.

  

Для того чтоб понять, что представляет из себя закон Дальтона , рассмотрим для этого воздух в комнате. Он представляет собой смесь нескольких газов: азота (80%), кислорода (20%). Парциальное давление каждого из этих газов — это давление, которое имел бы газ, если бы он один занимал весь объем. К примеру, если бы все газы, кроме азота, удалили из комнаты, то давление того, что осталось, и было бы парциальным давлением азота. Закон Дальтона утверждает, что общее давление всех газов вместе взятых равно сумме парциальных давлений каждого газа в отдельнсти. (Строго говоря, закон применим только к идеальным газам, но с достаточно хорошим приближением он описывает также и реальные газы.)

10 вопрос

Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:

Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.

Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме: 

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила названиевечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.

Применим первый закон термодинамики к изопроцессам в газах.

1. В изохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно, 

   Q = ΔU = U (T2) – U (T1).

2. Здесь U (T₁) и U (T₂) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).

3. В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением 

   A = p (V2 – V1) = p ΔV.

4. Первый закон термодинамики для изобарного процесса дает: 

   Q = U (T2) – U (T1) + p (V2 – V1) = ΔU + p ΔV.

5. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T₂ < T₁; внутренняя энергия убывает, ΔU < 0.

6. В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.

Первый закон термодинамики для изотермического процесса выражается соотношением 

Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.

Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называются адиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими.

В адиабатическом процессе Q = 0; поэтому первый закон термодинамики принимает вид 

По своему физическому смыслу первое начало термодинамики представляет собой закон сохранения (изменения) энергии в термодинамике. Если, согласно закону изменения энергии в механике, работа неконсервативных сил равна приращению механической энергии системы (в частности, имеющая отрицательный знак работа сил трения равна уменьшению механической энергии системы), то согласно первому началу термодинамики, приращение внутренней энергии термодинамической системы равно сумме работы внешних сил, совершенной над системой, и энергии, переданной системе путём теплопередачи. Энтальпия (от греч. enthalpo – нагреваю) — это свойство вещества, указывающее количество энергии, которую можно преобразовать в теплоту. Энтальпия — это термодинамическое свойство вещества, которое указывает уровень энергии, сохраненной в его молекулярной структуре. Это значит, что, хотя вещество может обладать энергией на основании температуры и давления, не всю ее можно преобразовать в теплоту. Часть внутренней энергии всегда остается в веществе и поддерживает его молекулярную структуру. Часть кинетической энергии вещества недоступна, когда его температура приближается к температуре окружающей среды. Следовательно, энтальпия — это количество энергии, которая доступна для преобразования в теплоту при определенной температуре и давлении. Единицы энтальпии — британская тепловая единица или Джоуль для энергии и Btu/lbm или Дж/кг для удельной энергии. 11 вопрос

13)Анализ изобарного термодинамического процесса.

Q=Cp (Т2-Т1)

Cp-изобарная теплоемкость

Ср=Cv+R – уравнение Майера

R- газовая постоянная- работа одного кг идеального газа в изобарном процессе при изменении температуры на 1 градус

Ro – универсальная газовая постоянная – работа одного моля идеального газа в изобарном процессе при изменении температуры на 1 градус

Δu=Cv (Т2-Т1)=qv

Q=i

i-энтальпия (функция состояния) Дж/кг Дж/моль

i=u+pv

L=p(v2-v1)

Δs=Cp ln(T2/T1)

изобара

14)Анализ Адиабатического процесса

Q=0

L=-Δu

P1V1^k=P2V2^k

PV^k=const

K=Cp/Cv К-показатель адиабаты

Q=Cад.(дельта)Т Cад.=0

Δu=Cv (T2-T1)

L=(R/(k-1))*(T1-T2)

Δs=0

15)Анализ политропного процесса

Обобщающий термодинамический процесс

P1V1ⁿ=P2V2ⁿ

PVⁿ=const n=(Cn-Cp)/(Cn-Cv) n-показатель политропы

Q=Cn ΔТ

L=(R/(n-1))*(T1-T2)

Δu=Cv(T2-T1)

Δs=Cv*((n-k)/(n-1))ln(T2/T1)

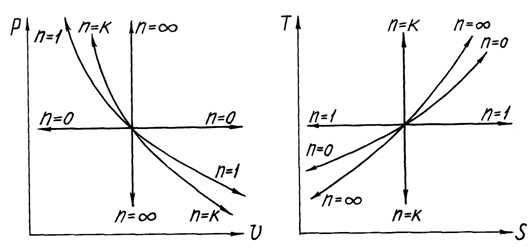
16)Второй закон термодинамики

А)Теплота самопроизвольно передается только в одном направлении: из области с большей температурой(теплоотдатчик) в область с меньшей температурой(теплоприемник). Чтобы передать теплоту в обратном направлении нужно приложить энергию(совершить работу)

Б)Невозможно в тепловом двигателе превратить всю теплоту в работу, так как часть ее должна быть отдана теплоприемнику.Таким образом термический КПД любого цикла не может быть равен единице

Qподведенная=Lполная+Qотведенная

КПД=Lполная/Qподведенная=(q подведенная-Iq отведеннаяI)/q подведенная

КПД=1-(q2/q1)

Энтропия- функция состояния термодинамической системы, т.е. непрерывная функция двух аргументов

S, s Дж/(кг К)

dS>=0 только для изолированной системы

мера упорядоченности системы (беспорядка)

dS=dQ/T

dQ=TdS

TdS=Cv(дельта)T+R(дельта)Т

Обратимый цикл Карно в тепловой машине, работающей по принципу Карно, имеются три тела: холодильник, нагреватель, рабочее тело (газ). Изменение энтропии газа в тепловой машине так как газ возвращается в исходное состояние. Изменение энтропии нагревателя: 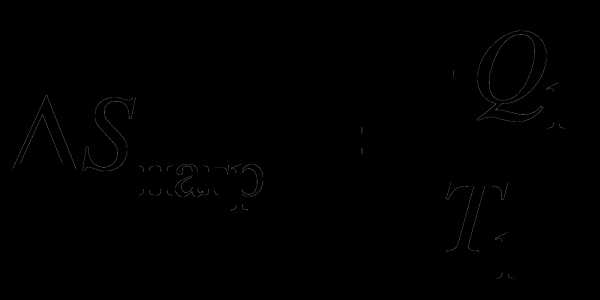. Для холодильника: 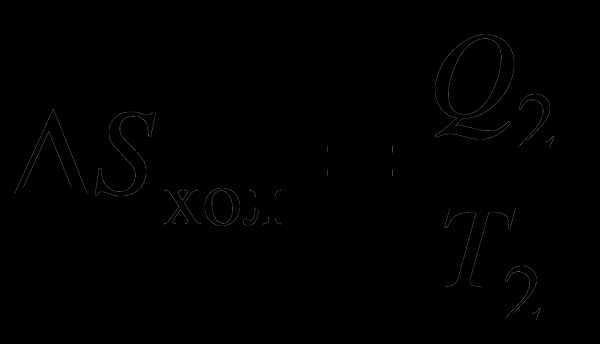. . .    т.е. S – константа. Таким образом, мы пришли к выражению называемому равенство Клаузиуса. Необратимый цикл Мы знаем, что т.е. 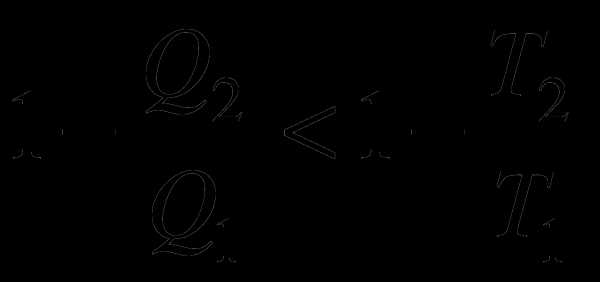Отсюда тогда . Таким образом,   Это выражение называют неравенством Клаузиуса: при любом необратимом процессе в замкнутой системе энтропия возрастает (dS > 0).

studfiles.net

Определения по МКТ и термодинамике

АБСОЛЮТНАЯ ВЛАЖНОСТЬ – физическая величина, равная отношению массы водяного пара в воздухе к его объему.  Практической единицей А.в. является .Иногда под А.в. понимают парциальное давление водяного пара. В этом случае ее измеряют в паскалях (Па).

АБСОЛЮТНАЯ ТЕМПЕРАТУРА – температура, измеряемая по абсолютной термодинамической шкале, не зависящей от свойств термометрического вещества. Отсчитывается от абсолютного нуля. Единица А.т. в СИ Кельвин (К).

АБСОЛЮТНЫЙ НУЛЬ – начало отсчета абсолютной температуры; находится на 273.16 К ниже температуры тройной точки воды, для которой принято значение 0.01^оС. При А.н. прекращается поступательное и вращательное движение атомов и молекул, но они находятся не в покое, а в состоянии “нулевых” колебаний. Из законов термодинамики следует, что А.н. практически недостижим.

АВОГАДРО ЗАКОН – один из основных законов идеальных газов: в равных объемах различных газов при одинаковой температуре и давлении содержится одинаковое число молекул. Открыт в 1811 году итал. физиком А.Авогадро(1776-1856).

АВОГАДРО ПОСТОЯННАЯ (число) – число частиц в единице количества вещества (в 1 моль): N_A=6,022^. 10²³ моль^-1.

АГРЕГАТНЫЕ СОСТОЯНИЯ ВЕЩЕСТВА – состояния одного и того же вещества, отличающиеся характером теплового движения частиц. Обычно различают 3 А.с.в.: газ, жидкость и твердое тело; иногда сюда относят и плазменное состояние. Вещество в любом А.с. существует при определенных внешних условиях  (температура, давление), изменение которых приводит к переходу из одного А.с. в другое.

АДИАБАТИЧЕСКИЙ (АДИАБАТНЫЙ) ПРОЦЕСС – модель термодинамического процесса, при котором отсутствует теплообмен между рассматриваемой системой и окружающей средой. Реальный термодинамический процесс может рассматриваться как А., если он происходит либо в теплоизолирующей оболочке, либо настолько быстро, чтобы теплообмен не успел произойти.

АДИАБАТА – линия, изображающая на любой термодинамической диаграмме равновесный адиабатический  процесс. Уравнение а. для идеального газа имеет вид  – показатель адиабаты, а с_p  и  с_v теплоемкости при постоянном давлении и объеме соответственно.

АМОРФНОЕ СОСТОЯНИЕ – состояние твердого вещества, при котором отсутствует дальний порядок  расположения молекул. Поэтому а. вещество обладает изотропией, т.е. имеет одинаковые физические свойства по всем направлениям, и не имеет определенной точки плавления.

АНЕРОИД –  барометр-анероид, прибор для измерения атмосферного давления, приемной частью которого служит металлическая коробка, внутри которой создано сильное разряжение. При изменении атм. давления изменяется деформация коробки, которая с помощью связанной с ней пружины и системы рычагов, вызывает поворот стрелки-указателя.

АНИЗОТРОПИЯ – зависимость физических свойств вещества от направления (в противоположность изотропии). Связана с внутренним упорядоченным строением сред и обнаруживается в явлениях упругости, тепло- и электропроводности, распространения звука и света в твердых телах. Может быть присуща и физическому пространству при наличии электромагнитного, гравитационного и других полей.

АТМОСФЕРНОЕ ДАВЛЕНИЕ – давление, которое оказывает атмосфера Земли на все находящиеся в ней предметы. Определяется весом вышележащего столба воздуха и является наиболее важной величиной, описывающей состояние земной атмосферы. Единицы А.д. в СИ – Па, мм рт.ст. Нормальное А.д. равно 760 мм рт.ст. или 1013 гПа.

БАРОМЕТР – прибор для измерения атмосферного давления. Наиболее часто встречаются деформационные Б., к которым, например, относится Б.-анероид (1844 г., Л.Види). В таком Б. при изменении атмосферного давления прогибается мембрана, закрывающая коробку, из которой откачан воздух, при этом происходит отклонение стрелки, связанной с мембраной через систему рычагов. Действие жидкостного Б. (например, ртутный Б. Э.Торричелли, 1644 г.) основано на уроавновешивании сиалы атмосферного давления весом столба жидкости.

БЛИЖНИЙ ПОРЯДОК – упорядоченное расположение атомов или молекул в пределах расстояний, близких к межатомным; характерен для аморфных веществ и некоторых жидкостей. (Ср.дальний порядок).

БОЙЛЯ-МАРИОТТА ЗАКОН – один из законов идеального газа: для данной массы данного газа при постоянной температуре произведение давления на объем есть величина постоянная. Формула: pV=const. Описывает изотермический процесс.

БОЛЬЦМАНА ПОСТОЯННАЯ – одна из основных физических постоянных, равная отношению универсальной газовой постоянной R к Авогадро постоянной N_A .Б.п. .Входит в ряд важнейших соотношений статистической физики: связывает ср. кинетическую энергию частиц и температуру, энтропию физической системы и ее термодинамическую вероятность.

БРОУНОВСКОЕ ДВИЖЕНИЕ – беспорядочное движение мелких макроскопических частиц, взвешенных в жидкости или газе, происходящее под влиянием теплового движения молекул. Наглядное подтверждение молекулярно-кинетической теории. Открыто Р.Броуном в 1827 г. Объяснено А. Эйнштейном и М. Смолуховским в 1905 г. Теория проверена в опытах Ж. Перрена в 1906-11 г.

ВАКУУМ –  состояние заключенного в сосуд газа, имеющего давление значительно ниже атмосферного. В зависимости от соотношения между длиной свободного пробега атомов или молекул и линейным размером сосуда различают сверхвысокий, высокий, средний и низкий вакуум.

ВЛАЖНОСТЬ ВОЗДУХА – явление наличия в воздухе водяного пара. Описывается физическими величинами абсолютной иотносительной В., которые измеряются  гигрометрами.

ВНУТРЕННЯЯ ЭНЕРГИЯ – энергия тела, зависящая только от его внутреннего состояния; складывается из энергии беспорядочного (теплового) движения атомов, молекул или других частиц и энергии внутриатомных и межмолекулярных движений и взаимодействий. (См.первый закон термодинамики). В МКТ энергия внутриатомных частиц и их взаимодействий не учитывается.

ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ – один из основных законов термодинамики, согласно которому невозможен периодический процесс единственным результатом которого является совершение работы, эквивалентной количеству теплоты, полученному от нагревателя. Другая формулировка: невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от менее нагретого тела к более нагретому. В.з.т. выражает стремление системы, состоящей из большого количества хаотически движущихся частиц, к самопроизвольному переходу из состояний менее вероятных в состояния более вероятные. Еще один способ формулировки в.з.т: невозможно создание вечного двигателя второго рода.

ГАЗ – одно изагрегатных состояний вещества, в котором его частицы слабо связаны между собой силами молекулярного притяжения и движутся хаотически, заполняя весь возможный объем, поэтому газы легко сжимаемы, летучи. Для описания свойств газа используются модели с различной степенью приближения к реальности. Так при малых плотностях Г. практически можно считать идеальным газом. Ср.жидкость, твердое тело. См. также Клапейрона-Менделеева уравнение.

ГАЗОВАЯ ПОСТОЯННАЯ УНИВЕРСАЛЬНАЯ (R) – одна из основных физических постоянных, входящая в уравнение состояния (См. Клапейрона-Менделеева уравнение). R=(8,31441±0,00026) Дж/(моль·К). Физический смысл: работа расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 К.

ГАЗОВЫЙ ТЕРМОМЕТР – прибор для измерения температуры, действие которого основано на зависимости давления или объема газа от температуры.

ГЕЙ-ЛЮССАКА ЗАКОН – один из законов идеального газа: для данной массы данного газа при постоянном давлении отношение объема к абсолютной температуре есть величина постоянная:  (или: объем прямо пропорционален абсолютной температуре: , где α – температурный коэффициент давления). Описывает изобарный процесс.

ГИГРОМЕТР – прибор для измеренияабсолютной  или относительной влажности воздуха. Г. подразделяют на весовые (для определения абсолютной влажности), конденсационные (для определения точки росы), волосовые (относительная влажность), а также Г. психрометрические или психрометры (относительная влажность).

ГРАДУС ЦЕЛЬСИЯ – внесистемная единица температуры по Международной практической температурной шкале, где температура тройной точки воды равна 0,01 градуса Цельсия, а температура кипения при нормальном атмосферном давлении 100 градусов Цельсия.

ДАЛЬНИЙ ПОРЯДОК – упорядоченное расположение частиц (атомов или молекул) во всем объеме тела; характерен для кристаллических веществ. Ср.ближний порядок.

ДАЛЬТОНА ЗАКОН – один из основных законов идеального газа: давление смеси химически не взаимодействующих газов равно сумме парциальных давлений этих газов.

ДЕФЕКТЫ В КРИСТАЛЛАХ – несовершенства кристаллического строения, нарушения строгого периодического расположения частиц ( атомов, молекул, ионов) в узлах кристаллической решетки. К ним относятся вакансии (точечные дефекты), дислокации (линейные дефекты), объемные дефекты: трещины, поры, раковины и т.д. Оказывают существенное влияние на физические свойства кристаллов.

ДИСЛОКАЦИИ – линейные дефекты кристаллической решетки, нарушающие правильное чередование атомных плоскостей. В двух измерениях имеют размеры порядка размеров атома, а в третьем – могут проходить через весь кристалл.

ДИССОЦИАЦИЯ – процесс распада молекул на более простые части – атомы, группы атомов или ионы. Может происходить при повышении температуры (термическая Д.), в растворе электролитов (электролитическая Д.) и под действием света (фотохимическая Д.).

ДИФФУЗИЯ – процесс распространения вещества в какой-либо среде в направлении убывания его концентрации, обусловленное тепловым движением атомов, молекул, ионов и др. более крупных частиц. (Посмотреть фильм “Диффузия“)

ЖИДКИЕ КРИСТАЛЛЫ – состояние вещества, в котором обнаруживаются структурные свойства, промежуточные между твердым кристаллом ижидкостью. Образуются в веществах с молекулами продолговатой формы, взаимная ориентация которых обусловливает анизотропию их физических свойств. Применяются в технике, биологии и медицине.

ЖИДКОСТНЫЙ ТЕРМОМЕТР – прибор для измерения температуры, действие которого основано на тепловом расширении жидкости. Ж.т. в зависимости от температурной области заполняют ртутью, этиловым спиртом и др. жидкостями.

ЖИДКОСТЬ – одно из агрегатных состояний вещества, промежуточное между твердым и газообразным. Ж., как и твердое тело, обладает малой сжимаемостью, большой плотностью и в то же время. подобно газу, характеризуется изменчивостью формы (легко течет). Молекулы ж., как и частицы твердого тела, совершают тепловые колебания, однако их положение равновесия время от времени меняется, что и обеспечивает текучесть жидкости.

ИДЕАЛЬНЫЙ ГАЗ – мысленная модель газа, в которой силами взаимодействия между частицами и размерами этих частиц можно пренебречь. Т.е. частицы принимаются за материальные точки, а все взаимодействие сводится к их абсолютно упругим ударам. Разреженные газы при температурах, далеких от температуры конденсации, близки по своим свойствам к И.г. Уравнением состояния служит Клапейрона – Менделеева уравнение.

ИЗОБАРА – линия постоянного давления, изображающая на диаграмме состояния равновесный  изобарный процесс.

ИЗОБАРНЫЙ ПРОЦЕСС (изобарический) – мысленная модель термодинамического процесса, протекающего при постоянном давлении. Для идеальных газов описывается законом Гей-Люссака.

ИЗОПРОЦЕССЫ – физические процессы, протекающие при постоянстве какого-либо из описывающих состояние системы параметоров (см. изобарный, изотермический, изохорный процесс).

ИЗОТЕРМА – линия постоянной температуры, изображающая на диаграмме состояния равновесный изотермический процесс.

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС – модель термодинамического процесса, протекающего при постоянной температуре. Напр., кипение химически однородной жидкости, плавление химически однородного кристалла при постоянном внешнем давлении. Для идеальных газов описывается Бойля-Мариотта законом. Ср.изобарный, изохорный, адиабатный процесс.

ИЗОТРОПИЯ, изотропность – одинаковость физических свойств во всех направлениях. Связано с отсутствием упорядоченного внутреннего строения сред и присуща газам, жидкостям (кроме жидких кристаллов) и аморфным телам. Ср. анизотропия.

ИЗОХОРА – линия постоянного объема, изображающая на диаграмме состояния равновесный изохорный процесс.

ИЗОХОРНЫЙ ПРОЦЕСС, изохорический процесс – термодинамический процесс, происходящий при постоянном объеме системы. Для идеальных газов описывается Шарля законом.

ИСПАРЕНИЕ – процесс парообразования со свободной поверхности жидкости при температуре ниже температуры кипения. И. с поверхности твердых тел называют возгонкой. (Ср. кипение, парообразование).

КАЛОРИМЕТР – прибор для определения различных калориметрических величин: теплоемкости, теплоты сгорания, теплоты парообразования и т.д.

КАПИЛЛЯР – узкий сосуд с характерным размером поперечного сечения менее 1 мм.

КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ – явления, вызываемые влиянием сил межмолекулярного взаимодействия на равновесие и движение свободной поверхности жидкости, поверхности раздела несмешивающихся жидкостей и границ жидкостей с твердыми телами. Например, поднятие или опускание жидкости в очень тонких трубках (капиллярах) и в пористых средах.

КАРНО ЦИКЛ – мысленная модель обратимого кругового процесса, состоящего из двух изотермических и двух адиабатных процессов. При изотермическом расширении (температура нагревателя T_н) рабочему телу (идеальному газу) сообщается количество теплоты Q_н, а при изотермическом сжатии (температура холодильника Т_х) – отводится количество теплоты Q_x. Кпд К.ц. не зависит от природы рабочего тела и равен .

КИПЕНИЕ – процесс интенсивного парообразования не только со свободной поверхности жидкости, но и по всему ее объему внутрь образующихся при этом пузырьков пара. Температура К. зависит от природы жидкости и внешнего давления и находится между тройной точкой и критической температурой (см. критическое состояние).

КЛАПЕЙРОНА-МЕНДЕЛЕЕВА УРАВНЕНИЕ – уравнение состояния идеального газа:  ,где p– давление, V– объем, T – абсолютная температура, m – масса, M – молярная масса газа, R – универсальная газовая постоянная. Из К.-М.у. вытекают законы Авогадро, Бойля-Мариотта, Шарля и Гей-Люссака.

КОЛИЧЕСТВО ВЕЩЕСТВА – количество молей, физическая величина, равная отношению числа структурных элементов (напр., атомов, молекул и т.д.) к Авогадро числу. Единица в СИ – моль.

КОЛИЧЕСТВО ТЕПЛОТЫ –физическая величина, равная части внутренней энергии, переданной в процессетеплообмена от одного макроскопического тела к другому без совершения работы. Единица в СИ – джоуль.

КОНДЕНСАЦИЯ – процесс перехода вещества из газообразного состояния в жидкое или кристаллическое. Сопровождается выделением теплоты. Процесс обратный парообразованию (испарению, кипению и возгонке). Играет важную роль в природе (образование облаков, тумана, росы, инея).

КРИСТАЛЛИЗАЦИЯ – процесс образования кристаллов из паров, растворов, расплавов в специальных установках или при химических реакциях. Играет важную роль в природе ( напр., образование минералов) и технике (выплавка металлов, получение полупроводниковых, оптических и др. материалов, нанесение тонкопленочных покрытий и т.д. В школьном курсе часто используется как синоним отвердевания, т.е. процесс, обратный плавлению.

КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА – мысленная модель, дающая возможность представить расположение атомов, ионов и молекул, характеризующееся периодической повторяемостью в пространстве и присущее твердым телам (кристаллам). Период К.р. составляет 0,1-0,5 нм для простых соединений, 1 – 2 нм для сложных неорганических и органических соединений, 10 нм для белков и вирусов.

КРИСТАЛЛЫ – твердые тела с упорядоченным взаимным расположением образующих их частиц – атомов, ионов, молекул. См. монокристаллы, поликристаллы.

КРИТИЧЕСКОЕ СОСТОЯНИЕ – состояние вещества, при котором две различные фазы (жидкая и газообразная), находящиеся между собой в равновесии, становятся тождественными по всем своим свойствам. Характеризуется критическим Давление, температуру и объемом, соответствующие К.с. называют критическими..

КРУГОВОЙ ПРОЦЕСС – цикл, модель термодинамического процесса, в результате которого рабочее тело возвращается в первоначальное состояние. Пример – Карно цикл.

МАЙЕРА УРАВНЕНИЕ – соотношение, устанавливающее связь между молярными теплоемкостями идеального газа при постоянном давлении с_p и при постоянном объеме с_V:  с_P =с_V + R. где R – газовая постоянная.

МАКСВЕЛЛА РАСПРЕДЕЛЕНИЕ – закон распределения по скоростям молекул идеального газа, находящегося в состоянии термодинамического равновесия.

МАНОМЕТР – прибор для измерения давления жидкостей и газов. Различают М. для измерения абслютного давления, отсчитываемого от нуля, и М. для измерения избыточного давления (разности между абсолютным и атмосферным давлением). Различают жидкостные, поршневые, деформационные и пружинные М. в зависимости от принципа действия.

МЕНИСК – искривленная поверхность жидкости в узкой трубке (капилляре) или между близко расположенными твердыми стенками (см.капиллярные явления).

МОДУЛЬ ЮНГА – постоянная для данного материала физическая величина, являющаяся коэффициентом пропорциональности между механическим напряжением и относительным удлинением в Гука законе: . М.Ю. Е равен механическому напряжению, возникающему в деформированном теле при увеличении его длины в 2 раза. Единица измерения в СИ – паскаль.

МОЛЕКУЛА – наименьшая устойчивая частица вещества, обладающая всеми химическими свойствами и состоящая из одинаковых (простое вещество) или разных (сложное вещество) атомов, объединенных химическими связями. Ср. атом.

МОЛЕКУЛЯРНАЯ МАССА – масса молекулы, выраженная в атомных единицах массы. Ср. молярная масса.

МОЛЕКУЛЯРНАЯ ФИЗИКА – раздел физики, изучающий физические свойства тел, особенности агрегатных состояний вещества и процессы фазовых переходов в зависимости от молекулярного строения тел, сил межмолекулярного взаимодействия и характера теплового движения частиц (атомов, ионов, молекул). См. статистическая физика, термодинамика.

МОЛЯРНАЯ МАССА – масса одного моля вещества; скалярная величина, равная отношению массы тела к количеству вещества (числу молей), которое в нем содержится. В СИ м.м. равна молекулярной массе вещества, умноженной на 10^-3 и измеряется в килограммах на моль (кг/моль).

МОНОКРИСТАЛЛЫ – одиночные кристаллы с единой кристаллической решеткой. Образуются в природных условиях или искусственно выращиваются из расплавов, растворов, парообразной или твердой фазы. Ср. поликристаллы.

НАСЫЩЕННЫЙ ПАР – пар, находящийся в динамическом равновесии с жидкой или твердой фазой. Под динамическим равновесием понимают такое состояние, при котором среднее число молекул, покидающих жидкость (твердое тело), равно среднему числу молекул пара, возвращающихся в жидкость (твердое тело) за то же время.

НЕОБРАТИМЫЙ ПРОЦЕСС – процесс, который может самопроизвольно протекать только в одном направлении. Все реальные процессы являются н.п. и в замкнутых системах сопровождаются возрастанием энтропии. См. обратимый процесс, второй закон термодинамики.

НОРМАЛЬНЫЕ УСЛОВИЯ – стандартные физические условия, определяемые давлением P=101325 Па (760 мм рт.ст.) и абсолютной температурой T=273,15 К.

ОБРАТИМЫЙ ПРОЦЕСС – модель процесса, для которого возможен обратный процесс, последовательно повторяющий все промежуточные состояния рассматриваемого процесса. Обратимым является лишь равновесный процесс. Пример – Карно цикл. Ср. необратимый процесс.

ОТНОСИТЕЛЬНАЯ ВЛАЖНОСТЬ – физическая величина, равная отношению плотности (упругости) водяного пара, содержащегося в воздухе, к плотности (упругости) насыщенного пара при той же температуре. Выражается в процентах. Ср. абсолютная влажность.

ПАР – вещество в газообразном состоянии в условиях, когда путем сжатия можно добиться равновесия с тем же веществом в жидком или твердом состоянии, т.е. при температурах и давлениях ниже критических (см. критическое состояние). При низких давлениях и высоких температурах свойства пара приближаются к свойствам идеального газа.

ПАРАМЕТР СОСТОЯНИЯ, термодинамический параметр – физическая величина, которая служит в термодинамике для описания состояния системы. Напр., давление, температура, внутренняя энергия, энтропия и т.д. П.с. взаимосвязаны, поэтому равновесное состояние системы можно однозначно определить ограниченным числом параметров (см. уравнение состояния).

ПАРООБРАЗОВАНИЕ – процесс перехода вещества из жидкого или твердого состояния в газообразное. В замкнутом объеме идет до тех пор, пока не образуется насыщенный пар. Различают два вида П.: испарение и кипение.

ПАРЦИАЛЬНОЕ ДАВЛЕНИЕ – давление газа, входящего в состав газовой смеси, которое он оказывал бы, занимая один весь объем смеси и находясь при температуре смеси. См. Дальтона закон.

ПАСКАЛЯ ЗАКОН – основной закон гидростатики:давление, производимое внешними силами на поверхность жидкости или газа, передается одинаково по всем направлениям.

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ – один из основных законов термодинамики, являющийся законом сохранения энергии для термодинамической системы: количество теплоты Q, сообщенное системе, расходуется на изменение внутренней энергии системы ΔU и совершение системой работы A_сист против внешних сил. Формула: Q=ΔU+A_сист. На использовании П.з.т. основана работа тепловых машин. Можно сформулировать по-другому: изменение внутренней энергии системы ΔU равно сумме переданного системе количества теплоты Q и работы внешних сил над системой A_внеш. Формула: ΔU=Q+A_внеш. В указанных формулах A_внеш.= – A_сист.

ПЛАВЛЕНИЕ – процесс перехода вещества из кристаллического состояния в жидкое. Происходит с поглощением некоторого количества теплоты при температуре плавления, зависящей от природы вещества и давления. См. теплота плавления.

ПЛАЗМА – ионизированный газ, в котором концентрации положительных и отрицательных зарядов практически одинаковы. Образуется при электрическом разряде в газах, при нагревании газа до температуры, достаточной для термической ионизации. В состоянии плазмы находится подавляющая часть вещества Вселенной: звезды, галактические туманности и межзвездная среда.

ПЛАСТИЧНОСТЬ – свойство твердых тел под действием внешних сил изменять, не разрушаясь, свою форму и размеры и сохранять остаточные (пластические) деформации после того, как действие внешних сил прекратится. Ср. хрупкость.

ПЛОТНОСТЬ – скалярная величина, равная отношению массы тела к его объему:. Одна из основных величин, применяемых для описания и сравнения веществ. В СИ измеряется в .

ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ КОЭФФИЦИЕНТ – физическая величина равная отношению работы внешних сил по изменению площади поверхности жидкости к величине этого изменения площади при постоянной температуре: . Зависит от рода жидкости и температуры. Может изменяться под действием поверхностноактивных веществ (напр., мыло).

ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ – явление, выражающееся в стремлении жидкости к уменьшению площади своей поверхности. Обусловлено межмолекулярным взаимодействием и вызвано образованием поверхностного слоя молекул, энергия которых больше, чем энергия молекул внутри данной жидкости при той же температуре.

www.eduspb.com