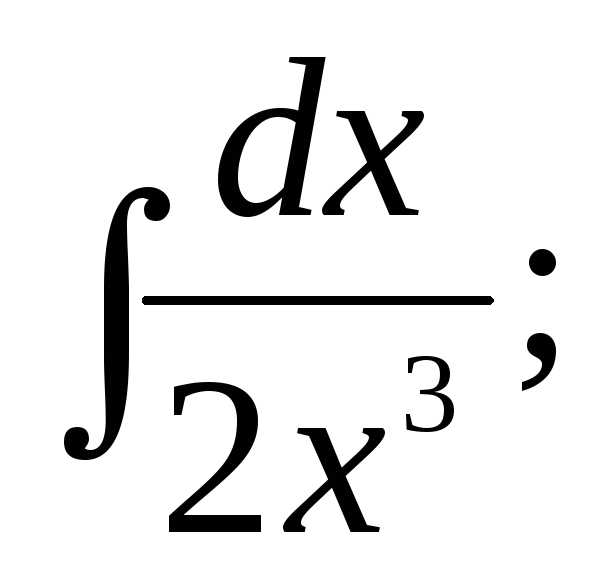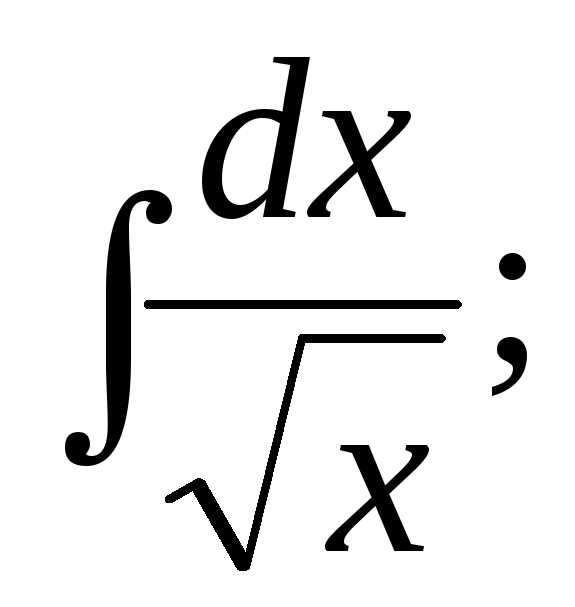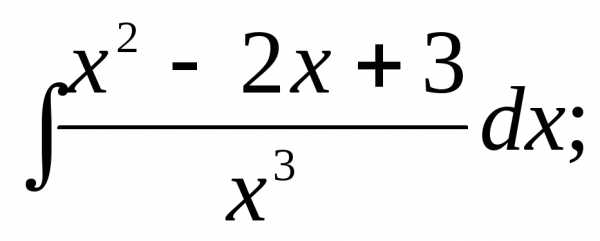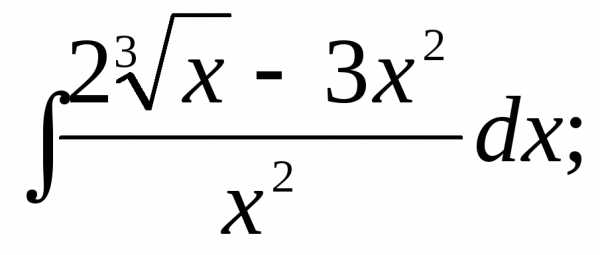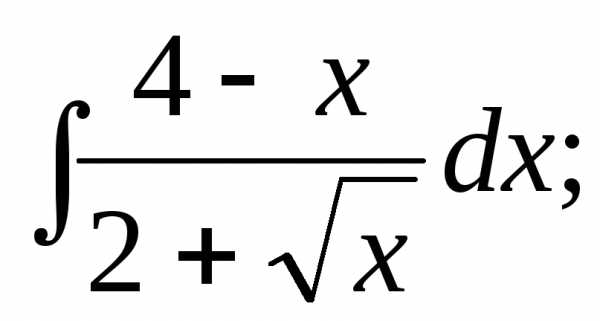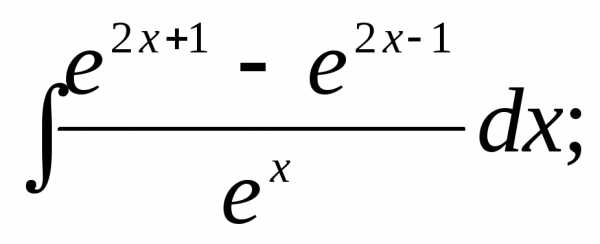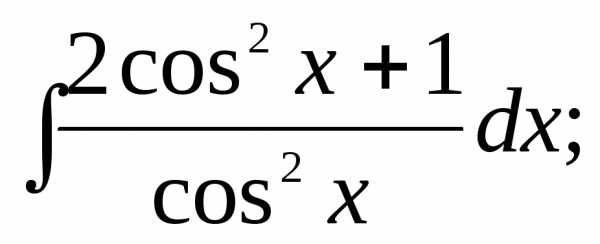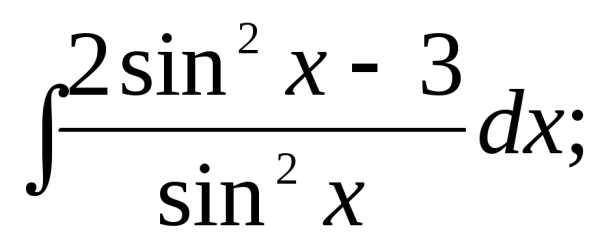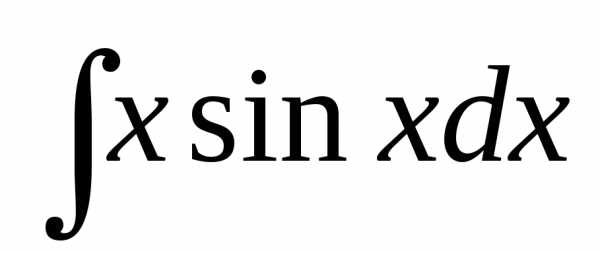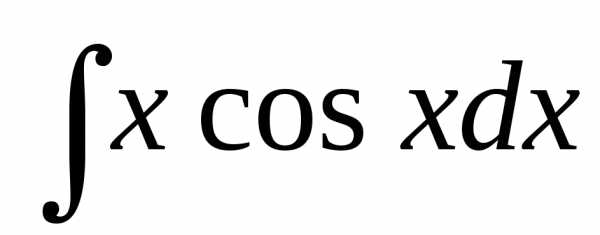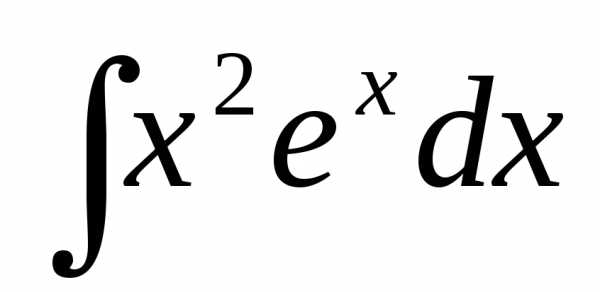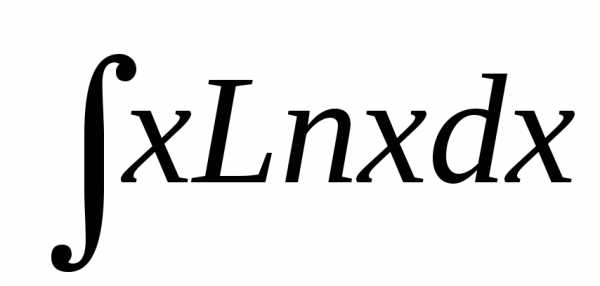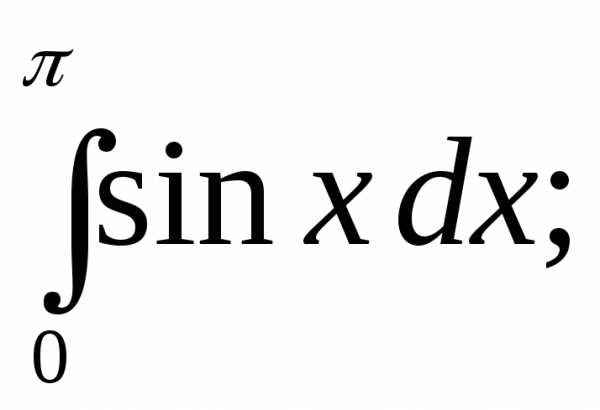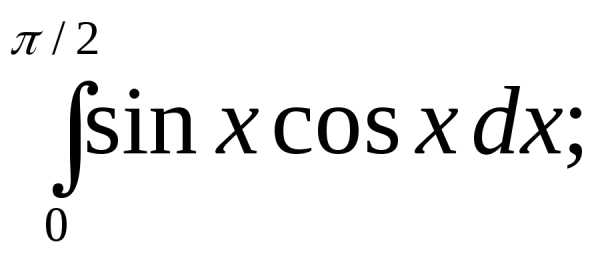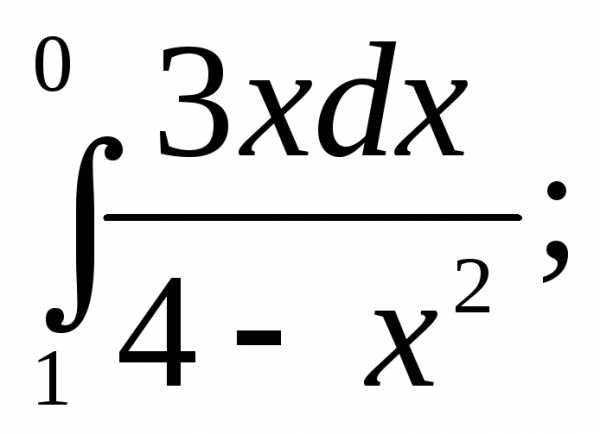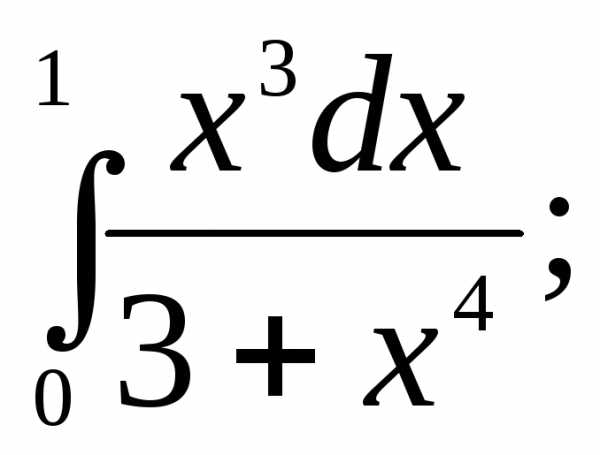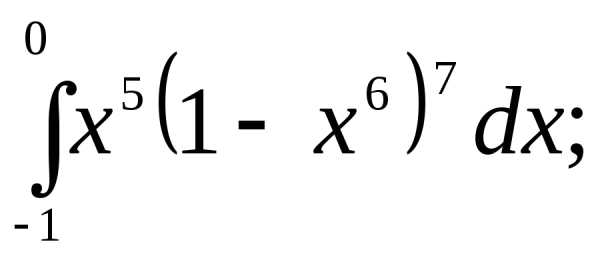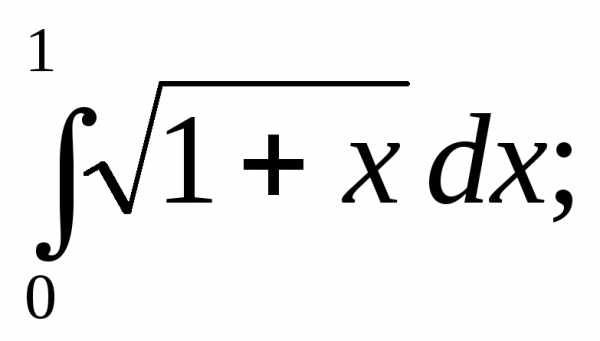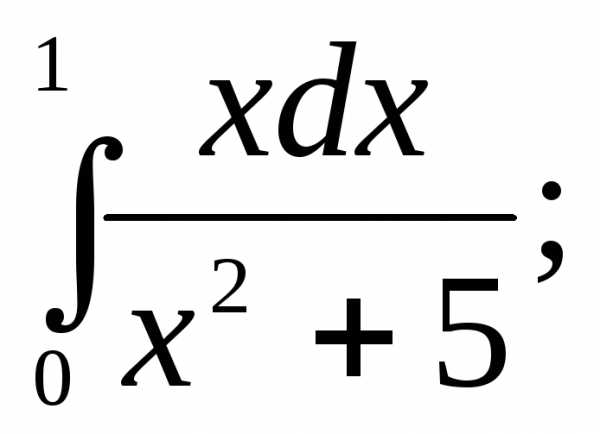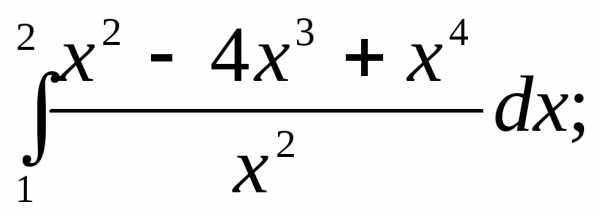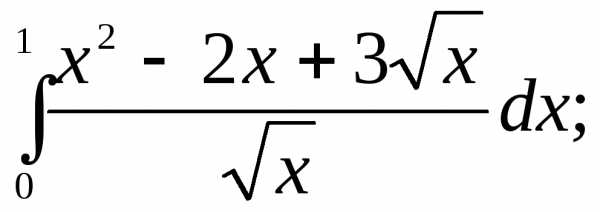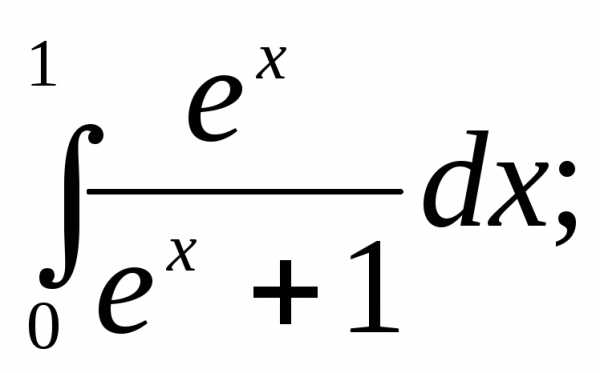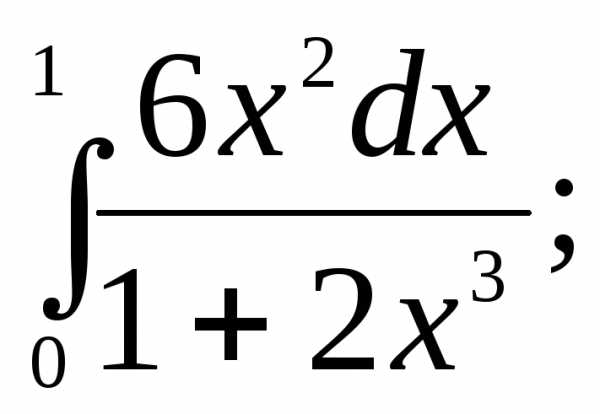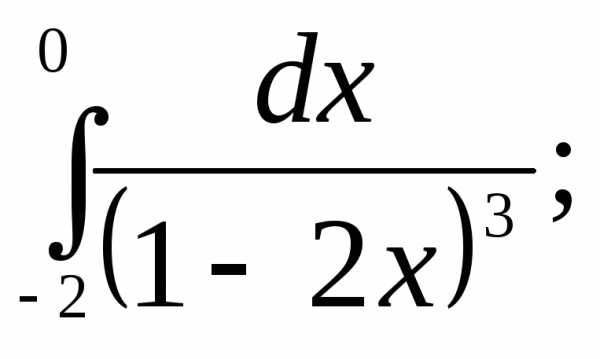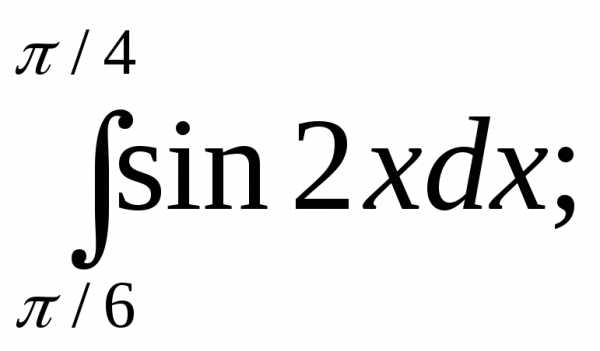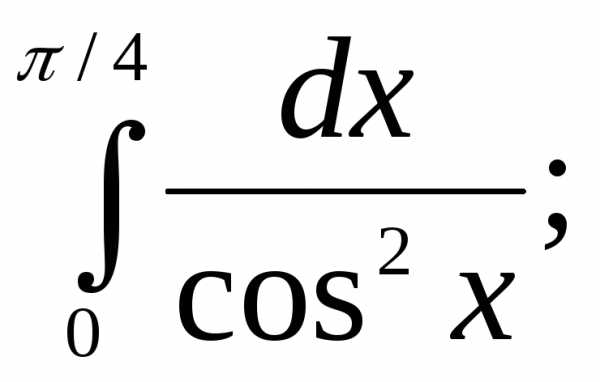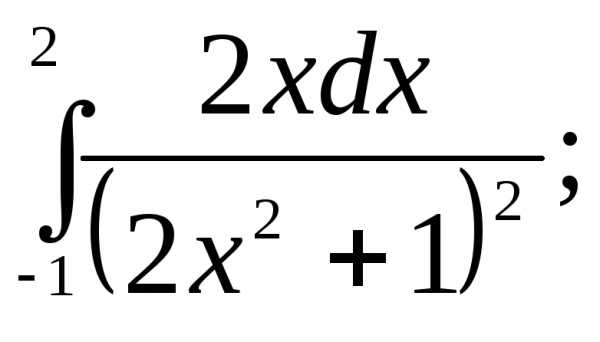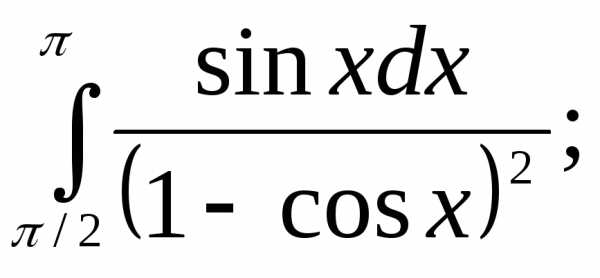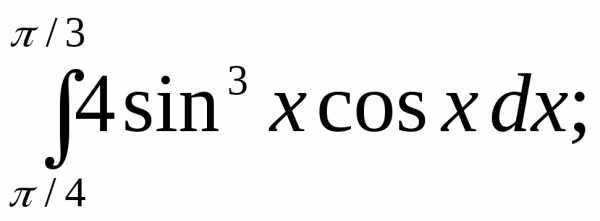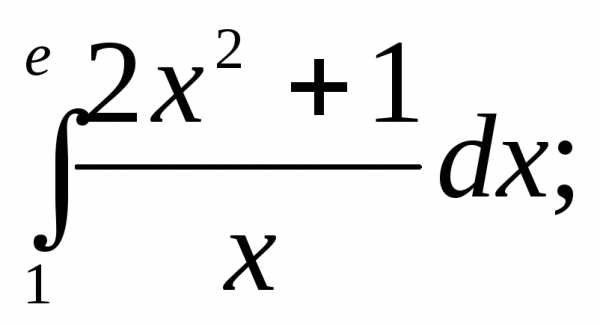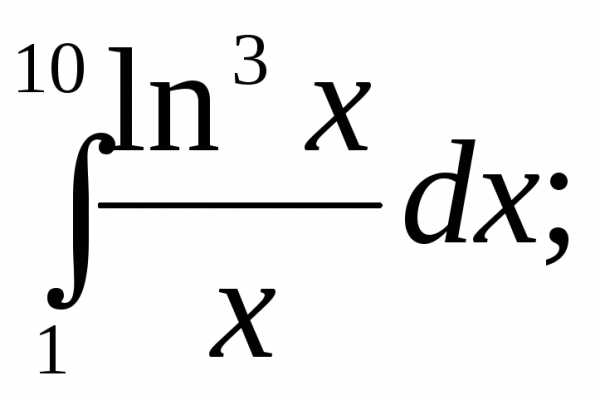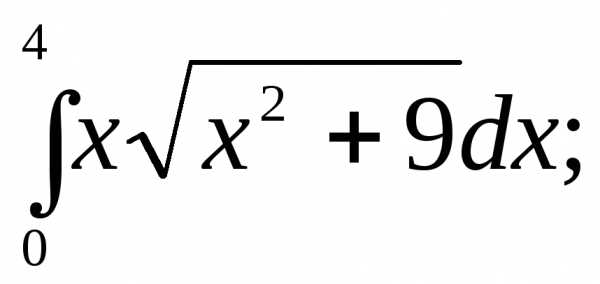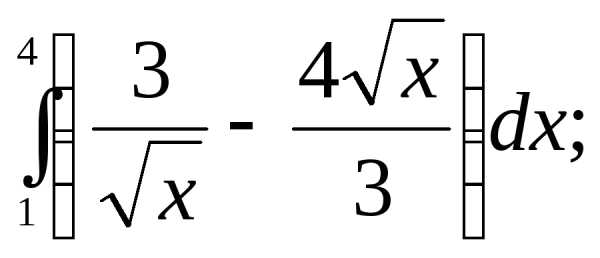§3. Основные правила интегрирования
I. .
II. .
III. Если , то.
Неопределенный
интеграл – это множество функций и
равенства I
и II
надо понимать как совпадение множеств.
Например, равенство I
означает следующее: чтобы получить
элементы множества  ,
надо каждый элемент множества
,
надо каждый элемент множества  умножить на число
умножить на число  .Правило
III
можно доказать так:
.
Тогда
.Правило
III
можно доказать так:
.
Тогда
,
т.е. .
Отметим,
что правило III
“работает” только тогда, когда вместо
переменной интегрирования 
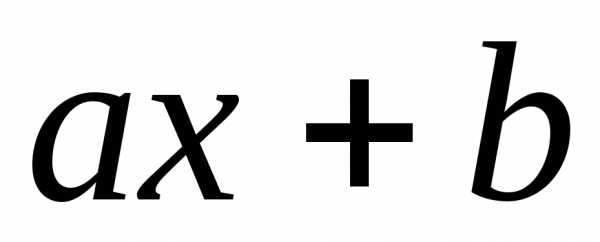 :
:,
но . Для этого интегралаправильный ответ имеет вид: .
Замечание. Правило III есть весьма частный случай замены переменной (см. следующий параграф).
§4. Основные методы интегрирования
I Непосредственное интегрирование
Так принято называть вычисление интегралов с помощью таблицы основных интегралов, правил интегрирования и тождественных преобразований подынтегральной функции.
Примеры.
1.
.
.
Можно предложить и другой способ:
.
Ответы по форме различны, но формулы тригонометрии позволяют доказать их тождественность.
3. .
4.Частный случай формулы 14 из §2:
.
5.Один полезный прием:
.
II Метод замены переменной
Существуют
две реализации этого метода: 1) в качестве
новой переменной интегрирования  рассматриваем некоторую функцию
рассматриваем некоторую функцию 
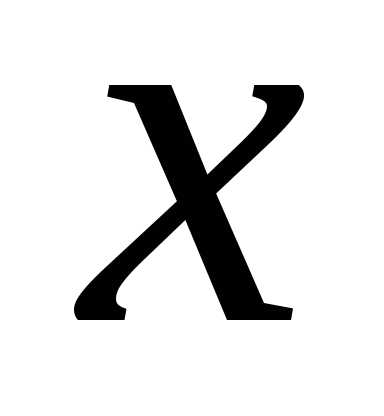 заменяем специально подобранной функцией
заменяем специально подобранной функцией .
.II.1 Подведение под знак дифференциала
Теорема
1. Пусть известно, что
.
Тогда, если функция – непрерывно-дифференцируема, то
– непрерывно-дифференцируема, то
. (1)
Доказательство.
Применяя правило дифференцирования сложной функции, получим
,
что и доказывает (1).
Чтобы воспользоваться этой теоремой на практике, необходимо вычленить в подынтегральной функции производную некоторой функции, объединить эту производную с дифференциалом переменной интегрирования и сделать замену. После вычисления интеграла вернуться к исходной переменной интегрирования.
Примеры.
6.
.
Замечание 1. Замену такого типа можно производить и без подведения под знак дифференциала.
7.
.
8.
.
Сразу отметим здесь, что такой простой заменой не всегда удается избавить-
ся
от иррациональности (попробуйте сами,
заменив в числителе 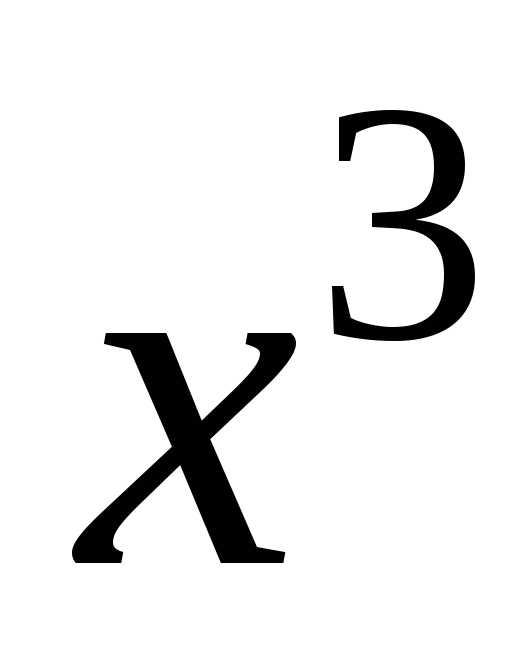 на
на ).
).
Замечание 2. Приведем две формулы, которые часто встречаются и их
лучше запомнить как табличные:
,
.
II.2 Метод подстановки
Теорема
2. Пусть требуется вычислить интеграл  и пусть
и пусть – непрерывно-дифференцируемая функция,
имеющая обратную
– непрерывно-дифференцируемая функция,
имеющая обратную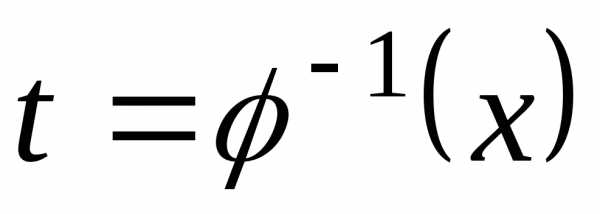 .
Тогда, если
.
Тогда, если
, (2)
то
. (3)
Доказательство. Равенство (2) означает, что . Тогда
.
Сравнение начала и конца этой цепочки равенств и доказывает равенство (3).
Пример.
9.
=
.
Ответ можно упростить, если учесть формулу синуса двойного угла:
.
III Интегрирование по частям
Теорема
3. Если  и
и – непрерывно-дифференци-руемые функции,
то справедлива формула
– непрерывно-дифференци-руемые функции,
то справедлива формула
. (4)
,
,
отсюда и следует формула интегрирования по частям (3).
При
практическом применении этого метода
подынтегральное выражение надо разбить
в произведение 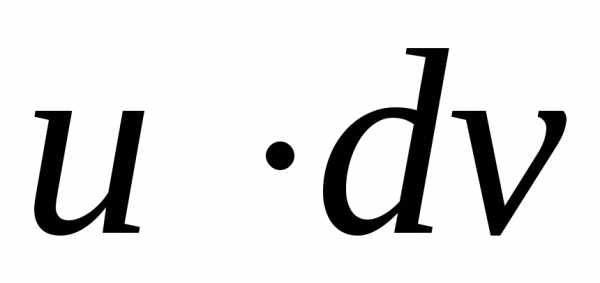 таким образом, чтобы функция
таким образом, чтобы функция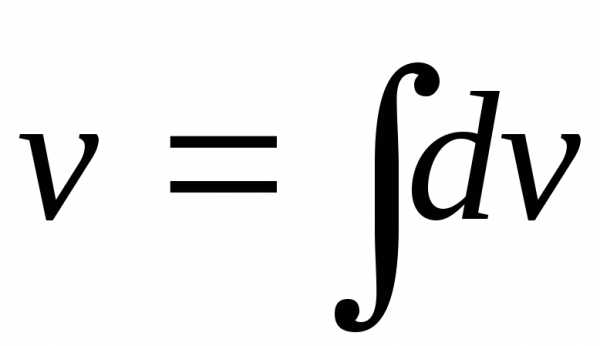 вычислялась просто, а интеграл в правой
части (4) был бы проще исходного.
вычислялась просто, а интеграл в правой
части (4) был бы проще исходного.
Примеры.
10.
.

.
Замечание
3. Если при вычислении интеграла  взять другую первообразную, например
взять другую первообразную, например ,
получим тот же результат:
,
получим тот же результат:
.
Замечание
4. Область применения этого метода в
основном исчерпывается интегралами
вида 
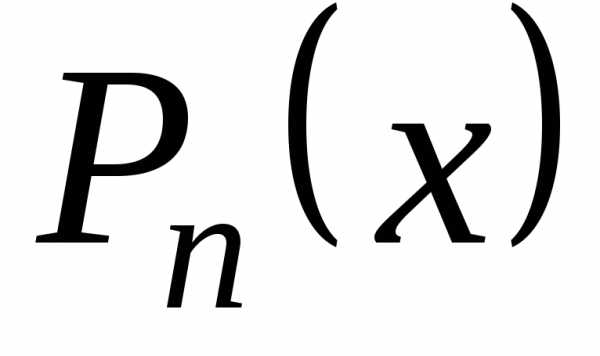 – многочлен, а
– многочлен, а – это: 1) показательные, тригонометрическиеи гипербо-лические функции; 2)
логарифмические и обратные тригонометрические
функции. При этом в качестве
– это: 1) показательные, тригонометрическиеи гипербо-лические функции; 2)
логарифмические и обратные тригонометрические
функции. При этом в качестве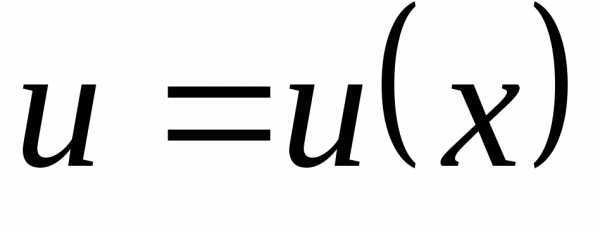 в случае 1) берем многочлен, а в случае
2)– логарифмы и аркфункции. Отметим,
что в случае 2) «многочлен» может
содержать степени переменной с
ненатуральными показателями.
в случае 1) берем многочлен, а в случае
2)– логарифмы и аркфункции. Отметим,
что в случае 2) «многочлен» может
содержать степени переменной с
ненатуральными показателями.Примеры.
12.
.
13.
.
Мы пришли к уравнению , из которого
получаем
.
14.Для интеграла путем двукратного интегриро-
вания по частям можно получить уравнение
,
из которого находим
.
Аналогичным образом можно найти интегралы
, 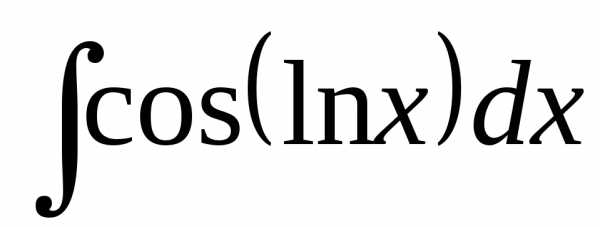 ,
, 
studfiles.net
Способы вычисления определенного интеграла Интегрирование по частям
Пусть  и
и – дифференцируемая функция от
– дифференцируемая функция от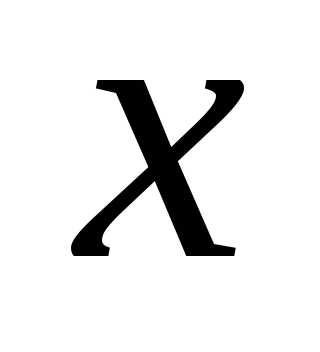 .
Тогда
.
Тогда
(8.21)
Проинтегруем
тождество (8.21) в границах от 
 ,
получим
,
получим(8.22)
Поскольку
,
то и равенство (8.22) приобретает вид
и равенство (8.22) приобретает вид

или
окончательно 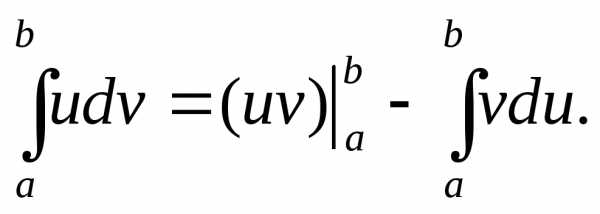 (8.23)
(8.23)
Формула (8.23) и выражает способ интегрирования по частям определенного интеграла. Видно, что она подобна формуле (7.12) интегрирования по частям неопределенного интеграла.
Пример.1. Вычислить 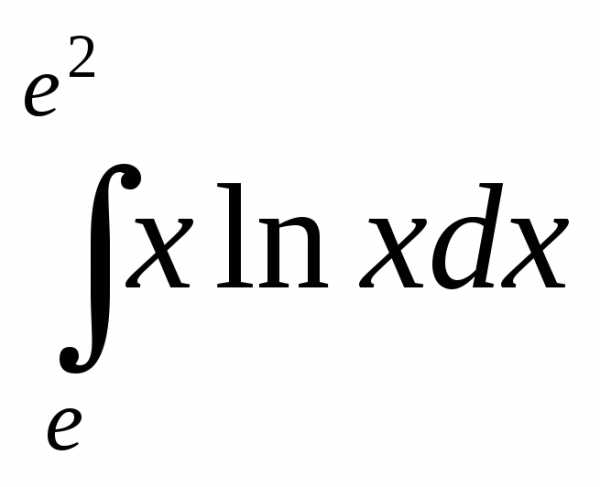 .
.
Решение
Пример 2. Вычислить  .
.
Решение.
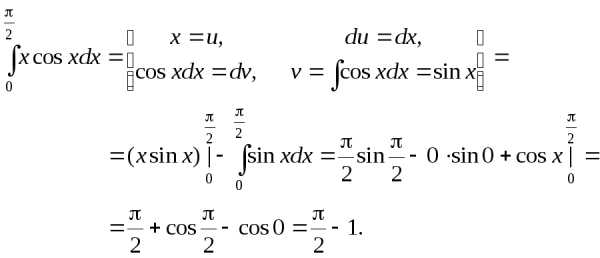
Интегрирование подстановкой
Пусть
надо вычислить определенный интеграл 
где 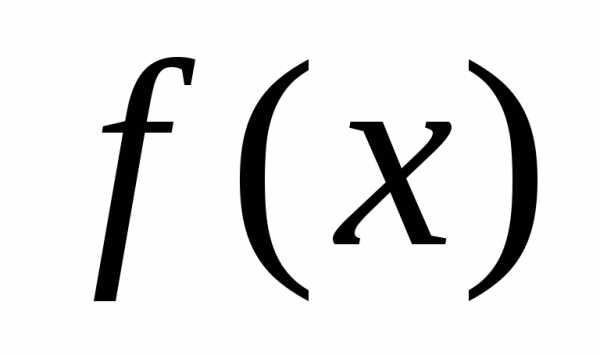 – непрерывная на
– непрерывная на функция, а первообразной для нее нет в
таблице простейших интегралов. Тогда
произведем замену переменной, а именно,
введем новую переменную
функция, а первообразной для нее нет в
таблице простейших интегралов. Тогда
произведем замену переменной, а именно,
введем новую переменную таким образом:,
где
таким образом:,
где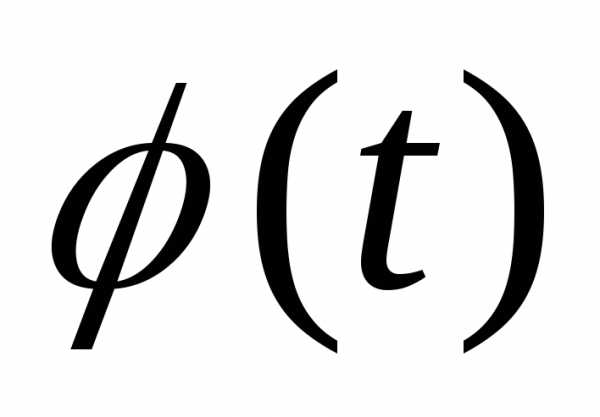 – непрерывно дифференцируема на
– непрерывно дифференцируема на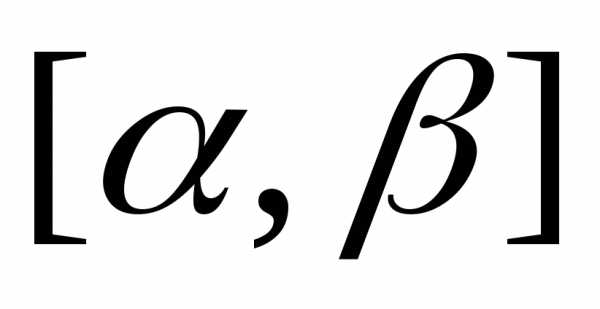 функция.
функция.
Если при этом будут выполняться такие условия:
при изменении
 от
от до
до переменная
переменная изменяется от
изменяется от до
до ,
то есть
,
то есть
. (8.24)
сложная функция
 определена и непрерывна на отрезке
определена и непрерывна на отрезке ,
то справедлива такая формула
,
то справедлива такая формула
(8.25)
Формула (8.25) и выражает собою суть метода подстановки.
Замечание. При вычислении определенного интеграла с помощью замены переменной нет необходимости возвращаться к старой переменной (как это нужно было делать при вычислении неопределенного интеграла) достаточно лишь учесть границы интегрирования соответственно (8.24).
Пример 8.3. Вычислить 
Решение
Введем
новую переменную  .
Тогда
.
Тогда
. Вычислим границы интегрирования и результат представим в виде табл. 1. Таблица 1
из
которой видно, что при
,
а при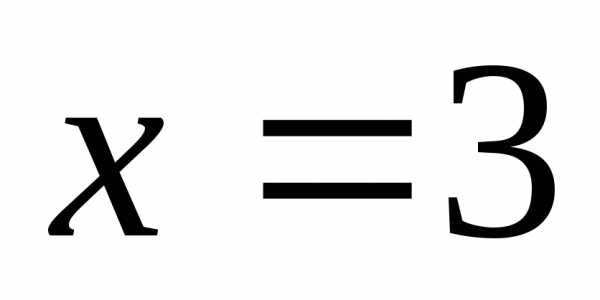 .
Итак, после введении новой переменной
получим
.
Итак, после введении новой переменной
получим
Пример 4.Вычислить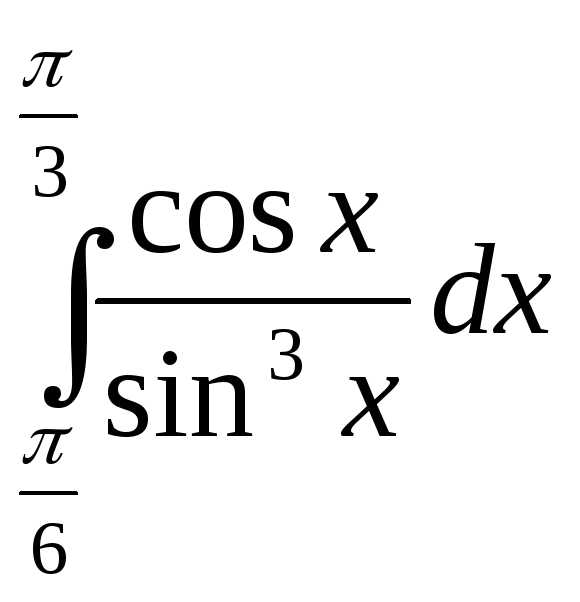 .
.
Решение.
Произведем замену переменной: . Тогда, а границы интегрирования приобретают значения: при
при
Итак, получаем

Таким образом, видим, что различие в применении метода замены переменной в неопределенном и определенном интеграле состоит в том, что в втором случае не надо возвращаться к старой переменной, поскольку при замене переменной изменяются также и границы интегрирования.
Приближенное вычисление определенного интеграла
Пусть
надо вычислить 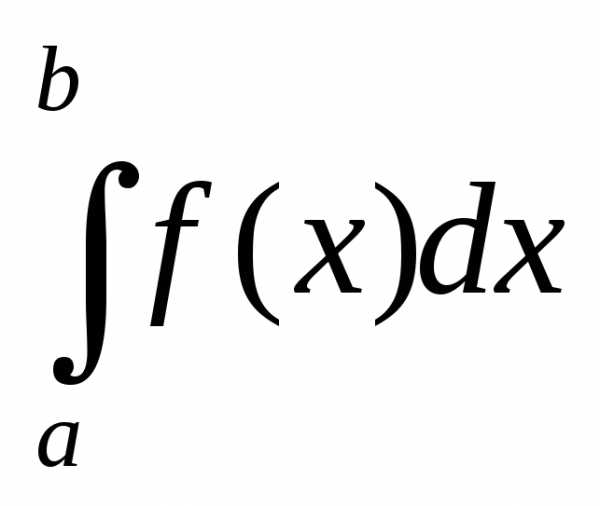 ,
но первообразная для функции
,
но первообразная для функции не выражается через элементарные
функции. Тогда применить формулу
Ньютона-Лейбница невозможно. В таких
случаях применяются методы приближенного
вычисления определенных интегралов.
Рассмотрим их, используя определение
интеграла как границы интегральной
суммы. Разделим отрезок
не выражается через элементарные
функции. Тогда применить формулу
Ньютона-Лейбница невозможно. В таких
случаях применяются методы приближенного
вычисления определенных интегралов.
Рассмотрим их, используя определение
интеграла как границы интегральной
суммы. Разделим отрезок точкамина
точкамина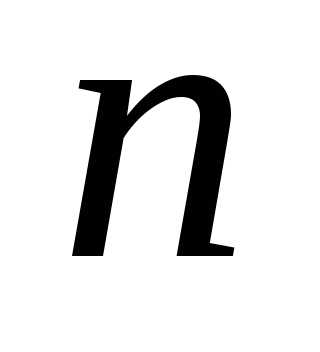 частичных отрезков равной длины.
Обозначим длину каждый из них через
частичных отрезков равной длины.
Обозначим длину каждый из них через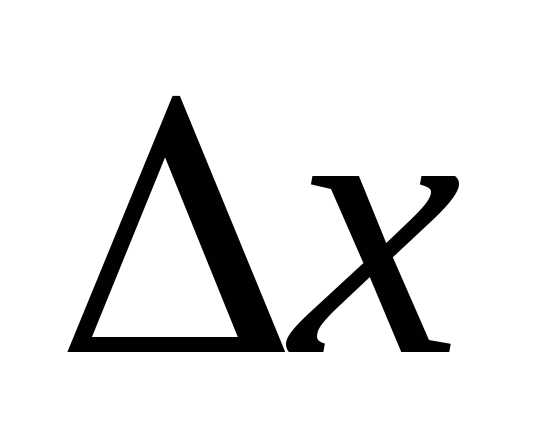 .
Тогда
.
Тогда

Обозначим
через
значения функции в точках,
то есть
в точках,
то есть
.
Составим суммы:
,
.
Каждая
из этих сумм представляет собой
интегральную сумму для  на отрезке
на отрезке и поэтому приближенно выражает интеграл
и поэтому приближенно выражает интеграл
 , (8.26)
, (8.26)
. (8.27)
Из
рис. 8.7 видно, что формула (8.26) выражает
площадь ступенчатой фигуры, составленной
из прямоугольников, вписанных в
криволинейную трапецию, а формула (8.27)
выражает площадь ступенчатой фигуры,
составленной из прямоугольников,
описанных вокруг криволинейной трапеции.
Поэтому формулы (8.26; 8.27) называются
формулами прямоугольников. Погрешность
при вычислении интегралов за формулами
прямоугольников будет тем меньше, чем
больше число n. Она выражается формулой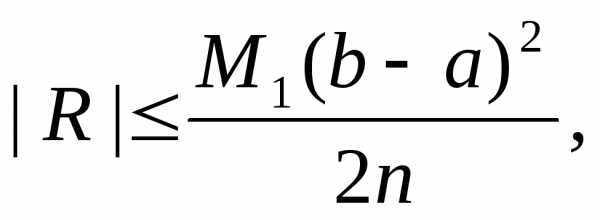
где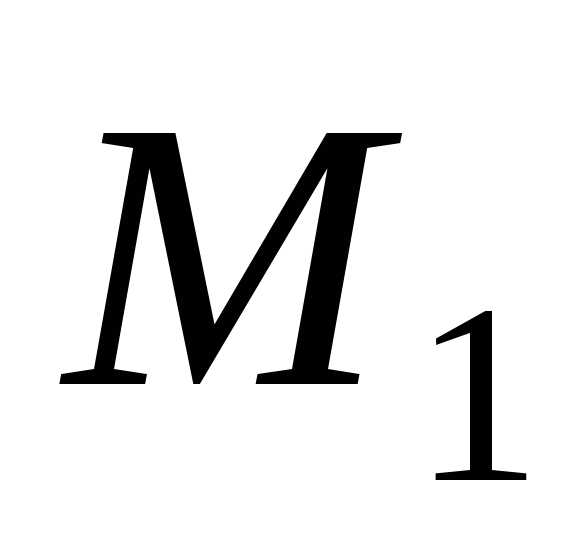 -максимальное значение
абсолютной величиныпроизводной
-максимальное значение
абсолютной величиныпроизводной на
на .
.
Более точное значение определенного интеграла получим, если данную кривую заменим не ступенчатой линией, как это делается в формуле прямоугольников, а вписанной ломаной (рис. 8.8).
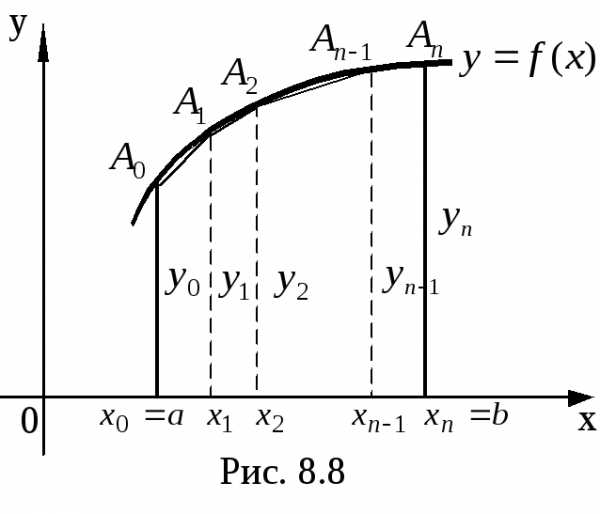 Тогда
площадь криволинейной трапеции
Тогда
площадь криволинейной трапеции  заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
Поскольку площадь первой из
этих трапеций равна  ,
площадь второй равняется
,
площадь второй равняется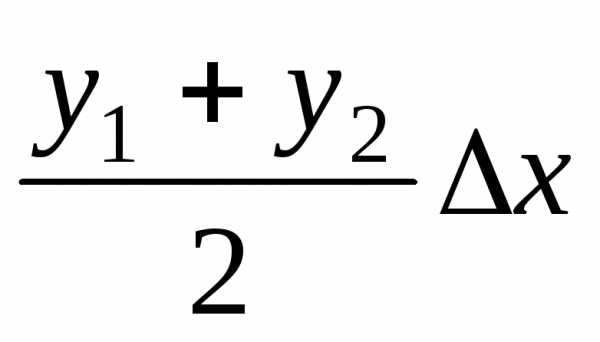 ,
то
,
то
или
. (8.28)
Легко
видеть, что она дает среднее арифметическое
из формул (8.26 и 8.27). Формула (8.28) называется
формулой трапеций. В этом случае
погрешность вычисляется по формуле 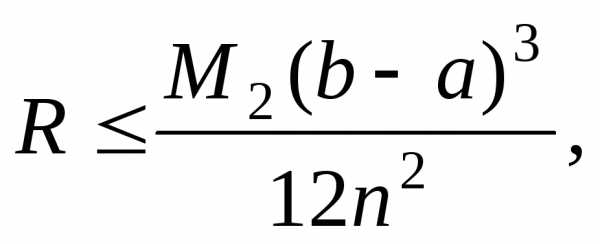
где 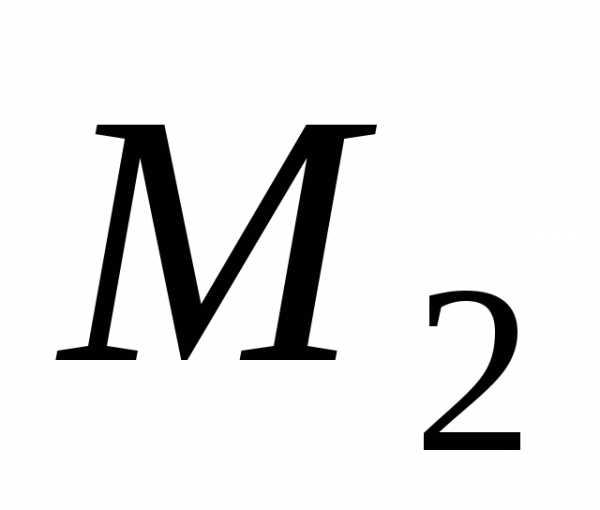 – минимальное значение абсолютной
величины второй производной
– минимальное значение абсолютной
величины второй производной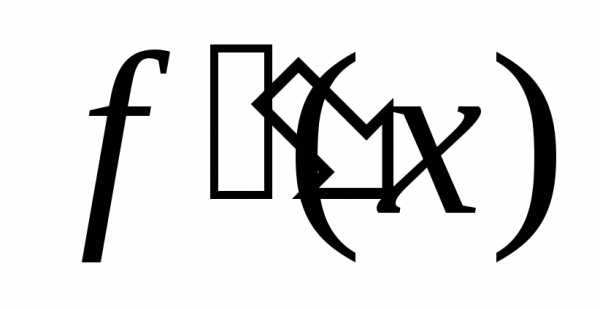 на
на .
.
Более точные результаты можно получить по формуле Симпсона (или формуле парабол), которая имеет вид:
(8.29)
При
этому надо обратить внимание на то, что
число  частичных отрезков, на которые разбивается
отрезок
частичных отрезков, на которые разбивается
отрезок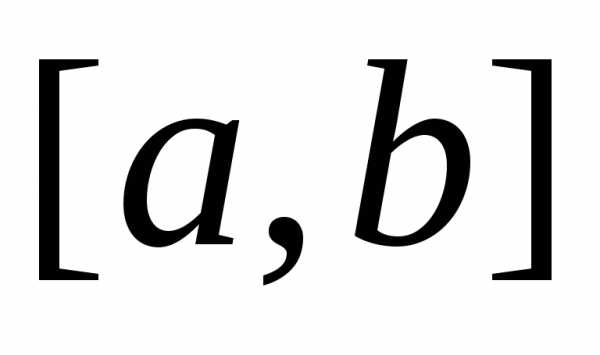 ,
должно быть обязательно четным, то есть
,
должно быть обязательно четным, то есть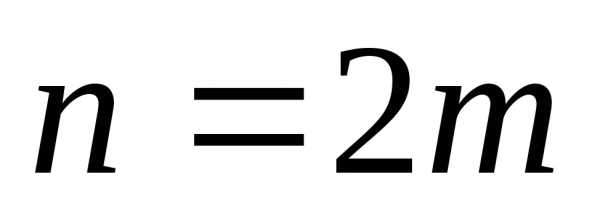 .
Тогда каждые две соседних криволинейных
трапеции, на которые разбилась вся
криволинейная трапеция
.
Тогда каждые две соседних криволинейных
трапеции, на которые разбилась вся
криволинейная трапеция (рис. 8.8), заменяютсяпараболической
трапецией, площадь
которой исчисляется по формуле
,
(рис. 8.8), заменяютсяпараболической
трапецией, площадь
которой исчисляется по формуле
,
гдеи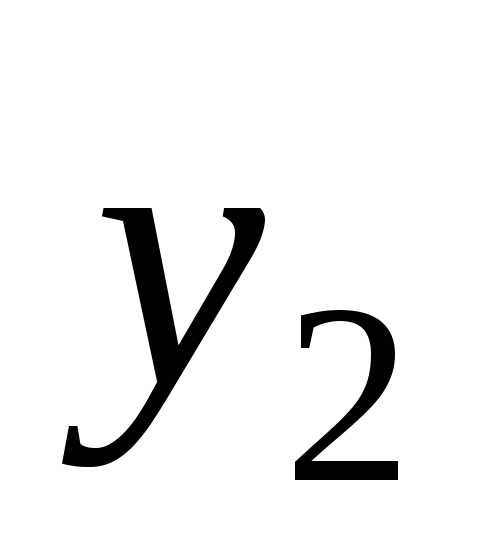 –
крайние ординаты,
–
крайние ординаты,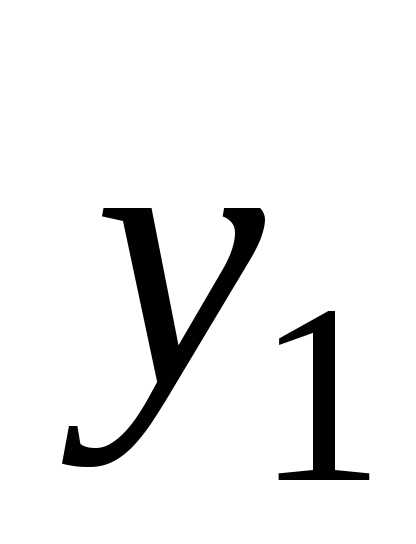 –
ордината кривой в середине отрезка, а
–
ордината кривой в середине отрезка, а – расстояние между ординатами
– расстояние между ординатами и
и (рис. 8.9).
(рис. 8.9).
Погрешность при этом может быть вычислена по формуле
где  – максимальное значение абсолютной
величины производной
– максимальное значение абсолютной
величины производной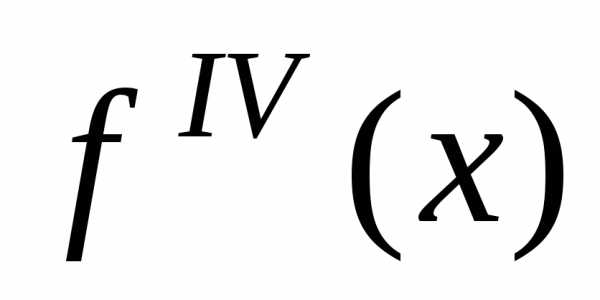 на отрезке
на отрезке .
.
Пример.5. Вычислить приближенно .
.
Точное
значение его 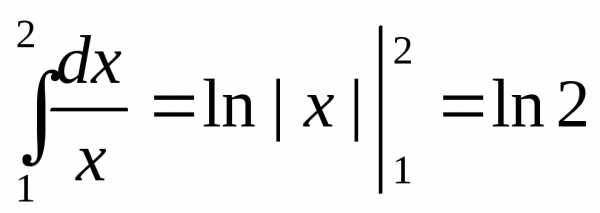 .
З точностью до седьмого знака.
Вычислим теперь его значение, пользуясь
формулами (8.26-8.29). Для этого разделим
отрезок
.
З точностью до седьмого знака.
Вычислим теперь его значение, пользуясь
формулами (8.26-8.29). Для этого разделим
отрезок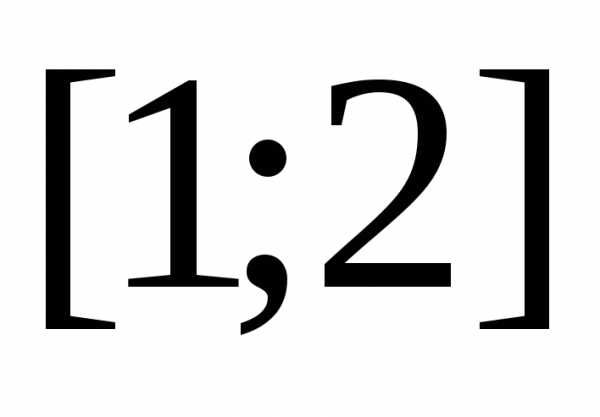 на 10 равных отрезков. Тогда длина каждого
из них будет
на 10 равных отрезков. Тогда длина каждого
из них будет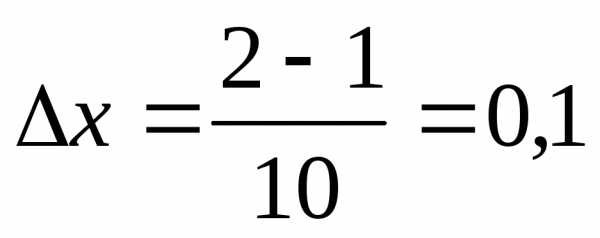 .
.
Составим табл. 2 значений подынтегральной функции в точках разбиения .
Таблица 2
Тогда по формуле (8.26) получим.
По формуле (8.27) .
По формуле (8.28) .
По формуле Симпсона (8.29)
Таким
образом, по формуле Симпсона при  получили 5 верных знаков, по формуле
трапеций – лишь три верных знака, за
формулами прямоугольников мы можем
быть уверены только в одном знаке.
получили 5 верных знаков, по формуле
трапеций – лишь три верных знака, за
формулами прямоугольников мы можем
быть уверены только в одном знаке.
studfiles.net
Определенный интеграл
Задание для студентов на практическое №3по теме
«Основы интегрального исчисления.Методы нахождения неопределенных интегралов. Вычисление определенных интегралов»
Цель занятия: Научиться решать примеры и задачи по данной теме
Вопросы теории ( исходный уровень)
Первообразная функции и неопределённый интеграл.
Интегрирование.
Методы нахождения неопределенных интегралов: приведение к табличному виду и метод замены переменной, интегрирование по частям.
Определённый интеграл, его применение для вычисления площадей фигур и работы переменной силы.
Вычисление определенных интегралов, правило Ньютона-Лейбница.
Примеры использования интегрального исчисления в медицинских задачах. (самостоятельная подготовка)
Содержание занятия:
1.ответить на вопросы по теме занятия
2.решить примеры
Примеры
Найти интегралы:
1) | 2) | 3) |
4) | 5) | 6) |
7) | 8) | 9) |
10) | 11) | 12) |
13) | 14) | 15) |
16) | 17) | 18) |
19) | 20) | 21) |
22) | 23) | 24) |
25) | 26) | 27) |
Вычислить интегралы:
1) | 2) | 3) |
4) | 5) | 6) |
7) | 8) | 9) |
10) | 11) | 12) |
13) | 14) | 15) |
16) | 17) | 18) |
19) | 21) | 22) |
23) | 24) | 25) |
26) | 27) | 28) |
29) | 30) | 31) |
32) | 33) | 34) |
35) | 36) | 37) |
38) |
Тема
Неопределенный интеграл
Функция F(x), имеющая данную функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции f(x). Совокупность всех первообразных функций для дифференциала f(x)dx называется неопределенным интегралом и обозначается символом ∫ f(x)dx.
Свойства неопределенного интеграла
∫f(x)dx=F(x)+C
∫[f(x)+φ(x)]dx=∫ f(x)dx+∫φ(x)dx
∫ d(F(x))=F(x)+C
(∫f(x)dx)=f(x)
∫f(x)dx= ∫f(t)dt
d∫f(x)dx=f(x)dx
∫af(x)dx+a∫f(x)dx
Основные интегралы
∫dx=x+C
∫xndx=xn+1/ (n+1) +C (n≠-1)
∫dx/x=ln|x|+C
∫axdx=ax/lna +C
∫exdx=ex+C
∫sin x dx=-cos x +C
∫cos xdx=sin x +C
∫dx/cos2x=tgx+C
∫dx/sin2x=-ctgx+C
∫dx/(1-x2)1/2=arcsinx=-arccosx
∫dx/(1+x2)= arctgx=- arcctgx
Интегрирование по частям
∫ udv = uv—∫ vdu.
Пример
Найти у = ∫ ln хdх.
Полагаем и=lпх, dv = dx, тогда dи =dx/x, v = x
Используя формулу интегрирования по частям, получаем
у = ∫ ln xdx = x ln х-∫ dх = xlnx-x+C
Пример метод непосредственного интегрирования
Найти у= ∫ (1+ 2x2)dx
На основании свойства интеграла суммы запишим
у= ∫ (1+ 2x2)dx = ∫ dx+2 ∫ x2dx =x+2x3/3+C
Пример; метод замены переменной( метод подстановки)
∫tgxdx=∫(sinx/cosx)dx обозначим cosx=t
Продифферинцируем праву и левую часть
-sinxdx=dt найдем dx=dt/(-sinx)
Запишим интеграл через новые переменные
∫(sinx/t) dt/(-sinx) =-∫dt/t= lnt+C или lncosx+C
Определенный интеграл функции f(x) на отрезке [а, b] представляет предел интегральной суммы
lim∑f(ki)Δxi ( от i=1 до n и Δx→0)
где ki — произвольная точка соответствующего отрезка.
Формула Ньютона — Лейбница
где F′ — первообразная функцию f(x), т е
F′(x)=f(x)
Некоторые свойства определенного интеграла
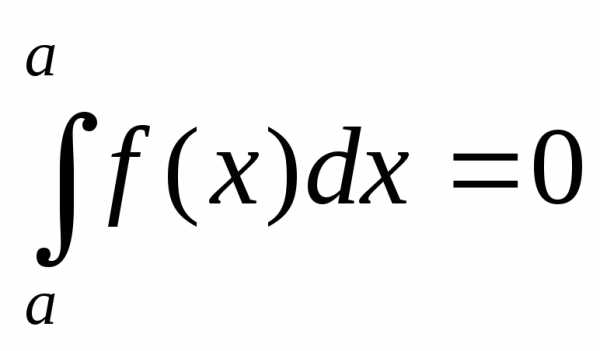
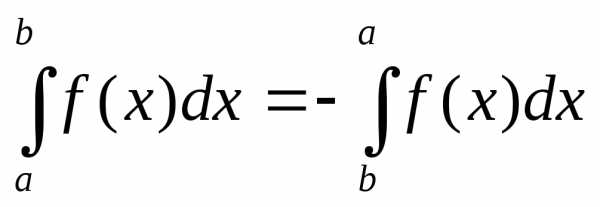
Площадь криволинейной трапеции, ограниченной графиком функции f(x), осью абсцисс и прямыми х=а и х=b,

Площадь фигуры, ограниченной двумя кривыми y=.f1(x) и у = = f2(x) [ f’2(x)≥f1(x)] и двумя прямыми х=а и х=b,
Дифференциальные уравнения
Общий вид дифференциального уравнения
F(x ,y,y′,y″,…yn) = О
Общee решение дифференциального уравнения
y=f(x, C1,C2, , Сn)
Общий вид дифференциального уравнения первого порядка
F(x,y,y’) = 0
Общее решение дифференциального уравнения первого порядка
y= f(x,C)
примеры
1 Дифференциальное уравнение типа y’=f(x)
dy/dx=f(х) , dx = f(x)dx
Общее решение
y=∫f(x)dx=F(x)+C
Дифференциальное уравнение типа
у’ = f(y)
dy/dx=f(y), dy/f(y)=dx
Общее решение
∫dy/f(y)=F(y)+C
Дифференциальное уравнение с разделенными переменными
f(x) dx + φ(y)dy = 0
Общее решение
∫f(x) dx + ∫φ(y)dy = C, F(х) + Ф(у) = С
Дифференциальное уравнение с разделяющимися переменными
f(x)φ(y)dx+ψ(x)Ф(y)dy=0
Приведем это уравнение к уравнению с разделенными переменными
(f(x)/ψ(x))dx+(Ф(y)/φ(y))dy=0
Общее решение
∫(f(x)/ψ(x))dx+∫(Ф(y)/φ(y))dy=C, F1(x)+F2(y)=C
Первообразная функции и неопределенный интеграл.
Из школьного курса математики известно, что математические операции образуют пары двух взаимно обратных действий (например, сложение и вычитание, умножение и деление, возведение в целую положительную степень и извлечение корня, логарифмирование и потенцирование).
Дифференцирование дает возможность для заданной функции F(x) находить ее производную F(x) или дифференциал dF = F (x)dx.
Cуществует действие, обратное дифференцированию, интегрирование нахождение функции F(x) по известной ее производной f(x) = F(x) или дифференциалу f(x)dx.
Функцию F(x) называют первообразной функции f(x), если для всех х из области определения функции F(x) = f(x) или dF(x)=f(x)dx.
Например, функция F(x) = x5 является первообразной функции f(x) = 5x4 для х , так как при любом х (х5) = 5х4 и dx5=5x4dx.
Для функции f(x) = 5x4 первообразной будет любая функция Ф(х) = х5 + С, где С – произвольное постоянное число, так как производная постоянной равна нулю.
В общем случае, если f(x) имеет первообразную функцию F(x), совокупность F(x) + C также будет первообразной для f(x):
(F(x) + C) = F(x) = f(x).
Cовокупность первообразных F(x) + С для данной функции f(x) или данного дифференциала f(x)dx называют неопределенным интегралом от функции f(x) и обозначают f(x)dx.
По определению, f(x)dx = F(x) + C (читается «неопределенный интеграл эф от икс дэ икс»).
Выражение f(x)dx называют подынтегральным выражением, функцию f(x) – подынтегральной функцией, а С – постоянной интегрирования.
Вычисление интеграла от данной функции называется интегрированием этой функции.
Пример. Найти неопределенный интеграл от функции f(x) = cos x, если при х = 0 F(0) = 0.
Решение. Функция cos x есть производная от функции sin x, поэтому cos xdx = sin x + C. Обозначим искомую первообразную F(x) = sin x + C. Подставив в последнее выражение начальные данные x = 0 и F(0) = 0, получим 0 = sin 0 + C, откуда C = 0. Искомая первообразная F(x) = sin x.
В геометрии с помощью неопределенного интеграла по закону углового коэффициента касательной в любой точке кривой можно найти уравнение кривой.
Пример. Угловой коэффициент касательной в любой точке кривой равен её абсциссе, то есть r = x. Составить уравнение кривой.
Решение. Так как угловой коэффициент r = tg = f(x) = x, то y= xdx = = x2/2 + C есть семейство парабол, отличающихся друг от друга на постоянную С.
studfiles.net
Основные правила интегрирования
Теорема:Любая непрерывная на интервале  функция
функция имеет на этом интервале первообразную.
Одной из первообразных является функция:
имеет на этом интервале первообразную.
Одной из первообразных является функция:
 ,
,
где  – любая фиксированная точка интервала
– любая фиксированная точка интервала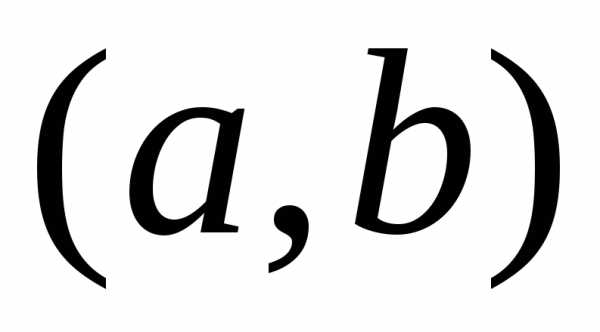 .
.
Так
как две первообразные данной функции  отличаются на постоянную, то согласно
теореме, любая первообразная
отличаются на постоянную, то согласно
теореме, любая первообразная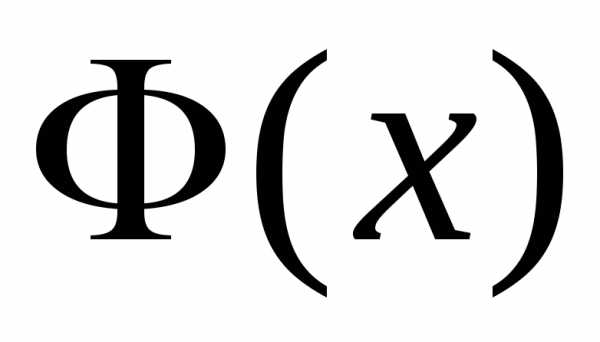 непрерывной на сегменте
непрерывной на сегменте функции
функции имеет вид:
имеет вид:

где  – некоторая постоянная.
– некоторая постоянная.
Полагая
в последней формуле сначала  ,
затем
,
затем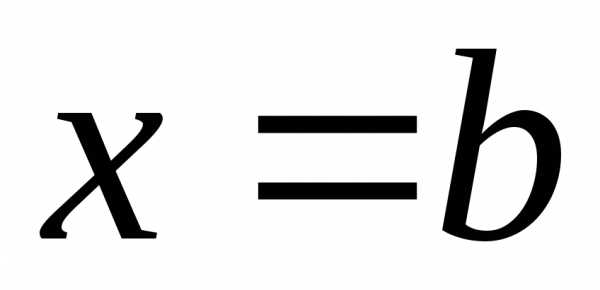 , и используя первое свойства
определенного интеграла, получим:
, и используя первое свойства
определенного интеграла, получим:
,  .
.
Из этих равенств вытекает соотношение:
,
которое называется основной формулой интегрального исчисления или формулой Ньютона – Лейбница.
Пусть выполнены следующие условия:
1)
Функция 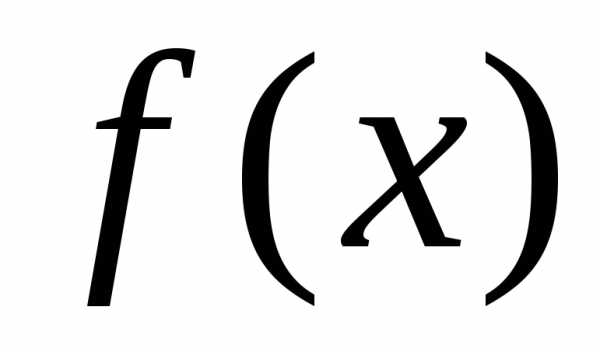 непрерывна на отрезке
непрерывна на отрезке ;
;
2)
отрезок  является множеством значений некоторой
функции
является множеством значений некоторой
функции ,
определенной на отрезке
,
определенной на отрезке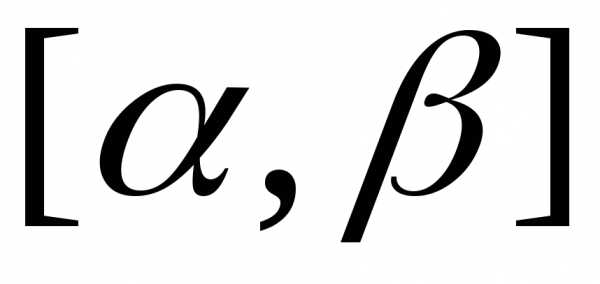 и имеющей на этом отрезке непрерывную
производную;
и имеющей на этом отрезке непрерывную
производную;
3) ,.
При этих условиях справедлива формула:
Указанная формула называется формулой замены переменной в определенном интеграле.
Пусть
функции  и
и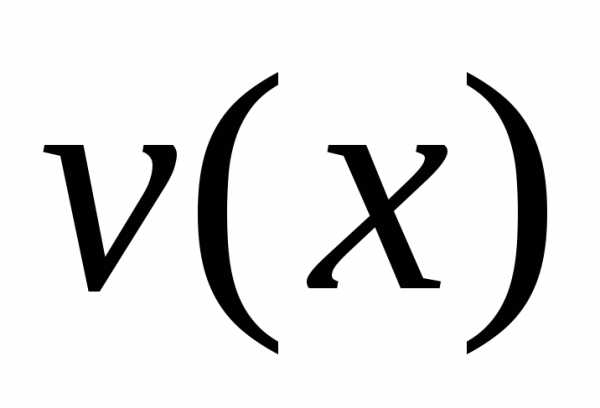 имеют непрерывные производные на
сегменте
имеют непрерывные производные на
сегменте .
Тогда имеет место следующая формула
интегрирования по частям для определенных
интегралов:
.
Тогда имеет место следующая формула
интегрирования по частям для определенных
интегралов:
.
Так как и, то эту формулу можно записать следующим образом:
 .
.
Приложения определенного интеграла Площадь плоской фигуры
Определение: Плоская
фигура  – часть плоскости, ограниченная простой
замкнутой кривой
– часть плоскости, ограниченная простой
замкнутой кривой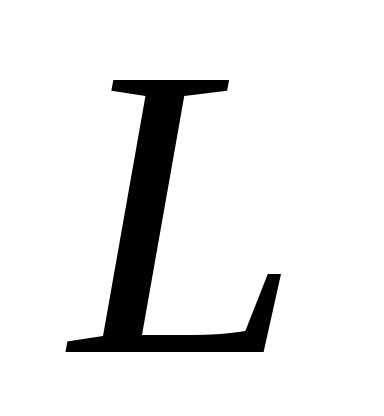 ,
при этом кривая
,
при этом кривая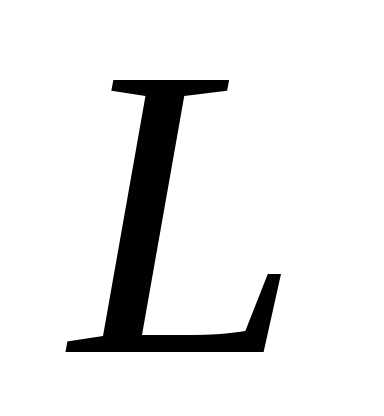 называется границей фигуры
называется границей фигуры .
.
Определение: Мы будем говорить, что многоугольник
вписан в фигуру  ,
если каждая точка этого многоугольника
принадлежит фигуре
,
если каждая точка этого многоугольника
принадлежит фигуре или ее границе.
или ее границе.
Определение: Если все точки плоской фигуры и ее
границы принадлежат некоторому
многоугольнику, то мы будем говорить,
что указанный многоугольник описан
вокруг фигуры  .
.
Замечание: Площадь любого вписанного в фигуру  многоугольника не больше площади любого
описанного вокруг фигуры
многоугольника не больше площади любого
описанного вокруг фигуры многоугольника.
многоугольника.
Пусть 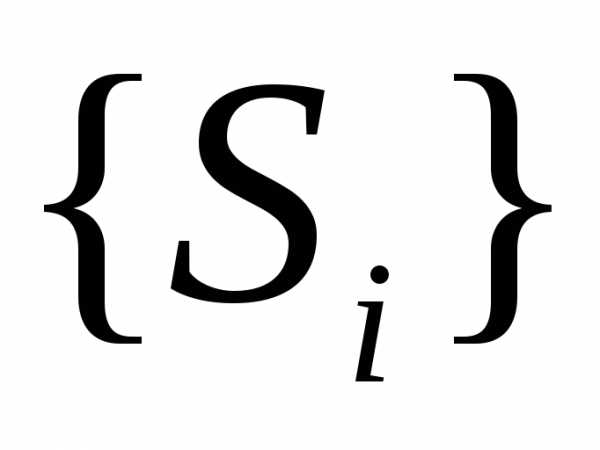 – числовое множество площадей вписанных
в плоскую фигуру
– числовое множество площадей вписанных
в плоскую фигуру многоугольников, а
многоугольников, а – числовое множество площадей описанных
вокруг плоской фигуры
– числовое множество площадей описанных
вокруг плоской фигуры многоугольников. Очевидно, что множество
многоугольников. Очевидно, что множество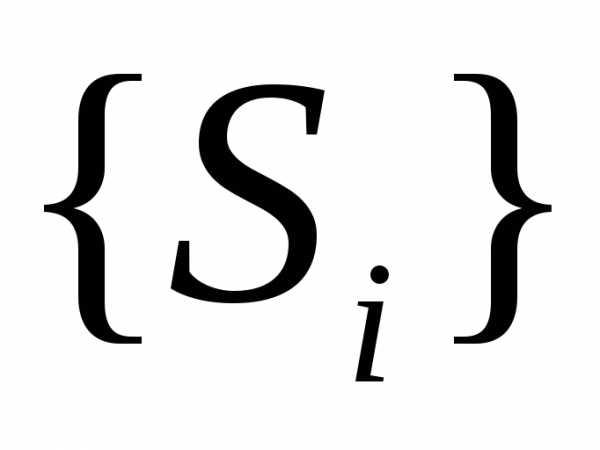 ограничено сверху (площадью любого
описанного вокруг фигуры
ограничено сверху (площадью любого
описанного вокруг фигуры многоугольника), а множество
многоугольника), а множество ограничено снизу (например, числом
нуль).
ограничено снизу (например, числом
нуль).
Обозначим
через 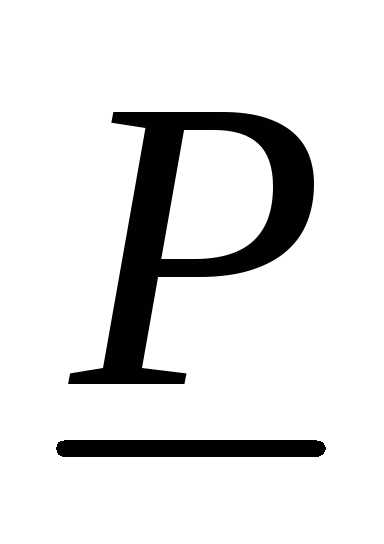 точную верхнюю грань множества
точную верхнюю грань множества ,
через
,
через точную нижнюю грань множества
точную нижнюю грань множества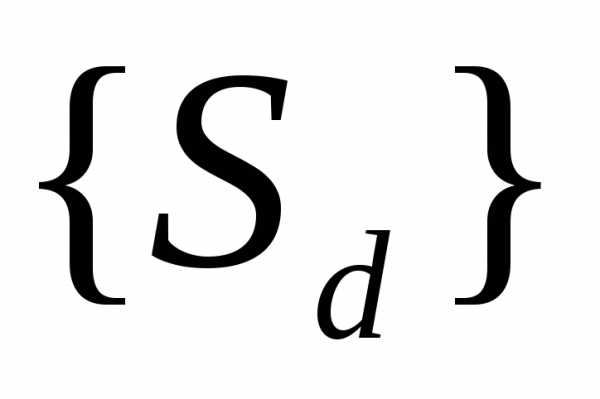 .
.
Числа  и
и называются соответственнонижнейплощадью иверхнейплощадью фигуры
называются соответственнонижнейплощадью иверхнейплощадью фигуры
Замечание: Нижняя площадь 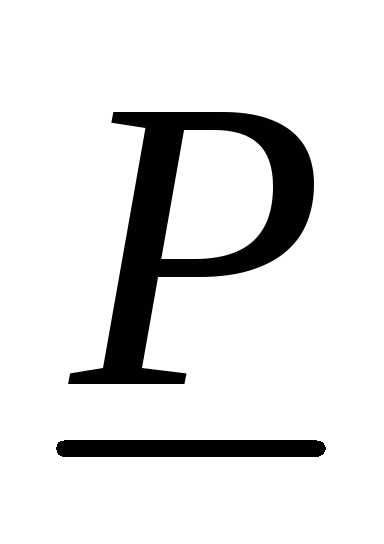 фигуры
фигуры не больше верхней площади
не больше верхней площади ,
т. е.
,
т. е. .
.
Определение. Плоская фигура  называетсяквадрируемой,
если верхняя площадь этой фигуры
совпадает с ее нижней площадью. При этом
число
называетсяквадрируемой,
если верхняя площадь этой фигуры
совпадает с ее нижней площадью. При этом
число 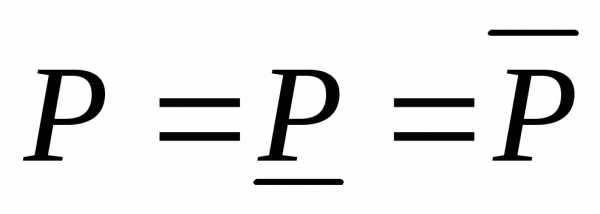 называетсяплощадью фигуры
называетсяплощадью фигуры  .
.
Теорема:Для того чтобы плоская фигура  была квадирируемой, необходимо и
достаточно, чтобы для любого положительного
числа
была квадирируемой, необходимо и
достаточно, чтобы для любого положительного
числа можно было указать такой описанный
вокруг фигуры
можно было указать такой описанный
вокруг фигуры многоугольник и такой вписанный в фигуру
многоугольник и такой вписанный в фигуру многоугольник, что разность
многоугольник, что разность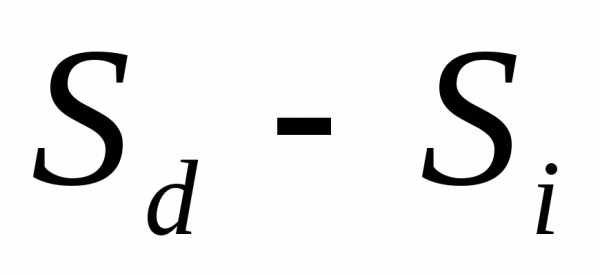 площадей которых была бы меньше
площадей которых была бы меньше ,.
,.
Определение:Криволинейной трапецией называется фигура, ограниченная графиком
заданной на сегменте  непрерывной и неотрицательной функции
непрерывной и неотрицательной функции ,
ординатами, проведенными в точках
,
ординатами, проведенными в точках и
и ,
и отрезком оси
,
и отрезком оси между точками
между точками и
и .
.
Теорема: Криволинейная трапеция представляет
собой квадрируемую фигуру, площадь  которой может быть вычислена по формуле:
которой может быть вычислена по формуле:
. Объемы тел вращения
Пусть  – некоторое конечное тело. Рассмотрим
всевозможные многогранники, вписанные
в тело
– некоторое конечное тело. Рассмотрим
всевозможные многогранники, вписанные
в тело ,
и всевозможные многогранники, описанные
вокруг тела
,
и всевозможные многогранники, описанные
вокруг тела .
.
Пусть 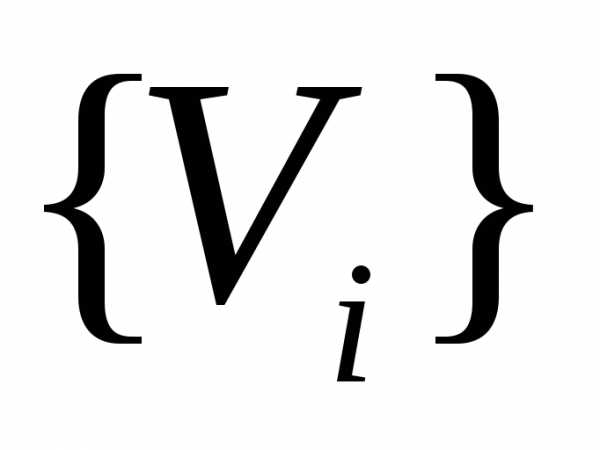 – числовое множество объемов вписанных
в тело
– числовое множество объемов вписанных
в тело ,
а
,
а – числовое множество объемов описанных
вокруг
– числовое множество объемов описанных
вокруг многогранников. Множество
многогранников. Множество ограничено сверху (объемом любого
описанного многогранника), а множество
ограничено сверху (объемом любого
описанного многогранника), а множество ограничено снизу (например, числом
нуль).
ограничено снизу (например, числом
нуль).
Обозначим
через  точную верхнюю грань множества
точную верхнюю грань множества ,
а через
,
а через точную нижнюю грань множества
точную нижнюю грань множества .
.
Числа  и
и называются соответственнонижним
объемом и верхним объемомтела
называются соответственнонижним
объемом и верхним объемомтела .
.
Замечание:Нижний объем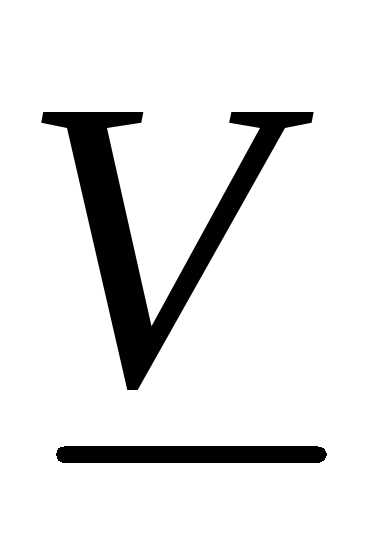 тела
тела не больше верхнего объема
не больше верхнего объема этого тела, т. е.
этого тела, т. е.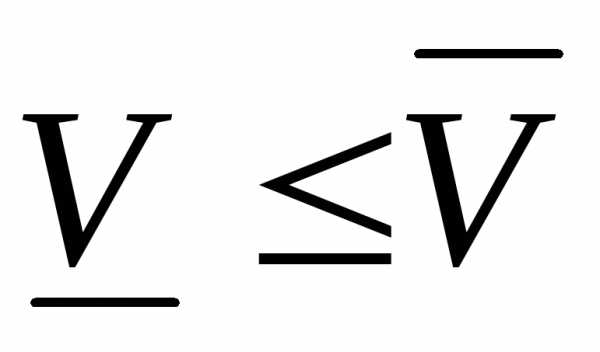 .
.
Определение:Тело  называется кубируемым, если верхний
объем
называется кубируемым, если верхний
объем этот тела совпадает с нижним объемом
этот тела совпадает с нижним объемом .
При этом число
.
При этом число называется объемом тела
называется объемом тела .
.
Теорема: Для того чтобы тело  было кубируемым, необходимо и достаточно,
чтобы для любого положительного числа
было кубируемым, необходимо и достаточно,
чтобы для любого положительного числа можно было указать такой описанный
вокруг тела
можно было указать такой описанный
вокруг тела многогранник и такой вписанные в тело
многогранник и такой вписанные в тело многогранник, разность
многогранник, разность объемов которых была бы меньше
объемов которых была бы меньше .
.
Теорема: Пусть функция 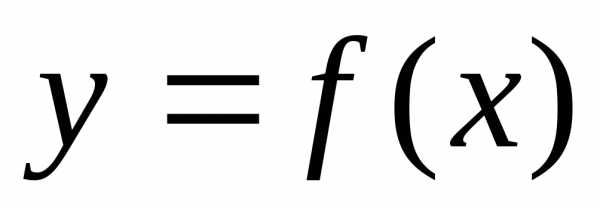 непрерывна на сегменте
непрерывна на сегменте .
Тогда тело
.
Тогда тело ,
образованное вращением вокруг оси
,
образованное вращением вокруг оси криволинейной трапеции, ограниченной
графиком функции
криволинейной трапеции, ограниченной
графиком функции ,
ординатами в точках
,
ординатами в точках и
и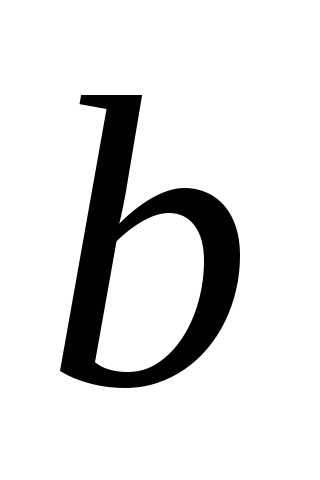 ,
и отрезком оси
,
и отрезком оси между точками
между точками и
и ,
кубируемо и его объем
,
кубируемо и его объем может быть найден по формуле:
может быть найден по формуле:
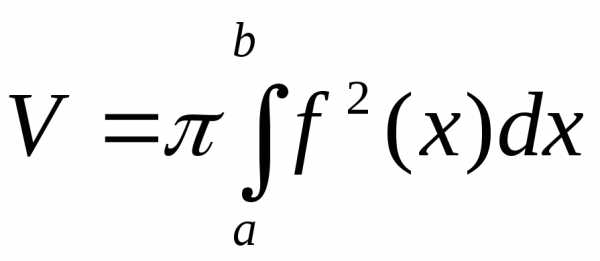 .
.
studfiles.net
2.2. Методы вычисления определенного интеграла
Вычисление определенных интегралов как пределов интегральных сумм связано в большими трудностями даже в тех случаях, когда подынтегральные функции являются простыми. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов.
Ниже будет сформулирована теорема Ньютона-Лейбница, позволяющая сводить вычисления определенного интеграла к неопределенному. Эта теорема играет фундаментальную роль в математическом анализе (см.подробнее [1] с.397).
2.2.1. Теорема Ньютона-Лейбница
Пусть f(x) непрерывна на сегменте [a,b] и F(x) одна из ее первообразных, тогда справедлива формула
Пример 34.
Вычислить  .
.
Решение. Используя формулу Ньютона-Лейбница, а также табличный интеграл 16, получим
.
2.2.2. Методы замены переменной в определенном интеграле
а) Необходимо
вычислить интеграл  ,
,
где f(x) непрерывная функция на [a,b].
Перейдем к новой
переменной t,
полагая  .
Пусть,
кроме того, при измененииt
от
до
значения функции
.
Пусть,
кроме того, при измененииt
от
до
значения функции  не выходят за пределы сегмента [a,b].
Предположим, что функция
не выходят за пределы сегмента [a,b].
Предположим, что функция  непрерывно дифференцируема на промежутке
[,],
то справедлива следующая формула замены
переменной
непрерывно дифференцируема на промежутке
[,],
то справедлива следующая формула замены
переменной
.
Пример 35. Вычислить 
Решение. Преобразуем подкоренное выражение, выделив полный квадрат
.
Введем новую переменную: тогда,
или
Найдем пределы интегрирования новой переменной t:
если 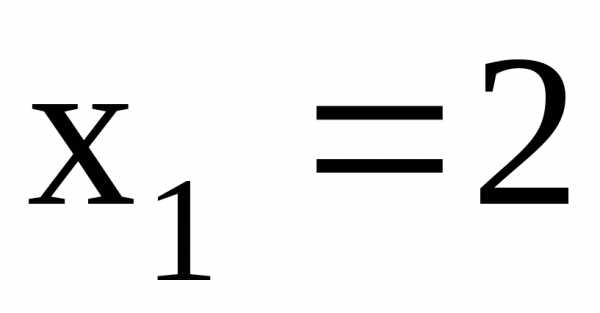 ,
то
,
то
если  ,
то.
,
то.
Воспользуемся формулой замены переменной в определенном интеграле, получим
Заметим, что в данном случае при применении формулы замены переменной отпадает необходимость возвращения к старой переменной х по сравнению с неопределенным интегралом. Это вполне объяснимо, ибо определенный интеграл есть некоторое постоянное число, в то время как неопределенный интеграл от той же самой функции есть некоторая функция.
б) Часто вместо
замены переменной  употребляют обратную замену переменной
употребляют обратную замену переменной .
На конкретном примере покажем, как это
делается.
.
На конкретном примере покажем, как это
делается.
Покажем это на конкретном примере.
Пример 36. Вычислить  .
.
Решение. Пусть  ,
тогда
,
тогда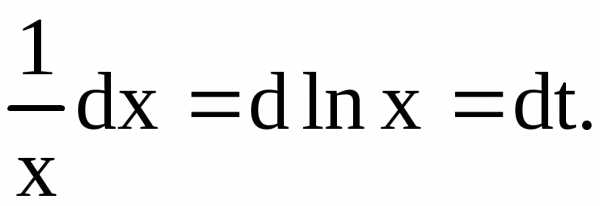
Если 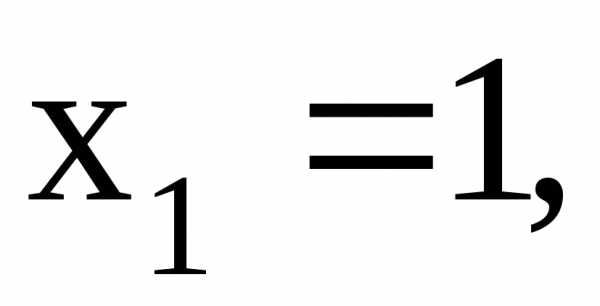 тоесли
тоесли ,
то
,
то
Следовательно,
2.2.3. Формула интегрирования по частям в определенном интеграле
Пусть 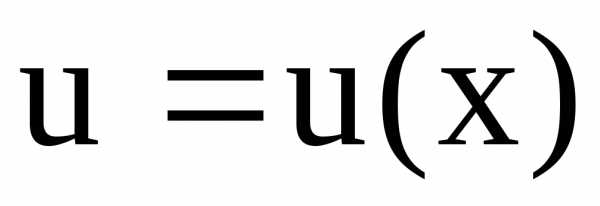 и
и
непрерывные функции вместе со своими
первыми производными на [a,b],
тогда справедлива формула интегрирования
по частям:
непрерывные функции вместе со своими
первыми производными на [a,b],
тогда справедлива формула интегрирования
по частям:

Пример 37. Вычислить интеграл 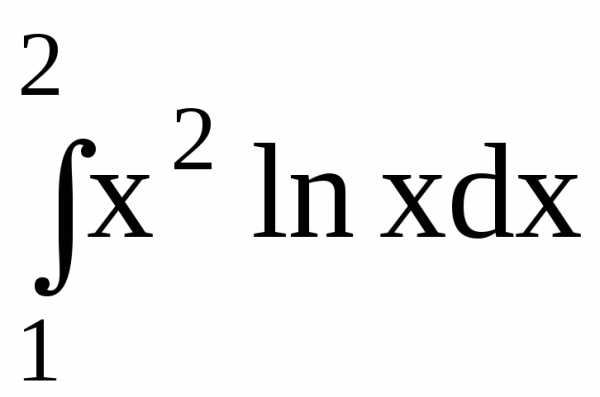 .
.
Решение. Применим полученную формулу

Подробнее о методах интегрирования в определенном интеграле см.[1] с.399-403.
3. Несобственные интегралы
Определение определенного интеграла, его свойства и методы интегрирования рассматривались в предположении, что промежуток интегрирования [a,b] конечен и функция f(x) непрерывна на нем.
Иногда приходится отказываться от одного или обоих этих предположений. В этом случае мы приходим к понятию несобственного интеграла.
3.1. Несобственные интегралы с бесконечными пределами интегрирования
Рассмотрим функцию 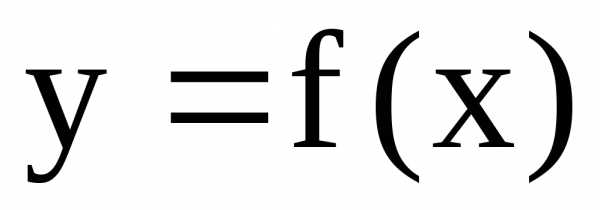 ,
непрерывную на бесконечном промежутке
,
непрерывную на бесконечном промежутке .
.
Несобственным
интегралом от функции f(x)
по промежутку 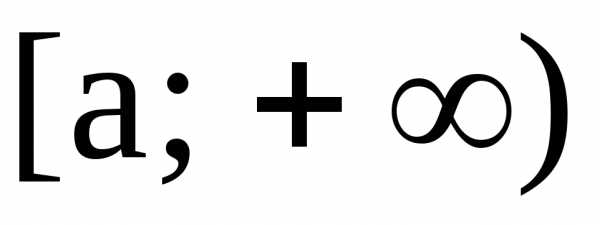 называется
называется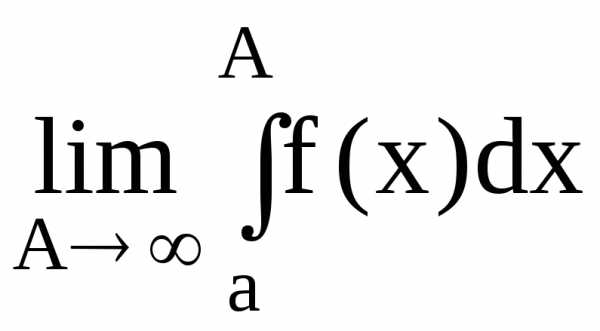 :
:
.
Если указанный предел существует и конечен, то несобственный интеграл с бесконечным пределом интегрирования называется сходящимся, в противном случае расходящимся.
Если 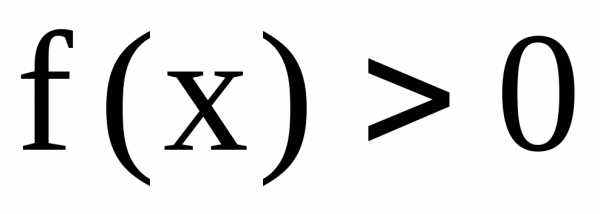 на
на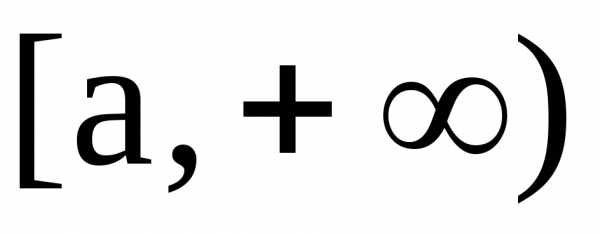 и
и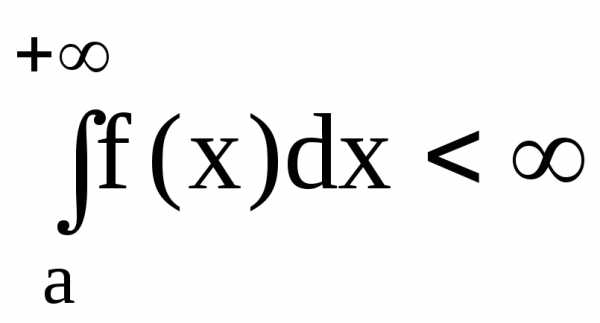 ,
то данный интеграл представляет собой
площадь бесконечной криволинейной
трапеции, ограниченной кривой
,
то данный интеграл представляет собой
площадь бесконечной криволинейной
трапеции, ограниченной кривой ,
прямой
,
прямой и бесконечным интервалом
и бесконечным интервалом .
.
Аналогично
определяется несобственный интеграл
на промежутке 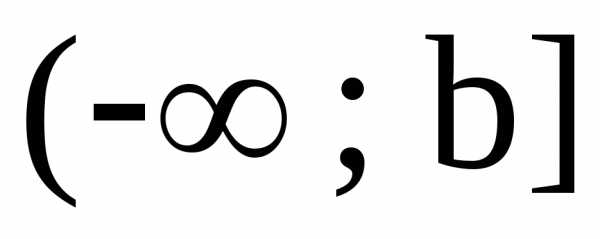 :
:
а на интервале определяется формулой
где с любое действительное число.
Если сравнить две
криволинейные трапеции на рис.3.1, то
конечность или бесконечность их
соответствующих несобственных интегралов
зависит от скорости убывания функции 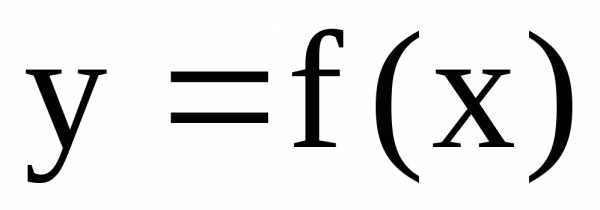 и
и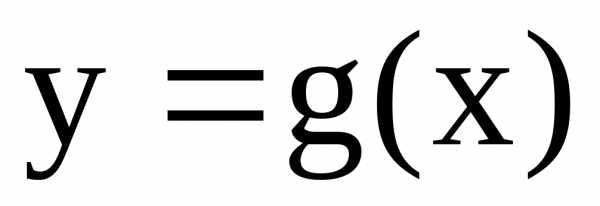 при.
при.
Так, например,  сходится при
сходится при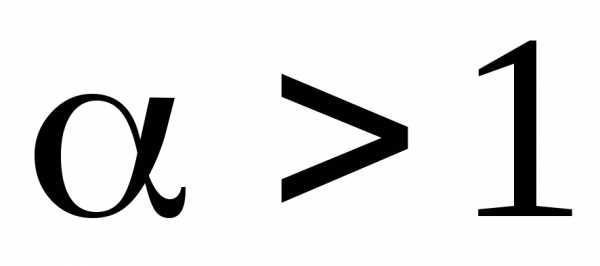 и расходится при
и расходится при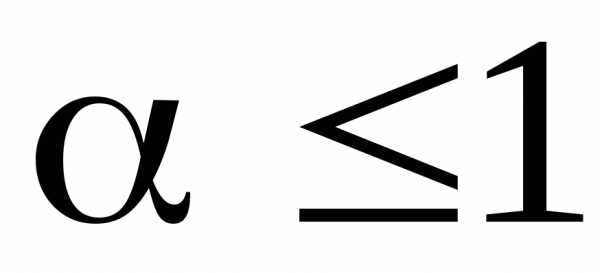 .
.
В этом легко
убедится, вычислив  ,
если.
,
если.
Если 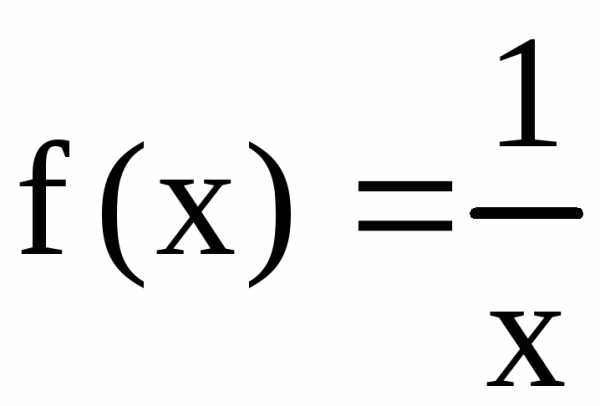 ,
топри,
поэтому
,
топри,
поэтому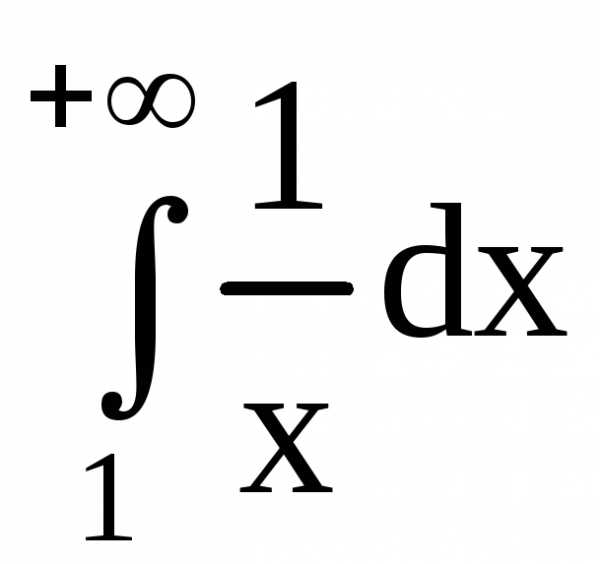
расходится, следовательно, и площадь
соответствующей криволинейной трапеции
бесконечна.
расходится, следовательно, и площадь
соответствующей криволинейной трапеции
бесконечна.
несобственный
интеграл сходящийся, следовательно,
площадь криволинейной трапеции,
ограниченной линиями 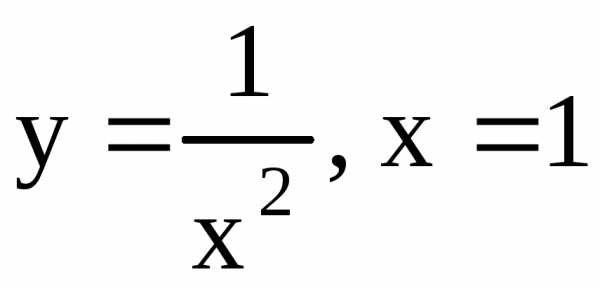 и бесконечным промежутком
и бесконечным промежутком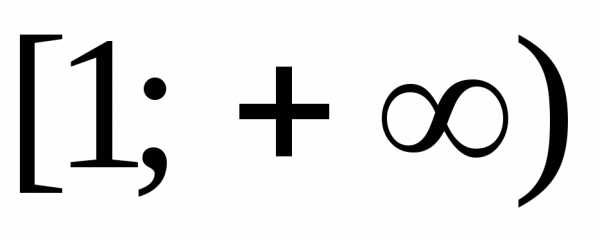 ,
является конечной и равна 1.
,
является конечной и равна 1.
Пример 38. Исследовать на сходимость несобственный
интеграл 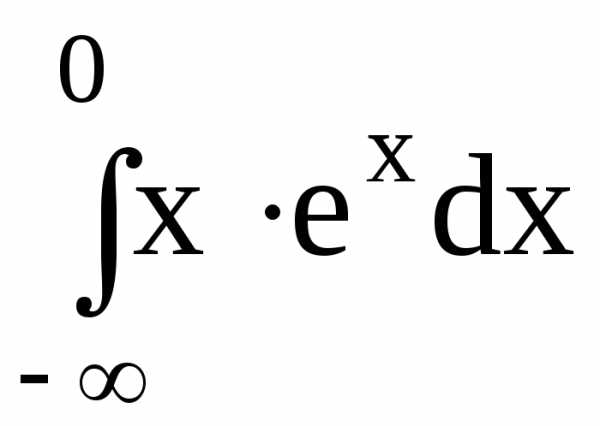 .
.
Решение. Воспользуемся определением несобственного интеграла с бесконечным нижним пределом интегрирования и далее формулой интегрирования по частям
.
Несобственный интеграл сходится.
Пример 39.
Вычислить несобственный интеграл или
установить его расходимость  .
.
Решение. Воспользуемся определением несобственного
интеграла с бесконечными пределами
интегрирования. Полагаем  .
.
Признак
сравнения. Пусть в промежутке  функцииf(x)
и g(x)
непрерывны и
.
Если
функцииf(x)
и g(x)
непрерывны и
.
Если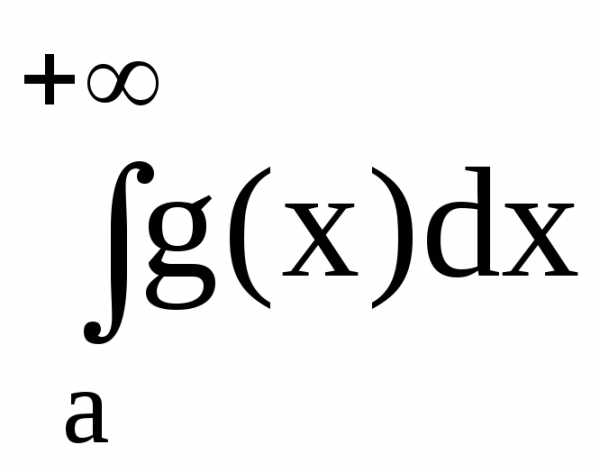 сходится, то сходится и интеграл
сходится, то сходится и интеграл .
Если интеграл
.
Если интеграл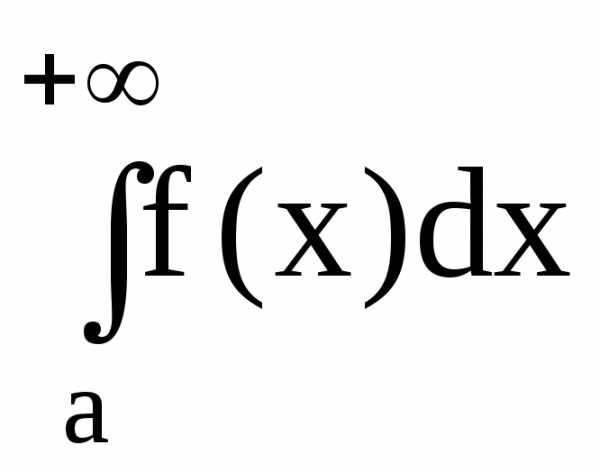 расходится, то и
расходится, то и также расходится.
также расходится.
Замечание. Аналогичное утверждение верно для несобственных интегралов и по другим бесконечным пределам интегрирования.
Пример 40.
Исследовать на сходимость несобственный
интеграл  .
.
Решение. Проведем сравнительный анализ подынтегральной функции при .
.
Но  сходится, т.к.
сходится, т.к.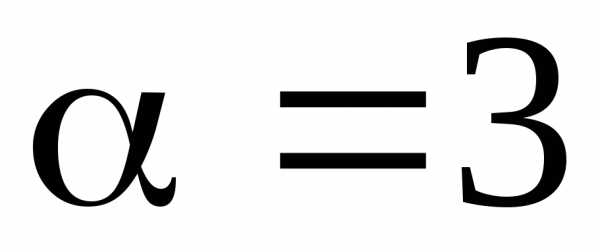 (см. рассуждения выше). Следовательно,
по признаку сравнения сходится и данный
интеграл.
(см. рассуждения выше). Следовательно,
по признаку сравнения сходится и данный
интеграл.
studfiles.net
Определенный интеграл | Высшая математика
Определенный интеграл | Высшая математика- Формула Ньютона-Лейбница:
, где - Формула интегрирования по частям в определенном интеграле:
- Замена переменной в определенном интеграле:
Если функция f(x) непрерывна на отрезке [a;b], а функция x=ϕ(t) непрерывно дифференцируема на отрезке [α;β], где a=ϕ(α), b=ϕ(β), то - Интегралы с бесконечными пределами:
- Признаки сходимости интегралов с бесконечными пределами (признаки сравнения):
1. Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
сходимость
≤
из расходимости расходимость
2. Если при a≤x≤+∞, f(x)>0, g(x)>0 и существует конечный предел ≠0, то интегралы сходятся или расходятся одновременно.
Эталоном сравнения служит интеграл:
он сходится при p>1 и расходится при p≤1. - Интегралы от неограниченных функций:
Если функция f(x) непрерывна при a≤x<b и
, то
. - Признаки сходимости несобственных интегралов от неограниченных функций:
Аналогичны признакам сходимости интегралов с бесконечными пределами. Эталоном сравнения служит интеграл он сходится при 0<p<1 и расходится при p>1.
- Приложения определенного интеграла
- Площадь плоской фигуры
1.1. Фигура ограничена графиком функции y=f(x)(f(x)≥0), прямыми x=a, x=b и осью Ox:
.
1.2. Фигура ограничена графиками функций y=f1(x) и y=f2(x), f1(x)≤2f2(x), и прямыми x=a, x=b:
.
1.3. Фигура ограничена кривой, имеющей параметрические уравнения x=x(t), y=y(t), прямыми x=a, x=b и осью Ox:
, где f=x(t1), b=x(t2), y(t)≥0 на отрезке [t1; t2].
1.4. Площадь криволинейного сектора, ограниченного графиком непрерывной функции ρ=ρ(ϕ), лучами ϕ=α, ϕ=β, где ϕ и ρ — полярные координаты:
. - Длина дуги кривой
2.1. Гладкая кривая задана явно, y=f(x), a≤x≤b:
.
2.2. Кривая задана параметрически, x=x(t), y=y(t), z=z(t), t1≤t≤t2:
(для плоской кривой z(t)≡0).
2.3. Кривая задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
. - Площадь поверхности вращения, образованной вращением вокруг оси Ox дуги кривой
3.1. Дуга задана явно, y=f(x), a≤x≤b:
.
3.2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
.
3.3. Дуга задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
. - Объем тела
4.1. Тело заключено между плоскостями x=a и x=b, площадь сечения тела плоскостью, перпендикулярной оси Ox – известная функция S=f(x), непрерывная на отрезке [a; b], f(x)≥0:
.
4.2. Криволинейная трапеция, ограниченная кривой y=f(x), a≤x≤b вращается вокруг оси Ox:
.
4.3. Криволинейная трапеция, ограниченная кривой x=g(y), c≤y≤d вращается вокруг оси Oy:
.
Формулы, уравнения, теоремы, примеры решения задач
matematika.electrichelp.ru
Основные правила интегрирования
1. Неопределённый интеграл от алгебраической суммы (или разности) конечного числа непрерывных функций равен алгебраической сумме (или разности) интегралов от этих функций:
.
2. Постоянный множитель можно выносить за знак интеграла:
, .
3. (Инвариантность формулы интегрирования)
Если , то и , где – произвольная функция, имеющая непрерывную производную.
Таблица основных интегралов
1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
10. .
11. .
12. .
13. .
14. .
В таблице переменная интегрирования может обозначать как независимую переменную, так и функцию от независимой переменной (согласно свойству инвариантности формулы интегрирования).
Непосредственное интегрирование
Непосредственным интегрированием называется метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (выражения) и применения свойств неопределенного интеграла сводится к табличному интегралу.
Примеры.
1. .
2. .
3. .
4. .
5. .
6. .
Интегрирование путем подведения под знак дифференциала и методом подстановки
При сведении интеграла к табличному часто используют метод интегрирования путем подведения под знак дифференциала. В данном случае используют следующую формулу:
,
где – функция, имеющая непрерывную производную на рассматриваемом промежутке.
Применяют также интегрирование методом подстановки.
Обозначим , тогда получим . Тогда
.
Подведение под знак дифференциала есть одна из реализаций метода замены переменной.
Удачная замена переменной позволяет упростить исходный интеграл, а иногда свести его даже к табличному.
Примеры.Вычислить следующие интегралы:
1. .
1 способ.
.
2 способ.
.
2. .
1 способ.
.
2 способ.
.
3. .
1 способ.
.
2. способ.
.
4. .
1 способ.
.
2 способ.
.
Метод интегрирования по частям
Пусть функции и имеют непрерывные производные на заданном интервале, тогда справедлива формула интегрирования по частям:
.
Метод интегрирования по частям целесообразно применять в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен, при этом за берется та функция, которая при дифференцировании упрощается, а за берется та часть подынтегрального выражения, интеграл от которой известен или может быть найден.
Выделяют следующие типы интегралов, которые удобно вычислять методом интегрирования по частям:
1. , , , где – многочлен степени , – число.
При вычислении данных интегралов формулу применяют n раз, обозначив за .
2. , , , , .
При вычислении интегралов второго типа удобно обозначить за .
3. , , – числа.
В данном случае обозначают .
Примеры.
1.
2.
.
Иногда формулу интегрирования по частям приходится применять более одного раза.
Пример.
.
Интегрирование простейших рациональных дробей
1. Интегралы вида сводят к табличным заменой .
2. Интегралы вида разбиваются на сумму двух интегралов и . Первый решается заменой . А второй представляет собой табличный интеграл.
3. Интегралы вида решаются с помощью выделения полного квадрата в знаменателе
.
Аналогично решаются интегралы вида .
Определенный интеграл
Пусть функция определена и ограничена на и произвольное разбиение этого отрезка на элементарных отрезков. На каждом отрезке выберем точку . Тогда сумма называется интегральной суммой для функции на отрезке .
Если предел интегральной суммы при стремлении к нулю существует и конечен, то он называется определенным интегралом от функции в пределах от до и обозначается:
.
Определенный интеграл не должен зависеть от способа выбора точек и точек
Для вычисления определенного интеграла используется формула Ньютона-Лейбница:
,
где любая первообразная функции на отрезке .
Таким образом, при вычислении определенного интеграла с использованием формулы Ньютона-Лейбница сначала, используя технику нахождения неопределенного интеграла, находят первообразную для подынтегральной функции , а затем вычисляют приращение первообразной на данном отрезке.
Примеры.
1.
2.
infopedia.su

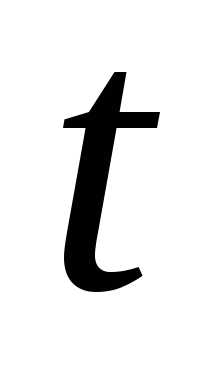 от
от до
до переменная
переменная изменяется от
изменяется от до
до ,
то есть
,
то есть определена и непрерывна на отрезке
определена и непрерывна на отрезке ,
то справедлива такая формула
,
то справедлива такая формула