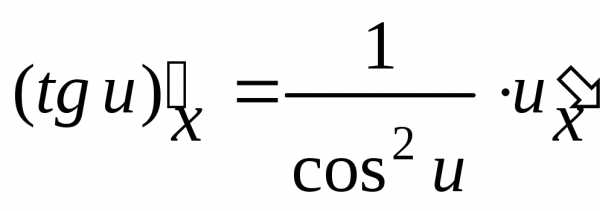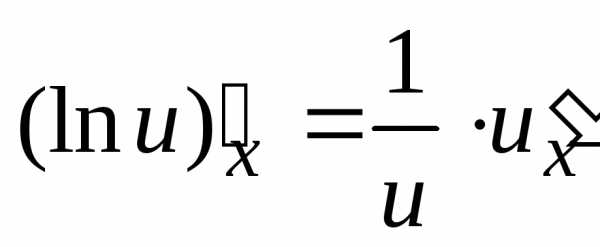1.3. Основные правила дифференцирования
Теорема 1.
Если функции 
и
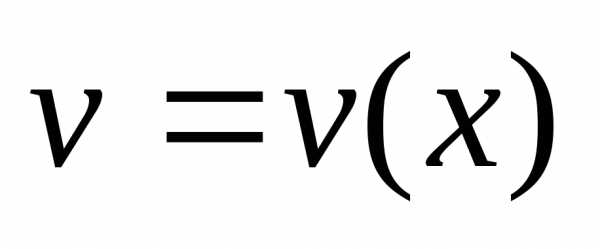дифференцируемы в данной точке, то в
той же точке дифференцируема и их сумма,
причем производная суммы равна сумме
производных слагаемых:
.
Формула обобщается на случай любого конечного числа слагаемых.
Теорема 2.
Если функци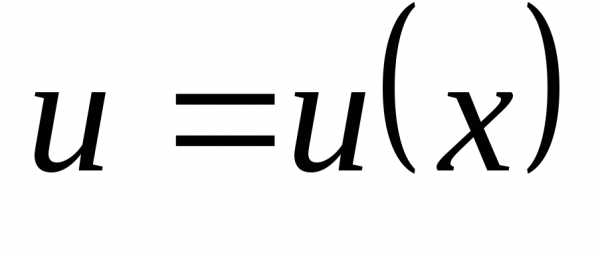и 
и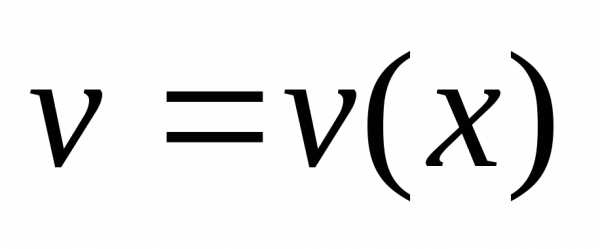
дифференцируемы в данной точкех,
то в этой же точке дифференцируемо и их
произведение, при этом:
.
Следствие. Постоянный множитель можно выносить за знак производной:
, где .
и
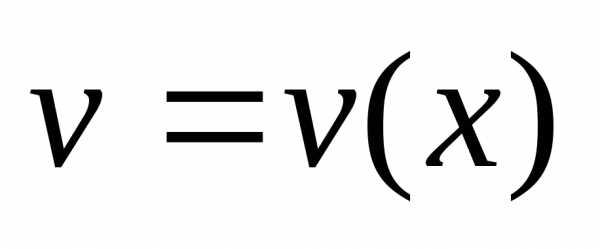дифференцируемы и
,
то в той же точке дифференцируемо и их
частное, причем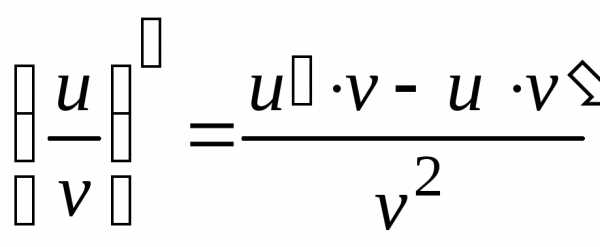
.
1.4. Обратная функция и ее производная
Рассмотрим функцию y = f (x) с областью определения (a, b) и множеством значений (c, d). Пусть эта функция такова, что всякая прямая, проходящая через точку интервала (c, d) параллельно оси Ох, пересекает ее график только в одной точке, т.е. уравнение
(c, d)
определяет единственное значение x
(a, b).
В этом случае каждому значению y
(c, d)
соответствует единственное значение x
(a, b),
т.е. на интервале (c, d)
задана функция, множество значений
которой есть интервал (a, b).
Эта функция называется обратной по
отношению к функции y = f
.
Очевидно, что для функции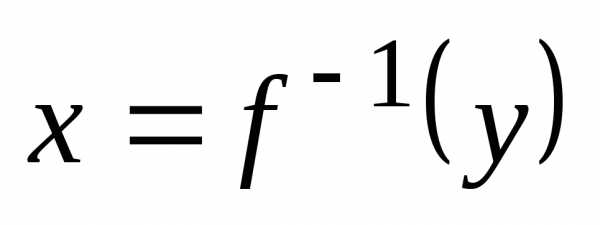
обратной является функция
.
Поэтому обе эти функции называютсявзаимно
обратными. Теорема. Если функция y = f (x)
монотонна и дифференцируема в некотором
интервале и имеет в точке x этого интервала производную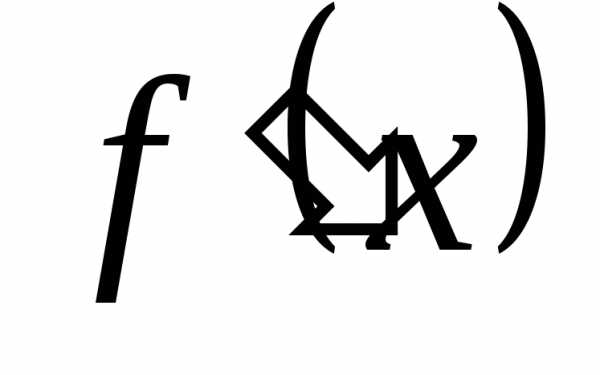 
,
не равную нулю, то обратная функция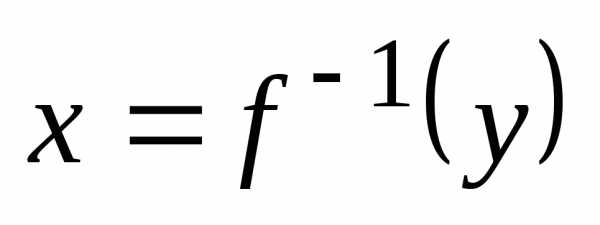
в соответствующей точке
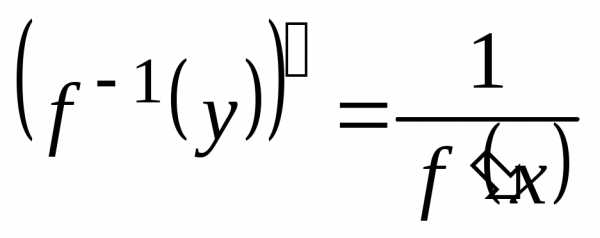или иначе
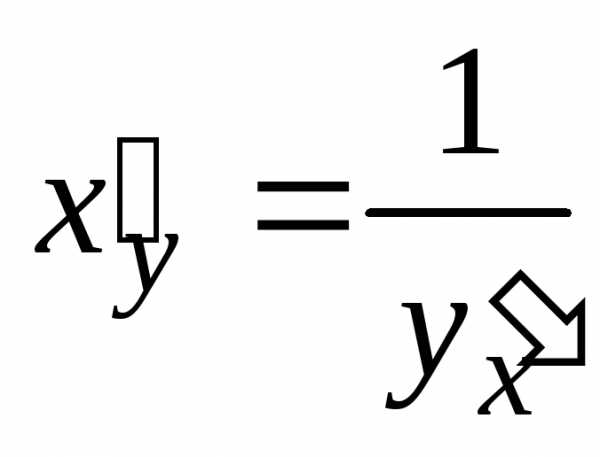.1.5. Производная сложной функции
Есл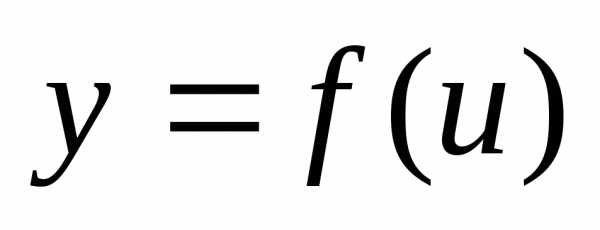и 
и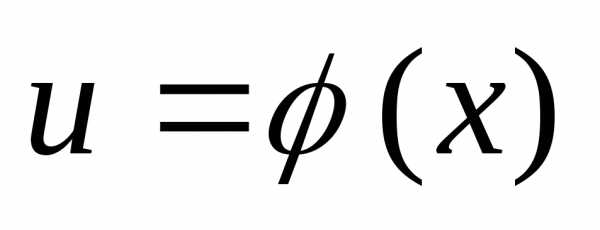
,
тоестьсложная
функция независимого аргумента x с промежуточным аргументом u.
Теорема.
Если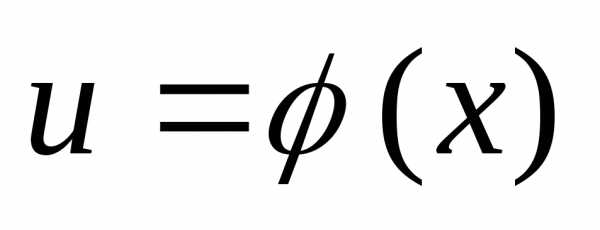 
имеет производную
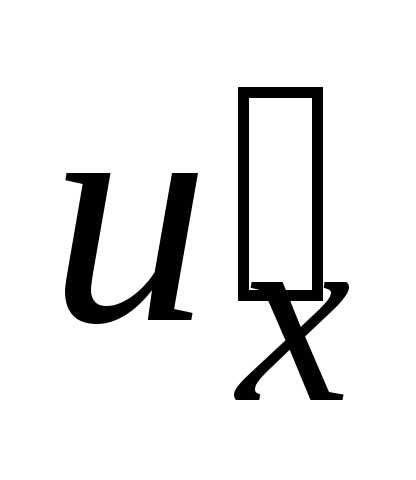в точкеx,
а функция 
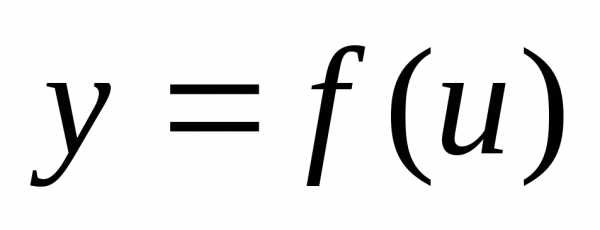
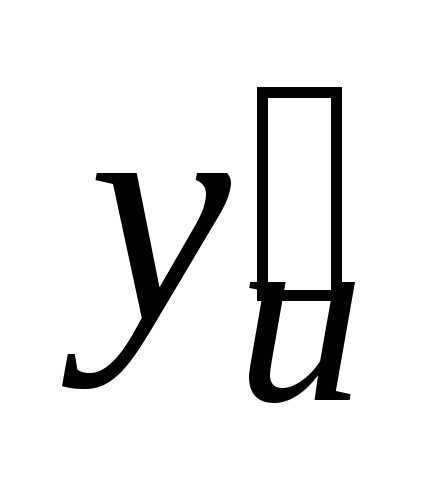в соответствующей точкеu,
то сложная функция
в данной точкеx имеет производную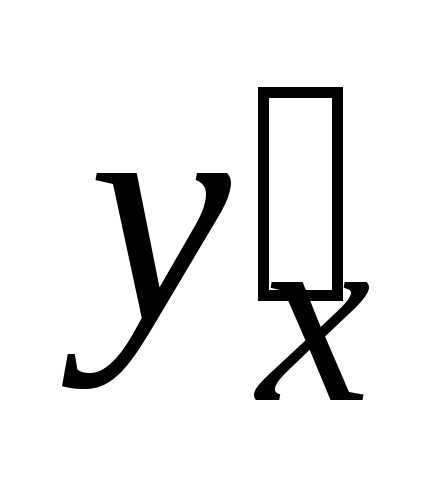 
,
которая находится по следующей формуле.Часто пользуются следующей формулировкой этой теоремы: производная сложной функции равна произведению производной внешней функции по промежуточному аргументу на производную внутренней функции по независимому аргументу.
Сложная функция может быть составлена не из двух функций, а из большого их числа. В таких случаях теорема применяется последовательно несколько раз.
В частности, если
функция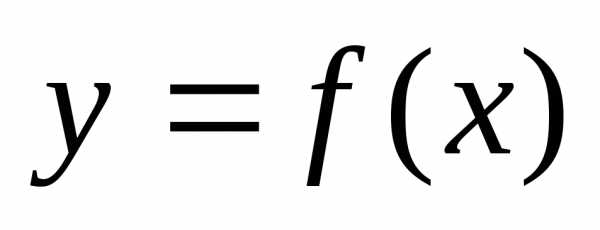 
,
,
,
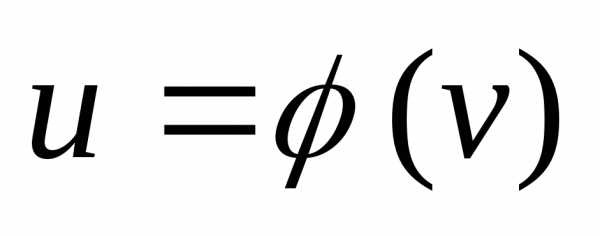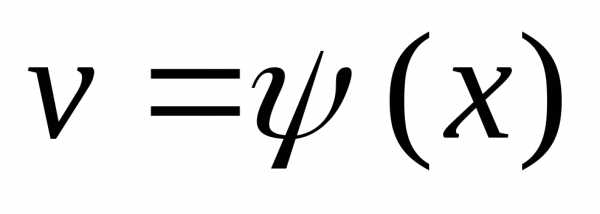то производная
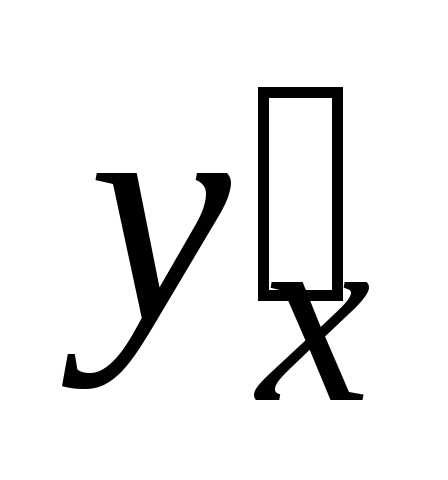находится по формуле.1.6. Производные основных элементарных функций.
Таблица производных
Используя определение производной, можно найти производные основных элементарных функций.
1. Производная степенной функции .
2. Производная показательной функции .
В
частности,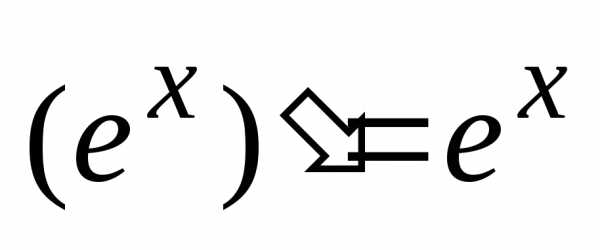 
3. Производная логарифмической
функци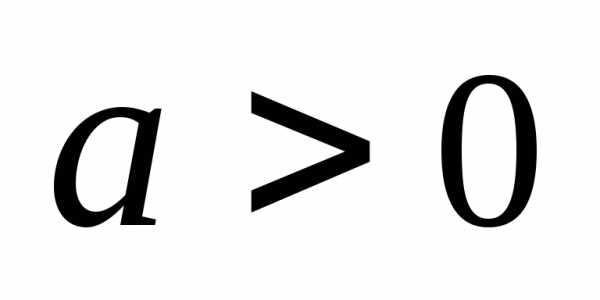и , 
,
.
В частности,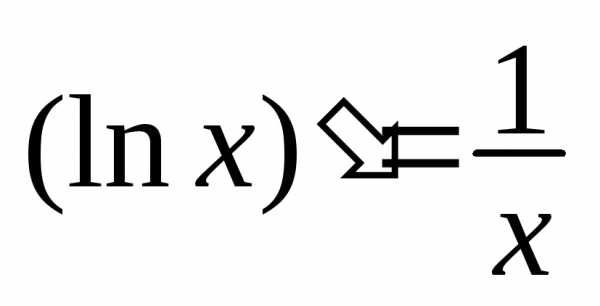
.
4. Производные тригонометрических
функций ,,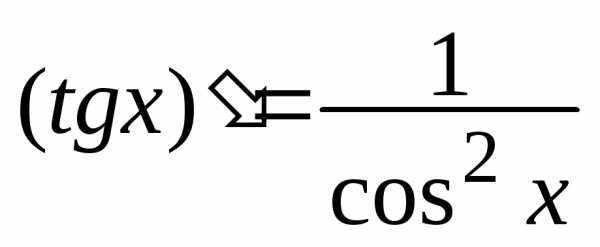
,
.
Найдем, например,
производную функции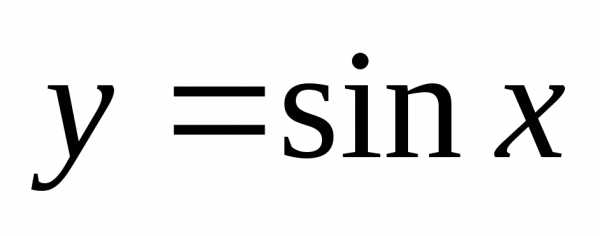 
.
По определению производной имеем:
.
Производную функции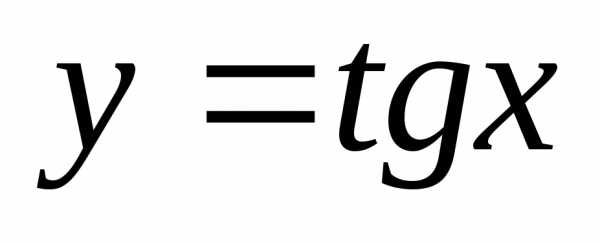 
.
5. Производные обратных тригонометрических функций ,.
Найдем, например,
производную функции
.
Функция,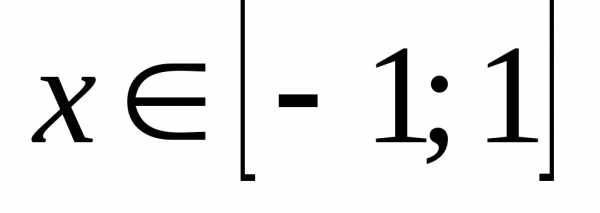
обратная к функции
,
.
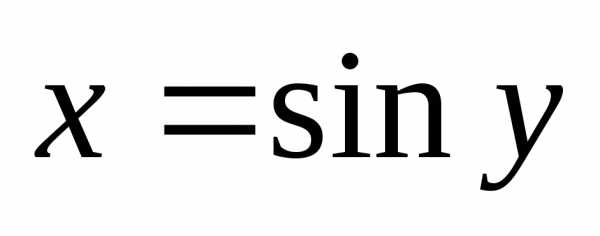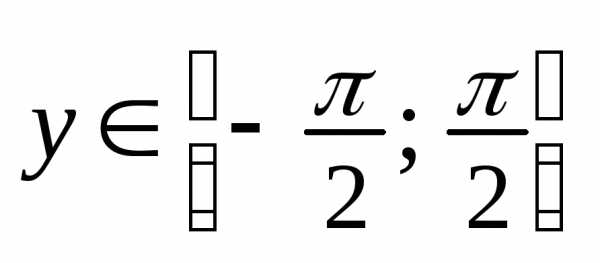По правилу дифференцирования обратной
функции
.
На интервале
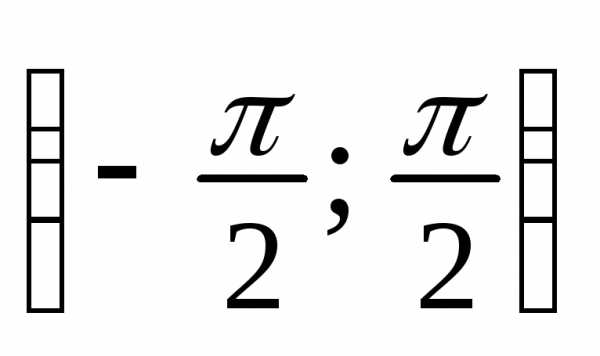имеем .
Запишем таблицу
производных для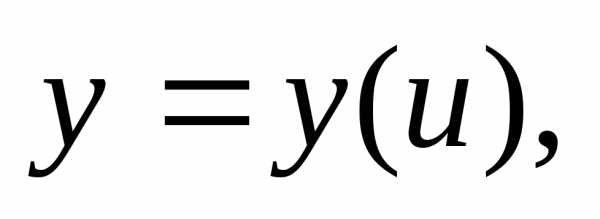 
где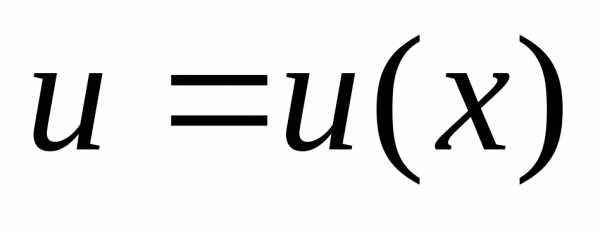
.
1. | 8. |
2. | 9. |
3. | 10. |
4. | 11. |
5. | 12. |
6. | 13. |
7. | 14. |
Применяя формулы и правила дифференцирования, найдем производные следующих функций:
1) .
Применим правило дифференцирования произведения двух функций:
.
2) 
.
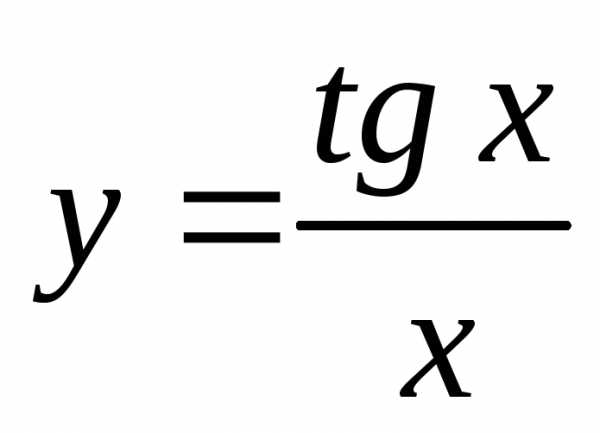Применим правило дифференцирования частного двух функций:
.
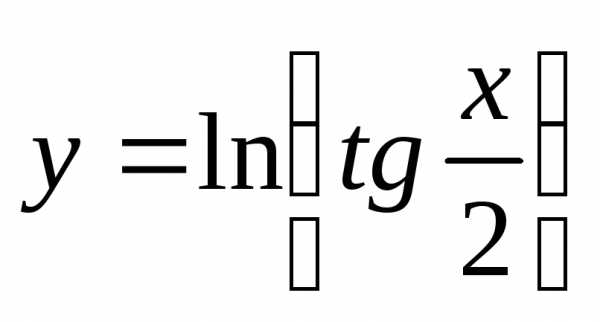.Применим правило дифференцирования сложной функции:
.
studfiles.net
18 Основные правила нахождения производной
19 Применение производной к нахождению нибольших и наименьших значений функций на отрезке.
Достаточное условие возрастания функции
Если в каждой точке интервала (a, b) f'(x)>0, то функция f(x) возрастает на этом интервале.
Достаточное условие убывания функции.
Если в каждой точке интервала (a, b) f'(x)<0, то функция f(x) убывает на этом интервале.
Определение:
x0 называется критической точкой функции f(x), если
1) x0 – внутренняя точка области определения f(x) ;
2) f'(x0)=0 или f'(x0) не существует.
Необходимое условие экстремума:
Если x0– точка экстремума функции f(x), то эта точка является критической точкой данной функции.
Достаточное условие экстремума:
Если при переходе через точку x0 производная функции меняет знак, то x0 – точка экстремума функции f(x).
Примеры экстремумов:
Схема исследования функции.
Найти область определения функции.
Проверить, не является ли функция четной или нечетной; проверить также, не является ли она периодической.
Найти, если это возможно, точки пересечения графика функции с осями координат и промежутки знакопостоянства функции. Иногда для уточнения построения графика следует найти две три дополнительные точки.
Найти производную функции и ее критические точки.
Найти промежутки монотонности и экстремумы функции.
Построить график функции, используя полученные результаты исследования.
Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].
Найти значения функции в концах отрезка, т.е. f(a) и f(b) ;
Найти значения функции в тех критических точках, которые принадлежат интервалу (a,b) ;
Из найденных значений выбрать наибольшее и наименьшее.
20 Функции 2 переменных. Частные производные. Перестановочность частных производных.Линии уровня.Градиент.
В естествознании встречаются ситуации, когда одна величина является функцией нескольких других:
,
– работа тока на участке цепи и др.
Далее остановимся на случае функции 2 переменных.
Определение 25.1.
Если каждой паре (x,y) значений двух, независимых друг от друга, переменных величин x и y , из некоторой области их изменений D, соответствует одно определенное значение величины z, то говорят, что z – есть функция двух независимых переменных x и y , определенная в области D (область определения функции).
Обозначение: z = f(x,y)=g(x,y)…
Способы задания функции
Табличный
S=S(x,y)
yx | 1 | 1.5 | 2 |
1 | 1 | 1.5 | 2 |
5 | 5 | 7.5 | 10 |
Аналитическое задание функции
.
Определение 25.2.
Областью определения функции z = f(x,y) называется множество {x,y}, для которых формула имеет смысл.
Пример 25.1.
Функция определена при.
Графическое задание функции.
Определение 25.3.
Пусть задана функция Графиком называется множество точек в пространстве , где-абсцисса,- ордината, а- аппликата, т.е. графиком являетсяповерхность.
Ранее изучали, что – верхняя часть сферы,
– параболоид, – плоскость.
Замечание 1. Любая поверхность в пространстве является графиком функции, если прямая, параллельная, пересекает ее в одной точке.
Предел функции двух переменных
Определение 25.4.
Множество точек , удовлетворяющих неравенству
называется -окрестностью точки.
Геометрический смысл
-окрестность точки – круг с центром в точкерадиуса.
Определение 25.5.
Функция имеет предел в точкеравный, т.е.
,
если она определена в некоторой окрестности точки , и для любого сколь угодно малогонайдется такое, что для всех точек, удовлетворяющих неравенствувыполняется неравенство
.
Замечание 2. Все правила нахождения пределов, сформулированные для функции одной переменной остаются в силе и для функции двух переменных.
Пример 25.2.
1) ,
2) .
Пусть
Определение 25.6.
Функция называетсябесконечно малой в точке
(или при ), если.
Если , то, где,
т.е. функция в окрестности точкиотличается от числана бесконечно малую функцию.
Замечание 3.
Сравнение бесконечно малых функций двух переменных производится также, как и бесконечно малых функций одной переменной, причем под символом будем понимать любую бесконечно малую в точкефункцию более высокого порядка малости, чем бесконечно малая в точкефункция, т.е..
studfiles.net
Формулы и основные правила дифференцирования функций
В основные правила дифференцирования функций входят вынесение констант за знак производной, сумма и разность, умножение и деление функций:
- Константу можно вынести за знак производной:
- Производная суммы/разности функций равна сумме/разности производных:
- Дифференцирование произведения двух функций выполняется по формуле:
- Дифференцирование частного двух функций выполняется по формуле:
| Пример 1 |
| С помощью основных правил дифференцирования найти производную: |
| Решение |
Берем производную: Так как присутствует константа, то по первому правилу дифференцирования можно вынести её за знак производной, а затем по таблице : |
| Ответ |
| Пример 2 |
| Найти производную суммы функций |
| Решение |
По второму правилу дифференцирования производная суммы функций равна сумме производных: Первое слагаемое дифференцируем по правилу степенной функции : Производная косинуса равна: Объединяем в сумму: |
| Ответ |
| Пример 3 |
| Найти производную произведения функций: |
| Решение |
По третьему правилу дифференцирования произведения двух функций расписываем: |
| Ответ |
| Пример 4 |
| Найти производную дроби |
| Решение |
Используя четвертое правило дифференцирования частного двух функций получаем: |
| Ответ |
Используя основные правила дифференцирования можно находить большинство производных функций.
xn--24-6kcaa2awqnc8dd.xn--p1ai