§ 10. Основные правила вычисления производных.
Теорема 10.1. Пусть функцияu=φ(x)
имеет в данной точкеx0производную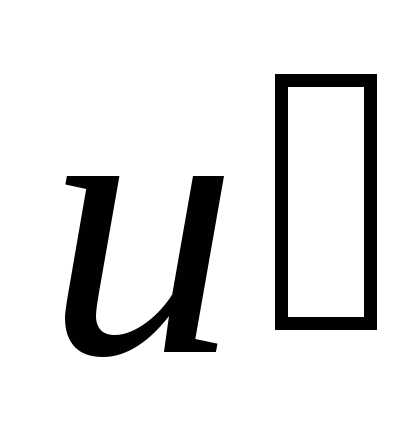 .
Тогда функцияy=c∙uимеет в точкеx0производную.
.
Тогда функцияy=c∙uимеет в точкеx0производную.
Здесь c– произвольная постоянная.
Доказательство. Дадим аргументу x приращение ∆ x. Тогда
∆ y=y(x0+∆ x) ─y(x0) =c∙ φ(x0+∆ x) ─c∙ φ(x0) =c∙[φ(x0+∆ x) ─ φ(x0)] =c∙∆φ.
Теорема доказана.
Теорема 10.2.Пусть функцииu(x) иv(x) имеют в данной точке
u(x)
∙v(x),
а также (еслиv(x0)≠0)
функция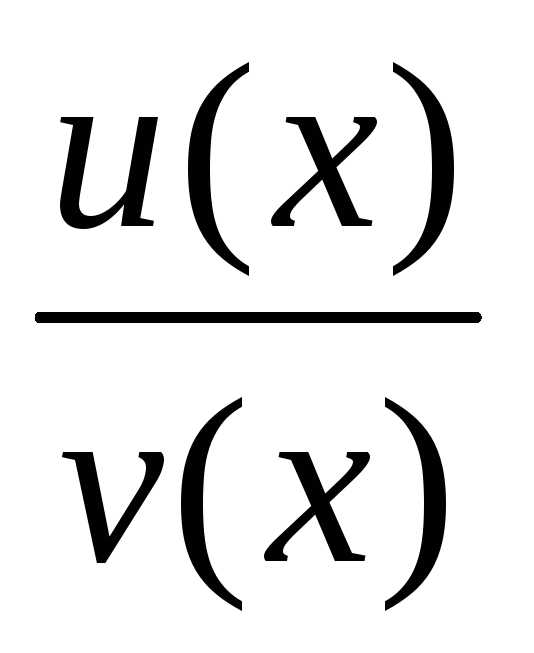 ,
,
причём (,,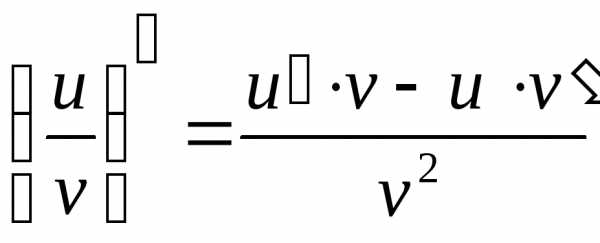 .
.
Доказательство. Пусть f(x) =u(x) +v(x). Тогда ∆ f=f(x0+∆ x) ─f(x0) =
= u(x0+∆ x) ─u(x0) +v(x0+∆
 (x0)
=
(x0)
= 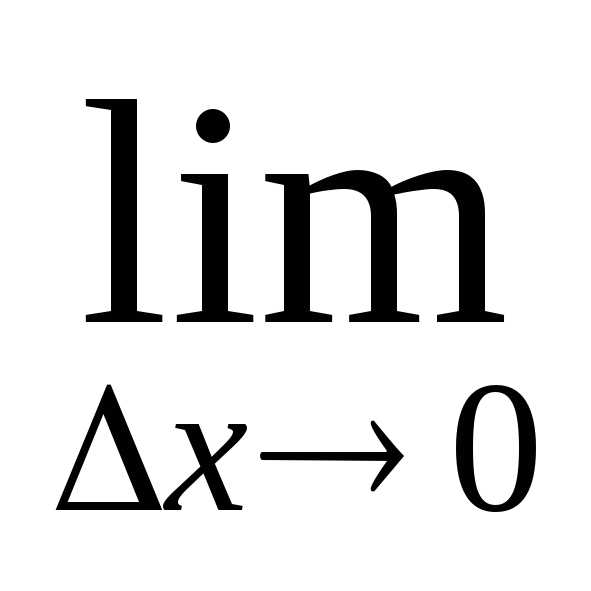
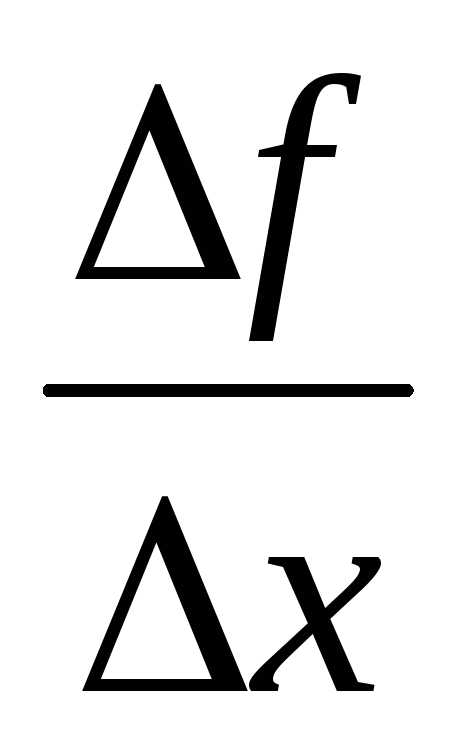 =
= 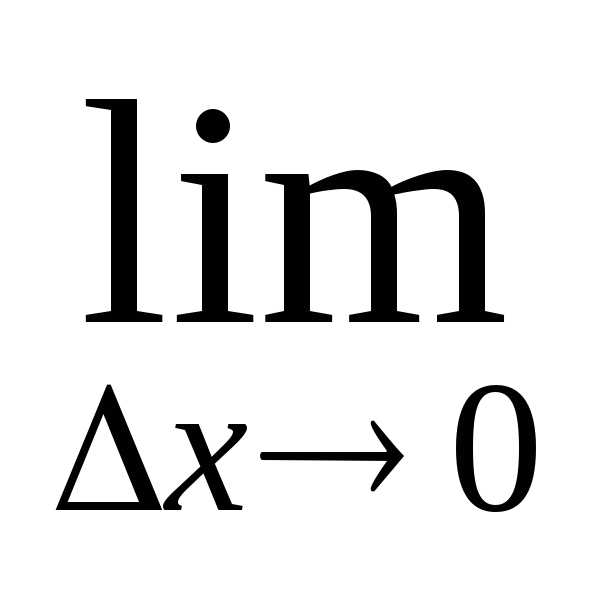
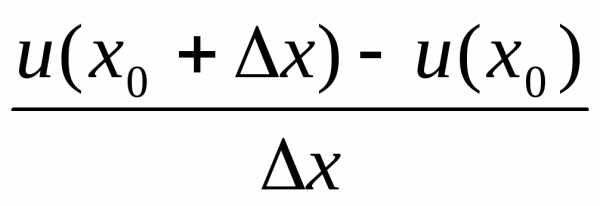 +
+ 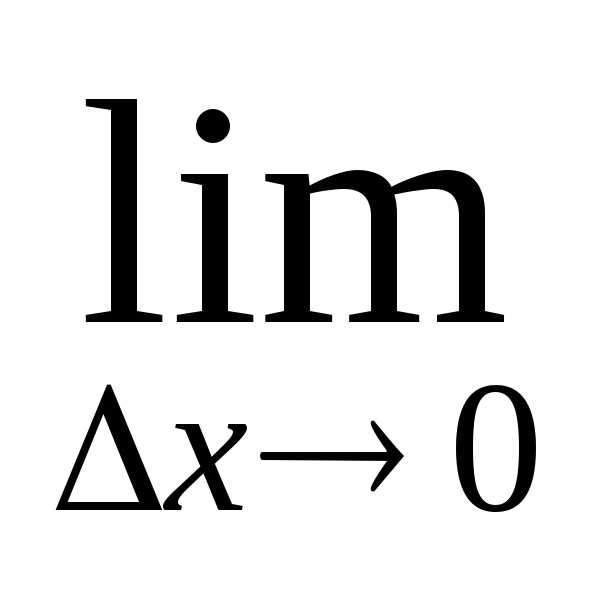
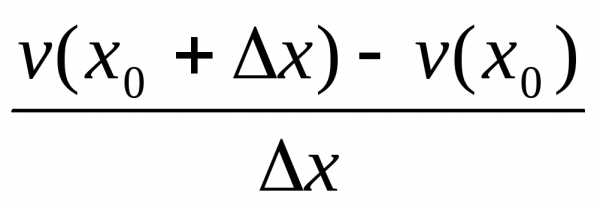 =
= .
Таким образом,.
.
Таким образом,.
Совершенно аналогично доказывается, что .
Пусть теперь f(x) =u(x) ∙v(x). Тогда
∆ f=f(x0+∆ x) ─f(x0) =u(x0+∆ x) ∙v(x0+∆ x) ─u(x0) ∙v(x0).
Введём для удобства обозначения: ∆u = u(x0+∆ x) ─u(x0), ∆v=v(x0+∆ x) ─v(x0),
u = u(x0),v = v(x0). Тогдаu(
∆f= (u+ ∆u) ∙ (v+ ∆v) ─u ∙v= ∆u ∙ (v+ ∆v) +u ∙ ∆v.
Так как функция v(x) дифференцируема (имеет производную) в точкеx0, то она непрерывна в этой точке. Следовательно, при ∆ x→0 и ∆v→0. Поэтому
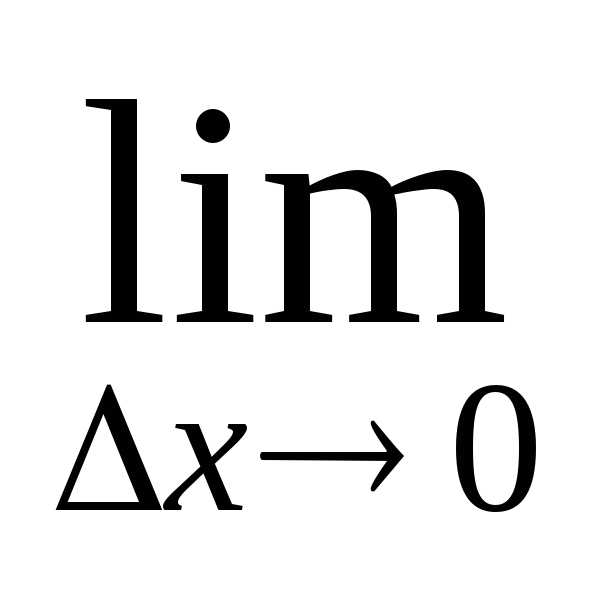
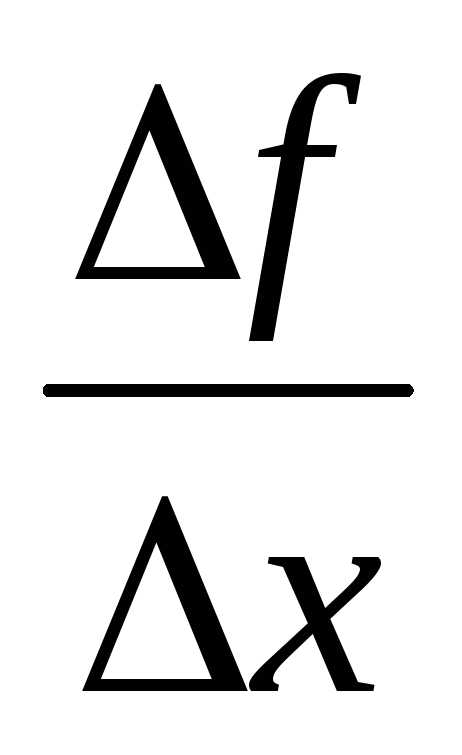 =
= 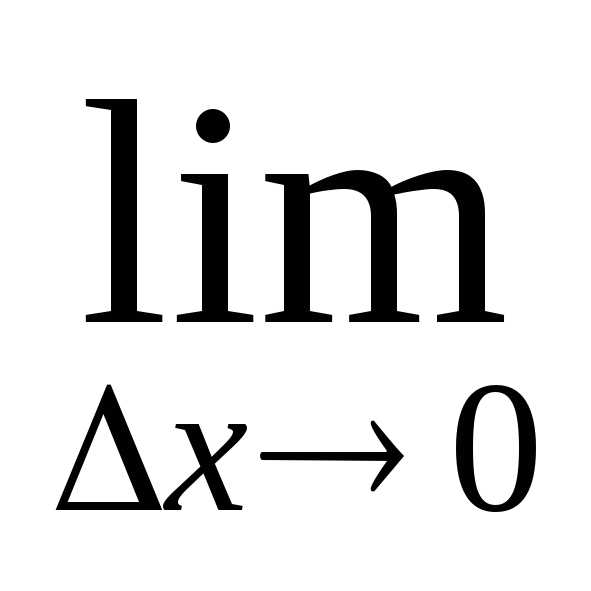
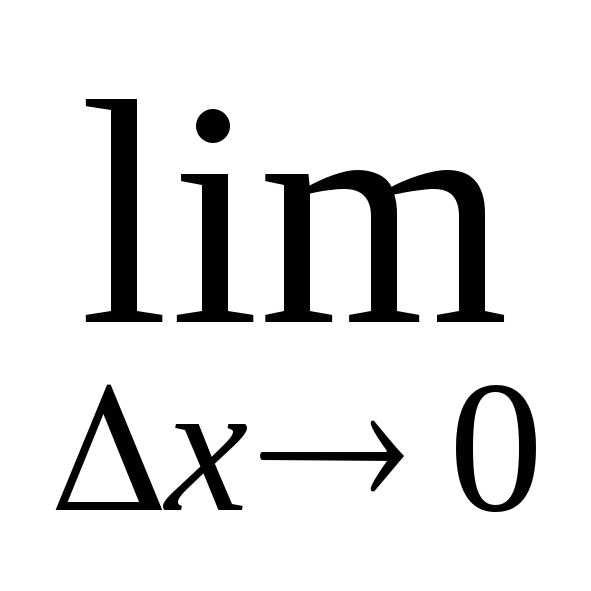
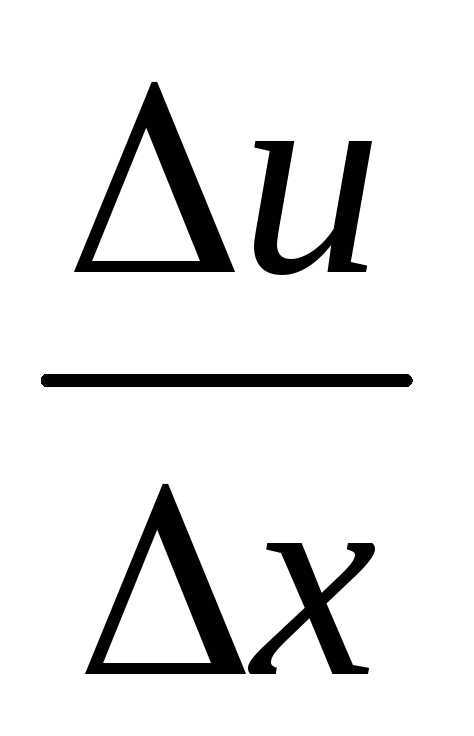 ∙v +u ∙
∙v +u ∙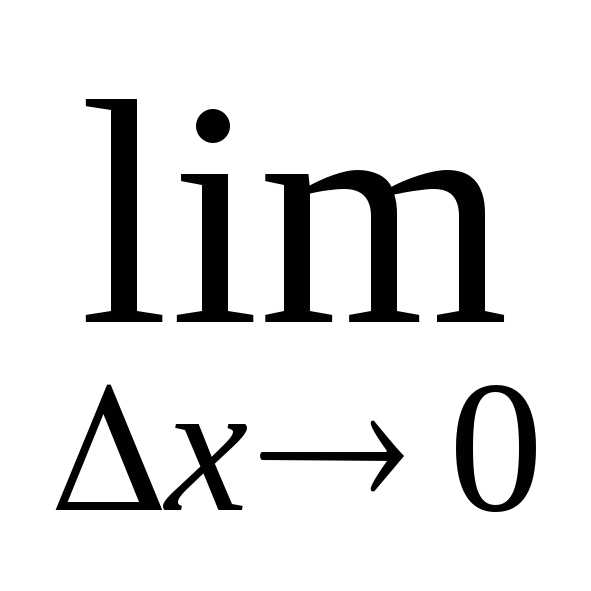
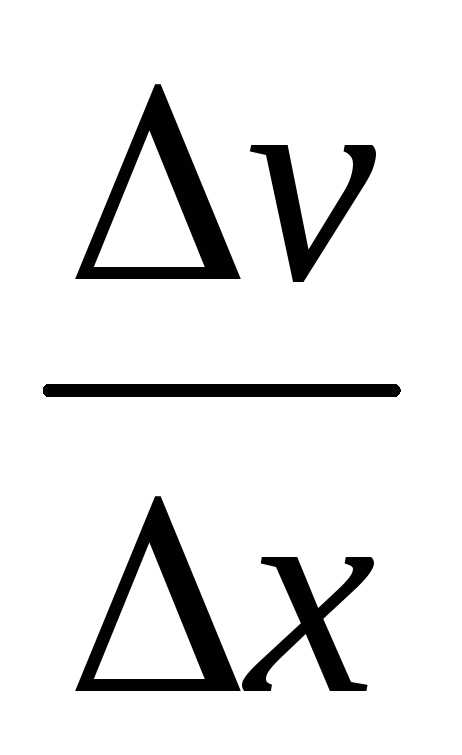 +
+ 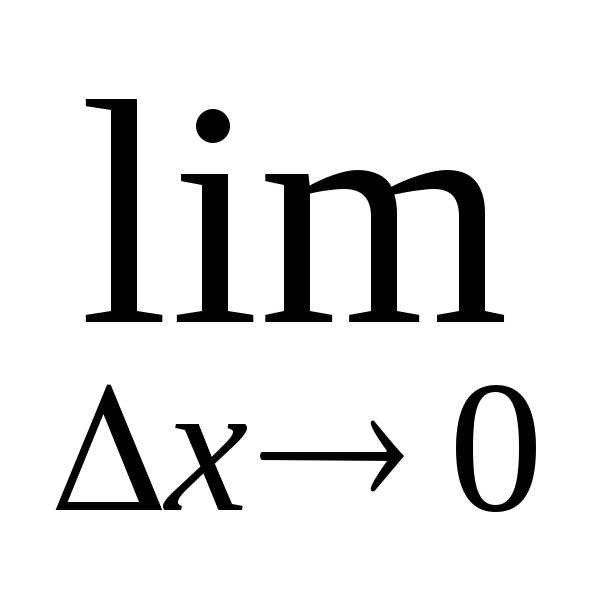
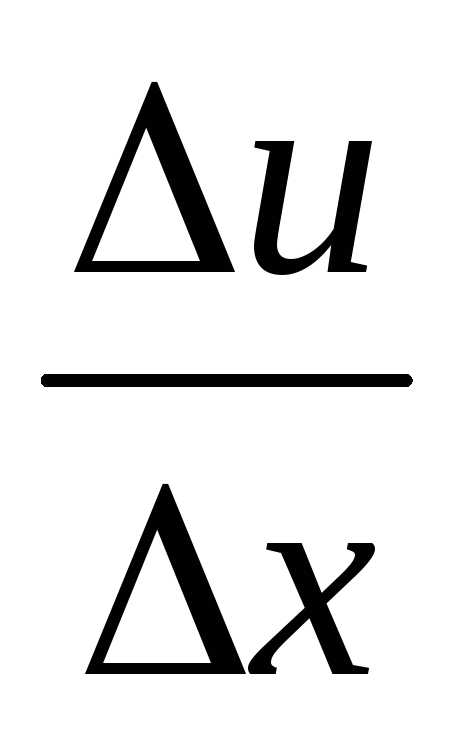 ∙
∙ 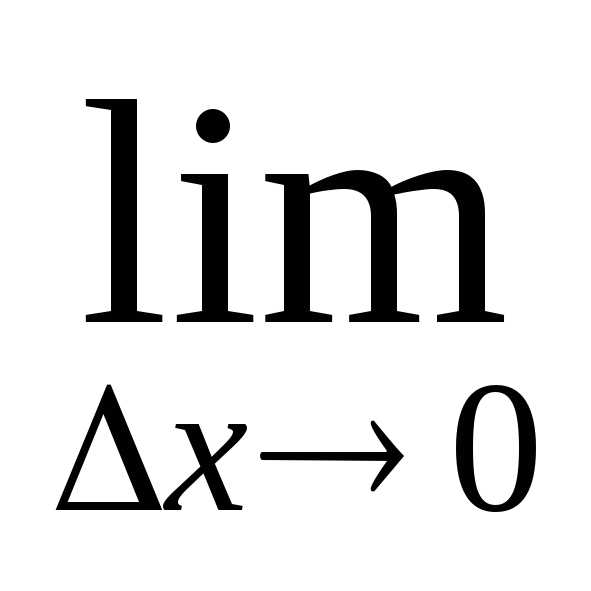 ∆v=
∆v==. Таким образом,.
Пусть далее f(x)
= .
Тогда
.
Тогда
∆ f=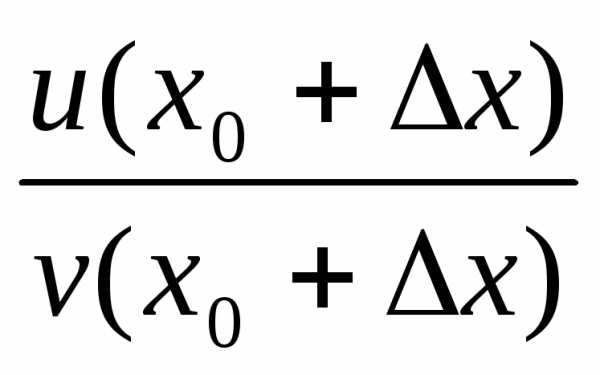 ─
─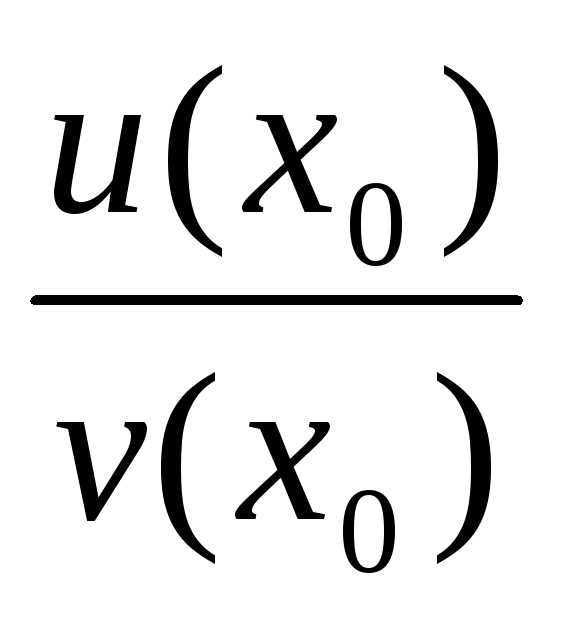 =(здесь обозначенияu,v, ∆u,
∆vимеют тот же смысл,
что и выше).
=(здесь обозначенияu,v, ∆u,
∆vимеют тот же смысл,
что и выше).
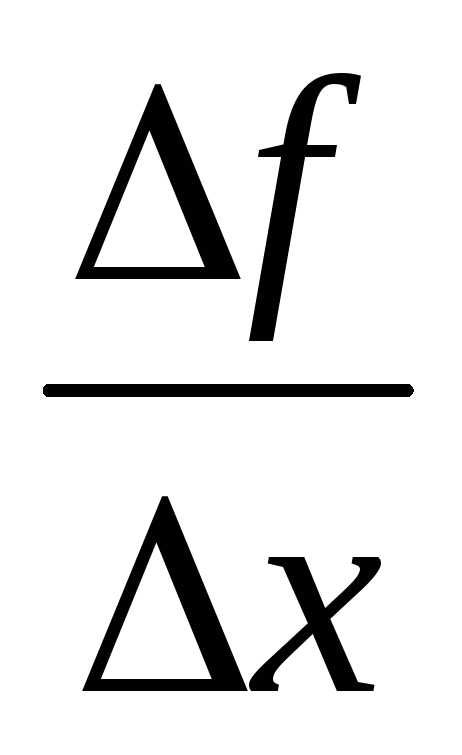 =
=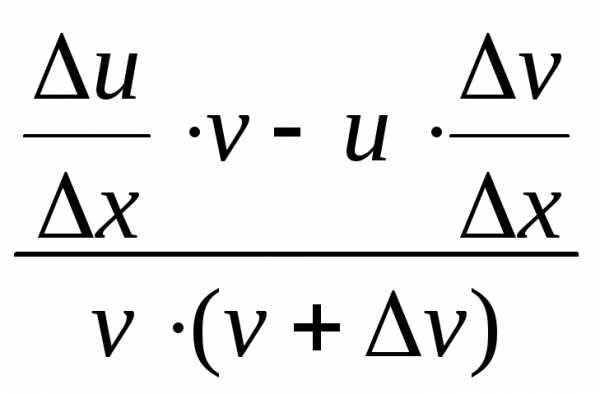 .
Так как
.
Так как 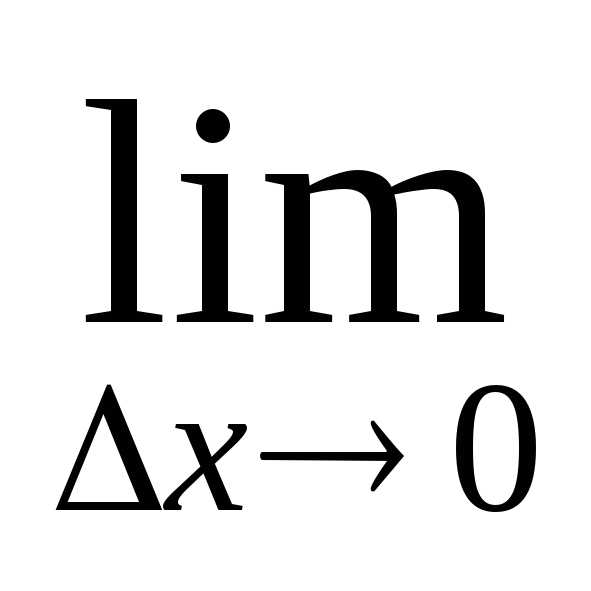 ∆v= 0, то
∆v= 0, то
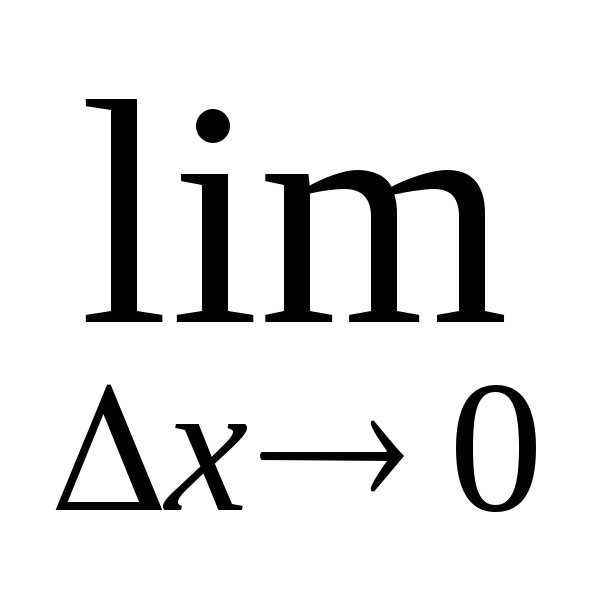
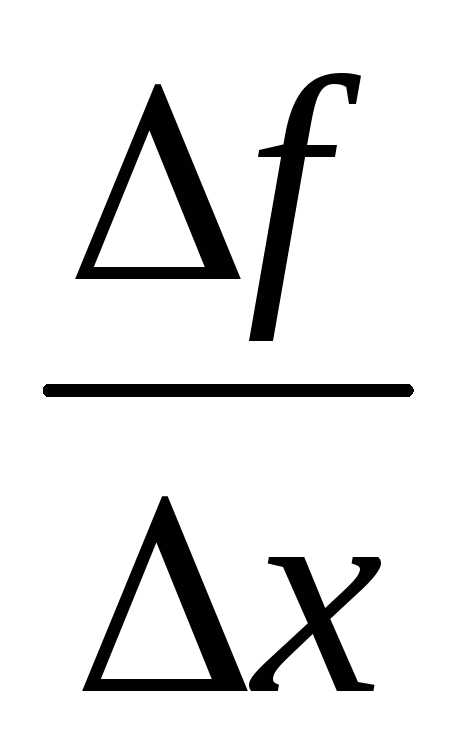 =
=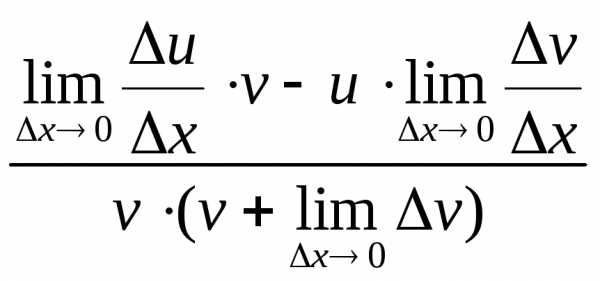
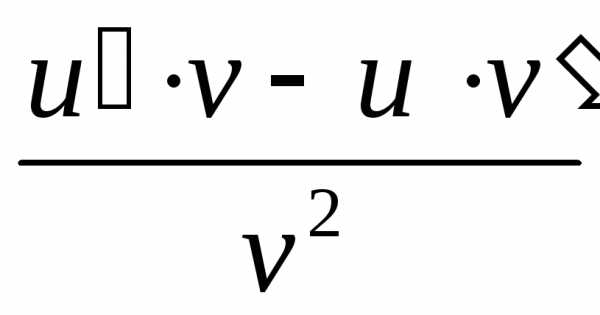 .
Таким образом,
.
Таким образом,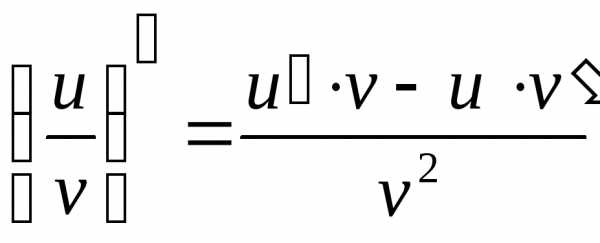 .
.Теорема доказана.
Рассмотрим несколько примеров применения основных правил вычисления производной.
Пример 10.1. Найти производную функции .
Решение.
.
Пример 10.2. Найти производную функции .
Решение.
.
Пример 10.3. Найти производную функции 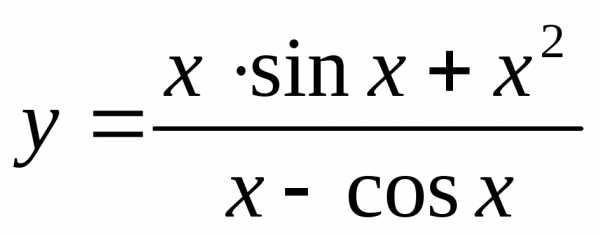 .
.
Решение.

§ 11. Производная обратной функции.
Справедлива следующая
 (x0).
Тогда на множестве значений этой функции,
соответствующем интервалу (a;b),
определена непрерывная обратная функцияx=φ(y),
которая в точкеy0= f(x0)
имеет производную
(x0).
Тогда на множестве значений этой функции,
соответствующем интервалу (a;b),
определена непрерывная обратная функцияx=φ(y),
которая в точкеy0= f(x0)
имеет производную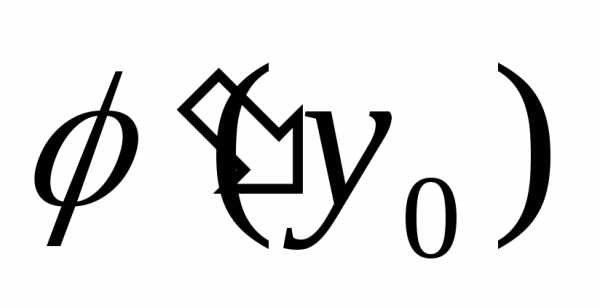
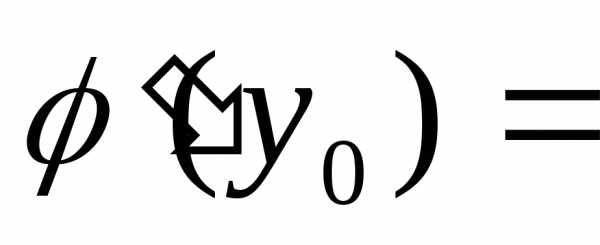
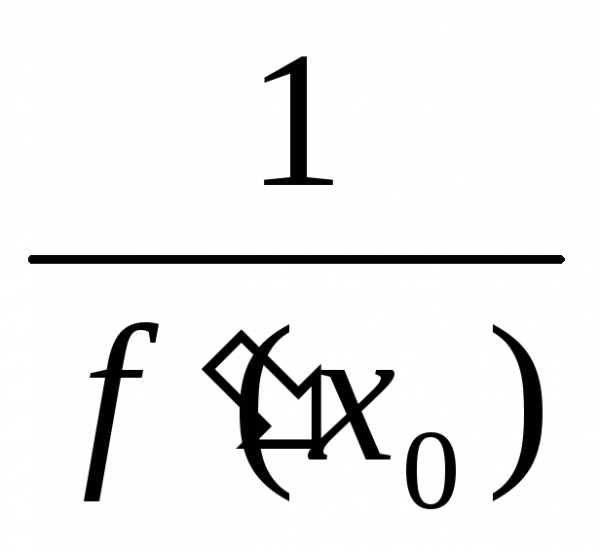 .
. Пример. Функция y = sin xудовлетворяет условиям последней
теоремы на интервале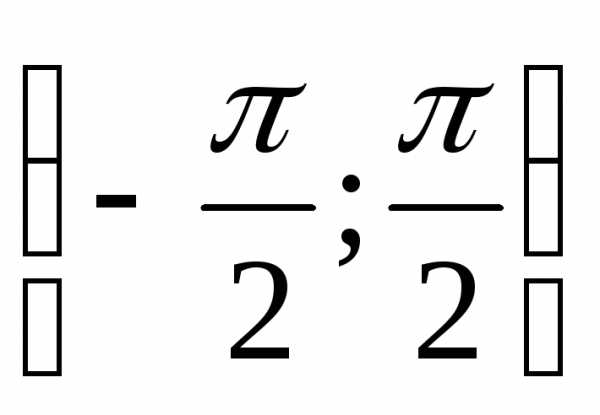 и всюду на этом интервале имеет отличную
от нуля производную:.
Поэтому на соответствующем интервале
значений этой функции (
и всюду на этом интервале имеет отличную
от нуля производную:.
Поэтому на соответствующем интервале
значений этой функции (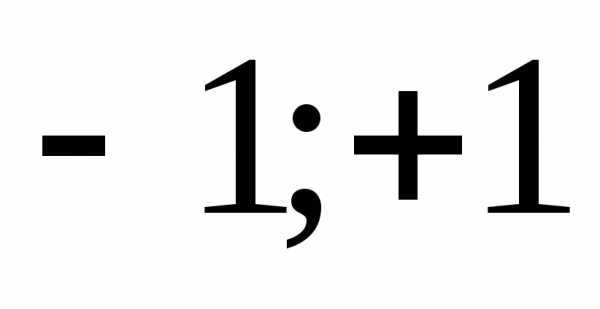 )
определена и дифференцируема обратная
функция
)
определена и дифференцируема обратная
функция
x = arcsin y, причём.
Здесь перед корнем взят знак плюс, так
как на интервале 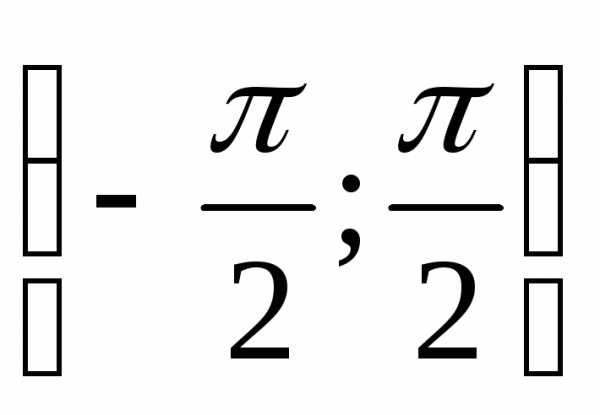
 положительна. Итак,
положительна. Итак,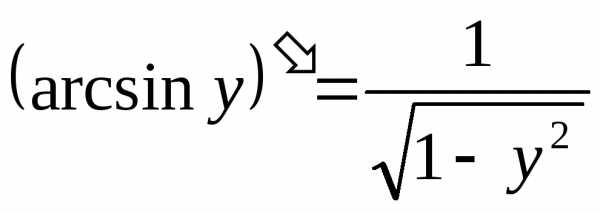 ,
или, если аргументy обозначить
,
или, если аргументy обозначить через x, 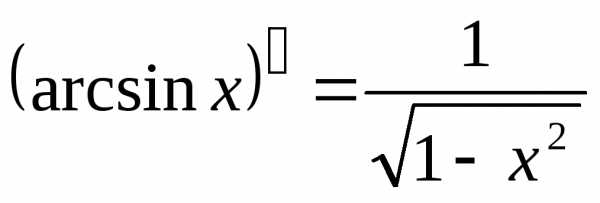 .
.
§ 12. Производная сложной функции.
Теорема 12.1 Пусть функция u =φ(x)
имеет в некоторой точкеx0производную,
а функция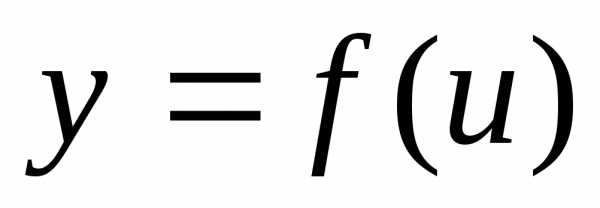 имеет в соответствующей точкепроизводную.
Тогда сложная функцияв точке
имеет в соответствующей точкепроизводную.
Тогда сложная функцияв точке
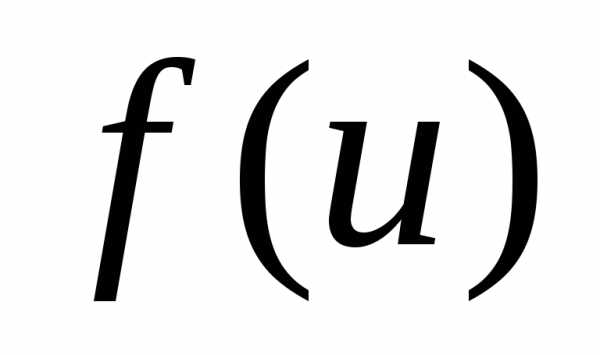 иφ(x):
иφ(x):.
Коротко это соотношение можно записать в виде .
Доказательство. Дадим аргументу x приращение ∆ x. Тогда функция u =φ(x)
получит приращение ∆ u,
а функция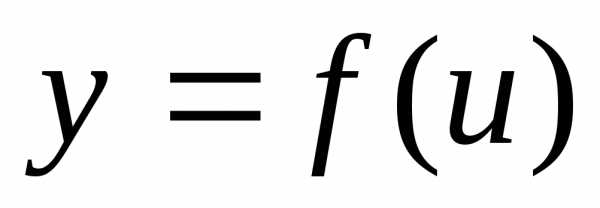 получит приращение ∆ y.
Так как функцииφ(x)
и
получит приращение ∆ y.
Так как функцииφ(x)
и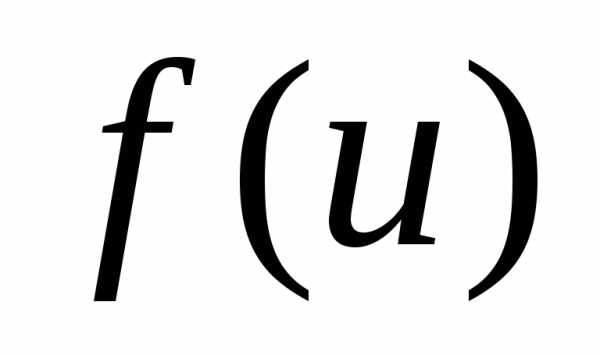 имеют производные, то есть дифференцируемы,
то,
а,
где
имеют производные, то есть дифференцируемы,
то,
а,
где
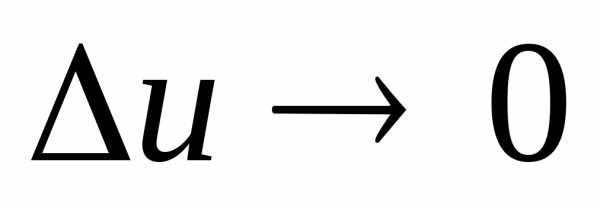 и
и при
при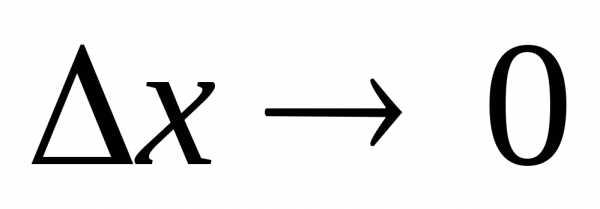 .
.Подставим выражение для ∆uв выражение для ∆y:
.
Разделим это равенство на ∆x:
.
Если 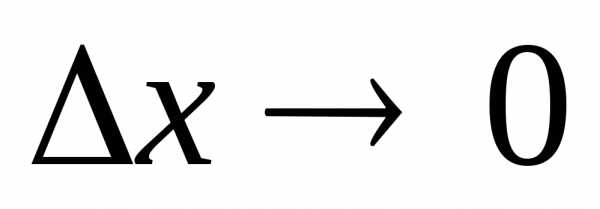 ,
то
,
то и (как следует из выражения для ∆ u)
и (как следует из выражения для ∆ u)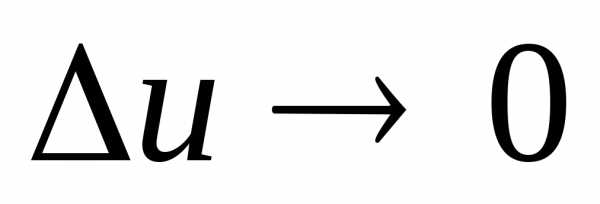
 .
Поэтому
.
Поэтому  =.
=.
Теорема доказана.
Остановимся на одном частном случае
применения этой теоремы. Пусть
,
гдеC– константа.
Тогда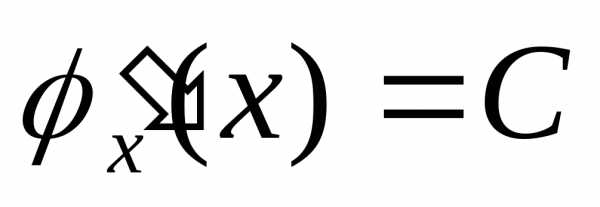 ,.
,.
Пусть, например,
.
Здесь,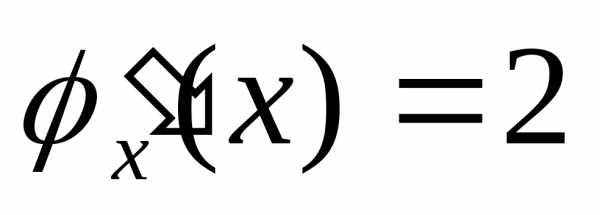 .
Введём обозначение,
тогда,.
.
Введём обозначение,
тогда,.
Рассмотрим примеры вычисления производной сложной функции.
Пример 12.1. Найти производную функции .
Решение. Введём промежуточную функцию
.
Тогда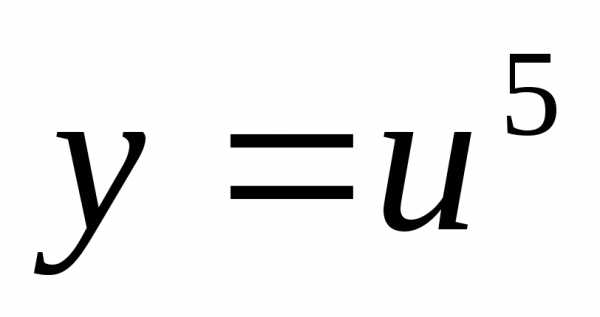 .
.
.
Пример 12.2. Найти производную функции .
Решение. Здесь ,.
.
Пример 12.3. Найти производную функции 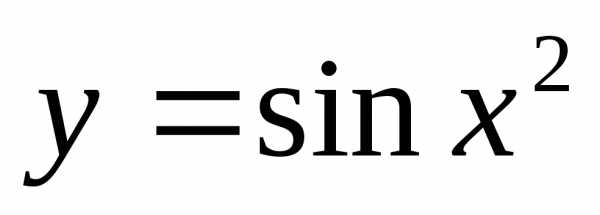 .
.
Решение. Здесь 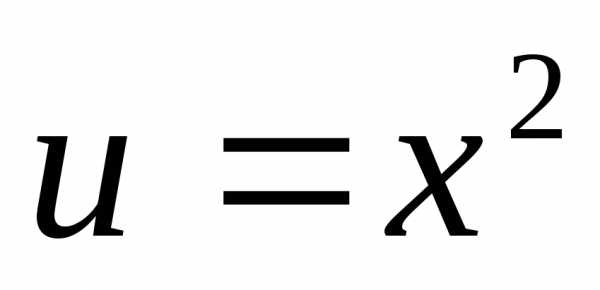 ,
,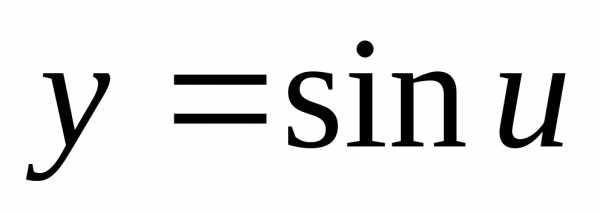 .
.
.
Пример 12.4. Найти производную функции 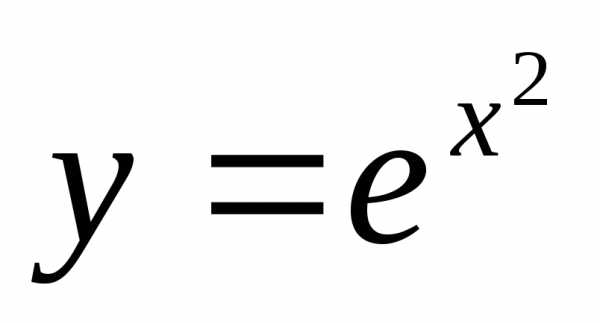 .
.
Решение. Здесь 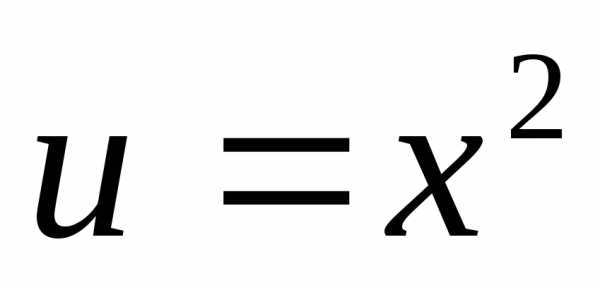 ,
,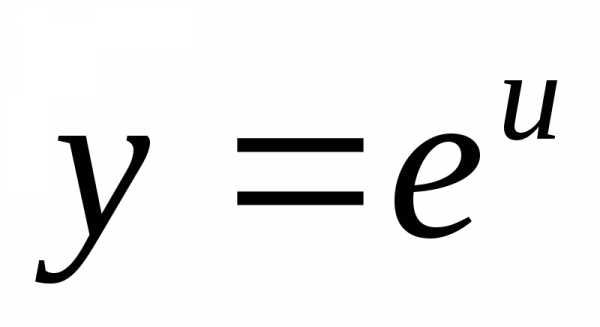 .
.
.
Пример 12.5. Найти производную функции 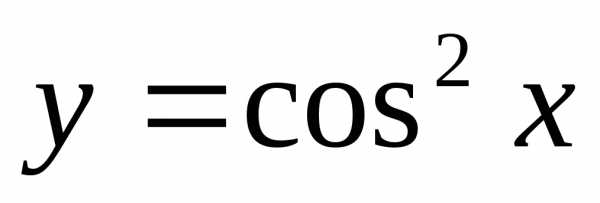 .
.
Решение.
(здесь подразумевается промежуточная функция ).
Пример 12.6. Найти производную функции .
Решение
Пример 12.7. Найти производную функции  .
.
Решение..
Если сложная функция получена в результате нескольких суперпозиций, то есть если она содержит несколько промежуточных аргументов, то теорема о производной сложной функции применяется последовательно требуемое число раз. Пусть, например,
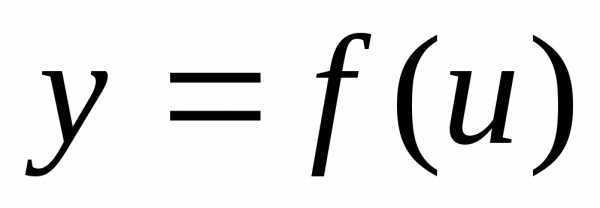 ,
,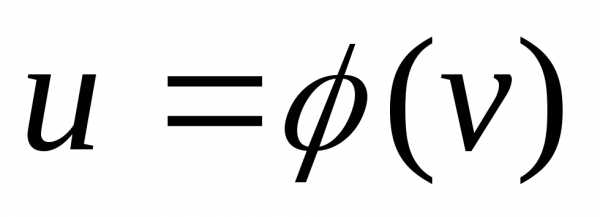 ,
а
,
а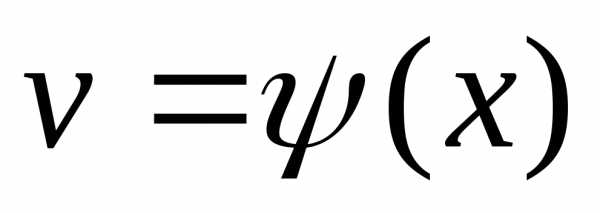 ,
то есть.
Тогда.
,
то есть.
Тогда.
То же самое можно записать иначе: .
Пример 12.8. Найти производную функции 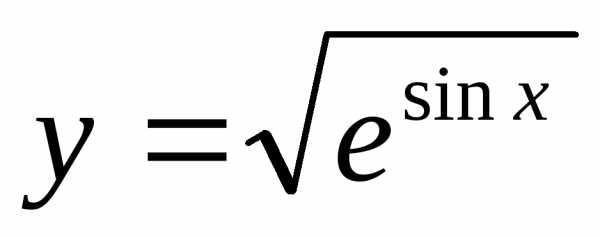 .
.
Решение. Здесь
,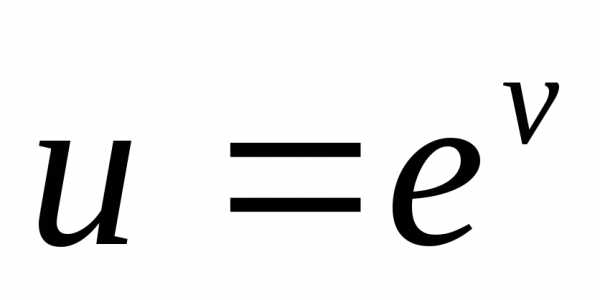 ,
тогда
,
тогда .
.
.
studfiles.net
§ 10. Основные правила вычисления производных.
Теорема 10.1. Пусть функцияu=φ(x)
имеет в данной точкеx0производную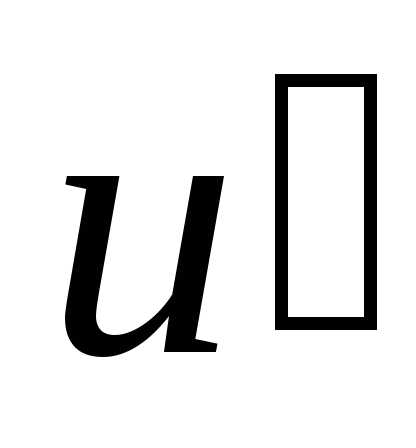 .
Тогда функцияy=c∙uимеет в точкеx0производную.
.
Тогда функцияy=c∙uимеет в точкеx0производную.
Здесь c– произвольная постоянная.
Доказательство. Дадим аргументу x приращение ∆ x. Тогда
∆ y=y(x0+∆ x) ─y(x0) =c∙ φ(x0+∆ x) ─c∙ φ(x0) =c∙[φ(x0+∆ x) ─ φ(x0)] =c∙∆φ.
Теорема доказана.
Теорема 10.2.Пусть функцииu(x) иv(x) имеют в данной точкеx0производные. Тогда в этой же точке имеют производные и функцииu(x) +v(x),u(x) ─v(x),
u(x)
∙v(x),
а также (еслиv(x0)≠0)
функция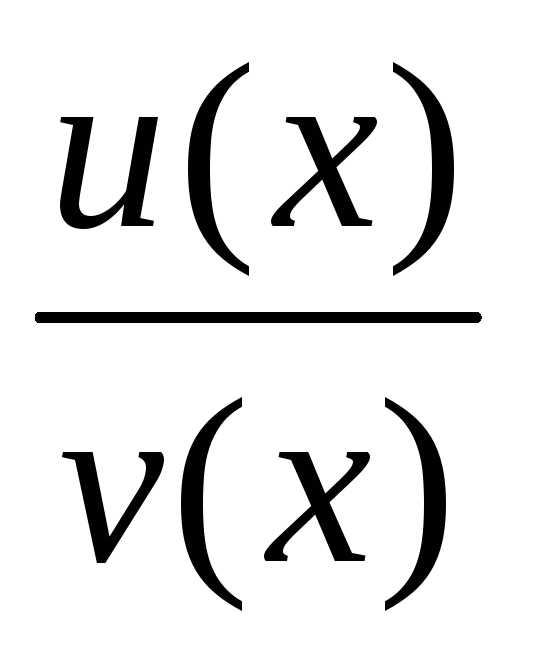 ,
,
причём (,,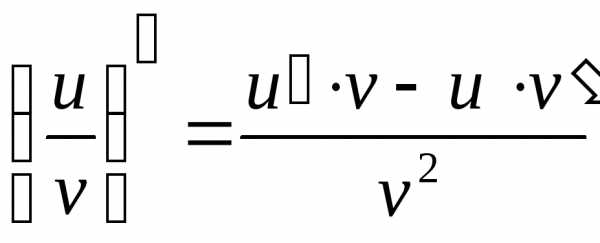 .
.
Доказательство. Пусть f(x) =u(x) +v(x). Тогда ∆ f=f(x0+∆ x) ─f(x0) =
= u(x0+∆ x) ─u(x0) +v(x0+∆ x) ─v(x0).
 (x0)
=
(x0)
= 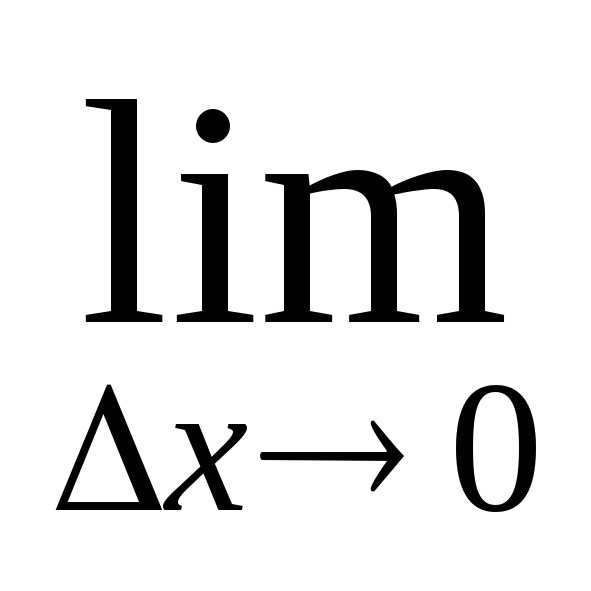
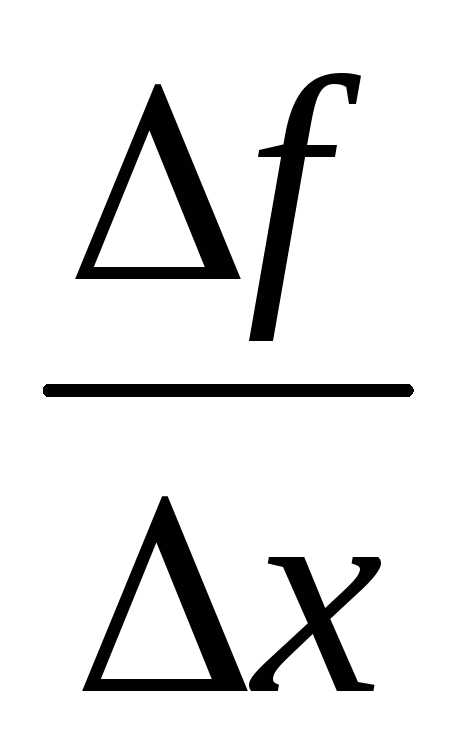 =
= 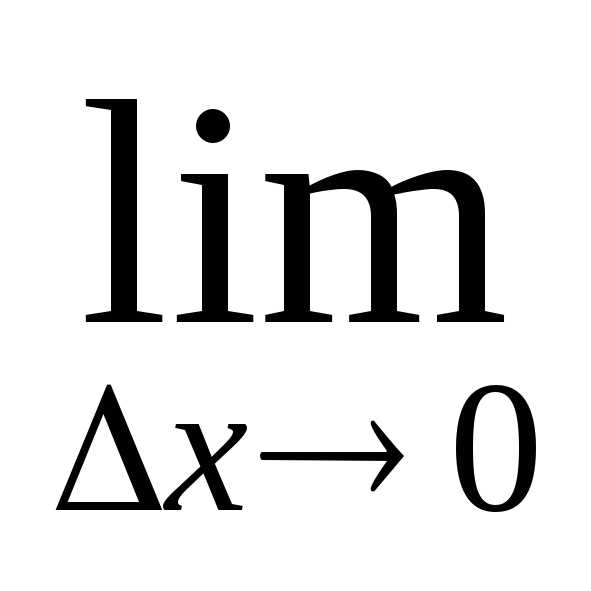
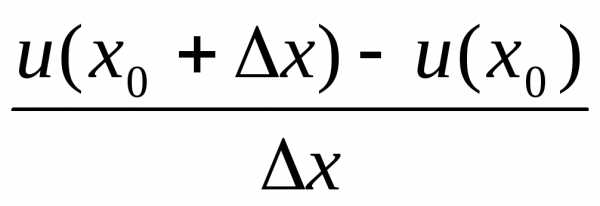 +
+ 
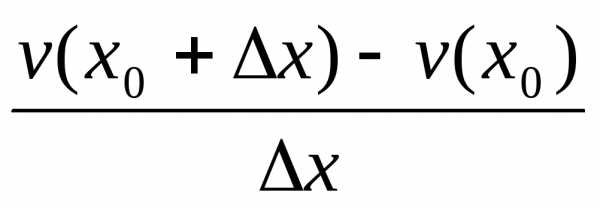 =
= .
Таким образом,.
.
Таким образом,.
Совершенно аналогично доказывается, что .
Пусть теперь f(x) =u(x) ∙v(x). Тогда
∆ f=f(x0+∆ x) ─f(x0) =u(x0+∆ x) ∙v(x0+∆ x) ─u(x0) ∙v(x0).
Введём для удобства обозначения: ∆u = u(x0+∆ x) ─u(x0), ∆v=v(x0+∆ x) ─v(x0),
u = u(x0),v = v(x0). Тогдаu(x0+∆ x) =u+ ∆u,v(x0+∆ x) =v+ ∆v,
∆f= (u+ ∆u) ∙ (v+ ∆v) ─u ∙v= ∆u ∙ (v+ ∆v) +u ∙ ∆v.
Так как функция v(x) дифференцируема (имеет производную) в точкеx0, то она непрерывна в этой точке. Следовательно, при ∆ x→0 и ∆v→0. Поэтому
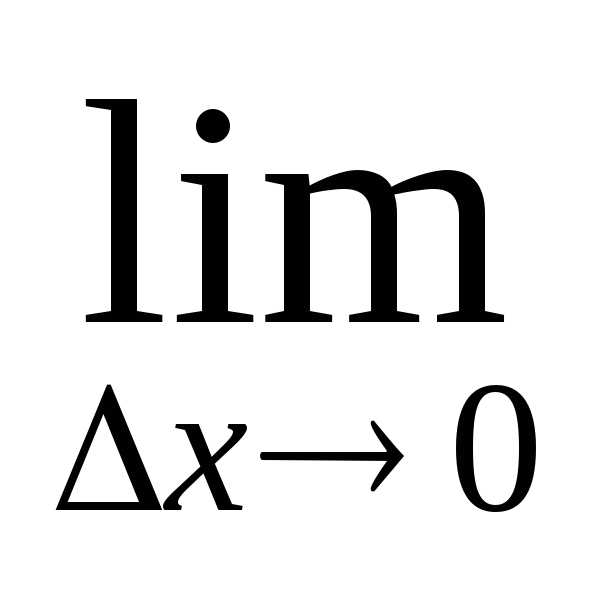
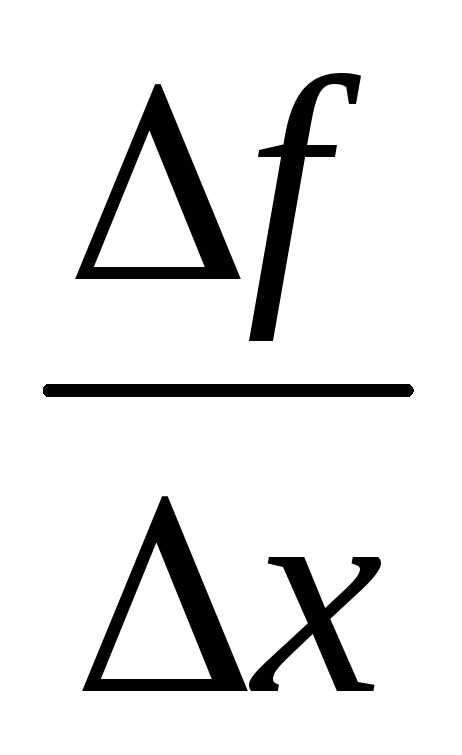 =
= 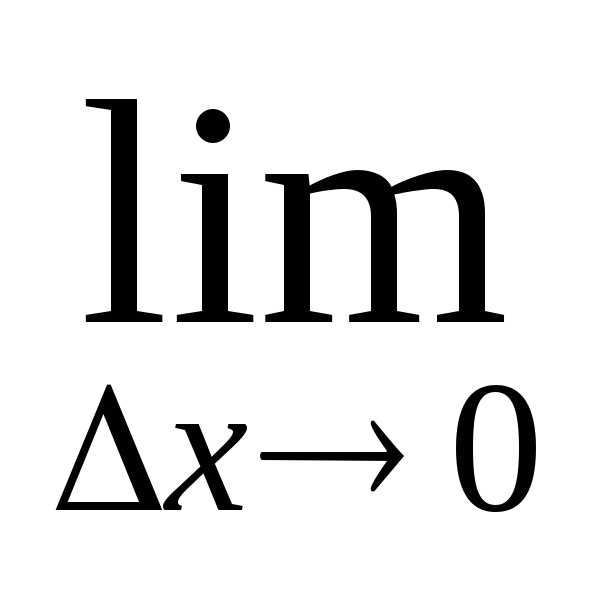
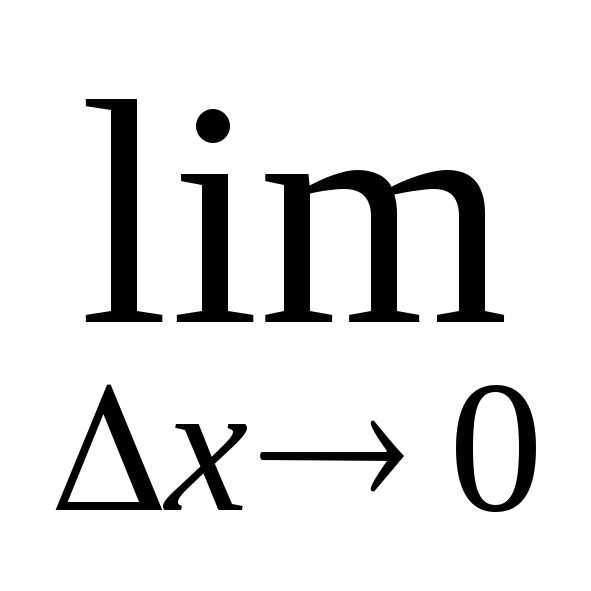
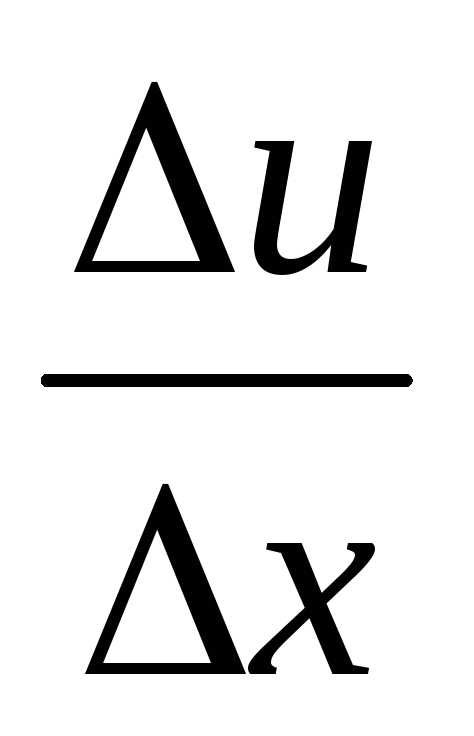 ∙v +u ∙
∙v +u ∙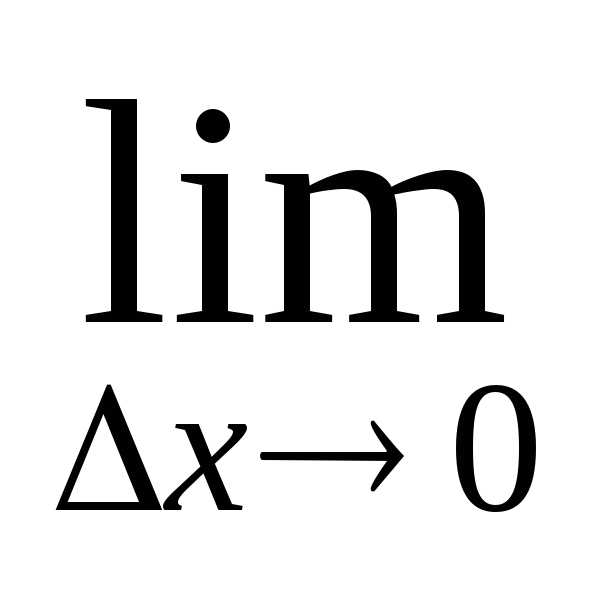
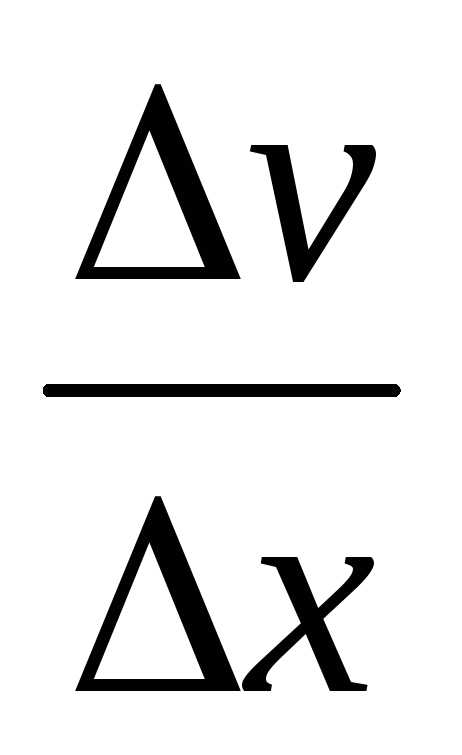 +
+ 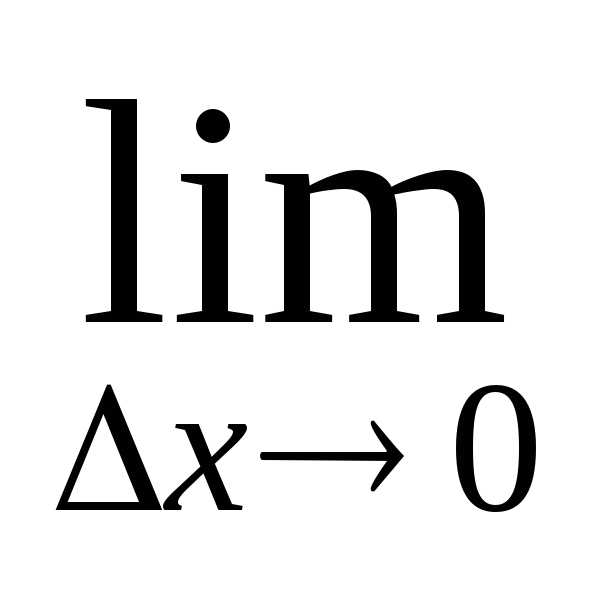
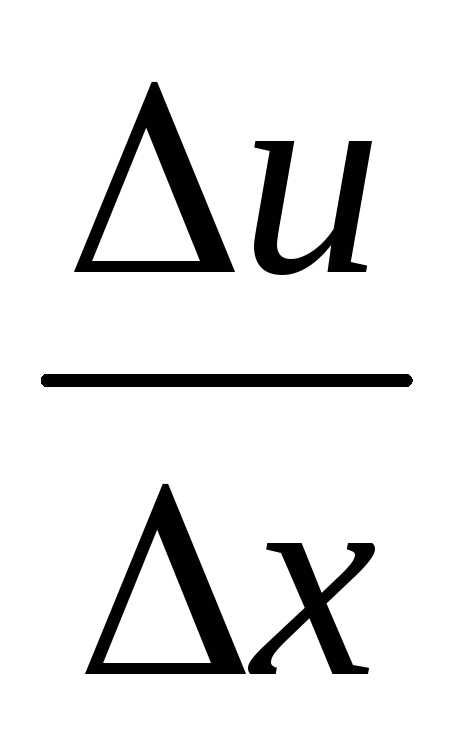 ∙
∙ 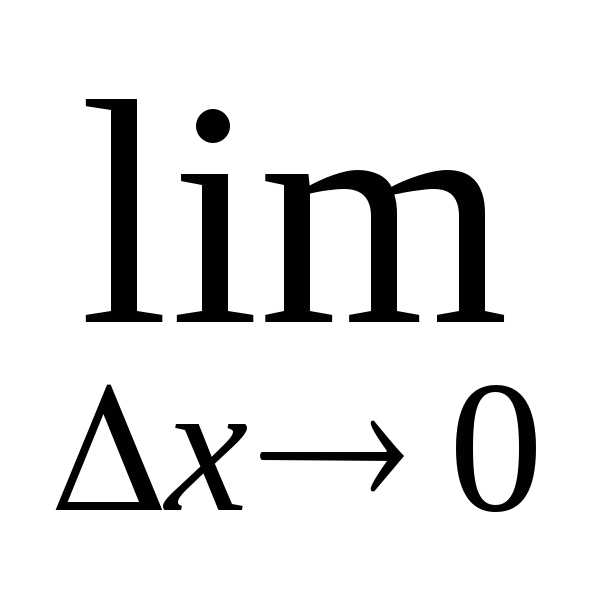 ∆v=
∆v=
=. Таким образом,.
Пусть далее f(x)
=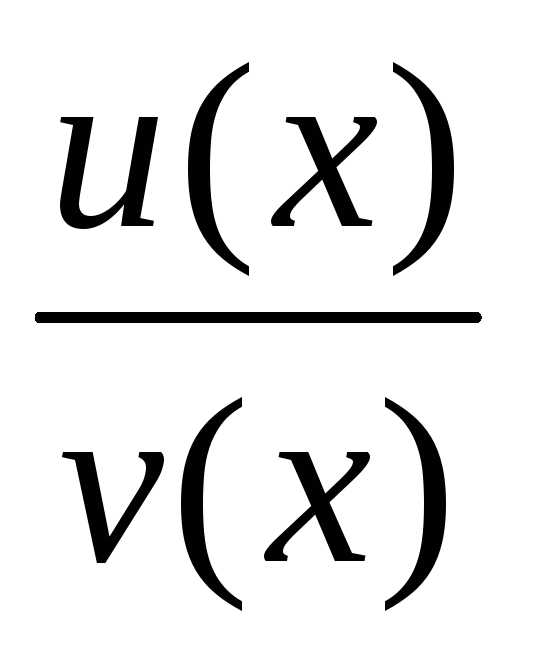 .
Тогда
.
Тогда
∆ f=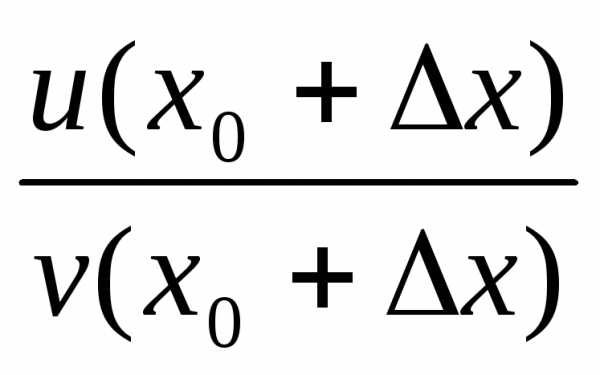 ─
─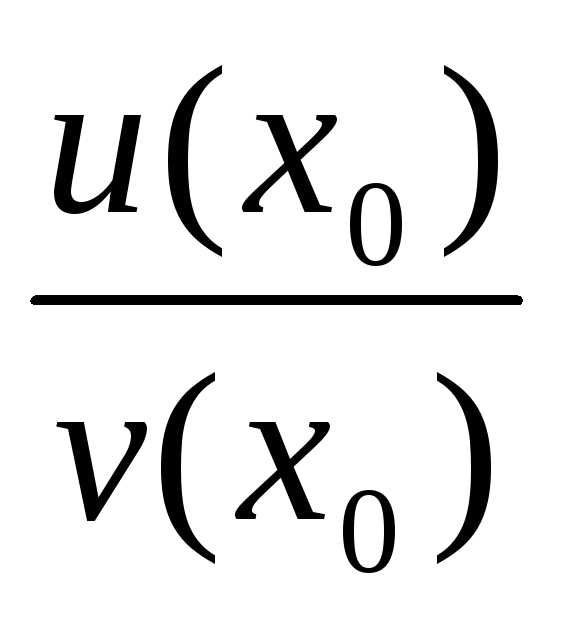 =(здесь обозначенияu,v, ∆u,
∆vимеют тот же смысл,
что и выше).
=(здесь обозначенияu,v, ∆u,
∆vимеют тот же смысл,
что и выше).
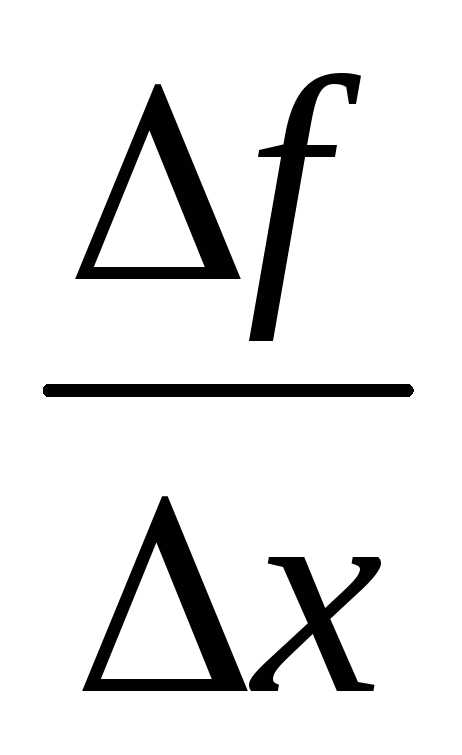 =
=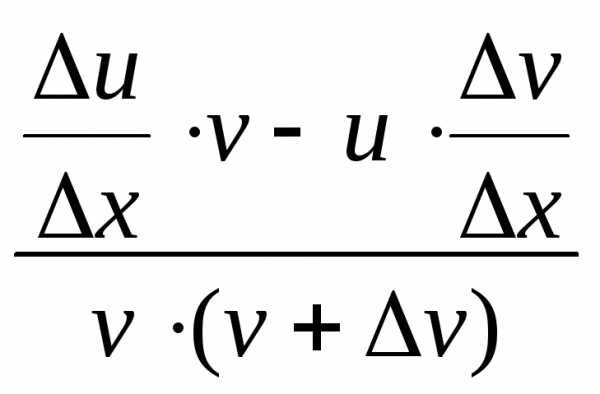 .
Так как
.
Так как  ∆v= 0, то
∆v= 0, то
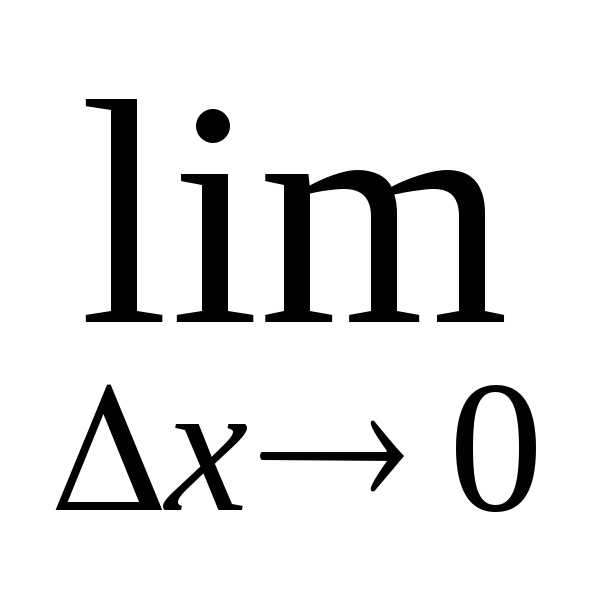
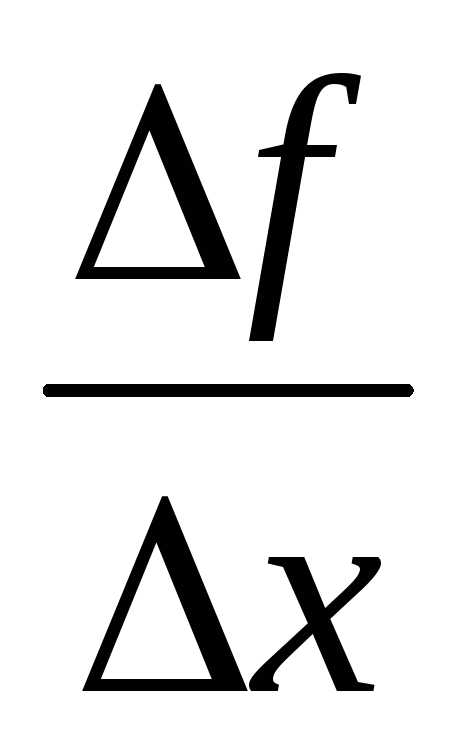 =
=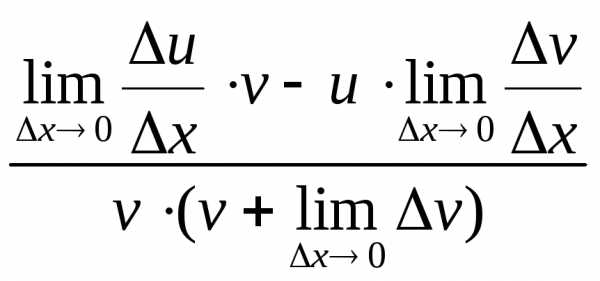 =
=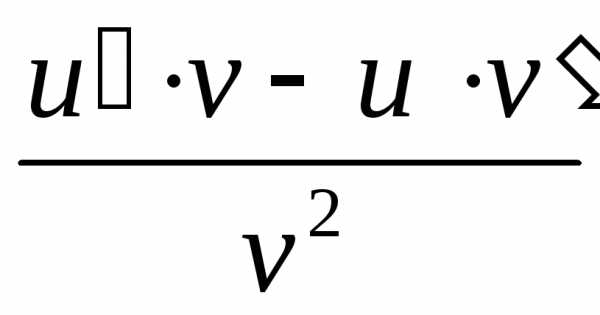 .
Таким образом,
.
Таким образом,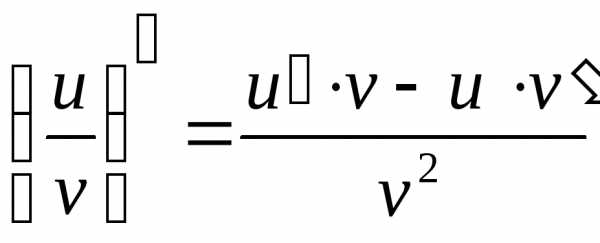 .
.
Теорема доказана.
Рассмотрим несколько примеров применения основных правил вычисления производной.
Пример 10.1. Найти производную функции .
Решение.
.
Пример 10.2. Найти производную функции .
Решение.
.
Пример 10.3. Найти производную функции 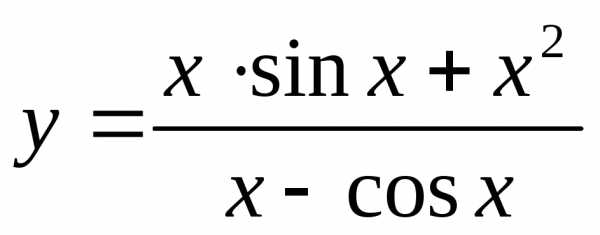 .
.
Решение.

§ 11. Производная обратной функции.
Справедлива следующая теорема. Пусть
функцияy=f(x)строго монотонна (т.е. является либо
возрастающей, либо убывающей) и непрерывна
на интервале (a;b)
и в точке x0из этого интервала
имеет отличную от нуля производную (x0).
Тогда на множестве значений этой функции,
соответствующем интервалу (a;b),
определена непрерывная обратная функцияx=φ(y),
которая в точкеy0= f(x0)
имеет производную
(x0).
Тогда на множестве значений этой функции,
соответствующем интервалу (a;b),
определена непрерывная обратная функцияx=φ(y),
которая в точкеy0= f(x0)
имеет производную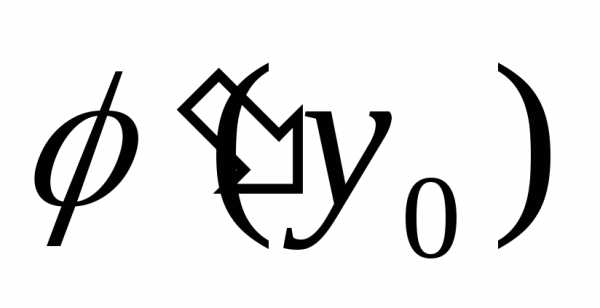 ,
причём
,
причём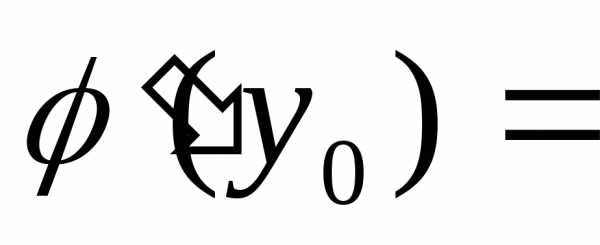
 .
.
Пример. Функция y = sin xудовлетворяет условиям последней
теоремы на интервале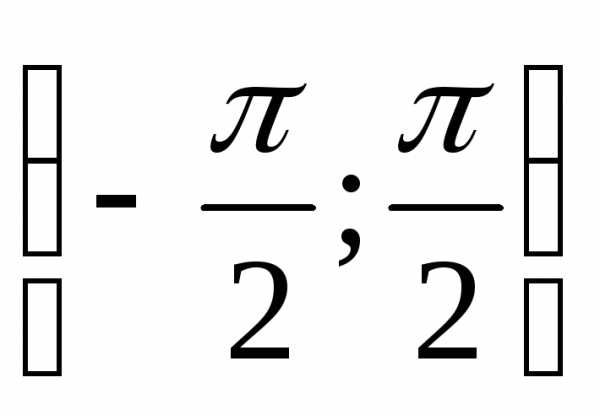 и всюду на этом интервале имеет отличную
от нуля производную:.
Поэтому на соответствующем интервале
значений этой функции (
и всюду на этом интервале имеет отличную
от нуля производную:.
Поэтому на соответствующем интервале
значений этой функции (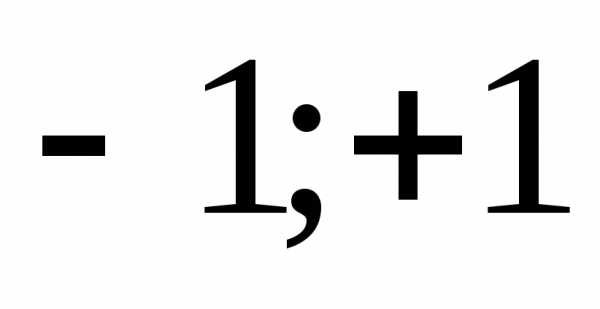 )
определена и дифференцируема обратная
функция
)
определена и дифференцируема обратная
функция
x = arcsin y, причём.
Здесь перед корнем взят знак плюс, так
как на интервале  функция
функция положительна. Итак,
положительна. Итак, ,
или, если аргументy обозначить
,
или, если аргументy обозначить
через x, 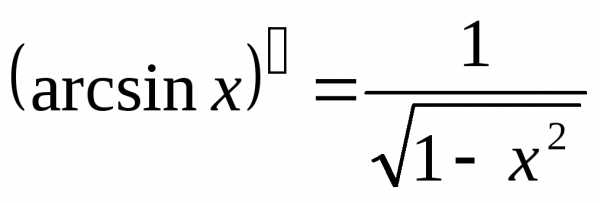 .
.
§ 12. Производная сложной функции.
Теорема 12.1 Пусть функция u =φ(x)
имеет в некоторой точкеx0производную,
а функция имеет в соответствующей точкепроизводную.
Тогда сложная функцияв точкеx0также имеет производную, равную
произведению производных функций
имеет в соответствующей точкепроизводную.
Тогда сложная функцияв точкеx0также имеет производную, равную
произведению производных функций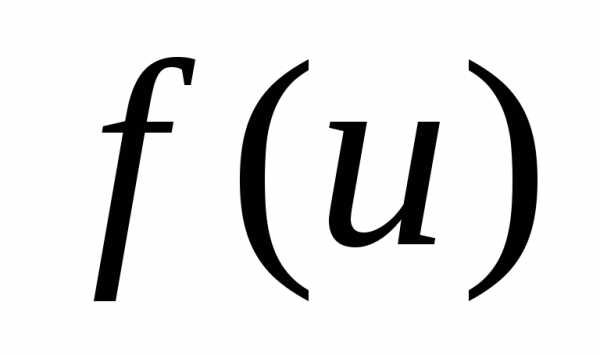 иφ(x):
иφ(x):
.
Коротко это соотношение можно записать в виде .
Доказательство. Дадим аргументу x приращение ∆ x. Тогда функция u =φ(x)
получит приращение ∆ u,
а функция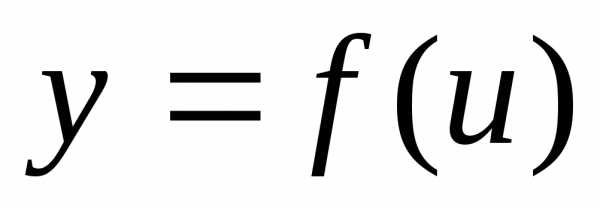 получит приращение ∆ y.
Так как функцииφ(x)
и
получит приращение ∆ y.
Так как функцииφ(x)
и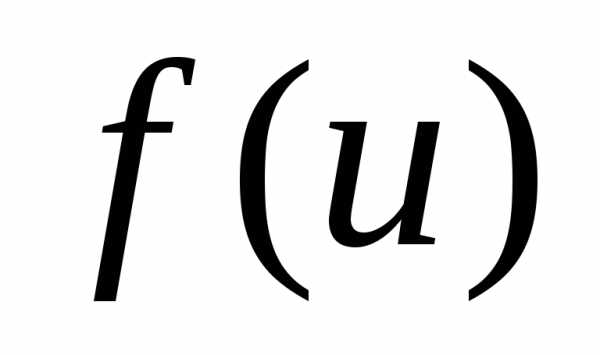 имеют производные, то есть дифференцируемы,
то,
а,
где
имеют производные, то есть дифференцируемы,
то,
а,
где при
при и
и при
при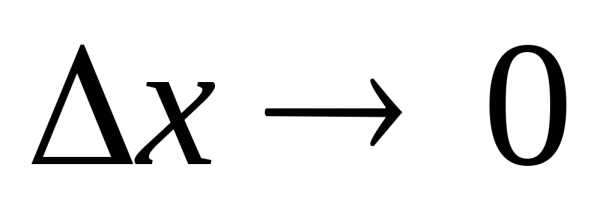 .
.
Подставим выражение для ∆uв выражение для ∆y:
.
Разделим это равенство на ∆x:
.
Если 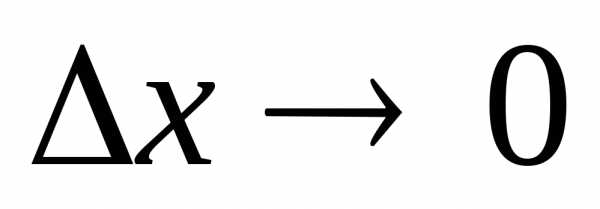 ,
то
,
то и (как следует из выражения для ∆ u)
и (как следует из выражения для ∆ u)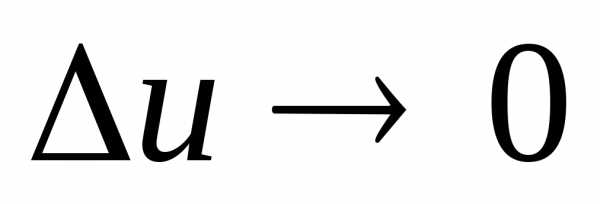 .
Но тогда и
.
Но тогда и .
Поэтому
.
Поэтому
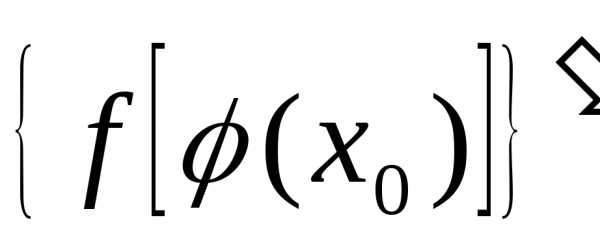 =.
=.
Теорема доказана.
Остановимся на одном частном случае
применения этой теоремы. Пусть
,
гдеC– константа.
Тогда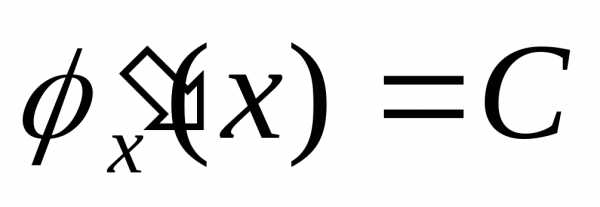 ,.
,.
Пусть, например,
.
Здесь,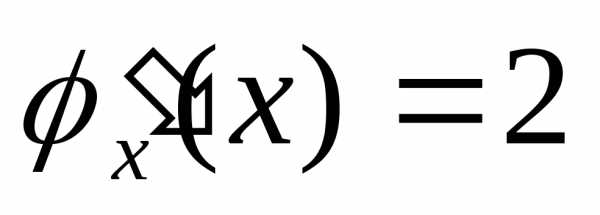 .
Введём обозначение,
тогда,.
.
Введём обозначение,
тогда,.
Рассмотрим примеры вычисления производной сложной функции.
Пример 12.1. Найти производную функции .
Решение. Введём промежуточную функцию
.
Тогда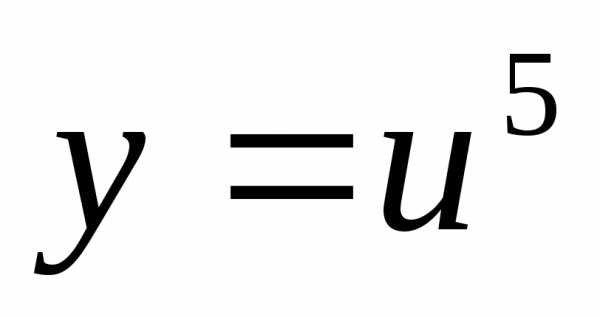 .
.
.
Пример 12.2. Найти производную функции .
Решение. Здесь
,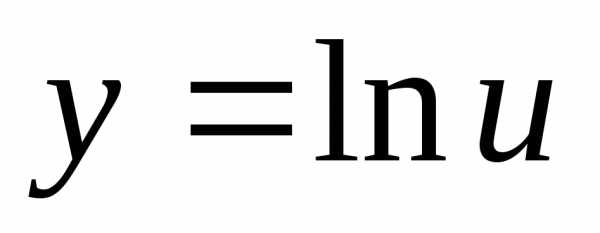 .
.
.
Пример 12.3. Найти производную функции 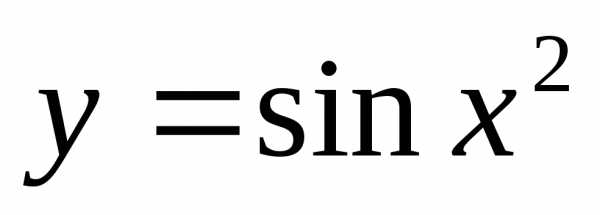 .
.
Решение. Здесь 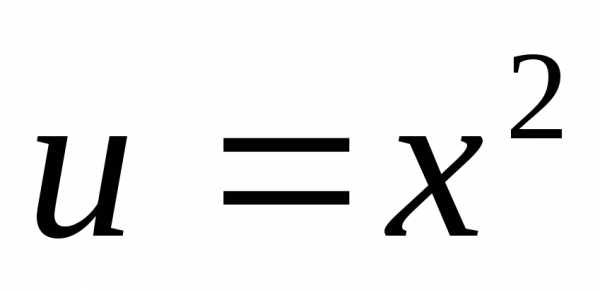 ,
,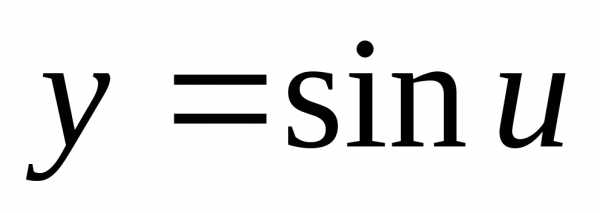 .
.
.
Пример 12.4. Найти производную функции 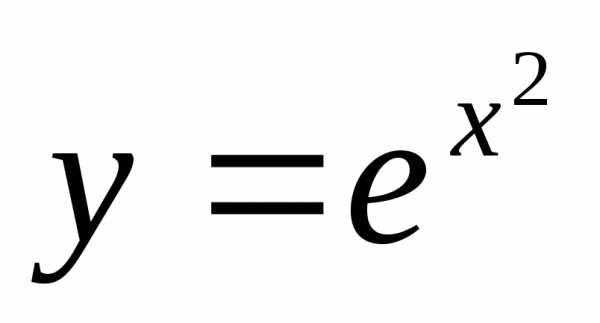 .
.
Решение. Здесь 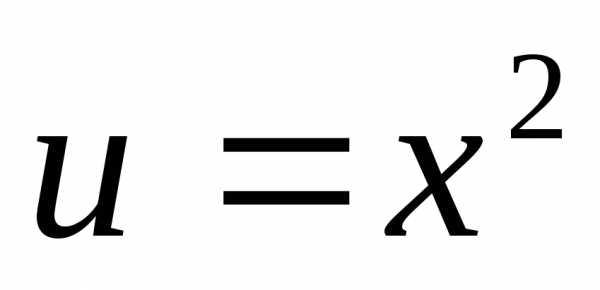 ,
,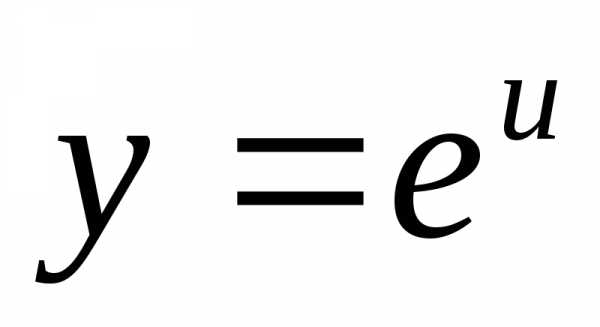 .
.
.
Пример 12.5. Найти производную функции 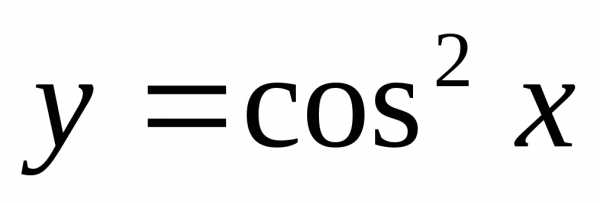 .
.
Решение.
(здесь подразумевается промежуточная функция ).
Пример 12.6. Найти производную функции .
Решение
Пример 12.7. Найти производную функции  .
.
Решение..
Если сложная функция получена в результате нескольких суперпозиций, то есть если она содержит несколько промежуточных аргументов, то теорема о производной сложной функции применяется последовательно требуемое число раз. Пусть, например,
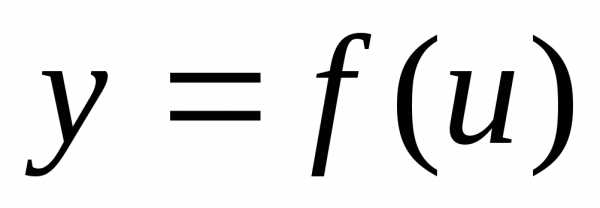 ,
, ,
а
,
а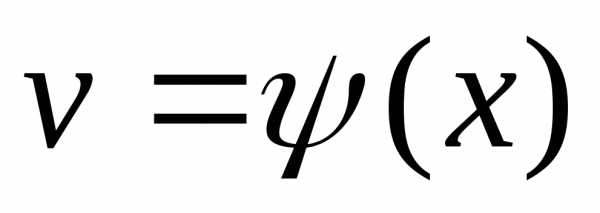 ,
то есть.
Тогда.
,
то есть.
Тогда.
То же самое можно записать иначе: .
Пример 12.8. Найти производную функции .
Решение. Здесь
,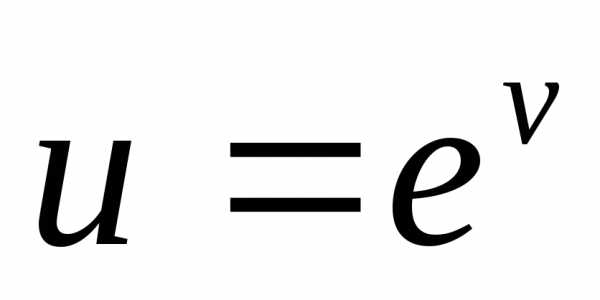 ,
тогда
,
тогда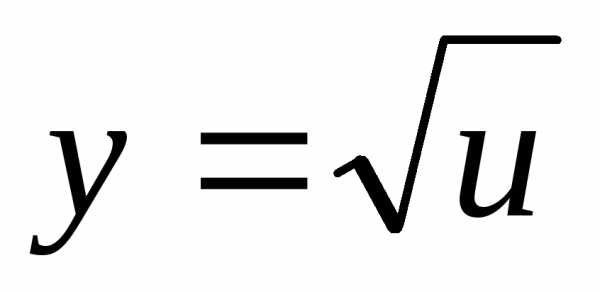 .
.
.
studfiles.net
Вычисление производных первого порядка.
Определение: Производной первого порядка функции $y=f(x)$ в точке $x_0$ называется предел
$$f'(x_0)=\lim\limits_{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}.$$
Основные формулы для вычисления производных.
$c’=0,\quad c=const;$
$(x^\alpha)’=\alpha x^{\alpha-1},$ $x\in\mathbb{R}, \alpha\neq 0;$
$(a^x)’=a^x\ln a,\quad a>0, a\neq 1, x\in \mathbb{R};$
$(e^x)’=e^x;$
$(\log_a x)’=\frac{1}{x\ln a}, \quad x>0;$
$(\log_a|x|)’=\frac{1}{x\ln a},\quad x\neq 0;$
$(\ln x)’=\frac{1}{x},\quad x>0;$
$(\sin x)’=\cos x, \quad x\in \mathbb{R};$
$(\cos x)’=-\sin x\quad x\in \mathbb{R};$
$(tg x)’=\frac{1}{\cos^2 x},$ $x\neq\frac{\pi}{2}(2n+1),\,\, n\in\mathbb{Z};$
$(ctg x)’=-\frac{1}{\sin^2 x},$ $x\neq\pi n,\,\, n\in\mathbb{Z};$
$(\arcsin x)’=\frac{1}{\sqrt{1-x^2}},\quad |x|<1;$
$(\arccos x)’=-\frac{1}{\sqrt{1-x^2}},\quad |x|<1;$
$(arctg x)’=\frac{1}{1+x^2},\quad x\in\mathbb{R};$
$(arcctg x)’=-\frac{1}{1+x^2},\quad x\in\mathbb{R};$
Правила вычисления производных.
1) Пусть $f=c_1 f_1+c_2f_2+…+c_nf_n.$ Тогда $f’=c_1f’_1+c_2f’_2+…+c_nf’_n.$
2) Пусть $f=f_1\cdot f_2.$ Тогда $f’=f’_1f_2+f_1f’_2.$
3) Если $f=f_1/f_2,$ то $f’=\frac{f’_1f_2-f’_2f_1}{f_2^2}.$
4) Если функция $y=f(x)$ имеет производную в точке $x_0,$ а функция $z=g(y) $ – в точке $y_0=f(x_0),$ то сложная функция $z=\varphi(x)=g(f(x)),$ также имеет производную в точке $x_0,$ причем $\varphi'(x_0)=g'(y_0)f'(x_0).$
Примеры.
Найти производную функции $y(x)$
1) ${ y=x^3+x^2+x+1}$
Решение.
$y’=3x^2+2x+1.$
2) ${ y=7x^{13}+13x^{-7}}$
Решение.
$y’=7\cdot 13x^{12}+13({-7})x^{-8}=91x^{12}-91x^{-8}=91(x^{12}-x^{-8}).$
3) ${y=\frac{x^2-5x+6}{x^2+x+7}}$
Решение.
$$y’=\frac{(x^2-5x+6)'(x^2+x+7)-(x^2+x+7)'(x^2-5x+6)}{(x^2+x+7)^2}=$$ $$=\frac{(2x-5)(x^2+x+7)-(2x+1)(x^2-5x+6)}{(x^2+x+7)^2}=$$ $$\frac{2x^3+2x^2+14x-5x^2-5x-35-2x^3+10x^2-12x-x^2+5x-6}{(x^2+x+7)^2}=$$ $$=\frac{6x^2+2x-41}{(x^2+x+7)^2}.$$
{jumi[*4]}
4) ${y=(x+1)tg x;}$
Решение.
$y’=(x+1)’tg x+(x+1)(tg x)’=tg x+\frac{x+1}{\cos^2 x};$
5) ${ y=(a+bx)^\alpha}$
Решение.
$y’=\alpha(a+bx)^{\alpha-1}(a+bx)’=$ $\alpha(a+bx)^{\alpha-1}b;$
6) ${y=\sqrt[3]{\frac{1-x^3}{1+x^3}}.}$
Решение.
$$y’=\frac{1}{3}\left(\frac{1-x^3}{1+x^3}\right)^{-\frac{2}{3}}\frac{(-3x^2)(1+x^3)-3x^2(1-x^3)}{(1+x^3)^2}$$
7) ${y=\ln\ln(x/2)}$
Решение.
$$y’=\frac{1}{\ln(x/2)}\cdot(\ln(x/2))’=\frac{1}{\ln(x/2)}\cdot\frac{2}{x}\cdot\frac{1}{2}=\frac{1}{x\log(x/2)}.$$
8) $y=\ln\frac{x^2+a}{\sqrt{x^4+b^2}}+\frac{a}{b}arctg\frac{x^2}{b}$
Решение.
$$y’=\frac{\sqrt{x^4+b^2}}{x^2+a}\cdot\left(\frac{x^2+a}{\sqrt{x^4+b^2}}\right)’+\frac{a}{b}\frac{1}{1+\frac{x^4}{b^2}}\cdot\left(\frac{x^2}{b}\right)’=$$
$$\frac{\sqrt{x^4+b^2}}{x^2+a}\cdot\frac{2x\sqrt{x^4+b^2}-1/2(x^4+b^2)^{-1/2}\cdot4x^3(x^2+a)}{x^4+b^2}+\frac{a}{b}\frac{1}{1+\frac{x^4}{b^2}}\cdot\frac{2x}{b}=$$
$$=\frac{2x(x^4+b^2)-2x^3(x^2+a)+2xa(x^2+a)}{(x^2+a)(x^4+b^2)}=\frac{2x(a^2+b^2)}{(x^2+a)(x^4+b^2)}.$$
9) ${y=x^x}$
Решение.
$y’=(x^x)’=(e^{\ln x^x})’=(e^{x\ln x})’=e^{x\ln x}(x\ln x)’=e^{x\ln x}(\ln x+x\cdot\frac{1}{x})=$ $=x^x(\ln x+1).$
10) ${y=\log_x 7}$
Решение.
$$y’=(\log_x 7)’=\left(\frac{1}{\log_7 x}\right)’=(\log_7^{-1} x)’=-\log_7^{-2}x\cdot\frac{1}{x\ln 7}=$$
$$-\frac{1}{(\frac{\ln x}{\ln 7})^2}\cdot\frac{1}{x\ln 7}=-\frac{1}{x\ln x\cdot\frac{\ln x}{\ln 7}}=-\frac{1}{x\ln x\log_7 x}.$$
Производная функции заданной параметрически.
Пусть функции $x=x(t)$ и $y=y(t)$ определены в некоторой окрестности точки $t_0$ и параметрически задают в окрестности точки $x_0=x(t_0) $ функцию $y=f(x).$ Тогда, если $x(t)$ и $y(t)$ имеют в точке $t_0$ производные и если $\frac{dx(t_0)}{dt}\neq 0,$ то функция $y=f(x)$ в точке $x_0$ также имеет производную, которая может быть задана по формуле
$\frac{df(x_0)}{dx}=\frac{\frac{dy(t_0)}{dt}}{\frac{dx(t_0)}{dt}},$ $y’_x(x_0)=\frac{y’_t(t_0)}{x’_t(t_0)}.$
Примеры.
1) ${ x=\sin^2 t,\,\, y=\cos^2 t,\quad t\in(0,\pi/2). }$
Решение.
$x’_t=2\sin t\cdot(\sin t)’=2\sin t\cdot\cos t;$
$y’_t=2\cos t\cdot(\cos t)’=2\cos t\cdot(-\sin t).$
$$y’_x=\frac{2\cos t\cdot(-\sin t)}{2\sin t\cdot\cos t}=-1.$$
2) ${ x=e^{-t}; \,\, y=t^3 \quad t\in (-\infty;\, +\infty) .}$
Решение.
$$y’_x=\frac{3t^2}{-e^{-t}}=-3t^2e^t.$$
3) ${ x=a\cos t;\,\, y=b\sin t,\quad t\in(0,\pi). }$
Решение.
$$y’_x=\frac{b\cos t}{-a\sin t}-\frac{b}{a}ctg t.$$
4) ${ x=(t^3-2t^2+3t-4)e^t,\,\, y=(t^3-2t^2+4t-4)e^t. }$
Решение.
$$y’_x=\frac{(3t^2-4t+4)e^t+e^t(t^3-2t^2+4t-4)}{(3t^2-4t+3)e^t+e^t(t^3-2t^2+3t-4)}=$$ $$\frac{t^3+t^2}{t^3+t^2-t-1}=\frac{t^2(t+1)}{t^2(t+1)-(t+1)}=\frac{t^2}{t^2-1}.$$
5) $x=ctg 2t,\,\, y=\frac{2\cos 2t-1}{2\cos t}\quad t\in (0, \pi/2).$ $x’_y -?$
Решение.
$$x’_y=-\frac{2}{\sin^2 2t}\cdot\frac{4\cos^2 t}{-4\sin 2t\cdot2\cos t+2\sin t(2\cos 2t-1))}=$$ $$\frac{-1}{\sin^2 t(-8\sin t\cos^2 t+\sin t(2(1-2\sin^2 t)-1))}=$$
$$\frac{-1}{-8\sin^3 t\cos^2 t-4\sin^5 t+2\sin^3 t-\sin^3 t}=$$
$$\frac{1}{\sin^3 t(8\cos^2 t+4\sin^2t-2+1)}=\frac{1}{\sin^3 t(4\cos^2 t+3)}.$$
Производная функции заданной неявно.
Если дифференцируемая на некотором интервале функция $y=y(x)$ задана неявно уравнением $F(x,y)=0,$ то ее производную $y'(x)$ можно найти из уравнения $\frac{d}{dx}F(x,y)=0.$
Примеры.
Найти производную функции $y'(x).$
1) ${ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 }$
Решение.
$$\frac{d}{dx}\left(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1\right)=0$$
$$\frac{2x}{a^2}+\frac{2y}{b^2}y’=0, \Rightarrow\quad y’=-\frac{b^2 x}{a^2 y}.$$
2) ${ y^5+y^3+y-x=0 }$
Решение.
$$\frac{d}{dx}(y^5+y^3+y-x)=0 \Rightarrow 5y^4y’+3y^2y’+y’-1=0\,\,\Rightarrow\,\,$$ $$\Rightarrow y’=\frac{1}{5y^4+3y^2+1}.$$
3) $ y-x=\varepsilon\sin y $
Решение.
$$\frac{d}{dx}(y-x-\varepsilon\sin y)=0\Rightarrow\,\, y’-1-\varepsilon\cos y\cdot y’=0 \Rightarrow y’=\,\frac{1}{1-\varepsilon\cos y}.$$
mathportal.net
Таблица производных и правила | Математика
На этой странице дана таблица производных и правила нахождения производных.
Таблица производных:
Правила вычисления производных:
Полезно помнить:
adminПроизводная
www.matematika.uznateshe.ru
ПРАВИЛА И ФОРМУЛЫ ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
Поиск ЛекцийКраевой колледж предпринимательства
Учебное пособие для выполнения
практических и контрольных работ по “Математике”
раздел “Дифференциальное исчисление”
Пермь 2009
“Дифференциальное исчисление”. Учебное пособие для выполнения практических и контрольных работ по дисциплинам “Элементы высшей математики”, “Математика” для студентов всех специальностей.
Разработал: преподаватель А.С. Ремизова
Пояснительная записка
Учебное пособие представляет собой руководство к решению задач раздела “Дифференциальное исчисление” курса “Элементы высшей математики” для студентов специальностей СПО на базе среднего (полного) общего образования.
Основное назначение пособия – помочь студенту самостоятельно, без помощи преподавателя изучить приемы решения основных задач, закрепить полученные навыки при выполнении практических работ и подготовиться к зачету (экзамену) по данному разделу.
ПРОИЗВОДНАЯ
Определение производной
Правила вычисления производных
Пусть дан график непрерывной функции y = f (x) (рис.)
Возьмем на кривой y = f (x) точки М (х; у) и М1 (х1; у1) , где х1 = х + ∆х, у1 = у + ∆у (∆х – приращение аргумента, ∆у – приращение функции). Проведем секущую ММ1, угловой коэффициент которой обозначим через k1, т.е. k1 = tg φ1. Из треугольника ММ1Р находим .
Предположим, что точка М остается неподвижной, а точка М1, перемещаясь по кривой, неограниченно приближается к М. Тогда:
1) Секущая ММ1 поворачивается вокруг точки М, приближаясь к положению касательной;
2) х1 → х, а следовательно, ∆х = (х1 – х)→0;
3) угол φ1 стремится к углу φ между касательной и осью Ох.
Пусть k – угловой коэффициент касательной, т.е. k =tgφ. Так как tg φ1 – непрерывная функция (случай, когда φ1 = , пока исключим из рассмотрения), то .
Итак, угловой коэффициент касательной определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю: .
Производной функции y = f (x) в данной точке х называют предел отношения приращения функции ∆у к соответствующему приращению аргумента ∆х при условии, что ∆х →0, т.е.
Вообще говоря, производная – это «новая» функция, произведенная от данной функции по указанному правилу.
ПРАВИЛА И ФОРМУЛЫ ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
Определение производной четко указывает действия, которые нужно выполнить для ее нахождения, что позволяет непосредственно вычислять производную любой элементарной функции. Непосредственное дифференцирование позволяет вывести основные правила и формулы дифференцирования.
Все правила и формулы дифференцирования сведем в таблицу и в дальнейшем будем пользоваться ею, подобно тому, как в арифметике пользуются таблицей умножения.

poisk-ru.ru
Правила вычисления производной функции — Мегаобучалка
Вычисление производной функции
Производная функции играет важную роль в различных приложениях математики, поэтому необходимо знать – в каких случаях можно вычислить производную и как это сделать.
Мы познакомились с основными элементарными и знаем, что все элементарные функции получаются из основных элементарных функций с помощью операций сложения, вычитания, умножения, деления и взятия функции от функции (суперпозиции функций). Мы научимся вычислять производную любой элементарной функции. Для этого будет обоснована таблица производных основных элементарных функций и выведены правила вычисления производной суммы, разности, произведения, частного и суперпозиции функций.
С понятием производной мы познакомились на прошлой лекции и следовали при этом истории появления понятий дифференциала и производной. Историческое развитие не всегда является прямолинейным. Поэтому в современном изложении этого материала вначале, как правило, появляется понятие производной, а только затем понятие дифференциала. И происходит это примерно следующим образом.
Производной функции называется предел отношения приращения функции к приращению аргумента, если этот предел существует. Это можно записать в виде , имея в виду, что величина является приращением аргумента, – приращением функции. Если этот предел не существует, то мы говорим, что функция не имеет производную в этой точке.
Затем вводится понятие дифференциала функции, как главной части приращения функции, если это приращение представляется в виде , где – функция, обладающая свойством . При этом также, как мы и делали, доказывается теорема о том, что функция дифференцируема тогда и только тогда, когда существует производная этой функции. При этом и для дифференциала функции справедлива формула . Заметим, что из дифференцируемости функции следует ее непрерывность. В частности, отсюда следует, что функция, имеющая производную в точке, непрерывна в этой точке.
Правила вычисления производной функции
Теорема 1. Пусть существуют производные функций и Тогда справедливы формулы: , , , .
Доказательство. Так как существуют производные функций и , то и . Докажем первую из формул. Рассмотрим и после простой группировки слагаемых получим . Вторая формула доказывается совершенно аналогично. Далее рассмотрим с учетом определения производной оказывается справедливой третья формула (с учетом непрерывности этих функций). Аналогично доказывается формула № 4, после чего теорема будет доказана.
Теорема 2. Пусть существуют производные функций и . Тогда существует производная функции и справедлива формула .
Доказательство. Сформулируем идею доказательства. Для функции рассмотрим отношение приращения функции к приращению аргумента функции . С учетом существования (по условию теоремы) производных соответствующих функций при переходе к пределу в этом равенстве (все приращения в силу непрерывности одновременно стремятся к 0) мы приходим к формуле . Теорема доказана.
Следствие. (Производная обратной функции) Пусть задана монотонная функция . Тогда существует обратная ей функция , т. е. функция, обладающая свойством , , и при этом справедлива формула .
Доказательство. Для сложной функции производная, с одной стороны, равна 1, а, с другой стороны, равна произведению производных , откуда .
Таблица производных основных элементарных функций
Теорема 3. Справедливы следующие формулы для производных основных элементарных функций.
Доказательство. Формула 1) очевидна, т. к. у константы приращение функции всегда равно 0. Рассмотрим теперь формулу 4) при , т. е. производную от натурального логарифма. Вычислим ее непосредственно:
.
Теперь заметим, что и справедлива формула . Формула 4) доказана.
Рассмотрим функцию , обратную к функции . Поэтому (производные берутся по соответствующим аргументам) . Теперь заметим, что , поэтому, с учетом правила вычисления производной сложной функции, . Формула 3) доказана.
Для вычисления табличной производной 2) применим так называемое правило логарифмического дифференцирования. Суть его заключается в том, что , и эта формула применяется, если производную от логарифма функции посчитать легче, чем от самой функции. В этом случае искомая производная вычисляется по формуле .
Итак, для функции рассмотрим соотношение-следствие или . Продифференцировав обе части полученного соотношения, получим , откуда и, наконец, . Формула 2) доказана.
Перейдем к доказательству формул второй строки таблицы. Вычислим производную функции после следующих преобразований: . Формула 5) доказана.
Формулы 6), 7), 8) являются прямым следствием формулы 5):
,
.
И, наконец, рассмотрим формулы третьей строки. Заметим, что функция является обратной к функции и поэтому . Учитывая, что в области определения арксинуса значения косинуса не могут принимать отрицательные значения, мы приходим к формуле . Далее, получим .
Теперь отметим, что функция является обратной к функции и поэтому . Вспомним формулу и поэтому . Далее, получим . Теорема 7 доказана.
megaobuchalka.ru
Правила вычисления производных
Пусть c-положительное число u=u(x), v=v(x) и кроме этого у этих функции существуют производные.
Тогда справедливы следующие формулы :
1). c´=0
2). (c · u(x))´=c · u´(x)
3). (u(x) v(x))´=u´(x) v´(x)
4). (u(x)· v(x))´= u´(x)·v(x)+u(x)·v´(x)
5). ()´=
Доказательство:
1). c´=0
c´=
c´=
c´=
c´= 0.
Упражнение.
Докажите формулу (c · u(x))´=c · u´(x) пен (u(x) v(x))´=u´(x) v´(x).
4). (u(x)· v(x))´= u´(x)·v(x)+u(x)·v´(x)
(u(x)· v(x))´=
(u(x)· v(x))´=
(u(x)· v(x))´= ()
(u(x)· v(x))´= ()
(u(x)· v(x))´= u(x)·v´(x)+v(x)·u´(x)
(u(x)· v(x))´= u´(x)·v(x)+u(x)·v´(x)
Упражнение.
Докажите 5-ю формулу.
tendey.kz
