Правило вычисления производной сложной функции – Определение производной функции. Вычисление производных основных элементарных функций. Вычисление производных сложных функций

Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике – Элементы математического анализа

Правила вычисления производных

     Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.

      Правило 1 (производная от произведения числа на функцию). Справедливо равенство

(c f (x))’ = c f ‘ (x) ,

где  c – любое число.

      Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.

      Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле

(f (x) + g (x))’ = f ‘ (x) + g’ (x),

то есть производная от суммы функций равна сумме производных этих функций.

      Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле

(f (x) – g (x))’ = f ‘ (x) – g’ (x),

то есть производная от разности функций равна разности производных этих функций.

      Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле

(f (x) g (x))’ = f ‘ (x) g (x) + f (x) g’ (x),

      Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.

      Правило 5 (производная частного двух функций). Производная от дроби (частного двух функций) вычисляется по формуле

,

      Определение. Рассмотрим функции   f (x)   и   g (x) .  Сложной функцией или «функцией от функции» называют функцию вида

f (g (x))

При этом функцию   f (x)   называют внешней функцией, а функцию   g (x)  – внутренней функцией.

      Правило 6 (производная сложной функции). Производная сложной функции вычисляется по формуле

[ f (g (x))]’ = f ‘ (g (x)) g’ (x)

      Другими словами, для того, чтобы найти производную от сложной функции   f (g (x))   в точке   x   нужно умножить производную внешней функции, вычисленную в точке   g (x) ,   на производную внутренней функции, вычисленную в точке   x .

Таблица производных часто встречающихся функций

      В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.

Функция	Формула для производной	Название формулы
y = c , где  c – любое число	y’ = 0	Производная от постоянной функции
y = x c , где  c – любое число	y’ = c xc – 1	Производная степенной функции
y = e x	y’ = e x	Производная от экспоненты (показательной функции с основанием   e)
y = a x где  a – любое положительное число, не равное 1	y’ = a x ln a	Производная от показательной функции с основанием   a
y = ln x ,   x > 0	,   x > 0	Производная от натурального логарифма
y = log a x ,   x > 0 где  a – любое положительное число, не равное 1	,   x > 0	Производная от логарифма по основанию   a
y = sin x	y’ = cos x	Производная синуса
y = cos x	y’ = – sin x	Производная косинуса
y = tg x ,	,	Производная тангенса
y = ctg x ,	,	Производная котангенса
y = arcsin x ,		Производная арксинуса
y = arccos x ,		Производная арккосинуса
y = arctg x		Производная арктангенса
y = arcctg x		Производная арккотангенса

Производная от постоянной функции

Функция: y = c , где  c – любое число Формула для производной: y’ = 0

Производная степенной функции

Функция: y = x c , где  c – любое число Формула для производной: y’ = c xc – 1

Производная от экспоненты (показательной функции с основанием   e)

Функция: y = e x Формула для производной: y’ = e x

Производная от показательной функции с основанием   a

Функция: y = a x где  a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a

Производная от натурального логарифма

Функция: y = ln x ,   x > 0 Формула для производной: ,   x > 0

Производная от логарифма по основанию   a

Функция: y = log a x ,   x > 0 где  a – любое положительное число, не равное 1 Формула для производной: ,   x > 0

Производная синуса

Функция: y = sin x Формула для производной: y’ = cos x

Производная косинуса

Функция: y = cos x Формула для производной: y’ = – sin x

Производная тангенса

Функция: y = tg x , где Формула для производной: ,

Производная котангенса

Функция: y = ctg x , где Формула для производной: ,

Производная арксинуса

Функция: y = arcsin x , Формула для производной:

Производная арккосинуса

Функция: y = arccos x , Формула для производной:

Производная арктангенса

Функция: y = arctg x Формула для производной:

Производная арккотангенса

Функция: y = arcctg x Формула для производной:

Таблица производных сложных функций

      В следующей таблице приведены формулы для производных сложных функций.

      В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид   f (x) = kx + b , где  k  и  b  – любые числа, .

Функция	Формула для производной
y = (kx + b) c , где  c – любое число.	y’ = kc (kx + b) c – 1 ,
y = ( f (x)) c , где  c – любое число.
y = ekx + b	y = kekx + b
y = e f (x)
y = akx + b где  a – любое положительное число, не равное 1
y = a f (x) где  a – любое положительное число, не равное 1
y = ln (kx + b) ,   kx + b > 0	, kx + b > 0
y = ln ( f (x)) ,   f (x) > 0	, f (x) > 0
y = log a (kx + b) ,   kx + b > 0 где  a – любое положительное число, не равное 1	,   kx + b > 0
y = log a ( f (x)) ,   f (x) > 0 где  a – любое положительное число, не равное 1	,   f (x) > 0
y = sin (kx + b)	y’ = k cos (kx + b)
y = sin ( f (x))
y = cos (kx + b)	y’ = – k sin (kx + b)
y = cos ( f (x))
y = tg (kx + b), где	,
y = tg ( f (x)), где	,
y = ctg (kx + b), где	,
y = ctg ( f (x)), где	,
y = arcsin (kx + b),
y = arcsin ( f (x)),
y = arccos (kx + b),
y = arccos ( f (x)),
y = arctg (kx + b)
y = arctg ( f (x))
y = arcctg (kx + b)
y = arcctg ( f (x))

Функция: y = (kx + b) c , где  c – любое число. Формула для производной: y’ = kc (kx + b) c – 1 ,

Функция: y = ( f (x)) c , где  c – любое число. Формула для производной:

Функция: y = ekx + b Формула для производной: y = kekx + b

Функция: y = e f (x) Формула для производной:

Функция: y = akx + b где  a – любое положительное число, не равное 1 Формула для производной:

Функция: y = a f (x) где  a – любое положительное число, не равное 1 Формула для производной:

Функция: y = ln (kx + b) ,   kx + b > 0 Формула для производной: ,   kx + b > 0

Функция: y = ln ( f (x)) ,   f (x) > 0 Формула для производной: ,   f (x) > 0

Функция: y = log a (kx + b) ,   kx + b > 0 где  a – любое положительное число, не равное 1 Формула для производной: ,   kx + b > 0

Функция: y = log a ( f (x)) ,   f (x) > 0 где  a – любое положительное число, не равное 1 Формула для производной: ,   f (x) > 0

Функция: y = sin (kx + b) Формула для производной: y’ = k cos (kx + b)

Функция: y = sin ( f (x)) Формула для производной:

Функция: y = cos (kx + b) Формула для производной: y’ = – k sin (kx + b)

Функция: y = cos ( f (x)) Формула для производной:

Функция: y = tg (kx + b), где Формула для производной: ,

Функция: y = tg ( f (x)), где Формула для производной: ,

Функция: y = ctg (kx + b), где Формула для производной: ,

Функция: y = ctg ( f (x)), где Формула для производной: ,

Функция: y = arcsin (kx + b), Формула для производной:

Функция: y = arcsin ( f (x)), Формула для производной:

Функция: y = arccos (kx + b), Формула для производной:

Функция: y = arccos ( f (x)), Формула для производной:

Функция: y = arctg (kx + b) Формула для производной:

Функция: y = arctg ( f (x)) Формула для производной:

Функция: y = arcctg (kx + b) Формула для производной:

Функция: y = arcctg ( f (x)) Формула для производной:

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Производные математических функций. Определение, таблица основных производных, правила их вычисления

Справочные материалы по теме «производная». Базовый школьный уровень.
Теоретические сведения для учеников, преподавателей и репетиторов по математике. В помощь к проведению занятий.

Определение: производной функции в точке называется предел отношения приращения функции к приращению переменной, то есть

Таблица производных основных математических функций:

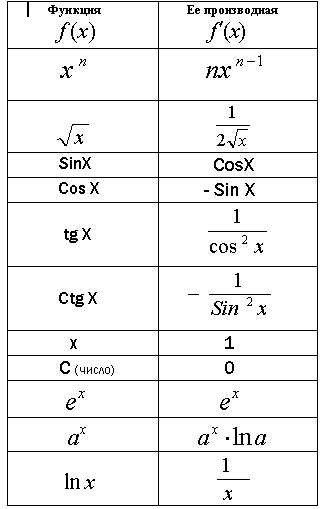
Правила вычисления производных

Производная суммы двух любых выражений равна сумме производных этих выражений (производная суммы равна сумме производных)

Производная разности двух любых выражений равна разности производных этих слагаемых (производная разности равна разности производных).

Производная от произведения двух множителей равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго (сумма поочередно взятых производных от множителей).

Комментарий репетитора по математике: когда я короткими фразами напоминаю ученику о правиле вычисления производной от произведения, я говорю так: производная первого множителя на второй плюс обмен штрихами!

Производная от частного двух выражений равна частному разности поочередно взятых производных от множителей и квадрата знаменателя.

Производная от произведения числа на функцию. Чтобы найти производную от произведения числа на буквенное выражение (на функцию) нужно умножить это число на производную этого буквенного выражения.

Производная сложной функции:

Для вычисления производной сложной функции необходимо найти производную внешней функции и умножить ее на производную внутренней функции.

Ваши комментарии и отзывы к странице с производными:
Александр С.
Очень нужна была таблица. В интернете одна из самых. За пояснения и правила тоже огромное спасибо. Хотя бы по одному примеру ещё к ним и вообще было бы отлично было. Еще раз огромное спасибо.

Колпаков А.Н, репетитор по математике: хорошо, постараюсь в ближайшее время дополнить страницу примерами.

Виртуальный математический справочник.
Колпаков Александр Николаевич, репетитор по математике.

Метки: Алгебра, Справочник репетитора, Ученикам

ankolpakov.ru

Производная сложной функции – примеры решений

Здесь мы приводим примеры вычисления производных от следующих функций:
;   ;   ;   ;   .

Если функцию можно представить как сложную функцию в следующем виде:
,
то ее производная определяется по формуле:
.
В приводимых ниже примерах, мы будем записывать эту формулу в следующем виде:
.
где .
Здесь нижние индексы или , расположенные под знаком производной, обозначают переменные, по которой выполняется дифференцирование.

Обычно, в таблицах производных, приводятся производные функций от переменной x. Однако x – это формальный параметр. Переменную x можно заменить любой другой переменной. Поэтому, при дифференцировании функции от переменной , мы просто меняем, в таблице производных, переменную x на переменную u.

Простые примеры

Пример 1

Найти производную сложной функции
.

Решение

Запишем заданную функцию в эквивалентном виде:
.
В таблице производных находим:
;
.

По формуле производной сложной функции имеем:
.
Здесь .

Ответ

.

Пример 2

Найти производную
.

Решение

Выносим постоянную 5 за знак производной и из таблицы производных находим:
.

Применяем формулу производной сложной функции:
.
Здесь .

Ответ

.

Пример 3

Найдите производную
.

Решение

Выносим постоянную –1 за знак производной и из таблицы производных находим:
;
Из таблицы производных находим:
.

Применяем формулу производной сложной функции:
.
Здесь .

Ответ

.

Более сложные примеры

В более сложных примерах мы применяем правило дифференцирования сложной функции несколько раз. При этом мы вычисляем производную с конца. То есть разбиваем функцию на составные части и находим производные самых простых частей, используя таблицу производных. Также мы применяем правила дифференцирования суммы, произведения и дроби. Затем делаем подстановки и применяем формулу производной сложной функции.

Пример 4

Найдите производную
.

Решение

Выделим самую простую часть формулы и найдем ее производную. .

Применяем правило дифференцирования сложной функции.

.
Здесь мы использовали обозначение
.

Находим производную следующей части исходной функции, применяя полученные результаты. Применяем правило дифференцирования суммы:
.

Еще раз применяем правило дифференцирования сложной функции.

.
Здесь .

Ответ

.

Пример 5

Найдите производную функции
.

Решение

Выделим самую простую часть формулы и из таблицы производных найдем ее производную. .

Применяем правило дифференцирования сложной функции.
.
Здесь
.

Дифференцируем следующую часть, применяя полученные результаты.
.
Здесь
.

Дифференцируем следующую часть.

.
Здесь
.

Теперь находим производную искомой функции.

.
Здесь
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 19-11-2016

1cov-edu.ru

Производная сложной функции, примеры решений

Достаточно часто студентам в контрольных работах по математике нужна производная сложной функции, примеры решений которой будут рассмотрены на практике в данном материале. Но сначала краткая теория.

Формула

Пусть есть функция , тогда производную сложной функции можно найти по формуле:

Проще говоря, нахождение производной сложной функции выполняется “по цепочке”. Сначала находим производную от внешней функции без изменения её аргумента и умножаем на производную аргумента. Если аргумент в свою очередь тоже является сложной функцией, то снова берем производную ещё и от него.

Рассмотрим на практике примеры решений производных сложных функций.

Примеры решений

Пример 1

Найти производную сложной функции:

Решение

Пользуемся формулой нахождения производной сложной функции. Сначала находим производную внешней функции без учета внутренней функции, а затем и производную от самой внутренней функции:

Ответ

Пример 2

Найти производную сложной функции:

Решение

Видим экспоненту в задаче, поэтому берем значение производной для неё из таблицы, а затем вычисляем производную от аргумента:

Ответ

Пример 3

Найти производную сложной функции:

Решение

Зная значение производной арктангенса из таблицы, находим производную сложной функции:

Ответ

Пример 4

Найти производную сложной функции:

Решение

Перед нами сложная функция, точнее натуральный логарифм от многочлена. Поэтому применим правило. Имеем:

Ответ

Пример 5

Найти производную от сложной функции:

Решение

Сложную функцию представляет натуральный логарифм, аргументом которого является сумма двух функций, обе тоже сложные функции. Вспоминаем формулу и приступаем: Производная суммы функций равна сумме производных этих функций: Первая функция  – это производная от сложной функции: Вторая функция  – это производная сложной функции: Продолжаем нахождение производной исходной функции:

Ответ

В статье: «Производная сложной функции: примеры решений» была приведена формула и её словесное толкование. Также разобрано решение задач по данной теме. 

xn--24-6kcaa2awqnc8dd.xn--p1ai

Производная сложной функции

Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле

           

Типичная ошибка при решении задач на производные – машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.

Посмотрите на формулу 9 в

таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению – промежуточным аргументом по независимой переменной x.

А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии – приготовлении запечёных яблок, фаршированных ягодами.

Итак, “яблоко” – это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной

x, в свою очередь, является “фаршем” (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на “яблоко”, поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, “яблока”. Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной “яблока” и производной “фарша”. Можно подавать!

Пример 1.Найти производную функции

Сначала определим, где здесь “яблоко”, то есть функция по промежуточному аргументу u, а где “фарш”, то есть промежуточный аргумент u по независимой переменной x. Определяем: возведение в степень – это функция по промежуточному аргументу, то есть “яблоко”, а выражение в скобках (разность двух тригонометрических функций) – это промежуточный аргумент, то есть “фарш”.

Тогда

Далее по таблице производных (производная суммы или разности, производные синуса и косинуса) находим:

Требуемая в условии задачи производная (готовое “фаршированое яблоко”):

Нахождение производной сложной логарифмической функции имеет свои особенности, поэтому у нас есть и урок “Производная логарифмической функции”.

Пример 2.Найти производную функции

Неправильное решение: вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:

Правильное решение: опять определяем, где “яблоко”, а где “фарш”. Здесь натуральный логарифм от выражения в скобках – это “яблоко”, то есть функция по промежуточному аргументу u, а выражение в скобках – “фарш”, то есть промежуточный аргумент u по независимой переменной x.

Тогда (применяя формулу 14 из таблицы производных)

Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок “Производная логарифмической функции”.

Пример 3.Найти производную функции

Неправильное решение:

Правильное решение. В очередной раз определяем, где “яблоко”, а где “фарш”. Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это “яблоко”, оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени – номер 3 в таблице производных) – это “фарш”, он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Результат:

Производная сложной логарифмической функции – частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок “Производная логарифмической функции”.

Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования. Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы. Ниже – два примера, как это делается.

Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций

,

то её производную следует находить как произведение производных каждой из этих функций:

.

Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 4.Найти производную функции

Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:

Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:

Второе слагаемое – корень, поэтому

Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного из слагаемых содержит сложную функцию: возведение в степень – сложная функция, а то, что возводится в степень – промежуточный аргумент по независимой переменной x.

Поэтому вновь применим правило дифференцирования сложной функции:

Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:

Теперь можем найти производную промежуточного аргумента, нужного для вычисления требуемой в условии задачи производной сложной функции y:

Тогда

Пример 5.Найти производную функции

Сначала воспользуемся правилом дифференцирования суммы:

Получили сумму производных двух сложных функций. Находим первую из них:

Здесь возведение синуса в степень – сложная функция, а сам синус – промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки:

Теперь находим второе слагаемое из образующих производную функции y:

Здесь возведение косинуса в степень – сложная функция f[g(x)], а сам косинус – промежуточный аргумент по независимой переменной x. Снова воспользуемся правилом дифференцирования сложной функции:

Результат – требуемая производная:

---

Для сложных функций на основании правила дифференцирования сложной функции формула производной простой функции принимает другой вид.

Поделиться с друзьями

Весь блок “Производная”

function-x.ru

Сложная функция. Производная сложной функции

В этой статье мы будем говорить о таком важном математическом понятии, как сложная функция, и учиться находить производную сложной функции.

Прежде чем учиться находить производную сложной функции, давайте разберемся с понятием сложной функции, что это такое, “с чем ее едят”, и “как правильно ее готовить”.

Рассмотрим произвольную функцию, например, такую:

Заметим, что аргумент , стоящий в правой  и левой части уравнения функции – это одно и то же число, или выражение.

Вместо переменной  мы можем поставить, например, такое выражение: . И тогда мы получим функцию

.

Назовем выражение  промежуточным аргументом, а функцию  – внешней функцией. Это не строгие математические понятия, но они помогают уяснить смысл понятия сложной функции.

Строгое определение понятия сложной функции звучит так:

Пусть функция   определена на множестве  и  – множество значений этой функции. Пусть, множество  (или его подмножество) является областью определения функции . Поставим  в соответствие каждому  из  число . Тем самым на множестве  будет задана функция . Ее называют композицией функций или сложной функцией.

В этом определении, если пользоваться нашей терминологией,   – внешняя функция,  – промежуточный аргумент.

Производная сложной функции находится по такому правилу:

Чтобы было более понятно, я люблю записывать это правило в виде такой схемы:

В этом выражении  с помощью обозначена промежуточная функция.

Итак. Чтобы найти производную сложной функции, нужно

1. Определить, какая функция является внешней и найти по таблице производных соответствующую производную.

2. Определить промежуточный аргумент.

В этой процедуре наибольшие затруднения вызывает нахождение внешней функции. Для этого используется простой алгоритм:

а. Запишите уравнение функции.

б. Представьте, что вам нужно вычислить значение функции при каком-то значении х. Для этого вы подставляете это значение х в уравнение функции и производите арифметические действия. То действие, которое вы делаете последним и есть внешняя функция.

Например, в функции

 последнее действие  – возведение в степень.

Найдем производную этой функции. Для этого запишем промежуточный аргумент

как 

Получим 

Ищем в таблице производных  производную показательной функции:

Получим:

    (1)

Теперь наша задача найти производную функции

Заметим, что здесь мы опять имеем дело со сложной функцией. В этом выражении последнее действие – возведение в квадрат, а промежуточный аргумент .

Получаем:

Смотрим в таблице производных производную синуса:

Получаем:

Подставим полученное значение производной в выражение (1):

И, наконец, упростим выражение, вспомнив формулу синуса двойного аргумента:

Таким образом,

Заметим, что функции иногда похожи на матрешку: промежуточный аргумент сам является сложной функции. Но тогда при нахождении производной промежуточного аргумента, нужно вновь применить правило нахождения производной сложной функции.

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Правила дифференцирования производной

К основным правилам дифференцирования относят:

1. Вынесение постоянного множителя за знак производной:

   

То есть константу можно выносить за знак производной.

2. Производная суммы, производная разности:

   

Производная суммы двух функций равна сумме производных от каждой из них.

Замечание. Это правило распространяется и на большее число функций.

Производная разности

   

равна разности производных от каждой из них.

3. Производная произведения:

   

Производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

4. Производная дроби (производная частного двух функций):

   

Итак, производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com