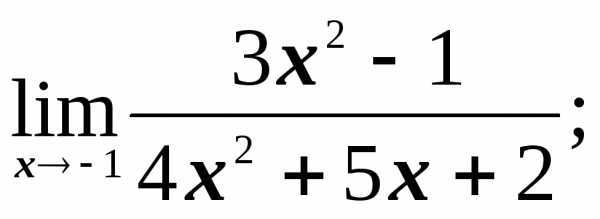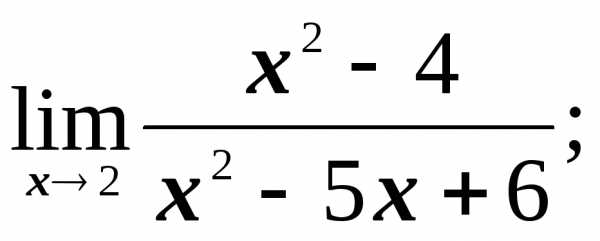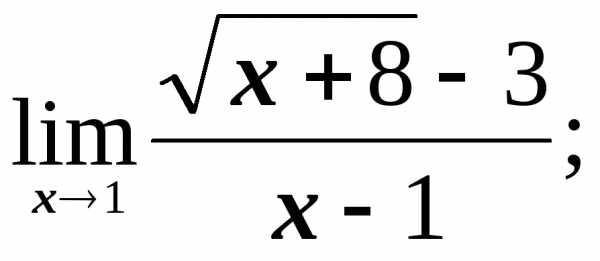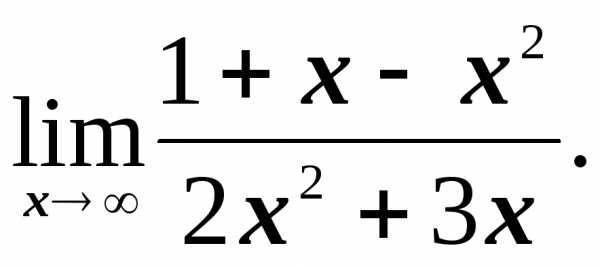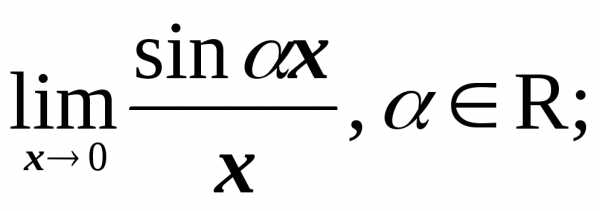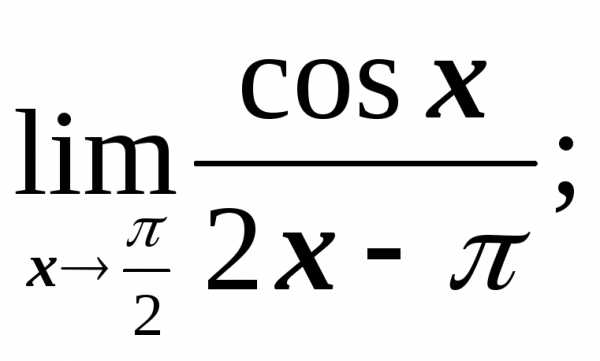пределы на бесконечность на бесконечность
Рассмотрим пределы на раскрытие неопределенности вида бесконечность на бесконечность.
Сначала учтем следующее:
— если при вычислении предела в числителе дроби стоит число, то
— или
Выражение вида
— это предел на неопределенность вида бесконечность, деленная на бесконечность (или просто бесконечность на бесконечность).
Чтобы найти предел, надо раскрыть неопределенность вида бесконечность на бесконечность. Для этого и в числителе, и в знаменателе выносим за скобки степень с наибольшим показателем. Затем сокращаем на нее.
1)
В дальнейшем просто делим почленно числитель и знаменатель (то есть каждое слагаемое) на старшую степень икса.
2)
3)
4)
А теперь сделаем выводы. Пределы на неопределенность бесконечность на бесконечность сводятся к одному из трех вариантов:
Примеры для самопроверки:
Показать решение
adminПредел функции
www.matematika.uznateshe.ru
Помогите решить / разобраться (М)
Потому что бесконечность — не число
Я сам хотел сказать ровно то же самое.
Поэтому не буду повторять, а немного добавлю.
Есть два разных понятия: число и точка.
Вначале для школьников они существуют по отдельности, как просто слова из разных миров: из арифметики / алгебры и из геометрии. Всё нормально.
Потом школьники изучают числовую прямую и координатную плоскость. И научаются сопоставлять На числовой прямой каждая точка – это какое-то число из множества – множества действительных чисел. И напротив, каждое число из – это какая-то точка на прямой.
А теперь, надо мысленно снова разделить эти понятия. Развести их. К прямой линии можно добавить ещё точки. Это будут “бесконечно удалённые точки”, одна или две. Это сделать можно, чисто геометрически (предел – это геометрическое понятие, например, в школьной геометрии постоянно встречаются пределы: при определении длины кривой линии, площади фигуры, при определении касательной). Но при этом, к множеству нельзя добавить таких чисел. Потому что числа “идут с другим комплектом”: чтобы какой-то новый элемент можно было назвать числом, его надо вписать во все арифметические операции, научиться проводить с ним всевозможные вычисления.
К множеству конечно, можно добавить ещё новые числа, но другие. Например, могут получиться комплексные числа. Или, может получиться так называемое “нестандартное множество действительных чисел”, в котором будут “актуальные бесконечности”. Но я не советую так делать. Главная проблема здесь в том, что вы не можете добавить числа по одному – вам придётся сразу добавлять бесконечно много новых чисел, сразу не меньше чем копию исходного множества а то и кучу таких копий.
—————-
Ещё я хотел бы подчеркнуть такую вещь. Добавление одной точки и добавление двух точек – это действия разные. Получатся разные результаты. И нельзя добавить и то и другое. То есть, вы должны рассматривать три разных конструкции:
– просто числовая прямая ;
– числовая прямая пополненная одной бесконечно удалённой точкой;
– числовая прямая пополненная двумя бесконечно удалёнными точками.
Эти конструкции используются неформально рядом, только чтобы “сообщить дополнительную уточнённую информацию”, когда это можно. Например, если вы считаете то вы можете написать ответ и будете абсолютно правы. Определению бесконечного предела это удовлетворяет. Но вы можете сделать большее, вы можете уточнить ответ, и написать (и именно это будет вам зачтено как решённая задача). И это тоже будет правильным ответом, и выполненным определением.
Но по сути, надо понимать, что мы имеем дело с тремя геометрическими фактами:
1. Если мы рассматриваем просто числовую прямую то в ней предел не существует. (Для вас это произносят как “не существует конечный предел”.)
2. Если мы рассматриваем числовую прямую то в ней предел существует, и равен
3. Если мы рассматриваем числовую прямую то в ней предел существует, и равен
Просто от вас ждут формулировки именно третьего факта, поскольку он “наиболее подробный”.
— 19.01.2016 11:44:05 —
А, ну и это уже arseniiv произнёс, и даже больше и подробней…
— 19.01.2016 11:50:19 —
—————-
Ещё добавлю. Если мы говорим про точки, то почему вообще пишем под знаком предела и другие формулы? На самом деле, конечно, в множестве или вычислять ничего нельзя. Но это было бы нам неудобно: мы хотим брать разные функции, и их исследовать, чтобы посмотреть, какие у них будут пределы. Поэтому, мы просто вычисляем что-то в рамках обычного а потом переносим эти числа уже в пополненные множества, по очевидному (естественному) сопоставлению.
dxdy.ru
Глава 1. Предел функции
1.1. Определение предела
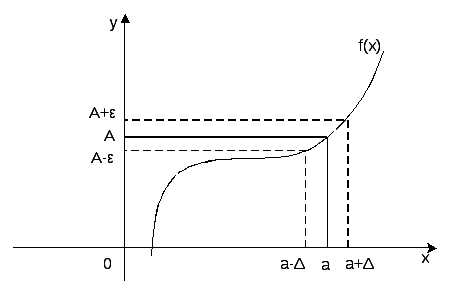
Рис. 1.1
Пусть функция f(x) определена в некоторой окрестности точки х =
Число А называется пределом функции f(x) при ха, если для любого >0 существует такое число >0, что для всех х таких, что 0 < x – a < верно неравенство f(x) – A< (рис. 1.1).
То же определение может быть записано в другом виде:
Если а – < x < a + , x a, то верно неравенство А –
Запись предела функции в точке: .
Если f(x) A1 при х а только при x < a, то называетсяпределом функции f(x) в точке х = а слева, а если f(x) A2 при х а только при x > a, то называетсяпределом функции f(x) в точке х = а справа
П
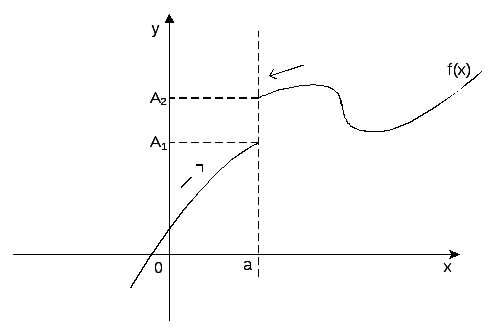
Рис. 1.2
риведенное выше определение относится к случаю, когда функцияf(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.Пределы А1 и А2 называются также односторонними
пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).
1.2. Операции над пределами
Предел постоянной есть сама постоянная:
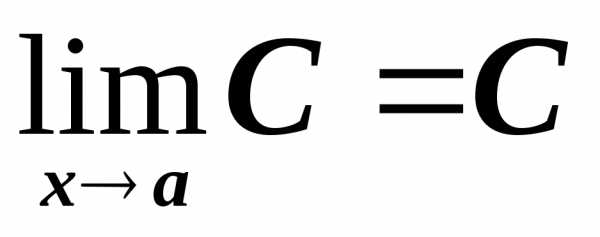 ,
гдеС = const.
,
гдеС = const.
Следующие свойства справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при ха;
Предел суммы (разности) равен сумме (разности) пределов:
;
Предел произведения равен произведению пределов:
;
Постоянную можно выносить за знак предела:
;
Предел отношения равен отношению пределов:
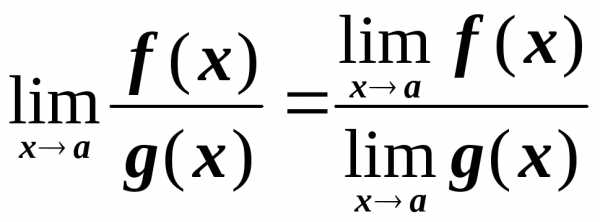
Если f(x)>0 вблизи точки х = а и , тоА>0.
Аналогично определяется знак предела при f(x) < 0, f(x) 0, f(x) 0;
Если g(x) f(x) u(x) вблизи точки х = а и , то и
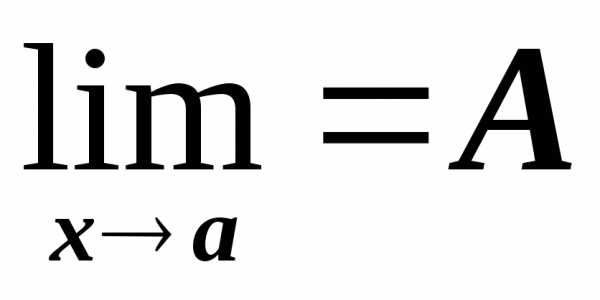 ;
;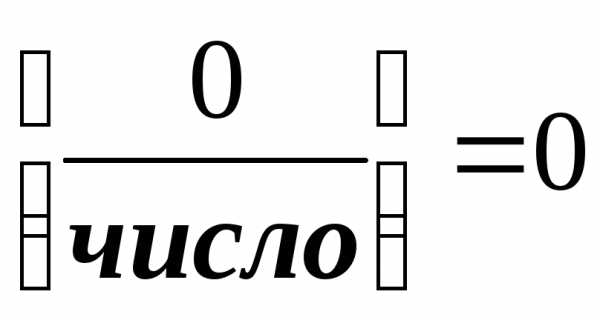 ;
;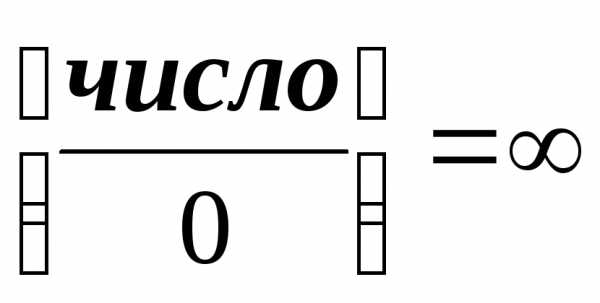
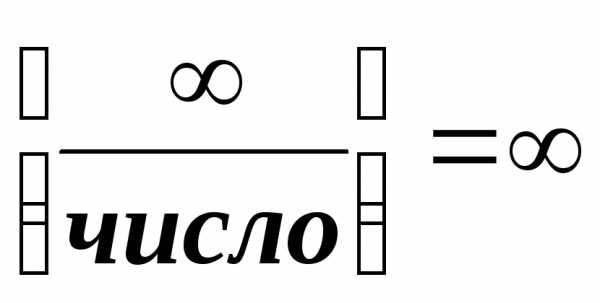 ;
; ;
;Неопределенность вида
 можно раскрыть, если числитель и
знаменатель дроби разделить на высшую
степень переменной;
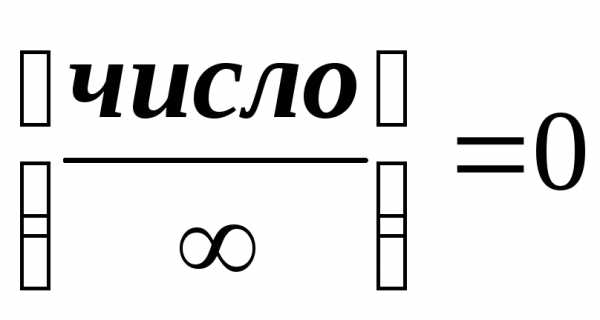
можно раскрыть, если числитель и
знаменатель дроби разделить на высшую
степень переменной;Неопределенность вида
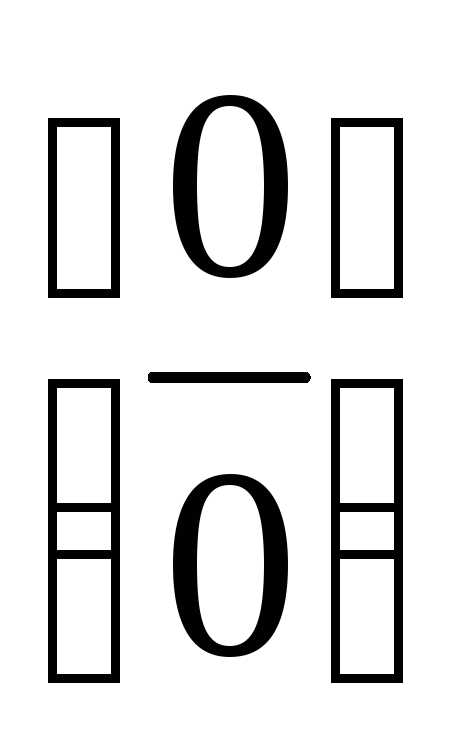 можно раскрыть, если числитель и
знаменатель дроби разложить на множители
и сократить.
можно раскрыть, если числитель и
знаменатель дроби разложить на множители
и сократить.
1.3. Замечательные пределы
Найдем
предел отношения двух многочленов, т.е. 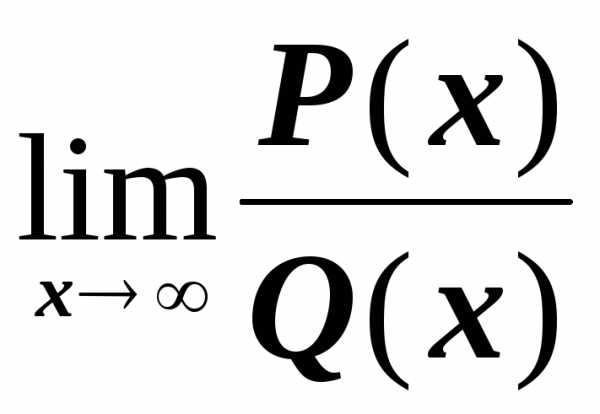 ,
где
,
где
P(x)
Таким
образом, 
Первый
замечательный предел: 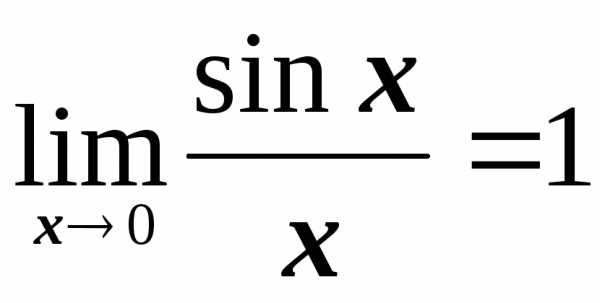
Второй
замечательный предел: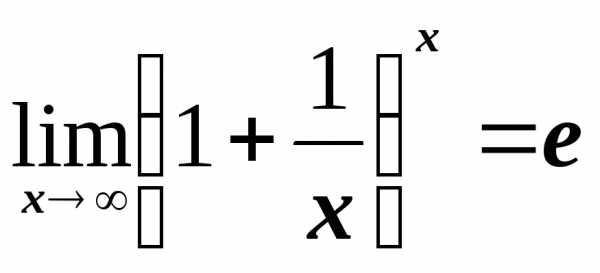 ,
гдее постоянная, которая приблизительно
равна 2,718281828…
,
гдее постоянная, которая приблизительно
равна 2,718281828…
Часто если непосредственное нахождение предела какой-либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
При решении многих задач используются следующие эквивалентности, верные при х0:
~ х
1–cos x ~
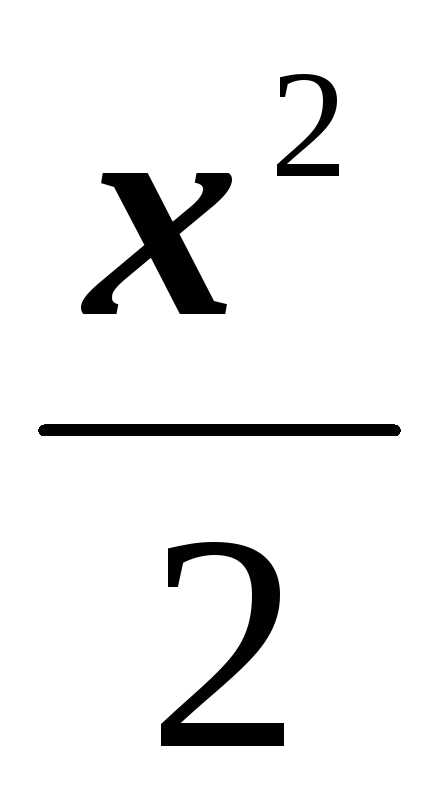 ;
;tg x ~ x;
arcsin x ~ x;
arctg x ~ x;
ln (1+x) ~ x;
ax–1 ~ xln a;
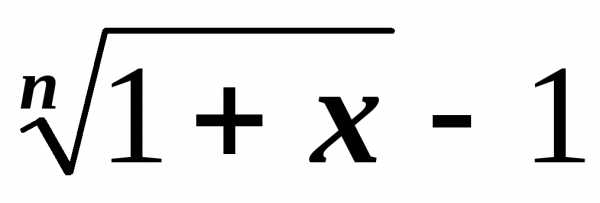 ~
~  .
.
1.4. Примеры
№1. Используя свойства пределов функций, найти следующие пределы:
Решение.
Применяя теорему о действиях над пределами функций, получим:
Так как пределы числителя и знаменателя при х2 равны нулю, то мы имеем неопределенность вида
 .
«Раскроем» эту неопределенность (т.е.
избавимся от нее), разложив числитель
и знаменатель на множители и сократив
их далее на общий множитель
.
«Раскроем» эту неопределенность (т.е.
избавимся от нее), разложив числитель
и знаменатель на множители и сократив
их далее на общий множитель
.
Здесь мы также имеем неопределенность вида
 .
Домножим числитель и знаменатель дроби
на выражение, сопряженное к числителю
(избавимся от иррациональности в
числителе):
.
Домножим числитель и знаменатель дроби
на выражение, сопряженное к числителю
(избавимся от иррациональности в
числителе):
Числитель и знаменатель дроби – бесконечно большие функции, поэтому здесь имеет место неопределенность вида
 .
Раскроем эту неопределенность. Поделим
числитель и знаменатель дроби на высшую
степеньх,
т.е. на
.
Раскроем эту неопределенность. Поделим
числитель и знаменатель дроби на высшую
степеньх,
т.е. на
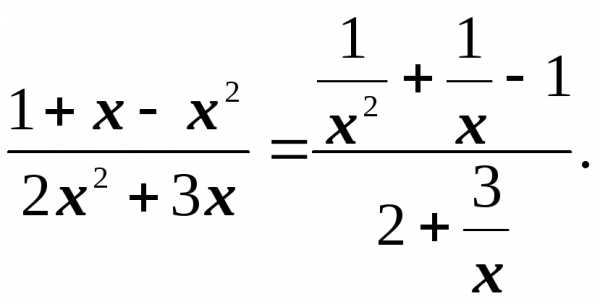
Таким образом,
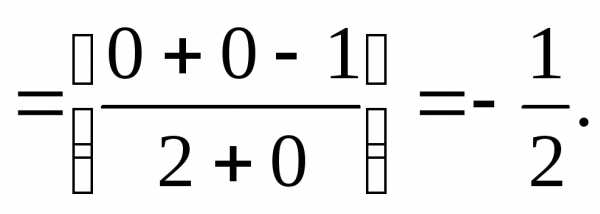
№2. Найти пределы:
Решение.
Сделаем замену у=αх; тогда у0 при х0 и . В последнем равенстве мы воспользовались первым замечательным пределом. Таким образом,
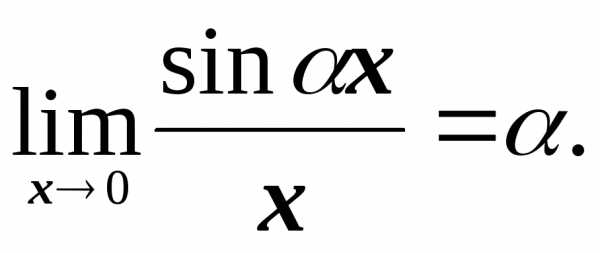
Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся предыдущим пунктом:
Сводя предел к первому замечательному пределу, сделаем замену у=х–
 .
Тогдау0
при х
.
Тогдау0
при х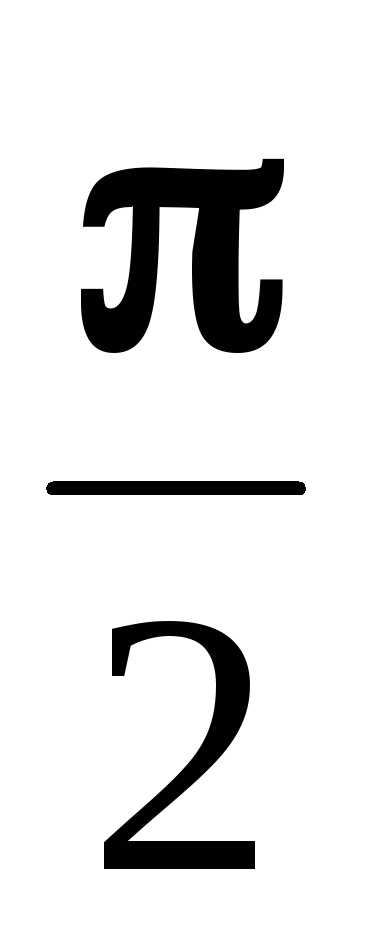 ,
ах=у+
,
ах=у+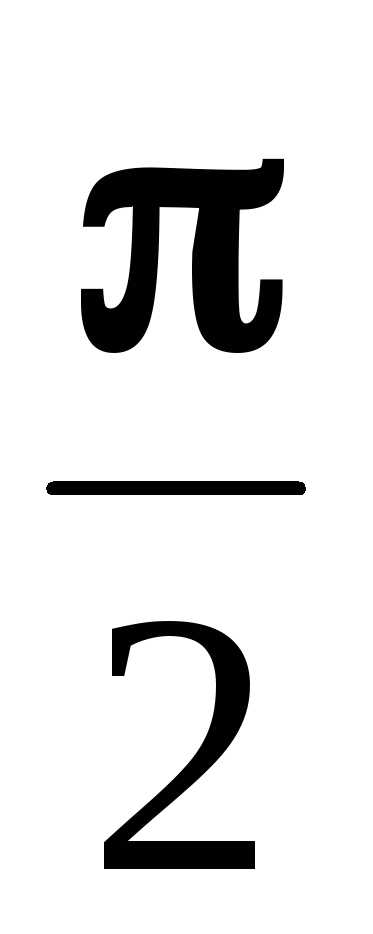 ,
откуда:
,
откуда:
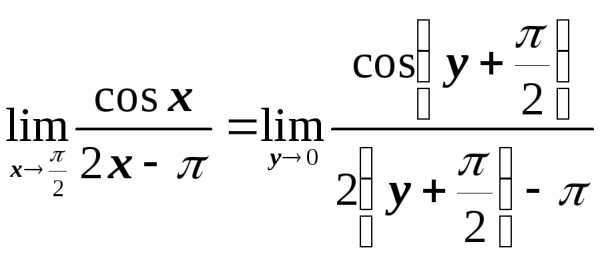
Во втором равенстве в этой цепочке мы использовали формулу приведения, а в последнем – первый замечательный предел.
Так как х0, то воспользуемся эквивалентностью №4:
.
studfiles.net
Предел функции с корнями
Среди примеров пределов функции часто встречаются функции с корнями, которые не всегда понятно как раскрывать. Проще когда есть пример границе с корневой функцией вида
Решение подобных пределов просто и понятно каждому.
Трудности возникают если есть следующие примеры функций с корнями.
Пример 1. Вычислить предел функции
При прямой подстановке точки x = 1 видно что и числитель и знаменатель функции
превращаются в ноль, то есть имеем неопределенность вида 0/0.
Для раскрытия неопределенности следует умножить выражение, содержащее корень на сопряженное к нему и применить правило разности квадратов. Для заданного примера преобразования будут следующими
Предел функции с корнями равен 6. Без приведенного правила ее трудно было бы найти.
Рассмотрим подобные примеры вычисления границы с данным правилом
Пример 2. Найти предел функции
Убеждаемся что при подстановке x = 3 получаем неопределенность вида 0/0.
Ее раскрываем умножением числителя и знаменателя на сопряженное к числителю.
Далее числитель раскладываем согласно правилу разности квадратов
Вот так просто нашли предел функции с корнями.
Пример 3. Определить предел функции
Видим, что имеем неопределенность вида 0/0.
Избавляемся ирациональносьти в знаменателе
Предел функции равна 8.
Теперь рассмотрим другой тип примеров, когда переменная в переделе стремится к бесконечности.
Пример 4. Вычислить предел функции
Много из Вас не знают как найти предел функции. Ниже будет раскрыта методика вычислений.
Имемем предел типа бесконечность минус бесконечность. Умножаем и делим на сопряженный множитель и используем правило разности квадратов
Границ функции равна -2,5.
Вычисление подобных пределов фактически сводится к раскрытию иррациональности , а затем подстановке переменной
Пример 5. Найти предел функции
Предел эквивалентен – бесконечность минус бесконечность
.
Умножим и разделим на сопряженное выражение и выполним упрощение
Пример 6. Чему равен предел функции?
Имеем неопределенность вида бесконечность минус бесконечность
Выполняем преобразования с корневыми функциями
предел функции равен -2.
Хорошо ознакомьтесь с методикой раскрытия неопределенностей, алгоритм достаточно прост и поможем найти сложную границу функции.
yukhym.com