Предел синуса на бесконечности – Математика всем и для всех
06:35 pm – Предел синуса на бесконечностиНапомним, что последовательность {xn} называется расходящейся, если никакое число не является пределом этой последовательности (Кудрявцев, МФТИ, том первый).
Докажем от противного, что последовательность sin(n) является расходящейся.
Пусть существует
Тогда последовательность sin(n) является фундаментальной и, в частности, верно, что
Учитывая то, что
,
получаем
откуда следует, что
Откуда получаем
но тогда, т.к. существует
должно быть верно, что
Однако из cos2(n) + sin2(n) = 1 и из того, что
следует, что должно выполнятся
Полученное противоречие доказывает требуемое.
fichtengolts.livejournal.com
Первый замечательный предел
Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.
Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:
Приведённое выше равенство основано на эквивалентности бесконечно малых . Следовательно, верно равенство и следующего отношения:
.
Это разновидность первого замечательного предела.
Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.
Пример 1. Найти предел .
Решение. Подстановка вместо x нуля приводит к неопределённости:
.
В знаменателе – синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:
.
В знаменателе – синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе, а, когда тройки сократятся, получится первый замечательный предел в чистом виде. Умножаем икс на три и тут же делим и далее решаем:
.
Пример 2. Найти предел .
Решение. Непосредственная подстановка вновь приводит к неопределённости “нуль делить на нуль”:
.
Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:
.
Решение. При подстановке вновь получаем неопределённость “нуль делить на нуль”:
.
Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:
.
Пример 4. Найти предел .
Решение. Вновь получаем неопределённость “нуль делить на нуль”:
.
Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:
Пример 5. Найти предел .
Решение. И вновь неопределённость “нуль делить на нуль”:
.
Помним из тригонометрии, что тангенс – это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:
.
Пример 6. Найти предел .
Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.
.
Так как , то и
Пример 7. Найти предел .
Решение. И вновь неопределённость “ноль делить на ноль” и синус под знаком предела. Значит надо приводить к первому замечательному пределу. Умножим числитель и знаменатель на выражение сопряжённое числителю и получим
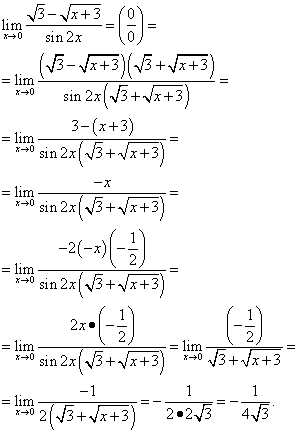
Пример 8. Найти предел .
Решение. Бороться с неопределённостью “ноль делить на ноль” будем приведением к первому замечательному пределу. Вспоминаем формулу тригонометрической единицы и подставляем её. Потом вспоминаем, что косинус в квадрате нуля и просто косинус нуля равны единице, а они у нас с противоположными знаками, значит взаимно уничтожаются. Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю. И дальнейшие преобразования. Всё вышеописанное выглядит так:
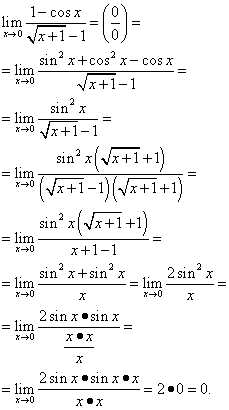
Начало темы “Предел”
Продолжение темы “Предел”
function-x.ru
пределы тригонометрических функций | Математика
Пределы тригонометрических функций чаще всего находятся с помощью 1-го замечательного предела и следствий из него. Проиллюстрируем решение пределов тригонометрических функций на конкретных примерах. Сам 1й замечательный предел
и одно из его следствий (есть и другие, но о них — позже):
(Здесь угол x выражен в радианах). Итак, примеры на пределы тригонометрических функций, которые решаются через 1й замечательный предел.
Найти пределы:
чтобы раскрыть неопределенность вида ноль на ноль, используем 1й замечательный предел:
Сокращаем числитель и знаменатель на x:
Так как по 1-му замечательному пределу
окончательно получаем, что
Решение пределов тригонометрических функций зачастую требует привлечения тригонометрических формул. Например, из тригонометрической единицы следует, что
используем формулу
В следующем пункте пределы тригонометрических функций будем находить с помощью следствий из 1-го замечательного предела.
www.matematika.uznateshe.ru
