Пределы с логарифмами примеры решения – Помощь студенту — практические примеры, задачи, теория: Предел отношения логарифмов - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

пределы логарифмов | Математика

Рассмотрим пределы логарифмов, которые можно найти с помощью следствия из 2-го замечательного предела.

Следствие 2-го замечательного предела:

Это следствие распространяется и на пределы логарифмов, в которых на месте x стоит некоторая функция f(x), если f(x)→0 при x→0, то есть

Рассмотрим, как находят пределы на логарифмы на примерах.

Найти предел функции:

Приводим выражени под знаком предела к такому виду, чтобы можно было применить нашу формулу (*):

так как по следствию из 2-го замечательного предела

Преобразуем выражение -1+cos x:

Продолжим

Теперь приведем предел с логарифмом к виду (*)

С пределом логарифма разобрались:

осталось убрать неопределенность 0 на 0, возникшую с появлением синуса. По 1-му замечательному пределу

Преобразовываем выражение так, чтобы применить этот замечательный предел:

Сокращаем дробь на x², имеем:

По теореме о разложении квадратного трехчлена на множители: x²-7x+10=(x-2)(x-5).

Сокращаем дробь на (x-2):

Так как при x→2 x²-7x+10→0, то

Значит, окончательный ответ

Дальше мы увидим, что пределы на логарифмы удобно находить, используя эквивалентность бесконечно малых величин.

www.matematika.uznateshe.ru

Сложные пределы и методы их решения

В этой статье собраны наиболее интересные и сложные случаи пределов, решение которых требует определенных навыков и знаний. В большинстве случаев, пределы, изучаемые в

базовом курсе высшей математики, просты и решаются в одно-два действия. Однако иногда приходится сталкиваться со сложными примерами пределов, которые чтобы решить
нужно знать хитростные способы. Рассмотрим же их!

Пример 1. Решить предел

Чтобы решить данный предел, необходимы знания по теме первый замечательный предел и эквивалентные бесконечно малые функции. Ну а в начале долгого пути, нам предстоит сделать преобразования в числителе, используя свойства тригонометрических функций, и в знаменателе, используя обманный ход, но обо всем по порядку. Начнем с числителя, представим

в равнозначной записи и запишем числитель уже в новой форме:

Тот факт, что x стремится к нулю, позволяет нам считать что в будущем можно будет использовать свойства эквивалентных бесконечно малых. Поэтому, обращаем внимание на
логарифм, стоящий в знаменателе. Если его немного «отредактировать» и привести к нужному виду, то его смело можно будет использовать для получения эквивалентных
значений. Обращаемся к таблице эквивалентных бесконечно малых величин и видим, что для счастья нам не хватает единицы. Вот здесь-то мы и используем способ (как я его
называю) «искусственного добавления» числа:

Все довольно просто, мы не нарушая баланса выражения, добавили и убавили единицу к косинусу. С учетом всех знаков , преобразуем выражение:

В результате наших действий, мы получили идеальных кандидатов на эквивалентные замены. В числителе вынесли знак минус за скобки, получив тем самым

в знаменателе подготовили выражение с логарифмом. С ними все понятно, что же делать в синусом? Все просто, используем первый замечательный предел и получаем законную
единицу. Вычисляем:

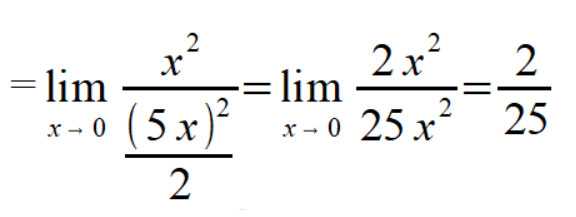
Краткие пояснения к тому, какие эквивалентные замены были произведены, а также как был использован первый предел:

— первый предел, при

Отдельной строкой хотелось бы остановиться на третьей формуле. Как известно, эквивалентная малая для логарифма выглядит следующим образом:

ln(1+x) ~x

В нашем случае, в роли х выступала вся скобка (-(1-cos(5x))).

Далее, мы повторно используем правило, но только уже для случая с косинусом:

при

В нашем случае, cos(x) — это cos(5x) и соответствующая замена была такой:

при

Ну вот и все. Предел был непростым, но интересным, и его решение, надеюсь, было вам понятным.

mathbaza.ru

12.Свойства пределов. Замечательные пределы | spiruk

12.Свойства пределов. Замечательные пределы

Обозначение предела

Предел функции обозначается как или через символ предела: .
Всюду ниже предполагается, что пределы функций существуют.

Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Расширенное правило суммы

Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

Предел произведения

Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

Расширенное правило произведения

Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Предел степенной функции

где степень p — действительное число. В частности,

Если f ( x ) = x, то

Предел показательной функции

где основание a > 0.

Предел логарифмической функции

где основание a > 0.

spiruk.wordpress.com

натуральный логарифм — ПриМат

Рассмотрим последовательность , .

Покажем, что последовательность ограничена и возрастает.

Сначала докажем монотонность. Воспользуемся биномом Ньютона:

Полагая, что , получим:

Из равенства следует, что с увеличением число положительных слагаемых в правой части увеличивается.

Кроме того, при увеличении число — убывает,

поэтому величины , , возрастают.

Поэтому последовательность {} = — возрастающая, при этом

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу. Правая часть увеличится, получим неравенство:

Усилим полученное неравенство, заменив числа , стоящие в знаменателях дробей, числом :

Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:

Поэтому:
Итак, последовательность ограничена, при этом для выполняются неравенства и :

Следовательно, на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемый обычно буквой :

Определение:

Числом называется предел последовательности т. е.

Это число иррациональное и приближенно равно . Логарифмы с основанием называются натуральными и обозначаются Данный предел называют вторым замечательным пределом. Многие примеры сводятся с помощью простых замен ко второму замечательному пределу. Рассмотрим пример решения на второй замечательный предел.

Пример.

Найти предел

Решение.

Преобразуем предел:

Литература

Портал знаний (Введение в анализ->Последовательности)

Вартанян Г.М. Конспект лекций по математическому анализу, стр.17 (часть 1)
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Издание четвертое. Стр. 74-76: М.Наука. — 1982, 616 стр.

Число е.

Лимит времени: 0

Информация

Тест на тему: Число е

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 4

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

максимум из 7 баллов
Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Ваш результат был записан в таблицу лидеров

С ответом
С отметкой о просмотре

Поделиться ссылкой:

ib.mazurok.com

Решение пределов | СпецКласс

Пределы – первая тема, с которой вам придется познакомиться в курсе высшей математики. Так что давайте рассмотрим все варианты задач, которые скорее всего попадутся вам по этой теме на контрольной или экзамене.

Что надо знать про пределы

Чтобы научиться решать примеры на пределы, надо знать две вещи:

Какой тип предела перед вами?
Каким способом решаются пределы такого типа?

Типы пределов

Тип предела часто подразумевает неопределенность, которая записана в примере.

Плохая новость – подходы к решению таких примеров различны.
Хорошая новость – эти подходы стандартные, и каждый из таких пределов вы сможете решить сами с помощью моих онлайн-уроков.

Вот 5 полезных ссылок, по которым вы найдете понятные решения пределов онлайн, и сможете самостоятельно решить свои пределы, просто повторив ход моего решения.

Предел с неопределенностью вида “бесконечность на бесконечность”

Предел с неопределенностью вида “ноль на ноль”

Предел с неопределенностью, решаемый через сопряженное

Предел с тригонометрическими функциями

Предел со степенями

Предел с логарифмом

Замечательные пределы

Отдельным пунктом любого учебника стоят так называемые замечательные пределы. Это всего две формулы, которые имеют массу вариантов примеров на замечательные пределы. Два коротких ролика помогут вам справиться с этими примерами:

Первый замечательный предел

Второй замечательный предел

При решении задач на замечательные пределы старайтесь “увидеть” их и свести к формулам этих пределов.

Правило Лопиталя

Еще одна группа примеров – это примеры на полезное правило, которое очень упрощает нахождение пределов – Решение пределов с помощью правила Лопиталя.

Правило Лопиталя – это нахождение производных, принцип которого объясняется здесь. Ну а как он работает в конкретных случаях, я расскажу отдельных видео, ссылки на которые также здесь выложу.

Первый ролик, который я выложил на своем канале Youtube, рассказывал о решение пределов:

specclass.ru

Натуральный логарифм, функция ln x

Определение

Натуральный логарифм – это функция y = ln x, обратная к экспоненте, x = e^y, и являющаяся логарифмом по основанию числа е: ln x = log_e x.

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x.

Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045…;
.

График натурального логарифма ln x

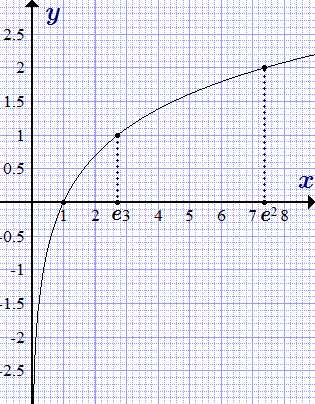
График функции y = ln x.

График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x.

Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x^a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.


Область определения	0 < x + ∞
Область значений	– ∞ < y < + ∞
Монотонность	монотонно возрастает
Нули, y = 0	x = 1
Точки пересечения с осью ординат, x = 0	нет
	+ ∞
	– ∞

Значения ln x

ln 1 = 0

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе “Логарифм”.

Обратная функция

Обратной для натурального логарифма является экспонента.

Если , то

Если , то .

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Интеграл вычисляется интегрированием по частям:
.
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z:
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n.

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 05-04-2014 Изменено: 20-03-2017

1cov-edu.ru

Замечательные пределы с экспонентой и логарифмом

На практике чаще встречаются пределы и особенно их частные случаи . Предела лично ни разу не видел, а может быть, и видел, да не помню.

Иногда перечисленные пределы называют третьим, четвёртым и пятым замечательным пределом, но своё негативное отношение к избыточной нумерации я уже высказал на урокеПравила Лопиталя, поэтому пусть это будут «просто» замечательные пределы без номеров.

Сама техника решения мало чем отличатся от первого замечательного предела:

Пример 10