Пример уравнения – Решение линейных уравнений с примерами

Решение линейных уравнений с примерами

Уравнение с одним неизвестным, которое после раскрытия скобок и приведения подобных членов принимает вид  

aх + b = 0, где a и b произвольные числа, называется линейным уравнением с одним неизвестным. Cегодня разберёмся, как эти линейные уравнения решать.

Например, все уравнения:

2х + 3= 7 – 0,5х;  0,3х = 0;  x/2 + 3 = 1/2 (х – 2) – линейные.

Значение неизвестного, обращающее уравнение в верное равенство называется решением или корнем уравнения.

Например, если в уравнении 3х + 7 = 13 вместо неизвестного х подставить число 2 , то получим верное равенство 3· 2 +7 = 13. Значит, значение х = 2 есть решение или корень уравнения.

А значение х = 3 не обращает  уравнение  3х + 7 = 13 в верное равенство, так  как  3· 2 +7 ≠ 13. Значит, значение х = 3 не является решением или корнем уравнения.

Решение любых линейных уравнений сводится к решению уравнений вида

aх + b = 0.

Перенесем свободный член из левой части уравнения в правую, изменив при этом знак перед b на противоположный, получим

aх = ‒ b.

Если a ≠ 0, то х = ‒ b/a .

Пример 1. Решите уравнение 3х + 2 =11.

Перенесем 2 из левой части уравнения в правую, изменив при этом знак перед 2 на противоположный, получим 
3х = 11 – 2.

Выполним вычитание, тогда
3х = 9.

Чтобы найти х надо разделить произведение на известный множитель, то есть     
х = 9 : 3.

Значит, значение х = 3 является  решением или корнем уравнения.

Ответ: х = 3

.

Если а = 0 и b = 0, то получим уравнение  0х = 0. Это уравнение имеет бесконечно много  решений, так как при умножении любого числа на 0 мы получаем 0,но b тоже равно 0. Решением этого уравнения  является любое число.

Пример 2. Решите уравнение 5(х – 3) + 2 = 3 (х – 4) + 2х ‒ 1.

Раскроем скобки:
5х – 15 + 2 = 3х – 12 + 2х ‒ 1.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
5х – 3х ‒ 2х =  – 12  ‒ 1 + 15 ‒ 2.

Приведем подобные члены:
0х = 0.

Ответ: х –  любое число.

Если а = 0 и b ≠ 0, то получим уравнение  0х = – b. Это уравнение решений не имеет, так как при умножении любого числа на 0 мы получаем 0, но  b ≠ 0 .

Пример 3. Решите уравнение х + 8 = х + 5.

Сгруппируем  в левой части члены, содержащие неизвестные, а в правой ‒ свободные члены:
х – х = 5 ‒ 8.

Приведем подобные члены: 
0х = ‒ 3.

Ответ: нет решений.

На рисунке 1 изображена схема решения линейного уравнения

Составим общую схему решения уравнений с одной переменной. Рассмотрим решение примера 4.

Пример 4. Пусть надо решить уравнение 

1) Умножим все члены уравнения на наименьшее общее кратное знаменателей, равное 12.

2) После сокращения получим
4 (х – 4) + 3·2 (х + 1) ‒ 12 = 6·5 (х – 3) + 24х – 2 (11х + 43)

3) Чтобы отделить члены, содержащие неизвестные и свободные члены, раскроем скобки:
4х – 16 + 6х + 6 – 12 = 30х – 90 + 24х – 22х – 86 .

4) Сгруппируем в одной части члены, содержащие неизвестные, а в другой – свободные члены:
4х + 6х – 30х – 24х + 22х = ‒ 90 – 86 + 16 – 6 + 12.

5) Приведем подобные члены:
‒ 22х = ‒ 154.

6) Разделим на  – 22 , Получим
х = 7.

Как видим, корень уравнения равен семи.

Вообще такие уравнения можно решать по следующей схеме:

а) привести уравнение к целому виду;

б) раскрыть скобки;

в) сгруппировать члены, содержащие неизвестное, в одной части уравнения, а свободные члены ‒ в другой;

г) привести подобные члены;

д) решить уравнение вида aх = b,которое получили после приведения подобных членов.

Однако эта схема не обязательна для всякого уравнения. При решении многих более простых уравнений приходится начинать не с первого, а со второго (Пример. 2),  третьего (Пример. 1, 3) и даже с пятого этапа, как в примере 5.

Пример 5. Решите уравнение 2х = 1/4.

Находим неизвестное  х = 1/4 : 2,
х = 1/8 .

Рассмотрим решение некоторых линейных уравнений, встречающихся на основном государственном экзамене.

Пример 6. Решите уравнение 2 (х + 3) = 5 – 6х.

Решение

2х + 6 = 5 – 6х

2х + 6х = 5 – 6

8х = ‒1

х = ‒1 : 8

х = ‒ 0, 125

Ответ: ‒ 0, 125

Пример 7. Решите уравнение – 6 (5 – 3х) = 8х – 7.

Решение

– 30 + 18х = 8х – 7

18х  – 8х =  – 7 +30

10х = 23

х = 23 : 10

х = 2,3

Ответ: 2,3

Пример 8. Решите уравнение

 

Решение:

3(3х – 4) = 4 · 7х + 24

9х – 12 = 28х + 24

9х – 28х = 24 + 12

-19х = 36

х = 36 : (-19)

х = – 36/19

Ответ: – . 

Пример 9. Найдите f(6), если f (x + 2) = 3^7-х

Решение

Так как надо найти f(6), а нам известно f (x + 2),
то х + 2 = 6.

Решаем линейное уравнение х + 2 = 6,
получаем х = 6 – 2, х = 4.

Если х = 4, тогда
f(6) = 3^7-4 = 3³ = 27

Ответ: 27.

Если у Вас остались вопросы, есть желание разобраться с решением уравнений более основательно, записывайтесь на мои уроки в РАСПИСАНИИ. Буду рада Вам помочь!

Также TutorOnline советует посмотреть новый видеоурок от нашего репетитора Ольги Александровны, который поможет разобраться как с линейными уравнениями, так и с другими.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Алгебра. Урок 4. Уравнения, системы уравнений

 

Содержание страницы:

 

Линейное уравнение

– уравнение вида ax=b, где x — переменная, a и b некоторые числа, причем a≠0.

Примеры:

Линейными уравнениями называют не только уравнения вида ax=b, но и любые уравнения, которые при помощи преобразований и упрощений сводятся к этому виду.

Как же решать уравнения, которые приведены к виду ax=b? Достаточно поделить левую и правую часть уравнения на величину a. В результате получим ответ: x=ba.

Как распознать, является ли произвольное уравнение линейным или нет? Надо обратить внимание на переменную, которая присутствует в нем. Если старшая степень, в которой стоит переменная, равна единице, то такое уравнение линейное.

Для того, чтобы решить линейное уравнение, необходимо раскрыть скобки (если они есть), перенести «иксы» в левую часть, числа – в правую, привести подобные слагаемые. Получится уравнение вида ax=b. Решение данного уравнения: x=ba.

Примеры:

1. 2x+1=2(x−3)+8

Это линейное уравнение, так как переменная стоит в первое степени.

Попробуем преобразовать его к виду ax=b:

Для начала раскроем скобки:

2x+1=4x−6+8

В левую часть переносятся все слагаемые с x, в правую – числа:

2x−4x=2−1

−2x=1

Теперь поделим левую и правую часть на число (-2):

−2x−2=1−2=−12=−0,5

Ответ: x=−0,5

 

1. x2−1=0

Это уравнение не является линейным, так как старшая степень, в которой стоит переменная x равна двум.

 

1. x(x+3)−8=x−1

Это уравнение выглядит линейным на первый взгляд, но после раскрытия скобок старшая степень становится равна двум:

x2+3x−8=x−1

Это уравнение не является линейным.

 

Особые случаи (в 4 задании ОГЭ они не встречались, но знать их полезно)

Примеры:

1. 2x−4=2(x−2)

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2x−4=2x−4

2x−2x=−4+4

0=0

И как же здесь искать x, если его нет? После выполнения преобразований мы получили верное равенство (тождество), которое не зависит от значения переменной x . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда получается верное равенство (тождество). Значит x может быть любым числом.

Ответ: x∈(−∞; +∞)

 

1. 2x−4=2(x−8)

Это линейное уравнение. Раскроем скобки, перенесем иксы влево, числа вправо:

2x−4=2x−16

2x−2x=−16+4

0=−12

В результате преобразований x сократился, но в итоге получилось неверное равенство, так как . Какое бы значение x мы ни подставляли бы в исходное уравнение, в результате всегда будет неверное равенство. А это означает, что нет таких значений x, при которых равенство становилось бы верным.

Ответ: x∈∅

 

Квадратное уравнение — уравнение вида ax2+bx+c=0, где x — переменная, a,b и c — некоторые числа, причем a≠0.

Алгоритм решения квадратного уравнения:

1. Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: ax2+bx+c=0
2. Выписать, чему равны в числах коэффициенты: a=…b=…c=…
3. Вычислить дискриминант по формуле: D=b2−4ac
4. Если D>0, будет два различных корня, которые находятся по формуле: x1,2=−b±D2a
5. Если D=0, будет один корень, который находится по формуле: x=−b2a
6. Если D<0, решений нет: x∈∅

Примеры:

1. −x2+6x+7=0

a=−1,b=6,c=7

D=b2−4ac=62−4⋅(−1)⋅7=36+28=64

D>0 — будет два различных корня:

x1,2=−b±D2a=−6±642⋅(−1)=−6±8−2=[−6+8−2=2−2=−1−6−8−2=−14−2=7

Ответ: x1=−1,x2=7

 

1. −x2+4x−4=0

a=−1,b=4,c=−4

D=b2−4ac=42−4⋅(−1)⋅(−4)=16−16=0

D=0 — будет один корень:

x=−b2a=−42⋅(−1)=−4−2=2

Ответ: x=2

 

1. 2×2−7x+10=0

a=2,b=−7,c=10

D=b2−4ac=(−7)2−4⋅2⋅10=49−80=−31

D<0 — решений нет.

Ответ: x∈∅

 

Квадратный трехчлен можно разложить на множители следующим образом:

ax2+bx+c=a⋅(x−x1)⋅(x−x2)

где a — число, коэффициент перед старшим коэффициентом,

x — переменная (то есть буква),

x1 и x2 — числа, корни уравнения ax2+bx+c=0, которые найдены через дискриминант.

Если уравнение имеет только один корень , то разложение выглядит так:

ax2+bx+c=a⋅(x−x0)2

Примеры:

1. −x2+6x+7=0⇒x1=−1, x2=7

−x2+6x+7=(−1)⋅(x−(−1))(x−7)=−(x+1)(x−7)=(x+1)(7−x)

 

1. −x2+4x−4=0;⇒x0=2

−x2+4x−4=(−1)⋅(x−2)2=−(x−2)2

 

Если квадратный трехчлен является неполным, ( (b=0 или c=0) то его можно разложить на множители следующими способами:

• b=0⇒ применить формулу сокращенного умножения для разности квадратов.

 

Пусть f(x) и g(x) — некоторые функции, зависящие от переменной x.

Дробно рациональное уравнение – это уравнение вида f(x)g(x)=0.

Для того, чтобы решать дробно рациональные уравнения, надо вспомнить, что такое ОДЗ и когда оно возникает.

ОДЗ – область допустимых значений переменной.

В выражении вида f(x)g(x)=0

ОДЗ: g(x)≠0 (знаменатель дроби не может быть равен нулю).

Алгоритм решения дробно рационального уравнения:

1. Привести выражение к виду f(x)g(x)=0.
2. Выписать ОДЗ: g(x)≠0.
3. Приравнять числитель дроби к нулю f(x)=0 и найти корни.
4. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Пример:

Решить рациональное уравнение x2−42−x=1.

Решение:

Будем действовать в соответствии с алгоритмом.

1. Привести выражение к виду f(x)g(x)=0.

Переносим единичку в левую часть, записываем к ней дополнительный множитель, чтобы привести оба слагаемых к одному общему знаменателю:

x2−42−x−1\2−x=0

x2−42−x−2−x2−x=0

x2−4−(2−x)2−x=0

x2−4−2+x2−x=0

x2+x−62−x=0

Первый шаг алгоритма выполнен успешно.

1. Выписать ОДЗ:

g(x)≠0

2−x≠0

−x≠−2

x≠2

Обводим в рамочку ОДЗ, не забываем про него: x≠2

1. Приравнять числитель дроби к нулю f(x)=0 и найти корни:

x2+x−6=0 — Квадратное уравнение. Решаем через дискриминант.

a=1,b=1,c=−6

D=b2−4ac=12−4⋅1⋅(−6)=1+24=25

D>0 — будет два различных корня.

x1,2=−b±D2a=−1±252⋅1=−1±52=[−1+52=42=2−1−52=−62=−3

[x1=2×2=−3

 

1. Указать в ответе корни из числителя, исключив те корни, которые попали в ОДЗ.

Корни, полученные на предыдущем шаге:

[x1=2×2=−3

ОДЗ: x≠2

Значит, в ответ идет только один корень, x=−3.

Ответ: x=−3.

 

Системой уравнений называют два уравнения с двумя неизвестными (как правило, неизвестные обозначаются x и y), которые объединены в общую систему фигурной скобкой.

Пример системы уравнений

{x+2y=83x−y=−4

Решить систему уравнений — найти пару чисел x и y, которые при подстановке в систему образуют верное равенство в обоих уравнениях системы.

Существует два метода решений систем линейных уравнений:

1. Метод подстановки.
2. Метод сложения.

Алгоритм решения системы уравнений методом подстановки:

1. Выразить из любого уравнения одну переменную через другую.
2. Подставить в другое уравнение вместо выраженной переменной полученное значение.
3. Решить уравнение с одной неизвестной.
4. Найти оставшуюся неизвестную.

Пример:

Решить систему уравнений методом подстановки

{x+2y=83x−y=−4

Решение:

1. Выразить из любого уравнения одну переменную через другую.

{x=8−2y3x−y=−4

1. Подставить в другое уравнение вместо выраженной переменной полученное значение.

{x=8−2y3x−y=−4

{x=8−2y3(8−2y)−y=−4

1. Решить уравнение с одной неизвестной.

3(8−2y)−y=−4

24−6y−y=−4

−7y=−4−24

−7y=−28

y=−28−7=287=4

y=4

1. Найти оставшуюся неизвестную.

y=4

x=8−2y=8−2⋅4=8−8=0

Ответ можно записать одним из трех способов:

Ответ:

1. x=0,y=4
2. {x=0y=4
3. (0; 4)

 

Решение системы уравнений методом сложения.

Метод сложения основывается на следующем свойстве:

если

{a=bc=d

то

(a+c)=(b+d)

Идея метода сложения состоит в том, чтобы избавиться от одной из переменных, сложив уравнения.

Пример:

Решить систему уравнений методом сложения

{x+2y=83x−y=−4

Давайте избавимся в данном примере от переменной x. Суть метода состоит в том, чтобы в первом и во втором уравнении перед переменной x стояли противоположные коэффициенты. Во втором уравнении перед x стоит коэффициент 3. Для того, чтобы метод сложения сработал, надо чтобы перед переменной x оказался коэффициент (−3). Для этого домножим левую и правую часть первого уравнения на (−3).

{x+2y=8 | ⋅(−3)3x−y=−4

{(−3)⋅(x+2y)=(−3)⋅83x−y=−4

{−3x−6y=−243x−y=−4

Теперь, когда перед переменной  в обоих уравнениях стоят противоположные коэффициенты, при сложении левых частей уравнений переменная x исчезнет.

{−3x−6y=−243x−y=−4⊕

(−3x−6y)+(3x−y)=(−24)+(−4)

−3x−6y+3x−y=−24−4

−7y=−28

y=−28−7=287=4

Осталось найти переменную x. Для этого подставим y=4 в любое из двух уравнений системы. Например, в первое.

x+2y=8

x+2⋅4=8

x+8=8

x=8−8=0

Ответ можно записать одним из трех способов:

Ответ:

1. x=0,y=4
2. {x=0y=4
3. (0; 4)

 

 

Скачать домашнее задание к уроку 4.

 

epmat.ru

Линейные уравнения: решение, примеры, график

Линейные уравнения — относительно несложная математическая тема, довольно часто встречающаяся в заданиях по алгебре. Разберемся, что это такое, и как решаются линейные уравнения.

Как правило, линейное уравнение — это уравнение вида ax + c = 0, где а и с — произвольные числа, или коэффициенты, а х — неизвестное число.

К примеру, линейным уравнением будет:

2х + 4 = 0,

или

5х + 8 = 0,

или

4х + 1 = 0,

И так далее.

Решение линейных уравнений.

Как решать линейные уравнения?

Решаются линейные уравнения совсем несложно. Для этого используются такой математический прием, как тождественное преобразование. Разберем, что это такое.

Пример линейного уравнения и его решение.

Пусть ax + c = 10, где а = 4, с = 2.

Таким образом, получаем уравнение 4х + 2 = 10.

Для того чтобы решить его было проще и быстрее, воспользуемся первым способом тождественного преобразования — то есть, перенесем все цифры в правую часть уравнения, а неизвестное 4х оставим в левой части.

Получится:

4х = 10 – 2,

4х = 8.

Таким образом, уравнение сводится к совсем простенькой задачке для начинающих. Остается лишь воспользоваться вторым способом тождественного преобразования — оставив в левой части уравнения х, перенести в правую часть цифры. Получим:

Х = 8 : 4,

Х = 2.

Проверка:

4х + 2 = 10, где х = 2.

4 * 2 + 2 = 10.

8 + 2 = 10.

Ответ верный.

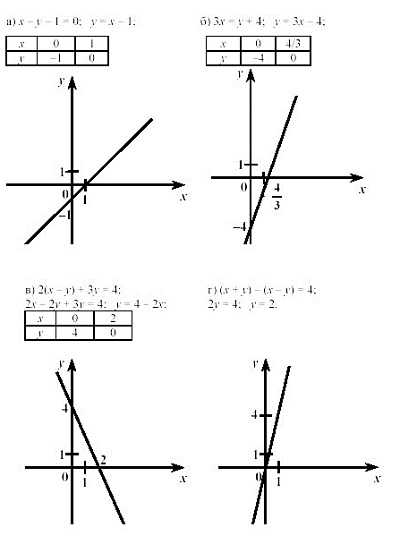
График линейного уравнения.

При решении линейных уравнений с двумя переменными также часто используется метод построения графика. Дело в том, что уравнение вида ах + ву + с = 0, как правило, имеет много вариантов решения, ведь на место переменных подходит множество чисел, и во всех случаях уравнение остается верным.

Поэтому для облегчения задачи выстраивается график линейного уравнения.

Чтобы построить его, достаточно взять одну пару значений переменных — и, отметив их точками на плоскости координат, провести через них прямую. Все точки, находящиеся на этой прямой, и будут вариантами переменных в нашем уравнении.

Похожие статьи

infoogle.ru

Решение уравнений, формулы и примеры

Определение и степень уравнения

Например. .

Например. Уравнение является уравнением седьмой степени, поскольку максимальную — седьмую — степень имеет одночлен .

Решение уравнения и его корни

Два уравнения называются равносильными, если они имеют одно и то же множество решений.

Основные свойства уравнений

1. Если хотя бы в одной части уравнения выполнить тождественные преобразования, то в результате получим уравнение, равносильное заданному.

   Например. .

2. Если из одной части уравнения перенести слагаемые в другую его часть, при этом изменив их знак на противоположный, то получим уравнение, равносильное заданному.

   Например. .

3. Если обе части уравнения умножить или поделить на одно и тоже ненулевое число, то получим уравнение, равносильное данному.

   Например. .

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Методы решения уравнений

Автор Сергей

Понедельник, Июль 9, 2012

Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.

Основные методы решения уравнений

Решить уравнение значит найти все его корни или доказать, что их не существует. Стандартных методов решения уравнений много, нестандартных — еще больше. Последние подходят для решения небольшого количества (часто вообще одного) типа уравнений. При решении уравнений почти всегда приходится прибегать к тождественным преобразованиях алгебраических выражений. Поэтому целесообразно разобраться сперва с этим материалом, прежде чем переходить к решению уравнений. В данной статье разобраны в основном стандартные методы решения уравнений. Некоторые нестандартные методы кратко охарактеризованы в завершающей части статьи. Также на сайте есть отдельные статьи о решении тригонометрических, логарифмических и показательных уравнений, с которыми я также рекомендую читателю ознакомиться.

Метод разложения на множители

Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.

Пример 1. Решите уравнение методом разложения на множители:

Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную за скобки:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, или Из последнего уравнения получаем: или

Ответ:  и

Задача для самостоятельного решения №1. Решите уравнение методом разложения на множители:

Показать ответ

Ответ: 0 или Пример 2. Решите уравнение методом разложения на множители:

Решение. Для разложения на множители используем прием деления многочленов столбиком (или, как еще иногда говорят, уголком). Несложно догадаться, что — корень многочлена Следовательно, по

yourtutor.info

Квадратные уравнения, примеры решений

Теория по квадратным уравнениям

ОПРЕДЕЛЕНИЕ Квадратным уравнением называется уравнение вида , где .

Возможны такие случаи:

, тогда имеем квадратное уравнение вида и .

, тогда имеем квадратное уравнение вида , если ; если – корней нет.

, тогда имеем квадратное уравнение вида .

, тогда имеем полное квадратное уравнение , которое решается или с помощью дискриминанта:

   

Или по теореме Виета:

   

Примеры

ПРИМЕР 1

Задание	Решить следующие неполные квадратные уравнения
Решение	1) В уравнении вынесем за скобки . Произведение равно нулю, если один из сомножителей равен нулю, следовательно:     или     2) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :     3) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :     У данного квадратного уравнения нет корней. 4) уравнение равносильно уравнению , которое имеет два совпадающих корня .
Ответ	Корней нет

ПРИМЕР 2

Задание	Решить квадратное уравнение
Решение	Подсчитаем для заданного уравнения, чему равен дискриминант:     Так как , то уравнение имеет два совпадающих корня:
Ответ

ПРИМЕР 3

Задание	Решить уравнение
Решение	Вычислим дискриминант для исходного уравнения, получим:     Так как , данное уравнение решений не имеет.
Ответ	Корней нет.

ПРИМЕР 4

Задание	Решить квадратное уравнение
Решение	Дискриминант заданного уравнения, равен     Следовательно, уравнение имеет два различных корня
Ответ

ПРИМЕР 5

Задание	Решить уравнение, используя теорему Виета:
Решение	Пусть и – корни квадратного уравнения, по следствию из теоремы Виета     Проанализируем полученные равенства. Произведение корней отрицательно, следовательно, корни имеют разные знаки. Разложим –12 на множители, учитывая, что они должны быть числами разного знака. Возможны такие варианты: –12 и 1; 12 и –1; –6 и 2; 6 и –2; –4 и 3; 4 и –3. Так как сумма корней равна 1, то корнями будут числа и .
Ответ

ru.solverbook.com

Более сложные примеры уравнений | Математика

52. Более сложные примеры уравнений.
Пример 1.

5/(x – 1) – 3/(x + 1) = 15/(x² – 1)

Общий знаменатель есть x² – 1, так как x² – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x² – 1. Получим:

или, после сокращения,

5(x + 1) – 3(x – 1) = 15

или

5x + 5 – 3x + 3 = 15

или

2x = 7 и x = 3½

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x² – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

Пример 2.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

или

2x² + 6x – 2x – 6 = 2x² + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x². Однако, мы можем от обеих частей уравнения вычесть по 2x² — от этого уравнение не нарушится; тогда члены с x² уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

3x = 3 или x = 1

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

что невозможно.

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

6x + 10 = 2x + 18

или

4x = 8 и x = 2

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x² + 4x – 10 = 2x² + 16x – 18.

Здесь уже члены с x² не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

4x² – 12x = –8

или

x² – 3x = –2

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2² – 3 · 2 = –2 и 2) 1² – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Пример 3.

Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x² – 5x + 6 = x² – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x² – x – 2 = x² – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x² – 2x – 3 = x² – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Отсюда получим:

–x = –13 и x = 13.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

или

3x + 3 – 2x + 6 = x – 2

или

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

0 = –11,

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

maths-public.ru