Примеры с решениями на пределы – Пределы с иррациональностями. Примеры раскрытия неопределённостей. Первая часть. - Санкт-Петербургское государственное бюджетное учреждение социального обслуживания населения

Содержание

Примеры на вычисление пределов функции

ПРИМЕРЫ НА ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ

ФУНКЦИИ

На основании изложенного выше рекомендуется следующий порядок нахождения предела функции:

1. Если заданная функция непрерывна в точке x₀, нахождение предела сводится к вычислению значения функции в точке x₀.

2. Если при подстановке значения x₀в выражение функции оказалось, что имеет место одна из ситуаций, которые рассмотрены в п.4.3, 4.5 и 4.6, нужно воспользоваться соответствующими теоремами о пределах и свойствами бесконечно малых и бесконечно больших величин.

3. Если оказалось, что при x → x₀ имеет место неопределенное выражение (п. 4.4, 4.6, 4.7, 4.9), следует, установив вид неопределенности, найти специальный прием, позволяющий, как принято говорить, раскрыть данное неопределенное выражение. Специальные приемы раскрытия неопределенностей будут рассмотрены при решении задач.

Нахождение пределов в случае отсутствия

неопределенности

Пример 1. .

Использована непрерывность функции в точке x = 1

(п. 1.1).

Пример 2. .

Использована теорема о пределе частного.

Пример 3. .

Использовали то, что величина обратная бесконечно малой, является бесконечно большой.

Пример 4. .

Использовали то, что величина, обратная бесконечно большой, является бесконечно малой.

2. Раскрытие неопределенностей вида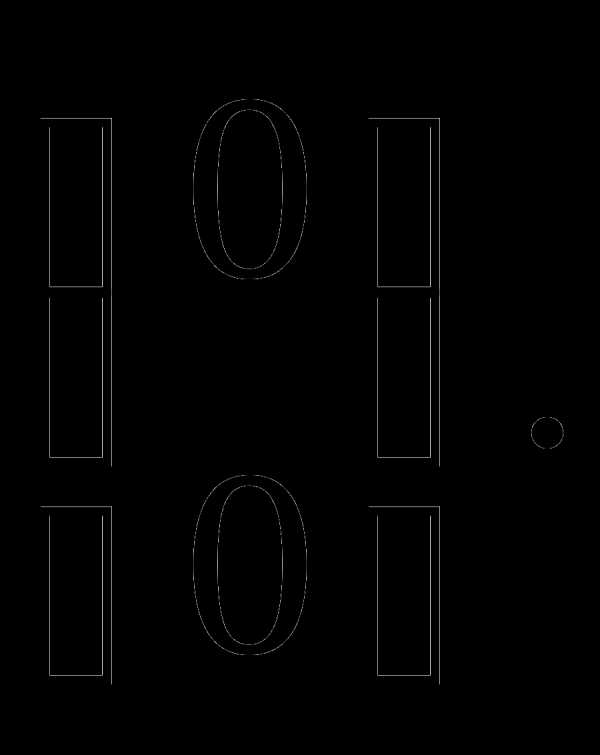

Способ нахождения зависит от того, каким классам функций принадлежат функции f(x) и g(x).

2.1. Нахождение

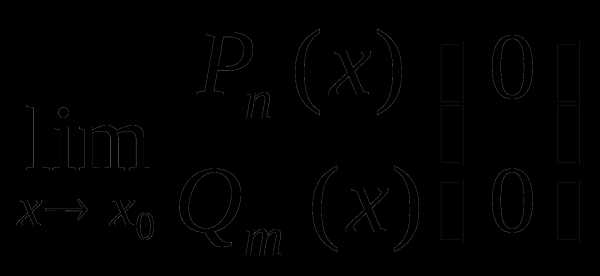, где P_n(x) и_{Q_m(x) неко-
торые многочлены, путем разложения
числителя и
знаменателя на множители
Напомним, что если число x₁ является корнем многочлена P_n(x),
то этот многочлен можно представить в
виде
В частности, если x₁ и x₂ корни
уравнения
,
то
Пример 1. Найти .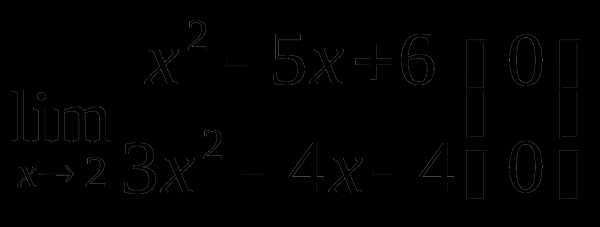
Решение. Найдем корни трехчленов и
разложим числитель и знаменатель на
множители. Тогда
.
Пример 2. Найти .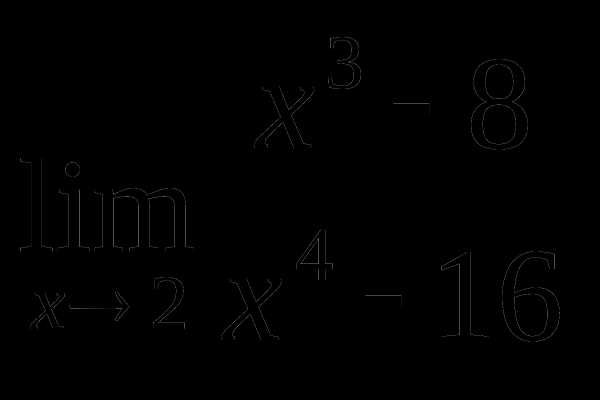
Решение. Воспользуемся формулами
и
.
Тогда
2.2. Раскрытия иррациональных
неопределенностей вида

В этом случае проводятся преобразования,
позволяющие далее использовать формулы:
;
Пример 1. Найти
Решение.
Пример 2. Найти
Решение.

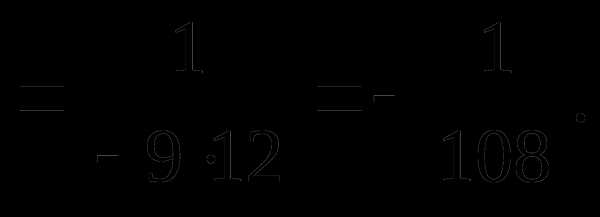
2.3. Раскрытие неопределенных выражений
вида с помощью первого замечательного предела
и его следствий

Первым замечательным пределом принято
называть:
(1) 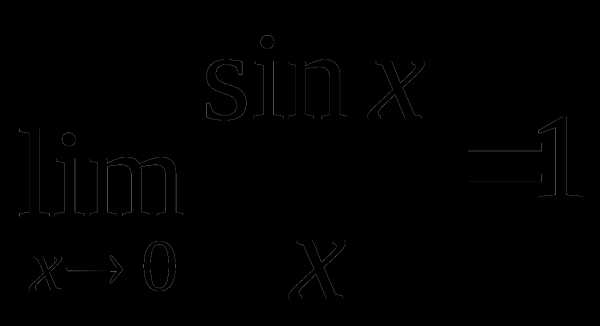или ,
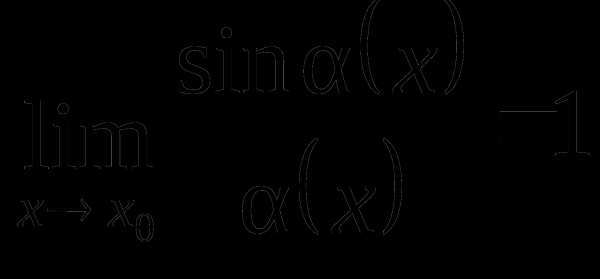(2)
где 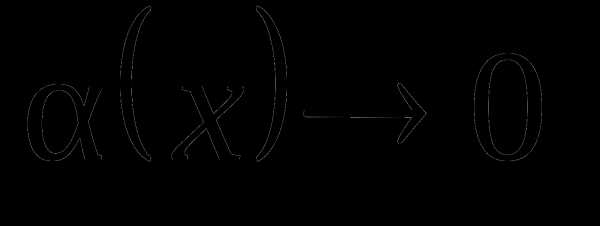при .
Предел замечателен тем, что он позволяет
сделать вывод: для значений аргумента,
близких к 0, величина синуса практически
не отличается от величины своего
аргумента.
Подчеркнем (это важно
!), что предел
отношения синуса некоторого аргумента
к своему аргументу равен 1, лишь когда
аргумент синуса стремится к 0.
Например,
,
,
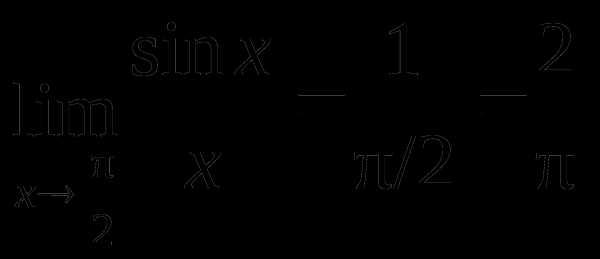и только .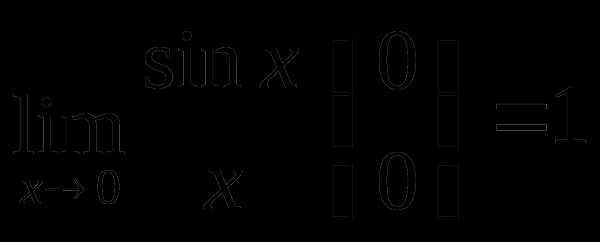
На конкретных примерах покажем, как
формально просто используется
замечательный предел при раскрытии
тригонометрических неопределенностей
вида
.
Пример 1. Найти

Решение.
Пример 2. Найти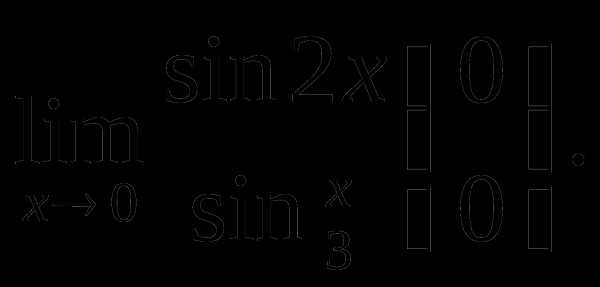
Решение. 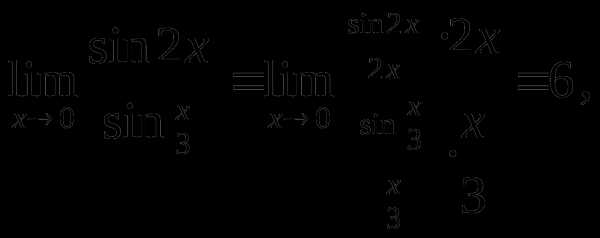так как
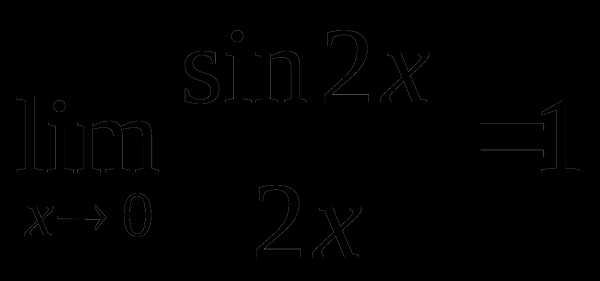и .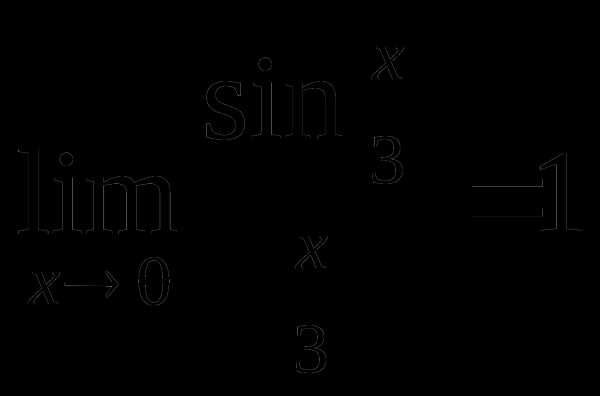
Пример 3. Найти
Решение.
Использованы формула и первый замечательный предел.
Пример 4. Найти
Решение.
так как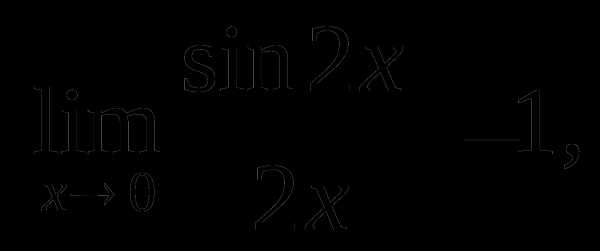

Пример 5. Найти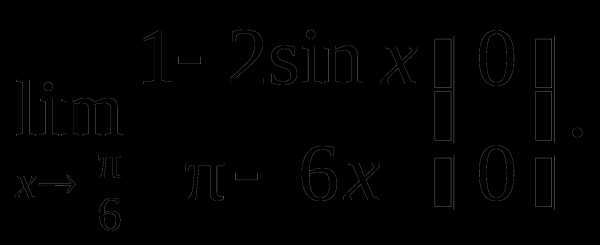
Решение.
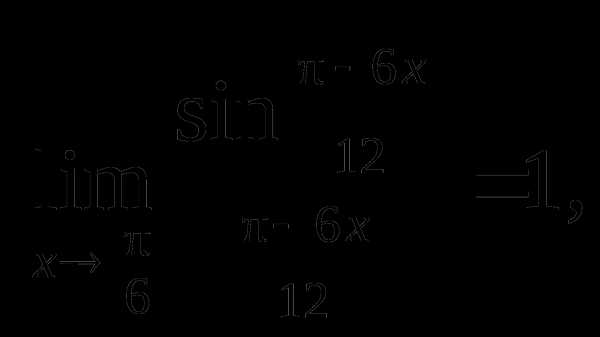так кака .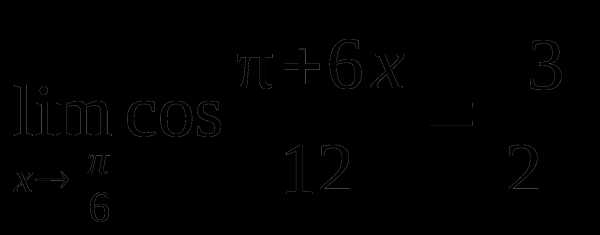
Примеры 6–7 решены с использованием
следствий первого замечательного
предела:
Пример 6.
Пример 7. Найти
Решение.

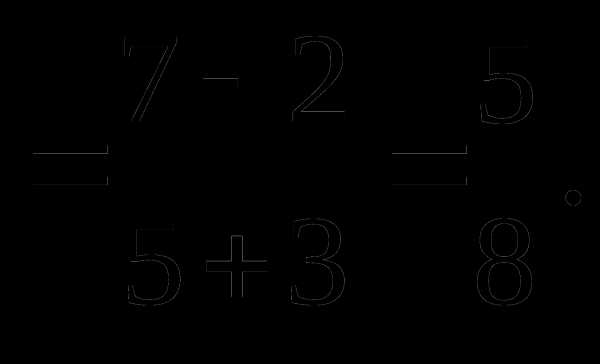
2.4. Введение новой переменной
Во многих случаях, чтобы найти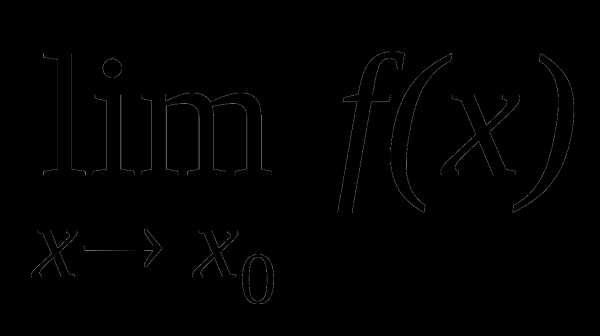
,
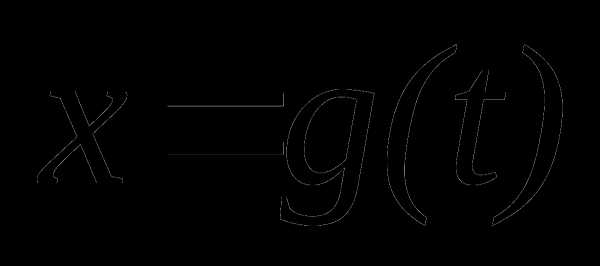имеет смысл сделать замену ,
при этом если 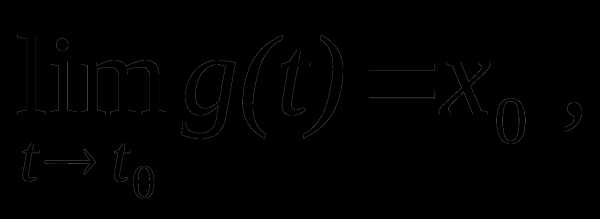то
.
Пример 1. Найти
Решение. Введем новую переменную или Очевидно, при переменная

Тогда
Использованы формулы приведения и
первый замечательный предел.
Пример 2. Найти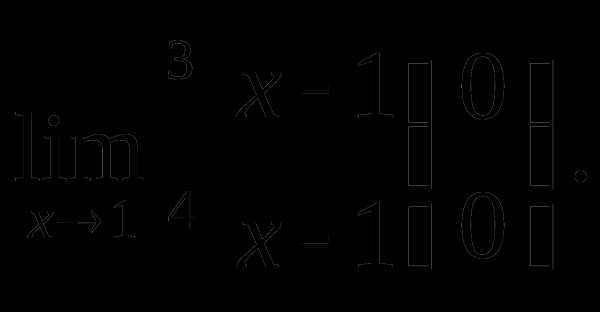
Решение. Введем новую переменную
При переменная
Тогда
3. Раскрытие неопределенностей вида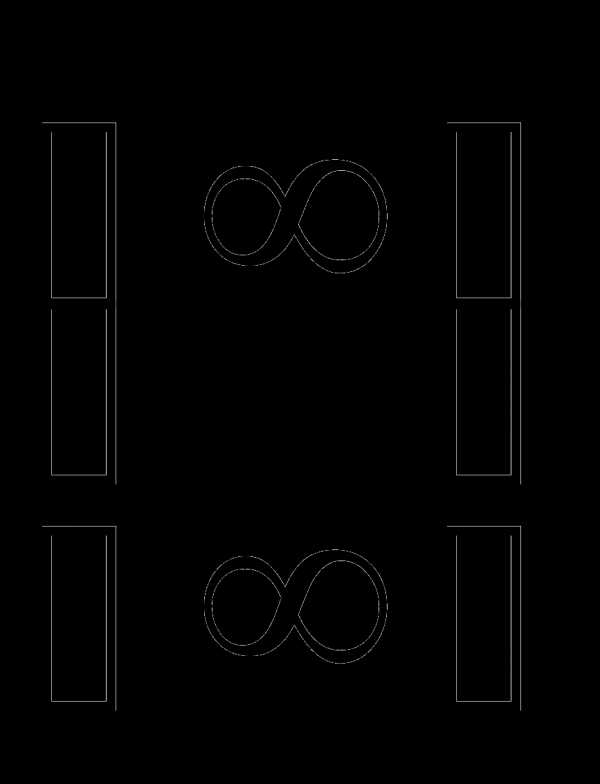

При нахождении ,
где P_n(x) и Q_m(x) – многочлены, используется метод
деления числителя и знаменателя на x^k , где k – наибольшее
из чисел m и n.
Аналогичный прием используется и при
нахождении пределов иррациональных
неопределенностей вида .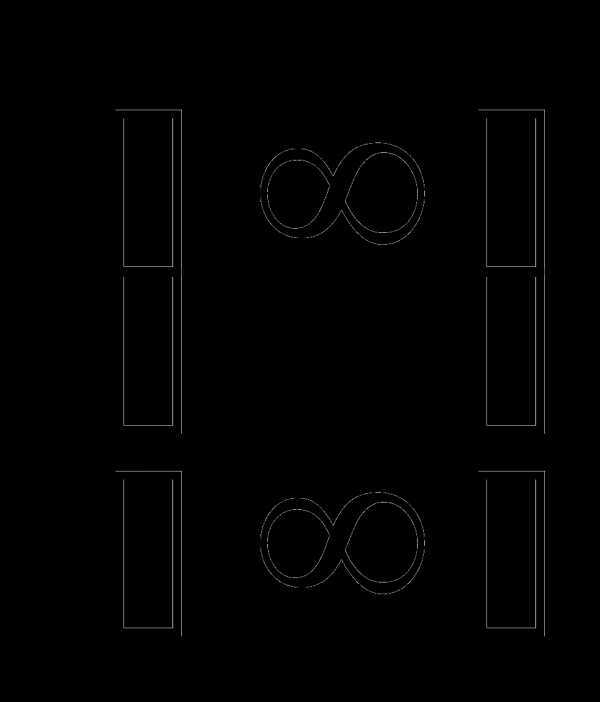
Пример 1.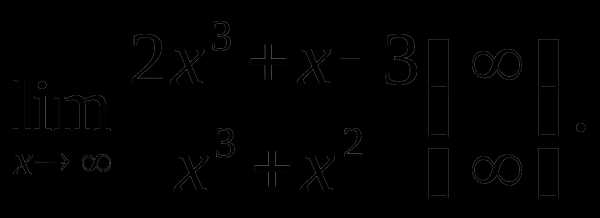
Решение. Разделим числитель и
знаменатель дроби на x³.
Тогда
так как 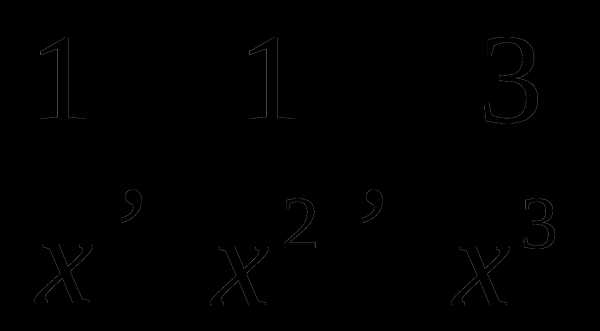– бесконечно малые величины при .
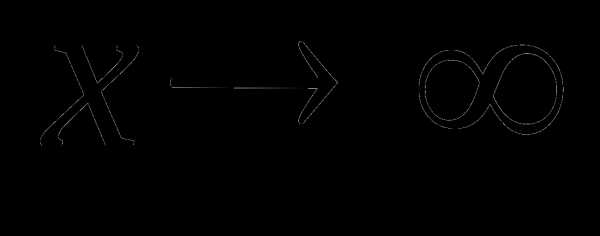Пример 2.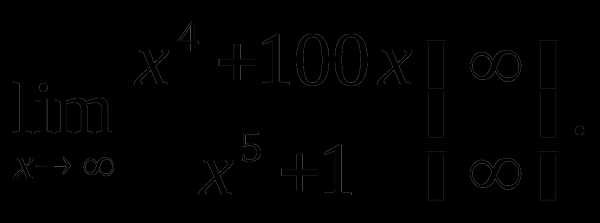
Решение. Разделим числитель и
знаменатель дроби на x⁵.
Тогда
Пример 3.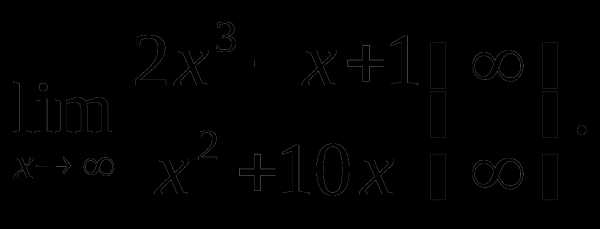
Решение. Разделим числитель и
знаменатель дроби на x³.
Тогда
Сравнивая полученные в примерах 1–3
результаты, можно сделать вывод:

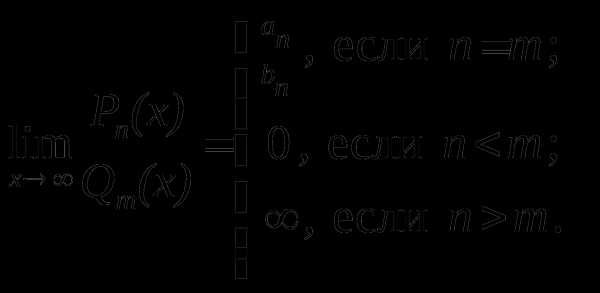
(a_n и b_n – коэффициенты при xⁿ многочленов P_n(x) и Q_n(x) соответственно).
Этот вывод позволяет в простейших
случаях находить 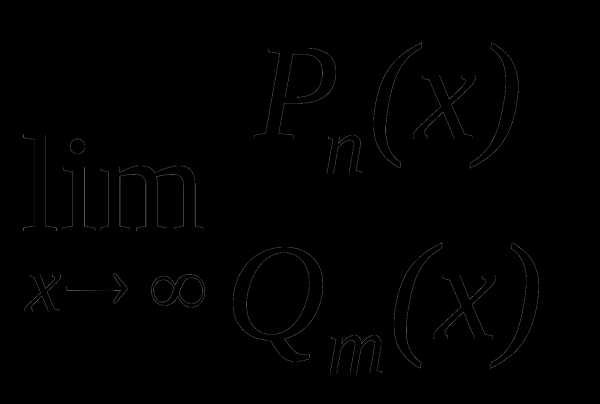без
каких-либо преобразований.
Например,

Перейдем к решению более сложных
примеров.
Пример 4.
Решение. Разделим числитель и
знаменатель дроби на
:

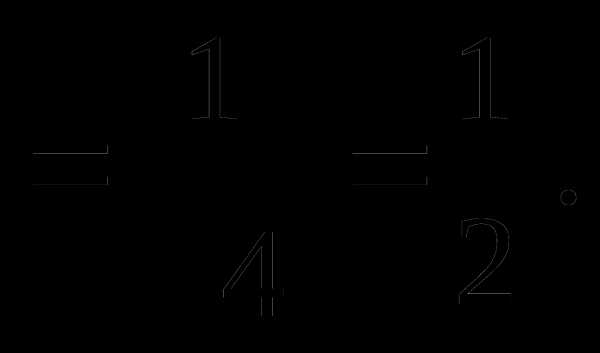
Заметим, что в этом примере наивысшие
степени переменной в числителе и
знаменателе равны (и там, и там это ),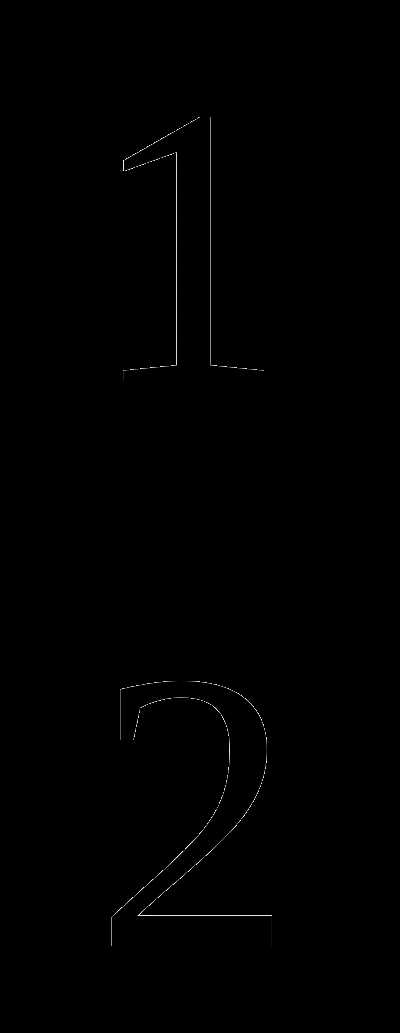
поэтому ответ оказался равным отношению
коэффициентов при
.
Пример 5.
Решение. Напомним, что Разделим почленно числитель на
знаменатель:
4. Раскрытие неопределенностей вида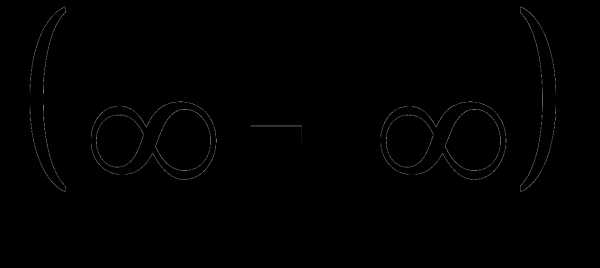
и
Каждую из неопределенностей 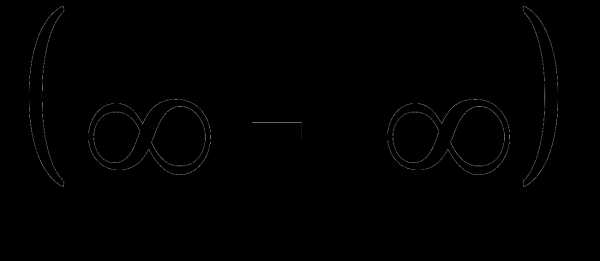и стараются свести к неопределенностям и .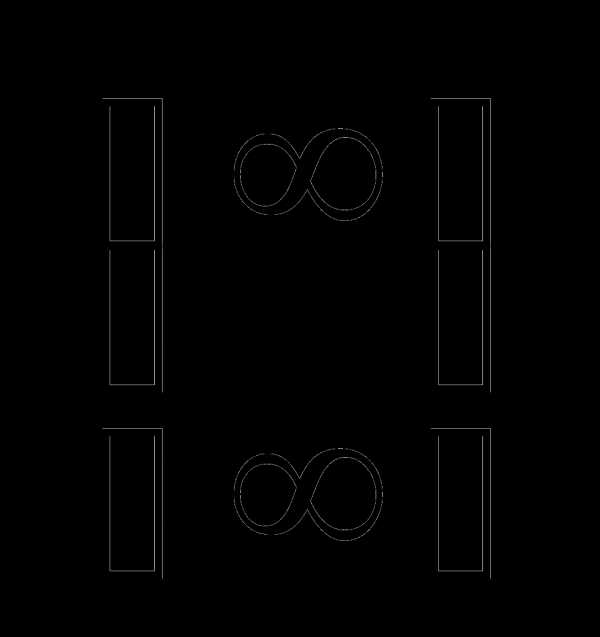
Далее используют соответствующий способ
раскрытия неопределенного выражения
полученного вида.
Пример 1. Найти
Решение. Вынесем знак минуса из
знаменателей за общую скобку и приведем
разность к общему знаменателю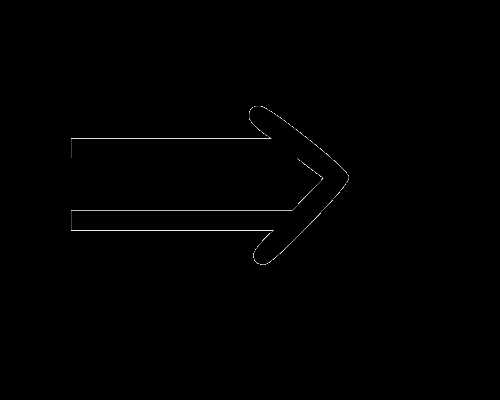
Пример 2. Найти
Решение.
Осталось воспользоваться первым
замечательным пределом
Пример 3. Найти
Решение. Умножим и поделим заданное
выражение на сумму Тогда
Пример 4. Найти
Решение.
Использован первый замечательный
предел:
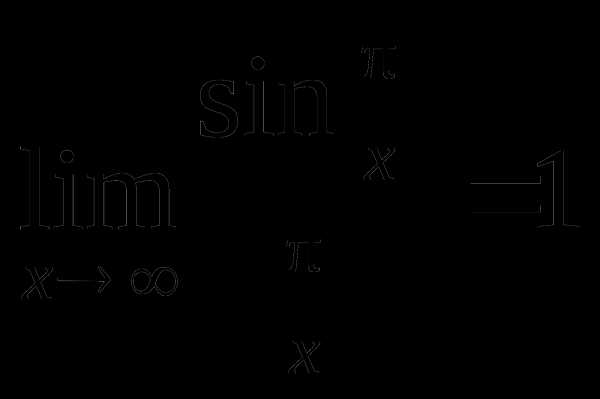( при ).
При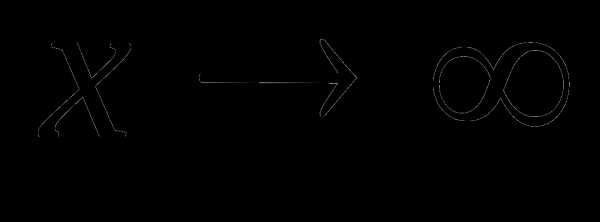мер 5. Найти
Решение. Воспользуемся тем, что
Тогда
Использованы непрерывность логарифмической
функции и первый замечательный предел.
5. Раскрытие неопределенностей вида
Неопределенности вида раскрываются с помощью второго
замечательного предела, который можно
записывать двумя способами:
(3) 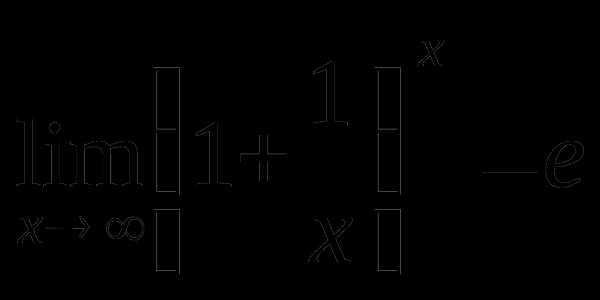или .
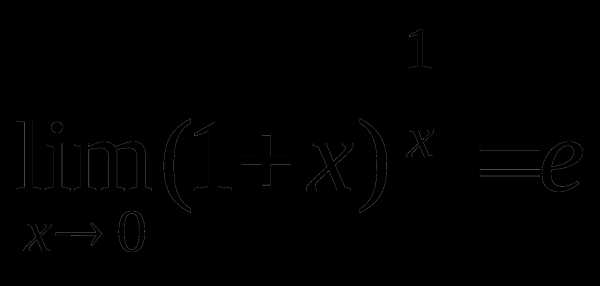(4)
Напомним, что второй замечательный
предел получен на основании равенства
,
gigabaza.ru
Примеры решения: Предел функции
Теория Предел функции Пример 1. Найти предел
Решение. Предел знаминателя равен нулю. Подстановка числа х=1 под знак предела призводит к неопределенности вида . Разложим числитель и знаменатель на множители и сократим на :

Пример 2. Найти предел
Решение. Имеем определенность вида . В подобных ситуациях следует числитель и знаменатиль разделить на наивысшую степень х

Пример 3. Найти предел
Решение.

Пример 4. Найти предел
Решение. Согласно формуле тригонометрии . Поскольку при эквивалентно , и эквивалентно эквивалентно , тогда

anet.lectra.me
5.07.3 Примеры на вычисление пределов функций
Вычислить указанные пределы:
1. .
2.
.
3. . Так как числитель и знаменатель обратились в нуль при , то – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет . Получаем
.
4.
.
5.
.
6. – не существует, так как .
7. . Обозначим , причем заметим, что при . Получим
.
8. . (Ответ получается непосредственно подстановкой вместо .)
9. . Здесь следует рассмотреть односторонние пределы:
; .
Следовательно, – не существует (так как у функции разные односторонние пределы).
Для самостоятельного решения.
1) ; Ответ:.
2) ; Ответ: .
3) ; Ответ: .
4) ; Ответ: .
5) . Ответ: не существует.
6) ; Ответ: .
7) ; Ответ: .
8) Найти в точке односторонние пределы функции ; Ответ: .
9) ; Ответ: .
< Предыдущая Следующая >
matica.org.ua
Замечательные пределы и их примеры
Примеры пределов содержащие неопределенности вида ноль на ноль часто встречаются в тригонометрических функциях. Для их раскрытия используют первый замечательный предел суть которого заключается в том, что предел отношения синус функции к аргументу, когда тот стремится к нулю равен единице
На основе этой формулы можно получить ряд полезных для практики пределов
1)
2)
3)
Второй замечательный предел позволяет раскрыть неопределенности вида .
Коротко он имеет следующую запись
где –экспонента.
На основе второго замечательного предела получают следующие формулы
1)
2)
Примеры, которые сводятся к первому и второму замечательному пределу встречаются довольно редко, однако без них такие примеры не решить.
Рассмотрим некоторые примеры из сборника задач Дубовика В.П., Юрика И.И. “Высшая математика” которые приводят к применению замечательных пределов.
———————————–
Пример 1. Найти пределы функций.
1) (4. 388)
2) (4. 393)
3) (4. 399)
4) (4. 432)
5) (4. 437)
6)
7)
Решение.
1) Домножим числитель и знаменатель на аргумент и сведем к первой замечательной границы
2) Разделим числитель и знаменатель на аргумент и сократим
3) Согласно разложению корня в окрестности единицы
знаменатель возможно превратить следующим образом
На основе этого и находим предел
4) Сведем к второму замечательному пределу
5) Сведем к правильной дроби выражение в скобках
и подставим в предел
Вычислим первый множитель
Второй предел равна единице
Окончательно получим
6) Сведем решение к первому замечательному пределу
7) Преобразуем показатель для применения второго замечательного предела
Подобных примеров можно привести много, они встречаются в контрольных, тестах, екзаменах. Их решения позволит закрепить Вам лучшие практические навыки поэтому пробуйте решать самостоятельно. Если в обучении вам встретятся тяжелые пределы посчитать которые Вы не в состоянии обращайтесь к нам. Мы Вам в этом поможем!
———————————–
Посмотреть материалы:
yukhym.com}