Примеры сложных функций – Производная сложной функции. Примеры нахождения производных сложных функций.

Примеры сложных функций | Математика

Сложная функция — это функция от функции. Если u — функция от x, то есть u=u(x),  а f — функция от u:  f=f(u), то функция y=f(u) — сложная.

А  u  в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней. Лучший способ понять, что такое сложная функция — рассмотреть примеры сложных функций.

1) y=sin x — эта функция «простая». Синус зависит от x. Как только вместо x под знаком синуса появится выражение, зависящее от x, даже самое простое — такая функция называется сложной. То есть y=sin u — сложная функция, если u — некоторая функция от x. Примеры сложных функций с синусом:

y=sin (x+1). Эта функция — сложная. Внутренняя функция u здесь равна x+1, а внешняя функция f — это синус. То есть u=x+1, f=sin u.

y=sin (5x-2x³+3). Внутренняя функция u=5x-2x³+3, внешняя функция f=sin u.

y=sin (x/7). Внутренняя функция u=x/7, внешняя функция f=sin u.

2) y=cos x — «простая» функция

. y=cos u — сложная функция, если u — некоторая функция, зависящая от x. Примеры сложных функций с внешней функцией — косинусом:

y=cos (4-11x). Внутренняя функция u=4-11x, внешняя функция — косинус: y=cos u.

y=cos (7x³ -4x²). Внутренняя функция u=7x³ -4x², внешняя — y=cos u.

3) y=tg x — «простая» функция. y = tg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — тангенс:

y=tg(17+5x²). Внутренняя функция u=17+5x², внешняя — y=tg u.

y=tg(9-x). Внутренняя u=9-x, внешняя — y=tg u.

4) y=ctg x — «простая» функция. y=ctg u — сложная функция, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — котангенс:

y=ctg(2x+6). Внутренняя функция u=2x+6, внешняя — y=ctg u.

y=ctg(√x).  u=√x, f=ctg u.

5) y=√x — «простая» функция. y=√u — сложная, если u=u(x). Примеры сложных функций для случаев, когда внешняя функция — квадратный корень:

   

Здесь внутренняя функция y=sin x, а внешняя — f=√u.

   

Здесь u=9x³-12x+5, f=√u.

6) y=xⁿ — «простая» функция. y=uⁿ — сложная, если u=u(x). Примеры сложных функция для случая, когда внешняя функция — степенная.

y=sin³x. Внутренняя функция y=sin x (так как sin³x=(sin x)³), внешняя — у=u³.

   

7) y=arcsin x — «простая» функция. y=arcsin u — сложная, когда u=u(x).

Например, y=arcsin (3x-9) — сложная функция. Внутренняя функция u=3x-9,  внешняя — f=arcsin u.

y=arcsin (17-5x³).  u=17-5x³, f=arcsin u.

8) y=arccos x — «простая» функция. y=arccos u — сложная, при u=u(x).

Например, y=arccos (34x+5) — сложная функция. Внутренняя функция u=34x+5, внешняя — f=arccos u.

9) y=arctg x — «простая» функция. y=arctg u — сложная, при u=u(x).

Например, y= arctg (6x+2x³-7). Внутренняя функция u =6x+2x³-7, внешняя — f=arctg u.

10) y=arcctg x — «простая функция. При u=u(x) функция y=arcctg u — сложная.

Например, y= arcctg(2-11x+x²) — сложная функция. u=2-11x+x², f= arcctg u.

11) y=ln x — «простая» функция. y= ln u — сложная, при u=u(x).

Например, y=ln(4+32x-2x³). Внутренняя функция y=4+32x-2x³, внешняя — f=ln u.

   

Это — «простая» функция. А вот при u=u(x) получаем логарифм сложной функции:

   

Например,

   

   

Эта функция — «простая» (называется экспонента). А вот если в показателе стоит не x, а некоторая функция от икса: u=u(x), то это — уже экспонента сложной функции:

   

Например,

   

   

Эта функция — «простая». А вот если в показателе стоит не x, а некоторое выражение с x — функция u=u(x), то это уже степень сложной функции:

   

Например,

   

Эта функция — сложная. Внутренняя функция u=8x³+5x, а внешняя — степень сложной функции

   

Следует добавить, что внутренняя функция u, в свою очередь, может быть сложной функцией. И таких «вложенных» функций может быть несколько (теоретически — сколько угодно).

Например,

1) y=cos³(3x-12). Здесь внутренняя функция u =cos(3x-12), а внешняя функция f=u³. Но внутренняя функция y=cos(3x-12), в свою очередь, тоже является сложной функцией. Для нее внутренняя функция u=3x-12, а внешняя f=cos x.

   

Сначала рассмотрим эту функцию, как логарифм сложной функции. Тогда внутренняя функция

   

внешняя — логарифм:

   

В свою очередь, функция

   

— тоже сложная. Это — синус сложной функции, то есть

   

Но u — снова сложная функция. Здесь уже внутренняя  функция u=2x²+5x, а внешняя f=√u.

 

www.matematika.uznateshe.ru

Сложная функция

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (1,4 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

“Сложный, составной, сложенный или составленный из разных частей…”.
Толковый словарь В.И. Даля.

Мы часто в повседневной речи считаем слова “сложный” и “трудный” синонимами. Иногда можно услышать от тех учеников, которым нелегко дается математика, что сложная функция потому так называется, что она “трудная”. Но на самом деле “сложный” и “трудный” далеко не всегда означают одно и то же.

Понятие сложной функции встречается в курсе алгебры и начал математического анализа в 10 классе [3]. Для сложной функции выводится формула дифференцирования. Ученики без предварительной подготовки этот материал воспринимают с большим трудом. На чисто формальном уровне можно дать много примеров на нахождение внутренней и внешней функции для данных сложных функций. При определенной практике они начинают хорошо различаться и производную можно вычислять. Беда в том, что при этом учащиеся погружаются в технику дифференцирования, а само понятие сложной функции как композиции нескольких функций отходит на задний план.

Чтобы сложная функция предстала в более наглядном виде, и сделана данная презентация.

В зависимости от подготовленности класса этот материал может быть предложен и на факультативных занятиях, и на уроках, причем в некоторых случаях непосредственно в теме “Производная”, а в некоторых и раньше. Самое главное, чтобы основные свойства функций (в первую очередь – монотонность) к этому времени учащимися были хорошо усвоены и чтобы графики элементарных функций стали легко узнаваемы.

К этому времени учащимся будет и легче воспринимать само понятие функции как соответствие между множествами.

Несмотря на весь абстрактный характер понятия “функция” с ним нужно разобраться, постепенно вводя логические уточнения и учитывая возможности класса. А сложную функцию нужно изучать как композицию двух функций. Это понятие важно для определения взаимно обратных функций. В связи с этим в сильных классах данный материал целесообразно вводить до того, как изучаются обратные функции – например, обратные тригонометрические функции. Для классов со слабой подготовкой, где обратные тригонометрические функции вводятся на более простом уровне, разговор о сложной функции пойдет в теме “Производная”. Но и в этом случае должно быть подробное рассмотрение определения этой функции.

Поведение элементарных функций лучше всего иллюстрируется с помощью графика, поэтому и для исследования сложной функции наилучший, как мне кажется, подход – это дать представление о ее графике, построенном с использованием графиков внутренней и внешней функций.

При построении графиков сложных функций в презентации для большей наглядности используются анимационные эффекты, дающие представление о последовательных шагах, которыми характеризуется композиция нескольких соответствий.

Важно подчеркнуть, что при исследовании функций с помощью производной ученики получают более совершенный аппарат для построения графика, но и элементарные методы имеют свои преимущества: они позволяют учащимся на более простом материале воспринимать основные функциональные изменения и дают возможность “прочувствовать” поведение сложной функции. Построение графиков без производной может осуществляться с разных точек зрения. Примеры получения достаточно трудных графиков описаны, например, в [1]. Те приемы, которые предложены в данной презентации, с одной стороны, касаются именно сложных функций, но с другой демонстрируют достаточно наглядные рассуждения, которые могут помочь в исследовании функций при решении различных задач. Например, изученные приемы могут пригодиться в тех случаях, когда требуется узнать промежутки монотонности сложной функции, множество ее значений. Причем предложенный метод достаточно нагляден и не использует громоздких преобразований с формулами.

В предлагаемой презентации можно выделить три части:

1. Введение понятия сложной функции.
2. Построение графиков сложных функций.
3. Нахождение множества значений сложной функции.

1. Для того чтобы подробно описать, как “действует” сложная функция, сначала нужно повторить определение функции как соответствия между множествами, при котором каждому элементу первого множества соответствует не более одного элемента второго множества. То, что на слайде изображены круги Эйлера, не случайно: на них более ярко можно показать соответствие между элементами множеств.

Понятие функции к 10 классу должно быть сформировано, но ученикам с низкой мотивацией иногда трудно его запоминать, и в данном случае можно подробнее остановиться на контрольных вопросах, например, почему окружность или вертикальная прямая в системе координат не могут быть графиками функций (хотя их и можно задать уравнениями).

Сложную функцию рассматриваем как композицию двух функций, то есть как последовательное выполнение двух соответствий. По рисунку можно проследить, как некоторому элементу множества Х соответствует элемент множества Т, этот закон устанавливается внутренней функцией. А затем для элемента множества Т внешняя функция указывает соответствующее значение элемента из множества У. Таким образом, для первоначального х₀ мы находим t₀, а затем у₀. Устанавливается зависимость: x₀t₀у_0.

После того, как чертеж с тремя множествами и соответствиями подробно разобран, переходим к рассмотрению конкретных сложных функций. Рассматриваем примеры, где сложная функция задается формулой. Ученикам предлагается назвать внутреннюю и внешнюю функцию.

Аналогичные задания приводятся и в учебнике [3], но практика показывает, что если ограничиваться только рассмотрением формул, то от восприятия учеников ускользает структура самой композиции функций, последовательность в переходе от одного шага к другому, в итоге исчезает математическая суть сложной функции.

Восполнить этот пробел помогают графики.

2. Построим график функции (пример 1).

Укажем область определения: D(y) = (-∞; -2] U (2; +∞). Заметим, что это четная функция.

Внутренняя функция: g(x) = x² – 4, построим график в системе координат (х,t). Для простоты изложения мы строим всю параболу, но в дальнейшем рассматриваем только те х, которые входят в множество D(y).

Внешняя функция: f(t) =, построим график в системе координат (t,y).

График исходной сложной функции будем строить в системе координат (х,у).

Для наглядности на рисунке отмечено некоторое произвольное значение х₀, для него с помощью графика g(x) можно указать t₀=g(x₀), а для t₀ по графику внешней функции находим значение у₀=f(t₀), таким образом получаем цепочку соответствий: x₀t₀у₀, аналогичную той, которая была изображена на рисунке с кругами Эйлера.

После того, как два вспомогательных графика построены, переходим к главной задаче – построению графика сложной функции.

Пусть переменная х изменяется от 2 до бесконечности. По графику g(x) хорошо видно, что при этом переменная t изменяется от 0 до бесконечности. В силу возрастания квадратичной функции на данном участке об этом можно было догадаться и без графика, но график помогает в дальнейших рассуждениях.

Итак, переменная t изменяется от 0 до бесконечности. Переходим в систему координат с графиком внешней функции f(t). Значения функции, то есть у, меняются от 0 до бесконечности.

Все эти изменения приводятся в таблице на слайде.

Значит, для функции при увеличении аргумента от 2 до бесконечности получаем возрастание функции от 0 до бесконечности. И то, что мы выделили этот участок монотонности, уже очень важно! Можно хотя бы схематично изобразить график при х≥2.

Чтобы детям лучше был понятен этот переход, соответствующие участки на чертежах подчинены анимационным эффектам (слайд 10). Участки появляются по щелчку мыши последовательно, друг за другом, в определенном цвете. В результате в системе координат (х,у) выделяется промежуток [2; +∞) на оси абсцисс, а по оси ординат ему соответствует промежуток [0; +∞), функция возрастает. И появляется первый участок искомого графика.

В силу четности исходной функции получаем и второй участок графика, при х≤-2, отражая первый участок относительно оси ординат.

Но можно и другим способом получить ту же линию при х≤-2: рассмотреть изменение х от минус бесконечности до -2, тогда переменная t изменяется от +∞ до 0, а переменная у при этом изменяется от +∞ до 0. Значит, при изменении аргумента от -∞ до -2 значения сложной функции убывают – это мы и видим на графике. Данные рассуждения можно провести устно, но они хорошо иллюстрируются изображениями на слайдах.

Заметим, что в этих рассуждениях приходится намеренно отказываться от термина “промежутки” и от соответствующих скобок для их указания, потому что мы говорим именно об изменении величины, а не просто о множестве, на котором ее рассматриваем, то есть если переменная уменьшается, она изменяется, начиная с большего значения (а в промежутках на первом месте указывается меньшее значение).

Еще один вариант применения указанного способа построения графика – это подготовительный этап в изучении свойств растяжения и сжатия графиков. Например, чтобы ученик осмысленно и “своими руками” получил график у=sin2x, можно рассматривать данную функцию как сложную. Это построение разобрано в презентации (пример 2).

Не исключено, что гармонические колебания будут уже известны ученикам к моменту изучения сложной функции и, в частности, поведение графика у=sin2x. В этом случае можно предложить ученикам самостоятельно найти ответ на вопрос, как пользуясь свойствами внутренней и внешней функции, прийти к итоговому графику. Второй способ решения уже известной задачи ничуть не умаляет первый, а только лучше закрепляет полученную информацию.

В классах, где тригонометрические сведения усвоены не достаточно хорошо, весьма полезной будет повторение значений синуса для определенных углов и заполнение предложенной таблицы. В классах с высокой мотивацией в обучении эта работа достаточно легкая, таблицу можно заполнять устно, а в тетрадях только построить сам график, но действовать поэтапно.

Итак, рассматриваем функцию у=sin2x.

Замечаем, что она всюду определена, нечетная, периодична с наименьшим положительным периодом π.

Изображаем графики внутренней и внешней функции.

Начинаем с анализа изменения переменной х. Для каждого участка изменения указываем, как изменяется переменная t, а затем переменная у.

Рассматриваем участки изменения для переменной х: от 0 до π/4; от π/4 до π/2; от π/2 до 3π/4; от 3π/4 до π.

То, что нужны именно эти участки, можно объяснить поведением рассматриваемых функций. Мы должны указать такой участок для x, на котором характер изменения t не меняется – либо только увеличивается, либо только уменьшается, то есть важна монотонность внутренней функции, а при соответствующих t монотонность внешней функции тоже дает однозначный ответ, то есть можно определенно указать, что значения у либо увеличиваются, либо уменьшаются. Для простоты расчетов участки монотонности иногда дробятся на два – в данном случае учитываются нули – пересечение графика с осью абсцисс. Но характер монотонности на каждом отдельном участке постоянен.

Если у учеников появляются вопросы, то графические иллюстрации позволяют быстрее их разрешить, поэтому показ слайдов очень удобен – каждый участок можно проследить на подробном чертеже, выделение цветом помогает концентрировать внимание на обсуждаемом участке. Например, указывая изменение переменной х от 0 до π/4, мы видим, что t изменяется от 0 до π/2, а при этом изменении t значения синуса возрастают от 0 до 1 – соответствующий столбец таблицы приведен рядом с графиками на слайде.

Поскольку для большинства детей эта работа может оказаться непростой, в презентации сделаны отдельные слайды для каждого столбца с иллюстрациями на графиках. Таблица заполняется постепенно, один столбец следует за другим.

В итоге мы получаем заполненную таблицу (она приведена на отдельном слайде) и можем изобразить график у=sin2x сначала на участке от 0 до π, а затем, учитывая периодичность, и весь график.

С сильными учениками можно значительно сэкономить время, рассмотрев подробно один или два участка, а затем перейти к итоговому графику. Но в некоторых классах пригодится и более подробная работа. Учитель регулирует скорость изложения, учитывая состав и подготовленность учащихся.

В зависимости от того, какой материал по тригонометрии к этому моменту пройден в классе, можно подчеркнуть особенность сжатия графика, роль частоты и пр.

Общий вид графиков различных функций, в том числе и сложных, прекрасно можно получить, например, с помощью программы “АвтоГраф”. Они не требуют почти никаких затрат, если программа уже установлена. Когда ученики хорошо поймут сам принцип задания сложной функции и смогут хотя бы схематично указывать ее график, то для корректировки сделанного чертежа можно показать график, построенный более точно с помощью “АвтоГрафа”.

Такую работу я проводила уже на следующих уроках, когда проверяли домашнее задание и дети самостоятельно строили графики других сложных функций. Приятно было видеть, что они с большим азартом строили даже такие трудные графики, как .

Подчеркнем, что настоящая презентация ставит главную цель дать ученикам представление о самой сложной функции как композиции двух функций, о графике сложной функции, полученном с помощью внешней и внутренней функции. Эта работа требует осмысленного восприятия материала. “При осмысленном восприятии я вижу в предмете нечто большее, чем содержится в непосредственном зрительном акте, и восприятие предмета является уже в известной степени абстракцией, и в восприятии содержатся следы обобщения”, – эти слова Л.С. Выготского [2] характеризуют общие психологические особенности восприятия, но они, в частности, прекрасно иллюстрируют процесс изучения математики.

И сразу, без теоретической подготовки, предлагать ученикам только готовые графики преждевременно. С другой стороны, чисто формальные рассуждения, без графических иллюстраций затрудняют восприятие. Поэтому при изучении данного раздела нужно как можно больше наглядности и поэтапного погружения в материал.

После того, как в сознании учеников понятие сложной функции будет сформировано, можно проводить уроки по теме “Взаимно обратные функции” (в профильных классах), а также переходить к формуле производной сложной функции (если уже изучается тема “Производная”).

3. Как дополнительный вопрос в данной теме предлагается рассмотреть задачу о нахождении множества значений сложной функции. Эту задачу можно решить графически.

Например, требуется найти множество значений функции y=(3+sinx)^-1.

Выделяем внешнюю и внутреннюю функции. Замечаем, что внутренняя функция изменяется от 2 до 4 (так как -1≤sinx≤1). Значит, 2≤t≤4.

Отсюда следует важный факт: внешняя функция определена только для значений аргумента от 2 до 4.

Изображаем график внешней функции, выделяя соответствующий участок на гиперболе. И тогда легко видеть, что значения у находятся на промежутке [0,25; 0,5].

Значит, Е(у)= [0,25; 0,5].

Заметим, что в этой задаче участки монотонности не важны! Важно только множество значений внутренней функции для перехода к области определения внешней функции.

Итак, мы рассмотрели понятие сложной функции как композицию двух функций, внешней и внутренней. Научились выделять эти функции в конкретно заданной сложной функции. С помощью графиков внешней и внутренней функции строим график сложной функции. А также находим множество ее значений.

И в заключение отметим, что “сложный”, “сложенный” связаны с глаголами “сложить”, “складывать”. В словаре Даля читаем, что склад – это стройность, красота, порядок, устройство. “Складный ум – логичный, ясный и верный”. И я старалась, чтобы сложная функция для моих учеников оказалась в первую очередь не трудной, а интересно устроенной.

Работа учителя математики посвящена тому, чтобы не только облегчить ученикам восприятие трудного материала, но и дать им возможность почувствовать ту упорядоченность и красоту, которая всегда встречается в математике.

Литература.

1. Виленкин Н.Я.и др. Алгебра для 9 класса. – М.: Просвещение, 1996.
2. Выготский Л.С. Вопросы детской (возрастной) психологии // Собрание сочинений: в 6 т. – М.: Педагогика, 1984. – Т.4.
3. Колмогоров А.Н. и др. Алгебра и начала анализа. 10-11 класс. – М.: Просвещение, 2009.

xn--i1abbnckbmcl9fb.xn--p1ai

Сложная функция

Сложная функция

1. Если задана некоторая функция , например,, то это значит, что задано правило соответствия. Это правило предписывает произвести над значением аргументаопределенные действия, а именно, в нашем случае, умножить его на 2 и затем к произведению прибавить 1. В итоге получаем определенное число – соответствующее значение функции. Так, если, то, а если , то . Приполучаем. Областью определения функции является числовое множество, в нашем примере – это.

Рассмотрим следующее выражение , в котором вместо аргумента данной функции подставляется некоторая функция от другого аргумента, а именно. Можно записать это выражение в виде. Таким образом, мы имеем «функцию от функции». Аргументом этой новой функции является переменная. Значения функции, то есть, вычисляются следующим образом. Берется значение аргумента, например, равное 2, и находится значение функциипри. Имеем. Далее вычисляем значение функциипри. Получаем. Таким образом,. Для произвольного значенияимеем, то есть, значит. Поэтому формула функцииимеет вид. Отметим, что фактически вбыли проделаны те действия, которые предусматриваются правилом, однако эти действия были проделаны не над аргументом х, а над выражением. Функцияполучена в результате описанной операции называется сложной. Термин «сложная» используется здесь в смысле «составная», то есть сложная функция составлена из других функций. Дадим точное определение сложной функции.

Определение. Пусть функция определена на множестве, а функция– на множестве, причем множество значений функциисодержится в области определения функции.Поставим в соответствие каждому числуизчисло. Тем самым на множествебудет задана функция. Эту функцию называют сложной функцией или композицией функцийи.

При этом называют внешней, a— внутренней функцией композиции.

Пример 1. Пусть . Составьте сложную функцию, если

.

Решение. Подставим вместо в формулу функции, соответственно,и:

1. Получаем 1

. В итоге .

Пример 2. Даны две функции , соответственно,. Найдите сложную функцию

Решение. ,,.

Рассмотрим следующую задачу, в которой требуется найти композицию функций и, причем первая функция – внешняя, а вторая – внутренняя. Для удобства имеет смысл ввести новые обозначения для переменных второй функции, обозначив ее аргумент буквой, а зависимую переменную – буквой. Имеем. Важно понимать, что введение других обозначений переменных никак не повлияло на функцию. Записиипредставляют одну и ту же функцию, с областью определения, действие которой состоит в возведении аргумента в квадрат и прибавлении числа 2.

Композицией функций иявляется функция. В этом случае также ничего не мешает обозначить другой буквой аргумент сложной функции, а именно – буквой, то есть так, как обозначены аргументы обеих функций в условии задачи. Таким образом, получаем ответ:. Заметим, что тот же результат можно получить, если формально подставить в формулу первой функциивместовыражение. На практике, конечно, можно пользоваться этим приемом, при этом понимая математический смысл произведенной операции.

Пример 3. Найдите сложную функцию, составленную из функций и, где первая функция будет внешней, а вторая – внутренней.

Решение. В первую функцию вместо подставим выражение. В итоге получаем.

2. Пусть даны две функции и

В итоге получены две разные функции: и. Они имеют разные области определения, у первой, а у второй. Кроме того, функции принимают разные значения, например, при: значение первой равно, а второй равно. Таким образом, для заданных функцийиоказалось, что. На основании этого можно сделать вывод о том, что если в сложной функции внутреннюю и внешнюю функции поменять местами, то может получиться другая функция. На самом деле, практически всегда так и происходит, поэтому нужно внимательно следить в каком порядке берутся функции при составлении из них сложной функции.

3. Рассмотрим вопрос об области определения и множестве значений сложной функции. Возьмем функции и , графики которых изображены на рисунках 1 и 2 , и составим сложную функциюС помощью графиков проследим, каким образом находятся значения сложной функции.

Рассмотрим число , принадлежащее области определения внутренней функции . В нашем примере. Находим значение(рис.2). Далее нужно вычислить значение функции от числа , то есть(рис.1). Для этого необходимо, чтобы числопринадлежало области определения функции, то есть(рис.1). Если это условие не выполняется, то числоне входит вобласть определения сложной функции. Таким образом, число должно быть таким, чтоДля нашего примера множествоявляется отрезком(рис.1). Это значит, что. По графику функцииопределяем, что тогда(рис.2). Поэтому областью определения сложной функцииявляется отрезок, в то время как.

Итак, область определения сложной функции, как видно из приведенного примера, содержится в области определения внутренней функции, но может быть меньше ее. Точно также как и множество значений сложной функции в сравнении с множеством значений внешней функции.

Отметим, что не всякие функции могут составить сложную функцию. Так будет в случае, если множества не содержат общих точек, то есть их пересечение пусто (рис. 5)

Пример 4. Найти множество значений сложной функции , еслии

Решение. Формула сложной функции имеет следующий вид: . Решим эту задачу с привлечением графиков заданных функций. Напомним, что множество значений функции представляется проекцией графика на ось ординат. Множество значений внутренней функциисоставляет промежуток,то есть(рис. 6). Внешняя функцияопределена на всем промежутке(рис. 5). Исходя из ее свойств, заключаем, что функцияпринимает на этом промежутке все значения от нуля, не включая его, до единицы. Таким образом, множество значений сложной функции составляет промежуток. Ответ..

Упражнения

1. – Заданы функции ,. Найдите

2. Заданы функции ,

Найдите

3. Составьте сложные функции и , если

4. Заполните таблицу

Ответ:

.

5. Найдите множество значений сложной функции , еслии

6. Найдите множество значений функции

Ответ:

.

7. Найдите наибольшее значение функции Ответ: 1,5

8. Найдите наибольшее значение выражения

Ответ:

Дополнительные задания

1. Функции изаданы таблицами. Найти сложную функцию, в которой- внешняя функция, а– внутренняя

Функция f(x)	аргумент	-4	-3	-2	-1	0	1	2	3	4
	значение	2	0	-1	-4	-2	3	-4	-4	-3

Функция g(x)	аргумент	-4	-3	-2	-1	0	1	2	3	4
	значение	-2	4	1	0	2	2	1	3	2

Ответ.

Функция g(f(x))	аргумент	-4	-3	-2	-1	0	1	2	3	4
	значение	1	2	0	-2	1	3	-2	-2	4

2. Доказать, что композиция

• двух возрастающих функций – функция возрастающая

• двух убывающих функций – функция возрастающая

• убывающей и возрастающей – функция убывающая

• возрастающей и убывающей – функция убывающая

3. Заполните таблицу

Ответ: .

4. Функция возрастает на промежуткеи убывает на промежутке. Найдите промежутки возрастания и промежутки убывания функции.

Ответ. промежуток возрастания: , промежуток убывания:.

4. Функция возрастает на промежуткеи убывает на промежутке. Найдите промежутки возрастания и промежутки убывания функции.

Ответ. промежутки возрастания: ; .

промежутки убывания: ;.

4. Нарисуйте графики функций и , если

Ответ.

studfiles.net

§ 03. Сложная функция | Решение задач по математике и другим предметам!!

Познакомимся с понятием Суперпозиции функций, которое состоит в том, что в качестве аргумента одной функции используется другая функция. Полученная в результате суперпозиции функция называется Сложной функцией. Записывается сложная функция следующим образом: . Например: , . Тогда сложная функция . Чтобы найти значение сложной функции, подставляют сначала заданное значение во внутреннюю функцию и находят ее значение , а затем уже вычисляют соответствующее значение функции .

При выполнении суперпозиции функций считают, что множество значений внутренней функции содержится в области определения внешней функции .

Сложную функцию можно составить из большего числа более простых функций.

Пример 1. Сложную функцию представьте в виде цепочки элементарных функций.

Решение. Будем последовательно выполнять операции, которые заданы в формуле: , , . Следовательно, заданная в условии задачи функция является суперпозицией трех основных элементарных функций.

Пример 2. Даны функции . Запишите сложную функцию .

Решение. Подставляя последовательно функции одну в другую, получим сложную функцию .

< Предыдущая		Следующая >

matica.org.ua

03.8. Понятие сложной функции | Решение задач по математике и другим пре

Определение. Если на некотором промежутке Х определена функция Z = φ(X) с множеством значений Z и на множестве Z Определена функция У = F(Z), то функция У = F[φ(X)] называ­ется сложной функцией от X (или суперпозицией функций), а переменная Z — промежуточной переменной сложной функции.

Приведем примеры сложных функций.

Пример 1. У = cos —Сложная функция, определенная на полубесконечном интервале (—,1], так как У = F(Z) = Cos Z, Z = φ(X) = .

Пример 2. У = — сложная функция, определенная на всей числовой прямой, поскольку У = F(Z) = еZ , Z = φ(X) = —х2.

Пример 3. У = — сложная функция, определенная на полубесконечных интервалах (-,0) и (0, + ), так как Y = f(z) = z3/2, z = φ(x) = (1 + x) / x.

ТЕОРЕМА 8. Пусть функция Z = φ(X) непрерывна в точке X0, а функция у = F(z) непрерывна в точке Z0 = φ(x0). Тогда сложная функция у = F[φ{X)] непрерывна в точке X0 = 0.

Пример 4. Функция Y = tg (X2 + 2X) непрерывна в точке X = 0, так как функция Z = х2 + х непрерывна в точке Х = 0, а функ­ция У = tg Z непрерывна в точке Z = 0.

< Предыдущая		Следующая >

matica.org.ua

Понятие сложной функции

Определение. Если на некотором промежутке Х определена функция z = φ(x) с множеством значений Z и на множестве Z определена функция у = f(z), то функция у = f[φ(x)] называ­ется сложной функцией от x (или суперпозицией функций), а переменная z — промежуточной переменной сложной функции.

Приведем примеры сложных функций.

Пример 1.у = cos —сложная функция, определенная на полубесконечном интервале (— ,1], так как у = f(z) = cos z, z = φ(x) = .

Пример 2. у = — сложная функция, определенная на всей числовой прямой, поскольку у = f(z) = е^z , z = φ(x) = —х².

Пример 3. у= — сложная функция, определенная на полубесконечных интервалах (- ,0) и (0, + ), так как y = f(z) = z^3/2, z = φ(x) = (1 + x) / x.

ТЕОРЕМА 8. Пусть функция z = φ(x) непрерывна в точке x₀, а функция у = f(z) непрерывна в точке z₀ = φ(x₀). Тогда сложная функция у = f[φ{x)] непрерывна в точке x₀ = 0.

Пример 4. Функция y = tg (x^{2+ 2x) непрерывна в точке x = 0, так как функция z = х2 + х непрерывна в точке х = 0, а функ­ция у = tg z непрерывна в точке z = 0.}

 

Элементы аналитической геометрии на плоскости

 

Уравнение линии на плоскости

 

Пусть на плоскости задана система координат. Рассмот­рим уравнение вида

 

 

Говорят,что уравнение (3.9) определяет (задает) линию L в системе координат Оху. Вообще говоря, линии на координат­ной плоскости могут быть самыми различными.

 

Линии первого порядка

 

К линиям первого порядка относятся те линии, для кото­рых задающее их уравнение (3.9) содержит переменные x и у только в первой степени. Иными словами, такие линии описы­ваются уравнениями вида

 

 

где А, В и С — постоянные числа. Из этого уравнения можно выразить переменную у как функцию от аргумента х при В ≠ 0:

 

 

Уравнение (3.11) называют уравнением прямой с угловым ко­эффициентом k = tg φ, где φ — угол наклона прямой к положительному направлению оси Ох (рис. 3.9). Если k = 0, то прямая параллельна оси Ох и отстоит от нее на b масштабных единиц.

 

Рис. 3.9

 

 

Определим самые необходимые элементы знания о прямых на плоскости.

1. Кроме “классического” уравнения прямой (3.11) следует знать еще две его разновидности. Первая из них — это уравне­ние прямой с заданным угловым коэффициентом k, проходящей через заданную точку М₀(x₀, у₀):

 

 

Другой вид — это уравнение прямой, проходящей через две заданные точки на плоскости M₁(x₁, y₁) и М₂(х₂, у₂):

2. Угол между прямыми. Рассмотрим две прямые, заданные уравнениями у = k₁x + b₁ и у = k₂x + b2, где k₁ = tg φ₁и k₂ = tg φ₂ (рис. 3.10). Пусть φ — угол между этими прямы­ми. Тогда φ = φ₂ — φ₁ и мы получаем tg φ = tg (φ₂ — φ₁) = или, что то же самое,

 

 

Рис. 3.10

 

Формула (3.12) определяет один из углов между пересекающи­мися прямыми; второй угол равен π – φ.

Из равенства (3.12) вытекают условия параллельности и перпендикулярности прямых. В самом деле, если прямые па­раллельны, то

 

 

Если прямые перпендикулярны, то α₂ = π/2 + α₁, откуда tg α₂ = -ctg α₁ = -1 / tg α₁, или окончательно

 

Пример 1. Найти угол между прямыми, заданными уравне­ниями у = 2x – 5 и у = -3x + 4.

Решение. Подставляя в формулу (3.12) значения k₁ = 2 и k₂ = -3, имеем

 

 

откуда получаем, что один из углов равен φ = π / 4.

3. Расстояние от точки до прямой. Пусть прямая за­дана уравнением общего вида (3.10). Тогда расстояние dотпроизвольной точки М₀(x₀, y₀) до прямой (рис. 3.11)даетсяформулой

 

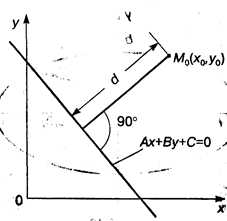
Рис. 3.11

Линии второго порядка

Рассмотрим здесь три наиболее используемыxвида линий:эллипс, гиперболу и параболу.

1. Эллипс. Линия, для всех точек которой сумма рассто­яний от двух данных точек, называемых фокусами, есть вели­чина постоянная и большая, чем расстояние между фокусами, называется эллипсом.

Согласно определению эллипса, сумма расстояний от произвольной точки М на этой линии до его фокусов F₁и F₂ по­стоянна (рис. 3.12):

 

 

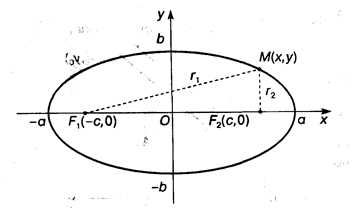
Рис. 3.12

 

Отсюда можно вывести уравнение эллипса в его основной (канонической) форме:

 

 

где а и b — полуоси эллипса, b² = а² — с², точка O (0,0) — центр эллипса, с — половина расстояния между фокусами эл­липса. Из уравнения (3.13) следует, что оси эллипса являются его осями симметрии, а точка их пересечения — центром его симметрии.

 

 

В частном случае, когда a = b, фокусы эллипса сливаются, т.е. с = 0, и мы имеем окружность радиуса а с центром в начале координат. Характеристикой эллипса, показывающей меру его вытянутости, является эксцентриситет — величина, определяемая отношением

 

 

2. Гипербола. Гиперболой называется линия, для всех то­чек которой модуль разности расстояний от двух данных то­чек, называемых фокусами, есть величина постоянная и мень­шая, чем расстояние между фокусами.

На рис. 3.13 показаны все основные элементы гиперболы. Разность расстояний от произвольной точки М на гиперболе до фокусов F₁ и F₂, согласно определению, есть величина по­стоянная:

 

 

Из этой основной предпосылки выводится каноническое урав­нение гиперболы, которое имеет вид

 

где b² = с² — а².

Нетрудно видеть, что прямые у = ± х являются наклонными асимптотами гиперболы. Линия (3.14) имеет две оси сим­метрии, точка пересечения которых является центром симмет­рии гиперболы.

3. Парабола. Параболой называется линия, все точки ко­торой находятся на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой дирек­трисой и не проходящей через фокус.

Согласно определению, точка М(х, у) лежит на параболе, если r₁ = r₂. Отсюда и выводится каноническое уравнение параболы, которое имеет вид

 

 

График параболы (3.15) показан на рис. 3.14. Нетрудно видеть, что перемена осей координат приводит к более привычному уравнению параболы вида у = Ах², где А — постоянное число.

 

Рис. 3.14

УПРАЖНЕНИЯ

 

Найти области определения функций, заданных следующими формулами.

3.1. у = 3x – 2.3.2. у = х² – 5x + 6.3.3. . 3.4. . 3.5. . 3.6. . 3.7. . 3.8. . 3.9. . 3.10. . 3.11. . 3.12. . 3.13. . 3.14. .

3.15.f(x) = x² + x – 2, найти f(0), f(1), f(-3).3.16.f(x)=arccos(lg x), найти f(1/10), f(1), f(10).3.17. .

3.18. Спрос и предложение на некоторый товар на рынке опи­сываются линейными зависимостями вида

 

 

1) Определить равновесную цену; 2) установить графичес­ким способом, является ли модель паутинного рынка “скручи­вающейся”. Варианты задания параметров зависимостей спро­са и предложения:

а) а = 19, b = 2, с = 3, d = 2; б) а = 15, b = 3, с = 1, d = 4;в)а = 11, b = 3, с = 3, d = 1; г) а = 23, b = 3, с = 5, d = 6.

 

Найти пределы.

 

3.19. . 3.20. . 3.21. . 3.22. . 3.23. . 3.24. . 3.25. . 3.26. . 3.27. . 3.28. . 3.29. . 3.30. . 3.31. . 3.32. . 3.33. .

 

Найти точки разрыва функций и определить типы разрывов.

3.34. .3.35. .3.36. . 3.37. .3.38. .3.39. .3.40. .

studopedya.ru

Сложная функция (композиция функций)

Термин сложная функция в действительности в математическом языке является «чисто рабочим»: так называют функцию, если она задана в виде у=f(g(x)) с внешней функцией f и внутренней функцией g. Из самого задания этой функции ясно, что для вычисления значения у сложной функции к значению аргумента х сначала применяется функция g, а затем к полученному значению g(x) применяется функция f — тогда и получается значение f(g(x)).

Владение этим термином, умение видеть сложную функцию для начал математического анализа исключительно — чтобы найти производную, функцию часто следует представить в виде сложной функции, причем функция может быть еще более «сложной», когда ее «история» более длинная, т.е., например, если функция задается формулой у=f(g(h(р(х))).

Для того чтобы подчеркнуть, что термин «сложная функция» относится не к самой функции, а к способу ее задания, приведем пример: функции $y=\sqrt[3]{x^3}$ и $y=x$ — это, очевидно, одна и та же функция, однако первую из них можно назвать сложной, а вторую — нет. Заметим также, что сложная функция может оказаться нигде не определенной, например,$y=\sqrt{-x^2-1}$ — под знаком радикала тут всегда стоит отрицательное выражение.

При желании заняться алгеброй функций, т.е. рассматривать операции, действия, которые можно осуществлять с функциями, изучать свойства этих операций, а иногда лишь для терминологического удобства сложную функцию у=f(g(x)) называют композицией функций f и g и обозначают обычно символом $f\circ g$ или, в обратном порядке, $g\circ f$ — математики, как ни странно, не могут, да и не пытаются, прийти к общему соглашению относительно этого обозначения. Далее мы применяем первый порядок f и g, т.е. $(f \circ g)(x)=f(g(x))$.

А между тем композиция двух функций зависит от их порядка: если, например, $f(x)=x^2$, $g(x)=\sqrt {x}$, то $f(g(x))=(\sqrt{x})^2=x, (x\geq 0)$ тогда как $g(f(x))=\sqrt{x^2}=|x|$, а значит, это две различные функции — они имеют даже разные области определения. Иными словами, равенство $f\circ g=g\circ f$ выполняется не для всех функций, так что в алгебре функций перестановочный (в математике, в отличие от школы, называют его коммутативным) закон для композиции не имеет места.

Интересно, что сочетательный (в математике говорят ассоциативный) закон остается в силе:

$[(f\circ g)\circ h](x)=(f\circ g)(h(x))=f(g(h(x)))$,

$[f\circ(g\circ h)](x)=f[(g\circ h)(x)]=f(g(h(x)))$

(мы здесь не стали рассматривать детали, связанные с областью определения рассматриваемых функций), а распределительный закон (в математике говорят дистрибутивный) распадается на два — из-за отсутствия перестановочного закона:

$f\circ(g+h)=(f\circ g)+ (f\circ h)$ и $(g+h)\circ f=(g\circ f)+(h\circ f)$

и, что удивительно, один из них выполняется в алгебре функций, а второй — нет.

Интересующиеся этими вопросами легко могут узнать, какой из них именно выполняется, рассмотрев какой-нибудь простой пример, и почти со стопроцентной вероятностью вы найдете ответ с первой попытки, если, конечно, вам не повезет попасть как раз на те функции, для которых выполняются оба закона. А доказать верный закон тоже будет небесполезным — с точки зрения будущего изучения высшей алгебры в вузе: для студентов она вовсе не проще, чем математический анализ, однако с его идеями вы более или менее знакомитесь в школе, а основные идеи алгебры, связанные со свойствами операций, полностью остаются в стороне.

Ну, а если вы хотели бы подтянуть разговорный английский язык, или вам нужна курсовая по английскому, обращайтесь. Так как этот язык уже стал международным и его знания будут полезны любому современному человеку.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com