Примеры вычисления производной обратной функции
⇐ ПредыдущаяСтр 6 из 89Следующая ⇒Пример
Задание. Найти производную функции
Решение. Искомая производная
Константу – 3 выносим за знак производной (согласно правилам дифференцирования):
Тогда, согласно формуле получаем:
Или после упрощения
Ответ.
Пример
Задание. Вычислить производную функции
Решение. В знаменателе заданной функции стоит функция , то есть
Поэтому необходимо найти производную сложной функции. Для этого находим производную от :
и умножаем на производную от функции :
Итак, имеем:
Производная суммы/разности равна сумме/разности производных. Тогда имеем:
Производная от независимой переменной равна единице: , а производная от единицы, как от константы, равна нулю:
Ответ.
7.Вопрос.Производные функций, заданнных параметрически, неявно.
Производная функции, заданной неявно
Определение
Если независимая переменная и функция связаны уравнением вида , которое не разрешено относительно , то функция называется неявной функцией переменной .
Пример
Всякую явно заданную функцию можно записать в неявном виде . Обратно сделать не всегда возможно.
Несмотря на то, что уравнение не разрешимо относительно , оказывается возможным найти производную от по . В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию как функцию от , а затем из полученного уравнения найти производную .
Пример
Задание. Найти вторую производную неявной функции .
Решение. Продифференцируем левую и правую часть заданного равенства, при этом помним, что является функцией переменной , поэтому производную от нее будем брать как производную от сложной функции. В итоге получаем:
Из полученного равенства выражаем :
Для нахождения второй производной продифференцируем равенство еще раз:
Подставив вместо найденное выше выражение, получаем:
После упрощения получаем:
Из полученного равенства выражаем вторую производную :
Ответ.
8 Вопрос.Логарифмическое дифференцирование,примеры.
Для функций вида для упрощения нахождения производной рациональнее использовать логарифмическое дифференцирование.
mykonspekts.ru
10 класс. Алгебра. Производная. Числовая последовательность. Дифференцирование функций. – Примеры вычисления основных производных. Таблица производных. Типовые задачи.
Комментарии преподавателя
Примеры вычисления производных. Функция f(x)=x^3. Типовые задачи.
1. Краткое повторение темы предыдущего занятия
На предыдущем уроке мы рассмотрели понятие производной и рассмотрели алгоритм нахождения производной. Он предусматривал: дать приращение аргументу, вычислить приращение функции, вычислить отношение , упростить, проанализировать, устремить к нулю и найти производную. Это было в общем виде, а теперь этот алгоритм рассмотрим на примере конкретных функций.
2. Функция f(x)=x^3
Пример 1 Дано:
Найти .
Зафиксируем точку и найдем значение производной от конкретной функции в конкретной точке. Действуем по алгоритму.
1)Вычисляем значение . Иллюстрируем все это графиком.
Рис. 1. Кубическая парабола.
Зафиксировав точку , вычислим значение функции в этой точке. Получим .
2) Даем аргументу приращение ,получаем – новое значение аргумента.
Примечание. В данном случае приращение положительное. Можно дать приращение отрицательное, тогда функция будет либо увеличиваться, либо уменьшаться. Важно, что –любое.
3) Вычислить значение функции в новой точке , подставив эту точку в функцию.
.
4) Найдем , то есть разность между значением функции в новой точке минус значение функции в старой точке.
.
Имеем две точки: значение аргумента и значение функции в точке , новое значение аргумента и значение функции при новом значении аргумента. Разность этих значений функции дает .
5) Найдем разностное отношение
.
Знаменатель для всех функций один и тот же, – приращение аргумента, а числитель – свой для каждой функции. Получили разностное отношение. Далее надо упростить его, сократить на и сделать дальнейший анализ.
Упрощать в данном случае можно по-разному. Можно применить формулу или куб суммы, или разность кубов. Напомним, что
. В данном случае – это , – это . Имеем
Раскрывая скобки, получили многочлен. Приведем подобные члены. Дальше надо преобразовать так, чтобы сократить. Вынесем за скобки, получим Теперь можно сократить на , ведь , оно не равно нулю. Имеем соотношение следующего вида
. Осталось узнать, что происходит, когда . В данном случае второй член выражения пропадет, и третий член пропадет. Останется , то есть .
Результат
, то есть смысл такой: 3 выносим как сомножитель и показатель уменьшили на единицу.
Итак, зафиксировали точку , нашли производную от конкретной функции в конкретной точке . Точка может быть любая.
Ответ: .
Итак, мы зафиксировали функцию – кубическую параболу. Была задача: найти производную этой функции в конкретной точке . Мы зафиксировали точку и действовали по алгоритму, который был изложен в общем виде, и применен к данной функции. Этот алгоритм можно применять к любой функции, а именно: вычислить значение функции в точке , подставив значение в закон соответствия, то есть в функцию, дать приращение аргумента, найти значение функции при новом значении аргумента и получить приращение функции, то есть разность между значениями функции в новой точке и старой. Далее, надо найти разностное отношение , упростить его так, чтобы вынести за скобку и сократить на . В результате получится выражение, члены которого зависят от и не зависят от него. Если члены, которые зависят от прямо пропорциональны ему, то они при стремятся к нулю, то есть пропадают. Остаются только члены, которые не зависят от . Таким образом получим значение производной.
Для знакомых с пределами .
Важно понять, что есть члены с члены и члены без . При этом члены с пропадают, остается то, что называется производной.
Итак, производная от кубической функции в любой точке – это .
3. Типовые задачи
Возьмем конкретный пример.
Дано:
Найти: , то есть конкретное значение функции в точке .
Решение.
1) Найти производную в любой точке . .
2) Найти . .
Физический и геометрический смысл решения задачи.
В момент , если двигаться (уезжать от дома) по закону , скорость равна 12. Если к этой кривой мы проведем касательную в точке , то эта касательная имеет угол наклона (см
www.kursoteka.ru
5.1.1.8. Примеры вычисления производных
По правилу дифференцирования частного двух функций, производную от заданной функции можно записать в виде:
.
Функции и – сложные. Поэтому производные от этих функций по переменной вычислим, используя правило дифференцирования суперпозиции функций
.
Производная от функции по переменной получится, если в табличную производную подставить переменную вместо переменной , то есть
.
Производная может быть вычислена по таблице, если учесть, что и использовать правило дифференцирования степенной функции, то есть
.
Тогда
.
Аналогично, по правилу дифференцирования суперпозиции функций вычисляется производная от функции .
.
Подставим вычисленные производные в формулу для производной частного и запишем производную от заданной функции в виде:
.
nww13.narod.ru
Производная функции по определению
Пример 1. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
Решение. Дадим х приращение , тогда у получит приращение :
Найдем приращение функции:
Находим отношение приращения функции к приращению аргумента:
Найдем предел этого отношения при
Следовательно, по определению производной
Пример 2. Исходя из определения производной (не пользуясь формулами дифференцирования), найти производную функции
Решение. Находим приращение функции: . Отсюда и
Таким образом,
Итак, .
Пример 3. Найти производную (добавлено по просьбам)
Решение. Исходную функцию желательно сразу сократить Находим приращение функции: . Отсюда и
Таким образом,
Итак, .
anet.lectra.me
Примеры на вычисление производной — Мегаобучалка
а) 2 в) Найти производную функции .
При нахождении производной используем формулы 6 (производная частного) и 7 (производная степенной функции).
;
т.к. , то
.
Функцию можно записать в виде произведения двух функций , и для вычисления производной использовать формулу 5.
.
г) .
Для вычисления производной степенно-показательной функции можно использовать следующую формулу: .
Эту формулу рекомендуется использовать в тех случаях, когда с помощью свойств логарифмов функцию удается преобразовать и сделать более простой для дифференцирования.
.
д) Производная функции , заданной параметрически , , вычисляется по формуле
,
где и – это производные функций по переменной .
Найдем производную функции, заданной параметрически: , .
.
131 – 140.Производная от производной функции называется производной второго порядка этой функции и обозначается или .
.
Вычислим производную второго порядка функции .
.
.
141 – 150. Если при выражение является неопределенностью типа или и
, то .
Этот способ вычисления называется правилом Лопиталя.
Неопределенности других типов с помощью алгебраических преобразований могут быть сведены к неопределенности или .
При вычислении пределов наряду с правилом Лопиталя следует использовать другие способы вычисления, а также свойства пределов.
Вычислим .
Так как , , то имеем неопределенность типа .
Для раскрытия такой неопределенности воспользуемся следующим утверждением.
Если при функция является неопределенностью типа и существует
,
то
.
В нашем случае , , .
;
применим правило Лопиталя:
;
еще раз используем правило Лопиталя:
.
Таким образом,
.
151 – 160. Полное исследование функции можно свести к 3 этапам.
1 этап. Найти область определения функции; исследовать функцию на чётность, нечётность, периодичность; найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции. Установить характер точек разрыва (если они существуют), а так же найти асимптоты графика функции: вертикальные и наклонные.
Наклонные асимптота кривой , если они существуют, задаются уравнениями вида y = kx+b , где параметры k и b определяются формулами:
, .
При этом пределы могут быть различными при x®+¥ или x®2¥ .
Для существования вертикальной асимптоты в точке x=x0
2 этап. Исследование функции с помощью производной. Найти производную y'(x) и её критические точки (т.е. точки из области определения функции, в которых производная равна нулю или не существует), определить промежутки возрастания и убывания функции и точки экстремума.
3 этап. Исследование функции с помощью производной второго порядка. Найти производную второго порядка (x) и её критические точки, используя знак производной, определить промежутки выпуклости, вогнутости графика и точки перегиба.
Используя результаты исследования нужно построить график функции.
Пример. Исследовать функцию
1 этап. D(y) = (2¥ ; +¥).
Точки пересечения графика с осями координат: х = 0, y = 0 (график проходит через начало координат). Функция не является чётной ( y(2x)¹ y(x)), нечётной (y(2x)¹2y(x)), периодической.
Интервалы знакопостоянства функции:
Границами интервалов, где функция сохраняет знак, могут быть только точки пересечения графика функции с осью Ох, точки разрыва и границы области определения функции.
Для исследуемой функции такой точкой является x = 0. При х<0 функция принимает отрицательные значения, при x>0 функция принимает положитель- ные значения.
Вертикальных асимптот график функции не имеет, так как она непрерывна на всей числовой прямой.
, наклонной асимптоты нет, но есть горизонтальная асимптота у=0, т.к. ;
(использовалось правило Лопиталя).
2 этап.
, , при . Это критическая точка.
При функция достигает минимума, .
3 этап.
;
при .
Точка x = -2 является точкой перегиба, так как производная второго порядка меняет знак в этой точке; при xÎ(-¥; -2) график является выпуклым, а на интервале (-2; +¥) – вогнутым.
y(-2) = -2 e –2 »-0.3 .
Построение графика лучше начинать с проведения асимптот (если они есть), потом отмечаются точки экстремума, точки перегиба, точки пересечения с осями. Если этих точек недостаточно, то можно найти ещё несколько дополнительных точек.
График данной функции изображен на рис. 4.
 |
1612170.В этих задачах величину, принимающую наибольшее или наименьшее значение, нужно записать как функцию некоторой переменной, а затем найти наибольшее или наименьшее значение этой функции.
Пример. Тело представляет собой цилиндр, завершенный сверху полушаром. Какую наименьшую площадь полной поверхности может иметь тело, если его объем равен ?
Решение.
Пусть – радиус основания цилиндра, – высота цилиндра. Тогда площадь полной поверхности тела , а объем тела ; отсюда .
Значит, . Таким образом, найдена площадь полной поверхности тела как функция радиуса . При этом можно заметить, что . Осталось найти наименьшее значение функции .
.
Следовательно, функция при имеет наименьшее значение.
.
Таким образом, наименьшая площадь поверхности тела равна .
Контрольная работа №4
171 – 180.Если закон движения точки на прямой задан функцией , то . Для нахождения нужно найти критические точки функции , вычислить значение в критических точках, принадлежащих отрезку , и на концах этого отрезка и выбрать из полученных значений наибольшее по модулю. Точно так же находим .
181 – 190.Функция называется первообразной для функции , если . Совокупность всех первообразных для функции называется неопределенным интегралом от функции и обозначается , при этом называется подынтегральной функцией, – подынтегральным выражением.
Можно доказать, что , где – некоторая первообразная для , – произвольная постоянная.
Для вычисления неопределенных интегралов нужно знать основные свойства, табличные интегралы и методы интегрирования.
Основные свойства неопределенных интегралов:
1. .
2. , где – постоянная, не равная нулю.
3. .
4. .
Свойства 3 и 4 показывают, что операции дифференцирования и интегрирования являются взаимообратными.
Таблица неопределенных интегралов
1)
2)
3)
Если , то .
4)
5)
6)
7)
8)
9)
10)
11)
Все формулы справедливы также в случае, если переменную заменить на некоторую другую функцию. Так, если в формуле 2 заменить на , то получим,
.
Перейдем к рассмотрению методов интегрирования.
megaobuchalka.ru
Примеры вычисления производных. Функция f(x)=x3. Типовые задачи
Дополнительные сочиненияНа уроке рассматривается тема «Примеры вычисления производных. Функция f(x)=x3. Типовые задачи». На этом занятии будут рассмотрены также практические примеры вычисления производных для конкретной функции f(x)=x3,будет решено ряд типовых задач.
Тема: Производная
Урок: Примеры вычисления производных. Функция f(x)=x^3. Типовые задачи.
1. Краткое повторение темы предыдущего занятия
На предыдущем уроке мы рассмотрели понятие производной и рассмотрели алгоритм нахождения производной. Он предусматривал: дать приращение аргументу, вычислить приращение функции, вычислить отношение , упростить, проанализировать, устремить к нулю и найти производную. Это было в общем виде, а теперь этот алгоритм рассмотрим на примере конкретных функций.
2. Функция f(x)=x^3
Пример 1 Дано:
Найти .
Зафиксируем точку и найдем значение производной от конкретной функции в конкретной точке. Действуем по алгоритму.
1)Вычисляем значение . Иллюстрируем все это графиком.
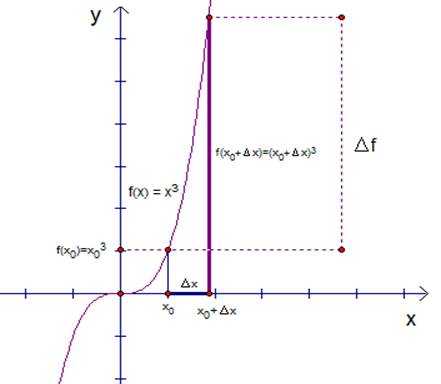
Рис. 1. Кубическая парабола.
Зафиксировав точку , вычислим значение функции в этой точке. Получим .
2) Даем аргументу приращение ,получаем – новое значение аргумента.
Примечание. В данном случае приращение положительное. Можно дать приращение отрицательное, тогда функция будет либо увеличиваться, либо уменьшаться. Важно, что –любое.
3) Вычислить значение функции в новой точке , подставив эту точку в функцию.
.
4) Найдем , то есть разность между значением функции в новой точке минус значение функции в старой точке.
.
Имеем две точки: значение аргумента и значение функции в точке , новое значение аргумента и значение функции при новом значении аргумента. Разность этих значений функции дает .
5) Найдем разностное отношение
.
Знаменатель для всех функций один и тот же, – приращение аргумента, а числитель – свой для каждой функции. Получили разностное отношение. Далее надо упростить его, сократить на и сделать дальнейший анализ.
Упрощать в данном случае можно по-разному. Можно применить формулу или куб суммы, или разность кубов. Напомним, что
. В данном случае – это , – это . Имеем
Раскрывая скобки, получили многочлен. Приведем подобные члены. Дальше надо преобразовать так, чтобы сократить. Вынесем за скобки, получим Теперь можно сократить на , ведь , оно не равно нулю. Имеем соотношение следующего вида
. Осталось узнать, что происходит, когда . В данном случае второй член выражения пропадет, и третий член пропадет. Останется , то есть .
Результат
, то есть смысл такой: 3 выносим как сомножитель и показатель уменьшили на единицу.
Итак, зафиксировали точку , нашли производную от конкретной функции в конкретной точке . Точка может быть любая.
Ответ: .
Итак, мы зафиксировали функцию – кубическую параболу. Была задача: найти производную этой функции в конкретной точке . Мы зафиксировали точку и действовали по алгоритму, который был изложен в общем виде, и применен к данной функции. Этот алгоритм можно применять к любой функции, а именно: вычислить значение функции в точке , подставив значение в закон соответствия, то есть в функцию, дать приращение аргумента, найти значение функции при новом значении аргумента и получить приращение функции, то есть разность между значениями функции в новой точке и старой. Далее, надо найти разностное отношение , упростить его так, чтобы вынести за скобку и сократить на . В результате получится выражение, члены которого зависят от и не зависят от него. Если члены, которые зависят от прямо пропорциональны ему, то они при стремятся к нулю, то есть пропадают. Остаются только члены, которые не зависят от . Таким образом получим значение производной.
Для знакомых с пределами .
Важно понять, что есть члены с члены и члены без . При этом члены с пропадают, остается то, что называется производной.
Итак, производная от кубической функции в любой точке – это .
3. Типовые задачи
Возьмем конкретный пример.
Дано:
Найти: , то есть конкретное значение функции в точке .
Решение.
1) Найти производную в любой точке . .
2) Найти . .
Физический и геометрический смысл решения задачи.
В момент , если двигаться (уезжать от дома) по закону , скорость равна 12. Если к этой кривой мы проведем касательную в точке , то эта касательная имеет угол наклона (см. рис.2). Так вот . Это говорит о том, что угол довольно большой, так как растет быстро (от дома мы уезжаем довольно быстро). Более того, чем дальше, тем быстрее скорость.
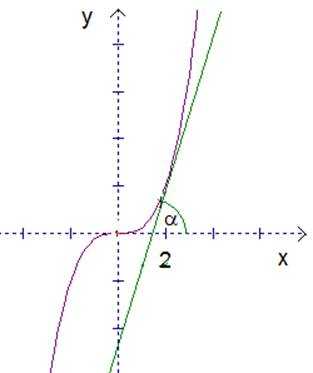
Рис. 2. Физический и геометрический смысл решения задачи.
4. Итог урока
Итак, рассмотрено подробное применение общего алгоритма нахождения производной для конкретной функции. Детализировано подробно каждое действие, решили одну из типовых задач, а именно, как находить значение производной функции в конкретной точке. Для этого нужно найти значение функции в произвольной точке, а потом найти значение производной в конкретной точке.
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н. Я., Ивашев-Мусатов О. С., Шварцбурд С. И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М. И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А. Г., Полонский В. Б., Якир М. С. Алгебраический тренажер.-К.: А. С.К., 1997.
7. ЗвавичЛ. И., Шляпочник Л. Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С. М., Гольдман А. М., Денисов Д. В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А. П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г. И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics. ru .
2. Портал Естественных Наук .
3. Интернет-портал Exponenta. ru .
Сделай дома
№ 40.3, 40.9 (а, б) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
Закрепите материал с помощью тренажёров
- Тренажёр 1 Тренажёр 2
dp-adilet.kz
Примеры вычисления производных.
Дом Примеры вычисления производных.просмотров – 907
Пример 1. Вычислить производную функции y=(3x3-2x+1)×sin x.
Решение. По правилу 3, y’=(3x3-2x+1)’×sin x + (3x3-2x+1)×(sin x)’ =
= (9x2-2)sin x + (3x3-2x+1)cos x.
Пример 2. Найти y’, y = tg x +.
Решение. Используя правила дифференцирования суммы и частного, получим: y’=(tgx + )’ = (tgx)’ + ()’ = + = .
Задание для практической работы по теме «Вычисление производных функций»: Вычислить производные функций:
практическое занятие №2
Тема 1.2: «Нахождение углового коэффициэнта касательной к графику функции в указанной точке. Составление уравнения касательной.»
Цель: Составить уравнение касательной к графику функции в заданной точке.
Теоретический материал:
Углом наклона прямой y = kx+b называют угол , отсчитываемый от положительного направления оси абсцисс до прямой y = kx+b в положительном направлении (то есть, против часовой стрелки). Угловым коэффициентом прямой y = kx+b называют числовой коэффициент k. Угловой коэффициент прямой равен тангенсу угла наклона прямой, то есть, .
Угол наклона прямой равен нулю, когда прямая параллельна оси абсцисс. В этом случае нулю равен и угловой коэффициент, так как тангенс нуля есть ноль. Следовательно, уравнение прямой будет иметь вид y = b.
Когда угол наклона прямой y = kx+b является острым ( ), то угловой коэффициент k является положительным числом (так как тангенс острого угла принимает положительные значения ) и указывает на возрастание графика прямой.
В случае, когда прямая располагается перпендикулярно оси абсцисс (параллельно оси ординат) и задается равенством x = c, где c – неĸᴏᴛᴏᴩᴏᴇ действительное число.
Когда угол наклона прямой y = kx+b является тупым ( ), то угловой коэффициент k является отрицательным числом и указывает на убывание графика прямой.
Касательной к графику функции y = f(x) в точке называют прямую, проходящую через точку , с отрезком которой практически сливается график функции при значениях х сколь угодно близких к . Для этого покажем, что будет происходить с секущей АВ, если точку В бесконечно приближать к точке А.
Рисунок ниже иллюстрирует данный процесс.
Секущая АВ (показана синей пунктирной прямой) будет стремиться занять положение касательной прямой (показана синей сплошной линией), угол наклона секущей (показан красной прерывистой дугой) будет стремиться к углу наклона касательной (изображен красной сплошной дугой). Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, касательная к графику функции y = f(x) в точке А – ϶ᴛᴏ предельное положение секущей AB при .
Читайте также
Пример 1. Вычислить производную функции y=(3×3-2x+1)×sin x. Решение. По правилу 3, y’=(3×3-2x+1)’×sin x + (3×3-2x+1)×(sin x)’ = = (9×2-2)sin x + (3×3-2x+1)cos x. Пример 2. Найти y’, y = tg x + . Решение. Используя правила дифференцирования суммы и частного, получим: y’=(tgx + )’ = (tgx)’ + ( )’ = + = . Задание для… [читать подробенее]
Пример 1. Найти производную сложной функции y= ,u=x4 +1. Решение. По правилу дифференцирования сложной функции, получим: y’x =y ‘u u’x =( )’u(x4 +1)’x =(2u + . Так как u=x4 +1, то y’x=(2 x4 +2+ . Пример 2. Найти производную функции y= . Решение. Представим функцию y= в виде суперпозиции двух функций: y… [читать подробенее]
Задание кривых и областей на комплексной плоскости. Управление карьерой с позиций системного подхода. Лекция 2. Карьерные цели и планирование карьеры. Этические проблемы карьеры молодых специалистов. Перед большинством современных работников необходимость… [читать подробенее]
Покажем на примерах, как, используя определение понятия производной, можно получать формулы дифференцирования различных функций. Задача 1.1.Найтипроизводная постоянной величины равна нулю: . (2.1) Решение. Для любого приращения величина . Отсюда следует: . Задача 1.2…. [читать подробенее]
10. Задано равенство: ln(x2 + y2) = arctg. Определяет ли это равенство функцию , и, если – да, то найти . Определим F(x, y) = ln (x2 + y2) – arctg= 0. Для нее якобиан J = существует везде кроме (0, 0), и точек, в которых и равен: J = = = –= ¹ 0 . Дифференцируем функцию F(x, y) по x, считая y функцией . = = 0; … [читать подробенее]
Производная сложной функции 1. Пусть z=f(x,y), x=x(t), y=y(t). Тогда z=f(x(t), y(t)) является сложной функцией одного переменного t, и ее производная по t может быть вычислена по формуле: . 2. Пусть z=f(x,y), x=x(u, v), y=y(u, v). Тогда z = f(x(u,v), y(u, v)) является сложной функцией двух переменных u и v, и… [читать подробенее]
1) . , поэтому у¢=0. 2) у=хп, где п – натуральное число. n=1: у¢=х¢=1, т.к. . п=2: у=х×х; у¢=(х)¢×х+(х)¢×х =2х. =3: у=(х2)×х; у¢=(х2)¢×х+(х)¢×х2 =2х2+х2=3х2. Во всех рассмотренных случаях (хп)¢=пхп-1. Для произвольного натурального п также (хп)¢=пхп-1. 3) … [читать подробенее]
oplib.ru
