Проинтегрировать дифференциальное уравнение – Дифференциальные уравнения первого порядка. Примеры решений. Дифференциальные уравнения с разделяющимися переменными

Методы интегрирования дифференциальных уравнений

1-й метод. Метод разделения переменных. Этот метод применяется к уравнениям вида , т. е. правая часть является произведением двух функций от разных переменных x и y. Такое уравнение записывается в виде

.

Выражения dy и dx называются дифференциалами переменных. Известно, что зависимость между этими величинами выражается равенством: dy =∙dx . Поэтому при умножении обеих частей этого уравнения на дробь получится равносильное дифференциальное уравнение (правда, при условии g(y)  0, но об этом позже):

,

в котором переменные x и y находятся в разных частях. Такое уравнение называется дифференциальным уравнением с разделёнными переменными

. К обеим частям этого равенства приписывают впереди символы интегралов, в результате получится так называемое равенство в квадратурах, которое теоретически считается решением рассматриваемого уравнения. А если эти интегралы будут вычислены, то получится общий интеграл этого уравнения

Замечание 1. При разделении переменных часто приходится делить обе части уравнения на некоторые выражения, содержащие неизвестную функцию. При этом надо обязательно предполагать, что делитель не равен 0. В результате некоторые значения переменной y становятся недопустимыми, и они могут не войти в полученное общее решение уравнения. В таких случаях надо отдельно рассматривать случаи, когда делитель равен 0. Часто полученные при этом значения

y являются особыми решениями исходного уравнения, и их прибавляют к общему решению.

2-й метод. Метод интегрирования однородных дифференциальных уравнений 1-го порядка. Такое уравнение имеет вид

y = f(x,y),

где правая часть является однородной функцией, которая удовлетворяет следующему условию: для любого множителя t имеет место:

f(t∙x, t∙y) = f(x,y).

Если в этом равенстве взять t = , то получится равенство: f(1,

) = f(x,y) .Тогда замена u = приводит это дифференциальное уравнение к виду:

u +x = f(1,u),

которое является с разделяющимися переменными. Находится решение этого уравнения и производится обратная замена y= x∙u.

3-й метод. Метод Бернулли. Он применяется к линейным уравнениям и к некоторым другим уравнениям.

Определение 4. Линейным дифференциальным уравнкнием 1-го порядка называется уравнение вида

+ p∙y = q,

где

p, q – некоторые функции от x. Согласно условиям существования решения задачи Коши, эти функции должны быть непрерывными.

Решение разыскивается в виде произведения двух неизвестных функций: производится замена: y=u∙v и . Получается уравнение

+ p∙u∙v = q.

Дальше решение разделяется на две части. 1-я часть. В полученном уравнении второе и третье слагаемые группируются вместе ( + p∙u∙v), выносится общий множитель u за скобку + p∙v)

и полученное в скобке выражение приравнивается к 0: + p∙v = 0. В результате исходное уравнение упрощается:. Но сначала, в качестве v подбирается функция, являющаяся решением предыдущего уравнения. Оно чвляется с разделяющимися переменными, получается: = –p∙v, тогда = – pdx и

 = –  pdx. Отсюда ln|v| = -pdx или v = , (здесь константу «с» не пишут).

2 -я часть. Найденную функцию v подставляют назад во вторую часть уравнения, получается . Отсюдаu =  + c. Функции u и найдены, и искомое решение равноy =

u∙v =( + c)().

4-й метод. Метод вариаций (или метод Лагранжа). Рассматривается линейное уравнение из предыдущего пункта. Ему соответствует уравнение вида

+ p∙y = 0,

которое называется линейным однородным уравнением. Оно решается методом разделения переменных так, как это было описано в первой части предыдущего пункта. В соответствующий момент получается общий интеграл вида: ln|y| = -pdx+ ln|c|, (параметр с не отбрасывается). Это равенство преобразуется к виду y = c∙. Далее, решение полного линейного уравнения отыскивается в виде

y = c(x)∙. Понимая под с некоторую функцию от x. Такое решение существует, действительно если эту функцию подставить в исходное уравнение, то получится:

∙+c(x)∙ + p∙ c(x)∙=q.

Здесь = –p∙, поэтому получилось уравнение: ∙= q.

Отсюда с(x) =(q∙)dx+, и у =( + )().

Пример 4. Найти общее решение +y∙tgx = 2xcosx.

Решение. Соответствующее линейное однородное уравнение +y∙tgx = 0 имеет решение y = c(x)∙cosx

. Функция c(x) удовлетворяет уравнению =2x. Поэтому с(x)=. Общее решение равноy=.

5-й Метод. Он применяется к так называемым уравнениям Бернулли, имеющим иид:

,

где p, q – непрерывные функции от x.

Это уравнение можно решать описанным выше методом Бернулли, или следующим более простым методом. Обе части уравнения делятся на и делается замена: , гдеz – новая неизвестная функция. В результате получается линейное уравнение относительно функции z: . Указанным выше методом находится общее решение этого уравнение, и делается обратная замена:y = .

studfiles.net

2.1. Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка

Не существует общих приемов, позволяющих проинтегрировать произвольное дифференциальное уравнение высшего порядка. Однако в некоторых случаях порядок дифференциального уравнения может быть понижен и его решение может быть сведено к последовательному интегрированию нескольких дифференциальных уравнений первого порядка. Остановимся на этих случаях.

I.Решение уравнения вида сводится ккратному интегрированию. Общее решение такого уравнения имеет вид

.

Пример. Найти решение уравнения , удовлетворяющее условиям

(2.3)

Решение. Последовательно интегрируя исходное уравнение, будем иметь

Значения постоянных найдем из условий (2.3). Для отысканияполучим систему уравнений

Итак, искомое решение имеет вид

II.Уравнение не содержит иего производных до порядкавключительно, то есть имеет вид .

Для понижения порядка уравнения применяется подстановка . После применения этой подстановки уравнение приобретает вид. Если удается найти общее решение последнего уравнения, то после-кратного интегрирования получим общее решение исходного уравнения.

Пример. Проинтегрировать уравнение .

Решение. Уравнение не содержит и его производных до третьего порядка включительно. Поэтому его порядок понижается путем введения заменыОтносительно новой переменной уравнение имеет вид

Последовательно интегрируя последнее равенство четыре раза, получим

III.Уравнение не содержит явно переменной , то есть имеет вид. В этом случае порядок уравнения понижается путем замены. Последовательно получим

.

Приходим к уравнению -го порядка

Если удалось найти общее решение последнего уравнения, то для отысканиябудем иметь уравнение с разделяющимися переменными

.

Пример. Проинтегрировать уравнение в области

Решение. Уравнение не содержит явно переменной . Поэтому выполним заменуУравнение примет вид. Разделив обе части этого уравнения на, получим– уравнение Бернулли относительно. Решение этого уравнения будем искать в виде произведения функций. Подставляя в уравнение, будем иметьВ качестве функциивозьмем решение уравненияТогда для отысканияполучим:

Итак,

Найден общий интеграл уравнения.

IY. Уравнение однородное относительно и его производных. Однородным называется уравнение , для которого выполнено

.

Порядок однородного уравнения понижается путем введения новой переменной по правилу . Тогда получим

.

При этом исходное уравнение принимает вид

.

Пусть найдено его решение . Для нахожденияполучаем уравнение с разделяющимися переменными, решение которого имеет вид. Заметим, что решениездесь не потеряно. Оно получается из последней формулы при.

Пример. Проинтегрировать уравнение

Решение. Левая часть уравнения– однородная функция относительно Выполним замену. Тогда уравнение примет вид

Общее решение последнего уравнения (линейного относительно ) имеет видТогдаРешениеполучается при

V. Уравнение имеет вид . Иными словами, левая часть этого уравнения представляет собой полную производную поот некоторой функции. Интегрируя обе части такого уравнения по, получим новое уравнение, порядок которого на единицу меньше, чем у исходного.

Пример. Проинтегрировать уравнение

Решение. Очевидным решением этого уравнения является функция Разделив обе части уравнения на, получим

.

При получаемПриполучаем линейное уравнение, общее решение которого имеет вид.

studfiles.net

Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка

Не существует общих приемов, позволяющих проинтегрировать произвольное дифференциальное уравнение высшего порядка. Однако в некоторых случаях порядок дифференциального уравнения может быть понижен и его решение может быть сведено к последовательному интегрированию нескольких дифференциальных уравнений первого порядка. Остановимся на этих случаях.

I. Решение уравнения вида сводится к кратному интегрированию. Общее решение такого уравнения имеет вид

.

Пример.Найти решение уравнения , удовлетворяющее условиям

(2.3)

Решение. Последовательно интегрируя исходное уравнение, будем иметь

Значения постоянных найдем из условий (2.3). Для отыскания получим систему уравнений

Итак, искомое решение имеет вид

 

II. Уравнение не содержит и его производных до порядка включительно, то есть имеет вид .

Для понижения порядка уравнения применяется подстановка . После применения этой подстановки уравнение приобретает вид . Если удается найти общее решение последнего уравнения , то после -кратного интегрирования получим общее решение исходного уравнения.

Пример.Проинтегрировать уравнение .

Решение.Уравнение не содержит и его производных до третьего порядка включительно. Поэтому его порядок понижается путем введения замены Относительно новой переменной уравнение имеет вид

Последовательно интегрируя последнее равенство четыре раза, получим

 

III.Уравнение не содержит явно переменной , то есть имеет вид . В этом случае порядок уравнения понижается путем замены . Последовательно получим

.

Приходим к уравнению -го порядка

Если удалось найти общее решение последнего уравнения , то для отыскания будем иметь уравнение с разделяющимися переменными

.

Пример.Проинтегрировать уравнение в области

Решение. Уравнение не содержит явно переменной . Поэтому выполним замену Уравнение примет вид . Разделив обе части этого уравнения на , получим – уравнение Бернулли относительно . Решение этого уравнения будем искать в виде произведения функций . Подставляя в уравнение, будем иметь В качестве функции возьмем решение уравнения Тогда для отыскания получим:

Итак,

Найден общий интеграл уравнения.

 

IV. Уравнение однородное относительно и его производных. Однородным называется уравнение , для которого выполнено

.

Порядок однородного уравнения понижается путем введения новой переменной по правилу . Тогда получим

.

При этом исходное уравнение принимает вид

.

Пусть найдено его решение . Для нахождения получаем уравнение с разделяющимися переменными , решение которого имеет вид . Заметим, что решение здесь не потеряно. Оно получается из последней формулы при .

Пример.Проинтегрировать уравнение

Решение. Левая часть уравнения– однородная функция относительно Выполним замену . Тогда уравнение примет вид

Общее решение последнего уравнения (линейного относительно ) имеет вид Тогда Решение получается при

V. Уравнение имеет вид . Иными словами, левая часть этого уравнения представляет собой полную производную по от некоторой функции . Интегрируя обе части такого уравнения по , получим новое уравнение, порядок которого на единицу меньше, чем у исходного.

Пример.Проинтегрировать уравнение

Решение.Очевидным решением этого уравнения является функция Разделив обе части уравнения на , получим

.

При получаем При получаем линейное уравнение, общее решение которого имеет вид .

Задание 7

Решить дифференциальные уравнения, используя методы понижения порядка. Найти общее или (если заданы начальные условия) частное решение.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

cyberpedia.su

4.3. Способы интегрирования уравнений первого порядка

Операцию отыскания решения дифференциального уравнения называют интегрированием уравнения. Мы рассмотрим лишь два простых класса дифференциальных уравнений, для которых находится общее решение.

Уравнения с разделяющимися переменными.К таким уравнениям относятся уравнения вида, где.

Для интегрирования уравнение запишем в виде

.

Простыми преобразованиями перепишем уравнение так:

.

Переменные разделились: слева записан дифференциал некоторой функции от y, а справа – отx. Проинтегрируем обе части полученного уравнения:или– получили общее решение уравнения (возможно, в неявном виде).

Замечание.При делении уравнения наh(y) предполагается, что(могли потерять решение уравнения).

Пример 1. .

Перепишем уравнение в виде .

Функции y=0 иy= –2являются решениями уравнения. Остальные решения найдем, разделив переменные и интегрируя полученное уравнение:

.

Произвольную постоянную здесь удобно записать как . Тогда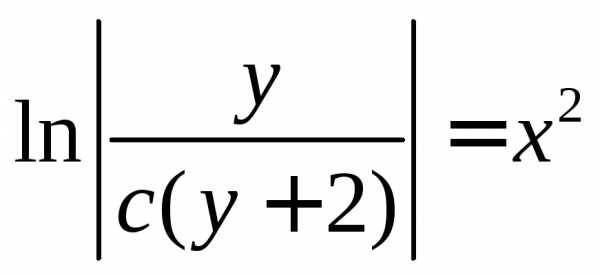или.

Линейные дифференциальные уравнения первого порядка.

Уравнение вида , гдеp(x) иq(x) – заданные непрерывные функции, называется линейным (функцииy(x) ивходят в уравнение лишь в первой степени).

Решение этого уравнения будем искать в виде или, коротко,, тогда; подставив в уравнение, получим

.

Выберем множитель u(x) так, чтобы, тогда исходное уравнение сводится к интегрированию двух уравнений с разделяющимися переменными:

, (1)

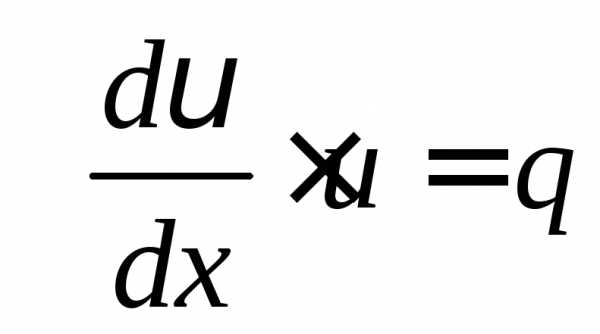. (2)

Найдем решение уравнения (1). Пусть u(x) – некоторое решение. Подставимu(x) во второе уравнение и найдем его общее решение. Тогда общим решением исходного уравнения будет функция.

Пример 2..

Ищем решение этого уравнения в виде . Имеем,.

Функцию uвыберем так, чтобы

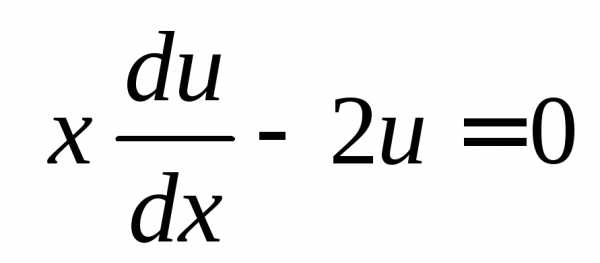(3)

Получили уравнение с разделяющимися переменными. Решим это уравнение:

или

Функция является решением этого уравнения. Функциюнаходим из уравнения, подставив найденную функциюu=x²:

. (4)

Вновь получили уравнение с разделяющимися переменными. Разделяя переменные, получим , или. Общим решением этого уравнения будет функция.

Следовательно, все решения исходного уравнения определяются формулой или.

4.4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами

Уравнение

,

Где – постоянные, называетсялинейным однородным дифференциальным уравнением с постоянными коэффициентами.

Решение этого уравнения будем искать в виде , тогда,. Подставив в уравнение, получим, так как, то функциябудет решением дифференциального уравнения, еслиrудовлетворяет алгебраическому уравнению

. (*)

Последнее уравнение называют характеристическим уравнением для исходного дифференциального.

Уравнение (*) имеет два корня .

Рассмотрим возможные случаи:

1) при D > 0 уравнение (*) имеет действительные различные корни . Функции– решения дифференциального уравнения, они образуют фундаментальную систему решений исходного дифференциального уравнения;

2) при D= 0 корни уравнения (*) действительные и кратные, т.е., тогда фундаментальная система решений состоит из функци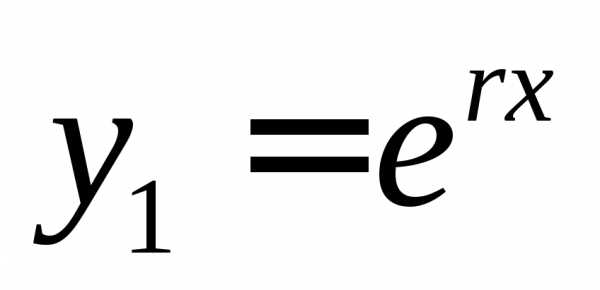йи;

3) при D<0 уравнение (*) имеет комплексно сопряженные корни, где, фундаментальная система решений состоит из функций.

Общее решение дифференциального уравнения с постоянными коэффициентами есть линейная комбинация решений фундаментальной системы, т.е. , где– произвольные постоянные.

Уравнение

называется линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами . Функцияf(x) называется правой частью уравнения. Уравнениес теми же коэффициентаминазывают однородным дифференциальным уравнением, соответствующим данному неоднородному. Общее решение неоднородного дифференциального уравненияY(x) есть сумма общего решения соответствующего однородногоy(x) и частного решения неоднородного:

.

Основная трудность состоит в нахождении 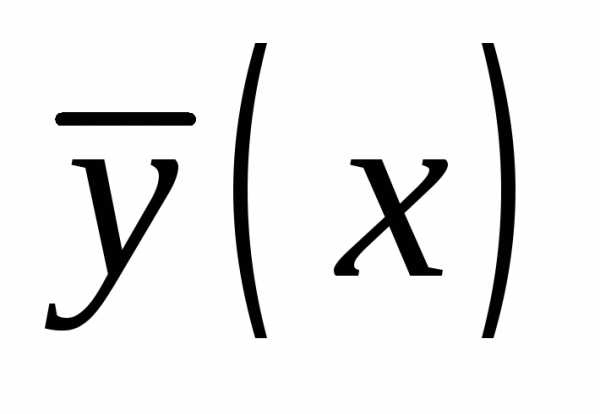. Однако существует простой способ нахождения частного решенияв том случае, когда правая частьf(x) имеет специальный вид. Способ этот заключается в подборе частного решения в зависимости от вида правой части (метод неопределенных коэффициентов).

1. Пусть правая часть уравнения имеет вид , где– заданный многочлен степениm,– действительное число.

Тогда частное решение ищем в виде, где– многочлен той же степениm, что и, но с неизвестными коэффициентами;k– кратность действительного корня α характеристического уравнения. Для отыскания коэффициентовследует подставитьв исходное уравнение, поделить обе части на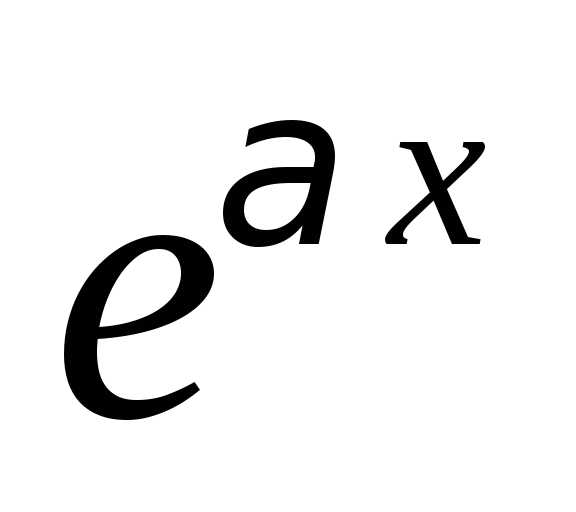и приравнять коэффициенты при одинаковых степеняхх. Получим систему линейных уравнений для определения неизвестных коэффициентов.

2. Пусть правая часть дифференциального уравнения имеет вид , где– заданные числа. Тогда частное решение 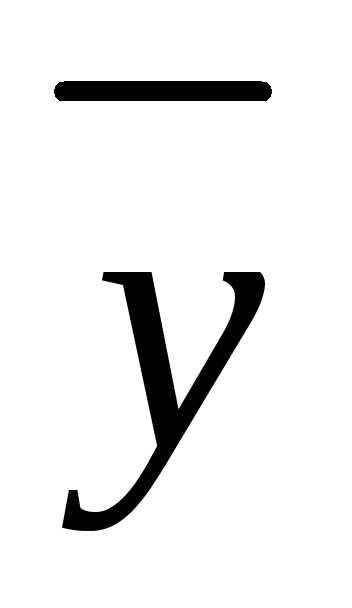следует искать в виде

,

где A,B– неизвестные постоянные,k– кратность комплексных корнейхарактеристического уравнения.

Разберем несколько примеров.

Пример 1.Найти общее решение уравнения.

Решение.Составим характеристическое уравнение; его корни(можно найти по теореме Виета), им соответствует фундаментальная система решений (ФСР)и общее решение имеет вид.

Пример 2.Найти общее решение уравнения.

Решение.Характеристическое уравнениеилиимеет кратный корень, ФСР:, общее решение.

Пример 3.Найти общее решение уравнения.

Решение.Характеристическое уравнение. Корни его найдем, используя общую формулу

.

Следовательно, . Корни характеристического уравнения комплексные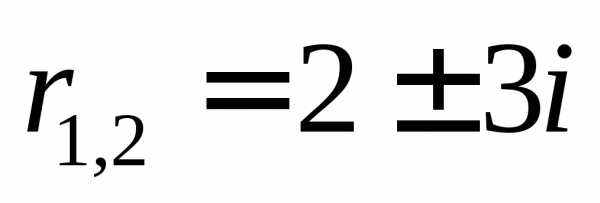, а потому им соответствуют частные решенияи, составляющие ФСР. Следовательно, общее решение есть

.

Пример 4.Найти общее решение неоднородного дифференциального уравнения с постоянными коэффициентами.

Решение.Характеристическое уравнение соответствующего однородного дифференциального уравненияимеет вид, его корнями будут числа; ФСР образуют функции, общее решение соответствующего однородного уравнения.

Частное решение исходного уравнения следует искать в виде , так как коэффициентом прислужит многочлен нулевой степени (, т.е. m=0), числоне является корнем характеристического уравнения (k= 0,k– кратность корня α = 5).

Итак, .

Подставим в данное уравнение , или, отсюда

12A= 1,и.

Общее решение исходного уравнения .

Пример 5.Найти общее решение неоднородного дифференциального уравнения.

Решение.Характеристическое уравнение соответствующего однородного уравненияимеет различные вещественные корни, а потому общее решение однородного уравнения.

Частное решение неоднородного уравнения следует искать в виде , так как правая часть уравнения,

и не является корнем характеристического уравнения,k=0.

Подставим решение в исходное уравнение (в колонке слева записаны коэффициенты прив данном уравнении):

или

.

Таким образом, имеем систему

,

т.е. A= –0,3;A= –0,9.

Получили частное решение .

Следовательно, общее решение данного уравнения имеет вид

.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

studfiles.net

Дифференциальные уравнения в полных дифференциалах

Дифференциальное уравнение первого порядка в полных дифференциалах – это уравнение вида:
(1)   ,
где левая часть уравнения является полным дифференциалом некоторой функции U(x, y) от переменных x, y:
.
При этом   .

Если найдена такая функция U(x, y), то уравнение принимает вид:
dU(x, y) = 0.
Его общий интеграл:
U(x, y) = C,
где C – постоянная.

Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1). Для этого умножим уравнение на dx. Тогда   . В результате получаем уравнение, выраженное через дифференциалы:
(1)   .

Свойство дифференциального уравнения в полных дифференциалах

Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2)   .

Доказательство

Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y. Точка x₀, y₀ также принадлежит этой области.

Докажем необходимость условия (2).
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U(x, y):
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что   . Необходимость условия (2) доказана.

Докажем достаточность условия (2).
Пусть выполняется условие (2):
(2)   .
Покажем, что можно найти такую функцию U(x, y), что ее дифференциал:
.
Это означает, что существует такая функция U(x, y), которая удовлетворяет уравнениям:
(3)   ;
(4)   .
Найдем такую функцию. Проинтегрируем уравнение (3) по x от x₀ до x, считая что y – это постоянная:
;
;
(5)   .
Дифференцируем по y считая, что x – это постоянная и применим (2):

.
Уравнение (4) будет выполнено, если
.
Интегрируем по y от y₀ до y:
;
;
.
Подставляем в (5):
(6)   .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.

В формуле (6), U(x₀, y₀) является постоянной – значением функции U(x, y) в точке x₀, y₀. Ей можно присвоить любое значение.

Как распознать дифференциальное уравнение в полных дифференциалах

Рассмотрим дифференциальное уравнение:
(1)   .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2):
(2)   .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет – то это не уравнение в полных дифференциалах.

Пример

Проверить, является ли уравнение в полных дифференциалах:
.

Решение

Здесь
,   .
Дифференцируем по y, считая x постоянной:


.
Дифференцируем по x, считая y постоянной:


.
Поскольку:
,
то заданное уравнение – в полных дифференциалах.

Методы решения дифференциальных уравнений в полных дифференциалах

Метод последовательного выделения дифференциала

Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d(u ± v);
v du + u dv = d(uv);
;
.
В этих формулах u и v – произвольные выражения, составленные из любых комбинаций переменных.

Пример 1

Решить уравнение:
.

Решение

Ранее мы нашли, что это уравнение – в полных дифференциалах. Преобразуем его:
(П1)   .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;

.
Подставляем в (П1):
;
.

Ответ

.

Метод последовательного интегрирования

В этом методе мы ищем функцию U(x, y), удовлетворяющую уравнениям:
(3)   ;
(4)   .

Проинтегрируем уравнение (3) по x, считая y постоянной:
.
Здесь φ(y) – произвольная функция от y, которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4):
.
Отсюда:
.
Интегрируя, находим φ(y) и, тем самым, U(x, y).

Пример 2

Решить уравнение в полных дифференциалах:
.

Решение

Ранее мы нашли, что это уравнение – в полных дифференциалах. Введем обозначения:
,   .
Ищем Функцию U(x, y), дифференциал которой является левой частью уравнения:
.
Тогда:
(3)   ;
(4)   .
Проинтегрируем уравнение (3) по x, считая y постоянной:
(П2)  
.
Дифференцируем по y:

.
Подставим в (4):
;
.
Интегрируем:
.
Подставим в (П2):

.
Общий интеграл уравнения:
U(x, y) = const.
Объединяем две постоянные в одну.

Ответ

.

Метод интегрирования вдоль кривой

Функцию U, определяемую соотношением:
dU = p(x, y) dx + q(x, y) dy,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки (x₀, y₀) и (x, y):
(7)   .
Поскольку
(8)   ,
то интеграл зависит только от координат начальной (x₀, y₀) и конечной (x, y) точек и не зависит от формы кривой. Из (7) и (8) находим:
(9)   .
Здесь x₀ и y₀ – постоянные. Поэтому U(x₀, y₀) – также постоянная.

Пример такого определения U был получен при доказательстве свойства уравнения в полных дифференциалах:
(6)   .
Здесь интегрирование производится сначала по отрезку, параллельному оси y, от точки (x₀ , y₀) до точки (x₀ , y) . Затем интегрирование производится по отрезку, параллельному оси x, от точки (x₀ , y) до точки (x, y) .

В более общем случае, нужно представить уравнение кривой, соединяющей точки (x₀ , y₀) и (x, y) в параметрическом виде:
x₁ = s(t₁);   y₁ = r(t₁);
x₀ = s(t₀);   y₀ = r(t₀);
x = s(t);   y = r(t);
и интегрировать по t₁ от t₀ до t.

Наиболее просто выполняется интегрирование по отрезку, соединяющим точки (x₀ , y₀) и (x, y). В этом случае:
x₁ = x₀ + (x – x₀) t₁; y₁ = y₀ + (y – y₀) t₁;
t₀ = 0;   t = 1;
dx₁ = (x – x₀) dt₁; dy₁ = (y – y₀) dt₁.
После подстановки, получается интеграл по t от 0 до 1.
Данный способ, однако, приводит к довольно громоздким вычислениям.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов.     Опубликовано: 10-08-2012   Изменено: 02-07-2015

1cov-edu.ru

Порядок дифференциального уравнения и его решения, задача Коши

Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию этой переменной и её производные (или дифференциалы) различных порядков.

Порядком дифференциального уравнения называется порядок старшей производной, содержащейся в нём.

Кроме обыкновенных изучаются также дифференциальные уравнения с частными производными. Это уравнения, связывающие независимые переменные , неизвестную функцию этих переменных и её частные производные по тем же переменным. Но мы будем рассматривать только обыкновенные дифференциальные уравнения и поэтому будем для краткости опускать слово “обыкновенные”.

Примеры дифференциальных уравнений:

(1) ;

(2) ;

(3) ;

(4) ;

(5) .

Уравнение (1) – четвёртого порядка, уравнение (2) – третьего порядка, уравнения (3) и (4) – второго порядка, уравнение (5) – первого порядка.

Дифференциальное уравнение n-го порядка не обязательно должно содержать явно функцию, все её производные от первого до n-го порядка и независимую переменную. В нём могут не содержаться явно производные некоторых порядков, функция, независимая переменная.

Например, в уравнении (1) явно нет производных третьего и второго порядков, а также функции; в уравнении (2) – производной второго порядка и функции; в уравнении (4) – независимой переменной; в уравнении (5) – функции. Только в уравнении (3) содержатся явно все производные, функция и независимая переменная.

Решением дифференциального уравнения называется всякая функция y = f(x), при подстановке которой в уравнение оно обращается в тождество.

Процесс нахождения решения дифференциального уравнения называется его интегрированием.

Пример 1. Найти решение дифференциального уравнения .

Решение. Запишем данное уравнение в виде . Решение состоит в нахождении функции по её производной. Изначальная функция, как известно из интегрального исчисления, есть первообразная для , т. е.

.

Это и есть решение данного дифференциального уравнения. Меняя в нём C, будем получать различные решения. Мы выяснили, что существует бесконечное множество решений дифференциального уравнения первого порядка.

Общим решением дифференциального уравнения n-го порядка называется его решение, выраженное явно относительно неизвестной функции и содержащее n независимых произвольных постоянных, т. е.

Решение дифференциального уравнения в примере 1 является общим.

Частным решением дифференциального уравнения называется такое его решение, в котором произвольным постоянным придаются конкретные числовые значения.

Пример 2. Найти общее решение дифференциального уравнения и частное решение при .

Решение. Проинтегрируем обе части уравнения такое число раз, которому равен порядок дифференциального уравнения.

,

,

.

В результате мы получили общее решение –

данного дифференциального уравнения третьего порядка.

Теперь найдём частное решение при указанных условиях. Для этого подставим вместо произвольных коэффициентов их значения и получим

.

Если кроме дифференциального уравнения задано начальное условие в виде , то такая задача называется задачей Коши. В общее решение уравнения подставляют значения и и находят значение произвольной постоянной C, а затем частное решение уравнения при найденном значении C. Это и есть решение задачи Коши.

Пример 3. Решить задачу Коши для дифференциального уравнения из примера 1 при условии .

Решение. Подставим в общее решение значения из начального условия y = 3, x = 1. Получаем

.

Записываем решение задачи Коши для данного дифференциального уравнения первого порядка:

.

При решении дифференциальных уравнений, даже самых простых, требуются хорошие навыки интегрирования и взятия производных, в том числе сложных функций. Это видно на следующем примере.

Пример 4. Найти общее решение дифференциального уравнения .

Решение. Уравнение записано в такой форме, что можно сразу же интегрировать обе его части.

.

Применяем метод интегрирования заменой переменной (подстановкой). Пусть , тогда .

Требуется взять dx и теперь – внимание – делаем это по правилам дифференцирования сложной функции, так как x и есть сложная функция (“яблоко” – извлечение квадратного корня или, что то же самое – возведение в степень “одна вторая”, а “фарш” – самое выражение под корнем):

Находим интеграл:

Возвращаясь к переменной x, получаем:

.

Это и есть общее решение данного дифференциального уравнения первой степени.

Не только навыки из предыдущих разделов высшей математики потребуются в решении дифференциальных уравнений, но и навыки из элементарной, то есть школьной математики. Как уже говорилось, в дифференциальном уравнении любого порядка может и не быть независимой переменной, то есть, переменной x. Помогут решить эту проблему не забытые (впрочем, у кого как) со школьной скамьи знания о пропорции. Таков следующий пример.

Пример 5. Найти общее решение дифференциального уравнения .

Решение. Как видим, переменная x в уравнении отсутствует. Вспоминаем из курса дифференциального исчисления, что производная может быть записана также в виде . В результате уравнение приобретает вид

,

то есть, в нём в некотором виде появился x.

Теперь вспомнаем одно из свойств пропорции: из пропорции выткают следующие пропорции:

,

то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.

Применяя это свойство, преобразуем уравнение к виду

,

после чего интегрируем обе части уравнения:

.

Оба интеграла – табличные, находим их:

и получаем решение данного дифференциалного уравнения первого порядка:

.

Эта статья представила необходимый минимум сведений о дифференциальных уравнениях и их решениях и должна помочь вам уверенно и увлечённо перейти к изучению различных видов дифференциальных уравнений.

Всё по теме “Дифференциальные уравнения”

Поделиться с друзьями

function-x.ru

Лекция 2. Решение различных видов дифференциальных уравнений первого порядка

 

Оглавление

 

§ 4. Уравнения первого порядка с разделяющимися переменными

Определение

Метод интегрирования

Пример 1

Пример 2

§ 5. Линейные дифференциальные уравнения первого порядка

Определение линейного дифференциальное уравнение первого порядка

Линейное однородное уравнение

Решение

Пример 3

§ 6. Однородные дифференциальные уравнения первого порядка

Определение однородного дифференциального уравнения первого порядка

Метод решения

Пример 4

§ 4. Уравнения с разделяющимися переменными

 

Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде

.

Правая часть этого уравнения представляет собой произведение двух множителей, каждый из которых является функцией только одного аргумента.

Например, уравнение есть уравнение с разделяющимися переменными, т.к. в нем можно принять и .

Точно так же, уравнение есть уравнение с разделяющимися переменными, т.к. его можно привести к виду или , где и .

Напротив, уравнение нельзя представить в виде произведения двух множителей , следовательно, оно не является уравнением с разделяющимися переменными.

Метод интегрирования уравнения с разделяющимися переменными заключается в следующем.

1. Приведем дифференциальное уравнение первого порядка к виду:

или .

2. Умножим обе части уравнения на dx и поделим на , получим:

.

3. Интегрируя, получим:

.

Полученное выражение представляет собой общий интеграл уравнения с разделяющимися переменными.

Пример 1. Решить уравнение .

Решение.

Разрешая уравнение относительно производной, получим или .

Умножим обе части уравнения на dx и поделим на у: .

Интегрируя, получим: или , где С₁ – произвольная постоянная.

Для упрощения полученного решения воспользуемся часто применяемым приемом: положим (С₂ > 0). Тогда

или

Полагая , окончательно получим

,

где С – произвольная постоянная.

Пусть требуется теперь из найденного общего решения выделить частное решение, удовлетворяющее условию . Заменяя в общем интеграле переменные х и у начальными условиями, получим: , откуда С = 2.

Таким образом, искомое частное решение имеет вид .

Пример 2. Приведем решение задачи об остывании тела (см. Задачу 1 из Лекции 1). Ранее, составляя математическую модель задачи, мы пришли к необходимости поиска частного решение дифференциального уравнения , при условиях Т (0) = 100, Т (10) = 60.

Найдем общее решение уравнения. Умножим обе части уравнения на dt и поделим на (Т – 10):

Проинтегрируем полученное равенство:

 

Получили общее решение дифференциального уравнения.

Для нахождения частного решения, воспользуемся начальным условием Т (0) = 100:

, откуда .

Подставив полученное значение в формулу общего решения, получим частное решение:

 

Полученное частное решение зависит от коэффициента пропорциональности k. В условии задачи он не определен, но его можно найти, если воспользоваться вторым начальным условием Т (10) = 60:

В результате, зависимость температуры от времени в заданных условиях имеет вид:

.

Теперь можно определить, через сколько минут температура тела станет равной 20 градусам, решив уравнение:

Таким образом, температура тела станет равной 20 градусам примерно через 37,4 минут.

 

 

§ 5. Линейные дифференциальные уравнения первого порядка

 

Дифференциальное уравнение первого порядка называется линейным, если его можно представить в виде

,

где P(x) и Q(x) – заданные непрерывные функции от х (или постоянные).

Название «линейное» не случайно, т.к. здесь и искомая функция, и ее производная находятся в первой степени (сравните с уравнением прямой линии: ).

Например, уравнения и будут линейными, а уравнение не является линейным.

Если Q(x) º 0, то линейное уравнение называется линейным однородным уравнением.

Решение линейного дифференциального уравнение первого порядка ищут в виде произведения двух функций от х:

или

.

Полученные выражения подставим в уравнение , получим:

.

Перенесем первое слагаемое правой части в левую часть уравнения, сгруппируем слагаемые и вынесем за скобки общий множитель:

Выберем функцию v такой, чтобы выражение в скобках равнялось нулю, т.е.

.

В этом случае дифференциальное уравнение примет вид:

.

Далее возвращаемся к уравнению (*) и, решая его, как уравнение с разделяющимися переменными, находим функцию v :

Для решения уравнения достаточно найти какое-нибудь частное решение уравнение (**), поэтому выберем С₁ = 0, тогда

Подставим найденное значение функции v = v* в уравнение (2.2) и решим его:

.

Возвращаясь к формуле и подставляя в нее найденные значения и , получим ответ:

, где .

Рассмотрим решение линейного дифференциального уравнение первого на примере.

Пример. Решить уравнение .

Решение.

Полагаем или , тогда . Уравнение примет вид:

.

Группируем второе и третье слагаемые левой части уравнения и выносим за скобки общий множитель:

.

Пусть , тогда

.

Полагая С₁ = 0, получим: .

Учитывая, что , подставим полученное значение в уравнение (***):

.

Окончательно имеем или

 

§ 6. Однородные дифференциальные уравнения первого порядка

 

Дифференциальное уравнение первого порядка называется однородным, если его можно представить в виде

.

Например, уравнения и являются однородными. Уравнение также однородное, т.к. деля числитель и знаменатель правой части на х³, получим .

В однородном уравнении переменные вообще говоря не разделяются. Однако оно легко может быть преобразовано в уравнения с разделяющимися переменными. В этом заключается метод решения таких уравнений.

Для разделения переменных введем новую функцию z, положив . Тогда y = x·z, следовательно, . В этом случае однородное уравнение примет вид:

.

В полученном уравнении переменные разделяются: . Предполагая, что , получим:

.

Найдя интеграл в левой части полученного уравнения и возвращаясь к первоначальной переменной у, получим общее решение однородного уравнения.

Пример. Проинтегрировать уравнение .

Разрешим уравнение относительно производной:

Числитель и знаменатель правой части уравнения поделим на х², получим:

Делая подстановку , получим и , следовательно,

В полученном уравнении разделим переменные и найдем общее решение:

Положим , тогда . Возвращаясь к исходной переменной, произведем обратную замену и получим:

 

Получили общий интеграл уравнения.

 

Существует и другие методы решения различных уравнений первого порядка, но мы остановимся на рассмотренных выше. Использование этих методов для интегрирования уравнений будет отработано на практическом занятии.

Дифференциальные уравнения



infopedia.su