как найти, вычислить и понять с нуля
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Геометрический смысл производной
Физический смысл производной: про
zaochnik.ru
Ответы@Mail.Ru: Объясните производную по-человечески, пожалуйста!
Производная – это скорость: движения, старения, глупения, выздоровления, ожирения и т. д.Начнём с функции. Так:
Функция – это любая зависимость чего-нибудь от чего-нибудь.
Например, вес портфеля зависит от количества учебников в нём.
Тяжесть похмелья по утрам зависит от объёма выпитого.
Количество волос на голове зависит от возраста.
Величина, которая зависит, называется функцией, а то, от чего она зависит, называется аргументом.
Т. е. возраст – аргумент (и довольно часто) , а количество волос на голове – функция.
Любому значению аргумента соответствует своё значение функции – так, например, в 25 лет у человека 100 тысяч волос, а в 55 лет (у того же человека) – их всего 100.
Понятно, что функция (пышность шевелюры) должна как-то изменяться при изменении её аргумента (число подаренных на 23 февраля галстуков, дезодорантов и бритв с носками) .
Волосы у человека выпадают каждый день по десятку штук.
Вот эта скорость изменения функции – минус 10 штук в день – и есть производная.
У разных людей своя собственная функция, заложенная природой, – волосы выпадают по-разному, кто-то лысеет в двадцать, а кто-то не лысеет в семьдесят, поэтому очевидно, что производная зависит от функции – у каждой функции она своя.
В математике значением производной в данной точке считается отношение изменения функции к изменению аргумента. Причём изменения аргумента должно быть как можно меньше (стремиться к нулю) .
Именно это записывается формулой: 
Производная тоже может меняться в разных точках.
Например, испугался человек – и быстро облысел, или, наоборот, витаминов налопался – лишние волосы повылазили.
В первом случае производная (одной и той же функции) отрицательная (число волос убывает) и большая (выпало много) , а во втором – положительная (растут новые волосы) и маленькая (выросло мало) .
Поэтому, в принципе, производная – это тоже функция.
Кроме механического смысла (скорость) у производной есть геометрический смысл – касательная к графику функции.
Если мы нарисуем график изменения числа волос у человека во времени, то получим что-то вроде этого (по горизонтальной оси время, по вертикальной – мохнатость) : 
Человек родился с каким-то количеством волос, потом они у него растут (производная положительна – количество волос увеличивается) , затем почему-то выпадают (наверное, попал под кислотный дождь) , а потом снова отрастают, а к старости уже выпадают.
Видно, что производная меняется.
Если мы проведём касательную к этому графику в какой-то точке, то получим график производной в этой точке (вернее, получим прямую, тангенс угла наклона которой численно равен значению производной в точке касания). 
otvet.mail.ru
Объясните, что такое производная, чтобы понял школьник : Вопросы преподавания
Что такое производная в данной точке :1)для простоты начертите параболу , её производная ;
2)возьмите точку на положительной части параболы, т.е. справа от нуля,
3)теперь через эту точку прочертите касательную к параболе и
4)обозначьте точку пересечения касательной с осью как ;
5)теперь опустите перпендикуляр из точки на ось ;
6)Вы должны наблюдать прямоугольный треугольник ;
7)обозначьте угол ;
8)так вот производная в точке , т.е. будет тангенсом .
, иначе говоря производная – это тангенс угла наклона касательной,
ведь косательная – это по сути прямая, т.е. имеет формулу , а это и есть .
dxdy.ru
Производная произведения и частного функции
Формула производной произведения функции имеет вид .
Формула производной частного функции имеет вид .
Однако было бы наивно надеяться, что на контрольной или экзамене Вам обязательно попадётся пример на нахождение производной такого частного: , где легко подставить простенькое выражение в формулу и выдать правильное решение.
В реальных задачах требуется найти производную таких произведений и частных, в которые вкрались тригонометрические выражения и логарифмы, не говоря уже о множителях (константах), и вообще о том, что может содержать произведение или частное функции. Поэтому примеры нахождения производной произведения и частного функций вынесены в эту отдельную статью.
Пример 1.Найти производную функции
.
Решение. От нас требуется найти производную произведения функций. Прежде всего вынесем множитель 2 за знак производной:
.
Теперь применяем формулу дифференцирования произведения:
Приводим слагаемые в скобках к общему знаменателю:
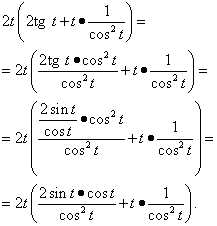
В числителе первого слагаемого можно заметить знакомое по школьной математике выражение двойного угла:
Существует также известное из школьной математики тождество:
.
Подставляем его в наш промежуточный результат и получаем:
.
Производная данного произведения найдена.
Найти производную произведения функций самостоятельно, а затем посмотреть решение
Пример 2.Найти производную функции
.
Пример 4.Найти производную функции
Решение. Перед нами сумма частных. Следовательно, каждое слагаемое будет дифференцировано как частное. Применяем правило дифференцирования частного, не забывая, чему равны производные числа(константы) и самой переменной x:
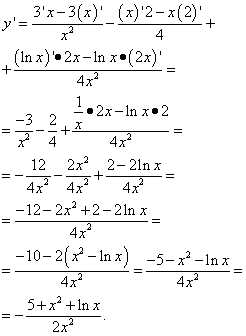
Пример 5.Найти производную функции
Шаг 1. Применим правило дифференцирования частного:
Шаг 2. Находим производную произведения в числителе:
Шаг 3. Находим производную суммы:
Шаг 4. Находим производную функции:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на x:
Найти производную частного функций самостоятельно, а затем посмотреть решение
Пример 6.Найти производную функции
.
Пример 8.Найти производную функции
Шаг 1. Применим правило дифференцирования произведения:
Шаг 2. Найдём производную частного, помня, что производная константы равна нулю, а корень из константы является также константой:
Шаг 3. Находим производную арктангенса (формула 12 в таблице производных):
Искомая производная:
Пример 9.Найти производную функции
Шаг 1. Применим правило дифференцирования частного:
Шаг 2. Дифференцируем по правилам для произведения и показательной функции (формула 17 в таблице производных):

Вновь настоятельно рекомендуем изучить производную сложной функции.
Поделиться с друзьями
Весь блок “Производная”
function-x.ru
Что такое производная. Практический смысл производной
Геометрический смысл производной
|
ОПРЕДЕЛЕНИЕ КАСАТЕЛЬНОЙ К КРИВОЙ Касательной к кривой y=ƒ(x) в точке М называется предельное положение секущей, проведенной через точку ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ Производная функции y=ƒ(x) в точке х0 численно равна тангенсу угла наклона к оси Ох касательной, проведенной к кривой y=ƒ(x) в точке М (х0; ƒ(x0)). |
ВИЗНАЧЕННЯ ДОТИЧНОЇ ДО КРИВОЇ Дотичною до кривої ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ Похідна функції y=ƒ(x) в точці х0 чисельно дорівнює тангенсу кута нахилу до осі Ох дотичної, проведеної до кривої y=ƒ(x) в точці М (х0; ƒ(x0)). |
Практический смысл производной
Прежде всего, производная – это основное понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке.
Что такое “скорость изменения”? Представим себе функцию f(x) = 5. Вне зависимости от значения аргумента (х) ее значение никак не изменяется. То есть, скорость ее изменения равна нулю.
Теперь рассмотрим функцию f(x) = x. Производная х равна единице. Действительно, легко заметить, что на каждое изменение аргумента (х) на единицу, значение функции прирастает также на единицу.
С точки зрения полученной информации теперь посмотрим в таблицу производных простых функций. Исходя из этого сразу же становится понятен физический смысл нахождения производной функции. Такое понимание должно облегчить решение практических задач.
Соответственно, если производная показывает скорость изменения функции, то двойная производная показывает ускорение.
Дифференциалы | Описание курса | Правила дифференцирования
profmeter.com.ua
Производная частного | Математика
При дифференцировании функций нахождение производной частного обычно вызывает наибольшие затруднения. Лучший способ разобраться и понять, как находится производная частного, — рассмотреть конкретные примеры с подробными пояснениями.
Именно этим мы сейчас и займемся. Для дифференцирования нам понадобится таблица производных. Напишем еще раз правило, по которому берется производная частного:
(Поначалу неплохо его выписать на листочек и держать перед глазами). В отличие от производной произведения, затруднений с определением, где здесь u, а где — v, в производной частного нет: понятно, что все, что вверху, в числителе — это u, а все что внизу, в знаменателе — v. Если u и v — табличные функции, производная частного может быть найдена легко: достаточно расписать все по формуле, найти каждую из производных, и упростить.
Пример. Найти производную частного:
Здесь u=2-4x, v=3x+7
Производную линейной функции полезно помнить: (kx+b)’=k, где k и b — числа, причем k — число, стоящее перех x. А можно найти как производную суммы: (kx+b)’=k·x’+b’=k·1+0=k. Таким образом, (2-4x)’=-4, (3x+7)’=3, и знак умножения перед скобкой и перед буквой обычно не пишется
Общий множитель в числителе выносим за скобку, затем дробь сокращаем:
u=2x³+7x-5, v=6x-8. Расписываем по формуле производной частного:
здесь числитель представляет собой сумму и разность функций. Как находить производную суммы и разности, мы уже знаем.
Здесь u=2lnx+1, v=2√x. Значит, производная частного равна
Примеры для самопроверки. Найти производную частного:
Показать решение
1) u=5x²-8x, v=7-x. Теперь ищем производную частного:
Пока что мы рассмотрели только самые простые примеры на производную частного. В более сложных примерах числитель и знаменатель дроби могут быть сложными функциями, либо являться, в свою очередь, производными произведения и частного. Такие примеры мы обсудим чуть позже.
www.matematika.uznateshe.ru
