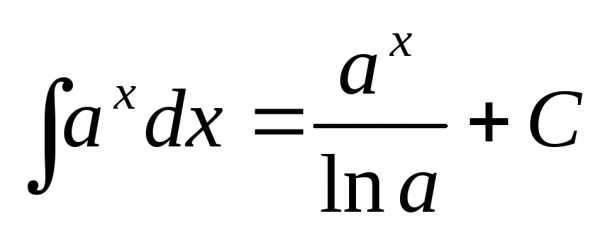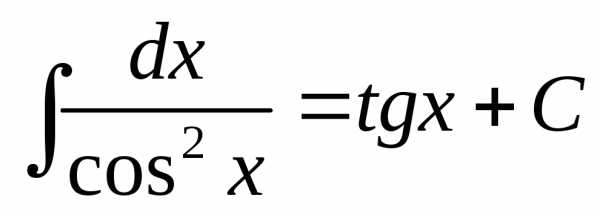Неопределенный интеграл.
Основной задачей дифференциального исчисления является нахождение производной или дифференциала от данной функции.
В интегральном
исчислении основной задачей является
обратная задача – отыскание функции  по заданной ее производной
по заданной ее производной или дифференциалу
или дифференциалу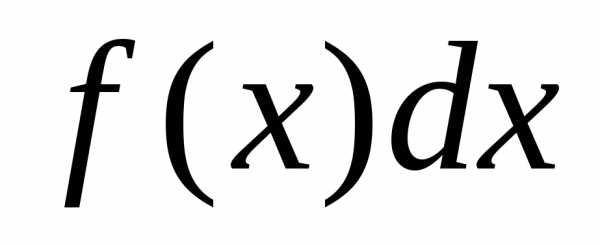 ,
т.е. для данной функции
,
т.е. для данной функции надо найти такую функцию
надо найти такую функцию ,
что:
,
что:
или
Функция 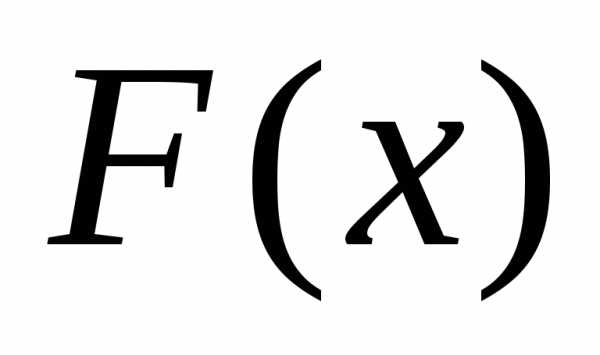
 на отрезке [a,b],
если во всех точках этого отрезка
выполняются равенства
на отрезке [a,b],
если во всех точках этого отрезка
выполняются равенстваили
Например, для
функции  первообразной будет функция
первообразной будет функция
 т.к.
т.к.
Легко видеть,
что если 
 ,
то функциятоже является первообразной для функции
,
то функциятоже является первообразной для функции ,
так как
,
так как Если
функция  является первообразной для функции
является первообразной для функции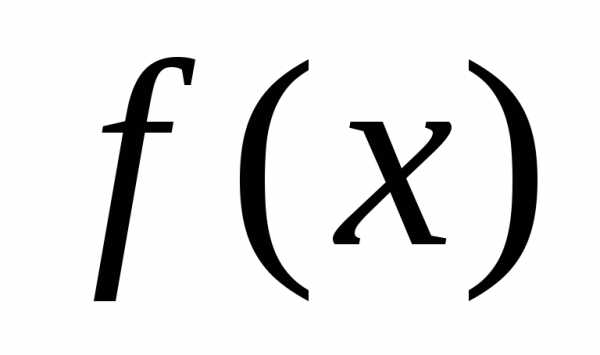 ,
то выражение называетсянеопределенным
интеграломот функции
,
то выражение называетсянеопределенным
интеграломот функции и обозначается символом
и обозначается символом
Функция  называется подынтегральной функцией,
называется подынтегральной функцией,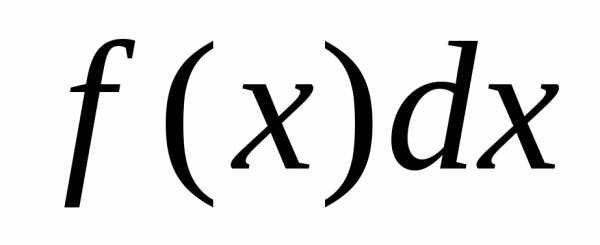 – подынтегральным выражением, С –
произвольная постоянная.
– подынтегральным выражением, С –
произвольная постоянная.
Нахождение первообразной для данной функции называется интегрированием.
Свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
Справедливость свойств 1 – 3 вытекает непосредственно из определения неопределенного интеграла.
4.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
Для доказательства достаточно найти производные от левой и правой частей этого равенства


5. Постоянный множитель можно выносить за знак интеграла
Для доказательства найдем производные от левой и правой частей равенства
6. Если функция  является первообразной для функции
является первообразной для функции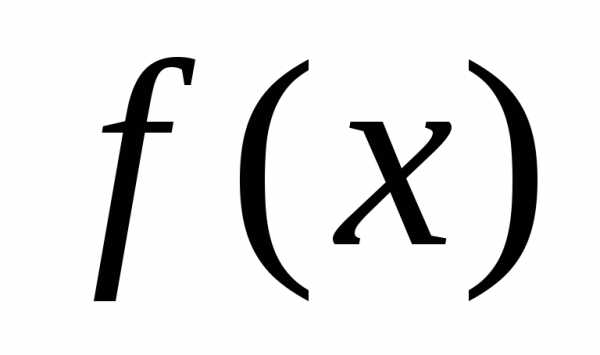 ,
то функция
,
то функция
 является первообразной для функции,
то есть, если,
то
является первообразной для функции,
то есть, если,
то
Для доказательства найдем производные от левой и правой частей равенства
Таблица интегралов.
 Таблица интегралов получается
непосредственно из определения
неопределенного интеграла и таблицы
производных. Для установления
справедливости указанных в таблице
формул достаточно найти производные
от правых частей равенств и получить
подынтегральные функции.
Таблица интегралов получается
непосредственно из определения
неопределенного интеграла и таблицы
производных. Для установления
справедливости указанных в таблице
формул достаточно найти производные
от правых частей равенств и получить
подынтегральные функции.
Заметим, что функций, стоящих в правых частях последних формул нет в таблице производных. Однако, эти интегралы часто встречаются в практических задачах, поэтому они помещены в таблицу. Справедливость их нетрудно проверить непосредственным дифференцированием функций, стоящих в правых частях равенств.
Например, формула 12 доказывается так:
Аналогично проверяются остальные формулы.
Непосредственное интегрирование.
Пользуясь таблицей интегралов, свойствами неопределенного интеграла и различными алгебраическими или трансцендентными преобразованиями подынтегральных функций можно вычислить многие интегралы.
Например:
Интегрирование методом подстановки.
Пусть
требуется найти интеграл  непосредственное интегрирование,
которого не дало окончательного
результата.
непосредственное интегрирование,
которого не дало окончательного
результата.
Заменим
переменную в подынтегральном выражении,
положив  ,
где
,
где непрерывная вместе со своей производной
функция. Получим
непрерывная вместе со своей производной
функция. Получим
.
Вычислим
полученный интеграл по переменной 
 перейдем к прежней переменной
перейдем к прежней переменной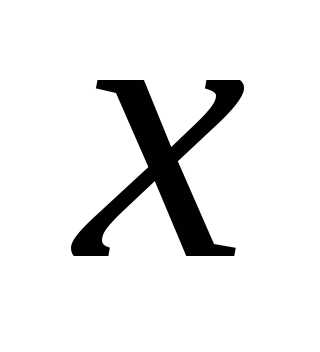 ,
вновь воспользовавшись формулой
,
вновь воспользовавшись формулой
Например:
1. 
Сделаем замену
переменной, положив 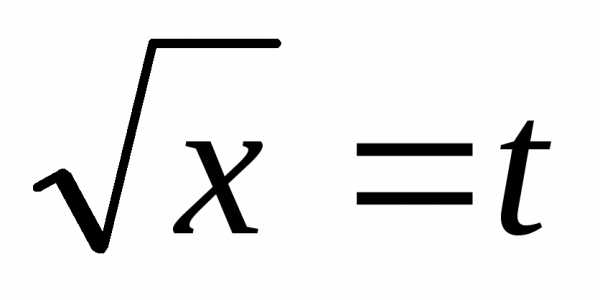
2. 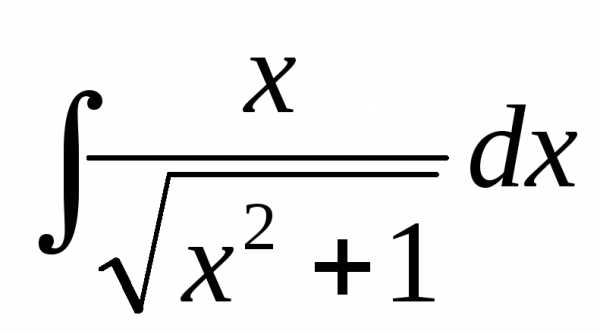
Положим  ,
отсюда выразим
,
отсюда выразим и найдем
и найдем
Тогда
3. 
Полагаем  ,
тогда
,
тогда
4. 
Положим 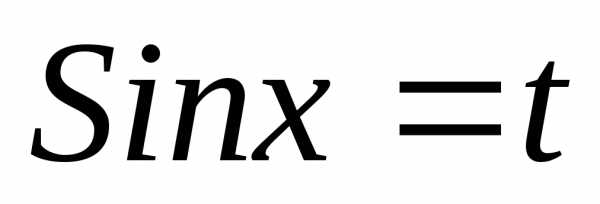 тогда
тогда
Заметим, что подобрать нужную подстановку удается не всегда быстро, необходимы определенные навыки и практический опыт.
studfiles.net
1) Производная от неопределённого интеграла равна подинтегральной функции:
Дифференциал от неопределённого интеграла равен подинтегральному выражению:
d(f(x)dx) = (f(x)dx)`dx = f(x)dx
2) Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
dF(x) = F(x) + C
В самом деле, т.к. dF(x) = F`(x)dx, то dF(x) = F`(x)dx = F(x) + C
/последнее равенство следует из того простого факта, что функция F(x) является первообразной для своей производной: [F(x)]` = F`(x)/
3) Неопределённый интегрл от алгебраической суммы нескольких интегрируемых функций равен алгебраической сумме неопределённых интегралов от отдельных слагаемых.
[f1(x)f2(x)…fn(x)]dx = f1(x)dx…fn(x)dx (1)
4) Можно выносить постоянный множитель из под знака неопределённого интеграла, т. е., если k = const, то kf(x)dx = kf(x)dx (2)
Свойства 3 и 4 доказываются аналогично. Докажем, например, свойство 4, т. е. справедливость равенства (2) /свойство 3 т. е. равенство (1) доказать самостоятельно, можно для простоты взять n = 2/.
На основании свойства 1 имеем:
(kf(x)dx) = kf(x)
и (kf(x)dx) = k(f(x)dx) = kf(x).
Таким образом, производные от обеих частей равенства (2) совпадают, но тогда совпадают и семейства первообразных, т. е. написанные неопределённые интегралы в левой и правой частях равенства (2). Именно в этом смысле и нужно понимать равенство (2) / и, соответственно, (1)/.
Замечание. Мы отмечали уже, что всякая непрерывная функция имеет первообразную, но одна и та же функция может иметь на разных промежутках разные первообразные. Например, функция f(x) = 1/x определена и непрерывна на ( – ,0) и (0,+ ).
На (0,+ ) первообразной для f(x) = 1/x будет очевидно F(x) = ln x , т. к. (ln x) = 1/x.
Следовательно для x (0,+ ) имеем (dx)/x = ln x + C. (3)
На ( – ,0) ln x не может быть первообразной для f(x) = 1/x, т. к. ln x там даже не существует. Однако, нетрудно заметить, что функция ln(-x) существует на
(- ,0) и будет там первообразной для f(x) = 1/x, т. к. (ln(-x)) = (1/(-x))(-1) = 1/x. Следовательно, для x ( – ,0) имеем (dx)/x = ln(-x) +C. (4)
Обычно пользуются формулой (dx)/x = ln |x| +C, (5)
которая справедлива для любых x 0 и, очевидно, объединяет формулы (3) и (4).
§2 Таблица основных неопределённых интегралов.
Таблица неопределённых интегралов от часто встречающихся элементарных функций может быть получена на основе определения 2(#1) и таблицы основных производных, которая была получена раньше. Доказательство всех формул / кроме номеров 7,8,11,13/ легко осуществляется на основе свойства 1 #1, согласно которому производная от правой части равенства должна равнятся подинтегральной функции.

1. ( – 1) /Здесь и во всех остальных формулах С означает произвольную постоянную/.
2. (dx)/x = ln |x| + C /Это верно согласно формуле (5) §1/.
3. sin x dx = – cos x + C. 10. (dx)/(a2+x2) = 1/a arctg x/a + C.
4. cos x dx = sin x + C. 10. (dx)/(1 + x2) = arctg x + C.
5. (dx)/(cos2 x) = tg x + C. 11. 11.
6. (dx)/(sin2 x) = – ctg x + C.
12.
7.tg x dx = – ln |cos x| + C.
12′. .
8.ctg x dx = ln |sin x| +C.
13.
9. ax dx =(ax)/(ln a) + C.
9. ex dx = ex + C.
Проверим, например, формулу 9.
(ax/ln a + C) = (1/ln a ax)‘ + 0 = (1/ln a ax ln a) = ax – Получим подинтегральнуюфункцию, что и доказывает верность формулы 9.
Самим проверить справедливость формул 1,3,4,5,6,9,9‘,10’,12‘.
Замечание. Формулы с абсолютной величиной 7,8,11,13,будут получены немного позже на основе общих результатов.
Вычисление неопределённых интегралов только с помощью таблиц основных интегралов и свойств 1 – 4(§1) называют прямым интегрированием.
Примеры 1) (3x2 + 4sin x – 3√x)dx = 3x2dx + 4sin x dx – 3√x dx =
= 3x2dx + 4sin x dx – 3x0,5dx = 3(x3/3) – 4cos x – 3(x1,5/1,5) + C =
= x3 – 4cos x – 3(x1,5/1,5) + C = x3 – 4cos x – 2x√x +C.

2) = 1/3 (2x + x-0,5 – 1/x) dx =
= 1/3[ 2x dx + x–0,5dx – (dx)/x] = 1/3[x2 + x0,5/0,5 – ln|x|] + C =
= 1/3 [x2 + 2√x – ln|x|] + C.
studfiles.net
Неопределенный интеграл.
Основной задачей дифференциального исчисления является нахождение производной или дифференциала от данной функции.
В интегральном
исчислении основной задачей является
обратная задача – отыскание функции  по заданной ее производной
по заданной ее производной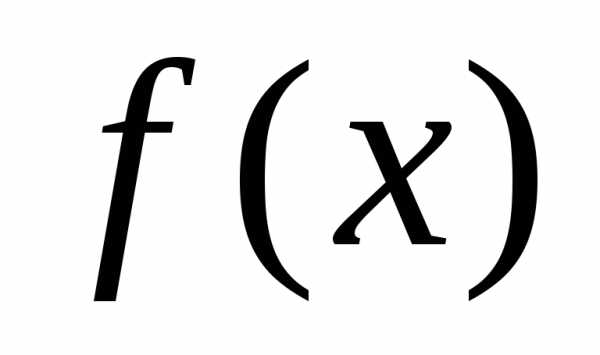 или дифференциалу
или дифференциалу ,
т.е. для данной функции
,
т.е. для данной функции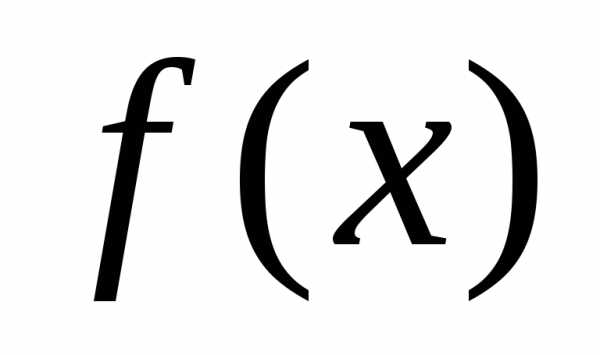 надо найти такую функцию
надо найти такую функцию ,
что:
,
что:
или
Функция  называетсяпервообразной для
функции
называетсяпервообразной для
функции на отрезке [a,b],
если во всех точках этого отрезка
выполняются равенства
на отрезке [a,b],
если во всех точках этого отрезка
выполняются равенства
или
Например, для
функции  первообразной будет функция
первообразной будет функция
 т.к.
т.к.
Легко видеть,
что если  первообразная для функции
первообразная для функции ,
то функциятоже является первообразной для функции
,
то функциятоже является первообразной для функции ,
так как
,
так как
Если
функция  является первообразной для функции
является первообразной для функции ,
то выражение называетсянеопределенным
интеграломот функции
,
то выражение называетсянеопределенным
интеграломот функции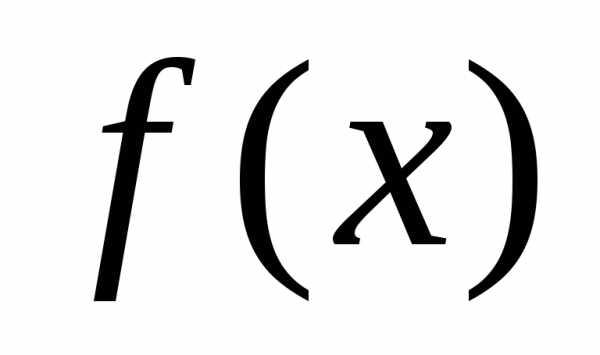 и обозначается символом
и обозначается символом
Функция  называется подынтегральной функцией,
называется подынтегральной функцией, – подынтегральным выражением, С –
произвольная постоянная.
– подынтегральным выражением, С –
произвольная постоянная.
Нахождение первообразной для данной функции называется интегрированием.
Свойства неопределенного интеграла.
1. Производная от неопределенного интеграла равна подынтегральной функции
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
Справедливость свойств 1 – 3 вытекает непосредственно из определения неопределенного интеграла.
4.Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
Для доказательства достаточно найти производные от левой и правой частей этого равенства


5. Постоянный множитель можно выносить за знак интеграла
Для доказательства найдем производные от левой и правой частей равенства
6. Если функция  является первообразной для функции
является первообразной для функции ,
то функция
,
то функция
 является первообразной для функции,
то есть, если,
то
является первообразной для функции,
то есть, если,
то
Для доказательства найдем производные от левой и правой частей равенства
Таблица интегралов.
 Таблица интегралов получается
непосредственно из определения
неопределенного интеграла и таблицы
производных. Для установления
справедливости указанных в таблице
формул достаточно найти производные
от правых частей равенств и получить
подынтегральные функции.
Таблица интегралов получается
непосредственно из определения
неопределенного интеграла и таблицы
производных. Для установления
справедливости указанных в таблице
формул достаточно найти производные
от правых частей равенств и получить
подынтегральные функции.
Заметим, что функций, стоящих в правых частях последних формул нет в таблице производных. Однако, эти интегралы часто встречаются в практических задачах, поэтому они помещены в таблицу. Справедливость их нетрудно проверить непосредственным дифференцированием функций, стоящих в правых частях равенств.
Например, формула 12 доказывается так:
Аналогично проверяются остальные формулы.
Непосредственное интегрирование.
Пользуясь таблицей интегралов, свойствами неопределенного интеграла и различными алгебраическими или трансцендентными преобразованиями подынтегральных функций можно вычислить многие интегралы.
Например:
Интегрирование методом подстановки.
Пусть
требуется найти интеграл  непосредственное интегрирование,
которого не дало окончательного
результата.
непосредственное интегрирование,
которого не дало окончательного
результата.
Заменим
переменную в подынтегральном выражении,
положив  ,
где
,
где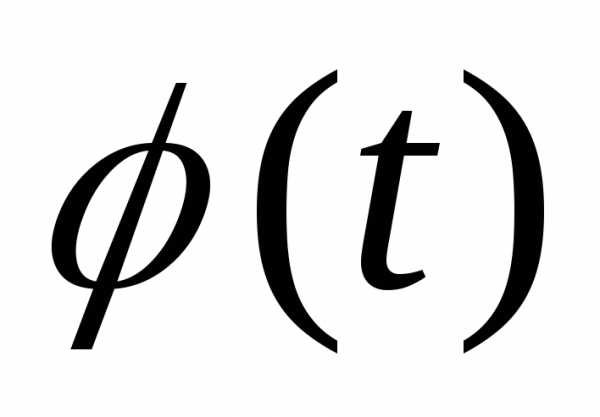 непрерывная вместе со своей производной
функция. Получим
непрерывная вместе со своей производной
функция. Получим
.
Вычислим
полученный интеграл по переменной 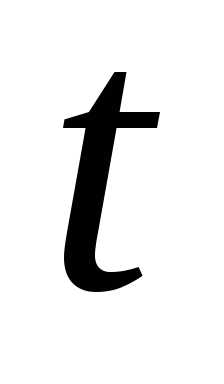 ,
а затем после интегрирования по переменной
,
а затем после интегрирования по переменной перейдем к прежней переменной
перейдем к прежней переменной ,
вновь воспользовавшись формулой
,
вновь воспользовавшись формулой
Например:
1. 
Сделаем замену
переменной, положив 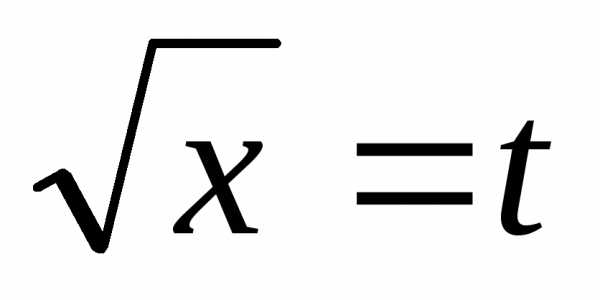 ,
тогда интеграл примет вид
,
тогда интеграл примет вид
2. 
Положим  ,
отсюда выразим
,
отсюда выразим и найдем
и найдем
Тогда
3. 
Полагаем  ,
тогда
,
тогда
4. 
Положим  тогда
тогда
Заметим, что подобрать нужную подстановку удается не всегда быстро, необходимы определенные навыки и практический опыт.
studfiles.net
1. Первообразная. Неопределённый интеграл
Основные формулы интегрирования получаются путём обращения формул для производных, поэтому перед началом изучения рассматриваемой темы следует повторить формулы дифференцирования1основных функций (т.е. вспомнить таблицу производных).
Знакомясь с понятием первообразной, определением неопределённого интеграла и сравнивая операции дифференцирования и интегрирования, студенты должны обратить внимание на то, что операция интегрирования многозначна, т.к. дает бесконечное множество первообразных на рассматриваемом отрезке. Однако фактически решается задача нахождения только одной первообразной, т.к. все первообразные данной функции отличаются друг от друга на постоянную величину
, (1.1)
где C – произвольная величина2.
Вопросы для самопроверки.
Дайте определение первообразной функции.
Что называется неопределённым интегралом?
Что такое подынтегральная функция?
Что такое подынтегральное выражение?
Укажите геометрический смысл семейства первообразных функций.
6. В семействе найдите кривую, проходящую через точку
.
2. Свойства неопределённого интеграла.
ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ
Здесь студенты должны изучить следующие свойства неопределённого интеграла.
Свойство 1. Производная от неопределённого интеграла равна подынтегральной3функции (по определению)
. (2.1)
Свойство 2. Дифференциал от интеграла равен подынтегральному выражению
, (2.2)
т.е. если знак дифференциала стоит перед знаком интеграла, то они взаимно уничтожаются.
Свойство 3. Если знак интеграла стоит перед знаком дифференциала, то они взаимно уничтожаются, а к функции добавляется произвольная постоянная величина
. (2.3)
Свойство 4. Разность двух первообразных одной и той же функции есть величина постоянная.
Свойство 5. Постоянный множитель можно выносить из-под знака интеграла
, (2.4)
где А – постоянное число.
Кстати, это свойство легко доказывается дифференцированием обеих частей равенства (2.4) с учётом свойства 2.
Свойство 6. Интеграл от суммы (разности) функции равен сумме (разности) интегралов от этих функций (если они порознь существуют)
. (2.5)
Это свойство также легко доказывается дифференцированием.
Естественное обобщение свойства 6
. (2.6)
Рассматривая интегрирование как действие, обратное дифферен-цированию, непосредственно из таблицы простейших производных можно получить таблицу следующую простейших интегралов.
Таблица простейших неопределённых интегралов
1. , где, (2.7)
2. , где, (2.8)
3. , (2.9)
4. , где,, (2.10)
5. , (2.11)
6. , (2.12)
7. , (2.13)
8. , (2.14)
9. , (2.15)
10. . (2.16)
Формулы (2.7) – (2.16) простейших неопределённых интегралов следует выучить наизусть. Знание их необходимо, но далеко не достаточно для того, чтобы научиться интегрировать. Устойчивые навыки в интегрировании достигаются только решением достаточно большого числа задач (обычно порядка 150 – 200 примеров различных типов).
Ниже приводятся примеры упрощения интегралов путём преобразования их к сумме известных интегралов (2.7) – (2.16) из вышеприведённой таблицы.
Пример 1.
.
Пример 2.
.
studfiles.net
Свойства неопределенного интеграла
Данные свойства используются для осуществления преобразований интеграла с целью его сведения к одному из элементарных интегралов и дальнейшему вычислению.
1. Производная неопределенного интеграла равна подинтегральной функции:
2. Дифференциал неопределенного интеграла равен подинтегральному выражению:
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме самой этой функции и произвольной постоянной:
4. Постоянный множитель можно выносить за знак интеграла:
, причем a ≠ 05. Интеграл суммы (разности) равен сумме (разности) интегралов:
6. Свойство является комбинацией свойств 4 и 5:
, причем a ≠ 0 ˄ b ≠ 07. Свойство инвариантности неопределенного интеграла:
Если , то8. Свойство:
Если , тоФактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной, который более подробно рассмотрен в следующем разделе.
Рассмотрим пример:
Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.
Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.
www.mathforyou.net
Первообразная. Неопределенный интеграл. Математика – повторение.
Все простейшие формулы интегралов будут иметь вид:
∫f (x) dx=F (x)+C, причем, должно выполняться равенство:
(F (x)+C)’=f (x).
Формулы интегрирования можно получить обращением соответствующих формул дифференцирования.
Действительно,
Показатель степени n может быть и дробным. Часто приходится находить неопределенный интеграл от функции у=√х. Вычислим интеграл от функции f (x)=√x, используя формулу 1).
Запишем этот пример в виде формулы 2).
Так как (х+С)’=1, то ∫dx=x+C.
3) ∫dx=x+C.
Заменяя 1/х² на х-2, вычислим интеграл от 1/х².
А можно было получить этот ответ обращением известной формулы дифференцирования:
Запишем наши рассуждения в виде формулы 4).
Умножив обе части полученного равенства на 2, получим формулу 5).
Найдем интегралы от основных тригонометрических функций, зная их производные: (sinx)’=cosx; (cosx)’=-sinx; (tgx)’=1/cos²x; (ctgx)’=-1/sin²x. Получаем формулы интегрирования 6) — 9).
6) ∫cosxdx=sinx+C;
7) ∫sinxdx=-cosx+C;
После изучения показательной и логарифмической функций, добавим еще несколько формул.
Основные свойства неопределенного интеграла.
I. Производная неопределенного интеграла равна подынтегральной функции.
(∫f (x) dx)’=f (x).
II. Дифференциал неопределенного интеграла равен подынтегральному выражению.
d∫f (x) dx=f (x) dx.
III. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С.
∫dF (x)=F (x)+C или ∫F'(x) dx=F (x)+C.
Обратите внимание: в I, II и III свойствах знаки дифференциала и интеграла (интеграла и дифференциала) «съедают» друг друга!
IV. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла.
∫kf (x) dx=k·∫f (x) dx, где k – постоянная величина, не равная нулю.
V. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.
∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.
VI. Если F (x) есть первообразная для f (x), а k и b — постоянные величины, причем, k≠0, то (1/k)·F (kx+b) есть первообразная для f (kx+b). Действительно, по правилу вычисления производной сложной функции имеем:
Можно записать:
Запись имеет метки: неопределенный интеграл
www.mathematics-repetition.com
2. Основные свойства неопределенного интеграла
а) Производная неопределенного интеграла равна подынтегральной функции
(’ =f(x).
Это свойство непосредственно вытекает из определения неопределенного интеграла, т. к , а.
Цепочка преобразований: .
Например, .
б) Дифференциал неопределенного интеграла равен подынтегральному выражению
=f(x)dx.
Это свойство также следует из определения неопределенного интеграла. Действительно, ,а,
Цепочка преобразований: .
Свойство б) означает, что знак дифференциала аннулирует знак интеграла.
Например, .
в) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной С, т.е.
или.
Действительно, dF(x)=f(x)dx.Возьмем интеграл от обеих частей равенства и получим
Но по определению,.
Цепочка преобразований: ==+С.
Например,
На основании этого свойства выводятся основные формулы интегрирования (см. ниже).
г) Постоянный множитель можно выносить за знак интеграла
(4) |
∆ Действительно, пусть F(x) – первообразная для f(x). В силу основной
формулы (3) имеем:
, | () |
где С1=аС, причем,С иС1– произвольные постоянные приа0. НоаF(x)есть первообразная для функцииаf(x), так какаF(x)’ =аF'(x)=аf(x).Поэтому из формулы () получаем требуемую формулу (4).
Коротко запишем: .
Действительно, производные обеих частей равенства равны:
и.
д) Неопределенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций в отдельности, т.е.
. | (5) |
В самом деле, пустьF‘(x) = f(x) иG‘(x) = g(x).
Тогдаи.
Поэтому
= , где С1+С2=С.
Здесь был использован тот факт, что производная алгебраической суммы функций равна алгебраической сумме производных этих функций и свойство а) неопределенного интеграла.
Свойство д) распространяется на случай алгебраической суммы любого конечного числа функций.
3. Таблица основных интегралов
Интегрирование есть действие, обратное дифференцированию. Поэтому, для того чтобы проверить, правильно ли найден данный интеграл, достаточно продифференцировать найденную первообразную. Если при этом получим подынтегральную функцию, то интеграл найден верно.
Из определения интеграла следует, что всякая формула для производной конкретной функции, т.е. формула вида (1) может быть записана в виде интегральной формулы (3). Формулы интегрирования получаются обращением соответствующих формул дифференцирования. Используя это соображение и таблицу производных, составим следующую таблицу неопределенных интегралов.
1.dх=+С(-1)
В частности, при = 0 имеем =x + С
2.=ln|х| +С
3.=+С,а0,а1
В частности,
3а. = ех + С
4.= –
5.=
6.=
7.=
8.
9.
Заметим, что формулы 2,6,7,8 справедливы лишь для тех значений х, при которых не происходит обращения в нуль знаменателя.
Для вывода этих формул, как уже отмечалось, используется свойство в) неопределенного интеграла, а именно, дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал -подынтегральное выражение.
Справедливость всех представленных интегралов легко проверить, если
продифференцировать их правые части.
Проверим, например, формулу 2.
Чтобы найти , заметим, что функциянепрерывна в промежуткахи, причем в каждом из них она имеет первообразную.
В промежутке этой первообразной, очевидно, является функцияlnx, т.к., т.епри.
В промежутке первообразной по отношению кявляется, т.е.
при. Действительно,существует при x<0 и.
Итак, оба промежутка непрерывности подынтегральной функции объединяются записью
.
Приведенные интегралы 1-9 принято называть табличными.
Лекция 2.
studfiles.net