Производная суммы | Математика
Производная суммы и разности функций берется по правилу (u±v)’=u’±v’. Если слагаемые — табличные функции, найти производную суммы несложно, гораздо легче, чем производную произведения или производную частного. Начнем с рассмотрения именно таких примеров, а более сложные задания разберем позже.
Таблицу производных можно посмотреть здесь.
Найти производные суммы и разности функций:
1) y=10x³+12x-4cosx+8.
y’=(10x³+12x-4cosx+8)’=
Поскольку производная суммы и разности равна сумме и разности производных, при нахождении производной суммы ищем отдельно производную каждого слагаемого:
=(10x³)’+(12x)’-(4cosx)’+8’=
Так как число выносится за знак производной, то в тех слагаемых, где перед функцией стоит числовой множитель, этот числовой множитель выносим за знак производной, то есть просто переписываем. Если слагаемое состоит только из числа, то его производная равна нулю: С’=0:
=10·(x³)’+12·x’+4·(c0sx)’+8’=
Теперь производную каждого слагаемого находим по таблице производных:
=10·3x² +12·1+4·(-sinx)+0=30x² +12-4sinx.
Если среди слагаемых встречаются степени, для их дифференцирования используется соответствующее правило для нахождения производной степени.
Так подробно примеры расписывают только в самом начале нахождения производной суммы и разности. В дальнейшем при нахождении производной суммы мы не будем каждое слагаемое заключать в скобки и ставить над ними штрих. Этот этап пропускается. Просто переписываем числовые множители, стоящие перед каждым слагаемым, а производную каждого слагаемого находим с помощью таблицы производных. Так как производная числа равна нулю, обычно при нахождении производных этот нуль тоже не пишут.
Прежде чем искать производную корня, его необходимо записать в виде степени (подробнее — здесь):
Теперь ищем производную суммы:
Мы рассмотрели самые простые примеры на производную суммы и разности. В свою очередь, производная каждого слагаемого может находиться как производная произведения, частного или производная сложной функции. Поэтому более сложные примеры мы рассмотрим позже, после того, как разберемся с другими правилами дифференцирования функций.
Упражнения для самопроверки: найти производные суммы и разности функций:
Показать решение
www.matematika.uznateshe.ru
Производная алгебраической суммы функций.
Теорема 1.
Производная алгебраической суммы двух дифференцируемых функций равна алгебраической сумме производных этих функций.
(u(x)+v(x))’ = u‘(x)+v‘(x).
(u(x)-v(x)’=u‘(x)-v‘(x).
Замечание. Можно доказать справедливость теоремы 1 для суммы любого конечного числа дифференцируемых функций, т.е.
Задача: Найти производную функции f(x)=x2+x-7.
Вычислить f (-1), f (0), f (3)
Решение
Производная произведения функций
Теорема 2.
Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой.
.
Эта формула называется формулой Лейбница.
Следствие 1. Постоянный множитель можно выносить за знак производной. .
Следствие 2
Задача. Найти производную функции f(x)=x3(x-1)
Решение:
Производная частного двух функций
Теорема 3. Производную частного двух дифференцируемых функций можно найти по формуле:
, где
Задача: Найти производную функции
Решение:
Упражнения
Найти производные функции:
1.
2.
3.
4.
5.
Похожие статьи:
poznayka.org
Производная – сумма – Большая Энциклопедия Нефти и Газа, статья, страница 1
Производная – сумма
Cтраница 1
Производная суммы равна z, так как все остальные члены суммы от п – не зависят. [1]
Производная суммы равна сумме производных. [2]
Производная суммы нескольких многочленов равна сумме их производных. [3]
Производная суммы векторов равна сумме производных от слагаемых векторов. [4]
Производная суммы функций равна сумме производных от этих функций. [5]
Производная суммы векторов равна сумме производных от слагаемых векторов. [6]
Производная суммы векторов равна сумме производных слагаемых. [7]
Производная суммы конечного числа функций равна сумме производных слагаемых. [8]
Правило производная суммы равна сумме производных устанавливается элементарно. [9]
Чему равна производная суммы, производная произведения, производная частного двух функций. [10]
Поэтому высказывание производная суммы равна сумме производных без предположения о существовании производной у каждого из слагаемых вообще говоря, неверно. [11]
Коротко говорят: производная суммы равна сумме производных. [12]
Таким образом, производная суммы функций равна сумме производных. [13]
Таким образом,
Доказать, что производная суммы любого фиксированного числа дифференцируемых функций равна сумме производных этих функций. [15]
Страницы: 1 2 3
www.ngpedia.ru
Производная суммы, разности, произведения и частного функций — Мегаобучалка
Нахождение производной функции непосредственно по определению (п.4.1) часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.
Теорема.
Если функции и дифференцируемы в точке х, то в этой точке дифференцируемы функции , , (при условии, что ) и при этом
;
;
, .
Следствия
1. , где .
2. Если , то .
3. , где .
Производная сложной функции
Пусть и , тогда − сложная функция с промежуточным аргументом u и независимым аргументом х.
Теорема.
Если функции имеет производную в точке х, а функция имеет производную в соответствующей точке , то сложная функция в точке х
или = .
Кратко это можно сформулировать так (правило цепочки): производная сложной функции равна произведению производных от функций ее составляющих.
Данное правило распространяется на сложные функции при любом (определенном) числе промежуточных аргументов.
Так, если , , , , то
.
Производная обратной функции
Если и − взаимо-обратные дифференцируемые функции и , то
или ,
т.е. производная обратной функции равна обратной величине производной данной функции.
Записывают:
или .
Пример
Найти производную функции .
, , тогда , . Имеем .
.
Итак, .
Таблица производных
Для удобства и упрощения процесса дифференцирования формулы производных основных элементарных функций и правила дифференцирования сведены в таблицу.
Примеры отыскания производных сложных функций
На практике чаще всего приходится находить производные от сложных функций. Покажем на примерах, как находить производные от таких функций.
1. , k − число.
;
.
2. .
;
.
;
.
4. .
;
.
5. .
;
.
6. .
;
;
.
7. .
.
8. .
;
.
9. .
.
10. .
;
.
Для случая дифференцирования сложных функций, таблицу производных можно переписать в более общем виде.
Формулы дифференцирования основных элементарных функций от промежуточного аргумента ( )
Производная функции, заданной параметрически
Зависимость между переменными х и y может быть задана параметрически в виде двух уравнений:
где t − вспомогательная переменная (параметр).
Функцию , определяемую этими уравнениями, можно рассматривать как сложную функцию , где .
По правилу дифференцирования сложной функции имеем:
.
Так как , то
.
Примеры
Найти производные функций:
1.
.
2.
.
Производная неявной функции
Если неявная функция задана уравнением , то для нахождения производной от у по х надо продифференцировать это уравнение по х, рассматривая при этом у как функцию от х, и затем, полученное уравнение разрешить относительно , выразив через х и у.
Пример
Найти производную функции: .
;
;
;
.
megaobuchalka.ru
3.5. Производная суммы, произведения и частного функций
ции, в силу чего равенство (3.10) играет большую роль как в теоретических исследованиях, так и в приближенных вычислениях.
Операции нахождения производной и дифференциала функции называются дифференцированием этой функции. Общее название обеих операций объясняется их очевидной зависимостью. В силу формулы (3.8) дифференциал функции получается простым умножением ее произ-
водной на величину | x = dx. |
|
Пример 3.2. | Найти приращение | и дифференциал функции |
y = 3×2 + x в точке | x =1 , еслиx = 0,1. | Вычислить абсолютную и от- |
носительную погрешности, которые возникают при замене приращения функции ее дифференциалом.
Найдём приращение и дифференциал функции
y = 3(x+ x)2 +(x+ x) −3×2 − x= 6x x+3( x)2 + x= (6x+1) x+( x)2.
Тогда dy = (6x +1) x . Вычислимy иdy в точкеx =1 , еслиx = 0,1 y = 7 0,1+3 0,01 = 0,73;dy = 7 0,1 = 0,7.
Абсолютная погрешность y −dy = 0,73 −0,7 = 0,03, а относительная погрешность
y= 00,,0373 ≈0,04.
Напомним известные из курса средней школы правила дифференцирования, которые позволяют в некоторых случаях находить производные функций, не прибегая непосредственно к определению.
Теорема 3.3. Если функцииu = u(x) иv = v(x)
в точке x , то в этой точке |
|
|
|
| ′ |
|
| ′ | ′ | |
|
|
|
|
|
|
|
| |||
|
|
|
| (u+v) | = u | +v | ||||
|
|
|
|
| ′ |
| ′ |
| ′ | |
|
|
|
| (uv) | = u v+v u; | |||||
u |
|
|
| ′ | ′ |
|
|
|
| |
= |
| u v −v u | ,v =v(x) ≠0. | |||||||
|
|
|
|
|
|
|
| |||
|
| v | 2 |
|
| |||||
v |
|
|
|
|
|
|
|
| ||
дифференцируемы
(3.11)
(3.12)
(3.13)
Умножив эти равенства почленно на dx , получим те же правила, записанные в терминах дифференциалов
d (u+ v)= du+ dv; | (3.14) |
d (uv) = udv+vdu; | (3.15) |
d |
| u |
| = | udv −vdu | . | (3.16) |
|
| ||||||
| v |
| v2 | ||||
Доказательство. Так как для всех частей теоремы доказательство проводится совершенно единообразно, докажем одну из них, например, вторую.
Обозначим y = uv. Придадимx приращениеx, и пусть
u,Δv,Δy будут приращения функцийu,v, y в точке | x , соответствую- | ||||||||
щие приращению |
| x, аргумента. Тогда |
|
|
|
| |||
y = (u+ u)(v+ v) −uv= v u+u v+ u v. | |||||||||
Учитывая, что u | и v – значения функций в точке | x не зависят от при- | |||||||
ращения аргумента | x, в силу определения (3.1) и свойств предельного | ||||||||
перехода (см. формулы (2.14),(2.15) находим |
|
|
|
| |||||
y′ =lim | y | = v lim | u | +u lim | v + lim | u | lim | v. | |
x→0 | x | x→0 | x | x→0 | x | x→0 | x | x→0 |
|
Функция v = v(x) | в рассматриваемой точке | x по условию теоремы диф- | |||||||
ференцируема, а значит, и непрерывна ( теорема 3.2), следовательно
lim | v = 0 (определение непрерывности 2.17) и предыдущее равенство | ||||||
x→0 |
|
|
|
| y′ = vu′+uv′+u′ 0. Подставив сюда | ||
дает выражение для производной: | |||||||
y = uv , придем к формуле (3.12). |
|
| y = C ( здесь | ||||
| Производная и дифференциал постоянной функции | ||||||
С – | постоянное число при всех x X ) | равны нулю. |
| ||||
| x X C | ′ | = 0; |
| ′ | (3.17) | |
|
| dC = C dx= 0. | |||||
Действительно, в любых точках множества X такая функция имеет одно | |||||||
и то же значение, в силу чего для нее | y ≡ 0 при любых | x иx таких | |||||
что | x, x + x X. Отсюда, |
| в силу определения производной и диффе- | ||||
ренциала, следуют формулы (3.17). |
|
|
| ||||
| Формула (3.11) обобщается на случай любого конечного числа сла- | ||||||
гаемых функций. |
|
|
|
|
|
| |
| При u = C , где | C −const , формулы (3.12) и (3.15), | в силу (3.17), | ||||
| ′ | ′ |
| d(Cv) = Cdv. То есть, постоянный множи- | |||
дают равенства: (Cv) | = Cv , |
| |||||
тель можно выносить за знаки производной и дифференциала.
Для случая трех сомножителей, последовательно применяя формулу
(3.12), находим
(uvw)′ = ((uv)w)′ = (uv)′w+(uv)w′+(u′v+uv′)w+uvw′ = = u′vw +uv′w +uvw′.
Аналогичное правило справедливо при дифференцировании произведения любого числа сомножителей.
В следующих пунктах будут получены производные основных элементарных функций.
3.6. Производные от тригонометрических функций
Найдем производные от тригонометрических функций, а именно
1. | ′ | = cosx | 2. | ′ | = −sinx | ||||
(sin x) | (cos x) |
| |||||||
| (tgx)′ = | 1 |
|
| (ctgx)′ |
| 1 | ||
3. |
|
| 4. | = − |
| ||||
| cos2 x |
| sin2 x | ||||||
Получим первую из них. Приращение функции y = sin x в точкеx , со-
ответствующее приращение | x | аргумента, будет |
| ||||||
y = sin(x+ | x)−sinx = 2sin | x cos(x + | x). | ||||||
Учитывая, что sin 2x | 2x при |
|
| 2 |
| 2 | |||
| x → 0 | и используя определение произ- | |||||||
водной, находим |
|
| 2sin 2x cos(x + | 2x) |
| ||||
y′ =lim | y = lim | = | |||||||
|
|
| |||||||
| x→0 | x | x→0 |
|
| x |
|
| |
= lim | 2 2x cos(x + | 2x) | = limcos(x + | x )= cosx. | |||||
|
| ||||||||
x→0 | x |
|
| x→0 |
| 2 |
| ||
Вторая формула доказывается аналогично. Третья и четвертая формулы получаются, если тангенс и котангенс выразить через синус и косинус и воспользоваться формулой (3.13).
3.7. Дифференцирование логарифмических функций
Имеют место формулы |
| 1 |
|
|
| 1 |
| ||
1. | ′ | = | loga e | ′ | = | . | |||
|
| ||||||||
(loga x) | x | 2.(lnx) | x | ||||||
|
|
|
|
|
|
| |||
Докажем первую из них. Приращение функции y = loga x в точкеx , со-
ответствующее приращению x | аргумента, будет |
| |||
y = loga (x + x)−loga x = loga |
| x + x | = loga (1+ | x)= loga eln(1+ | x); |
| x | ||||
|
|
| x | x | |
(мы воспользовались здесь тождеством loga A = loga eln A ).
Так как ln(1+ xx) xx | при | x → 0 | , то по определению производной | ||||||
получаем: | y = loga e lim |
| 1 |
|
| x)= | |||
y′ =lim |
| ln(1+ | |||||||
|
|
| |||||||
x→0 | x |
| x→0 |
| x | x | |||
= loga e lim | 1 | x | = | 1 | loga e. |
| |||
x | x |
|
| ||||||
| x→0 |
|
| x |
| ||||
3.8. Дифференцирование сложной функции.
Производные от степенной и показательной функций
Пусть сложная функция y аргументаx задана формуламиy = f (u),
u =ϕ(x) (см. пункт 1.4.3)
Теорема 3.4 (о производной сложной функции). Если функции
y = f (u),u =ϕ(x) дифференцируемы | в соответствующих | друг другу | |
точках u иx , то сложная функция | f [ϕ(x)] тоже дифференцируема в | ||
точке | x , причем | y′x =y′u u′x. |
|
| y′ =f ′(u)u′или | (3.18) | |
Доказательство. Независимой переменнойx придадим прираще- | |||
ние | x, тогда функцияu =ϕ(x) получит приращениеu , | что вызовет | |
приращение y функцииy = f (u) . Так как функцияy = f (u) по условию теоремы дифференцируема в рассматриваемой точкеu , то ее приращение в этой точке можно представить в виде (см.определение 3.4)
′ |
|
| u, гдеα( | u) → o приu →0. |
| ||
y = f(u) u+α( u) |
| ||||||
Отсюда: |
| y |
|
| u | u |
|
|
|
| ′ |
| |||
|
| x | = | f (u) | x +α(u) | x . |
|
Функция u =ϕ(x) | дифференцируема, а значит и непрерывна в точ- | ||||||
ке x , соответствующей рассмотренной выше точкеu | (теорема 3.2). | ||||||
Следовательно, | в | силу | непрерывности | lim u = 0, | а поэтому | ||
|
|
|
|
|
| x→0 |
|
lim α(u)= 0. |
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
Учитывая это, | при | переходе в | последнем | равенстве к | пределу при | ||
x → 0 , придем к (3.18).
Умножив равенство (3.18) почленно на dx , получим выражение для дифференциала сложной функции
70
dy = f′(u)du.
Замечание. Дифференциал функцииy = f (u) имел бы точно такой же вид и в том случае, если бы аргументu был не функцией, а независимой переменной. В этом состоит так называемоесвойство инвариантности (независимости) формы дифференциала по отношению к аргументу. Следует иметь в виду, что еслиu – независимая переменная, тоdu = u есть ее произвольное приращение, если жеu – промежуточный аргумент (то есть функция), тоdu – дифференциал этой функции, то есть величина, не совпадающая с ее приращениемu.
С помощью последней теоремы легко получить формулы дифференци-
рования степенной и показательной функции: |
|
| ′ |
|
| ||||||||||
α | ′ | α−1 | ; | 2). (a | x | ′ | = a | x | ln a; | 3). (e | x | x | . | ||
1). (x | ) =αx |
|
| ) |
|
| ) | = e | |||||||
Действительно, | предполагая | x > 0 , | прологарифмируем обе части | ||||||||||||
формулы y = xα ; ln y =α ln x. Здесьy | – это функция от x , в силу чего | ||||||||||||||
левая часть последнего равенства является сложной функцией отx . Продифференцировав обе части последнего равенства поx (левую – как сложную функцию), получим
1y y′ =a 1x ,
откуда
y′ =ayx =axxa =axa−1.
Легко показать, что этот результат верен и при x < 0 , если только при
этом xα имеет смысл. Ранее был получен результат для случаяα = n. Аналогично получается и вторая формула, из которой в частном случае приa = e вытекает последняя формула.
Замечание. Прием предварительного логарифмирования, который был использован при получении формулы дифференцирования степенной функции, имеет самостоятельное значение и называется в совокупности с последующим нахождением производной логарифма функции
логарифмическим дифференцированием.
Покажем его применение для дифференцирования функций вида y = u(x)v(x)
Пример 3.3. Найдем производную функцииy = xsin x .ln y = ln xsin x = sin xln x
ln y ‘= y ‘/y = (sinx)’lnx +sinx(lnx)’= cosxlnx + sinx x .
Следовательно,
y′ = xsin x(cosx lnx + sinx x)
Замечание. Правило дифференцирования сложной функции может быть применено и для отыскания производной функции, заданной неявно.
Действительно, если зависимость между x иy задана в формеF(x, y) = 0 и это уравнение разрешимо относительноy , то производнуюy′ можно найти из уравнения
|
|
|
| d | (F (x, y(x))= 0. |
|
|
| |
|
|
|
|
|
|
|
| ||
Пример 3.4. |
|
| dx |
|
| y = f (x) , заданной не- | |||
Найти производную функции | |||||||||
явно уравнением | arctg( y) − y+ x= 0 . | y функцией отx : | |||||||
Дифференцируем равенство по x , считая | |||||||||
| y′ |
| 1+y | ||||||
|
| − y′+1= 0, откуда | y′ = |
|
|
| |||
1+y2 |
| y2 |
| ||||||
3.9. Дифференцирование обратной функции.
Дифференцирование обратных тригонометрических функций
Пусть даны две взаимно обратные функции y = f (x) иx =ϕ(y)
(см.п. 1.4.8).
Теорема 3.5 (о производной обратной функции). Если функции
y = f(x), | x =ϕ( y) | возрастают (убывают) и в точке x функцияf (x) | |||||||||||||
дифференцируема, | причем | f ′(x) ≠ 0, то в соответствующей точке | y | ||||||||||||
функция ϕ( y) тоже дифференцируема (поy ), причем |
|
|
| ||||||||||||
|
|
| ϕ | ′ | = |
|
|
| 1 |
| . |
| (3.19) |
| |
|
|
|
|
|
| ′ |
|
| |||||||
|
|
| ( y) |
| f |
|
| ||||||||
|
|
|
|
|
|
| (x) |
|
| y. |
|
| |||
Доказательство. | В точке | y |
|
| зададим приращение | Так как | |||||||||
функция | x =ϕ( y) | возрастает |
| (убывает) | (см.п. | 1.4.7), | то | ||||||||
x =ϕ(y + y)−ϕ(y)≠ 0и | x = |
|
| 1 | . | В условиях теоремы | функция | ||||||||
|
|
| |||||||||||||
y |
|
| y | ||||||||||||
x =ϕ( y) |
|
|
|
|
|
|
|
| x |
| x →0 |
| y → 0 |
| |
непрерывна (теорема 3.2), в силу чего | при | и | |||||||||||||
studfiles.net
Производная алгебраической суммы, произведения и частного
Теорема
Если функции U = U(x) и V = V(x) дифференцируемы в некоторой точ
ке х0, то алгебраическая сумма, произведение и частное этих функций (при V(x) ± 0) также дифференцируемы в точке и имеют место следующие формулы:
(U ± V)¢ = U¢ ± V¢,
(U∙V)¢ = U¢V + UV¢,
при V¹0.
Доказательство
1. Для вывода формул воспользуемся определением производной функции и равенством: f(x + ∆x) = f(x) + ∆y и теоремой о пределах суммы, разности, произведения и частного двух функций, имеющих предел в точке.
2. Сначала докажем первую формулу: производную алгебраической суммы:
(U ±V)=
= /сгруппируем первое слагаемое с третьим, второе с четвертым/ =
/разобьём на две дроби/=
= /в числителе каждой дроби стоит приращение соответствующей функции, и по условию теоремы каждая из них имеет производную в точке х0, следовательно, существует конечный предел/=
= [35].
ч.т.д.
3. Докажем формулу № 2: производную произведения:
/заменим 1-й и 2-й сомножители первого слагаемого равенством / = /перемножим выражения в скобках/
/разделим каждое слагаемое числителя на / /так как множители V(x) и U(x) не зависят от , поэтому их можно вынести за знак предела/ /так как U(x) – дифференцируема по условию теоремы в точке х0, то она непрерывна в точке х0, следовательно, / = U′V(x)+U(x)V′+0 = U′V+ UV′.
ч. т. д.
4. Докажем третью формулу: производную частного:
/приведем к общему знаменателю дроби в числителе/ = /заменим U(x + ∆x) =
U(x) + ∆U и т.д./
/разделим числитель и знаменатель на ∆х/ = /предел частного равен частному пределов/ =
, V ≠ 0 [35].
ч.т.д.
Производные основных элементарных функций
1. f(x) = c, с′ = 0;
2. f(x) = xn, (xn)′= nxn-1;
3. f(x) = sinx, (sinx)′= cosx;
4. f(x) = cosx, (cosx)′ = – sinx;
5. f(x) = tgx, (tgx)′ = ;
6. f(x) = ctgx, (ctgx)′ = ;
7. f(x) = ax, (ax)′ = axlna;
8. f(x) = ex, (ex)′ = ex.
9. Производная логарифмической функции: f(x) = logax, a > 0, a ≠ 1, x > 0.
.
Доказательство
1. Для любого х .
2. Придадим аргументу х приращение ∆х, получим новое значение аргумента
х + ∆х.
3. Функция получит приращение ∆f(x) = ∆y = f(x+∆x) – f(x) = loga(x+∆x) –
– logax = .
4. Найдём предел отношения [35].
ч.т.д.
Следствие: Если f(x) =lnx, то (lnx)′ .
10. (lnx)′ ; 11. (arcsinx)′x = ;
12. (arccosx)′x = ; 13. (arctgx)′x = ;
14. (arcctgx)′x = [35].
Модуль
Тема №6
Дифференцируемость функции, производная и дифференциал. Правила дифференцирования
Лекция №2
1. Производная обратной функции.
2. Геометрический смысл производной обратной функции.
3. Производная сложной функции.
4. Дифференцирование логарифмических функций.
5. Логарифмическое дифференцирование.
6. Дифференцирование степенно – показательных выражений.
7. Производные высших порядков.
Производная обратной функции
Теорема
Пусть функция удовлетворяет условиям теоремы о существовании и непрерывности обратной функции. И пусть функция является для нее обратной. Тогда если функция имеет в точке производную, не равную нулю, , то и обратная функция также имеет в точке производную , причем она определяется по формуле:
.
Доказательство
1. Дадим аргументу обратной функции некоторое приращение в точке .
2. Тогда обратная функция получит приращение , причем в силу возрастания или убывания (т.е. в силу монотонности прямой и обратной функций) .
3. Составим отношение приращения функции к приращению аргумента:
.
4. Перейдем к пределу при в последнем равенстве
.
5. Так как обратная функция непрерывна в точке , то при (на основании определения №5 непрерывности функции в точке).
Поэтому , причем, по условию теоремы.
6. Так как предел правой части равенства существует и равен , то, следовательно, существует предел и левой части равенства. А он по определению производной функции в точке равен .
7. Таким образом, или [4].
ч.т.д.
Геометрический смысл производной обратной функции
Доказанная теорема имеет простой геометрический смысл.
1. Рассмотрим в некоторой окрестности точки х0 график функции у = f(x) или график обратной функции x = φ(y).
2. Пусть точка М имеет координаты М(х0, f(х0)) или М(φ(х0), у0).
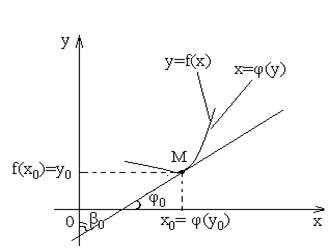
Рис.3.
3. Известно, что производная функции у = f(х) в точке х0f΄(х0) равна танген –
су угла φ0 наклона касательной, проходящей через точку М графика функции, к оси Ох: f΄(х0) = tg φ0.
4. Производная же обратной функции φ’(у0) будет равна тангенсу угла β0 наклона касательной, проходящей через точку М графика функции х = φ(у), к оси Оу: φ’(у0) = tg β0. Покажем это.
5. Так как углы φ0 и β0 в сумме составляют 90º, т.е. они являются дополнительными углами φ0 + β0 = , следовательно, можно записать:
,следовательно,
[4].
Производная сложной функции
Теорема
Если функция х = φ(t) имеет производную в точке t0, а функция у = f(x) имеет производную в соответствующей точке х0= φ(t0), то сложная функция f(φ(t)) = Ф(t) имеет производную в точке t0, причем справедлива следующая формула: Ф′(t0) = f′(x0)∙φ′(t0) или Ф′t = f′x∙ φ′t или у′t = у′x∙x′t.
Доказательство
1. Так как функция у = f(x) дифференцируема в точке х0, то приращение этой функции в точке х0 может быть записано так: , где бесконечно малая функция при .
2. Поделим данное равенство на ∆t, получим .
3. Последнее равенство справедливо при любых достаточно малых ∆х.
4. Возьмем ∆х, равным приращению функции х = φ(t), которое соответствует приращению ∆t аргумента t в точке t0.
5. Перейдём к пределу в равенстве пункта 2 при ∆t → 0.
6. Так как по условию теоремы функция х = φ(t) имеет производную в точке t0, то она непрерывна в точке t0. А следовательно, если ∆t стремится к нулю, то и ∆х стремится к нулю, т.е. на основании определения №5 непрерывности функции в точке.
7. Тогда при ∆t → 0 ∆х → 0 и, следовательно, α(∆х) → 0, так как .
8. Поэтому правая часть равенства пункта 2 примет вид:
= .
9. Если существует предел правой части равенства, то существует предел левой части того же равенства. А он по определению производной функции равен производной функции Ф(t) = f(φ(t)) в точке t0. Тем самым доказана дифференцируемость сложной функции в точке и установлена формула: Ф′(t0) = =f′(x0)∙φ′(t0) или у′(t0) = f′(x0)∙ φ′(t0) или у′t = у′x∙x′t.
ч.т.д.
Замечание
В данной теореме рассмотрена сложная функция, где у зависит от t через промежуточную переменную х. Возможна и более сложная зависимость – с двумя, тремя и большим числом промежуточных переменных, но правило дифференцирования останется прежним [35].
ч.т.д.
Пример.Найти производную функции.
[35].
infopedia.su
ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ ЧАСТНОГО ДВУХ ФУНКЦИЙ — Мегаобучалка
Для нахождения производных суммы, произведения и частного двух функций используются правила дифференцирования. Рассмотрим и решим примеры.
1. ПРОИЗВОДНАЯ ЛИНЕЙНОЙ ФУНКЦИИL (производная алгебраической суммы):
Производная алгебраической суммы равна алгебраической сумме производных.
2. ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ДВУХ ФУНКЦИЙ:
Если функции дифференцируемы в точке х0, то их произведение дифференцируемо в этой точке.
3. ПРОИЗВОДНАЯ ЧАСТНОГО ФУНКЦИЙ:
Если функции дифференцируемы в точке х0,то частное также дифференцируемо в этой точке, если v¹0
 ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ (примеры с решениями):
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ (примеры с решениями):
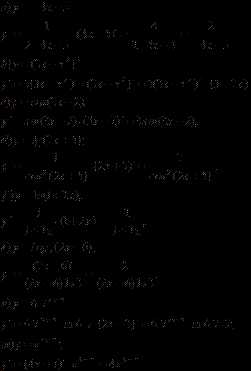
АЛГОРИТМ НАХОЖДЕНИЯ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИЙ:
| АЛГОРИТМ | ПРИМЕР: на отрезке [-3;4] |
| 1. Найти производную функции. 2. Найти критические точки функции (приравняем производную к нулю, и решим полученное уравнения; корни уравнения – критические точки). 3. Вычислить значения функции в критических точках и на концах данного отрезка. 4. Сравнить полученные значения: наибольшее из найденных является наибольшим значением функции на данном отрезке; аналогично – наименьшее является наименьшим на данном отрезке. | 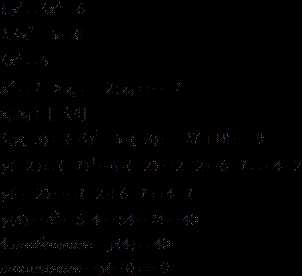 |
Исследовать функцию с помощью первой производной
Обратите внимание, как вариативно можно переформулировать фактически одно и то же задание.
Решение:
1) Функция терпит бесконечные разрывы в точках .
2) Детектируем критические точки. Найдём первую производную и приравняем её к нулю:
Решим уравнение . Дробь равна нулю, когда её числитель равен нулю:
Таким образом, получаем три критические точки:
3) Откладываем на числовой прямой ВСЕ обнаруженные точки и методом интервалов определяем знаки ПРОИЗВОДНОЙ:
Напоминаю, что необходимо взять какую-нибудь точку интервала, вычислить в ней значение производной и определить её знак. Выгоднее даже не считать, а «прикинуть» устно. Возьмём, например, точку , принадлежащую интервалу , и выполним подстановку: .
Два «плюса» и один «минус» дают «минус», поэтому , а значит, производная отрицательна и на всём интервале .
Действие, как вы понимаете, нужно провести для каждого из 6-ти интервалов. Кстати, обратите внимание, что множитель числителя и знаменатель строго положительны для любой точки любого интервала, что существенно облегчает задачу.
Итак, производная сообщила нам, что САМА ФУНКЦИЯ возрастает на и убывает на . Однотипные интервалы удобно скреплять значком объединения .
В точке функция достигает максимума:
В точке функция достигает минимума:
Подумайте, почему можно заново не пересчитывать второе значение.
При переходе через точку производная не меняет знак, поэтому у функции там НЕТ ЭКСТРЕМУМА – она как убывала, так и осталась убывающей.
! Повторим важный момент: точки не считаются критическими – в них функция не определена. Соответственно, здесь экстремумов не может быть в принципе (даже если производная меняет знак).
Ответ: функция возрастает на и убывает на В точке достигается максимум функции: , а в точке – минимум: .
Знание интервалов монотонности и экстремумов вкупе с установленными асимптотами даёт уже очень хорошее представление о внешнем виде графика функции. У графика функции есть две вертикальные асимптоты и наклонная асимптота . 
Постарайтесь ещё раз соотнести результаты исследования с графиком данной функции.
В критической точке экстремума нет, но существует перегиб графика (что, как правило, и бывает в похожих случаях).
Найти экстремумы функции:
Решение:
1. Находим производную функции
2. Приравниваем ее к нулю и решаем уравнение
критические точки функции х=1 и х=3.
3. Критические точки функции разбивают область определения на три интервала:
+ – +
1 3 х
определим знаки производной функции в каждом из полученных интервалов:
т.е. точка х=1 – точка максимума; х=3 – точка минимума.
4. Вычислим значения функции в критических точках:
5. Составим таблицу:
ИНТЕГРАЛ
Пример 1.
Вычислите определенный интеграл .
Решение.
Пример 2.
Вычислите определенный интеграл .
Решение.
.
Пример 3.
Вычислите определенный интеграл .
Решение.
.
Пример 4.
Вычислите определенный интеграл .
Решение.
.
Пример 5.
Вычислите определенный интеграл .
Решение.
.
megaobuchalka.ru
